Число π и длина окружности. Длина дуги окружности. Радианная мера угла

1. Число π и длина окружности. Длина дуги окружности. Радианная мера угла.

9 класс
ГЕОМЕТРИЯ
Число π и длина окружности.
Длина дуги окружности.
Радианная мера угла.

2. Ваша задача на сегодня:

• Ознакомиться с материалом слайдов 3 – 11.
• Выполни устно задания со слайдов 12 – 18,
сверься с ответами.
• Реши задачи со слайда 19.

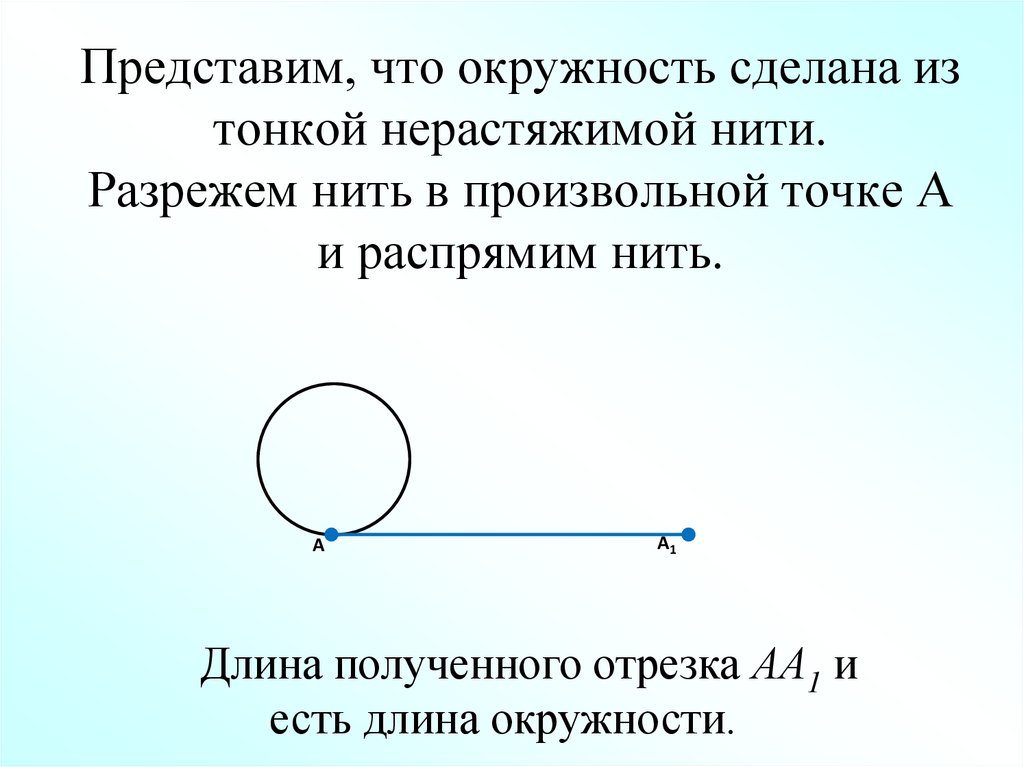
3. Представим, что окружность сделана из тонкой нерастяжимой нити. Разрежем нить в произвольной точке А и распрямим нить.

А
А1
Длина полученного отрезка АА1 и
есть длина окружности.

4.

Приближённым
значением
длины
окружности является периметр любого
правильного вписанного в окружность
многоугольника.
Чем больше число сторон у вписанного в
окружность правильного многоугольника, тем
точнее получим длину окружности, т.е.
многоугольник будет плотнее прилегать к
окружности.
Таким образом, можно сделать следующее
заключение. Точное значение длины окружности – это
предел, к которому стремится периметр правильного
вписанного в окружность многоугольника, при этом
количество сторон его может быть неограниченно
большим.

5. Расчет стороны правильного n-угольника , где an – длина стороны n-угольника; R – радиус описанной окружности; n – количество

сторон многоугольника.
Применяя эту формулу, выразим длину окружности через её
радиус.
Допустим, что С и С' длины окружностей, с радиусами,
соответственно R и R'.
В каждую окружность условно впишем правильный n-угольник с
периметрами Pn и P'n.
Соответственно стороны многоугольников обозначим an и a'n.
Получим следующие формулы периметров многоугольников:
- для первого многоугольника –
- для второго многоугольника –
Из данных формул следует равенство:

6.

Данное равенство будет справедливо при любом количестве сторон
правильного многоугольника.
При бесконечном увеличении количества, сторон многоугольника
предел периметра будет стремиться к длине окружности –
,
Таким образом, можно сделать вывод, что предел отношения
периметров будет равен пределу отношения длин окружностей:
Используя равенство (1) получим:
Таким образом, отношение длины окружности к
её диаметру есть одно и то же число для всех
окружностей. Такое число принято обозначать
греческой буквой π.

7.

Формула вычисления длины окружности
радиусом R будет записана следующим
образом:
С= пd,
.
Число π является бесконечной непериодической
десятичной дробью. При решении задач и в
практической деятельности, пользуются
приближенным значением числа π с точностью до
одной сотой: число
.

8.

Формула длины дуги l с произвольным углом α
Так как длина всей окружности равна
.
, то длина дуги в 1° равна
Длина дуги l с произвольным углом
:

9. Радианная мера угла

– отношение длины
соответствующей дуги к радиусу окружности.
Радиан – единица радианной меры углов.

10.

11.

12. Задание 1. Длина окружности больше диаметра в:

Варианты ответов:
а) п раз ;
б) 2п раз ;
Ответ:
в) 2 раза;
г) 0,5п раз.

13. Задание 2. Найдите длину окружности, радиус которой равен 36 см. Число π округлите до сотых.

Варианты ответов:
а) 318,07 см;
б) 121,3 см;
в) 116,18 см;
г) 226, 08 см.
Ответ: C=2пR=

14. Задание 3. Сколько сторон имеет правильный многоугольник, если каждый его угол равен 150°?

Варианты ответов:
а) 12 ;
б) 16;
в) 8;
Ответ:
г) 18.

15. Задание 4. Длина дуги окружности с радиусом 12 см и градусной мерой 100 равна:

Варианты ответов:
а)
;
б)
; в)
Ответ:
;
г)
.

16. Задание 5. Найдите углы правильного n-угольника, если n = 10.

Задание 5. Найдите углы
правильного n-угольника, если n = 10.
Варианты ответов:
а) 150°;
б) 144°;
Ответ:
в) 105°;
г) 135°.

17. Задание 6. Какое слово требуется убрать для того, чтобы получилось верное утверждение? Чем больше число правильных сторон у 

Задание 6. Какое слово требуется
убрать для того, чтобы получилось
верное утверждение?
Чем больше число правильных сторон у
вписанного в окружность правильного
многоугольника, тем точнее получим
длину окружности.
Ответ:

18. Задание 7. Найдите градусную меру угла, если его радианная мера равна .

Варианты ответов:
а) 150°;
б) 30°;
в) 180°;
Ответ:
г) 45°.

19. Реши задачи:

1. Найдите длину окружности, радиус которой
равен 24 см. Число π округлите до сотых.
2. Рассчитайте диаметр дачного бассейна, если
длина окружности составляет 8 метров.
3. Найдите градусную меру угла, если его
радианная мера равна .
4. По учебнику выполни № 1103.

20. Спасибо за внимание!