Способ Верещагина Формула Симпсона. (способы перемножения эпюр)

1.

Способ Верещагина
Формула Симпсона.
(способы перемножения эпюр)

2.

Способы вычисления интеграла
Мора.
Интеграл Мора, в котором подынтегральное выражение есть
произведение двух функций, может быть вычислен различными
методами в зависимости от вида этих функций. Заметим, одна из них,
связанная с эпюрой внутренних усилий от единичного сосредоточенного
воздействия, всегда линейная.
1. Непосредственное интегрирование – практически не имеет
ограничений по использованию.
2. Способ Верещагина – удобен на тех участках, на которых легко
можно определить центр тяжести одной из эпюр (обычно это относится к
эпюре от грузового воздействия).
3. Формула Симпсона – применима в случае квадратичного закона
изменения эпюры от грузового воздействия. Формула трапеций –
применяется в случае линейности обоих эпюр.
Способ Верещагина и формула Симпсона имеют ограничения, связанные
с тем, что жесткость балки в рамках расчетного участка считается
величиной постоянной. Интеграл Мора принимает следующий вид:
1
y
M xF M I dz
EI x l

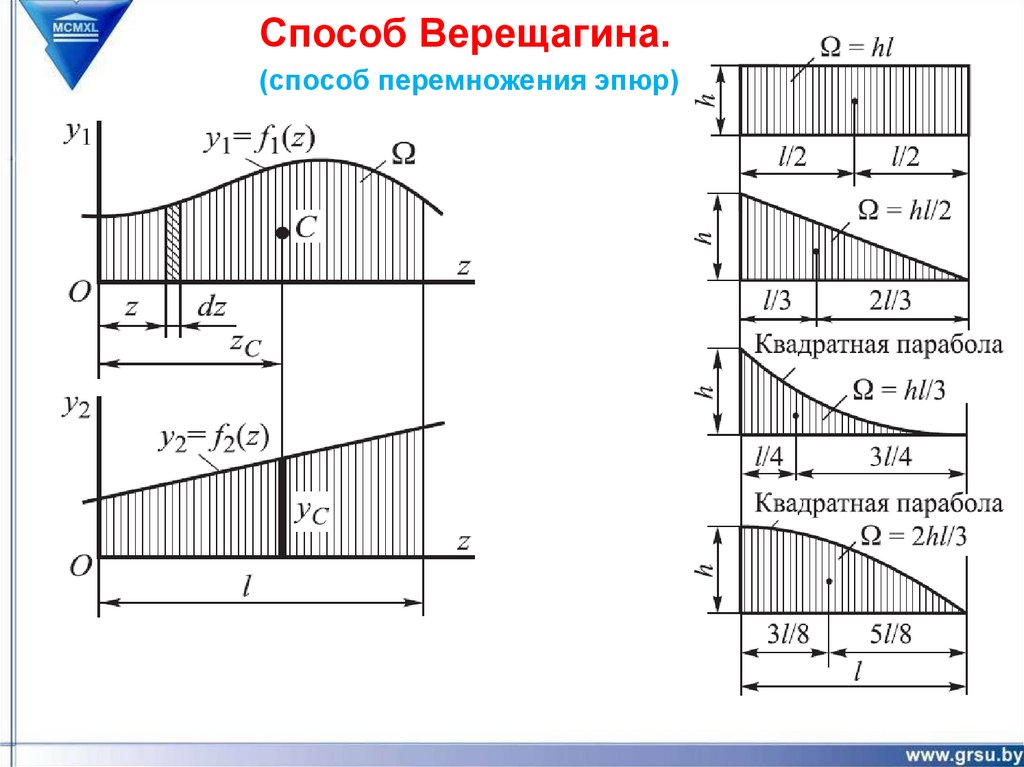
3. Способ Верещагина

• Предложен в 1925 году студентом
• Московского института инженеров
• железнодорожного транспорта
• А.Н.Верещагиным.
• ИСТОЧНИК:
• Дарков А.В. Шпиро Г.С. СОПРОТИВЛЕНИЕ
МАТЕРАЛОВ. Москва :Высшая школа, 1975- 654 с.
• (с.450)

4.

Способ (правило) Верещагина
:
Допустим, на участке стержня длиной l необходимо вычислить интеграл
от произведения двух функций
l
I f1 ( z ) f 2 ( z )dz
0
Рассмотрим условие, что хотя бы одна из этих функций линейная
(это условие всегда выполняется для единичных моментов , а также
для грузовых моментов на участках, где нет распределенной
нагрузки).
f 2 ( z ) b kz
Пусть
Тогда искомый интеграл
l
l
l
0
0
0
I f1 ( z )(b kz )dz b f1 ( z ) dz k f1 ( z ) z dz

5.

Способ (правило) Верещагина
:
Искомый интеграл
l
l
0
0
I b f1 ( z ) dz k f1 ( z ) z dz
Первый из интегралов правой части представляет собой
площадь Ωр, ограниченную кривой
или иначе – площадь эпюры
l
b f1 ( z ) dz b
0

6.

Способ (правило) Верещагина
Второй интеграл представляет собой статический
момент этой площади относительно оси ординат, т.е.
l
k f1 ( z ) z dz k zC
0
где ZC- координата центра тяжести первой
эпюры. Теперь получаем, что
Но
Следовательно
l
I f1 ( z ) f 2 ( z )dz yC
0

7.

Способ Верещагина.
(способ перемножения эпюр)
Для вычисления интеграла Мора вида:
y
1.
2.
1
M xF M I dz
EI x l
на отдельном участке балки, необходимо:
Рассчитать площадь нелинейной эпюры и умножить на ординату линейной
эпюры под центром тяжести нелинейной эпюры и разделить данное
произведение на жесткость EIх расчетного участка балки (в случае если обе
эпюры линейны безразлично для какой эпюры рассчитывать площадь, а для
какой ординату;
Произвести данный расчет на всех участках балки;
Просуммировать результаты.
Практические рекомендации по применению правила Верещагина:
В рамках расчетного участка эпюра для расчета площади не может быть
знакопеременной (необходимо разбить на доп. участки);
ПРАВИЛО ЗНАКОВ: Результат перемножения площади на ординату
считается положительным, если обе эпюры располагались по одну
сторону от оси эпюры.

8.

Способ Верещагина.
(способ перемножения эпюр)

9.

Способ Верещагина.
(способ перемножения эпюр)
Задача: определить перемещение и угол поворота для консольной
балки, нагруженной моментом на конце.
Решение:1. Строим грузовую эпюру
p M l
2. Строим единичную эпюру для
углов поворота (построена на сжатых
волокнах)
yC1 1
Перемножаем грузовую эпюру и
единичную для углов поворота
1
1
Ml
max
p yc
Ml 1
EI
EI
EI

10.

Способ Верещагина.
(способ перемножения эпюр)
Определяем перемещение на конце консольной балки, нагруженной
моментом
p
M l
2. Строим единичную эпюру
для перемещений
(построена на сжатых
волокнах)
l l
yc 1
2 2
3.Перемножаем грузовую эпюру и
единичную для перемещений
1
1 Ml l Ml 2
ymax
p yc
EI
EI 2
2 EI

11.

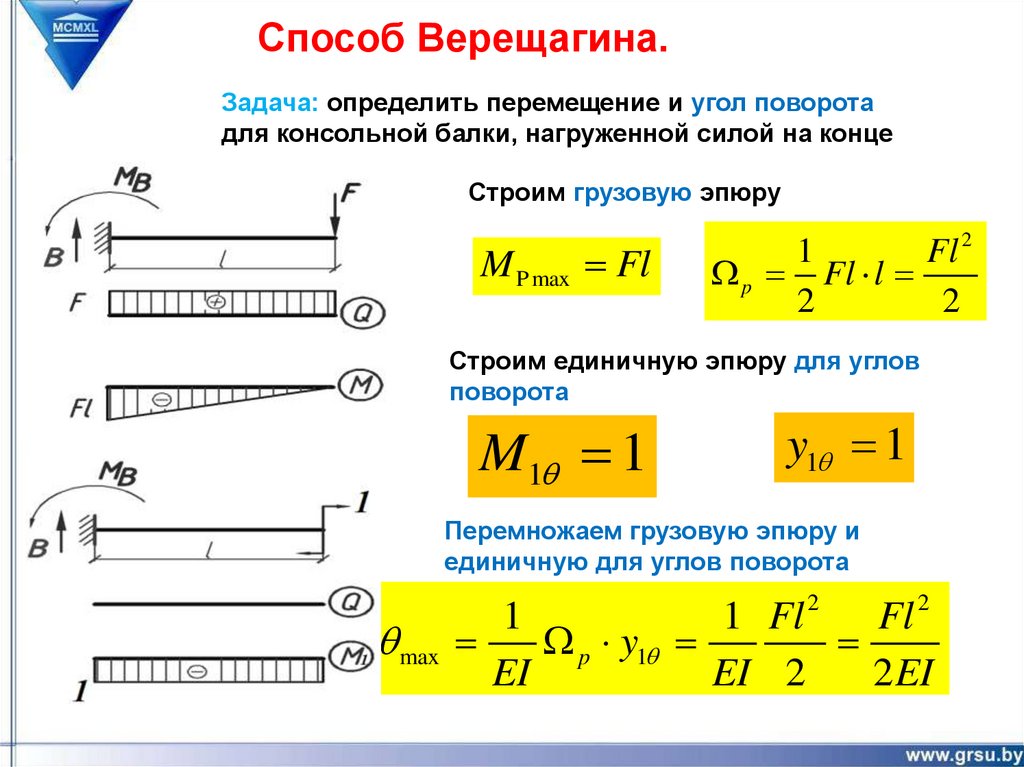
Способ Верещагина.
Задача: определить перемещение и угол поворота
для консольной балки, нагруженной силой на конце
Строим грузовую эпюру
M P max Fl
1
Fl 2
p Fl l
2
2
Строим единичную эпюру для углов
поворота
M1 1
y1 1
Перемножаем грузовую эпюру и
единичную для углов поворота
1
1 Fl 2 Fl 2
max
p y1
EI
EI 2
2 EI

12.

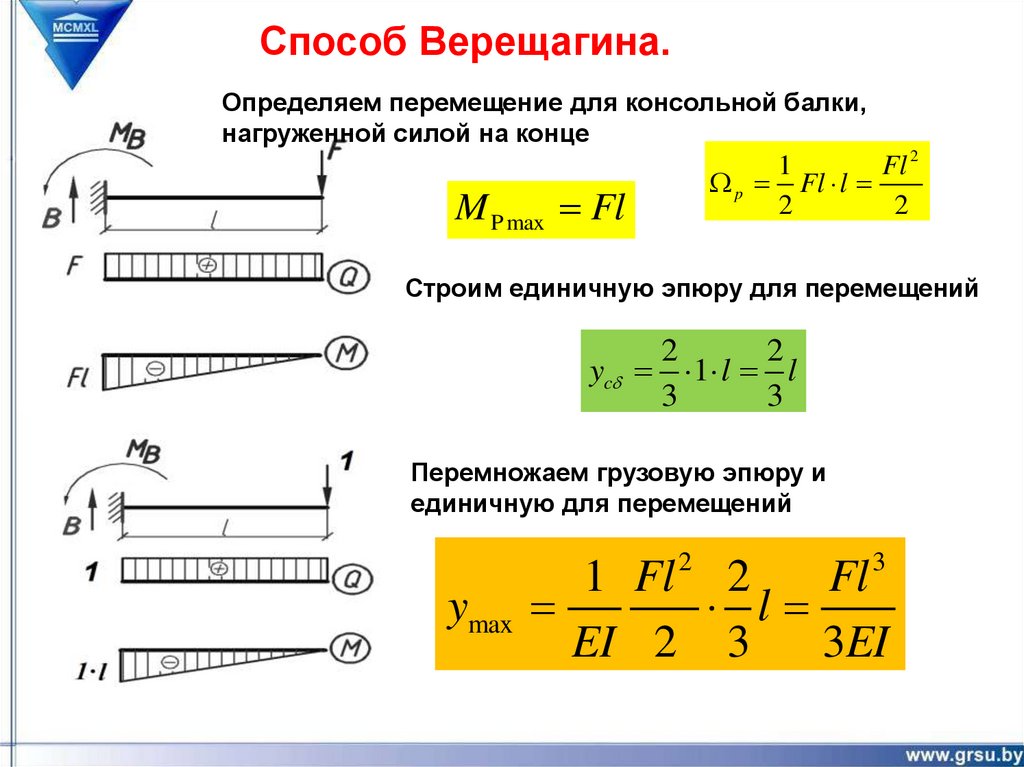
Способ Верещагина.
Определяем перемещение для консольной балки,
нагруженной силой на конце
M P max Fl
1
Fl 2
p Fl l
2
2
Строим единичную эпюру для перемещений
2
2
yc 1 l l
3
3
Перемножаем грузовую эпюру и
единичную для перемещений
1 Fl 2 2
Fl 3
ymax
l
EI 2 3
3EI

13.

Формула Симпсона.
(способ перемножения эпюр)
Интеграл Мора вида:
С помощью формулы Симпсона рассчитывается:
1
y
M xF M I dz
EI x l
a1
b1
Для перемножения нелинейного
участка с линейным:
l
a2
b2
l
l
0 M xF M I dz 6 (a1a2 4b1b2 c1c2 )
с1
l/2
c2

14.

Формула Симпсона.
(способ перемножения эпюр)
Интеграл Мора вида:
С помощью формулы Симпсона рассчитывается:
1
y
M xF M I dz
EI x l
Для перемножения двух линейных участков формула
трапеций:
a1
c1
l
l
0 M xF M I dz 6 (2a1a2 2c1c2 a1c2 a2c1 )
a2
l
c2

15.

Формула Симпсона.
(способ перемножения эпюр).
Оценка погрешности.
1.Линейная функция y=x; Точное решение
2 3
x
9 1
1 xdx 2 2 4
1
3
Приближенное решение
3 1
2
1 xdx 6 3 1 4 2 6 12 4
3

16.

Формула Симпсона.
(способ перемножения эпюр).
Оценка погрешности.
Квадратная парабола. Точное решение
3 3
x
27 1 26
1 x dx 3 3 3
1
3
2
Приближенное решение
3 1 2 2
2 26 26
2
1 x dx 6 3 1 4 2 6 3
3
2

17.

Формула Симпсона.
(способ перемножения эпюр).
Оценка погрешности.
Кубическая парабола. Точное решение
4 3
x
81 1
1 x dx 4 4 20
1
3
3
Приближенное решение
3 1 3 3
2
28 32
3
1 x dx 6 3 1 4 2 6 27 1 4 8 3 20
3
3

18.

Формула Симпсона.
(способ перемножения эпюр).
Оценка погрешности.
Четвертая степень. Точное решение
5 3
x
81 3 1 243 1 242
1 x dx 5 5 5 5 48, 4
1
3
4
Приближенное решение
2
82 4 16 82 64 146
4
81 1 4 2
48,67
6
3
3
3
Погрешность решения
48,67 48, 4 0, 27 2,7
0,5%
48, 4
48, 4 484

19.

Формула Симпсона.
(способ перемножения эпюр).
Оценка погрешности.
Синусоида. Точное решение
0
0
sin xdx cos x 1 1 2
Приближенное решение
2
0 sin xdx 2 0 sin xdx 2 2 6 0 1 4 2 6 1 2 2 2,0035
2
Погрешность решения зависит от интервала разбиения подинтегральной функции.

20.

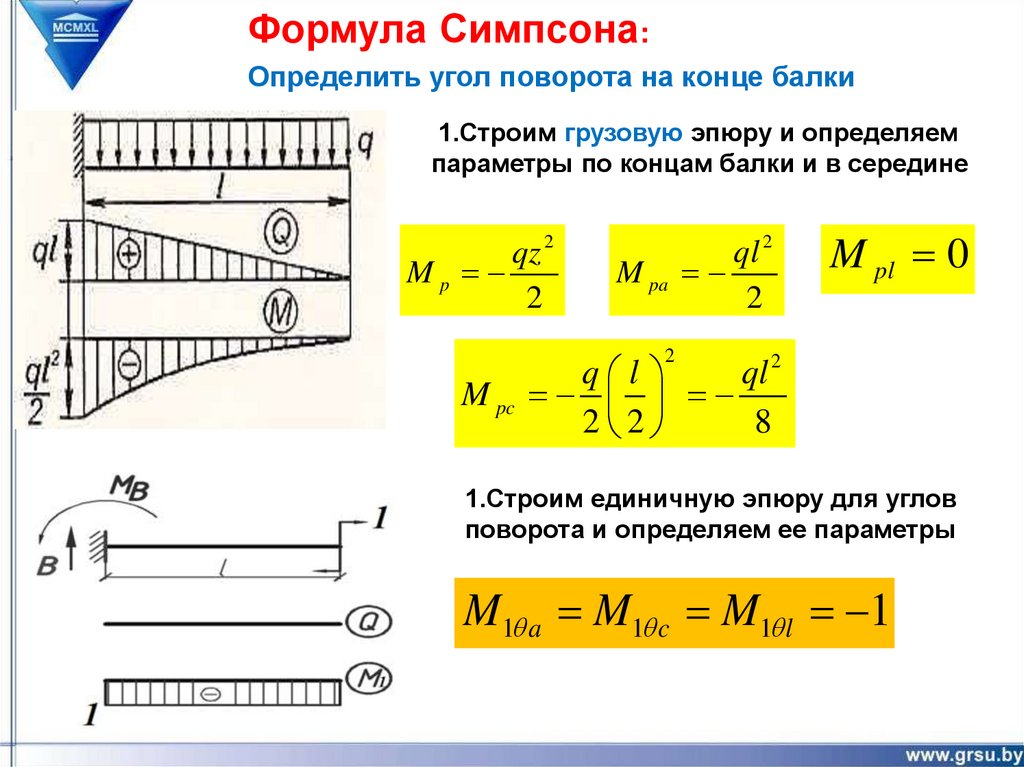
Формула Симпсона:
Определить угол поворота на конце балки
1.Строим грузовую эпюру и определяем
параметры по концам балки и в середине
qz 2
Mp
2
ql 2
M pa
2
M pl 0
2
q l
ql 2
M pc
2 2
8
1.Строим единичную эпюру для углов
поворота и определяем ее параметры
M1 a M1 c M1 l 1

21.

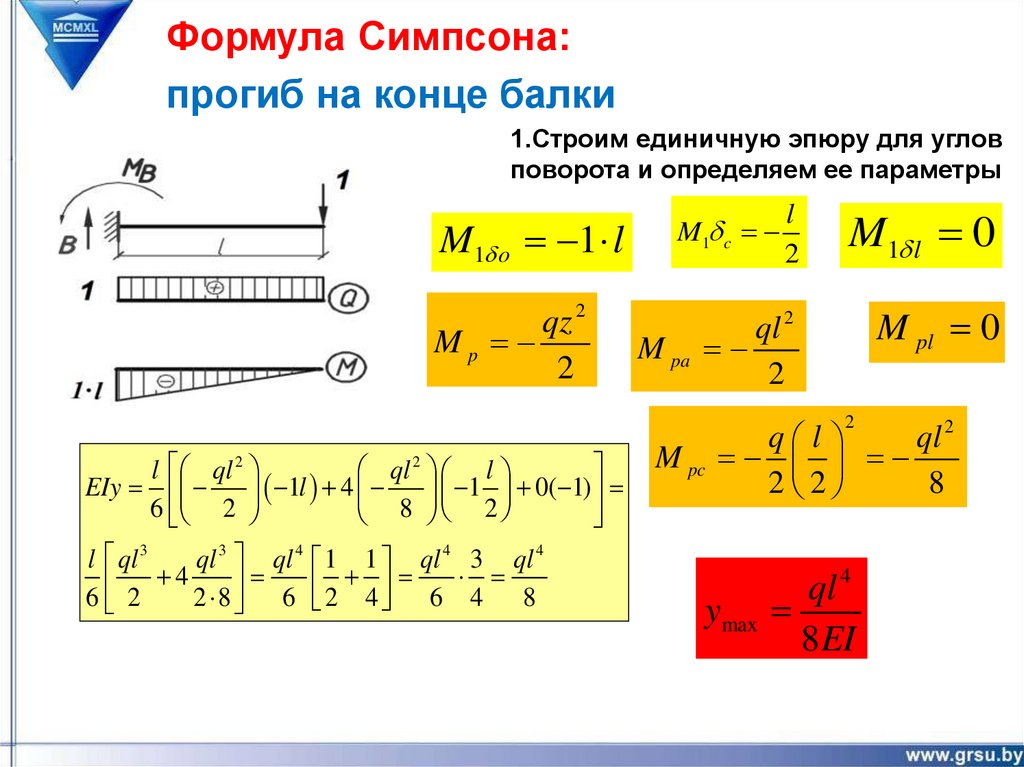
Формула Симпсона:
прогиб на конце балки
1.Строим единичную эпюру для углов
поворота и определяем ее параметры
M1 o 1 l
qz 2
Mp
2
l
2
M1 l 0
ql 2
M pa
2
M pl 0
M1 c
2
q l
ql 2
M pc
ql 2 l
l ql 2
2 2
8
EIy
1l 4
1 0( 1)
6
2
8
2
l ql 3
ql 3 ql 4 1 1 ql 4 3 ql 4
4
6 2
2 8 6 2 4 6 4 8
ql 4
ymax
8 EI

22.

Формула Симпсона:
угол поворота на конце балки
l
EI M xp M I dz
0
l
( M xpa M I a 4M xpc M I c M xpl M I l )
6
M1 a M1 c M1 l 1
2
Mp
qz
2
2
M pa
2
ql
2
q l
ql 2
M pc
2 2
8
l ql 2
ql 2
l ql 2
ql 2 ql 3
EI
1 4
1 0( 1) 4
6 2
8 6
8
6 2
M pl 0
ql 3
6 EI

23. УЧЕТ РАЗМЕРНОСТИ ПРИ РАСЧЕТЕ ДЕОРМАЦИЙ

N
];
2
mm
F kN F 103 N ;
E[ MPa ] E[
M[kN m] M[103 N 103 mm] M[106 Nmm];
kN
103 N
N
q[
] q[ 3
] q[
];
m
mm
10 mm
l[m] l[103 mm]; l 2 [m]2 l 2 [103 mm]2 l 2 [106 mm 2 ];
l 3 [m]3 l 3 [103 mm]3 l 3 [109 mm3 ];
I[cm 4 ] I[10 mm]4 I[10 4 mm 4 ]

24.

Формула Симпсона.
(способ перемножения эпюр)
2
ql 2
1
1 l1
ql
M p M 1
0 1 4
1
EI 0
EI 6 2
8
l
3
1 l ql 2
qe 2
l
ql
2
4
ql
EI 6 2
8 6 EI
6 EI
2
l
ql 2 l
1
1 l ql
M p M 1
0
1 l 4
EI 0
EI 6 2
8 2
l
ql 3 ql 3
l 3 3 ql 4
q1
0
6 EI
2
4 6 EI 4
8 EI