Похожие презентации:
Умножение и деление алгебраических дробей. Возведение алгебраических дробей в степень
1.
12.
Повторить правила умножения,деления и возведения в степень
числовых дробей;
Изучить алгоритм умножения и
деления алгебраических дробей;
Изучить правила возведения в
степень алгебраической дроби.
2
3.
Вспомним!Умножении числовых дробей :
a c a c
;
b d b d
Деление числовых дробей :
a c a d a d
:
.
b d b c b c
Возведение числовых дробей в степень :
n
a n a
( ) n.
b
b
3
4.
Примеры:1
1
1
3 4
3 4
1
.
8 15 82 155 2 5 10
3
3
2
1
12
16
12
15
12
15
2 :1
:
5
15
5 15
5 16
5 164
1
3 3 9
2 .
4
4
4
1
4
5.
Над алгебраическими дробями можно осуществлятьпреобразования аналогичные тем, которые указали
для обыкновенной дроби.
Внимание!
Прежде, чем выполнять умножение и деление
алгебраических дробей, полезно их числители
и знаменатели разложить на множители – это
облегчит сокращение той алгебраической дроби,
которая получится в результате умножения
или деления.
5
6.
Вспомним!Правила сокращения дробей, выполнив несколько примеров.
Сократить дроби:
2b
2 b
4 2 a b
8a b
.
a)
6
5
6
5
2
6
5
8 5
3a c
3 a c
41 3 a1 a c
12a c
2 7
1
1 2
1
7
7
1
7
3( a b )
3( b a )
1
б)
.
7
74
4
7
(
b
a
)
21( b a )
21
(
b
a
)
7
3
3
6
7.
1x 9
( x 3 )( x 3 ) ( x 3 )
в) 4
.
3
3
3
х 3x
x ( х 3)
x
2
1
Рассмотрим пример 1:
1
5
8
3
4
5 a x 3a b
6
2
7b
25 x
1
5 a x x 3 a b
4
2
2
7 b1 b 25
x1
5
5
1 2
6
3
4
a x 3 a
3a x
.
2
2
7 b 5
35 b
5
6
3
8
6
7
8.
c 6 c 36 c:
8
5 3
30 c
25 c d
3
Рассмотрим пример 2:
2
2
c (c 6 )
25 c d
8
30 c
( 6 c )( 6 c )
2
5
1
5
1
1
3
c ( c 6 ) 25 c d
8
306 c ( 6 c )( 6 c ) 1
2
5
3
3
5d
.
6c ( 6 c )
8
9.
Вспомним!Свойства степени с натуральным показателем.
(а, b > 0).
1 )a a
n
2 )a
n
m
:a
n
3 )( a )
m
m
a
n m
a
a
;
n m
n m
;
;
4 )( ab ) a b ;
n
n
n
n
24.06.2011
a n
a
5 )(
) n .
b
b
Кравченко Г. М.
9
10.
Например:(2х³)⁴ = 16х¹²;
(3а)² = 9а²;
(-5а⁷b)²= 25a¹⁴b²;
(-ху²)³ = -х³у⁶;
(x²y³z⁴)⁵= x¹⁰y¹⁵z²⁰;
Все свойства степени, которые известны, применимы
и для алгебраической дроби.
3
x 3 x
2
8
3
( ) 3 ; ( 4 ) 12 ;
y
y
a
a 2
8
3
x 4
x
27 a
3a 3
( 3 ) 9 ; ( y 5 ) y 20 .
b
b
24.06.2011
Кравченко Г. М.
10
11.
( a 3 )4a 2 6a 9 2
Рассмотрим пример 3:
:( 2
)
3
2
3a 6 a
a 4a 4
(a 3)
(a 3) 2
2
:(
)
2
3a ( a 2 ) ( a 2 )
4
2
(a 3)
(a 2 ) 2
2
(
)
2
3a ( a 2 ) ( a 3 )
4
1
2
(a 2 )
(a 3 ) (a 2 )
.
2
2
4
3a
3a ( a 12 ) ( a 1 3 )
24.06.2011
4
43
Кравченко Г. М.
3
11
12.
Рассмотрим пример 4:Рассмотрим решение сложной пропорции, в которой нужно
выразить переменную х.
2
2
9 4 a 4 ab b
3 2a b
;
2
4 a 2ab 3b 9
x
3 ( 4 a 4 ab b ) 3 2a b
;
2
( 4 a 9 ) ( 2ab 3b )
x
2
2
2
3 ( 2a b )
3 2a b
;
2
( 4 a 9 ) b( 2a 3 )
x
2
2
12
13.
3 ( 2a b )3 2a b
;
2
( 4 a 9 ) b( 2a 3 )
x
2
2
( 3 2a b )( 3 2a b )
3 2a b
;
( 2a 3 )( 2a 3 ) b( 2a 3 )
x
( 3 2 a b )( 3 2 a b ) 3 2 a b
;
( 2 a 3 )( 2 a 3 b )
x
13
14.
11
1
( 2 a 3 b )( 3 2 a b ) 3 2a b
;
( 2a 3 )( 2 a 3 1b )
x
1
1
;
2a 3 x
x ( 2a 3 ).
Ответ: x ( 2 a 3 ).
14
15.
1. Как выполнить умножение числовых дробей?2. Как выполнить деление числовых дробей?
3. Запишите свойства степеней (при а, b >0).
4.Сформулируйте основное свойство
алгебраической дроби.
5. Сформулируйте и запишите правила
умножения, деления и возведения в степень
алгебраических дробей.
15



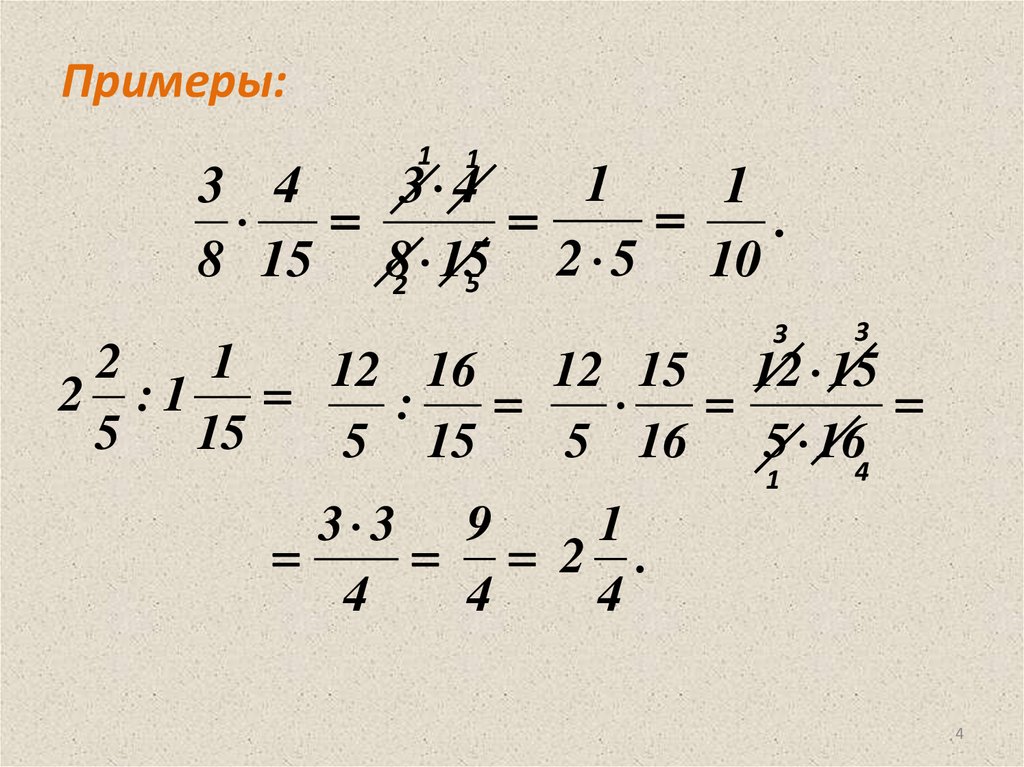



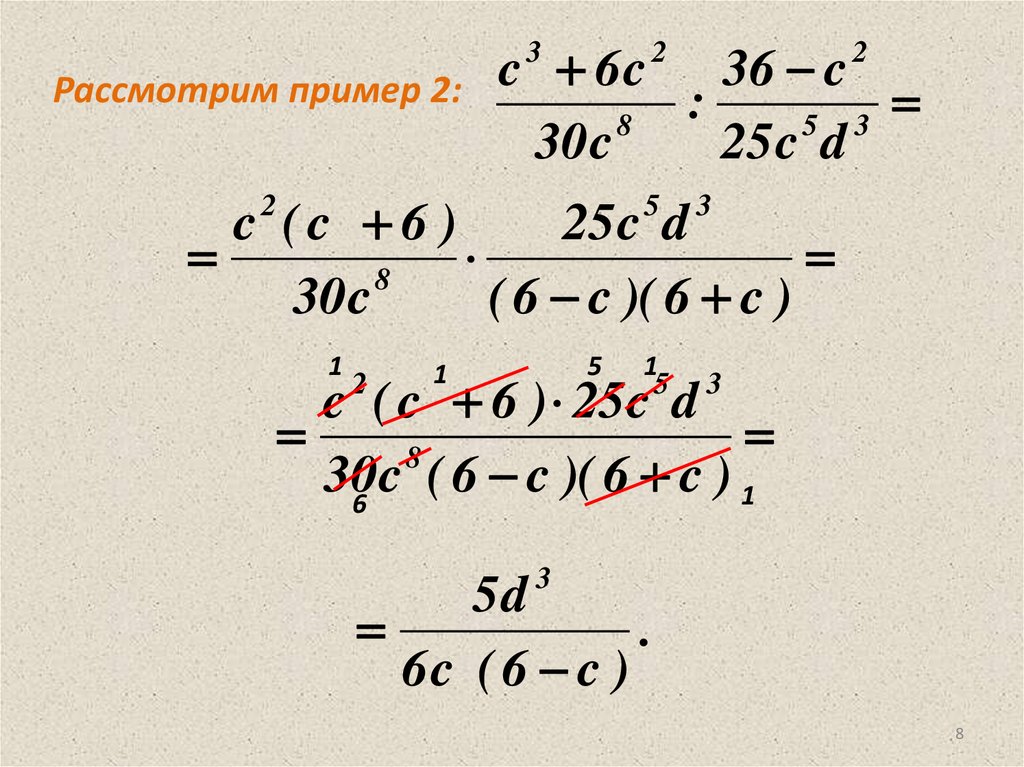




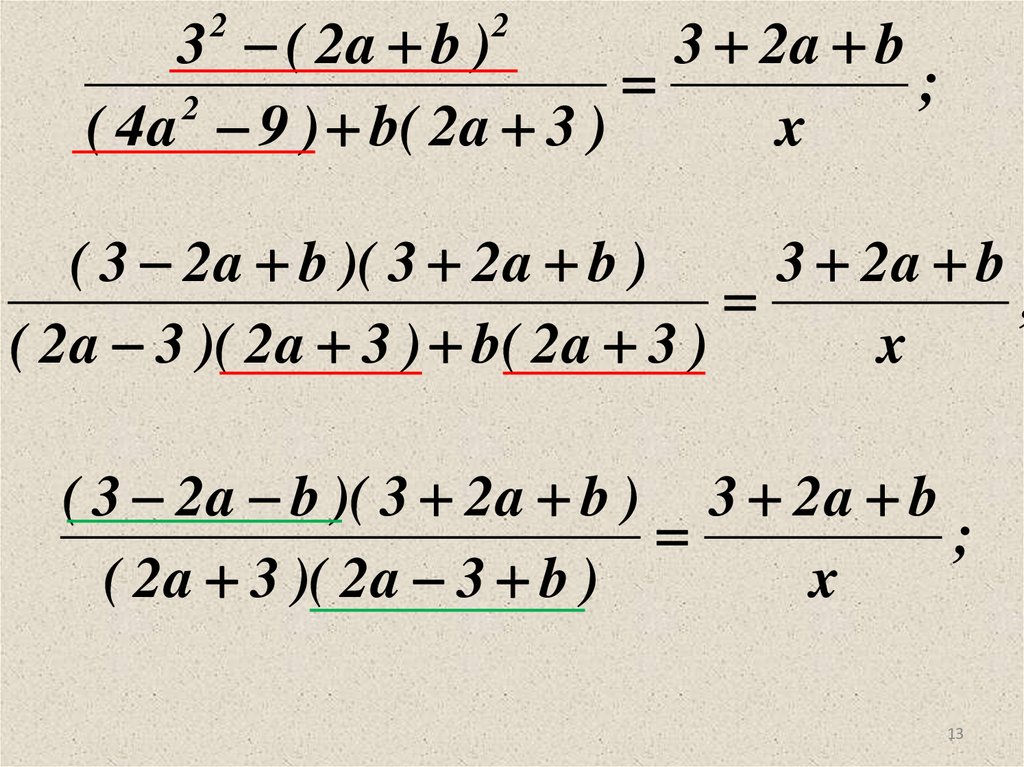
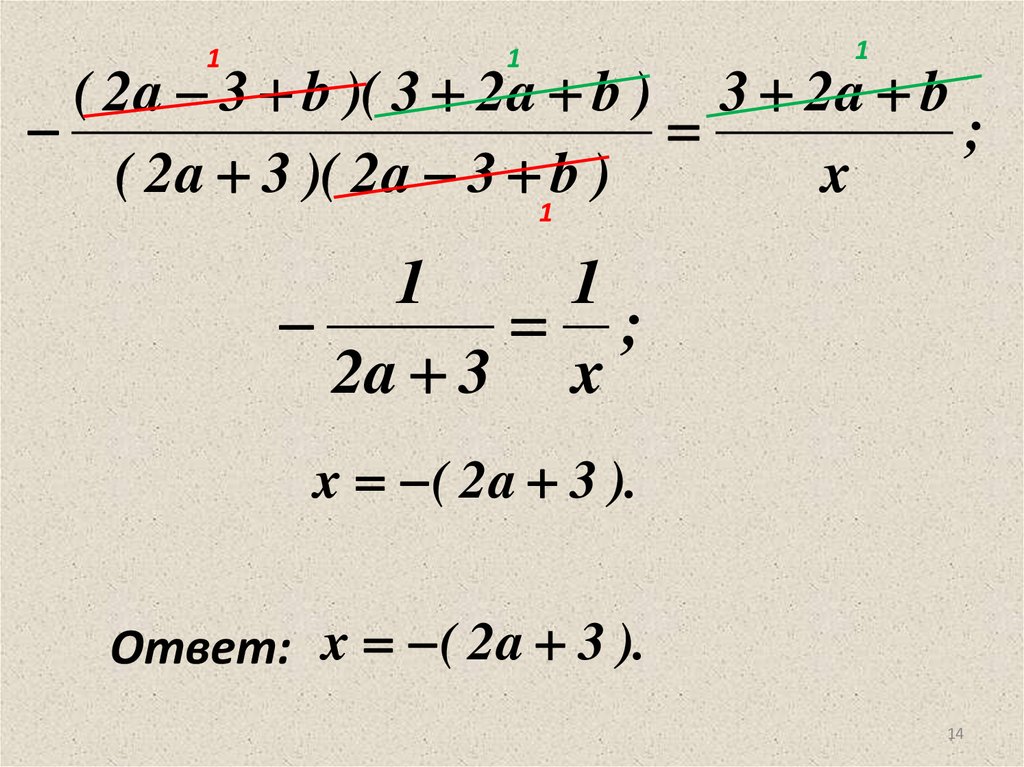

 Математика
Математика