Непрерывность функции. Функция с разрывом

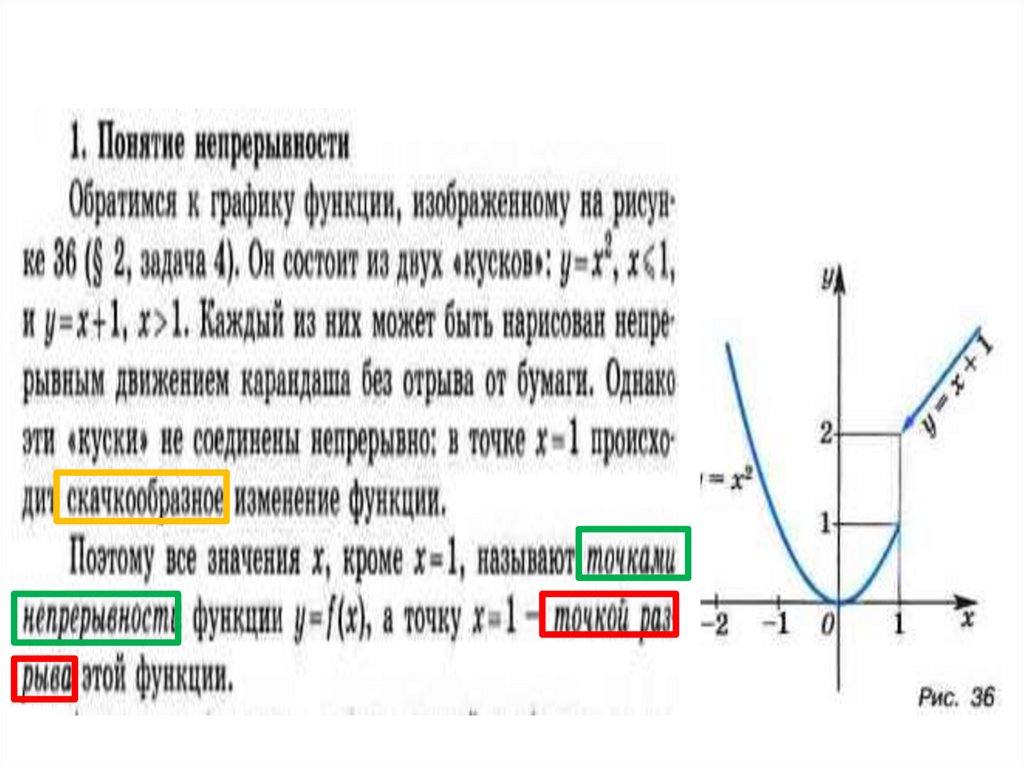
1. НЕПРЕРЫВНОСТЬ ФУНКЦИИ

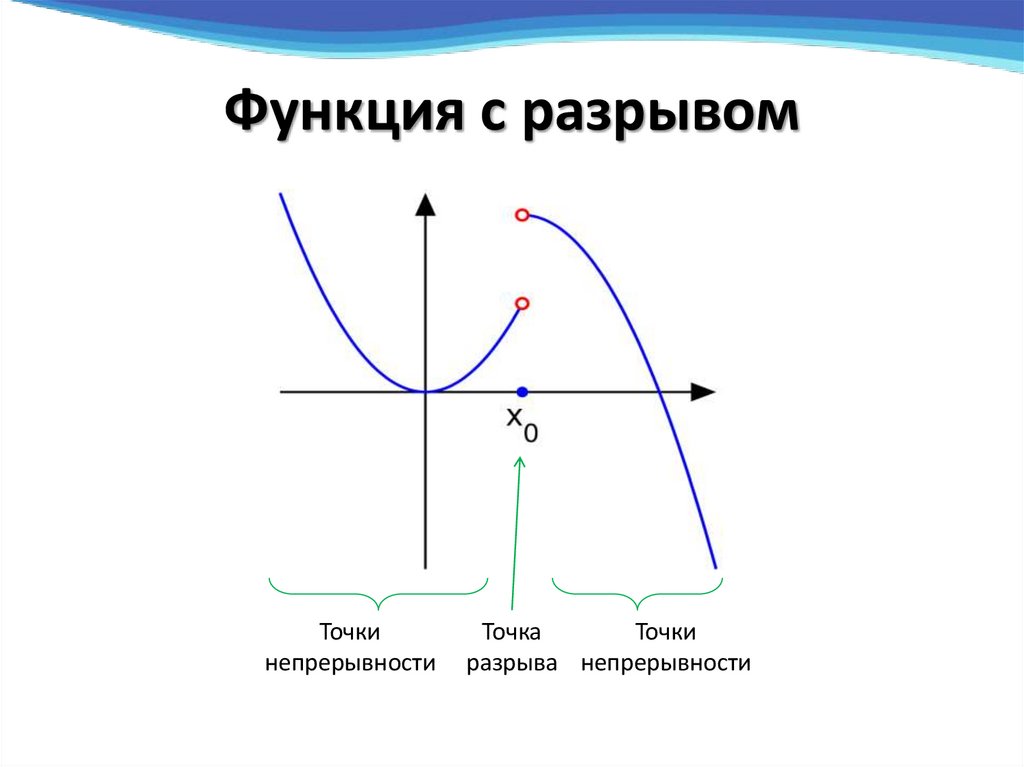
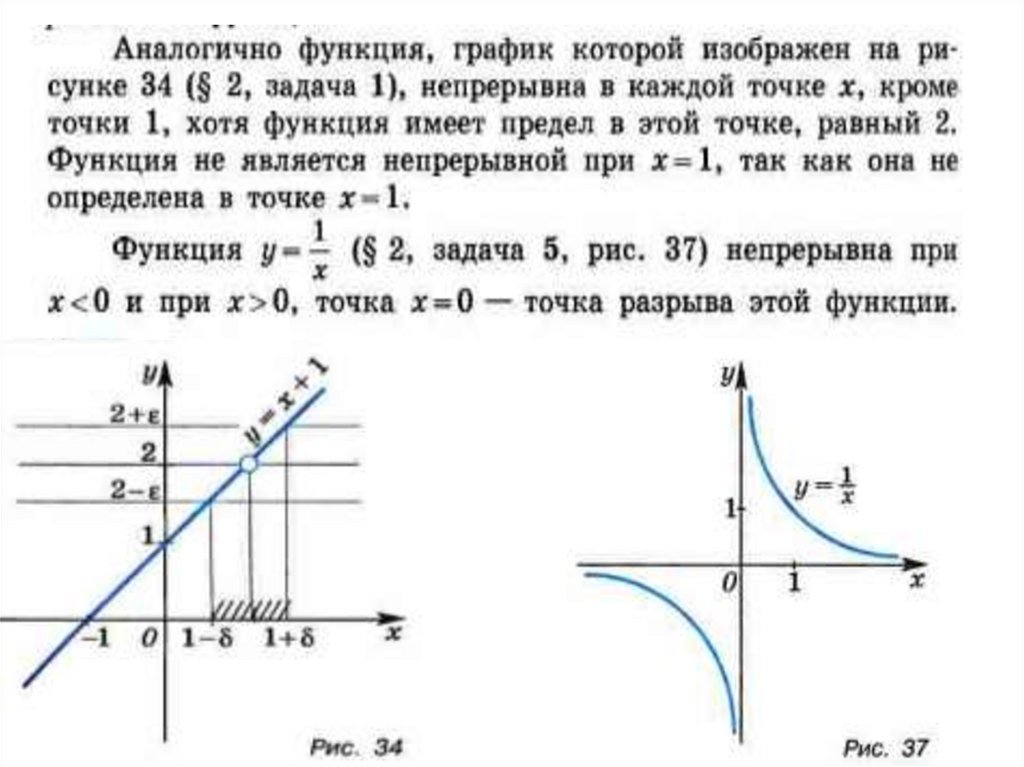
2. Функция с разрывом

Точки
непрерывности
Точка
Точки
разрыва непрерывности

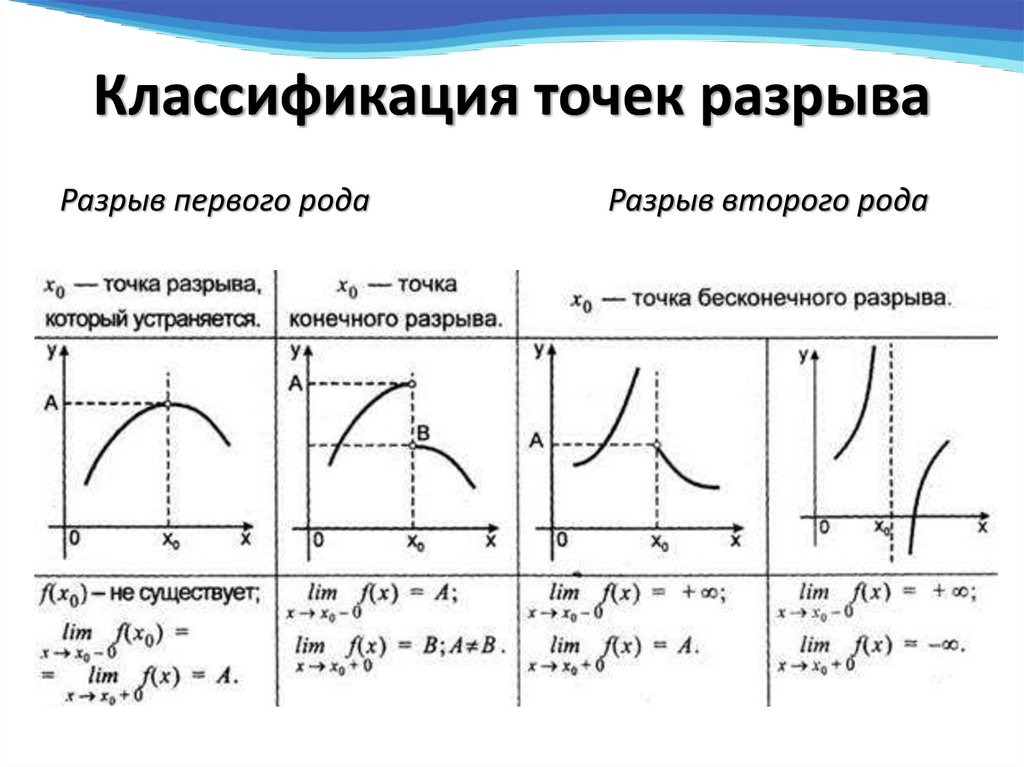
3. Классификация точек разрыва

Разрыв первого рода
Разрыв второго рода

4.

Найти область определения и
множество значений функции:
2 х
4) у
х 1
Что является графиком данной
функции?
Найдите горизонтальную и вертикальную
асимптоты функции.
Изобразите схематично график функции.

5.

Найти область определения и
множество значений функции:
2 х
4) у
...
х 1
Графиком данной функции
является …, имеющая две
асимптоты:
горизонтальную у=… и
вертикальную х= …

6.

Найти область определения и
множество значений функции:
2 х х 1 1
1
4) у
1
х 1 х 1
х 1
Графиком данной функции
является гипербола, имеющая
две асимптоты:
горизонтальную у=1 и
вертикальную х= -1

7.

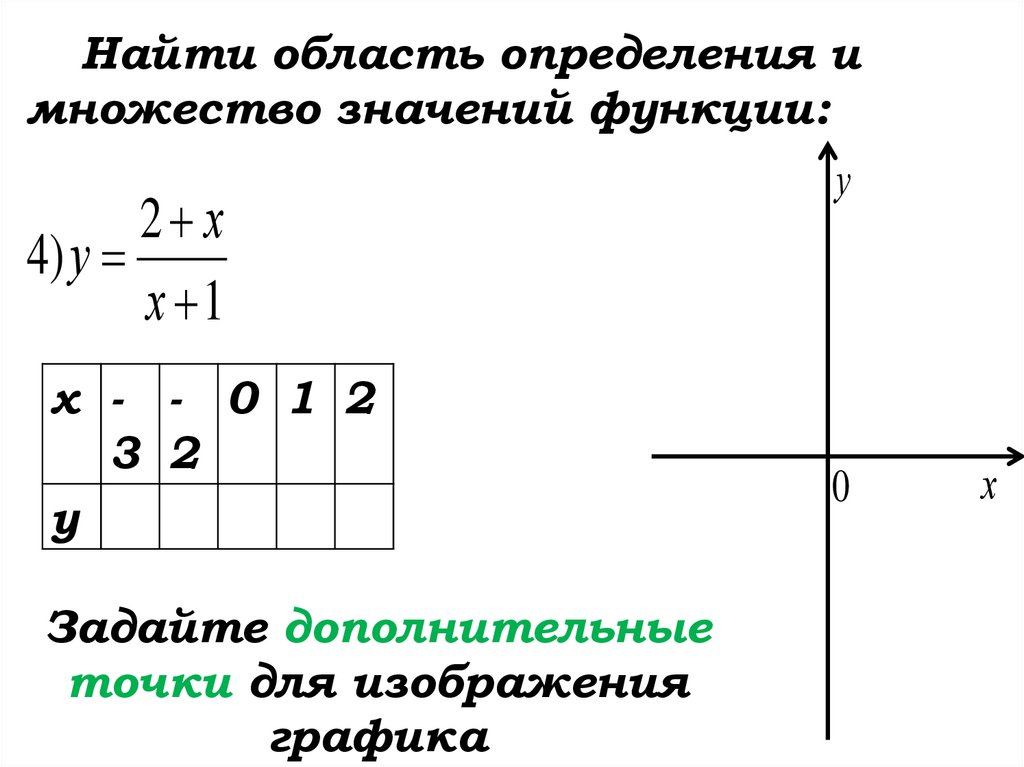
Найти область определения и
множество значений функции:
2 х
4) у
х 1
х - - 0 1 2
3 2
у
Задайте дополнительные
точки для изображения
графика
у
0
х

8.

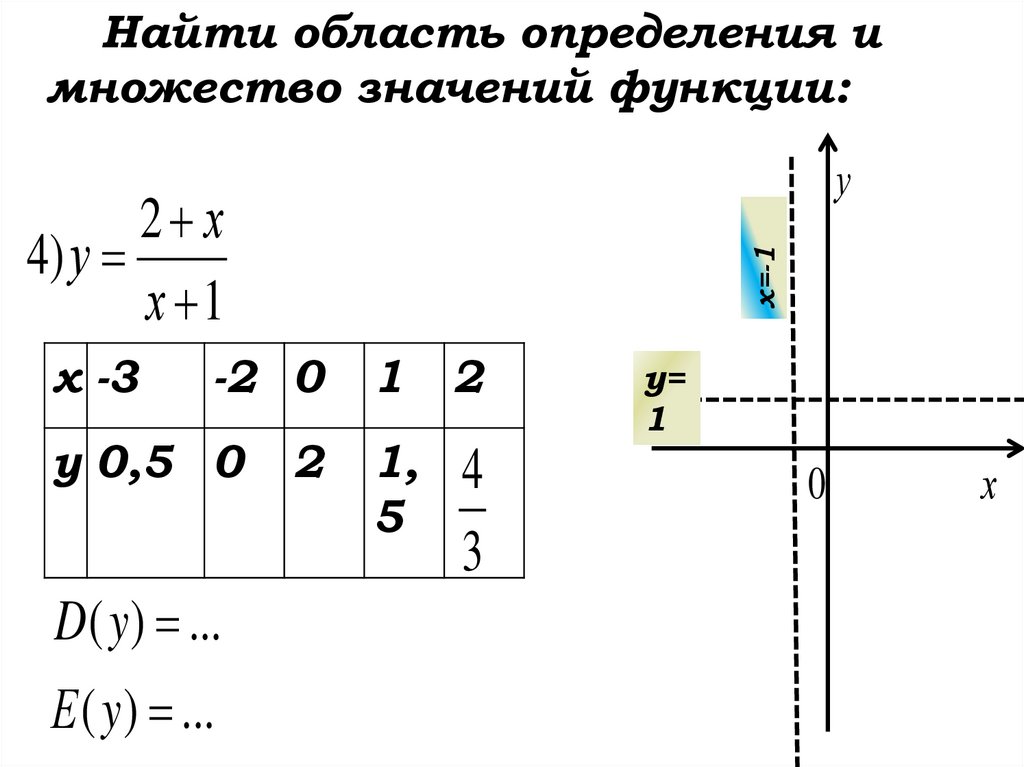
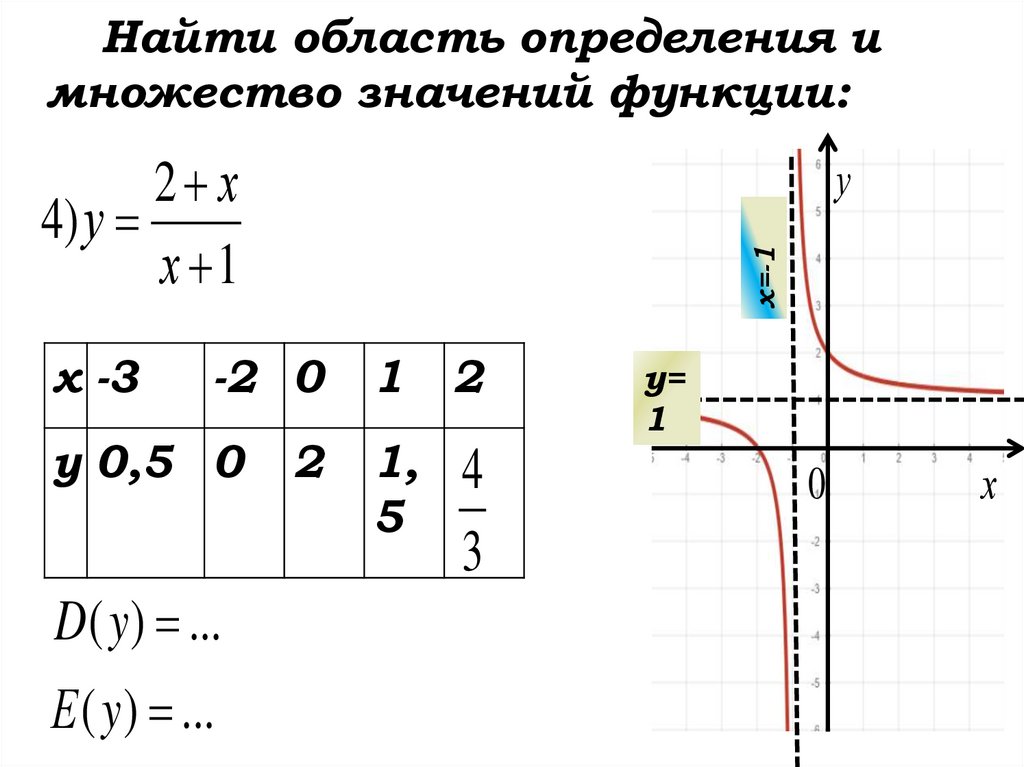
Найти область определения и
множество значений функции:
у
х -3
х=-1
2 х
4) у
х 1
-2 0
у 0,5 0
D( y ) ...
Е ( y ) ...
2
1
2
1,
5
4
3
у=
1
0
х

9.

Найти область определения и
множество значений функции:
2 х
4) у
х 1
х -3
х=-1
у
-2 0
у 0,5 0
D( y ) ...
Е ( y ) ...
2
1
2
1,
5
4
3
у=
1
0
х

10.

Найти область определения и
множество значений функции:
2 х
4) у
х 1
х -3
х=-1
у
-2 0
у 0,5 0
2
1
2
1,
5
4
3
D( y) ; 1 1;
Е( y) ;1 1;
у=
1
0
х

11.

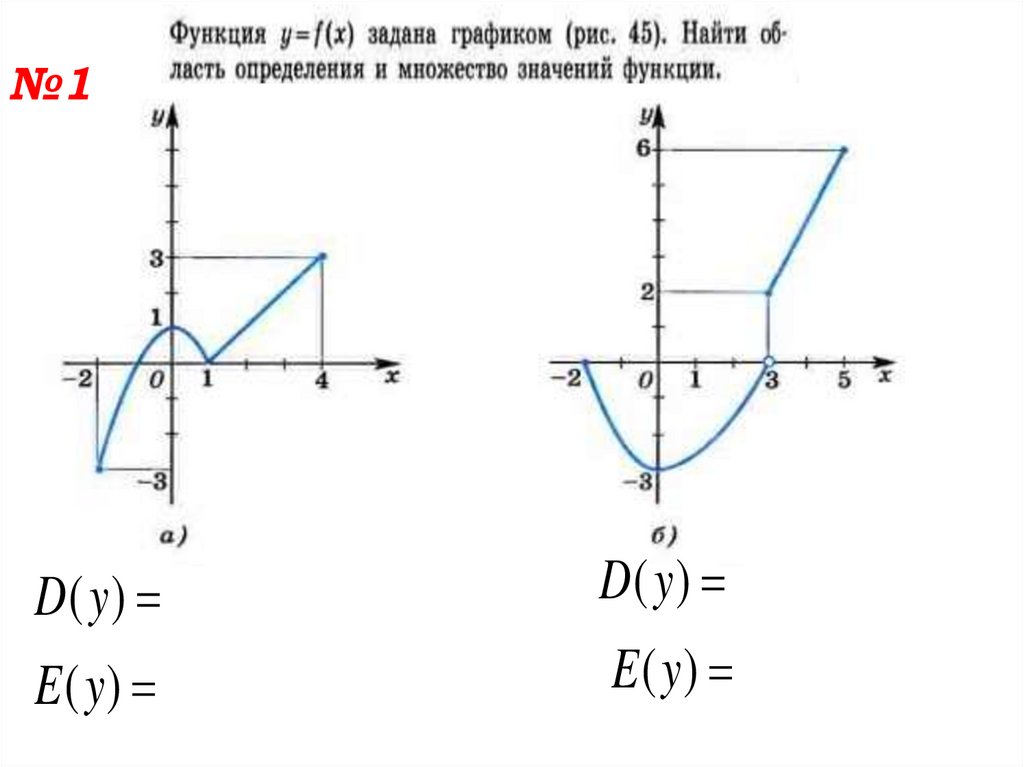
№1
D (y )
D (y )
E (y)
E (y)

12.

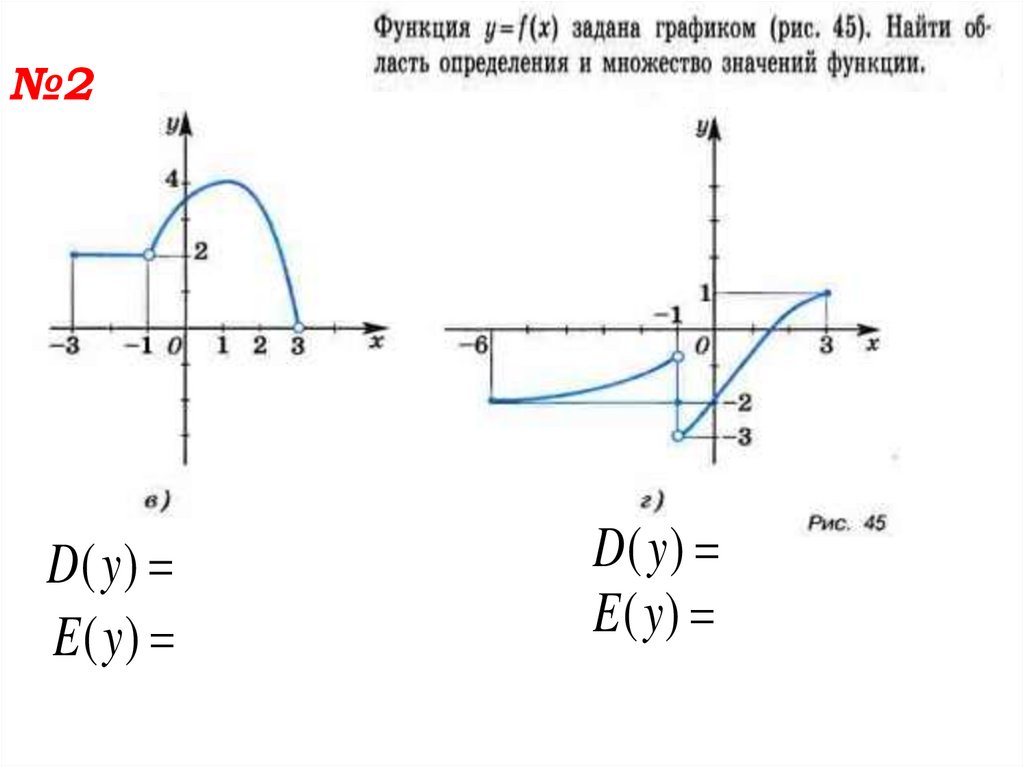
№2
D (y )
E (y)
D (y )
E (y)

13.

14.

15.

16.

1
2
3
Назовите точку
разрыва в каждом
случае и укажите
какие условия

17.

18.

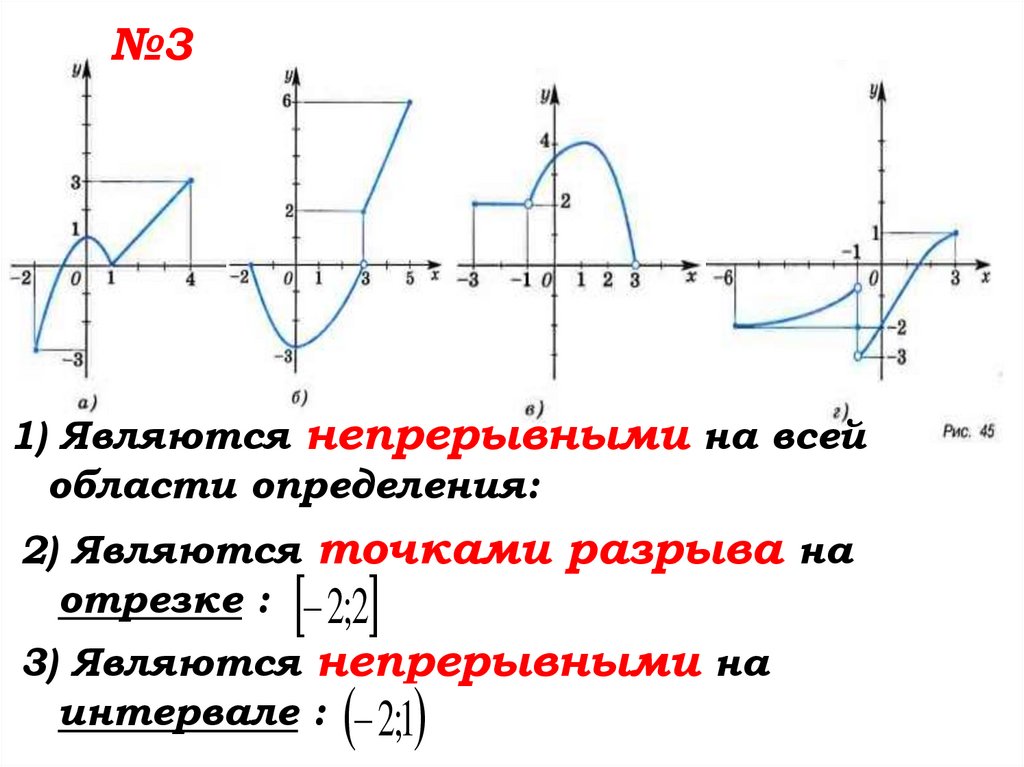
№3
1) Являются непрерывными на всей
области определения:
2) Являются точками разрыва на
отрезке : 2;2
3) Являются непрерывными на
интервале : 2;1