Похожие презентации:
Правила вычисления КРИ-2
1. Правила вычисления КРИ-2
2. 1 случай. Если линия задана уравнением в явном виде , и , тогда
a x by y( x)
P
(
x
,
y
)
dx
Q
(
x
,
y
)
dy
L
b
[ P( x, y( x)) Q( x, y( x)) y ( x)]dx
a
3. 2 случай. Если линия задана параметрическими уравнениями и тогда
2 случай.Если линия задана параметрическими
уравнениями x x t и t
тогда
y y t
P( x, y )dx Q( x, y )dy
L
( P( x(t ), y(t )) x (t ) Q( x(t ), y(t )) y (t )) dt
4.
Пример. Вычислитькриволинейный интеграл от
xdx
3
zydy
xydz
L
вдоль отрезка прямой, идущего от
точки М(3, 2, 1) до точки N(0,1 ,2).
5. Решение.
• Запишем уравнение прямой, проходящей черезточки М и N.
• Воспользуемся параметрическими уравнениями
прямой в пространстве
x x0 mt ,
y y0 nt ,
z z pt.
0
6.
• x , y ,-координатыточки, лежащей на прямой.
z
0
0
0
• Например, N(0,1 ,2).
x0 0, y0 1, z0 2
s ( m, n , p )
s NM (3 0; 2 1;1 2)
x x0 mt ,
y y0 nt ,
z z pt.
0
x 0 3t ,
y 1 1t ,
z 2 1 t .
7.
x 3t ,y 1 1t ,
z 2 t.
8. Пример
•Вычислить работу силывдоль
дуги
линии
F ( x 2)i xyj
от точки А(0;1) до точки В(1;3).
y 2x 1
2
9. п.3 Формула Грина
10. Д. Грин (14.07.1793 — 31.03.1841)
11.
Формула ГринаДжордж Грин
14.07.1793 – 31.05.1841
Джордж Грин в юности не получил образования,
математику изучал самостоятельно и только в
1833 г. поступил в Кембриджский университет,
который окончил в 1837 г. В сочинении "Опыт
применения математического анализа к
теориям электричества и магнетизма"
(1828 г.) развил теорию электричества и
магнетизма, опираясь на введенное в этой
работе понятие потенциала и соотношение
между интегралом по объему и интегралом по
поверхности, ограничивающей этот объем.
Независимо от Грина указанное соотношение в
том же году получил М.В. Остроградский.
12. Основные труды
«Математические исследования относительно законов
равновесия жидкостей, аналогичных электричеству»
(1833);
«Об определении внешнего и внутреннего притяжения
эллипсоидом неоднородной плотности» (1835);
«О распространении волн в узком и мелком канале»
(1837);
«Об отражении и преломлении звука» (1838);
«О законах отражения и преломления света на
поверхности, разделяющей две некристаллические
среды» (1838);
«О распространении волн в канале»; «О
распространении света в кристаллических средах»
(1839);
«Исследование о качании маятника в жидкости», 1833
13. Определение
L14. Определение
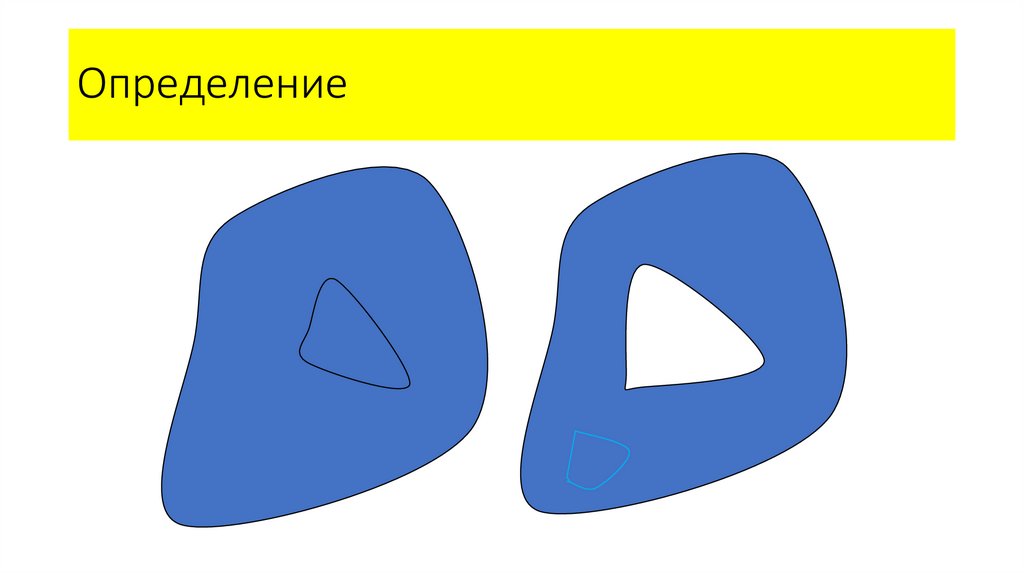
15. Определение
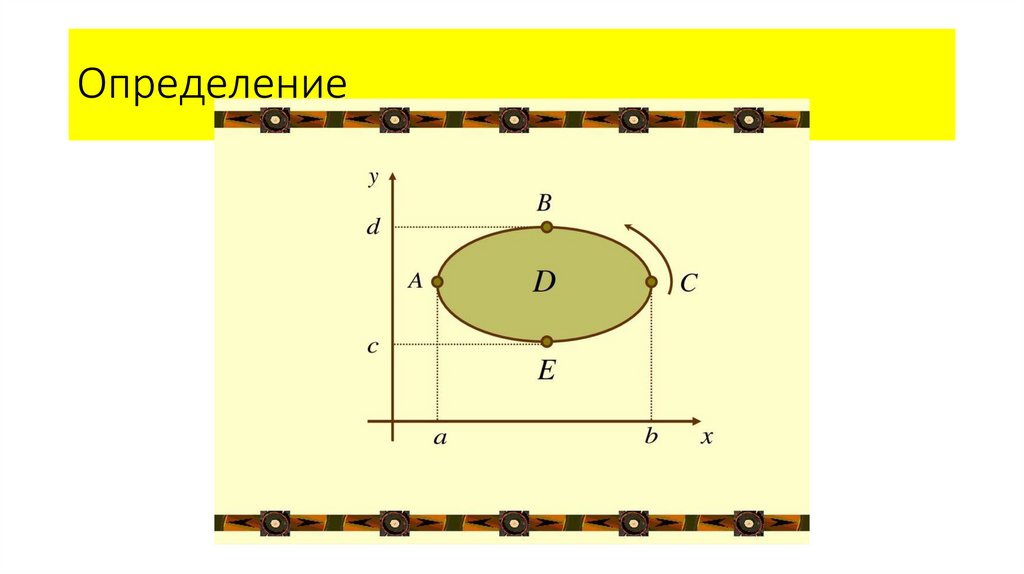
16. Формула Грина
P( x, непрерывныy), Q( x, y)вместе со своими
Если функции
частными производными в некоторой замкнутой
области
с границей L, то справедлива следующая
D
формула Грина:
Q(x,y) P(x,y)
P(x,y)dx Q(x,y)dy x y dxdy
L
D
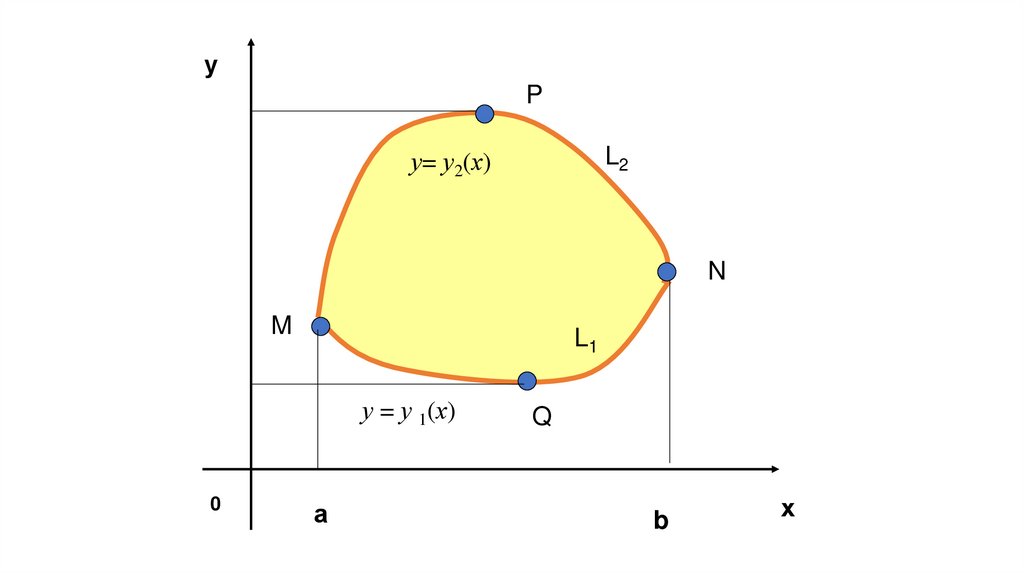
17.
уP
L2
у= у2(х)
N
M
L1
у = у 1(х)
0
а
Q
b
х
18.
P( x, y )dxdy
D y
P( x, y )
y2 ( x )
dx
dy P( x, y ) y ( x ) dx
1
y
a
y1 ( x )
a
b
y2 ( x )
b
b
P( x, y2 ( x)) P( x, y1 ( x)) dx
a
b
a
a
b
P( x, y1 ( x))dx P( x, y2 ( x))dx
19.
P( x, y)dx P( x, y)dx P( x, y )dxl1
l2
L
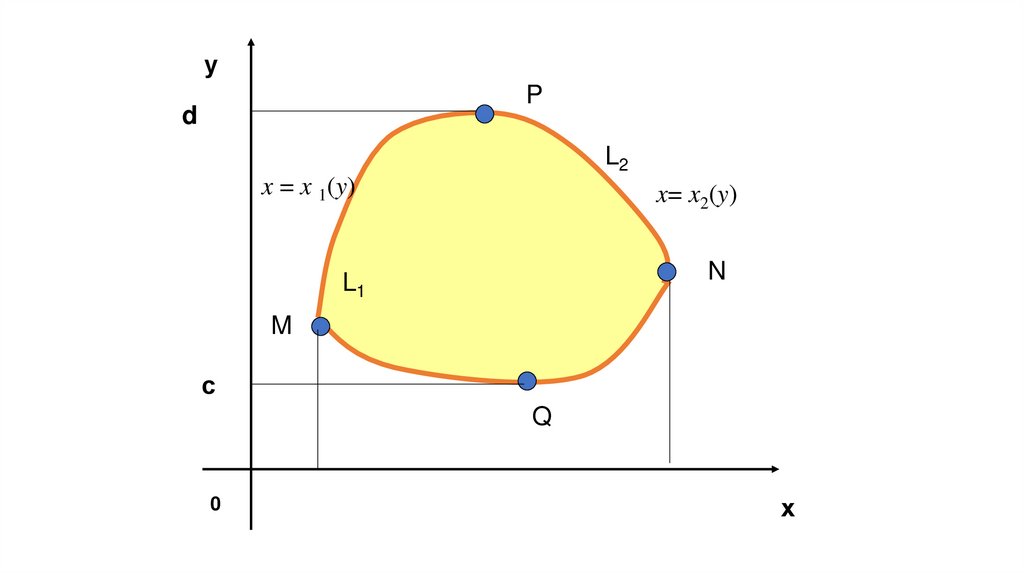
20.
уP
d
L2
x = x 1(y)
x= x2(y)
L1
N
M
с
Q
0
х
21.
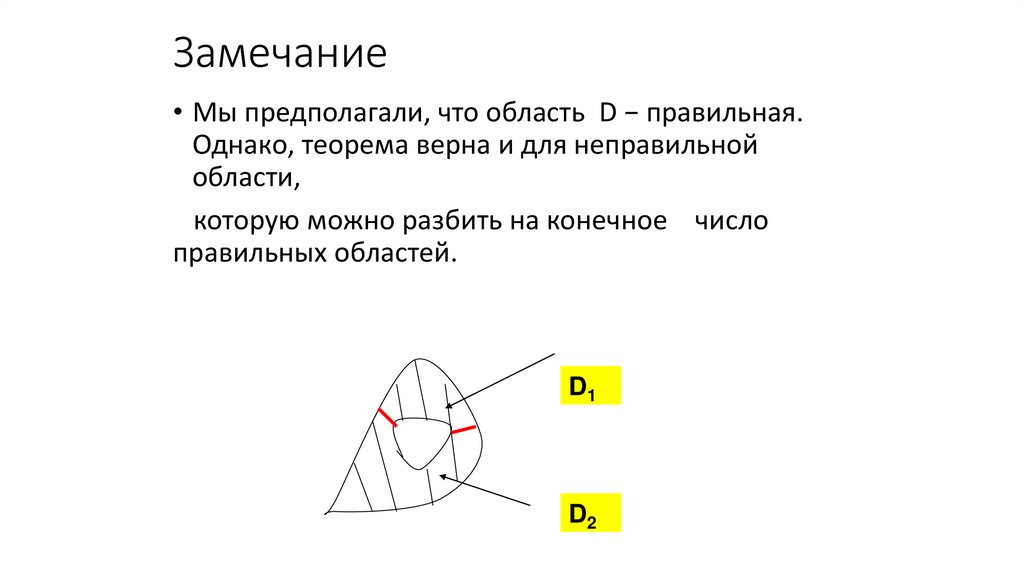
22. Замечание
• Мы предполагали, что область D − правильная.Однако, теорема верна и для неправильной
области,
которую можно разбить на конечное число
правильных областей.
D1
D2
23. Замечание
• Из формулы Грина следует, чтоydx xdy ( x) ( y) dxdy (1 1)dxdy 2 dxdy,
x
y
L
D
D
D
• т.е. площадь фигуры, ограниченной кривой , можно
найти по формуле
24. Пример
22
xy
y
dx
x
dy
Вычислить
, где L– контур
L
треугольника с вершинами в точках
А(–1, 0),
В(0, 2), С(1, 0).
25. Решение.
• Поскольку контур является замкнутым, применимформулу Грина. В нашем случае
26.
Q P(2
xy
y
)
dx
x
dy
dxdy
L
x y
2
2 x 2 x 1 dxdy
1
1
dxdy S AC OB 2 2 2
2
2
27. Пример:
28.
29. П.4 Независимость КРИ 2 от пути интегрирования
30. Теорема
Пусть функциивместе со своими
P( x, y), Q(непрерывны
x, y)
частными производными в односвязной области D, тогда
следующие условия эквивалентны:
1)
не dy
зависит от пути интегрирования,
P x,y dx Q x,y)
целиком Lлежащем в области D,
2)
P( x, y)dx Q( x, y)dy 0
L
3)
4)
P( x, y ) Q( x, y )
y
x
du( x, y) P( x, y)dx Q( x, y)dy
31. Пример
Вычислить интеграл4
3
2 2
4
(
х
4
xy
)
dx
6
x
y
5
y
dy
L
по ломаной ОАВ,
В(4;2)
если О(0;0), А(2; 1,5),
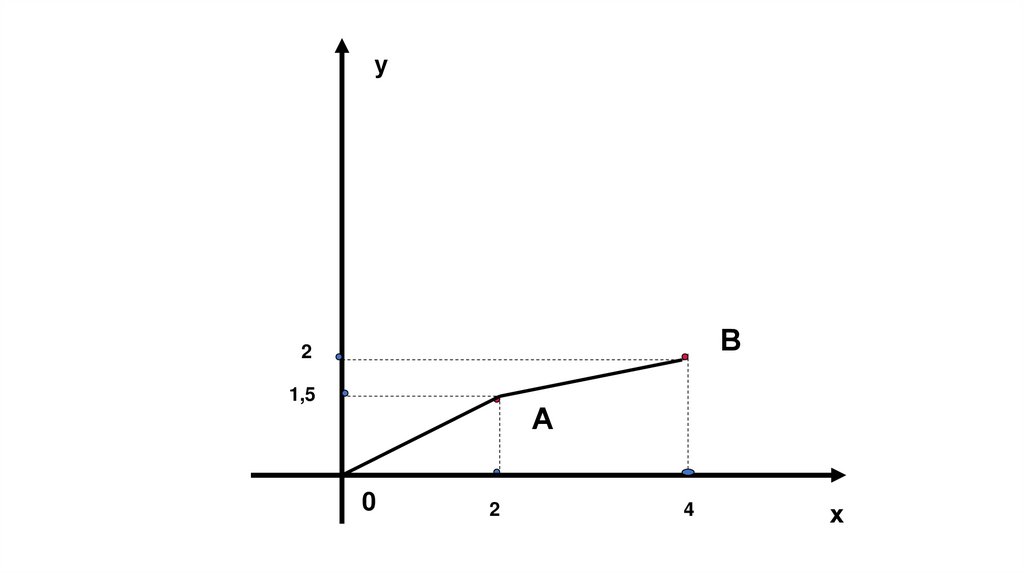
32.
уВ
2
1,5
А
0
2
4
х
33. Решение.
• Покажем, что криволинейный интеграл не зависитот пути интегрирования. В нашем случае
P( x, y ) х 4 xy
4
P( x. y )
2
12 xy
y
3
Q( x. y ) 6 x y 5 y
2
2
Q ( x. y )
2
12 x y
x
P( x. y ) Q ( x. y )
y
x
4
34.
• Значит, интеграл не зависит от путиинтегрирования.
• Следовательно, выбираем более удобный путь
интегрирования
(
х
4
xy
)
dx
6
x
y
5
y
dy
4
3
2
2
4
• Составляем
уравнение ОВ:
LOB
x x1
y y1
x2 x1 y2 y1
x 0 y 0
4 0 2 0
x
y
2
x y
4 2
35.
43
2 2
4
(
х
4
xy
)
dx
6
x
y
5
y
dy
LOB
y
x
2
1
x
dy dx dx
2
2
4
x 3 2 x 2
x 4 1
[ x 4 x( ) 6 x ( ) 5( ) ]dx
2
2
2 2
0
4
4
4
4
4
32
x
16
x
24
x
5
x
x
3x
x
4
dx
[x
5 ]dx
32
2
4
32
0
0
4
4
4
4
5
4
67 x 4 67 45 67 32
67 x
428,8
dx
5
32
32 5 0 32 5
0
4
4
36. П.5 Восстановление функции по ее полному дифференциалу
37. Определение
• Дифференциальное выражениеP( x, y)dx Q( x, y)dy
называется полным дифференциалом, если существует такая
функция u(x,y)
полный дифференциал которой равен данному выражению, т.е.
du( x, y) P( x, y)dx Q( x, y)dy
38.
• С другой стороныu
u
du( x, y)
dx
dy
x
y
• Сравнивая формулы, получаем
u
P( x, y) ,
• Далее находим x
u
Q( x, y) .
y
P 2u
,
• откуда заключаем, что y x y
Q 2u
,
x y x
P Q
y x
39. Теорема
• Для того, чтобы выражениеP( x, y)dx Q( x, y)dy
• было полным дифференциалом, необходимо и
достаточно выполнения равенства
P Q
.
y x
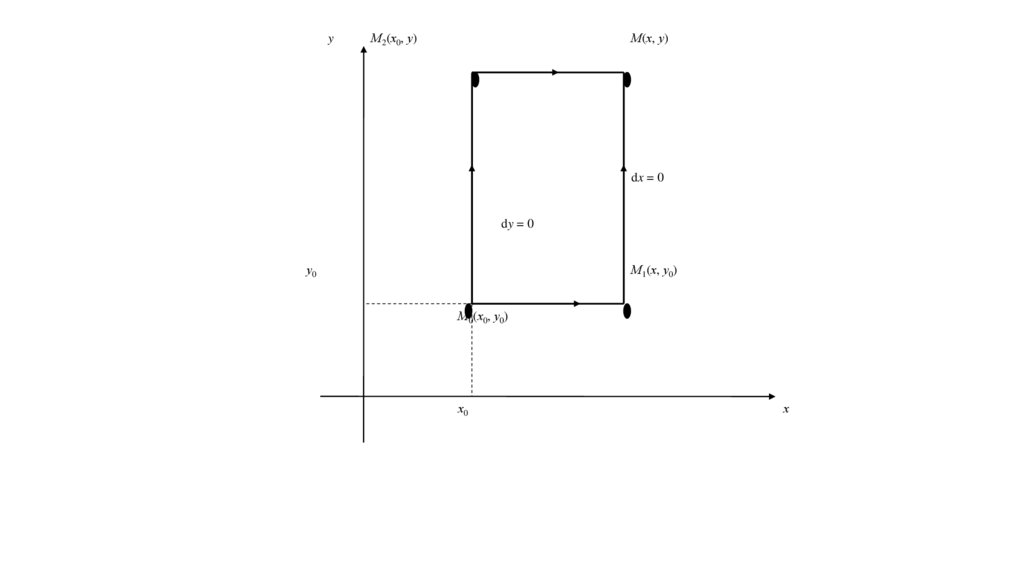
40.
yМ2(х0, у)
М(х, у)
dx = 0
dy = 0
у0
М1(х, у0)
М0(х0, у0)
х0
х
41.
du( x, y) P( x, y)dx Q( x, y)dyx
y
P( x, y 0 )dx Q( x, y )dy C ,
y0
x0
u ( x, y )
y
x
P( x, y )dx Q( x , y )dy C.
0
y0
x0
42. Пример
• Проверить является ли выражение полным дифференциалом иесли да, то восстановить функцию
4 x y y dx 3x y 2 xy dy
3
3
2
4
2
43. Решение.
• ОбозначимP( x ) 4 x y y
3
3
2
Q( x) 3x y 2 xy
4 2
P( x. y )
3 2
12 x y 2 y
y
Q ( x, y )
3 2
12 x y 2 y
x
44.
P Q• Так как
,
то данное выражение
y дифференциалом.
x
• является полным
• Найдем функцию
u
(
x
,
y
)
• Воспользуемся первой из формул, выбрав за
начальную точку О(0,0).
x
y
x0
y0
3
3
2
4 2
4
x
y
y
dx
3
x
0 0 y 2 xy dy x0 0. y0 0
y
3
2
y
y
y
4
3 3
2
4 2
2x )
4 x 0 0 dx 3x y 2 xy dy 0 (3x
3
2 0
0
0
x
x y xy C u( x. y )
4
3
2






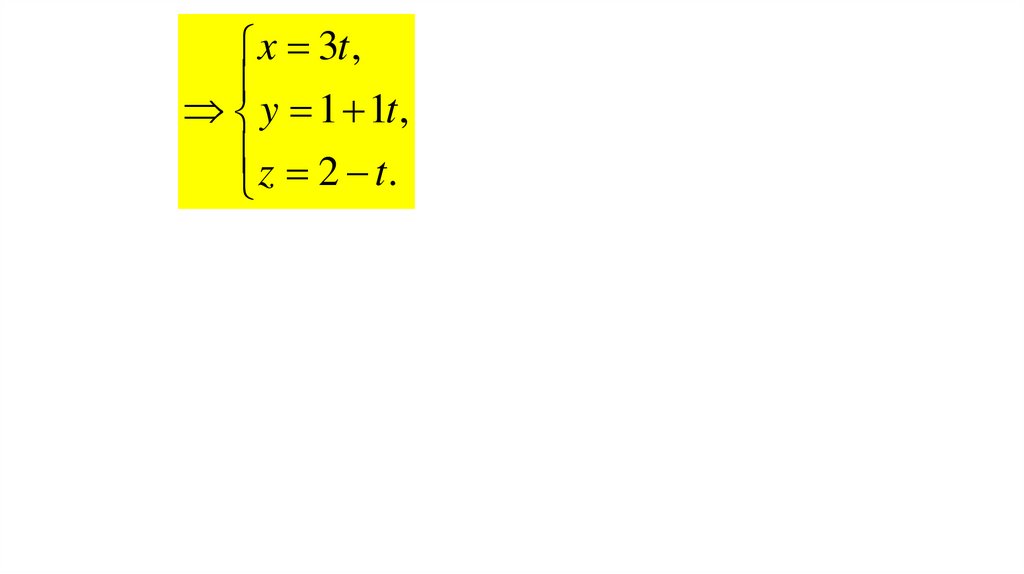






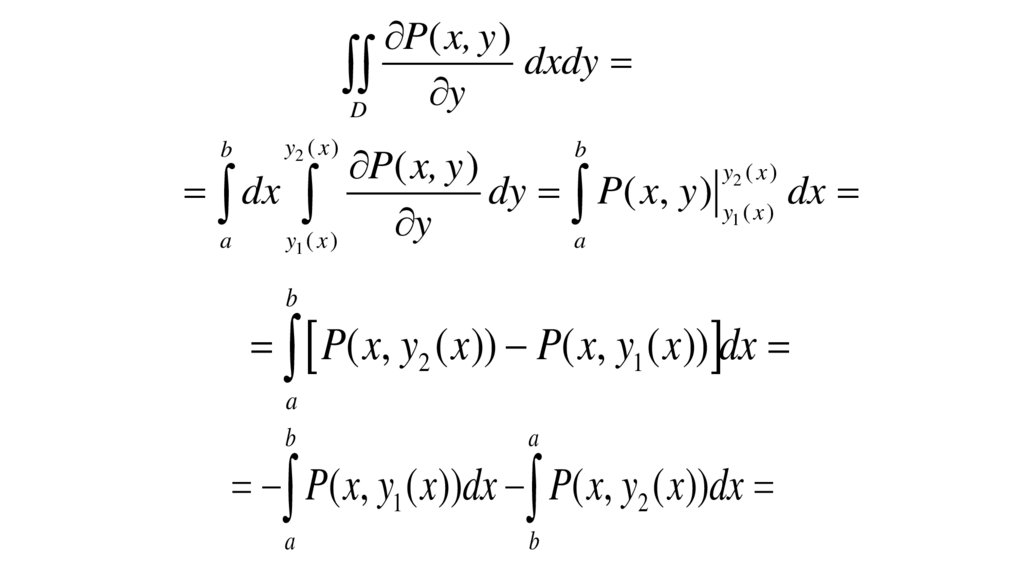
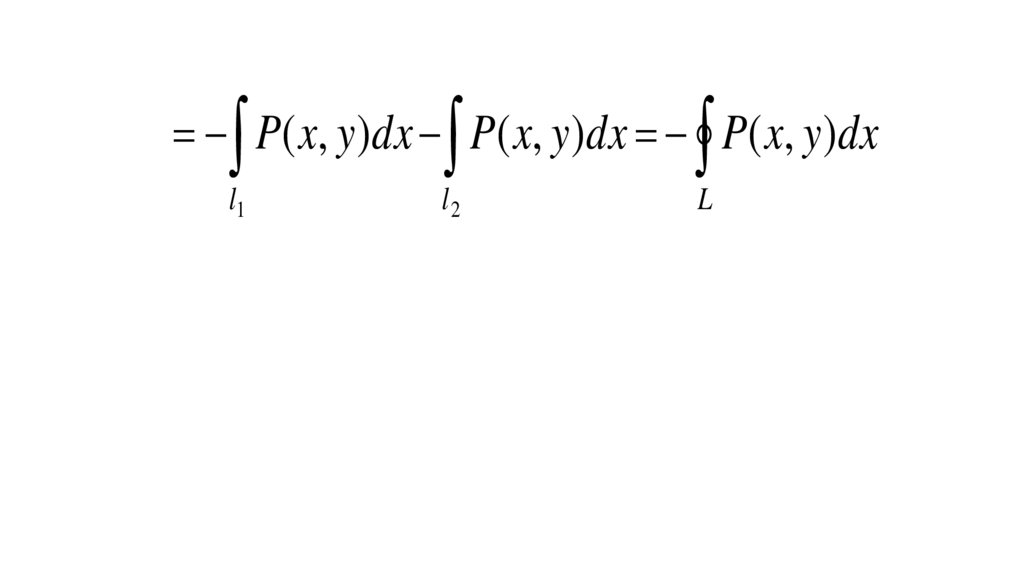




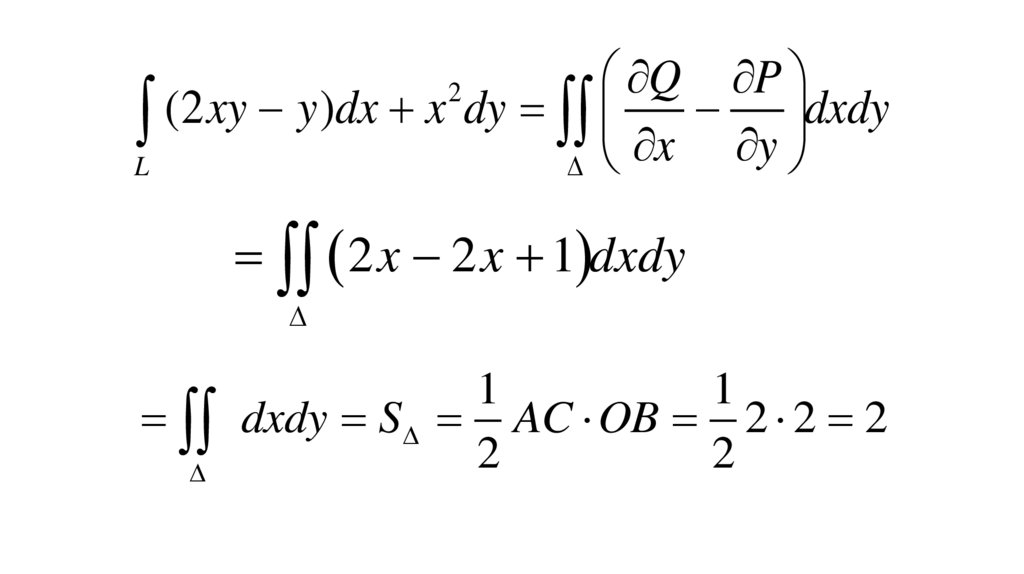












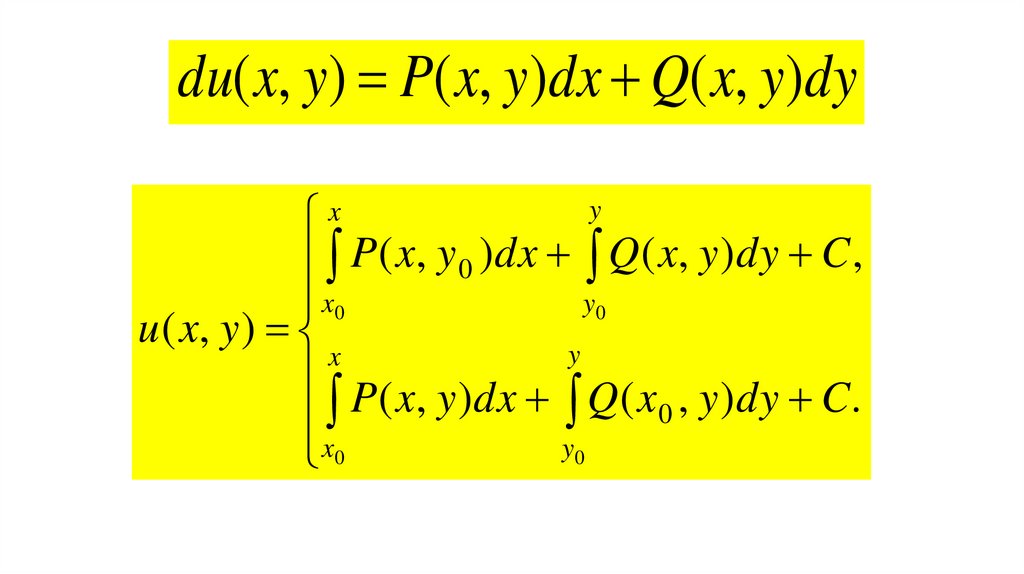



 Математика
Математика








