Похожие презентации:
Интеграл от функции комплексной переменной по кривой на комплексной плоскости
1. §5. Интеграл от функции комплексной переменной по кривой на комплексной плоскости.
п.1. Вспомогательные положения.Def. Кусочно-гладкая кривая-
z z( t ) x( t ) iy( t ); t a ,b , x(t ), y(t ) C a,b ,
'
'
x ( t ), y ( t ) кусочно-непрерывные на a ,b ,
x (t ) y (t )
'
2
'
2
нет точек возврата
0 и самопересечения.
Если x (a ) x (b ), y(a ) y(b )
замкнутая
кривая.
2. Криволинейные интегралы второго рода по кривой на плоскости (x,y).
* *x k , yk
zk
* *
x k , yk
zk 1
C
z k
x k
yk
2
2
z k x k yk
P x , y , Q x , y x , y C
3.
n* *
** **
S n P x k , yk x k Q x k , yk yk
k 1
lim
n
max z k 0
k
Sn P x , y dx Q x , y dy
C
Достаточные условия существования:
1) кусочная гладкость кривой C;
2) кусочная непрерывность и ограниченность
функций P и Q.
4. п.2. Основное определение.
Def. Интегралом от функции комплекснойпеременной f(z)=u(x,y)+iv(x,y) по кривой C
комплексной плоскости z называется
комплексное число
f z dz u x , y iv x , y dx idy
C
C
udx vdy i vdx udy .
C
C
5. Замечания.
1) Достаточные условие существования- кусочная гладкость контура C;
- кусочная непрерывность и ограниченность
u(x,y), v(x,y) .
2) lim
n
max z k 0
k
Sn f z dz ,
C
*
S n f z k z k .
n
k 1
6. п.3. Свойства
f z dzп.3. Свойства
C
1) f z dz f z dz;
C
C
2) af z bg z dz a f z dz
C
b g z dz;
C
n
C
3) f z dz f z dz;
n
Ck
k 1
k 1 C k
7.
4) f z dz f z dl MLC .C
C
b
5) f z dz f z t z t dt .
C
a
'
Пример.
z z0 R0 e i
dz
i
dz iR0 e d
z
z
0
z z0 R0
0
2
8.
2 iR e i2
0
d i d 2 i .
i
0 R0 e
0
6) Замена переменной. Пусть однолистная
z
C D : C
D.
f z dz f d .
'
C
9. §6. Теорема Коши.
п.1. Вспомогательные положения.Def. Область g R2 называется квадрируемой
*
если inf O P P* sup B .
*
Def. Число P P P* называется площадью
плоской области g (по Жордану).
Достаточное условие квадрируемости
- кусочная гладкость (спрямляемость) g.
10.
Для функции f(x,y) C(g) и |f(x,y)| Aв квадрируемой области g f x , y dxdy .
g
Def. Область g R2 называется односвязной,
если для замкнутого контура g ,
ограниченная им часть плоскости целиком g.
11. Формула Грина.
Пусть P(x,y), Q(x,y) C( g), g- кусочно- гладкийконтур и Px, Py, Qx, Qy C(g), тогда
Q P
Pdx Qdy dxdy .
x
y
g
g
12. п.2. Теорема 6.1 (Коши).
Если f z Cg
в односвязной области g, то
для замкнутого контура g
f z dz 0.
Доказательство.
по формуле
f z dz udx vdy i vdx udy Грина
P u
Q v
P v
Q u
13.
gg
v x u y dxdy i u x v y dxdy
g
f z C
g
g u x v y , u y v x
u y u y dxdy i v y v y dxdy 0
g
g
14. Замечания.
1) Односвязность области – важное требование!1
Пример. f z C 1 z 3 .
z
dz
2 i 0.
z
z 2
15.
Def. f(z) называется аналитической взамкнутой области g f(z) C ( g), если
f(z) C (g) и f(z) C ( g). Т.е. f(z) C ( g).
Определение справедливо и для многосвязной
области.
Теорема 6.2 (2-я теорема Коши).
Если f(z) C ( g), g-односвязная, то
f z dz 0.
g
Теорема переносится и на случай многосвязной
области.
16. Теорема 6.3 (теорема Коши для многосвязной области).
Пусть f(z) C (g), g-многосвязная, ограниченнаяизвне контуром C0, а изнутри- контурами C1,
C2,…Cn и пусть f(z) C ( g). Тогда
f z dz 0,
C
где С-полная граница g, С= C0 C1 C2… Cn,
проходящая в положительном направлении.
17.
Доказательство.C
C1
Cn
1
0
n
C2
2
18. п.3. Следствия теоремы Коши.
1)Если g- односвязная и f(z) C (g), то
для
z1, z2 g
z2
z2
z1
z1
f ( ) d f ( ) d .
z
При фиксированной z0
f ( ) d F ( z )
z0
функция только z !
19. 2) Неопределенный интеграл.
Пусть g-односвязная область, f(z) C(g),для замкнутого контура g
z
f z dz 0.
f ( ) d F ( z ) неопределенный интеграл f(z).
z0
20. Свойства неопределенного интеграла F(z).
Теорема 6.4 Если g-односвязная область,f(z) C(g), для замкнутого контура g
f z dz 0, то F ( z ) C g ,
z
F ( z ) f ( ) d .
z0
21.
Доказательство.F
1 z z
z z
f (z)
f
(
)
d
f
(
z
)
d
z
z
z z
z
z
z
1
f ( ) f ( z ) d
z z
z
max
f ( ) f ( z ) , z .
z z ,z z
F
lim
F z f z C g
z 0 z
F ( z ) C g .
22. Понятие первообразной
Def. Пусть f(z) C(g). Тогда первообразной F(z)функции f(z) в g называется F(z) C (g) такая,
что F'(z)=f(z).
23. Свойства неопределенного интеграла F(z).
1) Неопределенный интеграл F(z) водносвязной области g- первообразная для f(z).
2) Если первообразная F(z), то их много,
но F '1(z)- F '2(z)=0 => F1(z)=F2(z)+C.
3) Формула Ньютона-Лейбница. Если gодносвязная и f(z) C(g) и для замкнутого
контура g
z2
f z dz 0, то
f ( ) d F z2 F z2 ,
z1
где F первообразная.
24.
4) Формула конечных приращений, вообщеговоря не верна.
5) Формула Коши-Адамара.
Пусть g- односвязная и f(z) C (g)
и для замкнутого контура g
f(z)- первообразная для f '(z)=>
z z
f z dz 0.
f ( ) d f z z f z .
z
25.
z zz
z z , 0 1; d zd ;
1
f z z f z z f ( z z ) d
0
Формула Коши-Адамара
26.
6) При вычислении интеграла отаналитической функции контур
интегрирования можно деформировать так,
чтобы он не выходил из области
аналитичности подынтегральной функции.
Деформируя контур интегрирования так, как
это допускается теоремой Коши, можно легко
вычислить многие интегралы
27. Важный пример.
rei
C
0 1
dz
?
z
C
28.
z x , dz dxC
0 1
r
dz r dx
ln r
z
x
C
1
29.
rer
i
z re
C
i
i
dz ir e d
0
r
dz
i d i
z
C
0
30.
z reC
i
r
2
0 1
r
dz
ln r i 4 .
z
C
n
dz
ln r i 2 n ln z i arg z 2 n .
z
C
31. Замечание.
0, n 1n Z
z a dz
2 i , n 1
z a r
n
Аналитичность подынтегральной функции
внутри замкнутого контура интегрирования
не является необходимым условием равенства 0
интеграла по этому контуру.







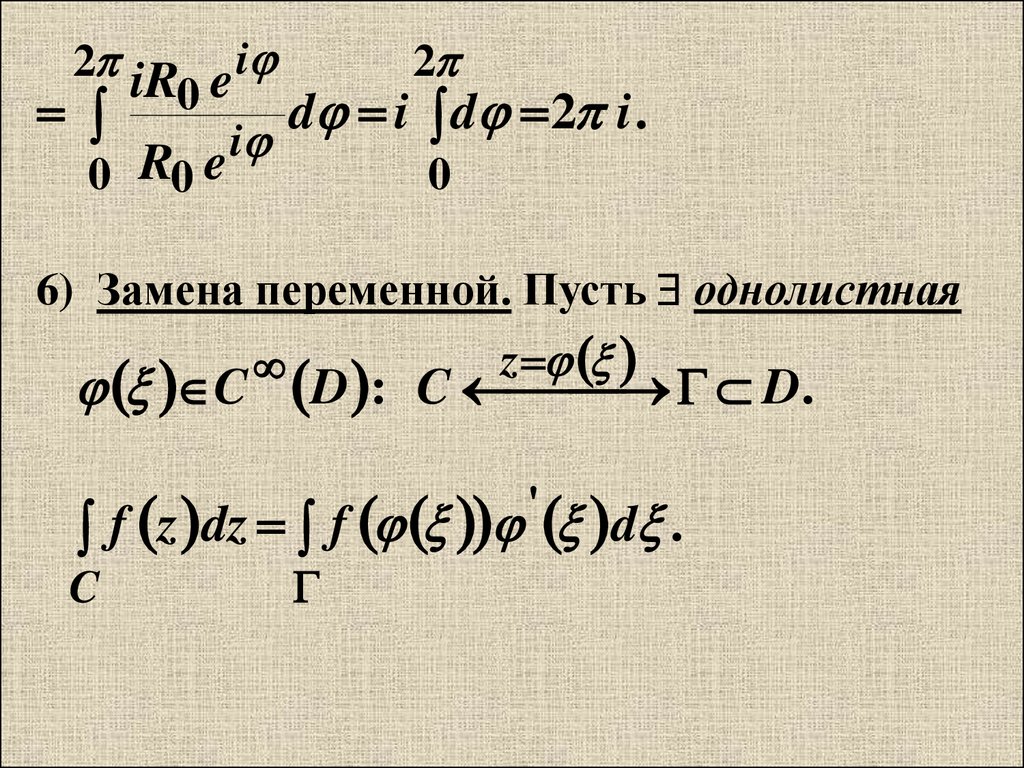




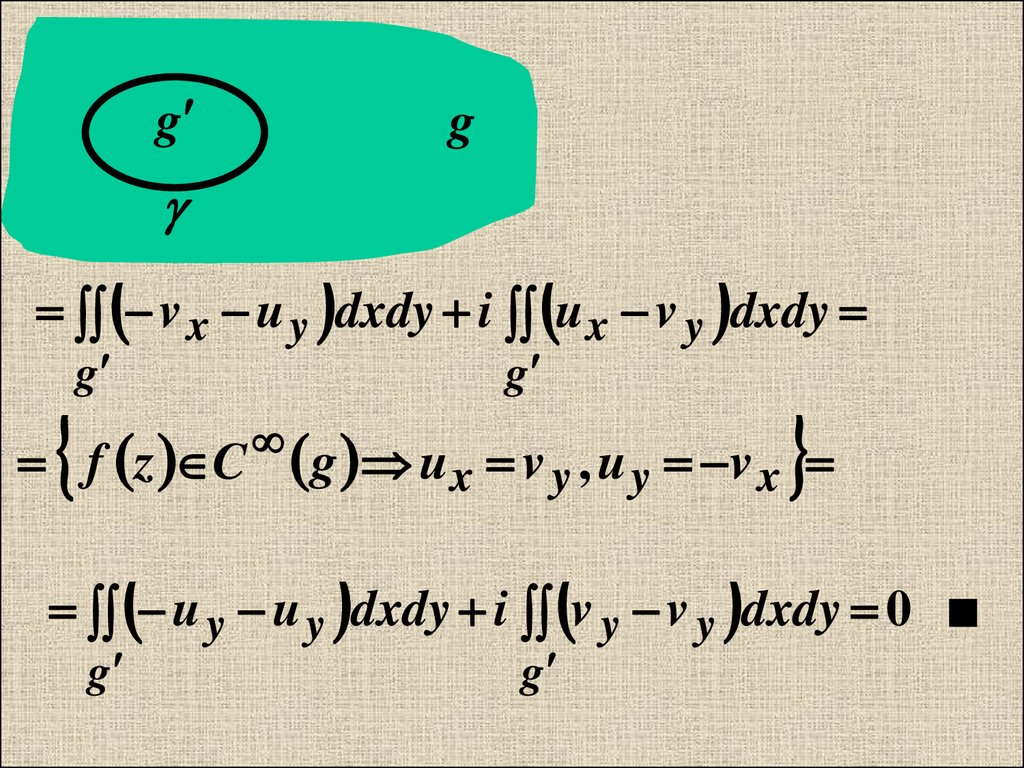


















 Математика
Математика








