Похожие презентации:
Непрерывные случайные величины. Лекция 15
1. Непрерывные случайные величины
Лекция 152. План лекции
• Непрерывные случайные величины.Закон распределения.
• Функции распределения и плотности
распределения вероятностей, их
свойства.
3. Непрерывные случайные величины
Случайные величины, возможные значениякоторых непрерывно заполняют некоторый
промежуток
Примеры:
- рост студента
- время безотказной работы прибора
- дальность полета снаряда
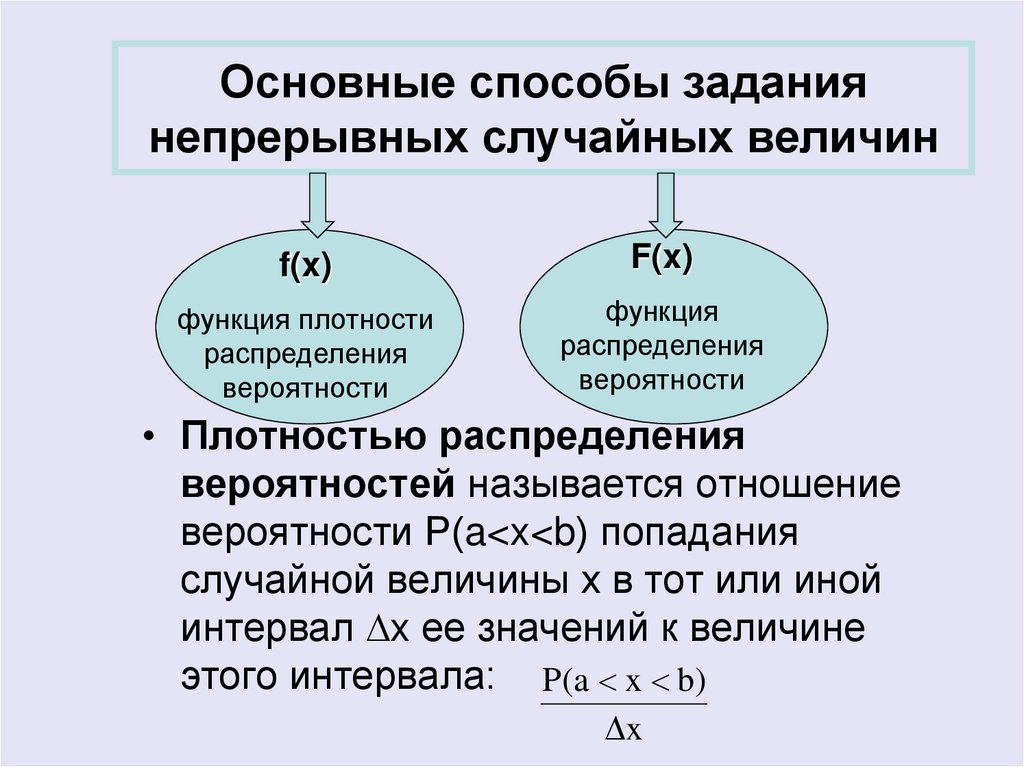
4. Основные способы задания непрерывных случайных величин
f(x)F(x)
функция плотности
распределения
вероятности
функция
распределения
вероятности
• Плотностью распределения
вероятностей называется отношение
вероятности Р(a<x<b) попадания
случайной величины x в тот или иной
интервал x ее значений к величине
этого интервала: P(a x b)
x
5. Плотность распределения
Плотностью распределениявероятностей называется отношение
вероятности Р(a<x<b) попадания
случайной величины x в тот или иной
интервал x ее значений к величине
этого интервала:
P ( a x b)
f ( x)
x
6. Свойства плотности распределения
7.
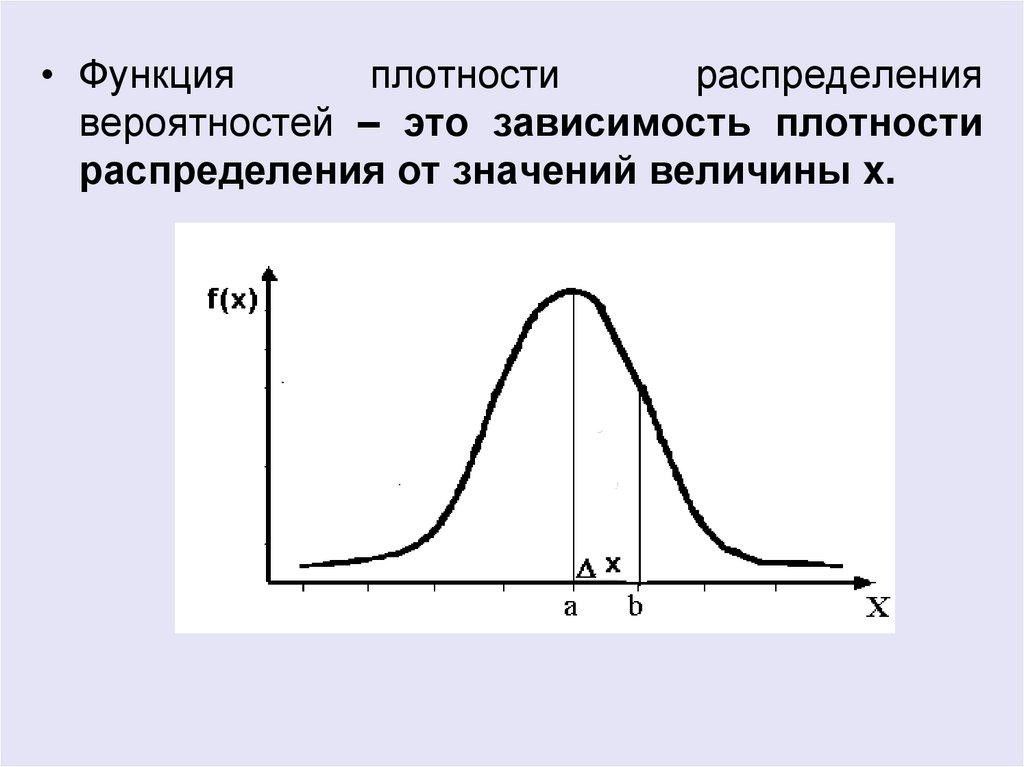
• Функцияплотности
распределения
вероятностей – это зависимость плотности
распределения от значений величины x.
8. Функция распределения
Функция F(х) распределения вероятностей(или накопленной вероятности) равна
вероятности того, что случайная
величина Х меньше наперед заданного
числа x.
F ( x) p ( X x)
9. Свойства функции распределения
У непрерывной случайной величины функция распределения тоженепрерывна.
10. Связь между f(x) и F(x)
f ( x) F ( x)x
F ( x) f (t )dt
11. Пример 1. Случайная величина задана своей функцией распределения F(x). Найти: 1. Функцию плотности распределения 2. Параметр а
3. Изобразить эти функции графически.0, x 0
2
F ( x) ax , 0 x 1
1, x 1
12. Решение
1. Согласно свойству f(x) f ( x ) F ( x )2
И с учетом того, что 0 0, ax 2ax, 1 0
получим функцию плотности
распределения:
0, x 0
f ( x) 2ax, 0 x 1
0, x 1
13. 2. Для нахождения параметра воспользуемся вторым свойством f(x)
bf ( x)dx 1
a
`
2axdx 1
0
1
2
x
0 2axdx 2a 2
Значит a 1
1
0
a1 0 a
2
2
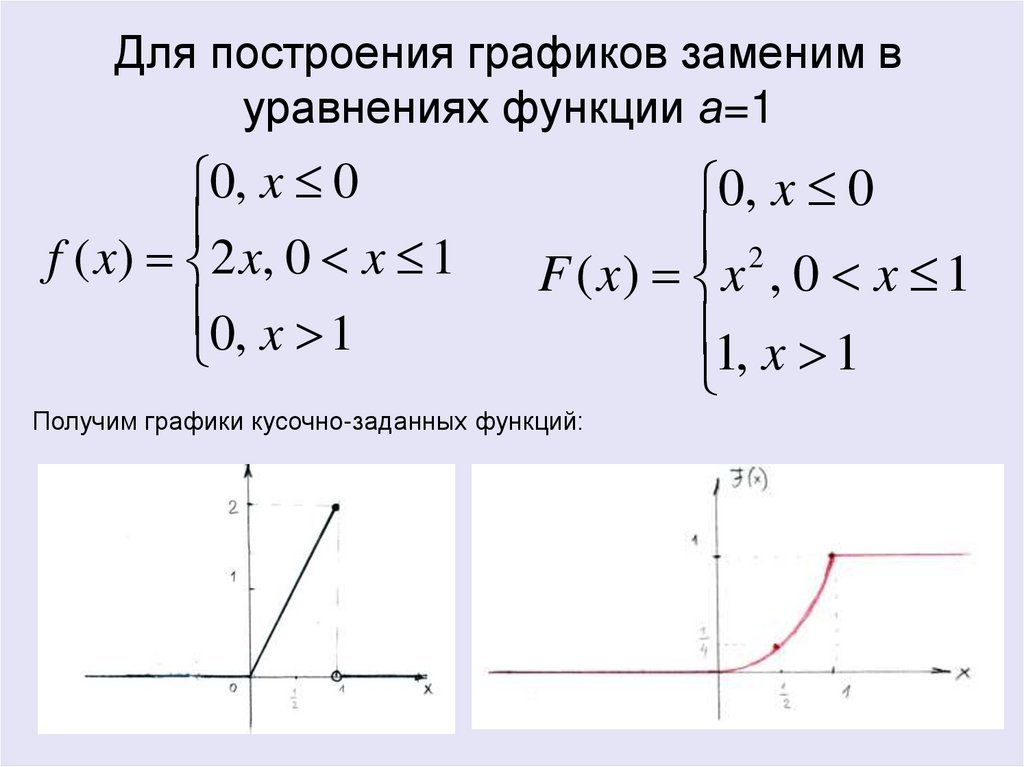
14. Для построения графиков заменим в уравнениях функции а=1
0, x 0f ( x) 2 x, 0 x 1
0, x 1
0, x 0
2
F ( x) x , 0 x 1
1, x 1
Получим графики кусочно-заданных функций:
15. Пример 2.
НСВ задана функцией плотностираспределения. Требуется найти:
1. Параметр с
2. Функцию F(x)
3. Построить графики этих функций
4. Вероятность p ( 2 x 1)
0 при х 0
f ( x) cx при 0 х 2
при х 2
0
16. Решение
1. Значение параметра с найдем аналогично предыдущему примеру:2
2
2
2
x
0 cxdx c 2
c
c
2 0 4 2c
0
2
2
1
Значит 2с 1 с
2
Запишем f(x) с данным значением параметра
0 при х 0
x
f ( x)
при 0 х 2
2
0
при х 2
17. 2. Функцию F(x) найдем согласно правилу
2. Функцию F(x) найдемxсогласно правилу F ( x) f (t )dt
x
x
2
1
t
f (t )dt 2 0 tdt 4
2
2
2
x 0
x
0
4 2
4
x
Получим функцию F(x):
0 при х 0
2
x
F ( x)
при 0 х 2
4
при х 2
1
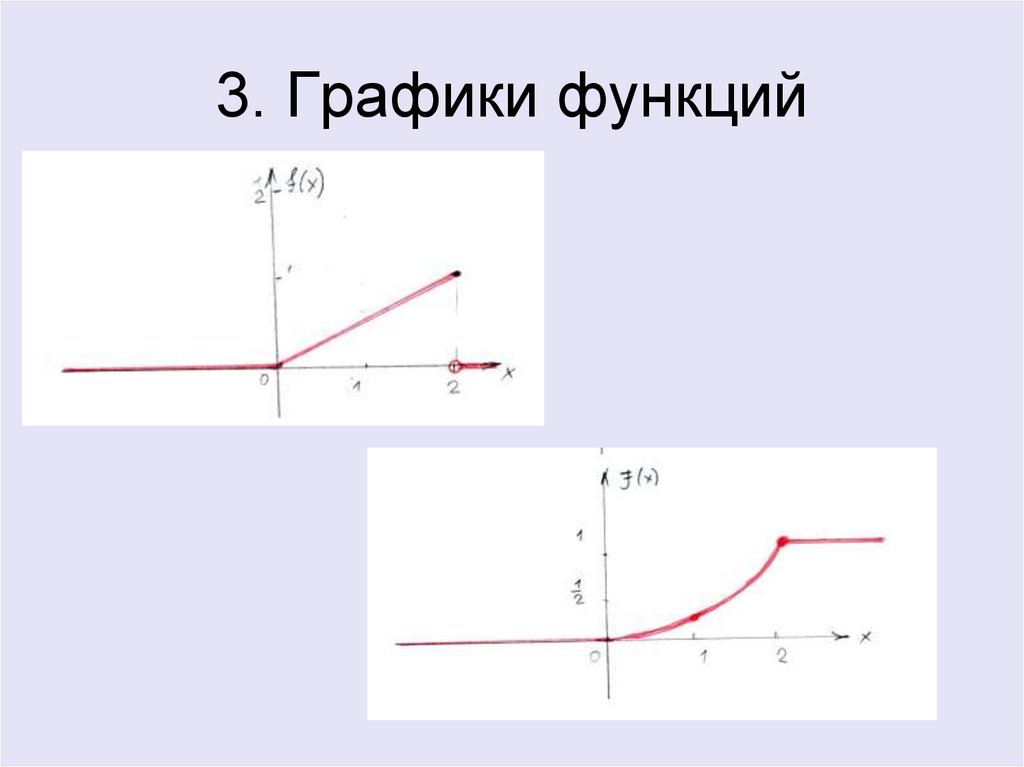
18. 3. Графики функций
19. 4. Вероятность
Согласно свойству F(x)p(a x b) F (b) F (a)
p( 2 x 1) F (1) F ( 2)
1
F (1)
4
F ( 2) 0
1
1
p( 2 x 1) F (1) F ( 2) 0
4
4







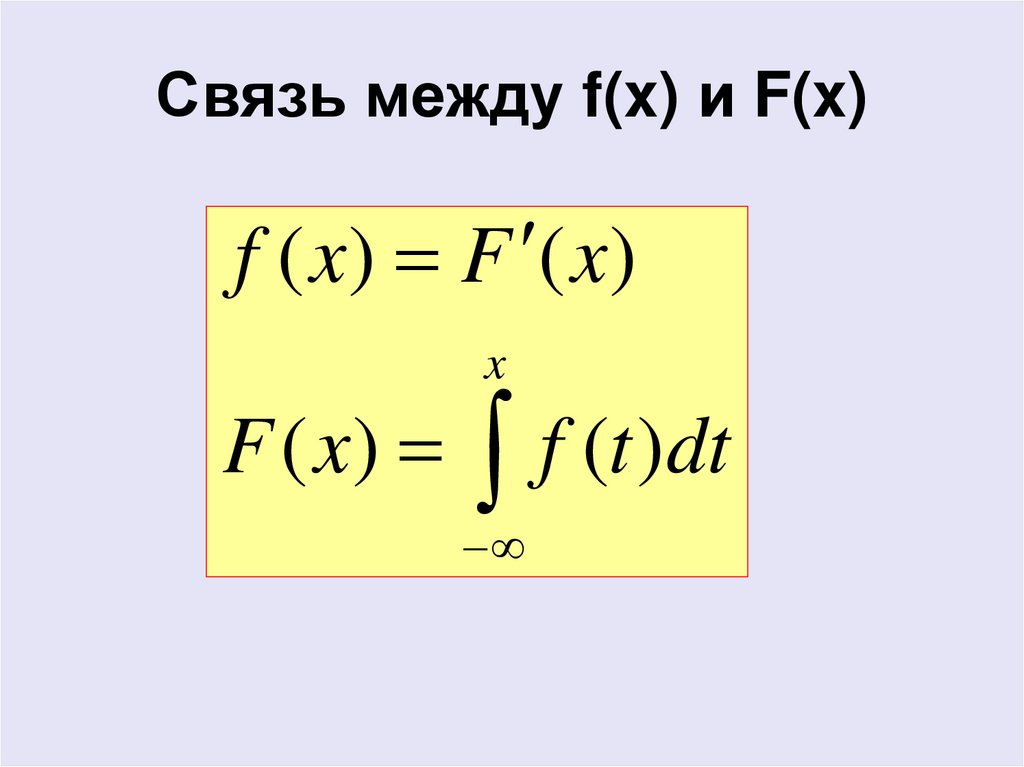








 Математика
Математика