Бинарный случайный опыт (испытание), успех и неудача. Серия независи­мых испытаний Бернулли

1. Бинарный случайный опыт (испытание), успех и неудача. Серия независи­мых испытаний Бернулли.

Бинарный случайный опыт
(испытание), успех и неудача.
Серия независимых испытаний
Бернулли.

2.

В этой главе мы будем изучать испытания
Бернулли. Это одна из наиболее важных
вероятностных моделей, которая используется для
решения многих практических задач. Впервые её
рассмотрел в своих работах швейцарский
математик Якоб Бернулли (1655—1705), один из
представителей многочисленного математического
семейства Бернулли.
Мы уже не раз сталкивались с испытаниями
Бернулли,
сами
того
не
подозревая.
Подбрасывание монеты или кубика, стрельба в
мишень, проверка деталей на соответствие
стандарту и многие другие серии случайных
опытов — всё это примеры таких испытаний.
Разберёмся, что объединяет все эти примеры и
почему для их изучения можно рассматривать одну
и ту же вероятностную модель.

3.

В теории вероятностей испытаниями Бернулли называют серию одинаковых
независимых случайных опытов, каждый из которых может завершиться одним
из двух исходов — успехом или неудачей.
Вероятности успеха и неудачи обозначают буквами p и q. Поскольку в каждом
испытании возможны только эти два исхода, то p + q = 1.
Важным требованием к испытаниям Бернулли является то, что вероятности p и q
остаются постоянными и не изменяются в процессе проведения испытаний.
Второе важное требование — независимость испытаний. Это означает, что
результаты предыдущих испытаний никак не влияют на вероятности появления
успеха и неудачи в последующих испытаниях. Понятно, что с монетой дело обстоит
именно так. Но если речь идёт о стрельбе в мишень на каких-то важных
соревнованиях, то в независимость может вмешаться психологический фактор: не
исключено, что, совершив промах, спортсмен занервничает, и вероятность успеха
в следующем выстреле может уменьшиться. Может быть и наоборот — он
соберётся, и тогда вероятность успеха увеличится. Здесь, как всегда при
построении математической модели, мы сами должны решить: существенна эта
зависимость или ею можно пренебречь.

4. Испытания до первого успеха

Рассмотрим опыт, в котором одинаковые испытания проводятся до наступления
первого успеха. Как только успех случился, испытания прекращаются.
ПРИМЕР 1. Монету бросают до тех пор, пока не выпадет орёл.
ПРИМЕР 2. Стрелок в тире стреляет по мишени до тех пор, пока не собьёт её.
ПРИМЕР 3. Мобильный телефон в условиях слабой связи пытается отправить
СМС. Если попытка неудачная, телефон предпринимает следующую . Так
продолжается до тех пор, пока очередная попытка не окажется удачной, либо
пока не кончится время, отведенное на попытки.
ПРИМЕР 4. Фрагмент файла загружается из Интернета в компьютер. Загрузка
идёт до тех пор, пока не пройдёт без ошибок.
ПРИМЕР 5. Самолёт осматривают перед каждым рейсом и допускают к полёту,
пока не обнаружено отклонение от нормы в работе жизненно важных систем.

5.

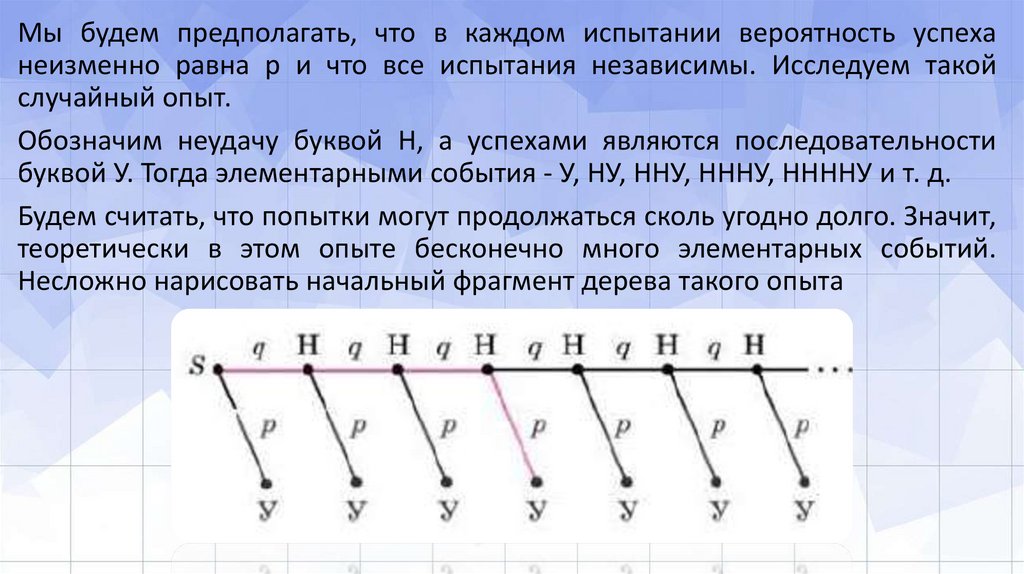
Мы будем предполагать, что в каждом испытании вероятность успеха
неизменно равна р и что все испытания независимы. Исследуем такой
случайный опыт.
Обозначим неудачу буквой Н, а успехами являются последовательности
буквой У. Тогда элементарными события - У, НУ, ННУ, НННУ, ННННУ и т. д.
Будем считать, что попытки могут продолжаться сколь угодно долго. Значит,
теоретически в этом опыте бесконечно много элементарных событий.
Несложно нарисовать начальный фрагмент дерева такого опыта

6.

Элементарные события изображаются цепочками, ведущими из точки S к
конечным вершинам. Например, элементарное событие НННУ (три
неудачи и затем успех) изображается в этом дереве цепочкой SHHHY
(выделена красным цветом).
Пользуясь правилом умножения, несложно найти вероятность каждого
элементарного события:

7.

8. Пример 6

Стрелок стреляет по мишени до первого попадания. Вероятность попадания
при каждом отдельном выстреле равна р = 0,2. Какова вероятность того, что
стрелку потребуется:
а) ровно два выстрела; б) не больше пяти выстрелов?

9. Испытания Бернулли

Рассмотрим элементарные события в последовательности из трёх
испытаний. Каждое испытание оканчивается либо успехом ( У) , либо
неудачей (Н). После трёх испытаний мы можем получить одно из восьми
элементарных событий:
УУУ, УУН, УНУ, НУУ, ННУ, УНН, НУН, ННН.
Отдельные испытания Бернулли независимы , поэтому вероятность
каждого элементарного события можно найти с помощью правила
умножения вероятностей.
Элеме УУУ
нтарно
е
событи
е
УУН
УНУ
НУУ
ННУ
УНН
НУН
ННН