Дифференциальные уравнения и численные методы. Лекция 3

1. Дифференциальные уравнения и численные методы

Лекция 3

2.

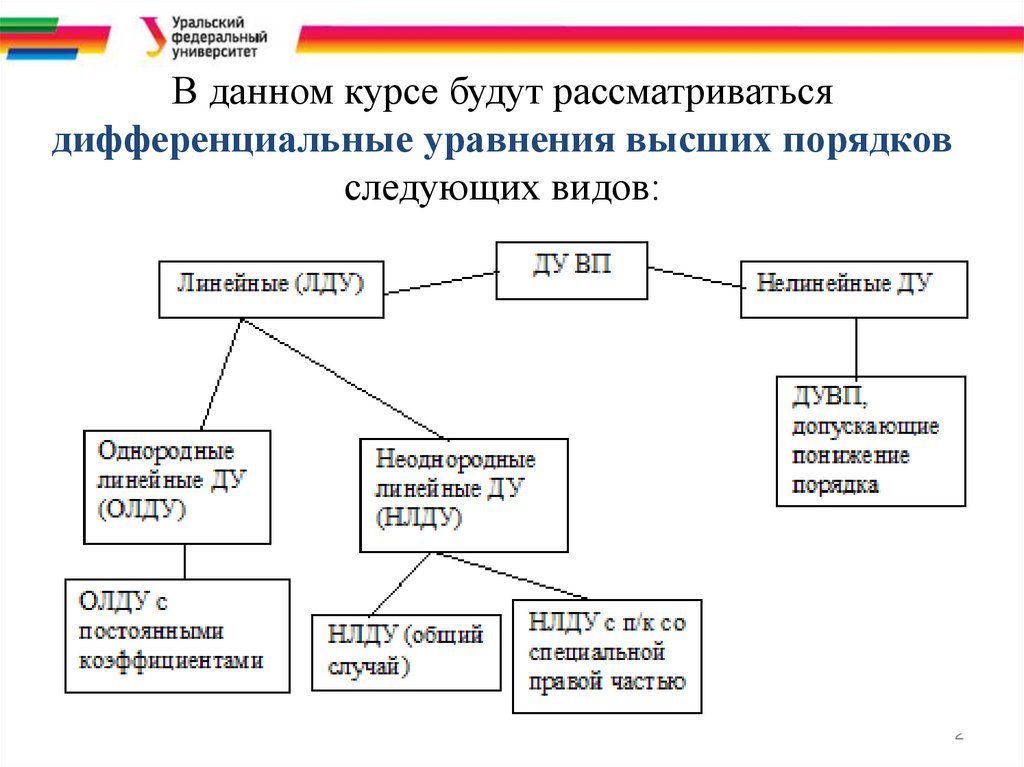
В данном курсе будут рассматриваться
дифференциальные уравнения высших порядков
следующих видов:
2

3.

Задача Коши ДУ ВП:
Пусть дано ДУ y(n)=f( x, y, y', y",…, y(n−1)),
НУ: у(х0)=у0, у'(х0)=у'0,…, у(n−1)(х0)=у0(n−1).
Требуется найти непрерывную и n раз
дифференцируемую функцию y = φ(x), x (a, b):
1) y = φ(x) является решением данного ДУ на (a, b),
т.е.
2) y = φ(x) удовлетворяет заданным, начальным
условиям:
3

4.

Теорема (существования и единственности решения
задачи Коши для ДУ ВП)
Если
1) f( x, y, y', y",…, y(n−1)) непрерывна (по совокупности
(n+1) аргументов) в области D̽ ;
2)
непрерывны (по совокупности
аргументов y, y', y",…, y(n−1)) в D̽ ,
то ! решение з. Коши для ДУ
y(n)=f( x, y, y', y",…, y(n−1)), удовлетворяющее
НУ: у(х0)=у0, у'(х0)=у'0,…, у(n−1)(х0)=у0(n−1),
( x0, y0, y'0,…, y0 (n−1) D̽ ).
Область D̽ называется областью единственности ДУ. 4

5.

Общим решением ДУ ВП называется
n-параметрическая функция φ(x, С1,…, Сn) = φ(x, ), где
С1,…, Сn такие что:
1)
– решение ДУ на (a, b);
2) н/у из области единственности
φ(x, 0) удовлетворяет заданным начальным условиям.
Соотношение вида F(x, y, С1,…, Сn)=0, неявно
определяющее общее решение ДУ на (a, b) называется
общим интегралом ДУ.
Частное решение ДУ получается из его общего
решения при фиксированном значении .
5

6.

Дифференциальные уравнения высших
порядков, допускающие понижение порядка
Одним из методов решения ДУ ВП является метод
понижения порядка.
Суть метода состоит в том, что с помощью замены
переменной данное дифференциальное уравнение
n−го порядка сводится к уравнению (n−1) го порядка.
Рассмотрим основные виды уравнений, допускающих
понижение порядка.
6

7.

1. Уравнение вида y(n)=f(x)
это неполное ДУ (в нем отсутствуют y, y', y",…, y(n−1)).
Способ понижения порядка:
n кратное интегрирование
и т.д.
7

8.

Пример. Решить уравнение y'''=sinx.
8

9.

2. Уравнение вида y(n)=f( x, y(k), y(k+1),…, y(n−1))
это неполное ДУ (в нем явно не содержится искомая
функция у(x) и ее (k−1) первых производных).
Способ понижения порядка:
замена y(k)=р(х) понижает порядок уравнения на k
единиц, при этом y(k+1)=р', y(n−1)= р(n−1−k), y(n)= р(n−k).
9

10.

Пример. Решить уравнение y'''=(y'')2.
10

11.

3. Уравнение вида y(n) = f( y, y', y",…, y(n−1))
это неполное ДУ (в нем явно не содержится аргумент
x искомой функции у(x)).
Способ понижения порядка:
замена y'=р(y) понижает порядок уравнения на
единицу, при этом y"=р'р, y'''= р" р2 +(р')2 р ...
11

12.

4. Уравнение вида y(n) = f( х, y, y', y",…, y(n−1)),
где f( х, y, y', y",…, y(n−1)) − однородная функция
относительно y, y', y",…, y(n−1)
(оно может быть полным и неполным).
Способ понижения порядка:
замена y'/ y =р(х) понижает порядок уравнения на
единицу, при этом y"=(р'+р2)y, y'''= (р"+3р'р+р3) y ...
12

13.

5. Уравнение в точных производных
(оно может быть полным и неполным).
Такое уравнение можно преобразовать к виду
(*)'=(**)',
где правая и левая части уравнения есть точные производные
некоторых функций.
Способ понижения порядка:
интегрирование правой и левой части уравнения по аргументу
понижает порядок уравнения на единицу.
13

14.

Пример. Решить задачу Коши yy''− (y')2 =y2, y(0)=1, y'(0)=0.
14

15.

yy''− (y')2 =y2, y(0)=1, y'(0)=0.
15

16.

yy''− (y')2 =y2, y(0)=1, y'(0)=0.
Решить другим способом- ДЗ
16

17.

17