Похожие презентации:
Фермы. Лекция
1. Лекция 5 ФЕРМЫ
2.
3.
4.
5.
6.
7.
8.
9.
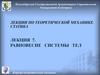
Ферма – это геометрически неизменяемая система,состоящая из прямолинейных стержней,
соединённых шарнирами (цилиндрическими
в плоской системе, шаровыми – в пространственной)
по концам, нагруженная сосредоточенными силами
в узлах.
Происхождение фермы как конструктивной формы
а
а
с
т
я
и
е
ж
е
н
Сжат.
Сжат.
Р
т
и
Сжат.
ж
Сжат.
С
Сжат.
s
е
10.
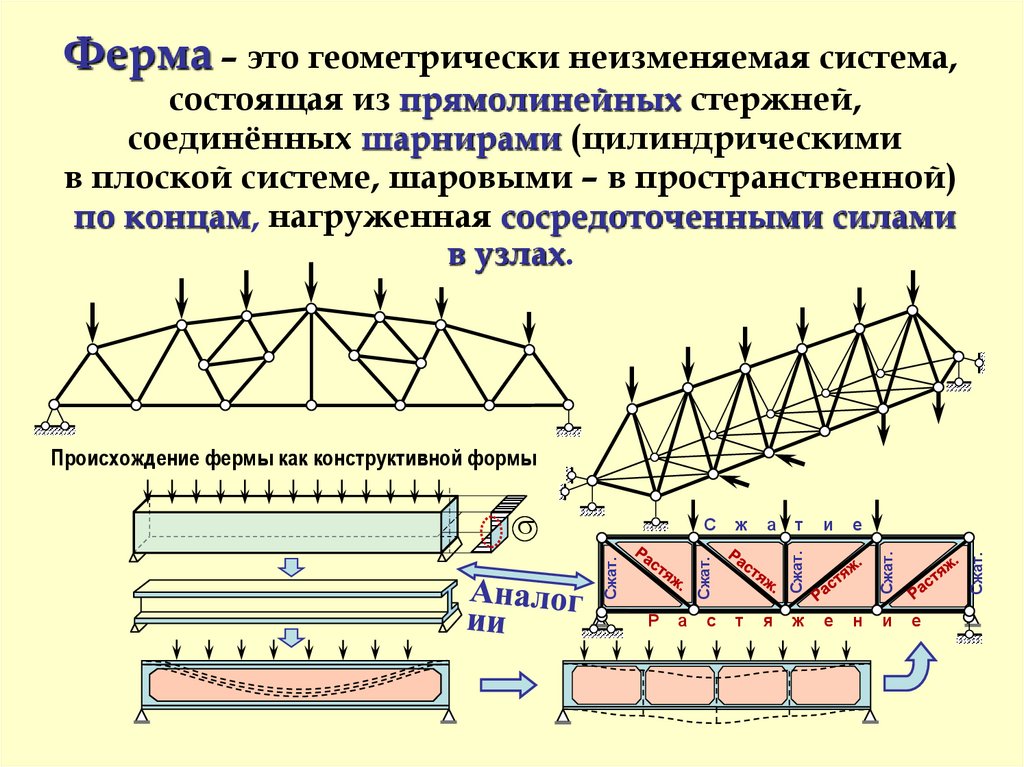
Панельверхнего пояса
d – длина панели
В е р х н и й
п о я с
Пояса фермы –
совокупность стержней,
образующих её внешний
контур
Раскосы –
Раскосы
наклонные
+
стержни между
стойки
поясами
h – высота
фермы
решётка
фермы
Стойки –
Н и ж н и й п о я с
вертикальные
l – длина пролёта
стержни между
поясами
пролёт фермы
Классификация ферм
По расположению элементов в пространстве плоские
пространственные
По очертанию поясов
По способу опирания
По назначению
- безраспорные (балочные)
однопролётные
треугольная
треугольная
раскосная
треугольная
с дополнительными стойками
- стропильные
- мостовые
- крановые
- башенные
полигонального очертания
полураскосная
трапецеидальная
серповидная
двухи многораскосные
шпренгельные
сложные
решётки
с параллельными поясами
простые
решётки
По типу решётки
консольные
многопролётные
- распорные
11.
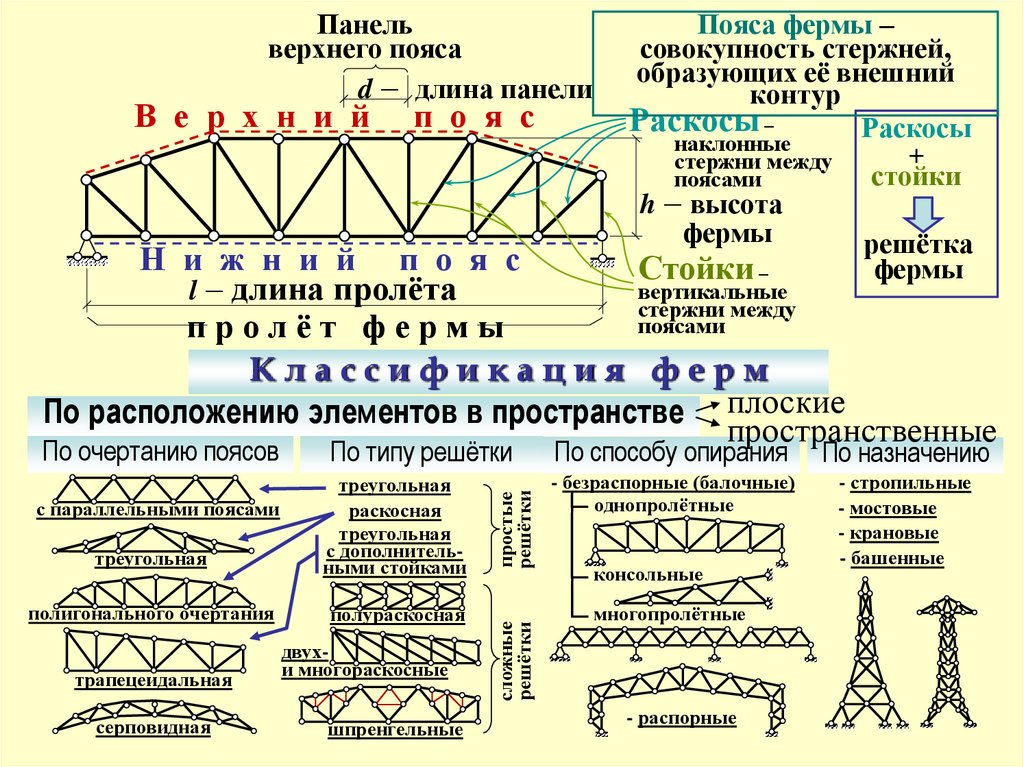
При проектировании и эксплуатации фермысоблюдаются следующие условия:
1. все стержни прямолинейны;
2. вес стержней пренебрежимо мал по
сравнению с эксплуатационной нагрузкой;
3. нагрузка прикладывается только к узлам
фермы.
12.
Присоблюдении
указанных
условий
усилиями, возникающими
при
изгибе
стержней, можно пренебречь по сравнению с
усилиями, возникающими при растяжении –
сжатии.
В реальной ферме крепления стержней в
узлах жёсткие. В расчётной схеме крепления
стержней считают шарнирными, что связано с
реализацией
принятого
упрощающего
предположения о возможности пренебречь
усилиями, возникающими при изгибе.
13.
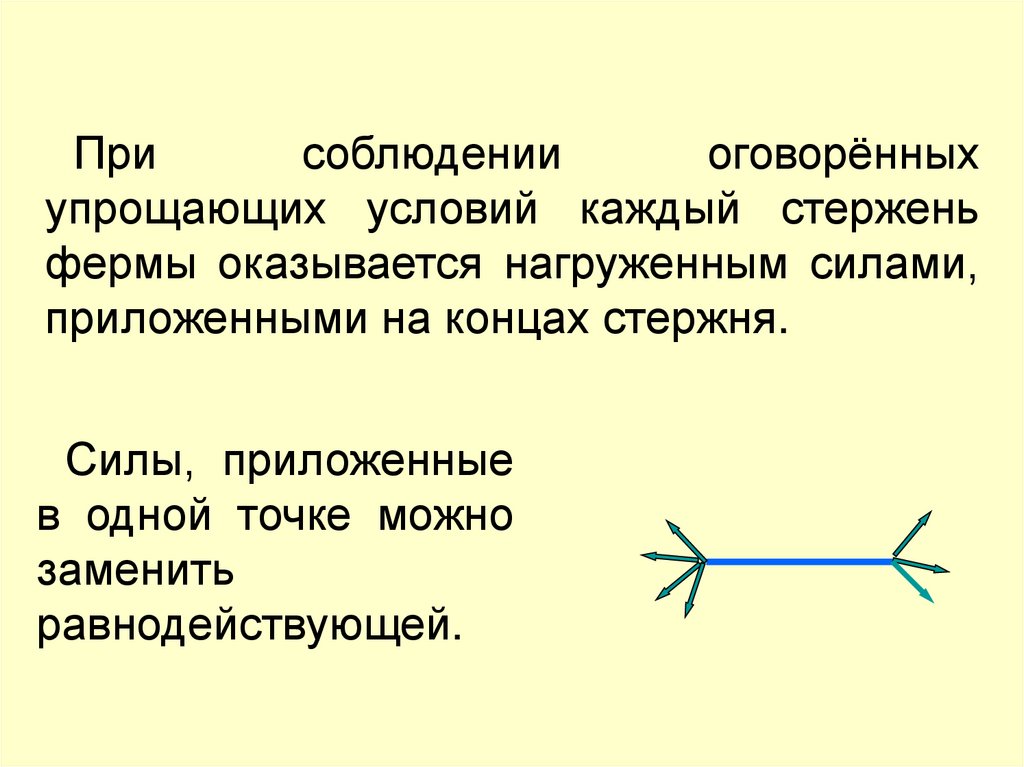
Присоблюдении
оговорённых
упрощающих условий каждый стержень
фермы оказывается нагруженным силами,
приложенными на концах стержня.
Силы, приложенные
в одной точке можно
заменить
равнодействующей.
14.
Передача нагрузки на фермуосуществляется через узлы, в
стержнях фермы возникают только
продольные внутренние усилия,
постоянные по длине стержня.
15.
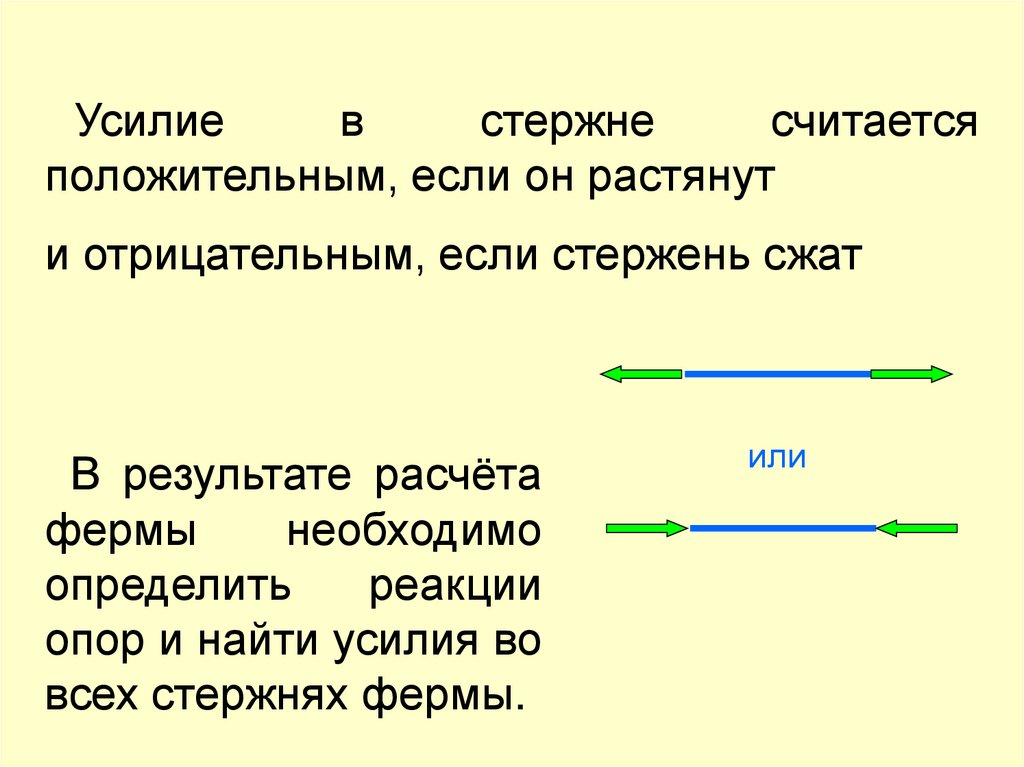
Усилиев
стержне
считается
положительным, если он растянут
и отрицательным, если стержень сжат
В результате расчёта
фермы
необходимо
определить
реакции
опор и найти усилия во
всех стержнях фермы.
или
16.
Количественный кинематическийанализ плоских ферм сводится к
выполнению условия
W=2Y – (С+С0) ≤ 0.
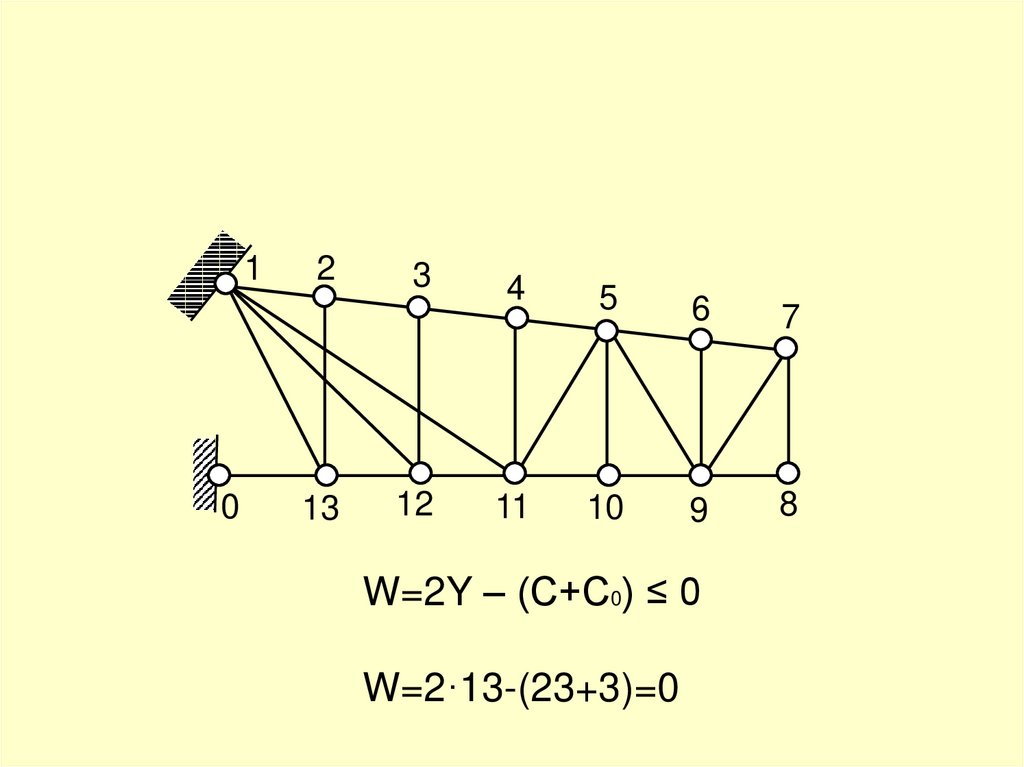
Здесь Y – количество узлов,
С – количество стержней системы,
С0 – количество опорных связей.
17.
Если W=0, то ферма являетсястатически определимой системой.
Условие W=0 является необходимым, но
не достаточным условием того, что ферма
является ГНС. Необходимо провести
структурный анализ
18.
Кинематическийанализ ферм
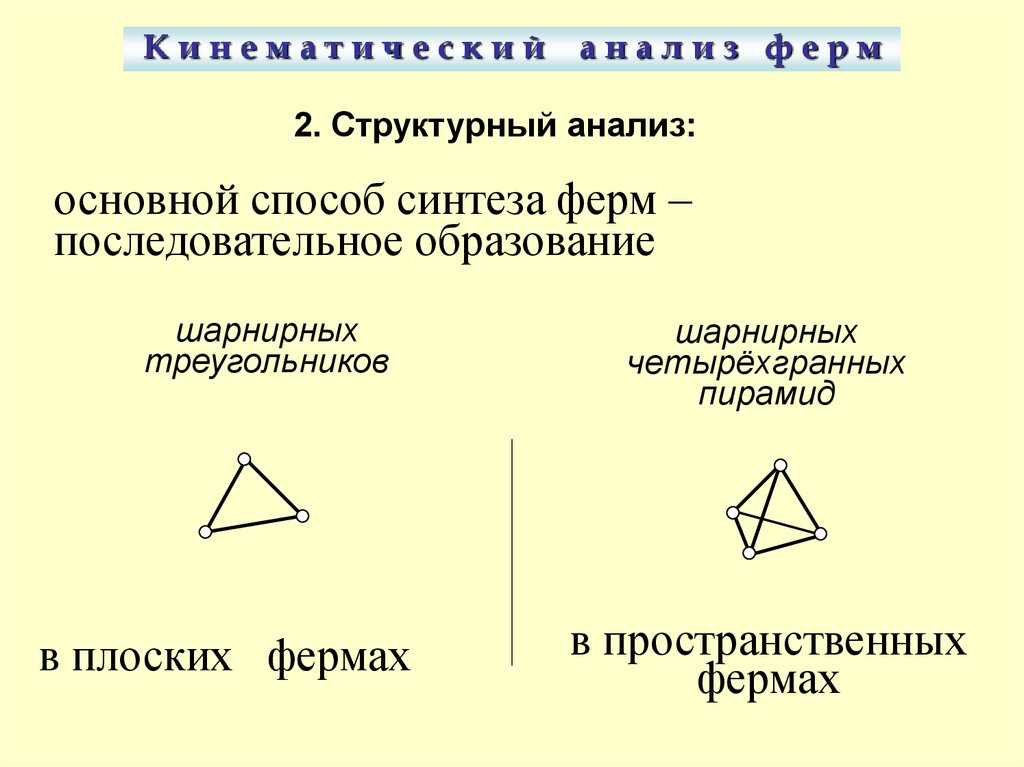
2. Структурный анализ:
основной способ синтеза ферм –
последовательное образование
шарнирных
треугольников
в плоских фермах
шарнирных
четырёхгранных
пирамид
в пространственных
фермах
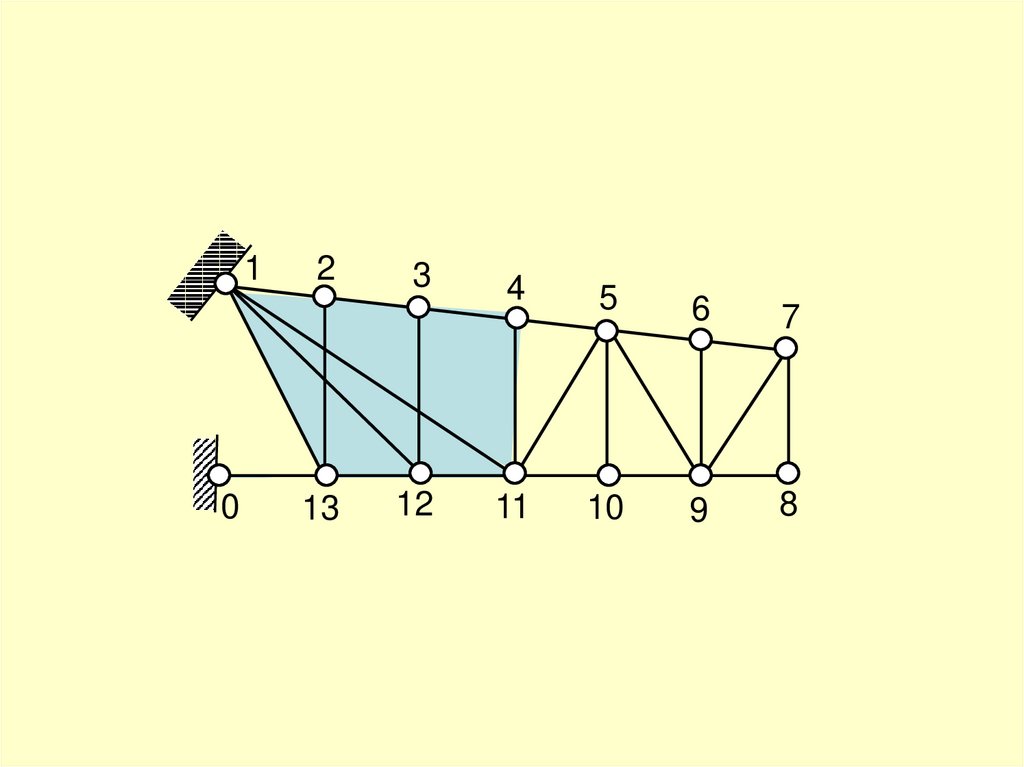
19.
10
2
13
3
12
4
5
6
7
11
10
9
8
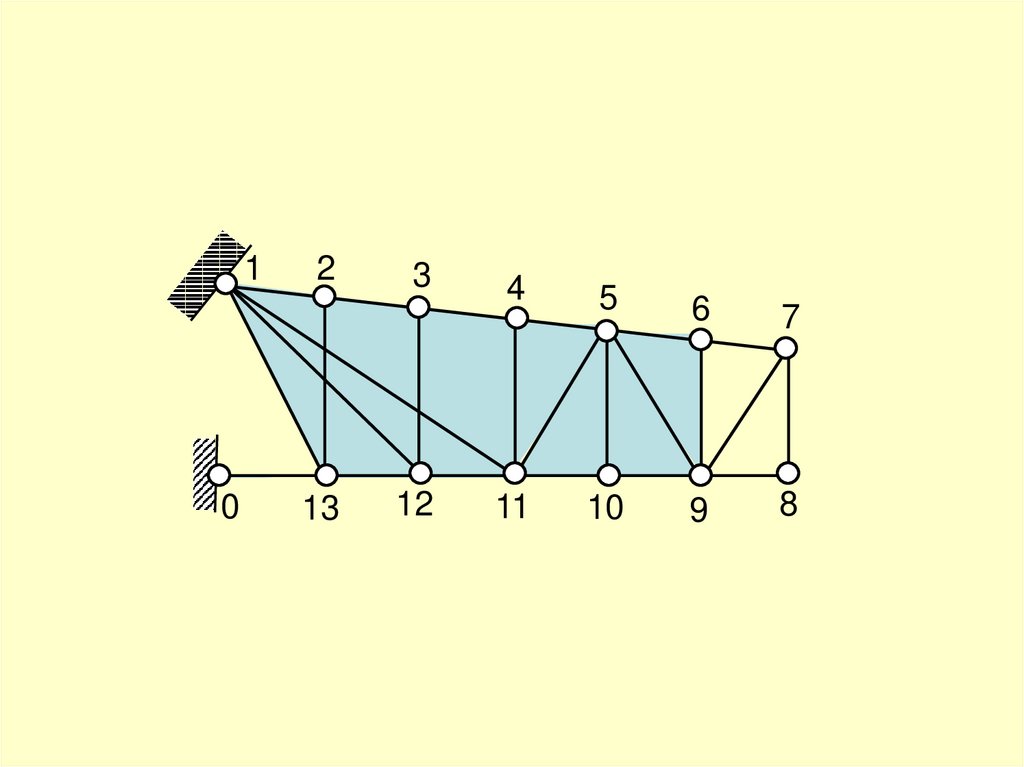
W=2Y – (С+С0) ≤ 0
W=2·13-(23+3)=0
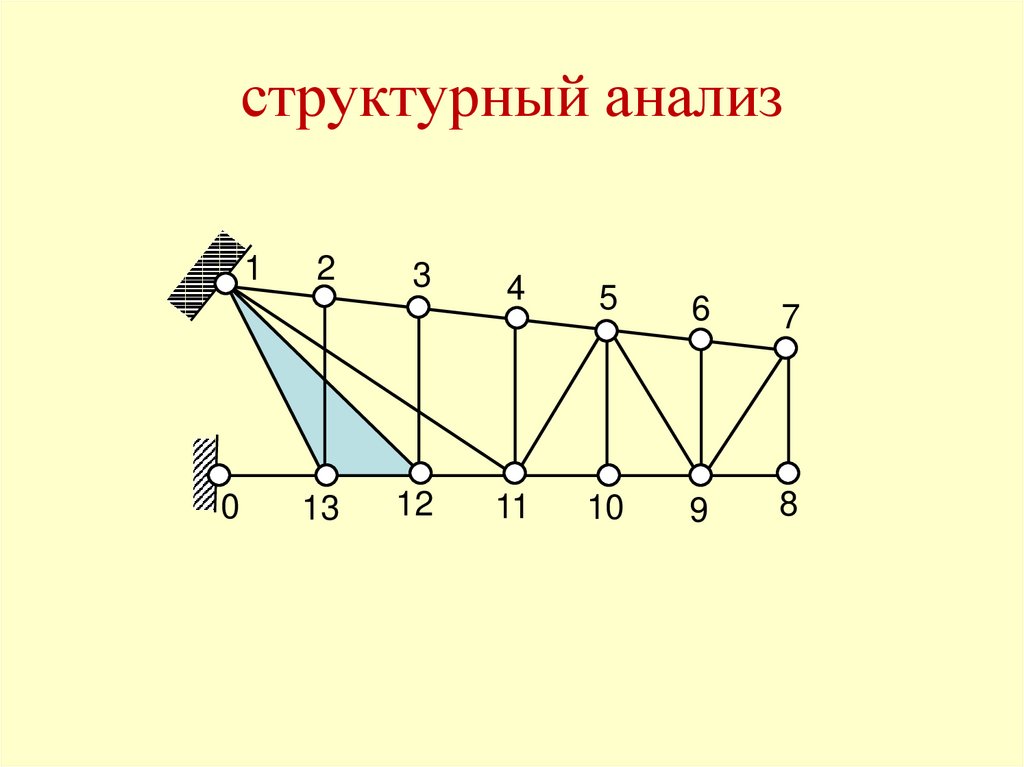
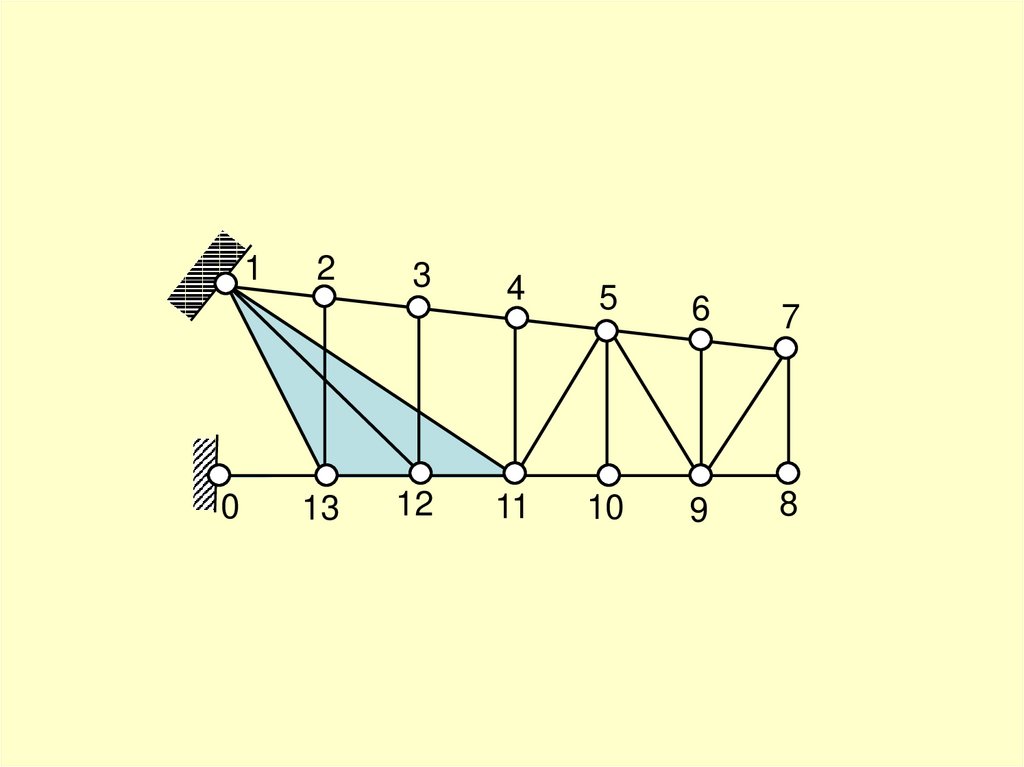
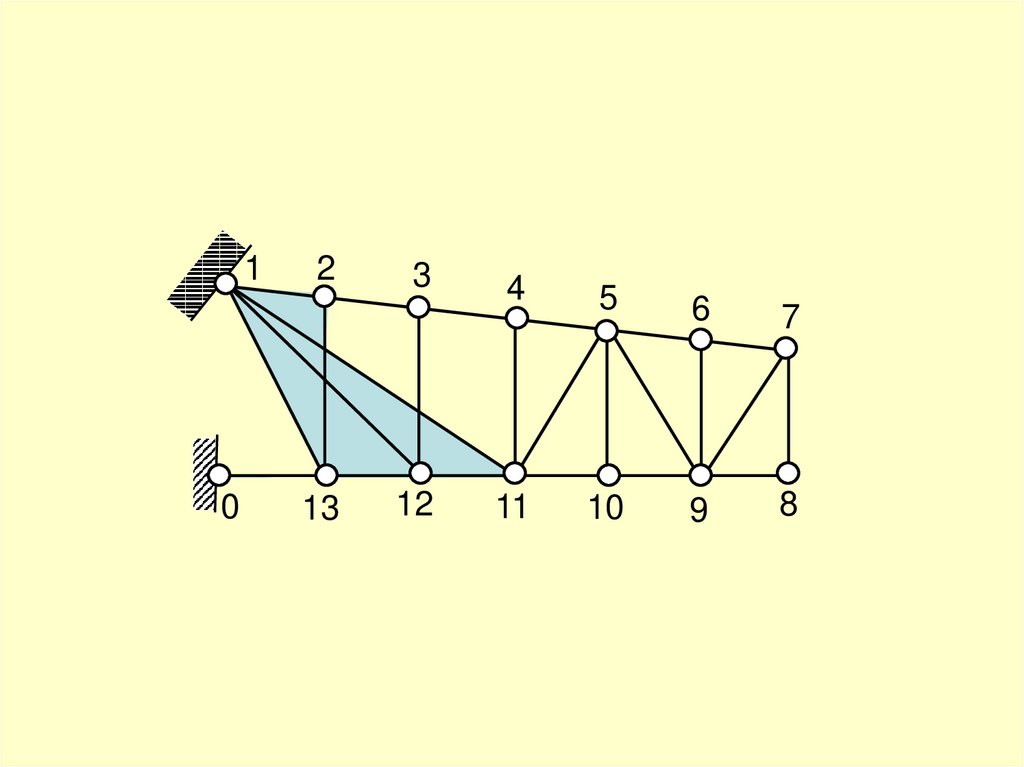
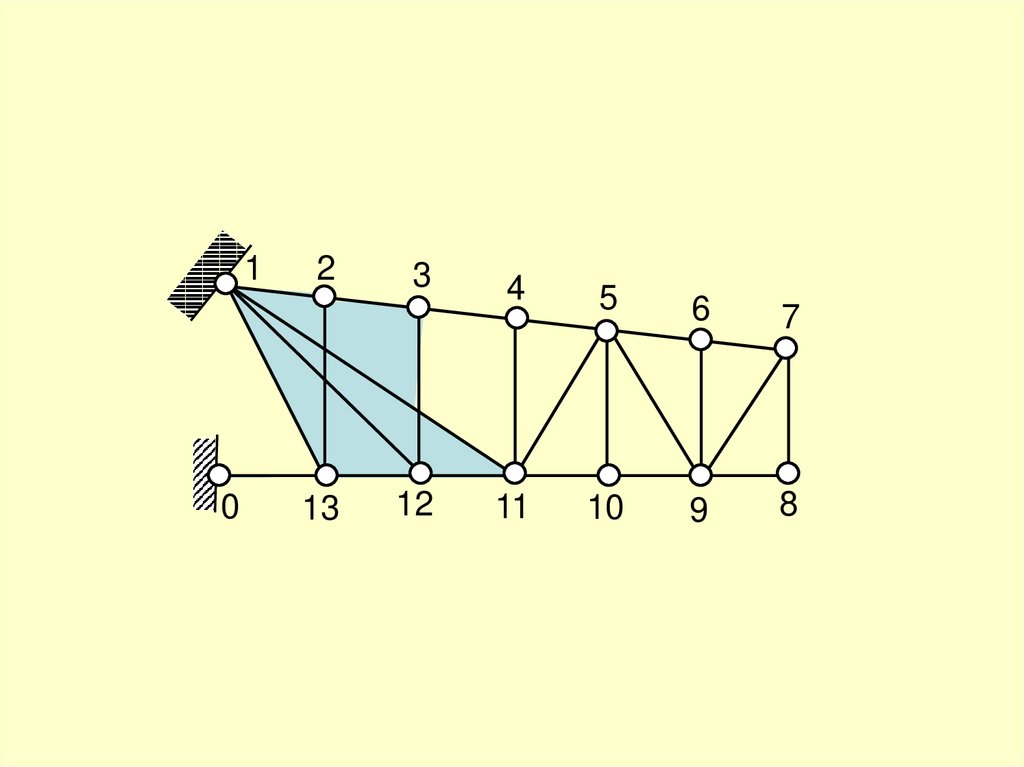
20.
структурный анализ1
0
2
13
3
12
4
5
6
7
11
10
9
8
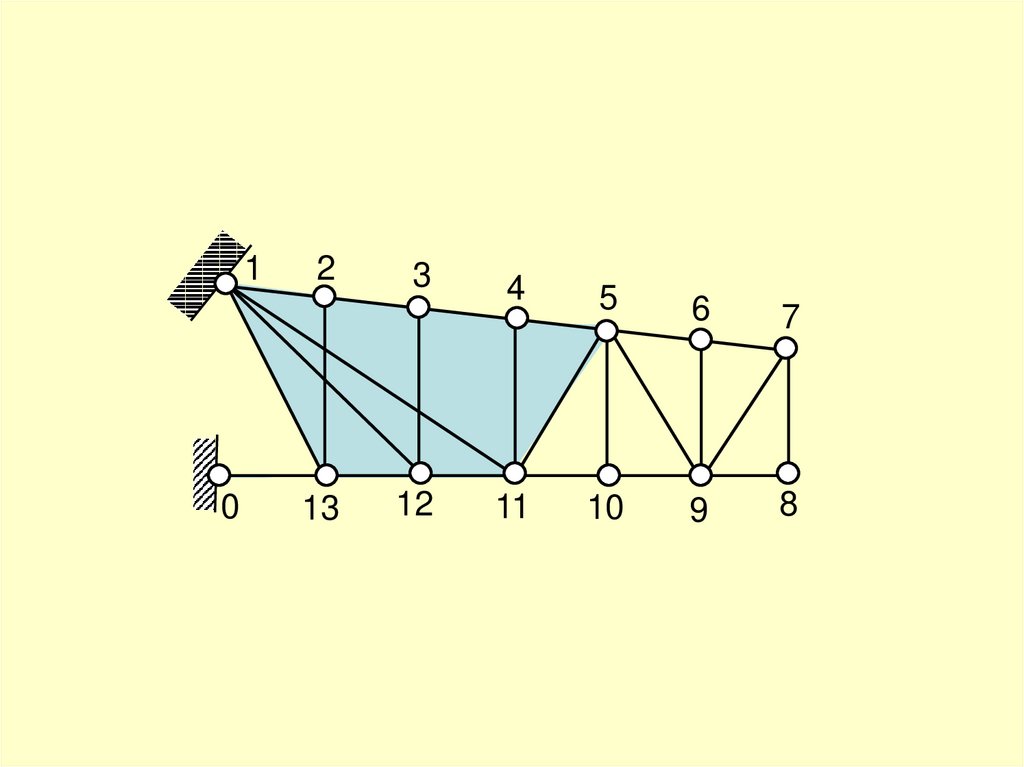
21.
10
2
13
3
12
4
5
6
7
11
10
9
8
22.
10
2
13
3
12
4
5
6
7
11
10
9
8
23.
10
2
13
3
12
4
5
6
7
11
10
9
8
24.
10
2
13
3
12
4
5
6
7
11
10
9
8
25.
10
2
13
3
12
4
5
6
7
11
10
9
8
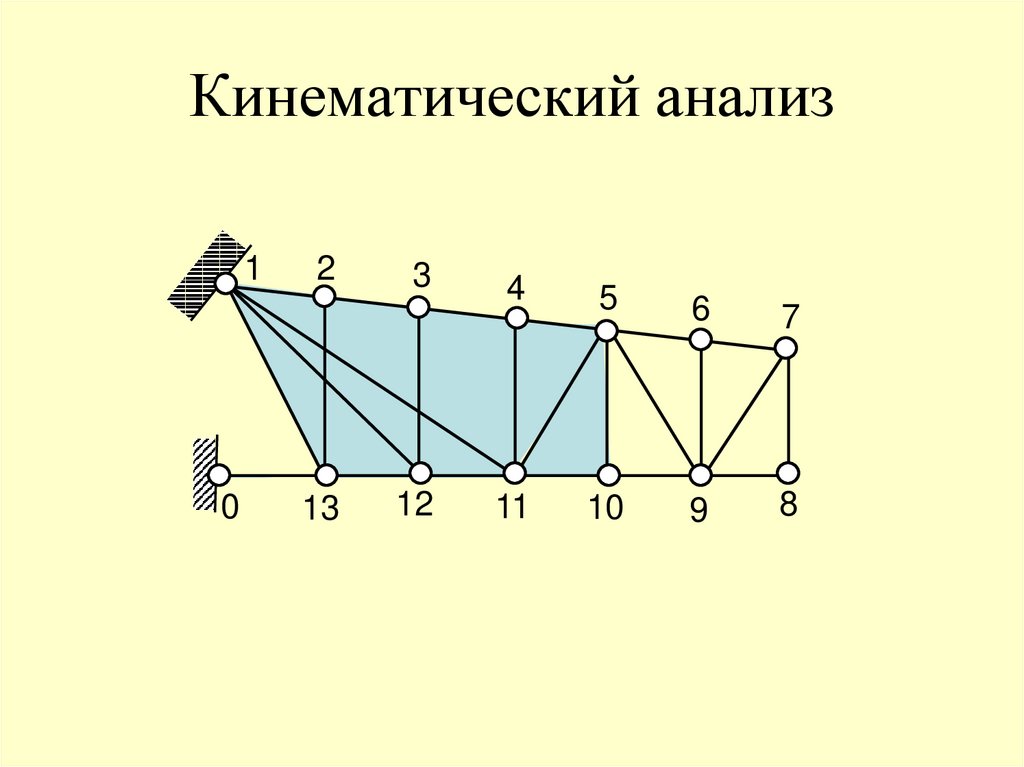
26. Кинематический анализ
10
2
13
3
12
4
5
6
7
11
10
9
8
27.
10
2
13
3
12
4
5
6
7
11
10
9
8
28.
10
2
13
3
12
4
5
6
7
11
10
9
8
29.
10
2
13
3
12
4
5
6
7
11
10
9
8
30.
10
2
13
3
12
4
5
6
7
11
10
9
8
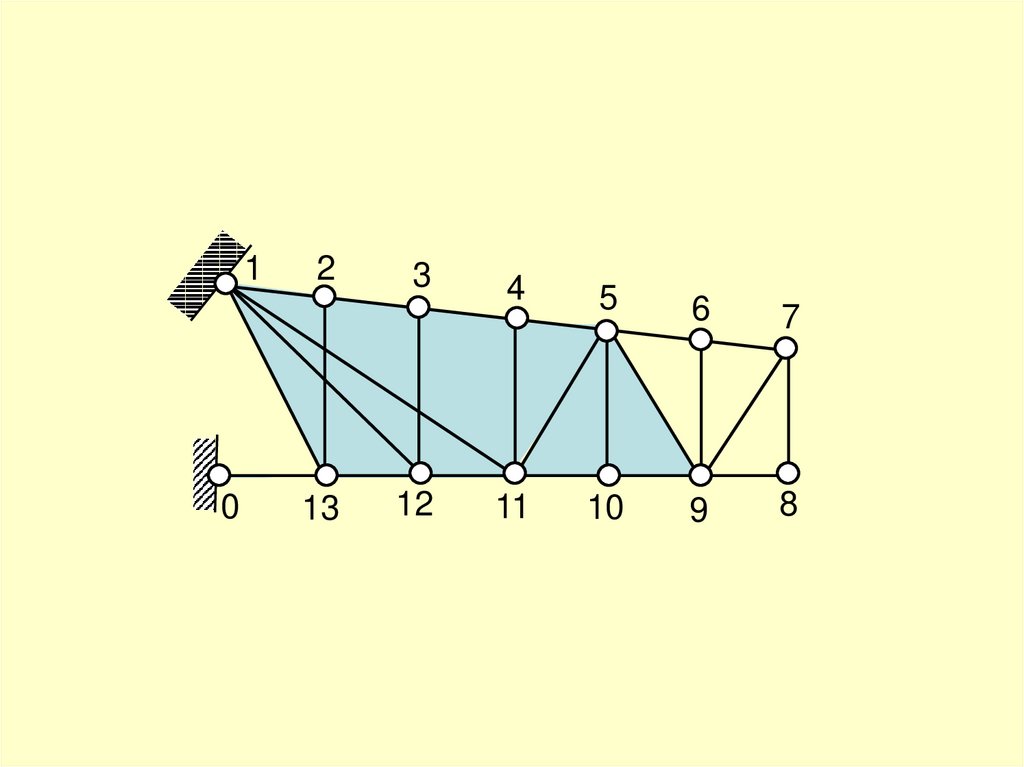
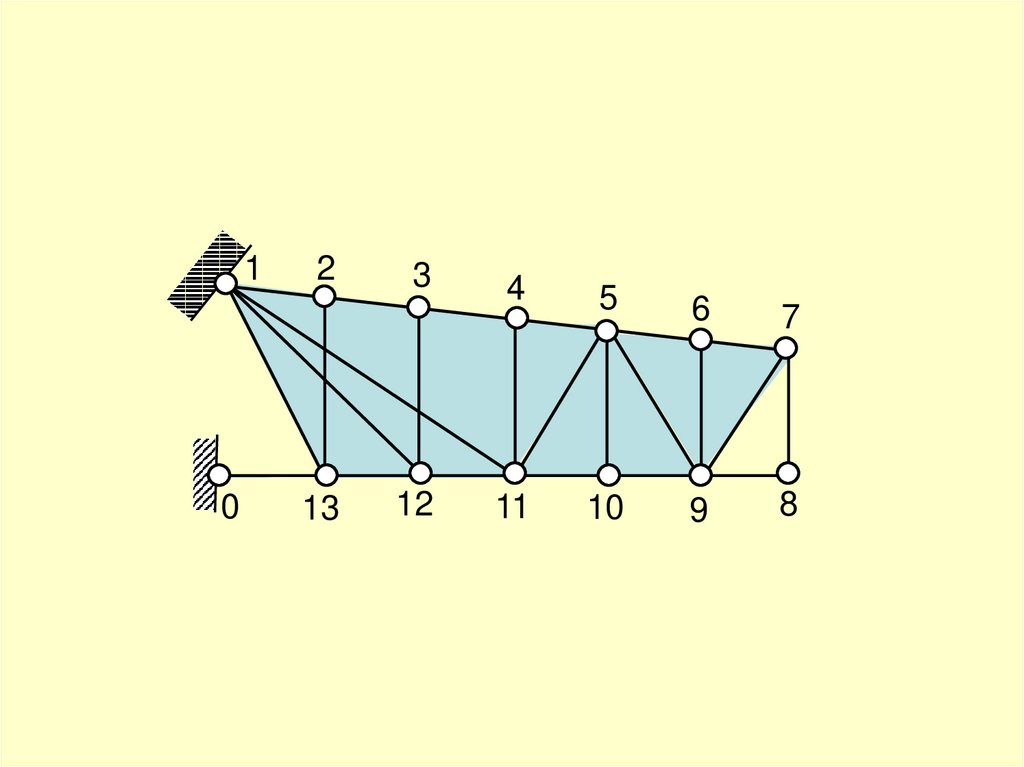
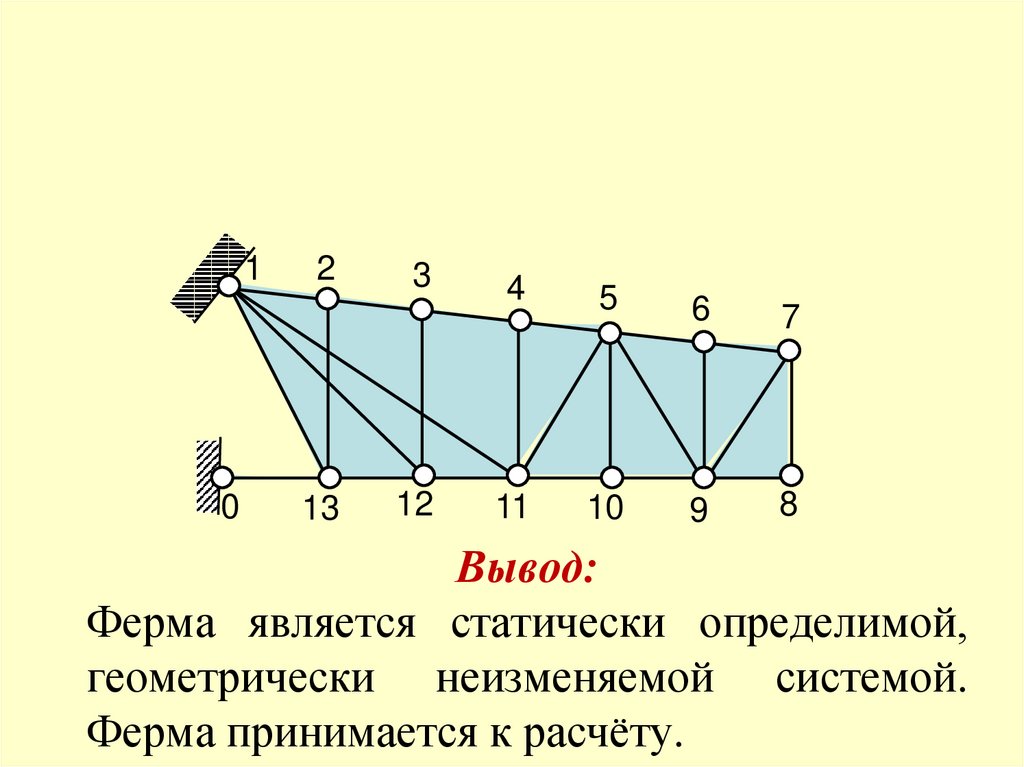
Вывод:
Ферма является статически определимой,
геометрически неизменяемой системой.
Ферма принимается к расчёту.
31.
Определение опорных реакций32.
Методы определения усилий(продольных сил) в стержнях ферм
- сечений;
- вырезания узлов;
- моментной точки (Риттера);
- проекций;
33.
Метод сечения:Если при действии внешних сил тело
находится в состоянии равновесия, то
любая отсеченная часть тела вместе с
приходящимися на нее внешними
и внутренними усилиями также будет
находится в равновесии, следовательно, к
ней применимы уравнения равновесия.
34.
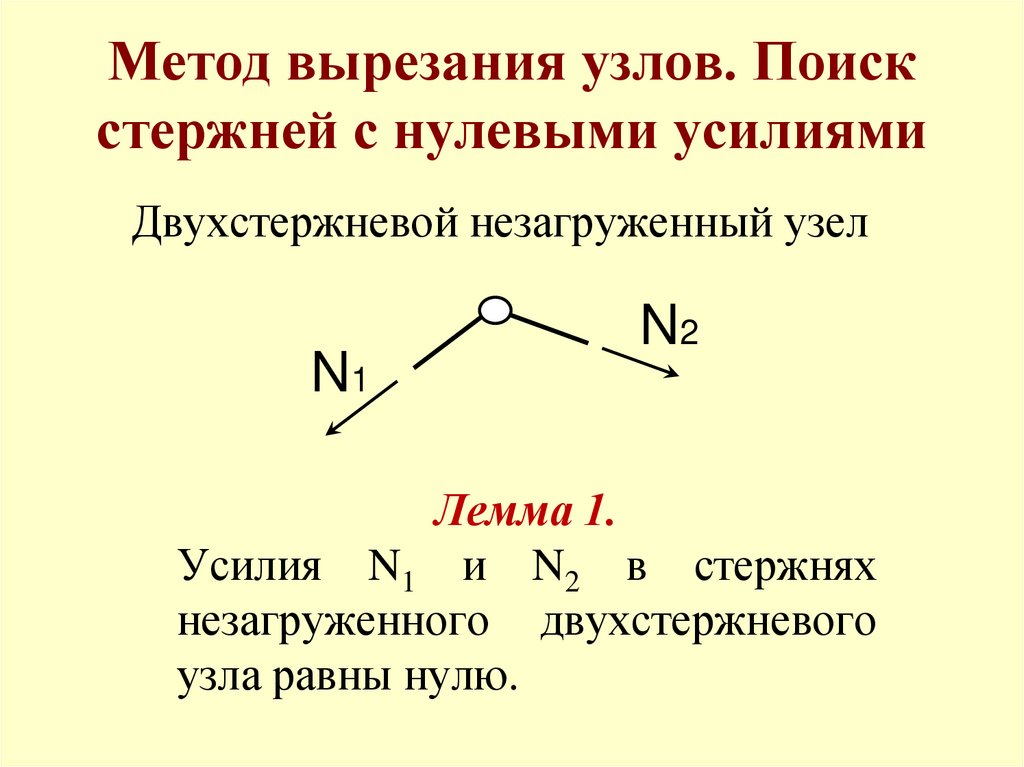
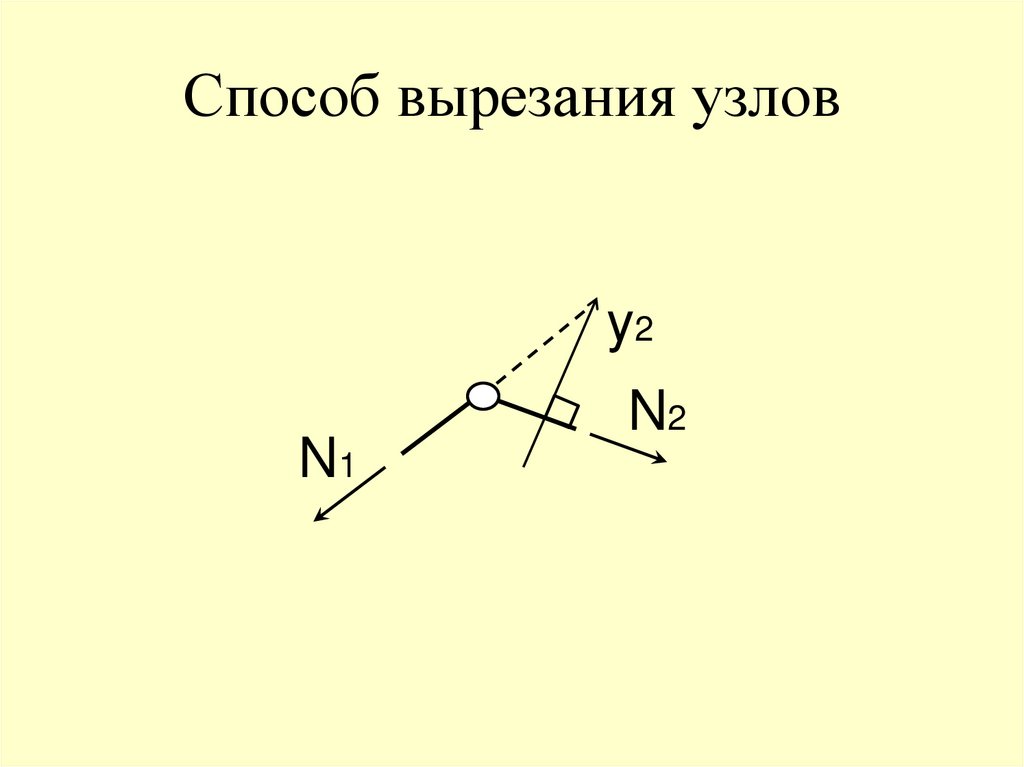
Метод вырезания узлов. Поискстержней с нулевыми усилиями
Двухстержневой незагруженный узел
N1
N2
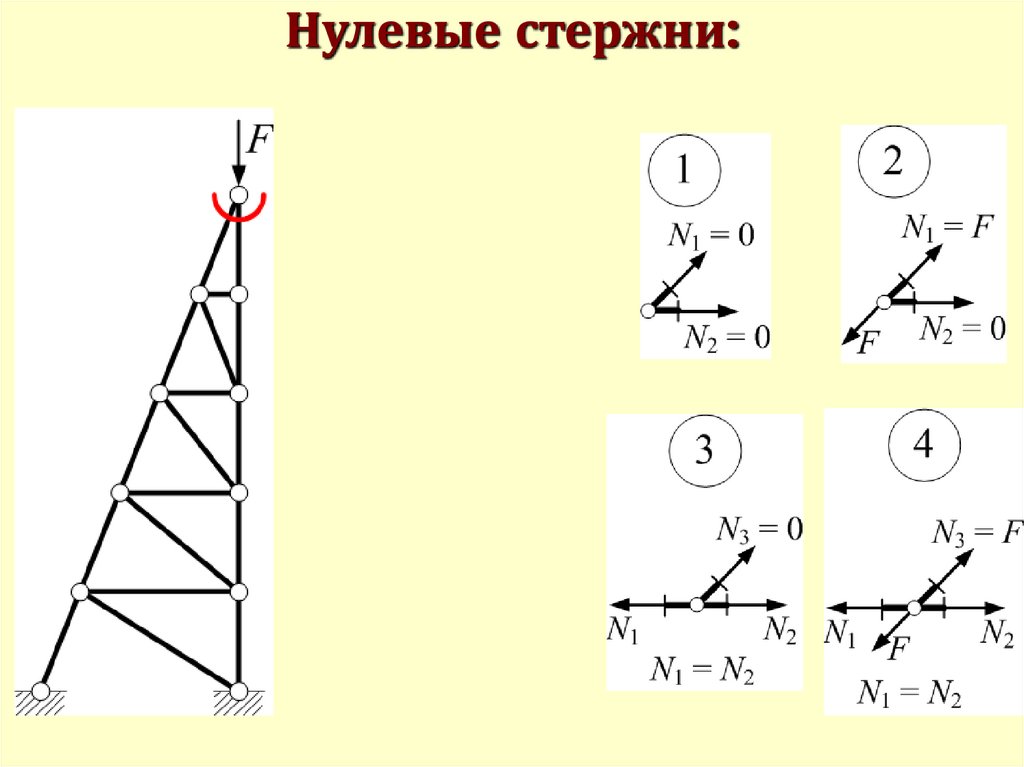
Лемма 1.
Усилия N1 и N2 в стержнях
незагруженного двухстержневого
узла равны нулю.
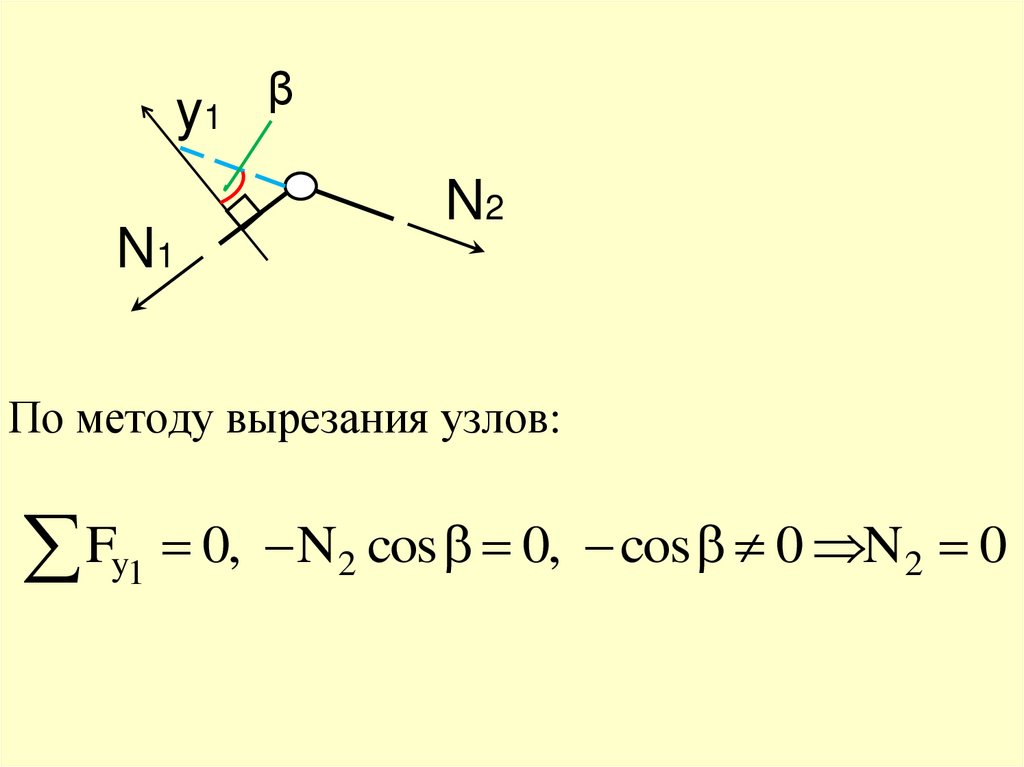
35.
y1N1
β
N2
По методу вырезания узлов:
Fy1 0, N2 cos 0, cos 0 N2 0
36.
N1y2
N2
Fy2 0, N1 cos 0, cos 0 N1 0
37.
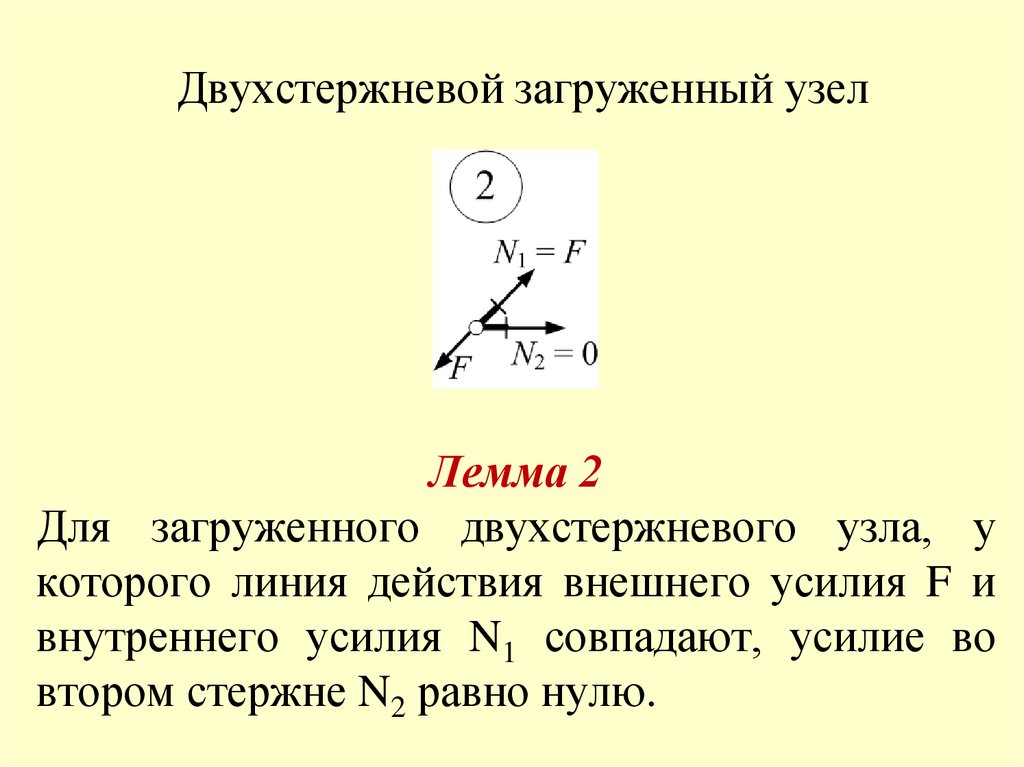
Двухстержневой загруженный узелЛемма 2
Для загруженного двухстержневого узла, у
которого линия действия внешнего усилия F и
внутреннего усилия N1 совпадают, усилие во
втором стержне N2 равно нулю.
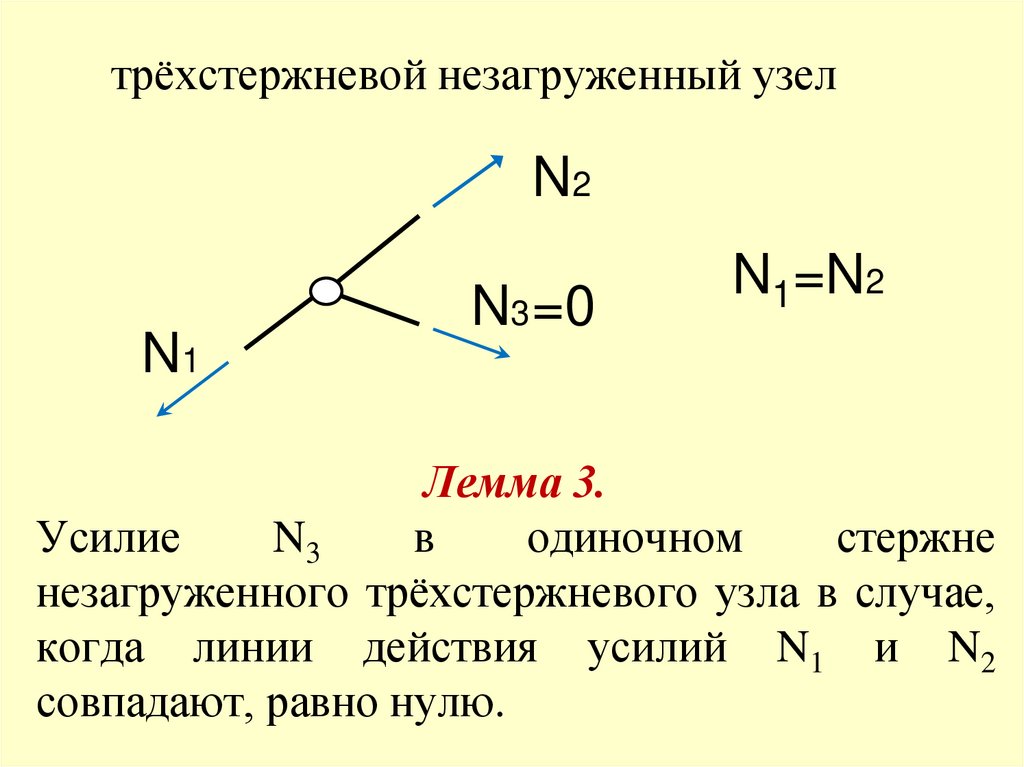
38.
трёхстержневой незагруженный узелN2
N1
N3 =0
N1=N2
Лемма 3.
Усилие
N3
в
одиночном
стержне
незагруженного трёхстержневого узла в случае,
когда линии действия усилий N1 и N2
совпадают, равно нулю.
39.
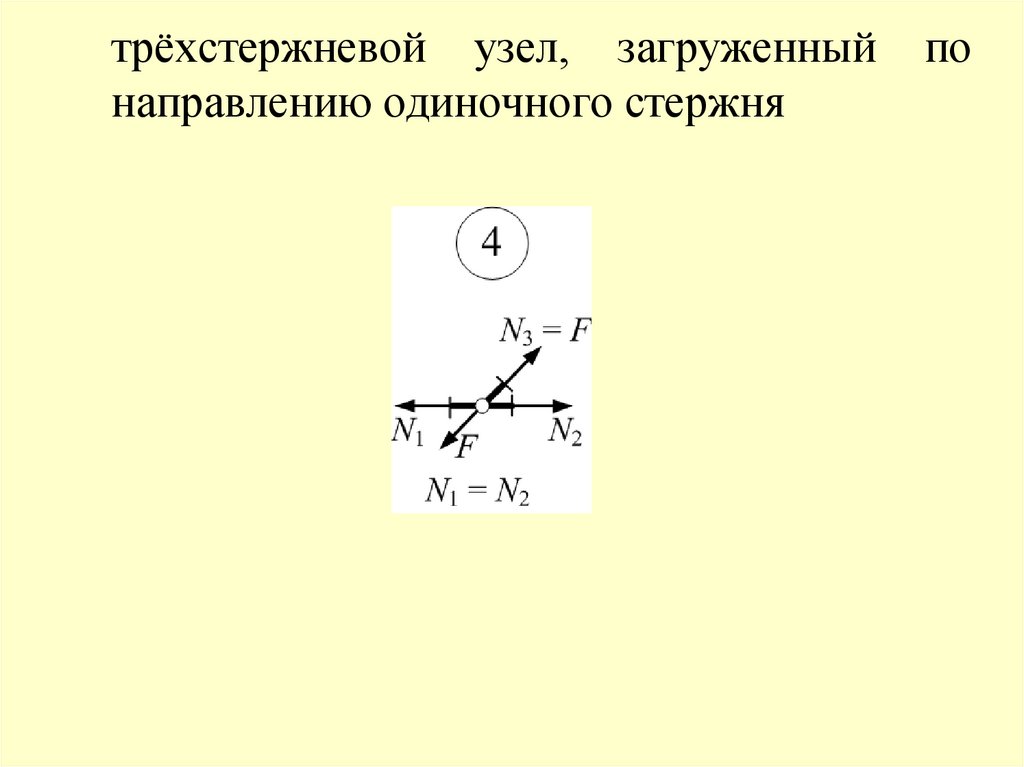
трёхстержневой узел, загруженныйнаправлению одиночного стержня
по
40.
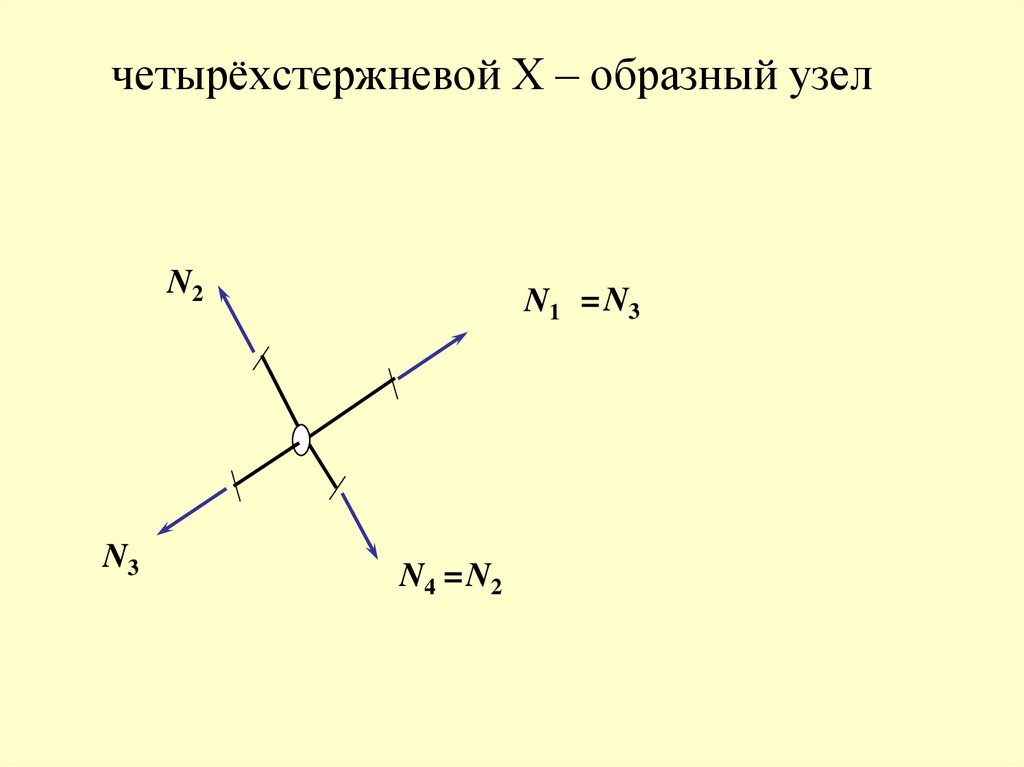
четырёхстержневой Х – образный узелN2
N3
N1 = N3
N4 = N2
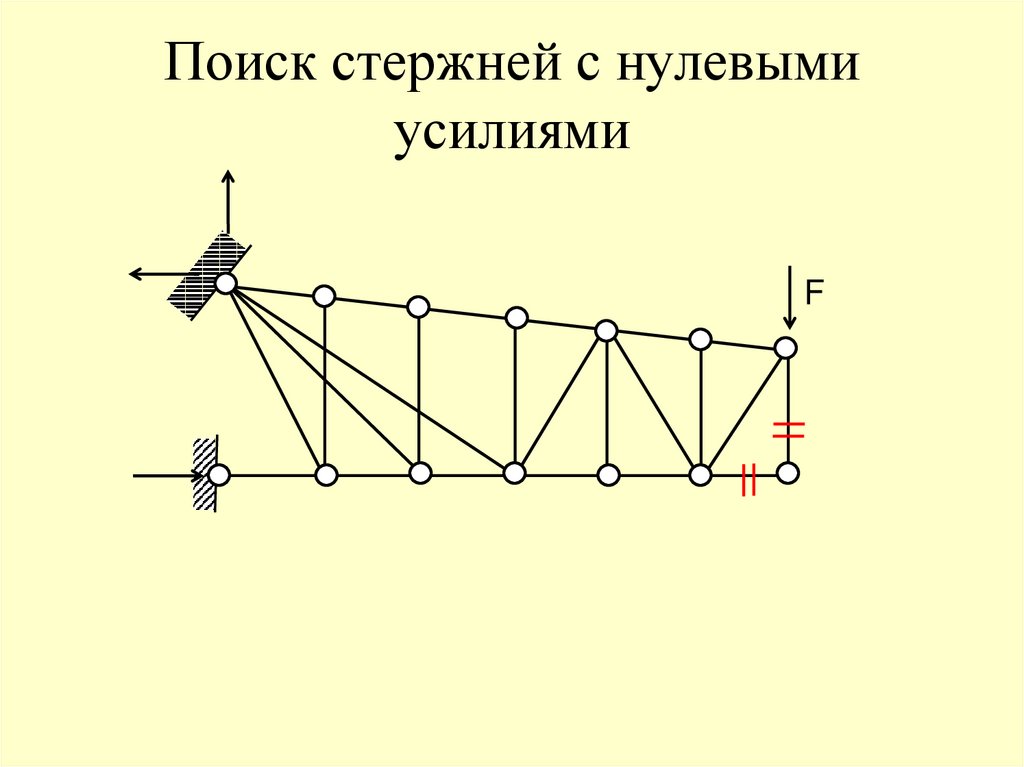
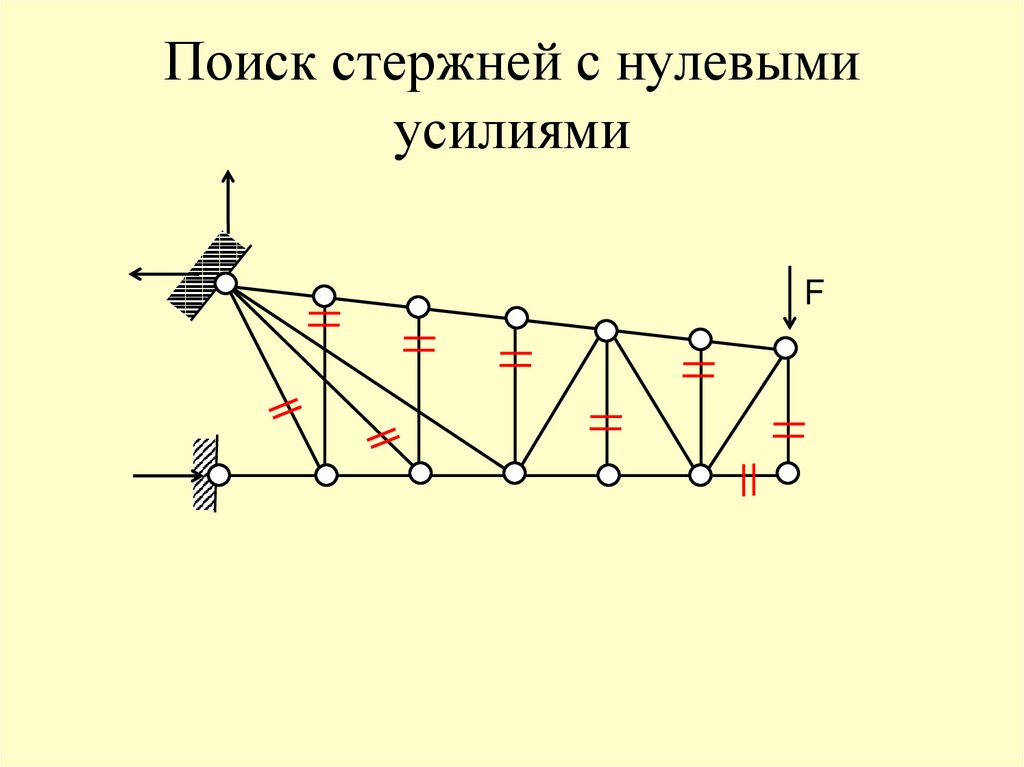
41. Поиск стержней с нулевыми усилиями
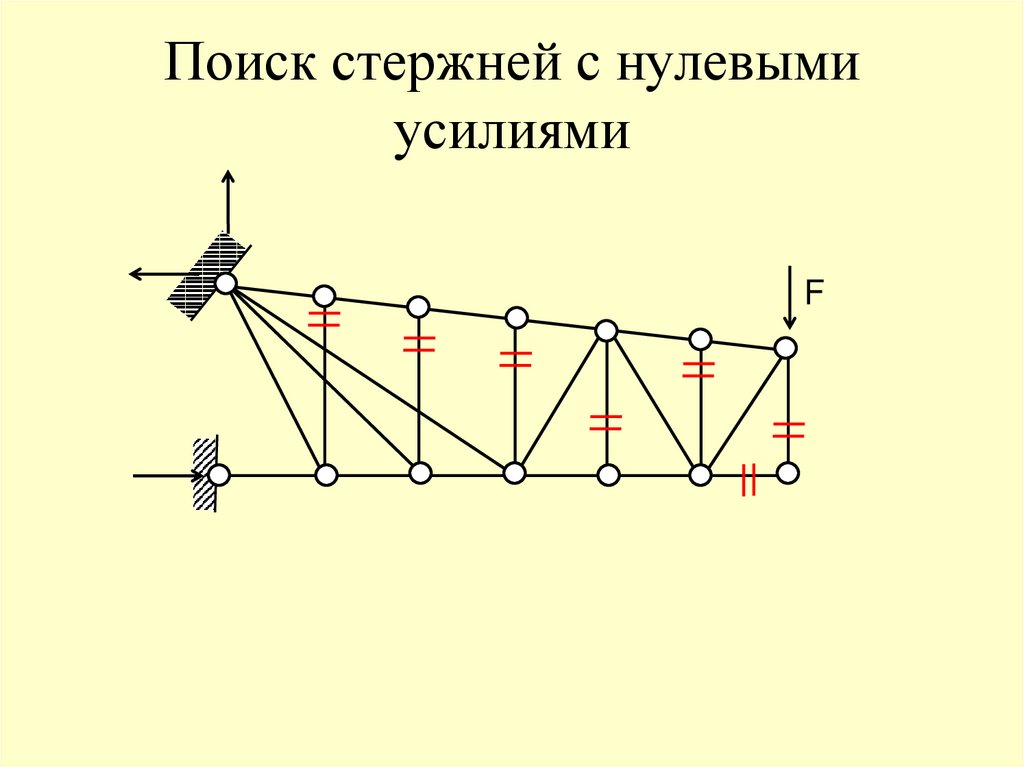
F42. Поиск стержней с нулевыми усилиями
F43. Поиск стержней с нулевыми усилиями
F44.
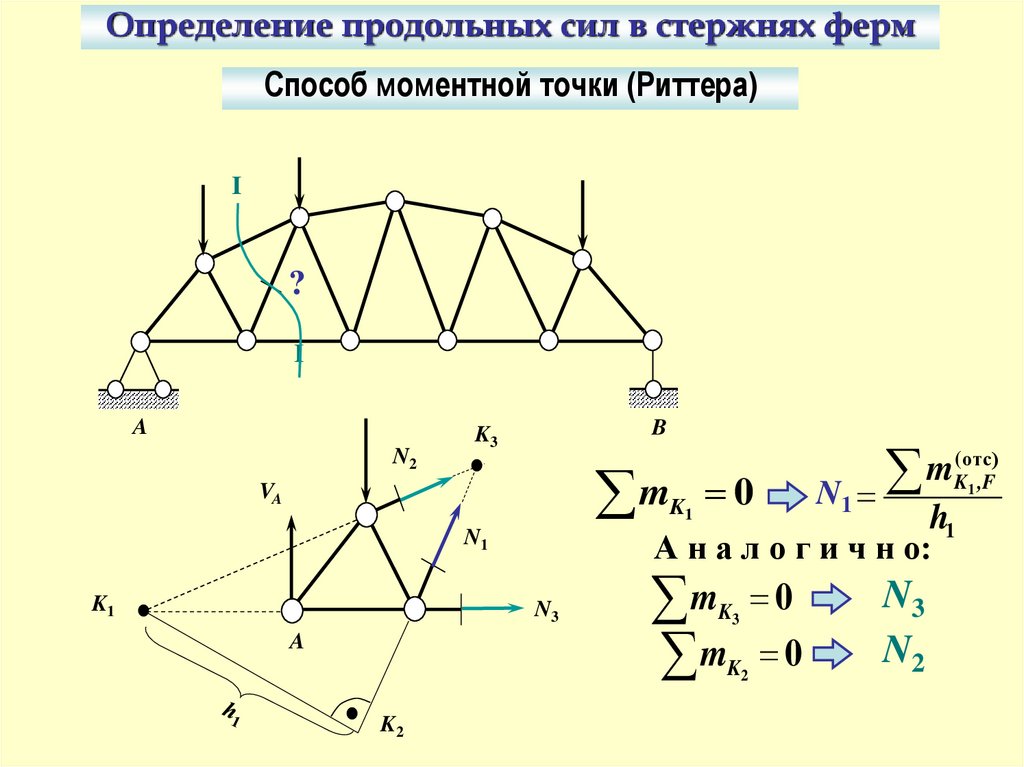
Определение продольных сил в стержнях фермСпособ моментной точки (Риттера)
I
?
I
A
N2
B
K3
VA
N1
K1
N3
A
( отс)
m
N1 K1 ,F
mK1 0
h1
А н а л о г и ч н о:
m 0
m 0
K3
K2
K2
N3
N2
45.
Сущность основного случая способа МТ(Р):если искомое усилие выявляется сечением,
которое разделяет ферму на отдельные части,
проходя по трём стержням (включая тот,
усилие в котором требуется найти), то для
определения усилия используется уравнение
равновесия
моментов
относительно
точки
пересечения линий действия двух других
продольных сил, выявленных сечением).
46.
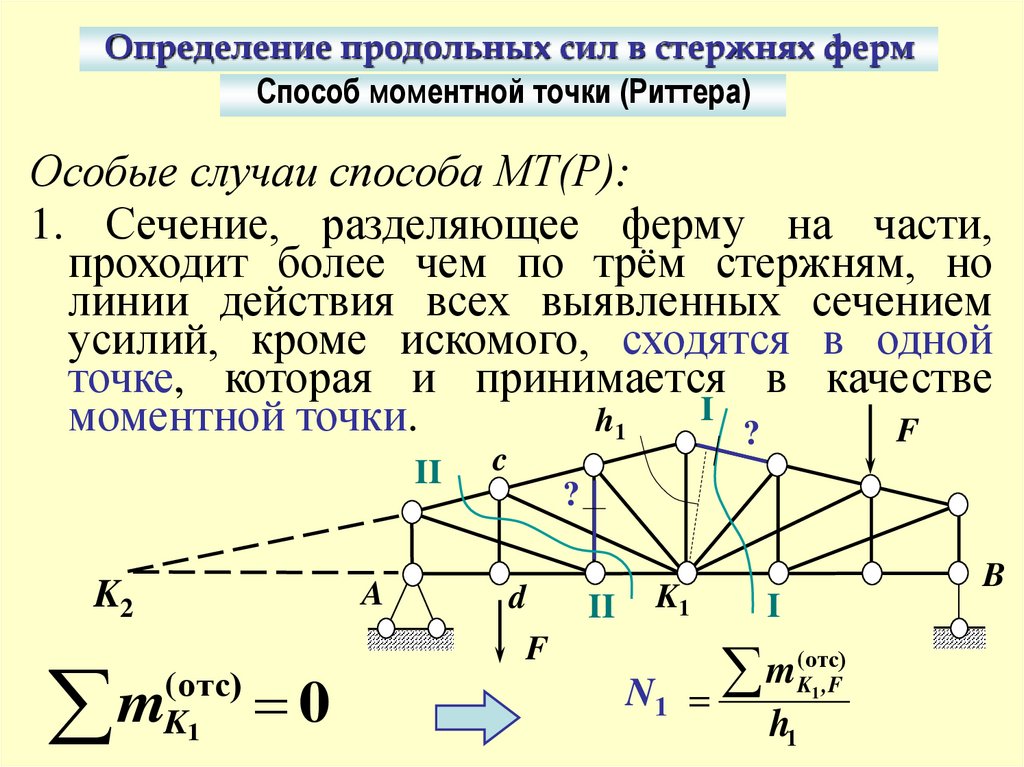
Определение продольных сил в стержнях фермСпособ моментной точки (Риттера)
Особые случаи способа МТ(Р):
1. Сечение, разделяющее ферму на части,
проходит более чем по трём стержням, но
линии действия всех выявленных сечением
усилий, кроме искомого, сходятся в одной
точке, которая и принимается в качестве
I
моментной точки.
h1
F
?
II
K2
A
m
(отс)
K1
0
c
?
d
F
II
K1
B
I
( отс)
m
N1 K1 ,F
h1
47.
2. Сечение проходит более чем по трёмстержням, но неизвестны усилия в трёх (или
менее) из них – остальные уже определены
ранее.
Ncd = F – из частного случая
равновесия Т-образного узла
m K(отс)
0
2
N2
48.
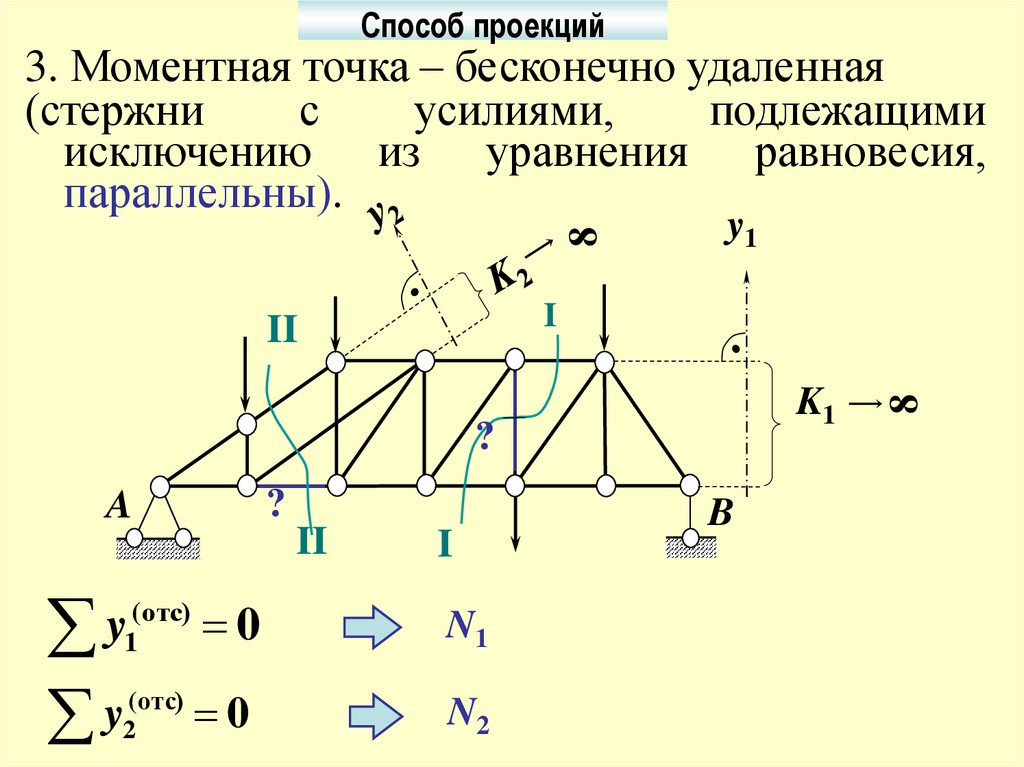
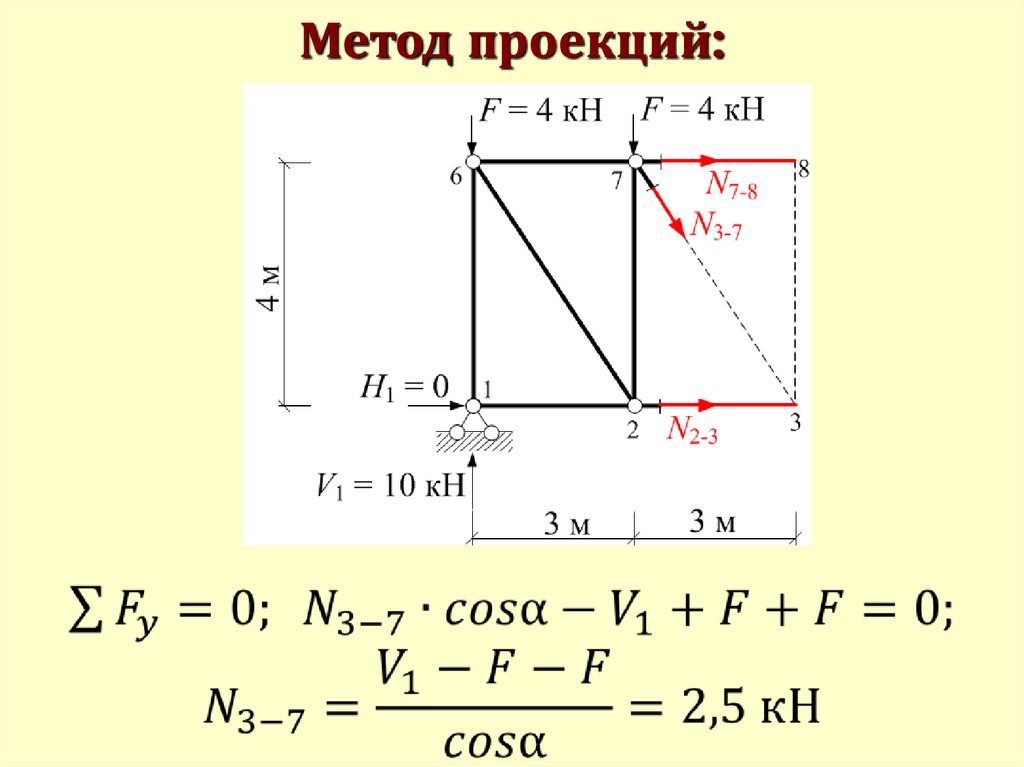
Способ проекций8
3. Моментная точка – бесконечно удаленная
(стержни
с
усилиями,
подлежащими
исключению из уравнения равновесия,
параллельны).
y1
K1
?
A
?
II
I
(отс)
y
1 0
N1
(отс)
y
2 0
N2
B
8
I
II
49.
50.
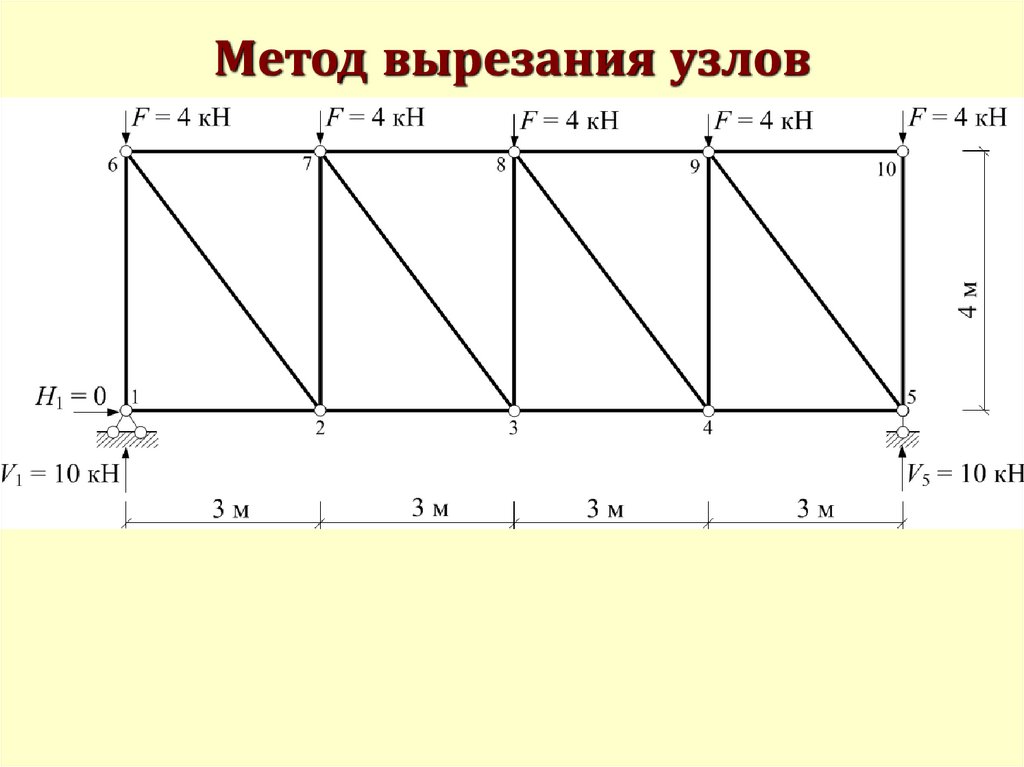
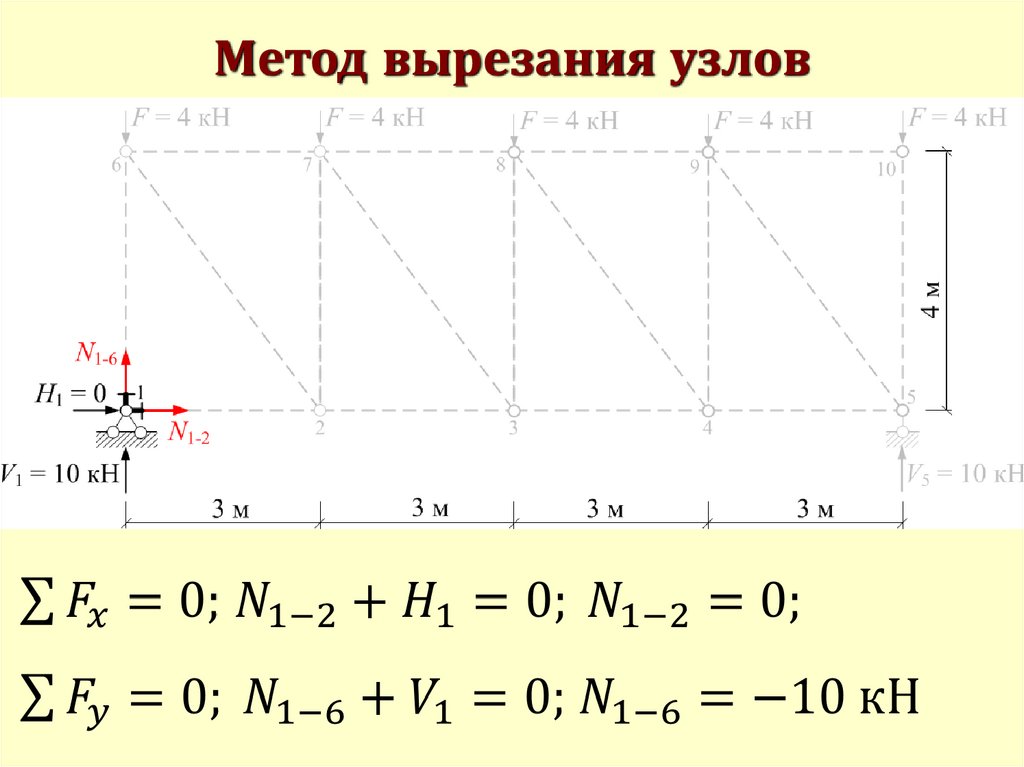
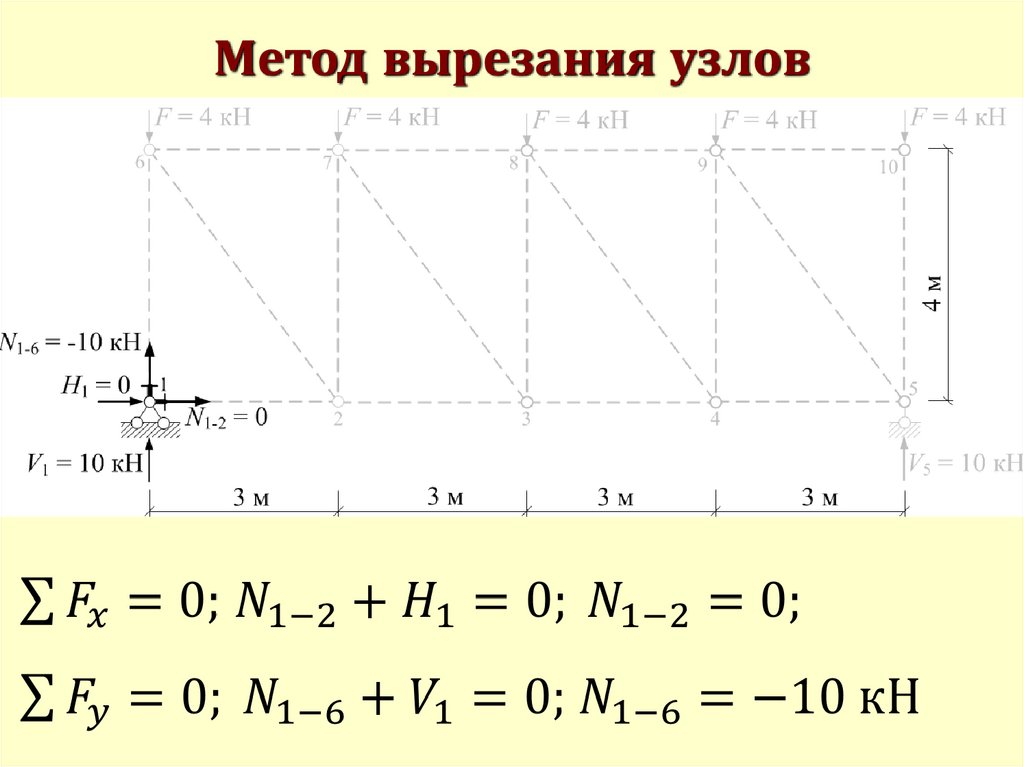
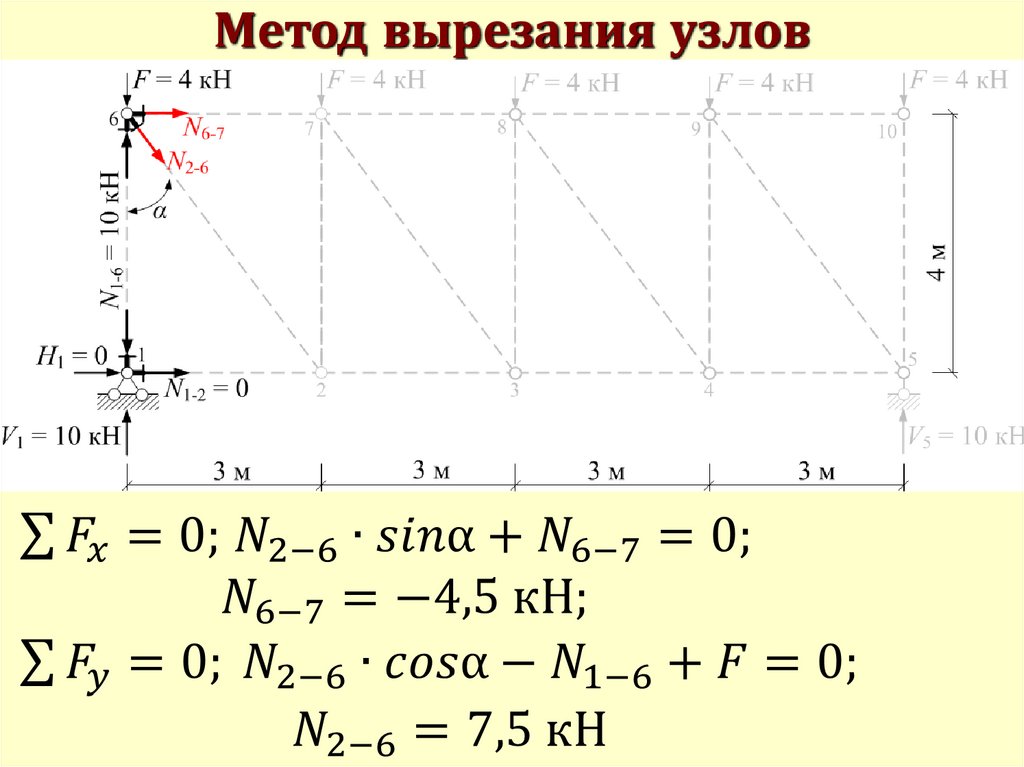
Метод вырезания узлов51.
Метод вырезания узлов52.
Метод вырезания узлов53.
Метод вырезания узлов54.
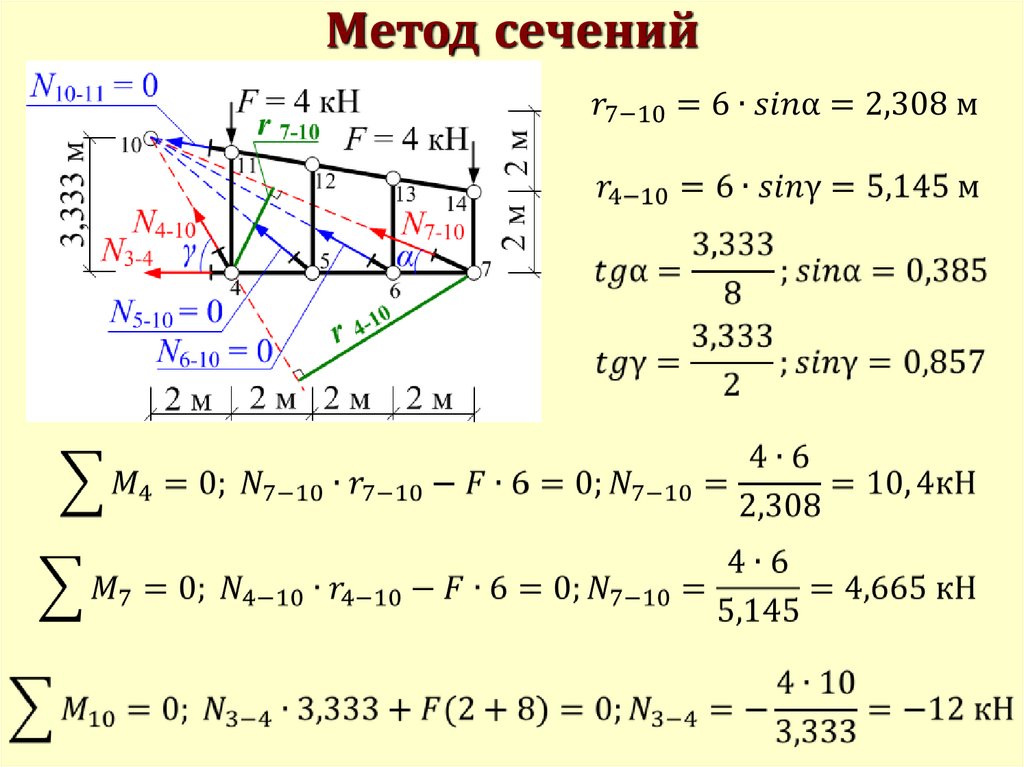
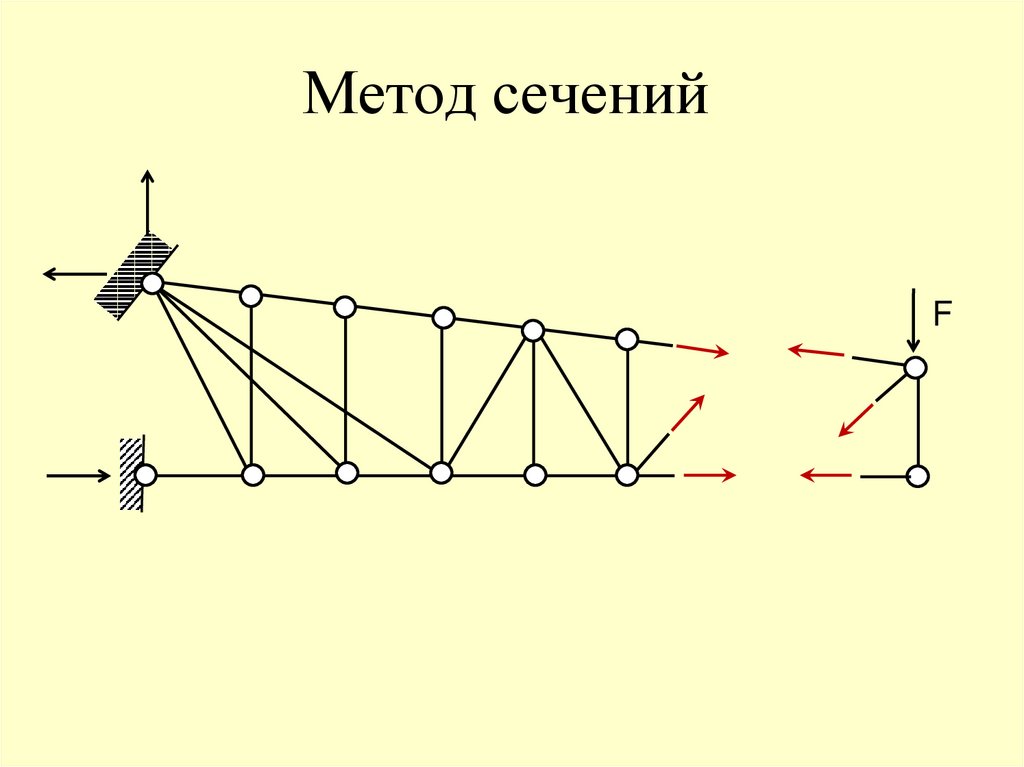
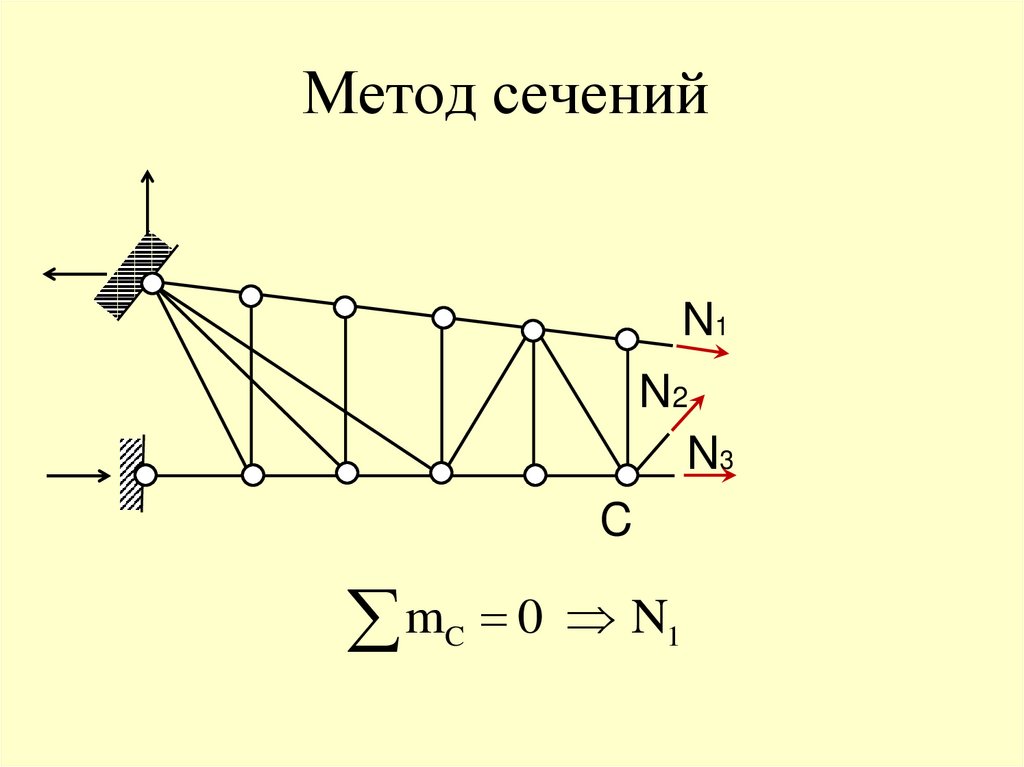
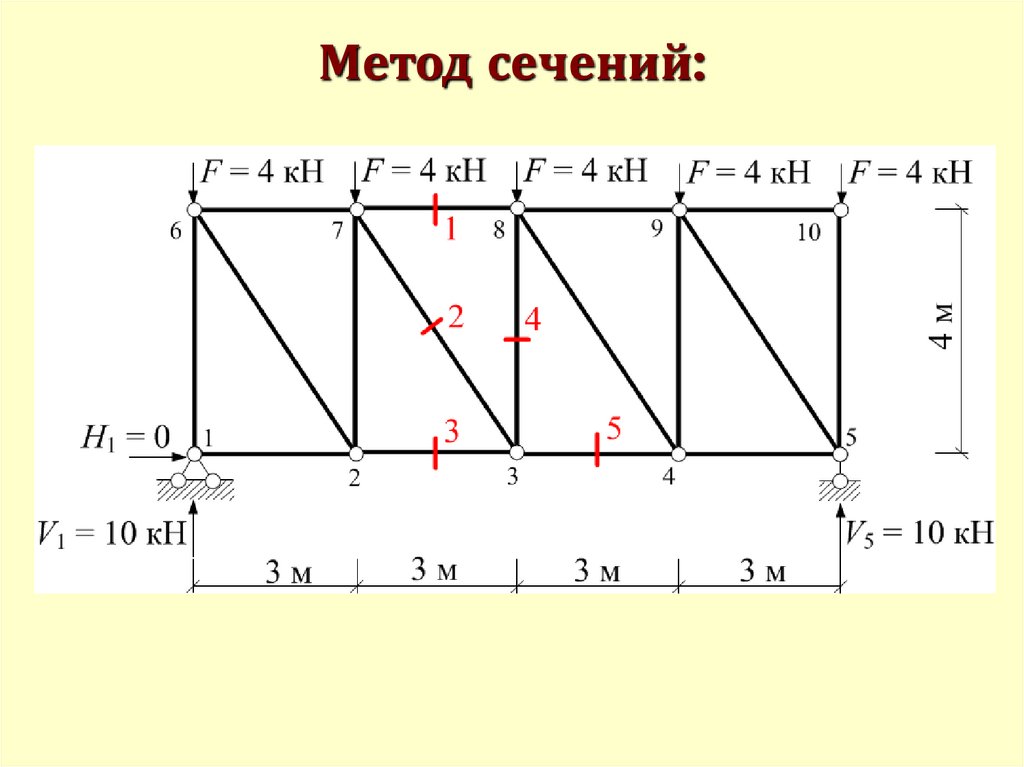
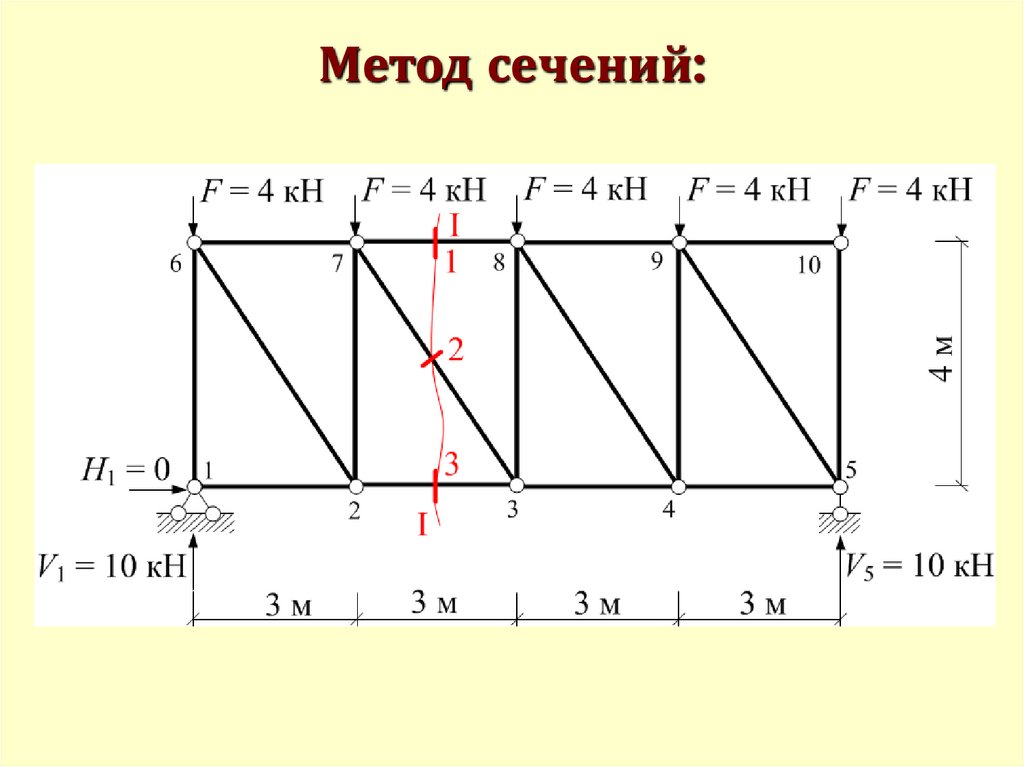
Метод сечений55.
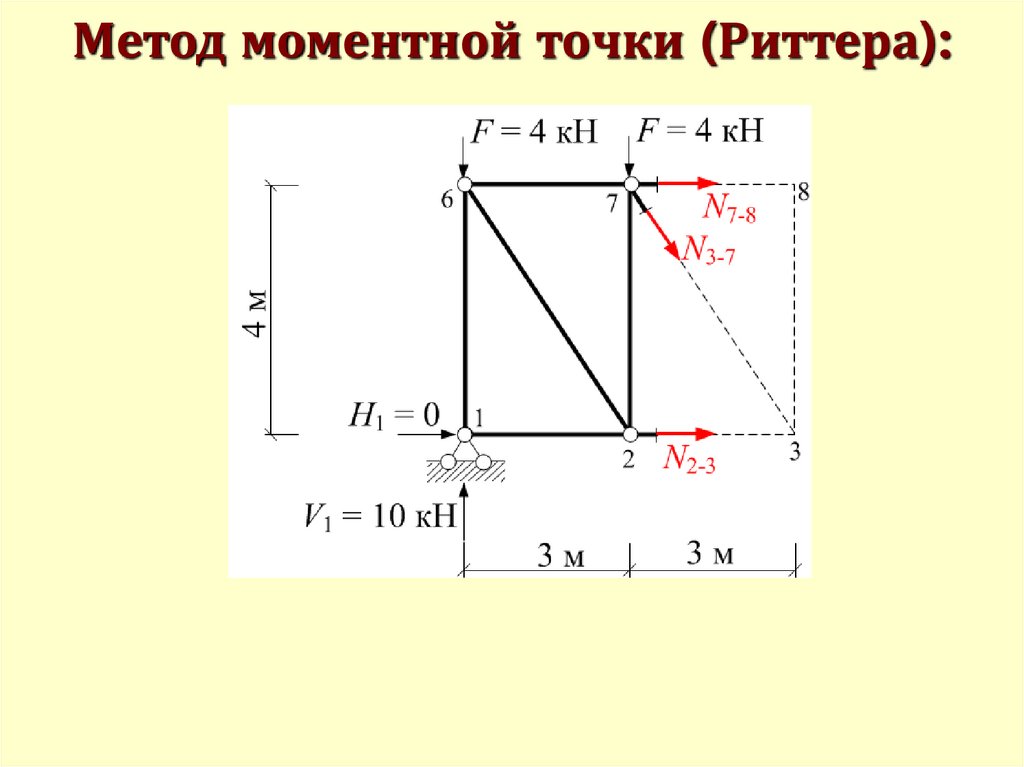
Метод моментной точки (Риттера):56.
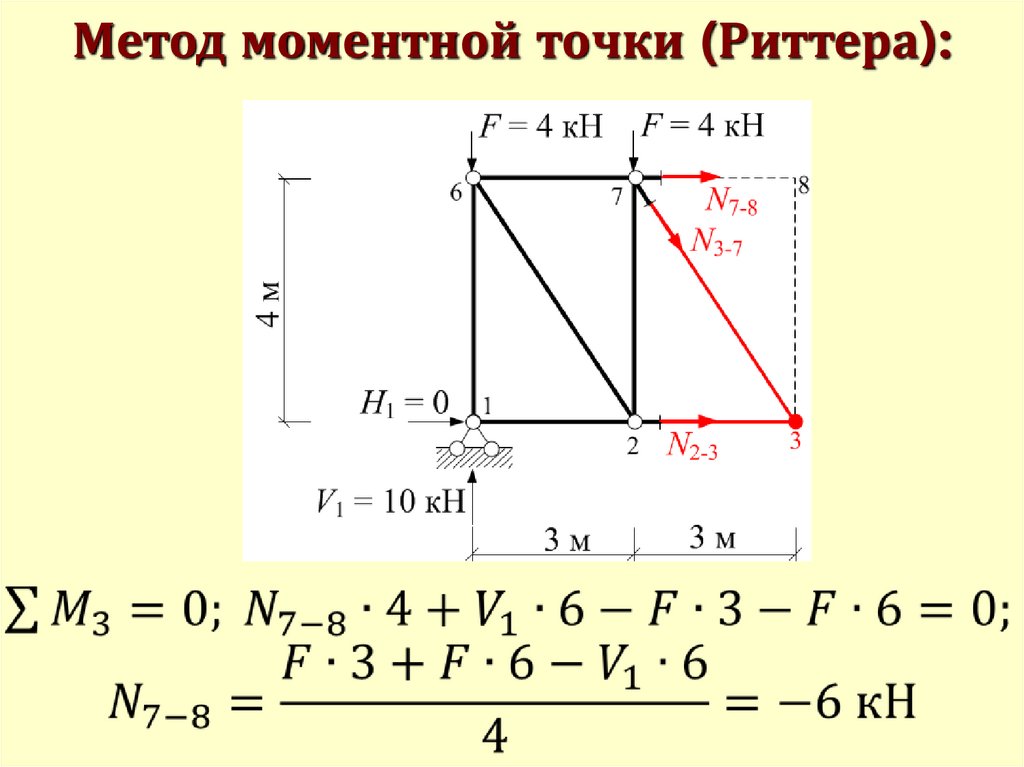
Метод моментной точки (Риттера):57.
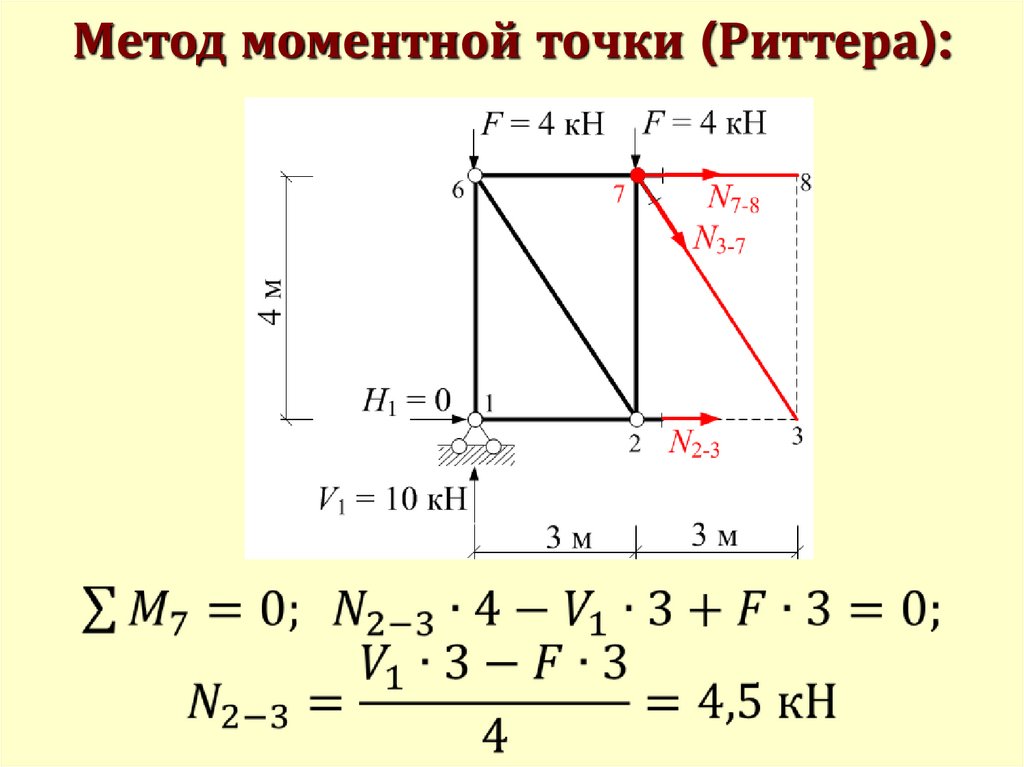
Метод моментной точки (Риттера):58.
Метод проекций:59. Способы определения усилий в стержнях ферм
• Графический• Аналитический
• Кинематический
60.
К аналитическому способуотносятся: способ вырезания
узлов, способ сечений, их
совместное применение, способ
замены стержней.
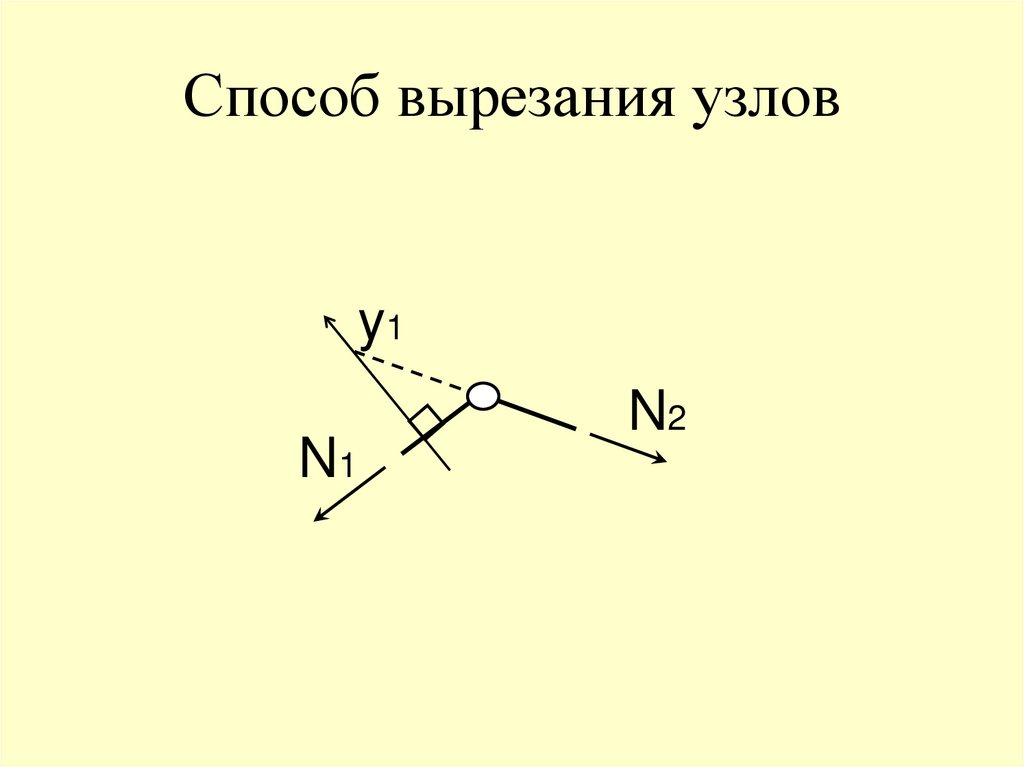
61. Способ вырезания узлов
62. Способ вырезания узлов
63. Способ вырезания узлов
y1N1
N2
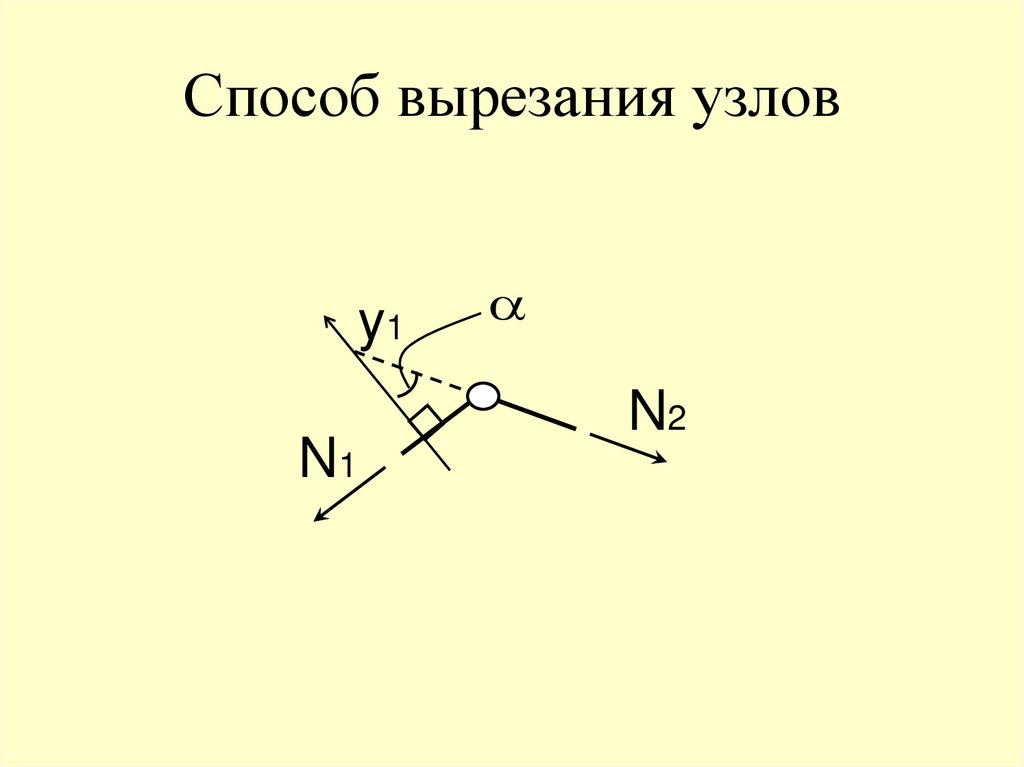
64. Способ вырезания узлов
y1N1
N2
65. Способ вырезания узлов
y1N1
N2
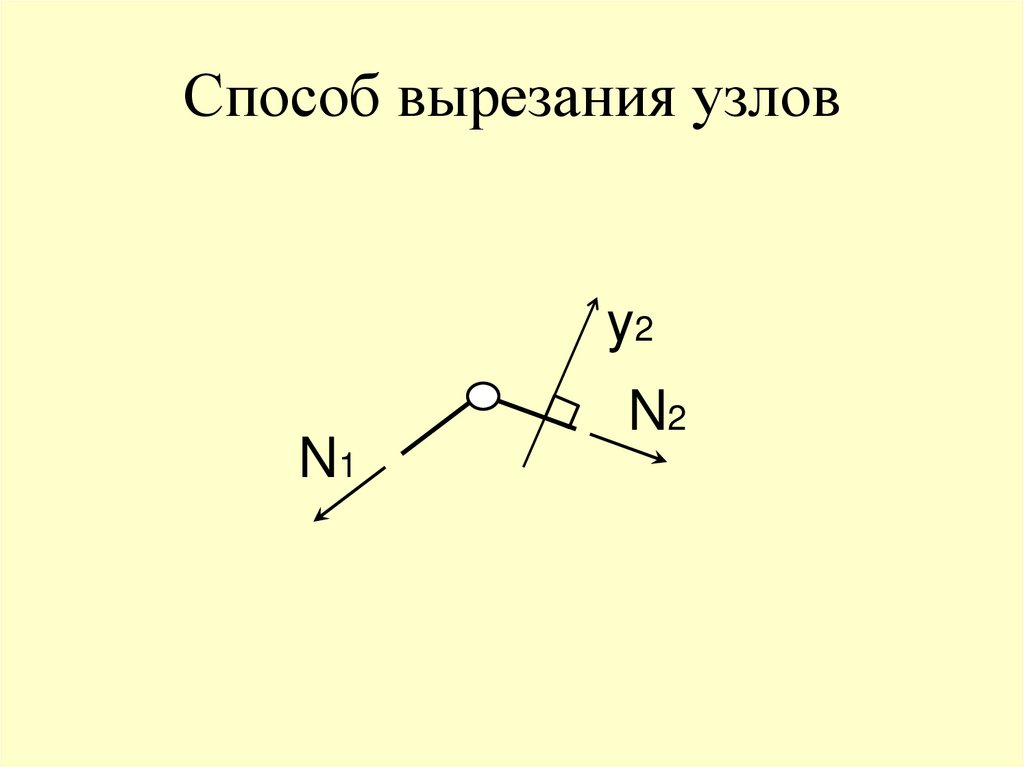
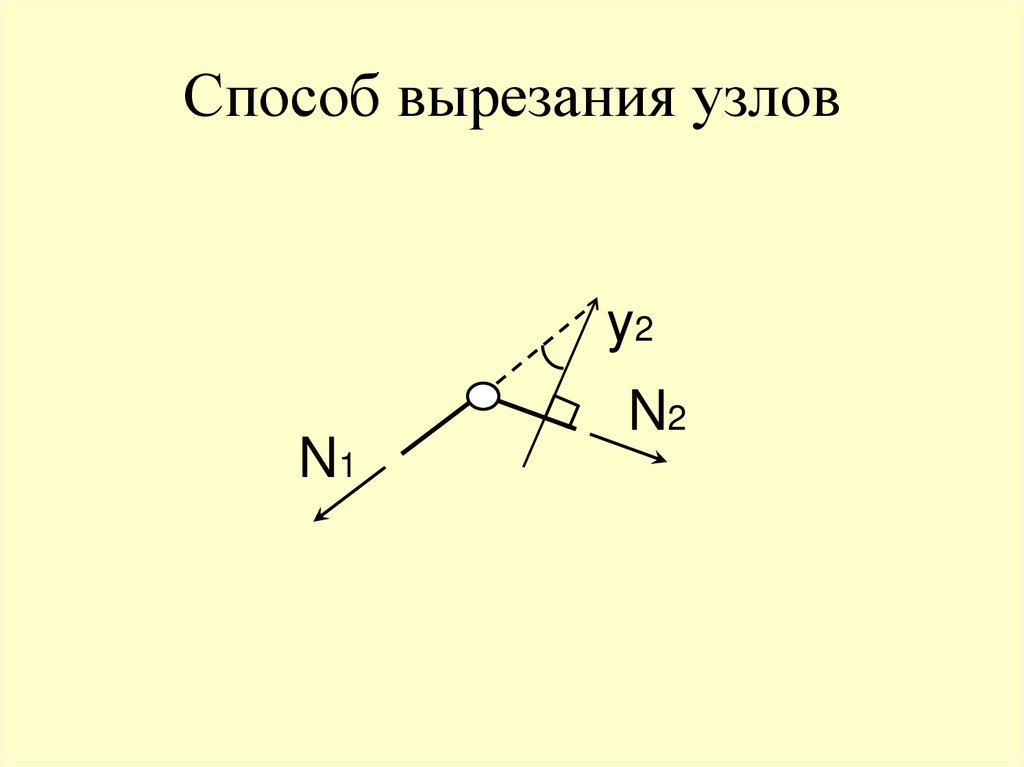
66. Способ вырезания узлов
y2N1
N2
67. Способ вырезания узлов
y2N1
N2
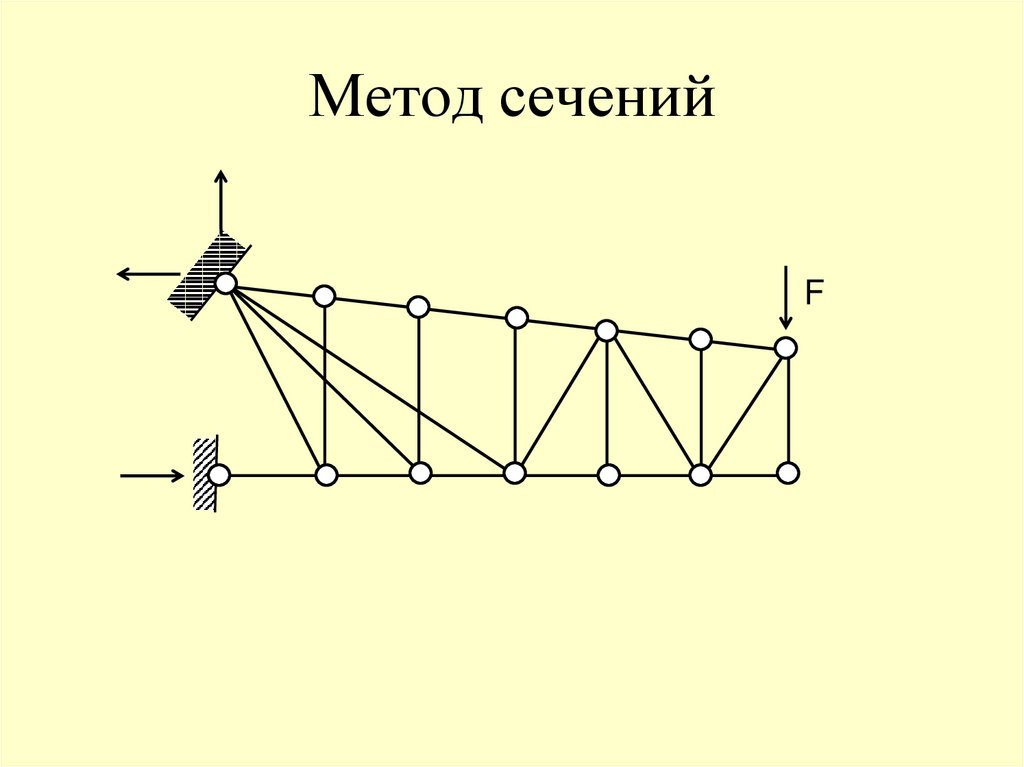
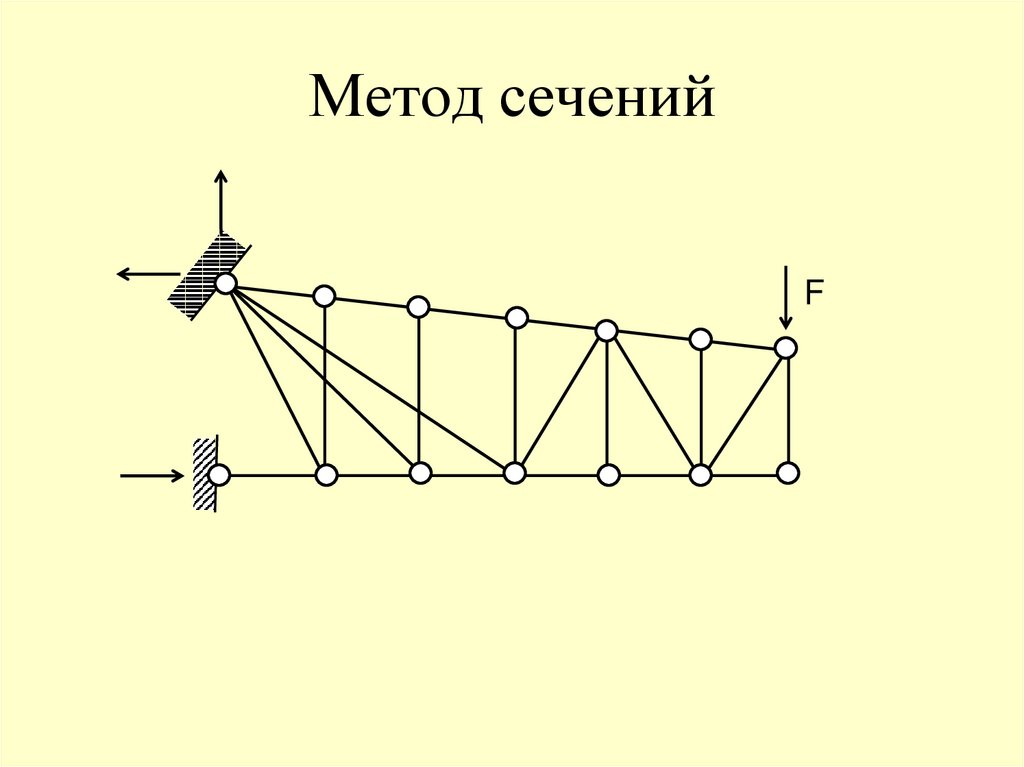
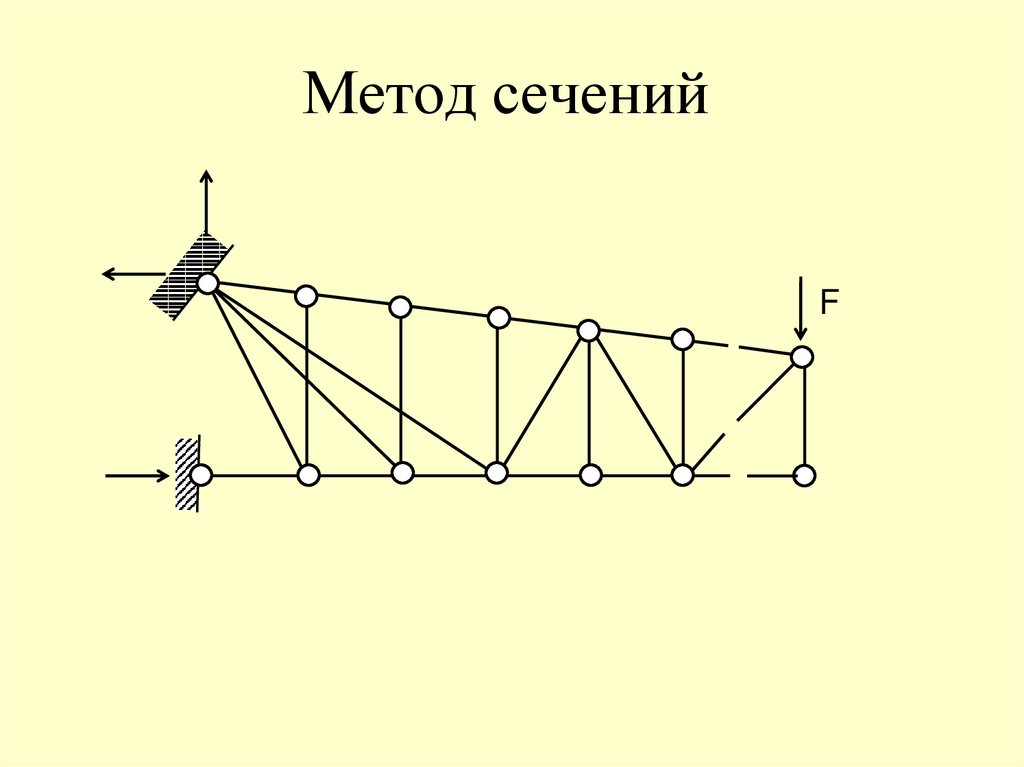
68. Метод сечений
F69. Метод сечений
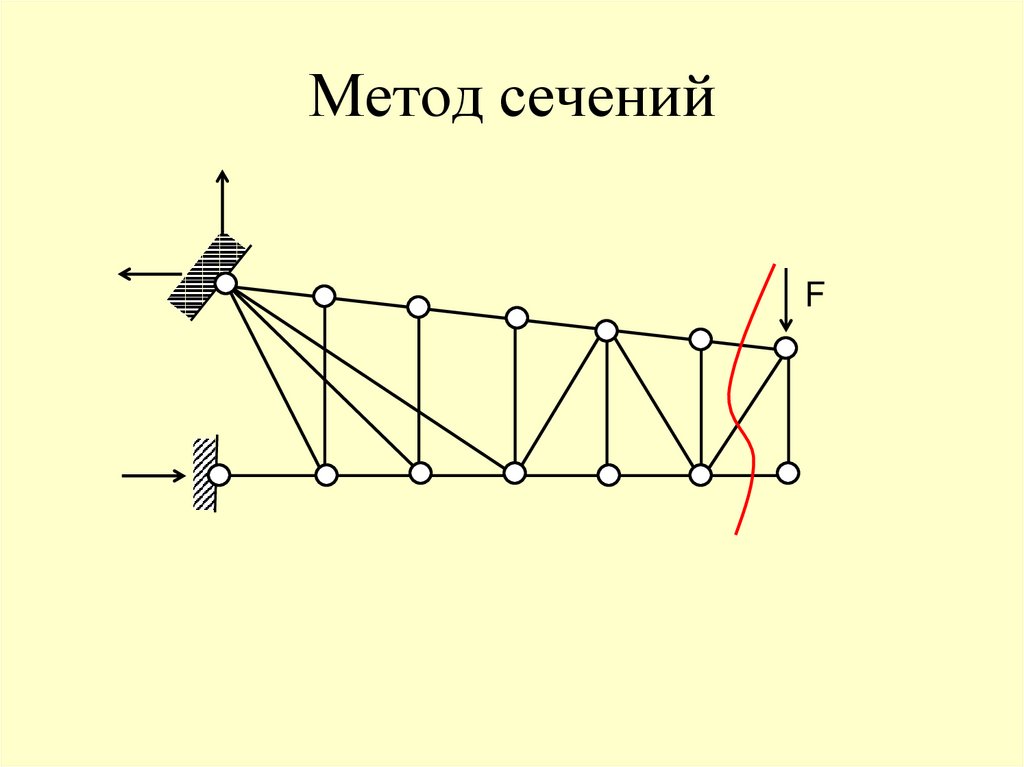
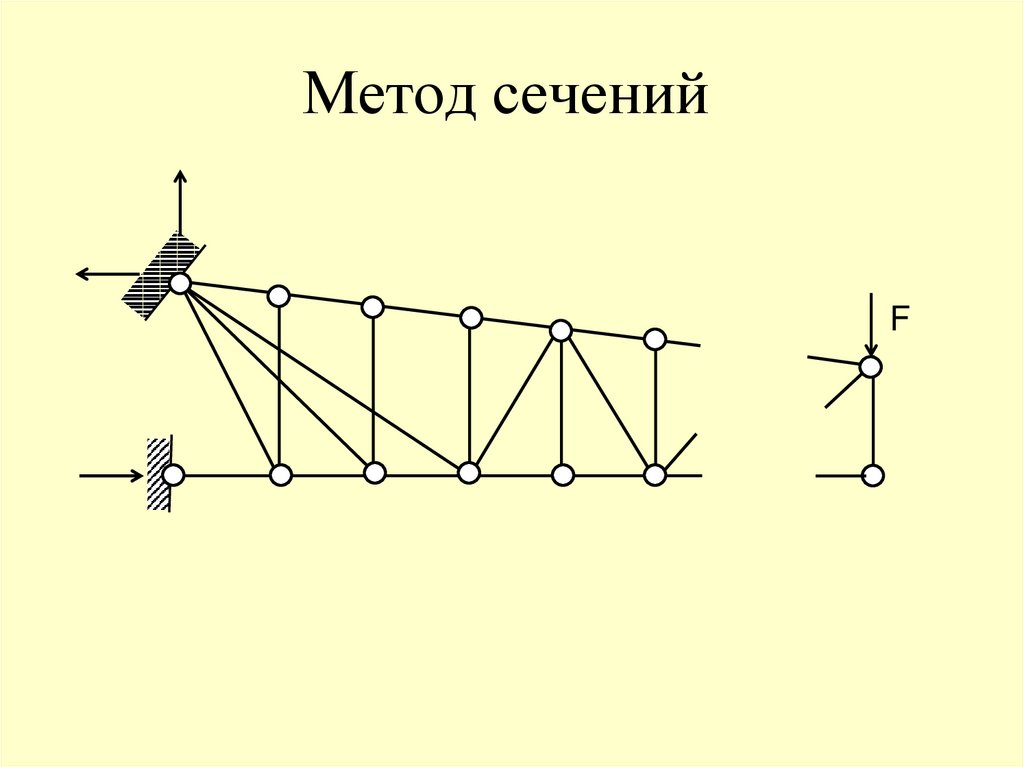
F70. Метод сечений
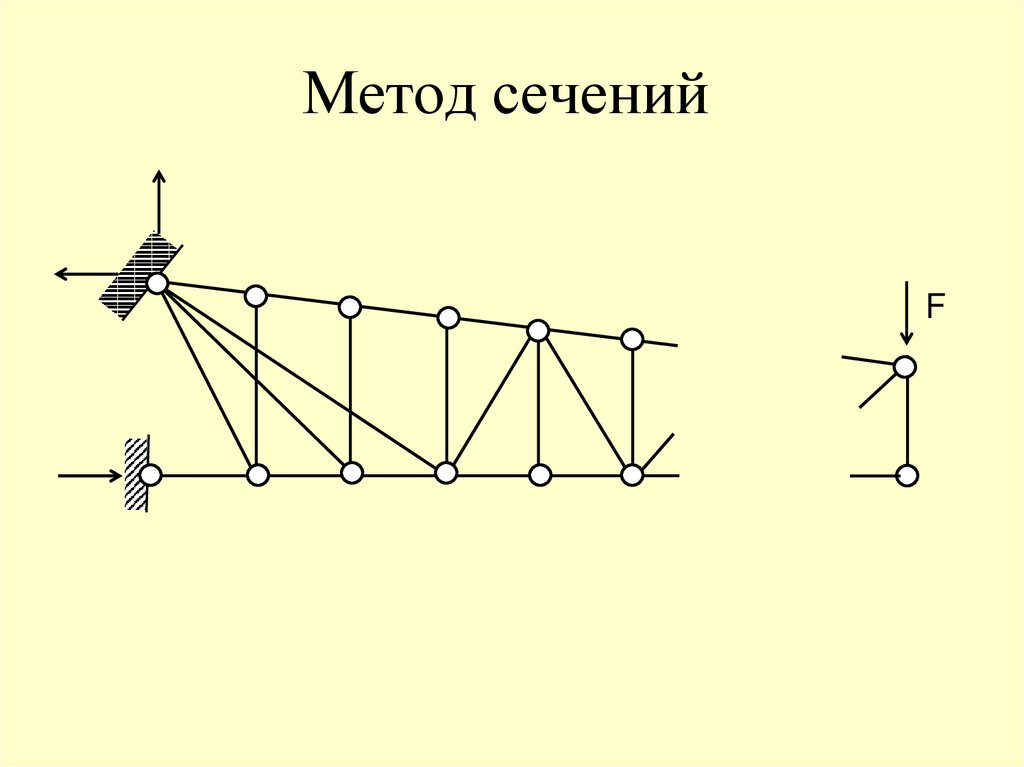
F71. Метод сечений
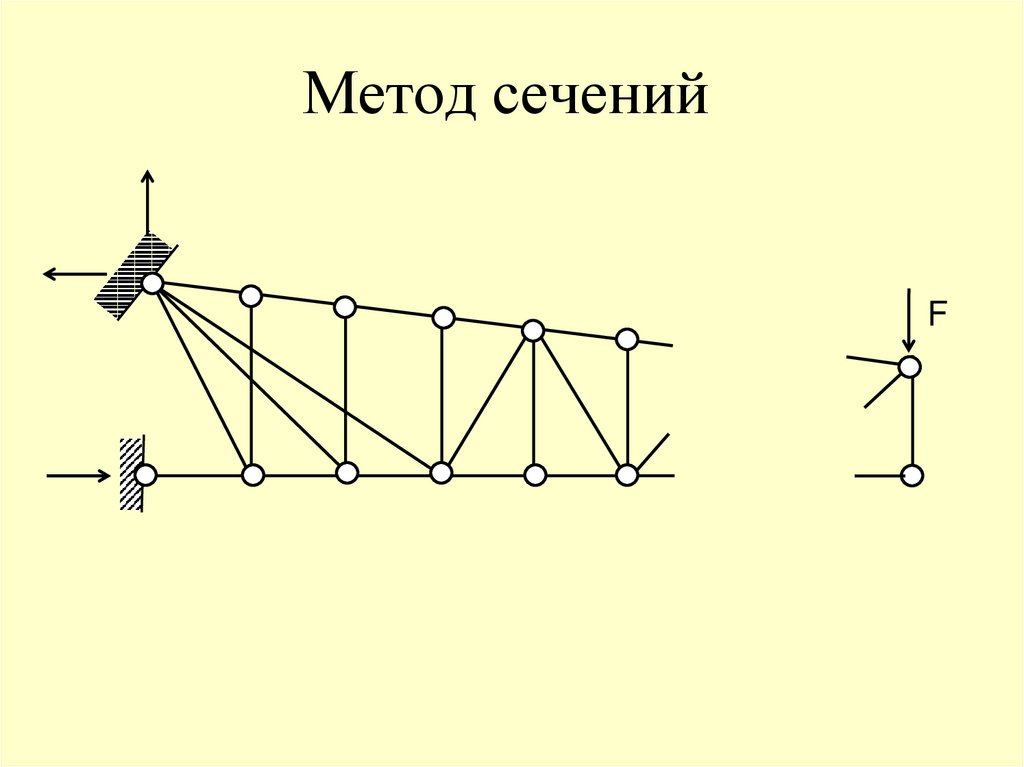
F72. Метод сечений
F73. Метод сечений
F74. Метод сечений
F75. Метод сечений
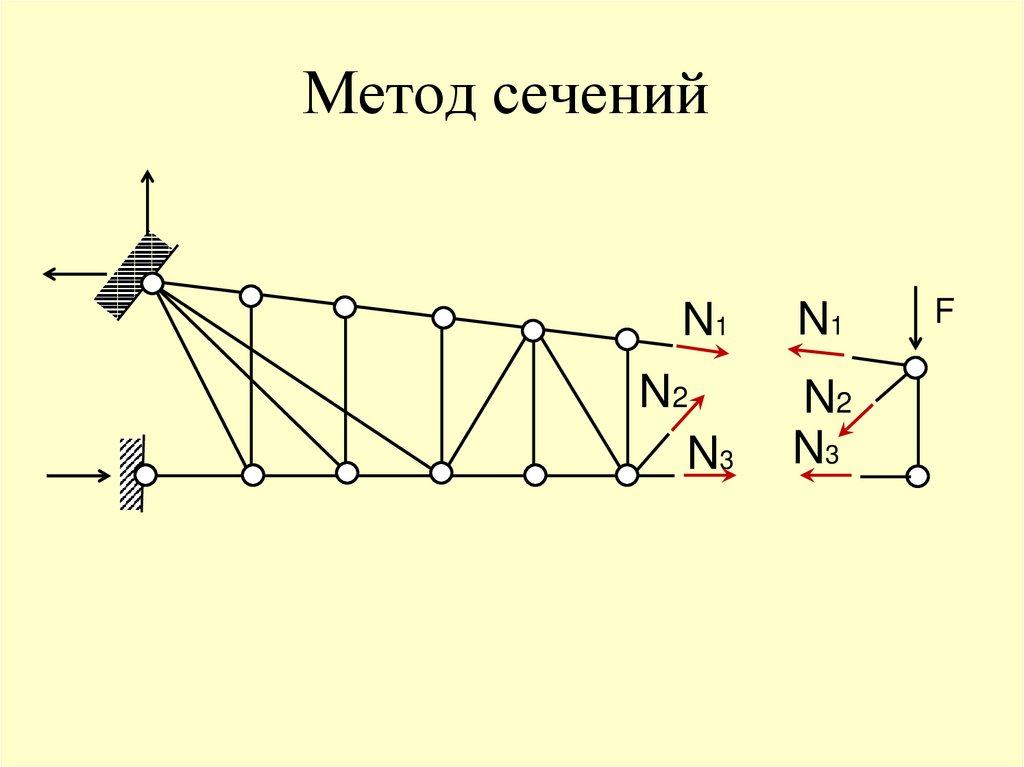
F76. Метод сечений
N1N1
N2
N3
N2
N3
F
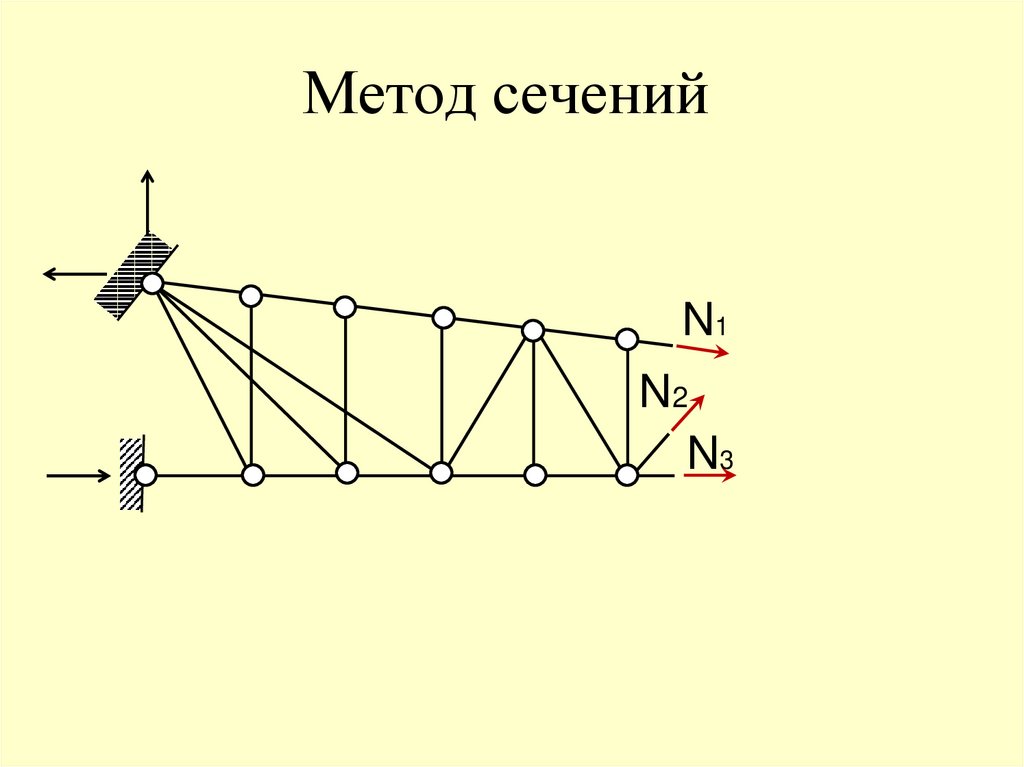
77. Метод сечений
N1N2
N3
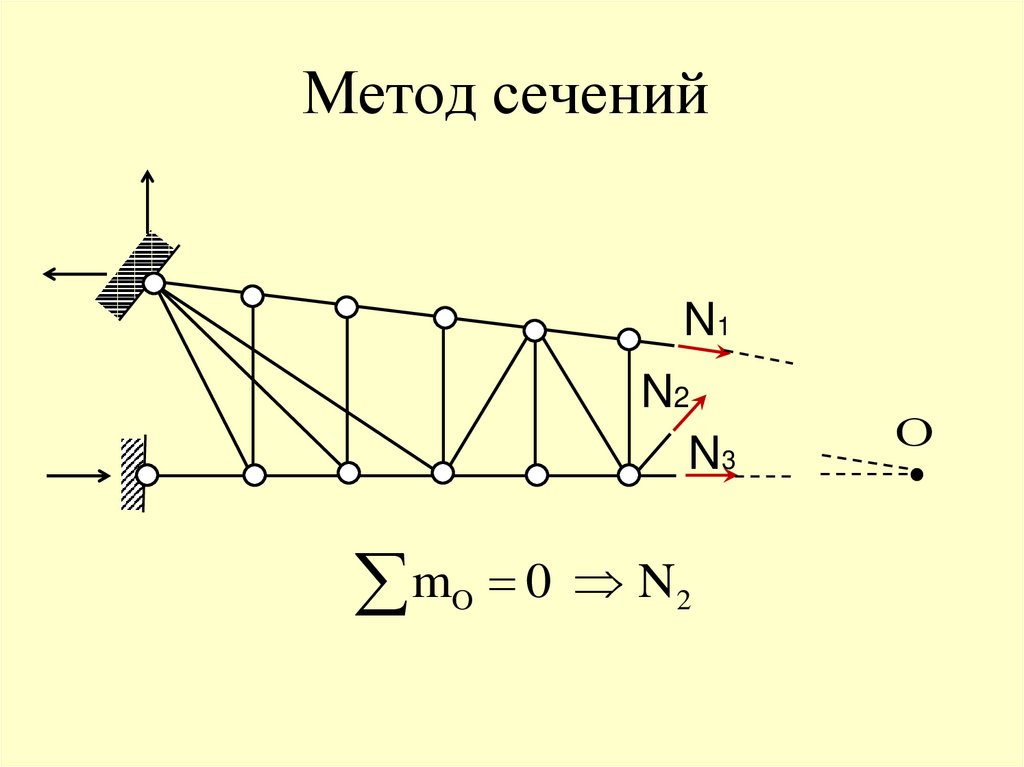
78. Метод сечений
N1N2
N3
m 0 N
O
2
О
79. Метод сечений
N1N2
N3
C
m 0 N
C
1
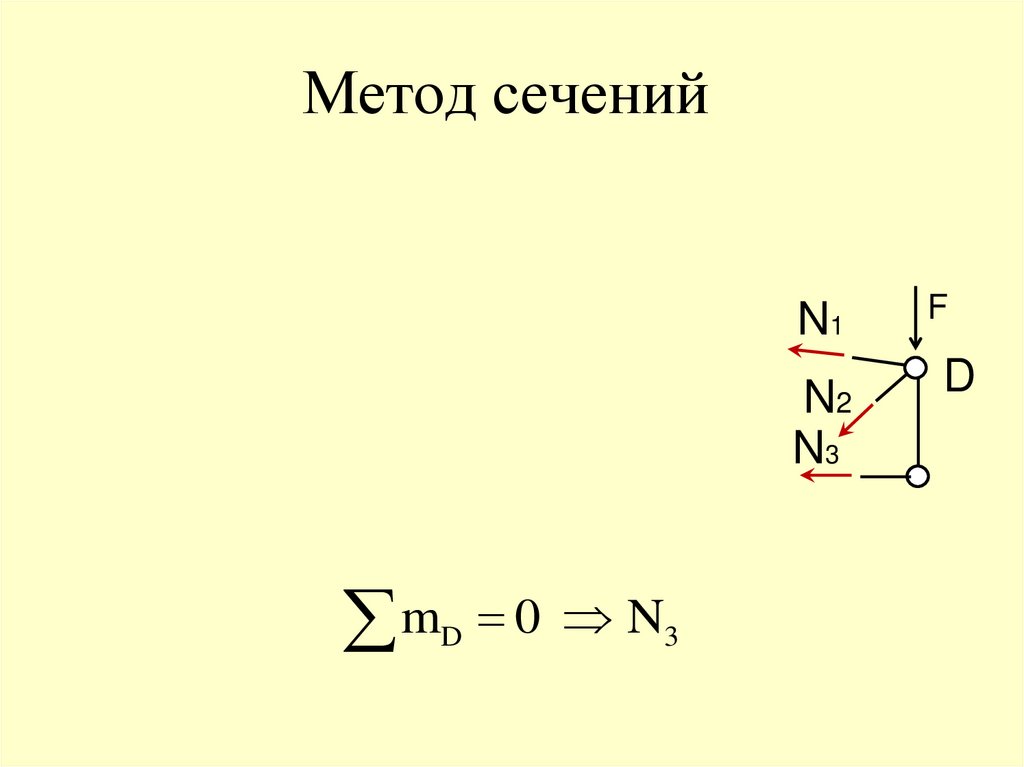
80. Метод сечений
N1N2
N3
m 0 N
D
3
F
D
81.
82.
83.
84.
РАСЧЁТ ФЕРМЕсли оси всех стержней и вся приложенная к ферме
нагрузка расположены в одной плоскости, ферма
называется плоской. В дальнейшем будем рассматривать
только плоские фермы.
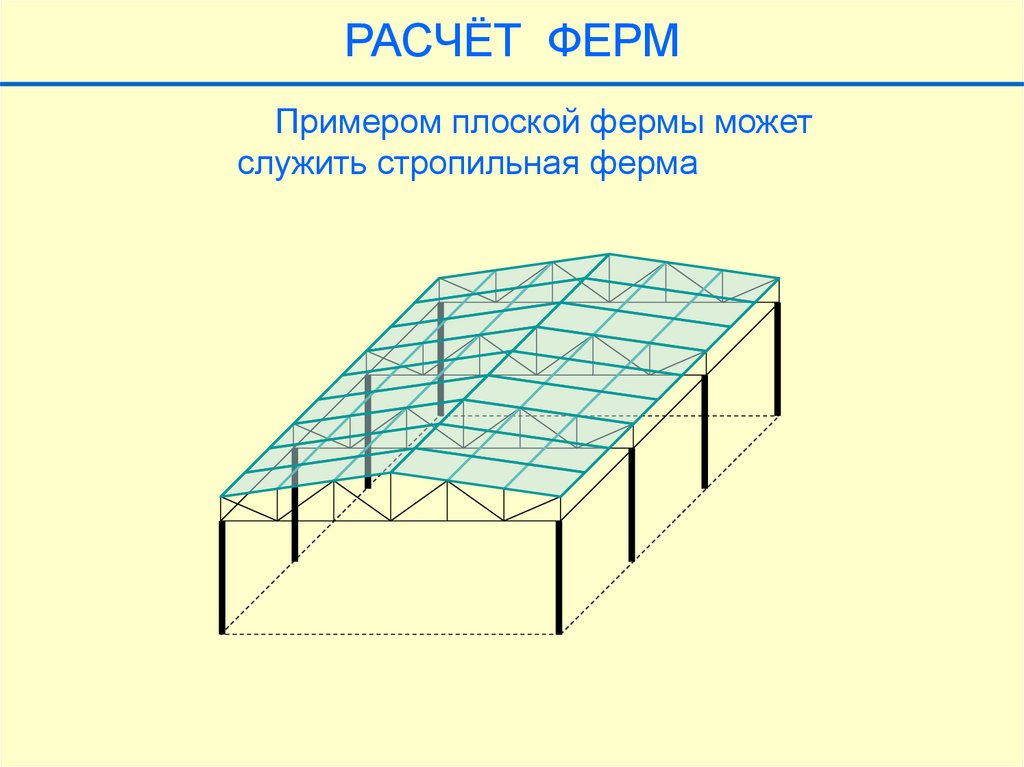
85.
РАСЧЁТ ФЕРМПримером плоской фермы может
служить стропильная ферма
86.
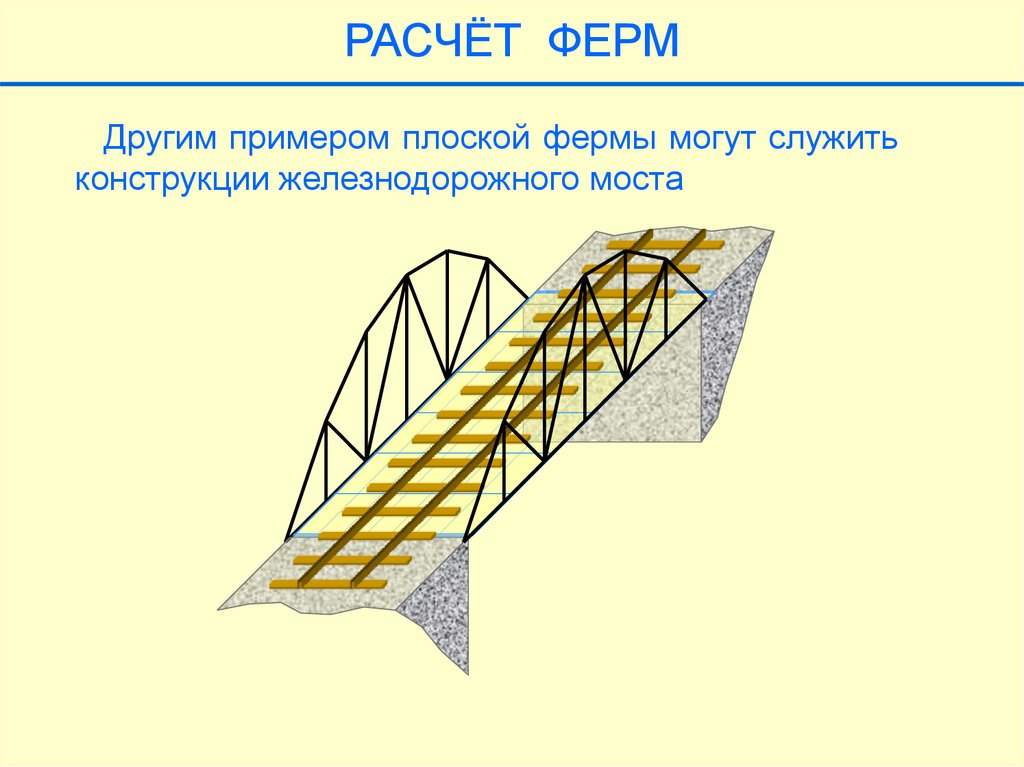
87.
РАСЧЁТ ФЕРМДругим примером плоской фермы могут служить
конструкции железнодорожного моста
88.
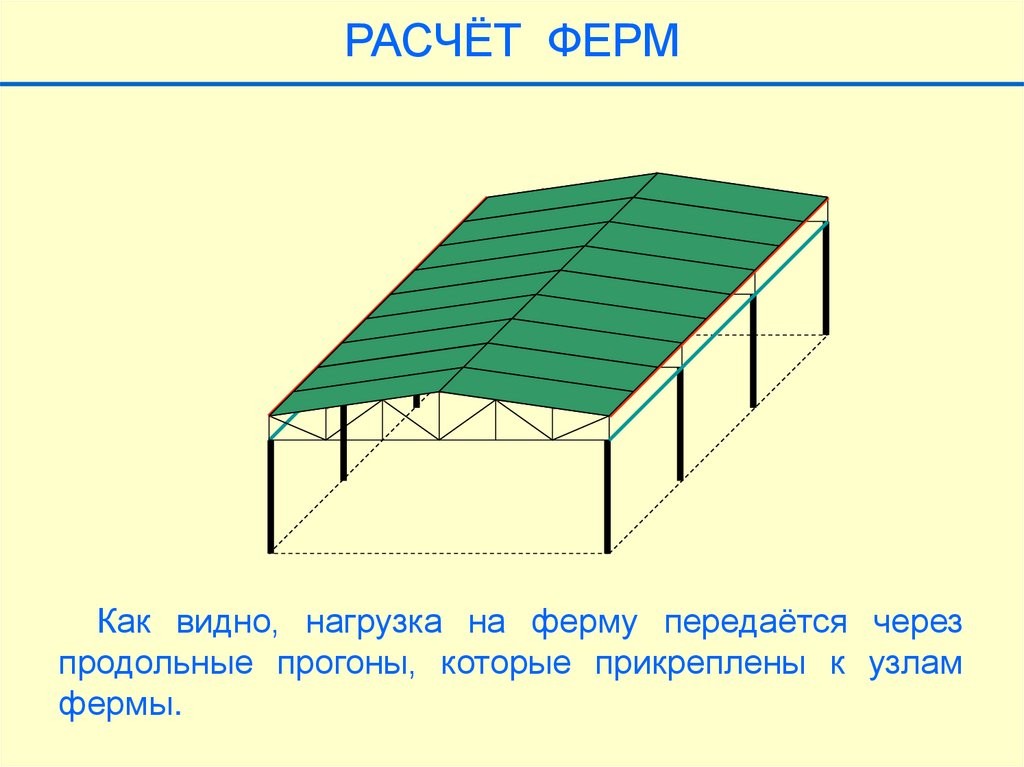
РАСЧЁТ ФЕРМКак видно, нагрузка на ферму передаётся через
продольные прогоны, которые прикреплены к узлам
фермы.
89.
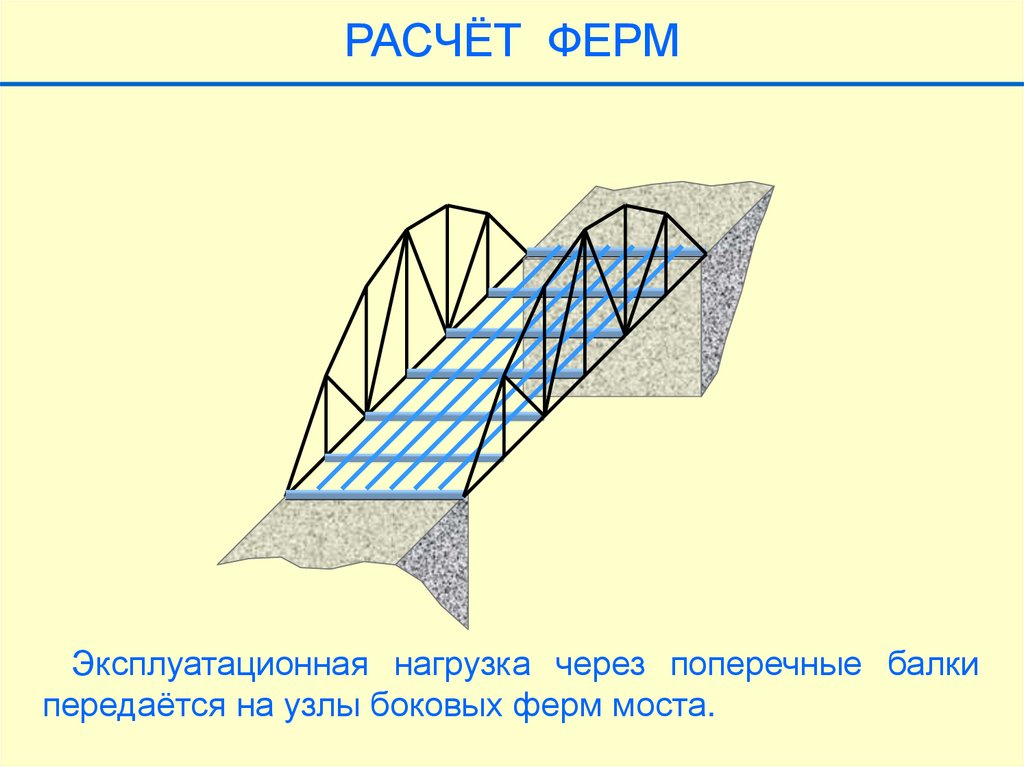
РАСЧЁТ ФЕРМЭксплуатационная нагрузка через поперечные балки
передаётся на узлы боковых ферм моста.
90.
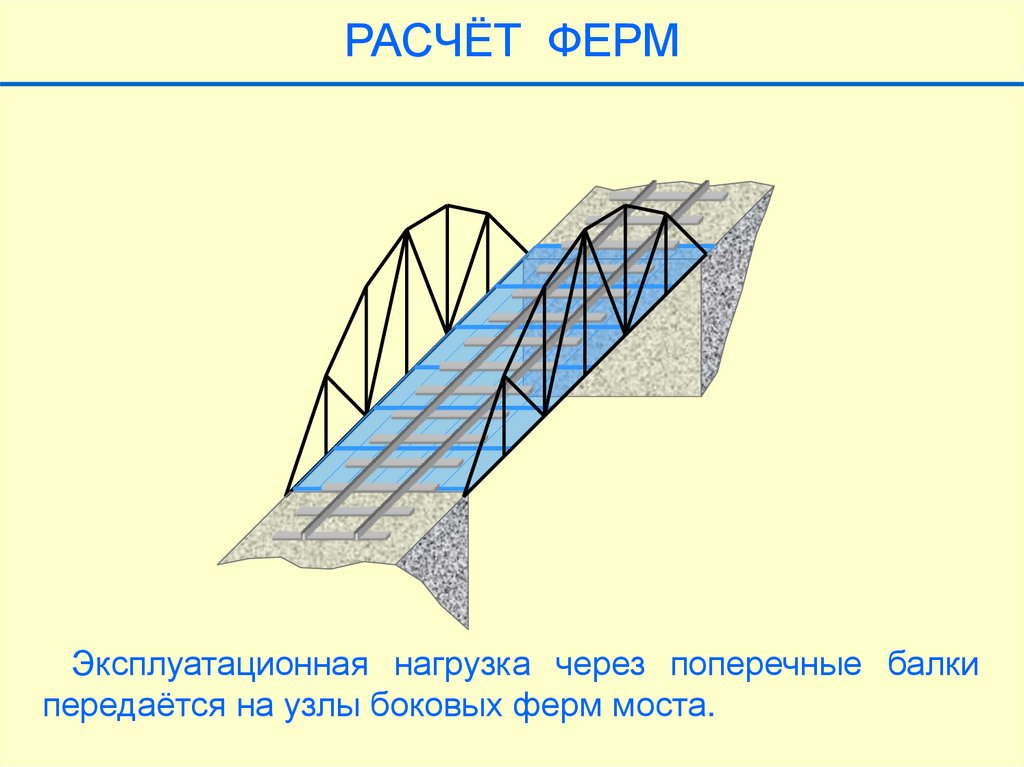
РАСЧЁТ ФЕРМЭксплуатационная нагрузка через поперечные балки
передаётся на узлы боковых ферм моста.
91.
РАСЧЁТ ФЕРМ?
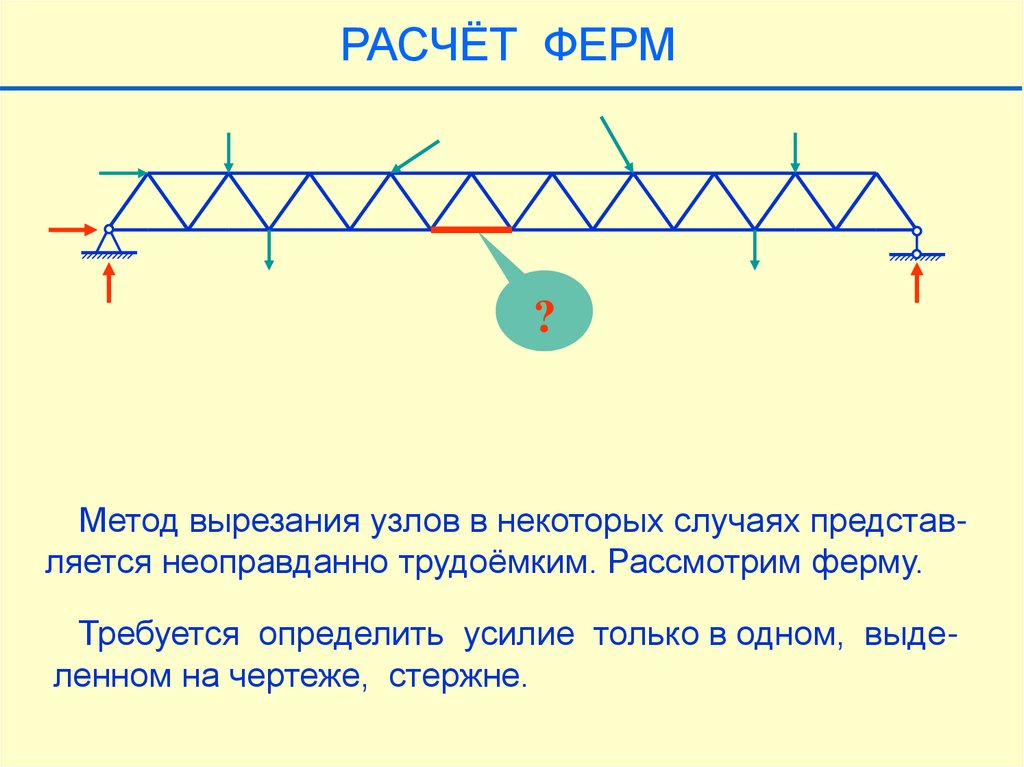
Метод вырезания узлов в некоторых случаях представляется неоправданно трудоёмким. Рассмотрим ферму.
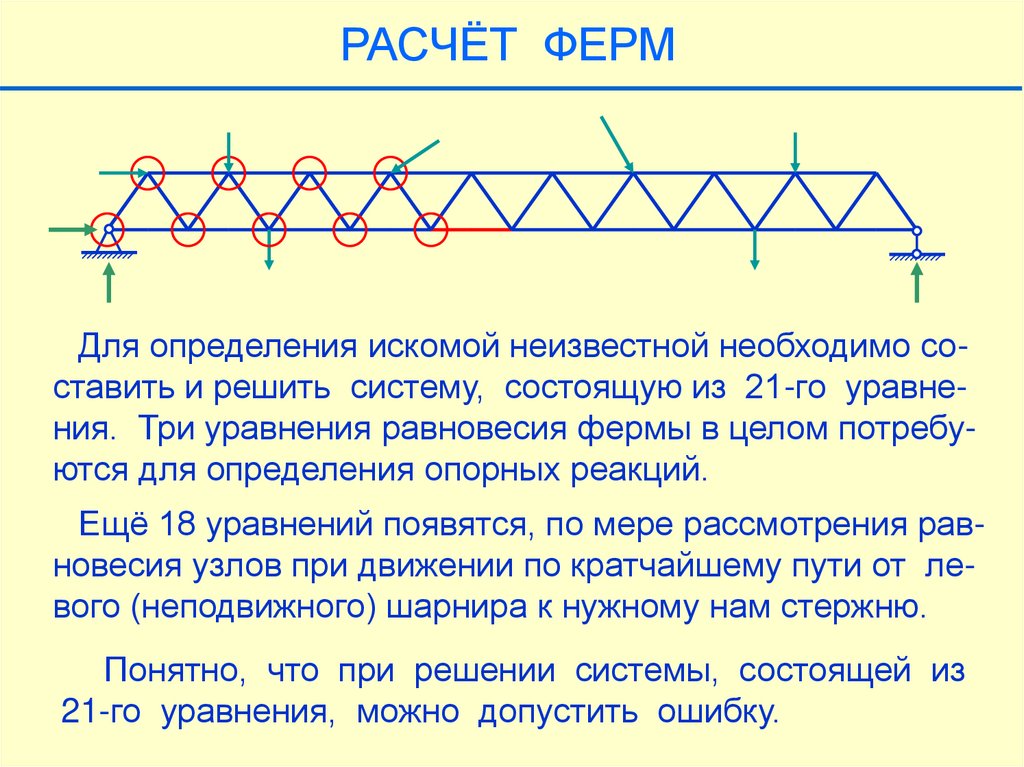
Требуется определить усилие только в одном, выделенном на чертеже, стержне.
92.
РАСЧЁТ ФЕРМДля определения искомой неизвестной необходимо составить и решить систему, состоящую из 21-го уравнения. Три уравнения равновесия фермы в целом потребуются для определения опорных реакций.
Ещё 18 уравнений появятся, по мере рассмотрения равновесия узлов при движении по кратчайшему пути от левого (неподвижного) шарнира к нужному нам стержню.
Понятно, что при решении системы, состоящей из
21-го уравнения, можно допустить ошибку.
93.
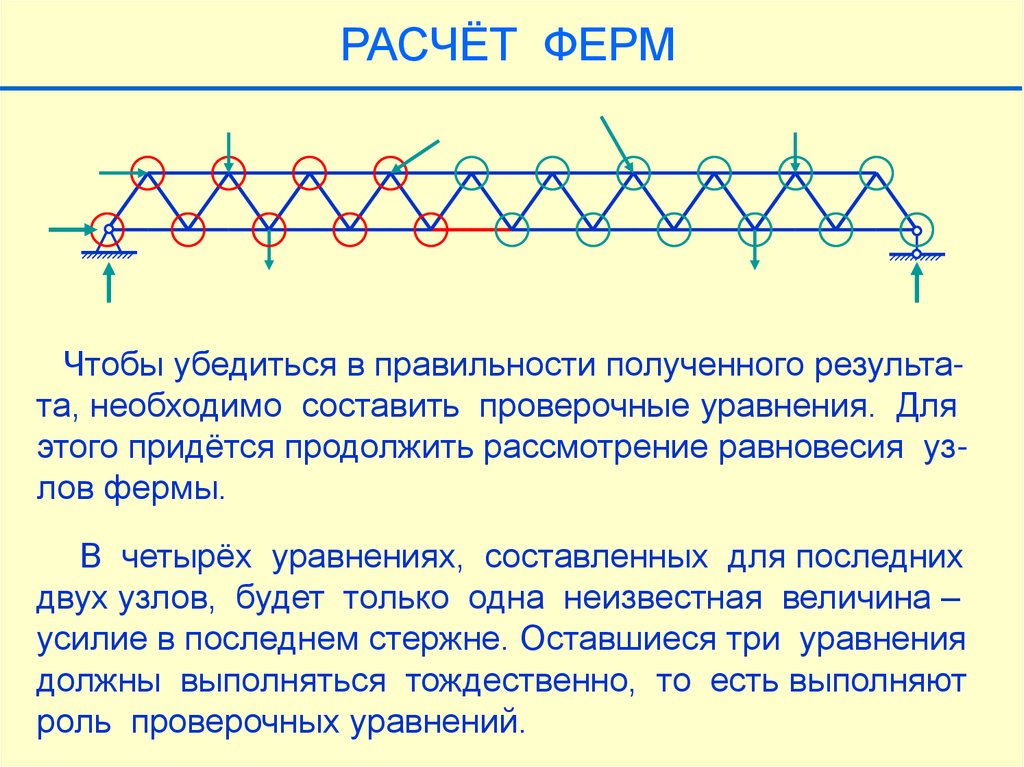
РАСЧЁТ ФЕРМЧтобы убедиться в правильности полученного результата, необходимо составить проверочные уравнения. Для
этого придётся продолжить рассмотрение равновесия узлов фермы.
В четырёх уравнениях, составленных для последних
двух узлов, будет только одна неизвестная величина –
усилие в последнем стержне. Оставшиеся три уравнения
должны выполняться тождественно, то есть выполняют
роль проверочных уравнений.
94.
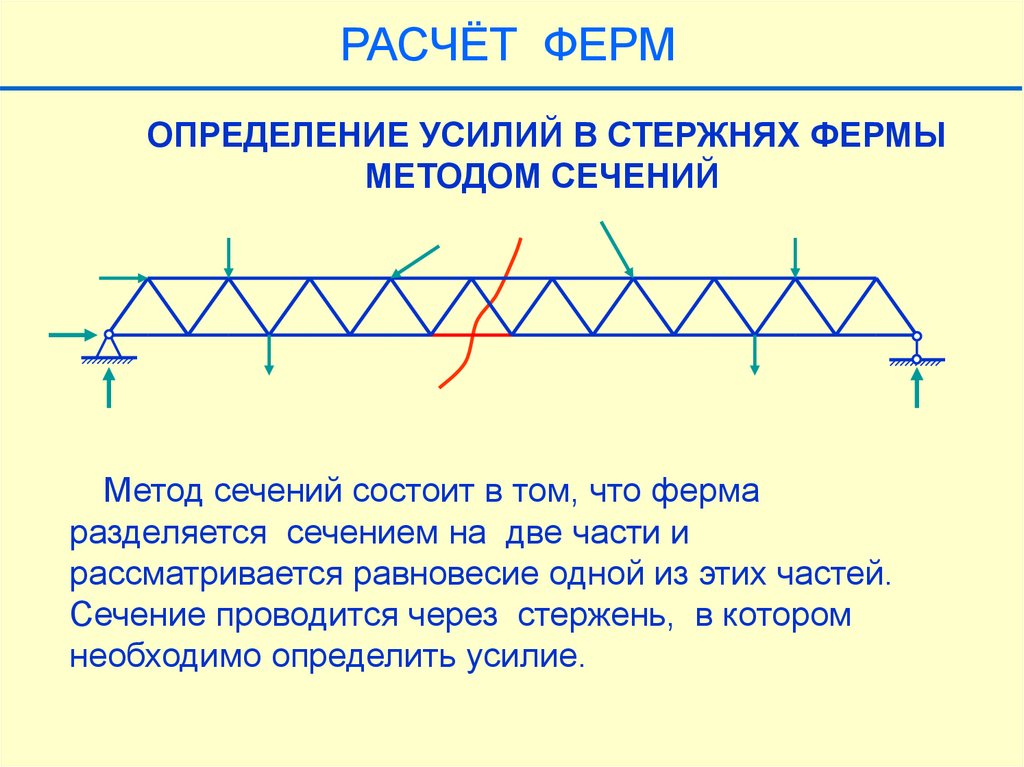
РАСЧЁТ ФЕРМОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ФЕРМЫ
МЕТОДОМ СЕЧЕНИЙ
Метод сечений состоит в том, что ферма
разделяется сечением на две части и
рассматривается равновесие одной из этих частей.
Сечение проводится через стержень, в котором
необходимо определить усилие.
95.
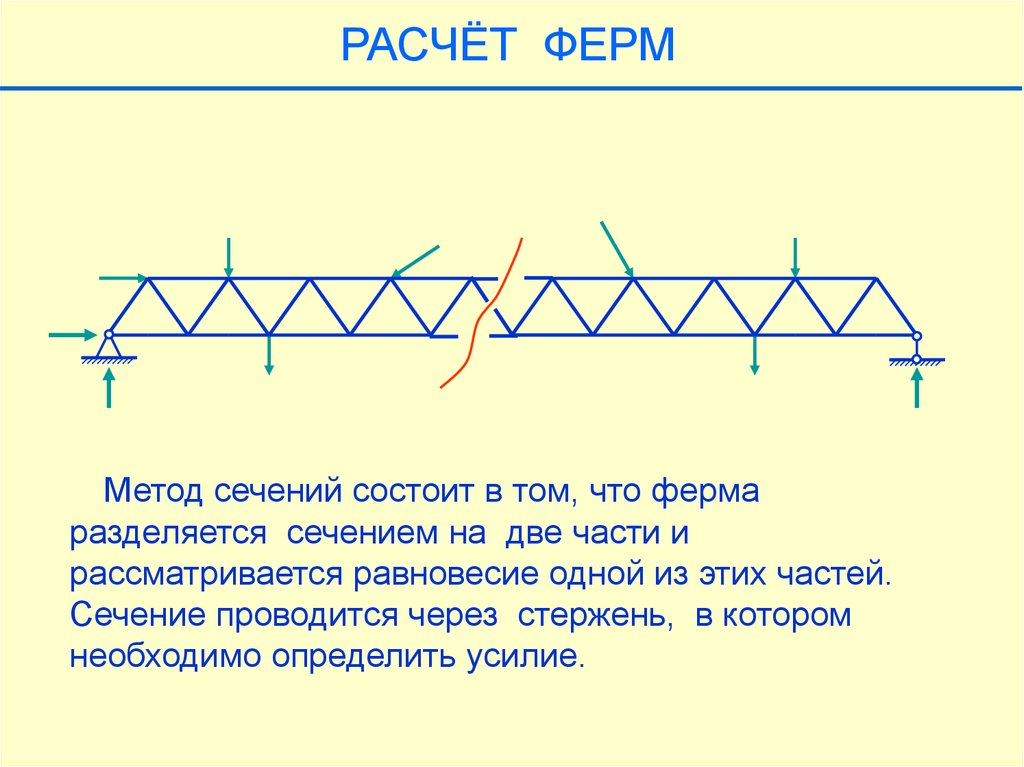
РАСЧЁТ ФЕРММетод сечений состоит в том, что ферма
разделяется сечением на две части и
рассматривается равновесие одной из этих частей.
Сечение проводится через стержень, в котором
необходимо определить усилие.
96.
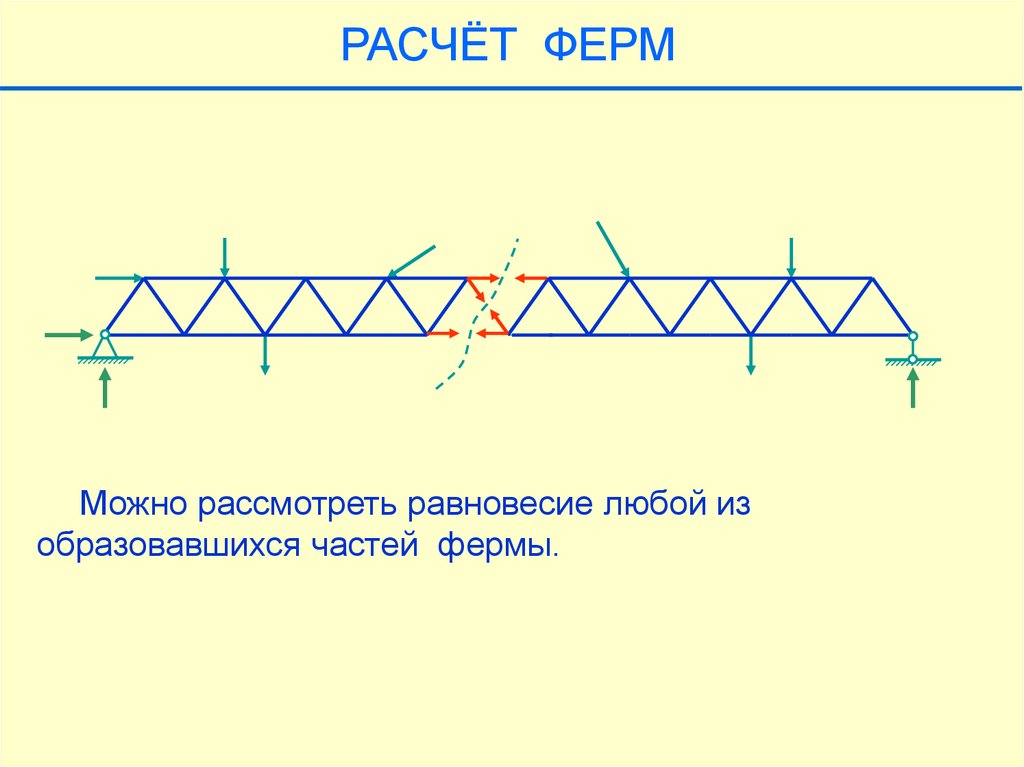
РАСЧЁТ ФЕРММожно рассмотреть равновесие любой из
образовавшихся частей фермы.
97.
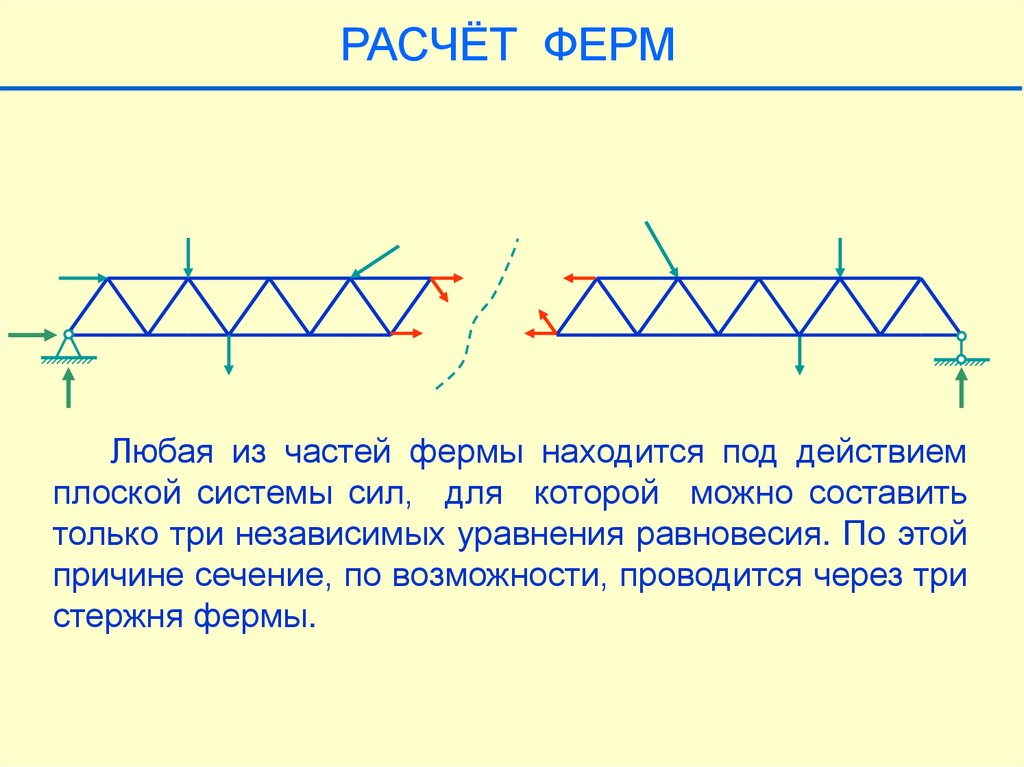
РАСЧЁТ ФЕРМЛюбая из частей фермы находится под действием
плоской системы сил, для которой можно составить
только три независимых уравнения равновесия. По этой
причине сечение, по возможности, проводится через три
стержня фермы.
98.
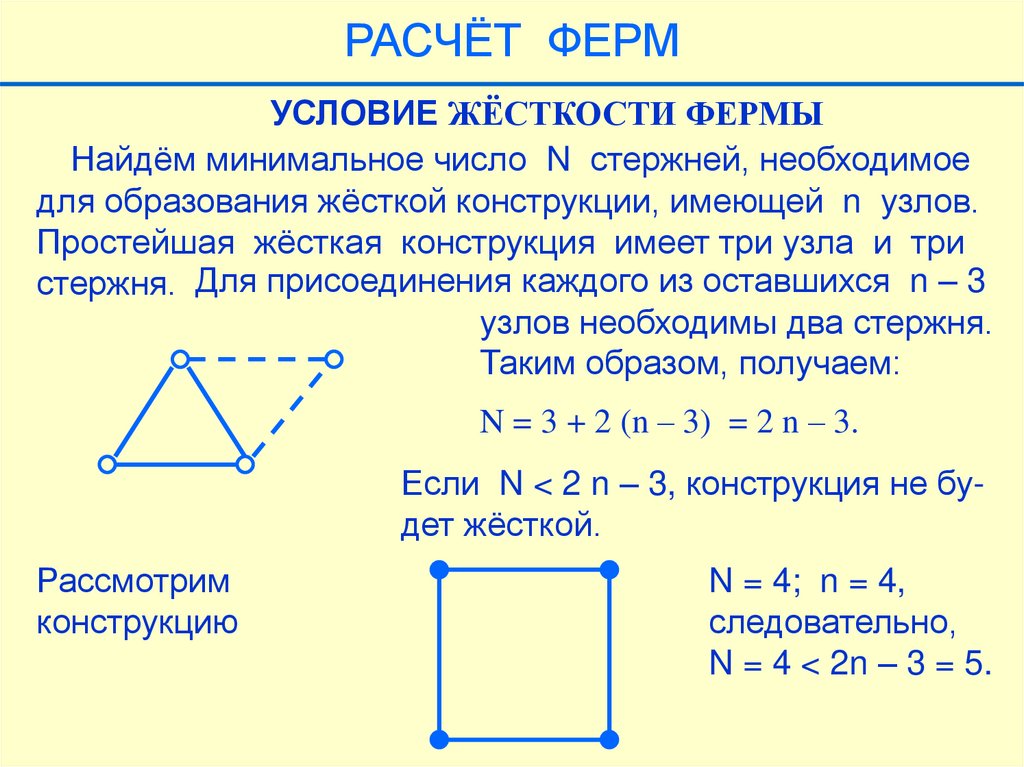
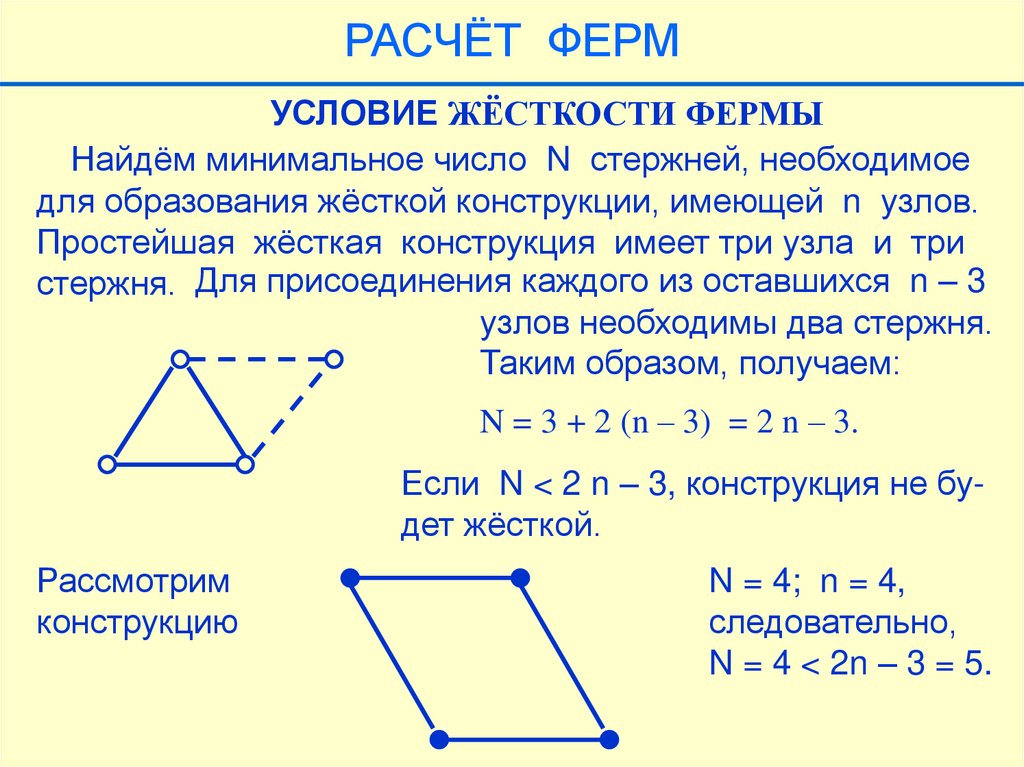
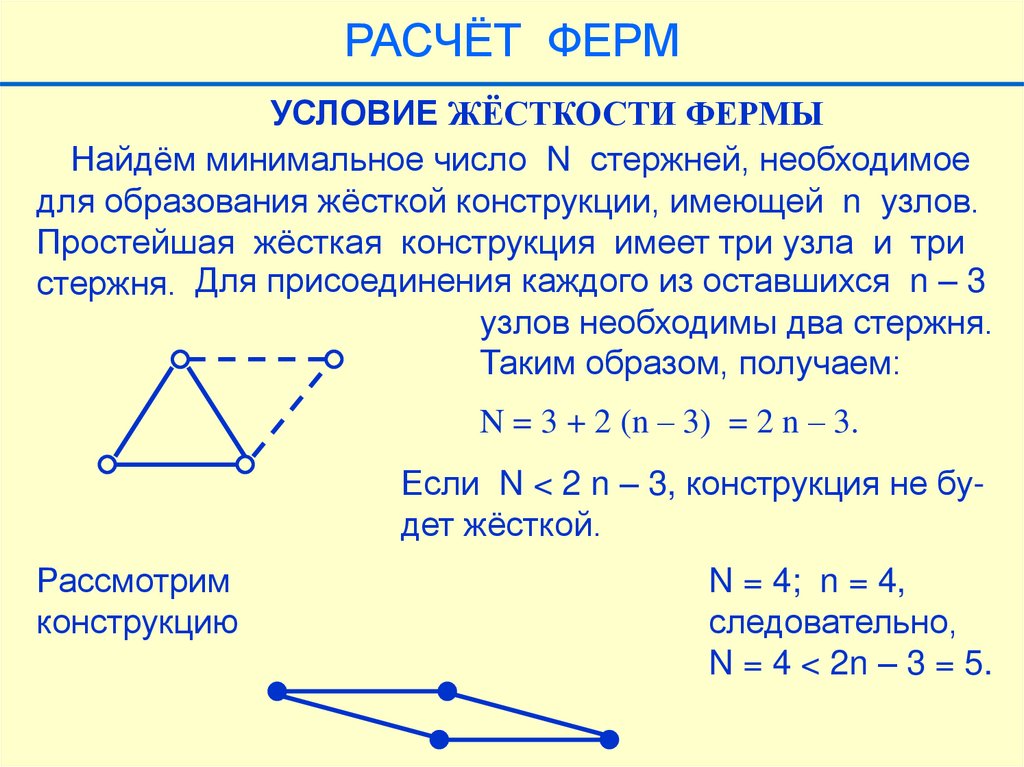
РАСЧЁТ ФЕРМУСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
Найдём минимальное число N стержней, необходимое
для образования жёсткой конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня. Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не будет жёсткой.
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
99.
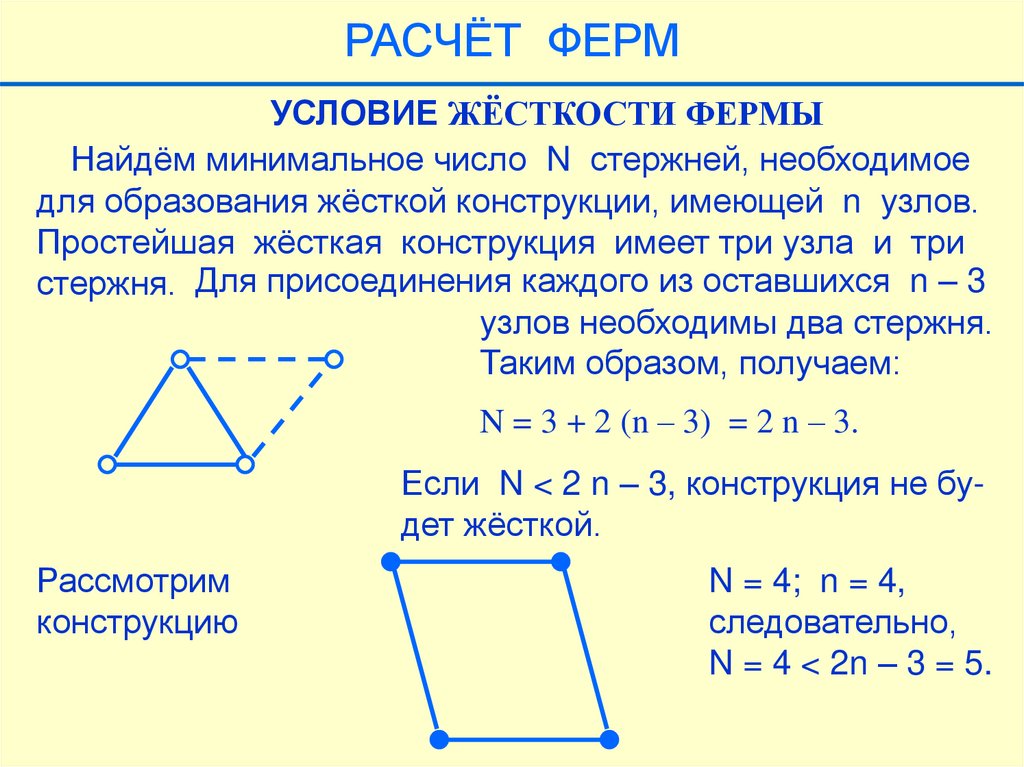
РАСЧЁТ ФЕРМУСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
Найдём минимальное число N стержней, необходимое
для образования жёсткой конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня. Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не будет жёсткой.
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
100.
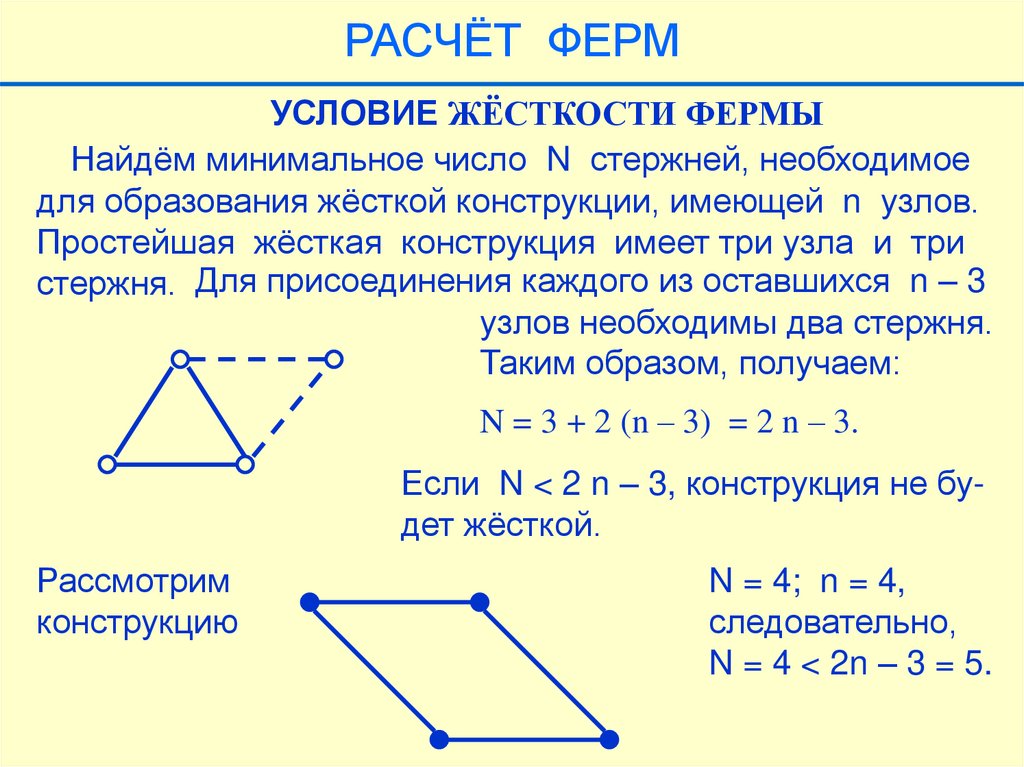
РАСЧЁТ ФЕРМУСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
Найдём минимальное число N стержней, необходимое
для образования жёсткой конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня. Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не будет жёсткой.
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
101.
РАСЧЁТ ФЕРМУСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
Найдём минимальное число N стержней, необходимое
для образования жёсткой конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня. Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не будет жёсткой.
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
102.
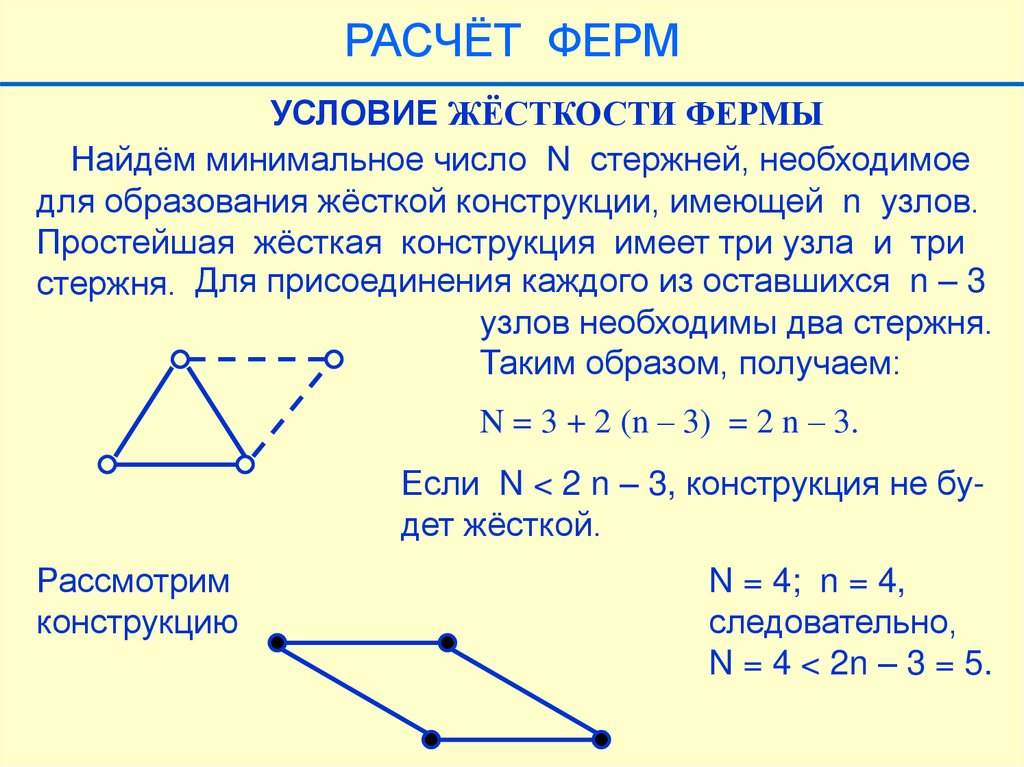
РАСЧЁТ ФЕРМУСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
Найдём минимальное число N стержней, необходимое
для образования жёсткой конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня. Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не будет жёсткой.
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
103.
РАСЧЁТ ФЕРМУСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
Найдём минимальное число N стержней, необходимое
для образования жёсткой конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня. Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не будет жёсткой.
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
104.
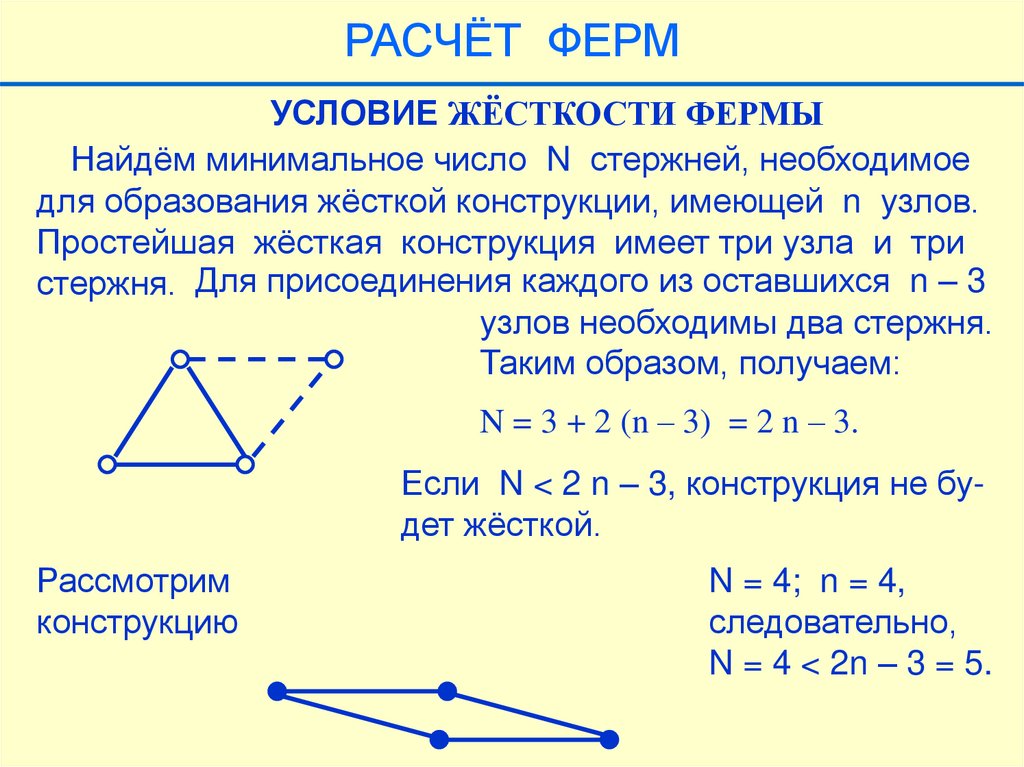
РАСЧЁТ ФЕРМУСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
Найдём минимальное число N стержней, необходимое
для образования жёсткой конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня. Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не будет жёсткой.
Рассмотрим
конструкцию
N = 4; n = 4,
следовательно,
N = 4 < 2n – 3 = 5.
105.
РАСЧЁТ ФЕРМУСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
Найдём минимальное число N стержней, необходимое
для образования жёсткой конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня. Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не будет жёсткой.
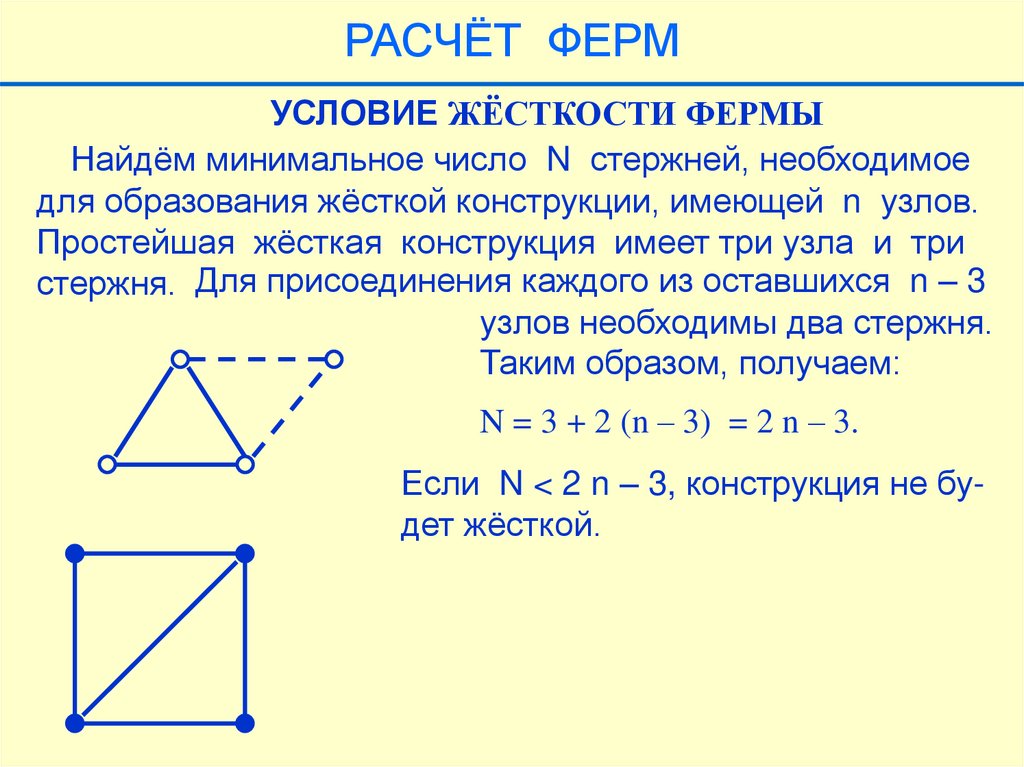
Такая конструкция не является фермой – это механизм.
Как следует из формулы N = 2n – 3, для обеспечения
жёсткости конструкции необходимо при том же количестве
узлов установить ещё один стержень.
106.
РАСЧЁТ ФЕРМУСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
Найдём минимальное число N стержней, необходимое
для образования жёсткой конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня. Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
N = 3 + 2 (n – 3) = 2 n – 3.
Если N < 2 n – 3, конструкция не будет жёсткой.
107.
РАСЧЁТ ФЕРМУСЛОВИЕ ЖЁСТКОСТИ ФЕРМЫ
Найдём минимальное число N стержней, необходимое
для образования жёсткой конструкции, имеющей n узлов.
Простейшая жёсткая конструкция имеет три узла и три
стержня. Для присоединения каждого из оставшихся n – 3
узлов необходимы два стержня.
Таким образом, получаем:
N = 3 + 2 (n – 3) = 2 n – 3.
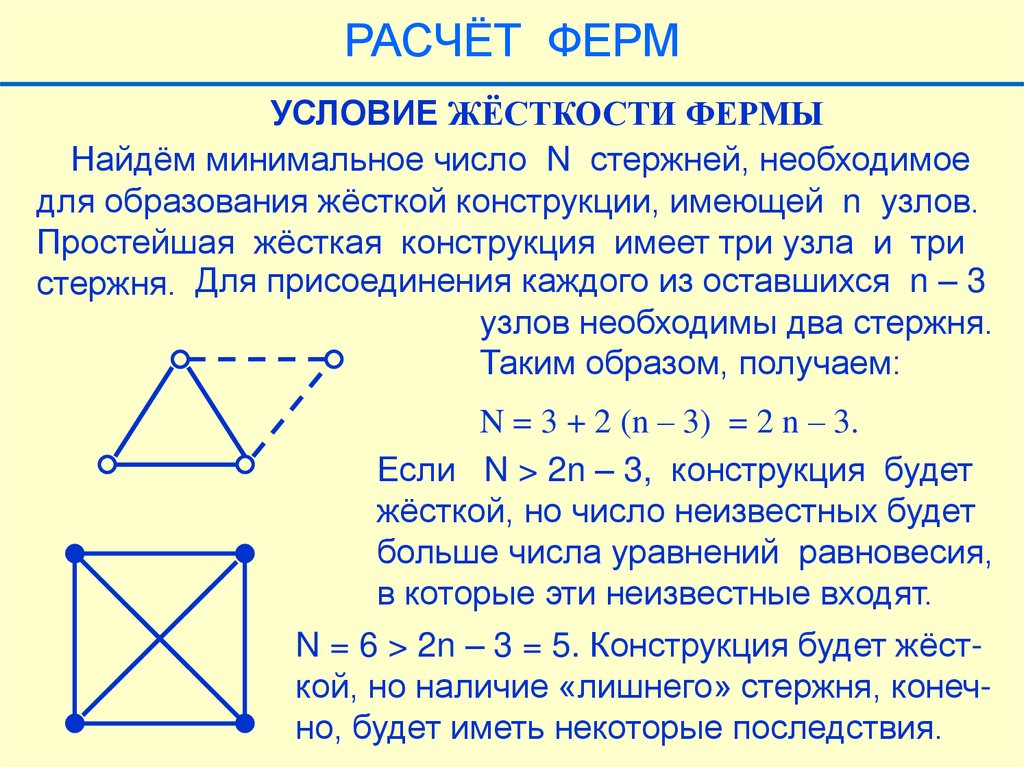
Если N > 2n – 3, конструкция будет
жёсткой, но число неизвестных будет
больше числа уравнений равновесия,
в которые эти неизвестные входят.
N = 6 > 2n – 3 = 5. Конструкция будет жёсткой, но наличие «лишнего» стержня, конечно, будет иметь некоторые последствия.
108.
РАСЧЁТ ФЕРМУСЛОВИЕ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ ФЕРМЫ
Ферма называется статически определимой, если число неизвестных равно числу уравнений равновесия, в которые эти неизвестные входят. Для фермы, имеющей n
узлов, можно составить 2n независимых уравнений равновесия. В число неизвестных входят N усилий в стержнях фермы и три составляющие реакций внешних опор.
Таким образом, ферма будет статически определимой
при выолнении условия
N = 2n – 3,
которое, как видно, совпадает с условием жёсткости.
109.
РАСЧЁТ ФЕРМУСЛОВИЕ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ ФЕРМЫ
«Лишние» опоры – ненужные для обеспечения
равновесия абсолютно твёрдого тела – могут появиться
по двум основным причинам.
Во-первых, причины могут быть технологическими:
перекрытие кладётся на две стены, хотя теоретически
можно было бы обойтись одной заделкой.
Во-вторых, дополнительные опоры приходится
устанавливать,
чтобы предотвратить недопустимо
большие
деформации, опасные для прочности
конструкции.
110.
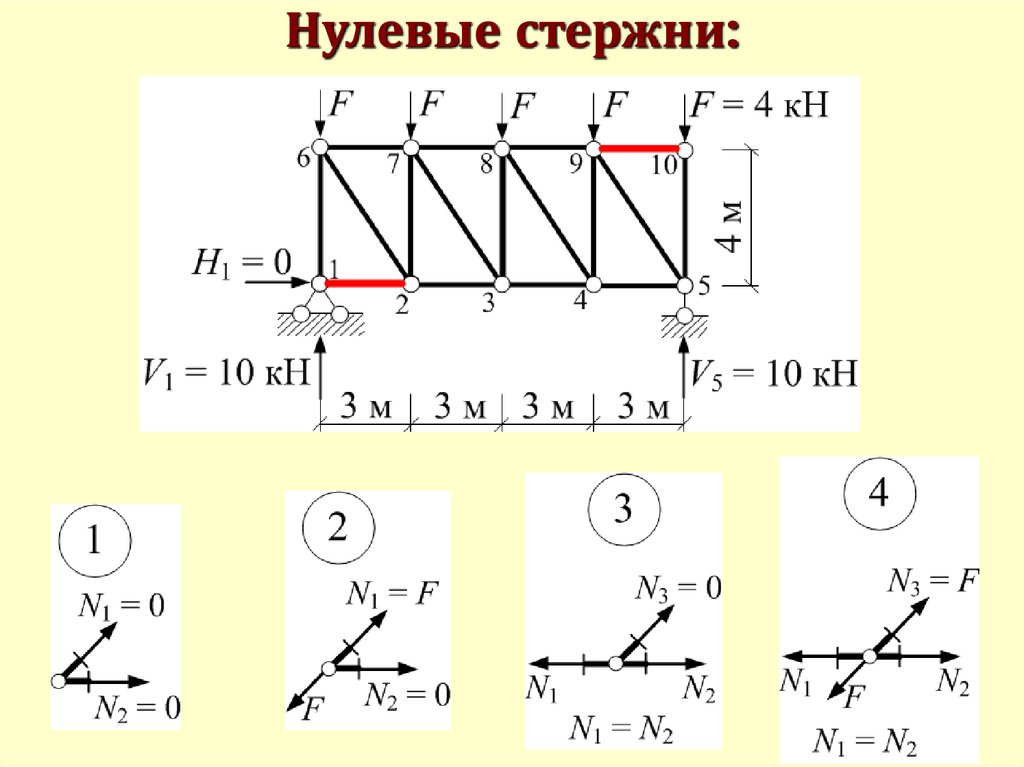
Нулевые стержни:111.
Нулевые стержни:112.
Нулевые стержни:113. Способ вырезания узлов
y2N1
N2
114.
Метод сечений:115.
Метод сечений:116.
117.
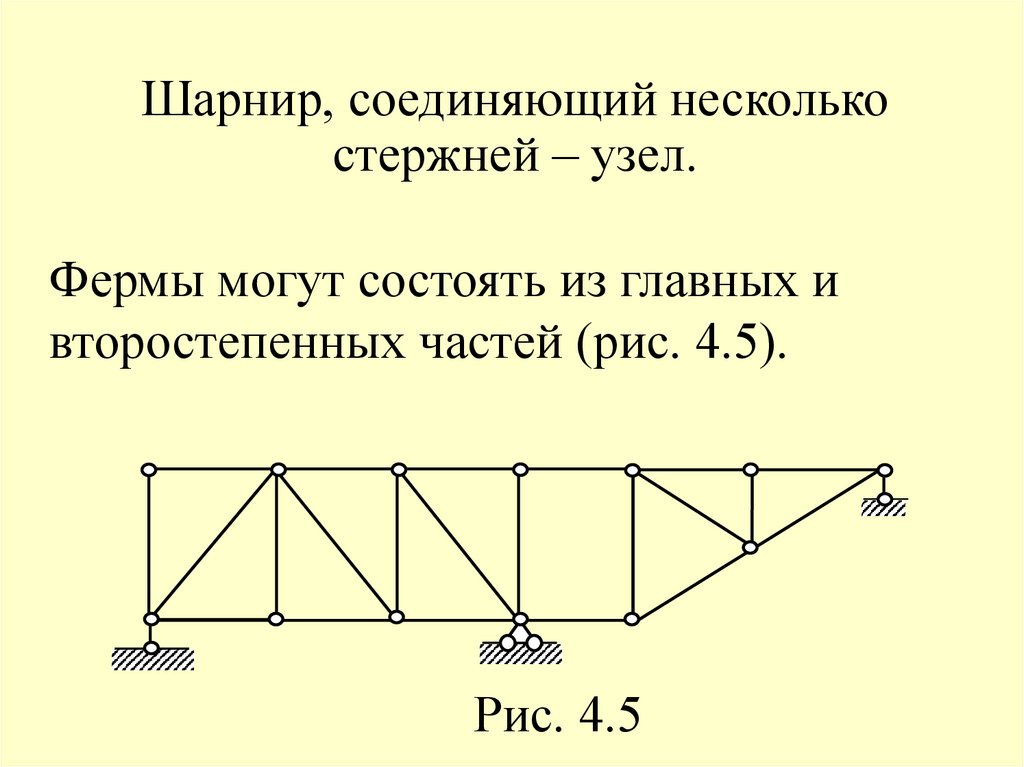
Шарнир, соединяющий несколькостержней – узел.
Фермы могут состоять из главных и
второстепенных частей (рис. 4.5).
Рис. 4.5
118.
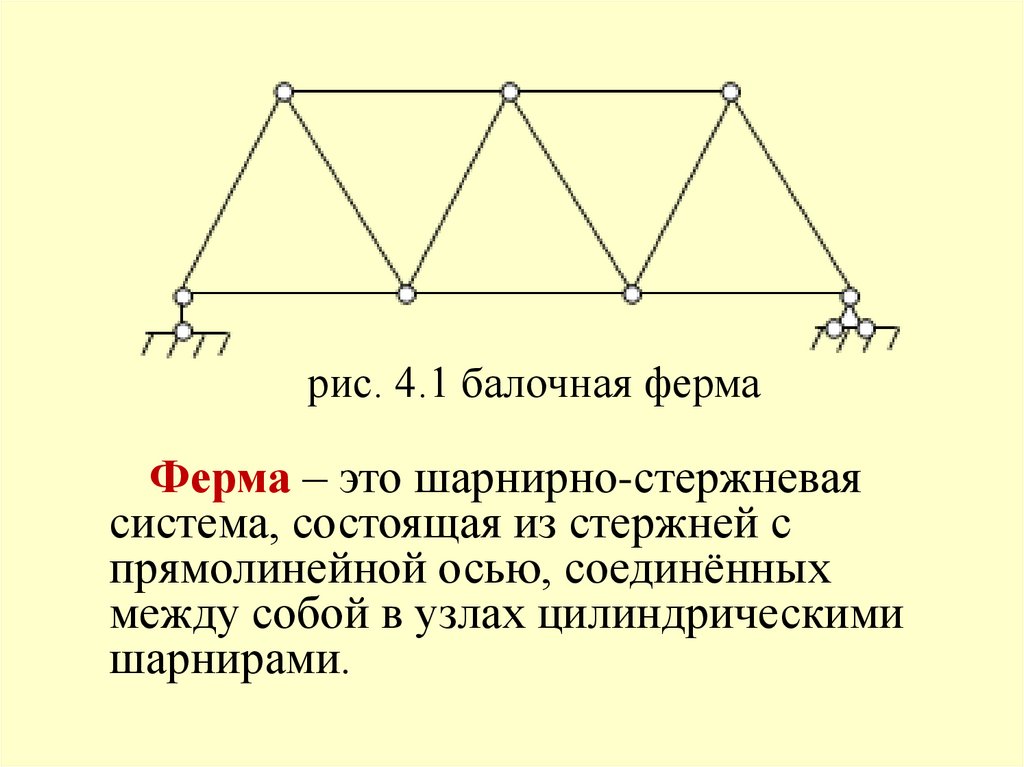
рис. 4.1 балочная фермаФерма – это шарнирно-стержневая
система, состоящая из стержней с
прямолинейной осью, соединённых
между собой в узлах цилиндрическими
шарнирами.
119.
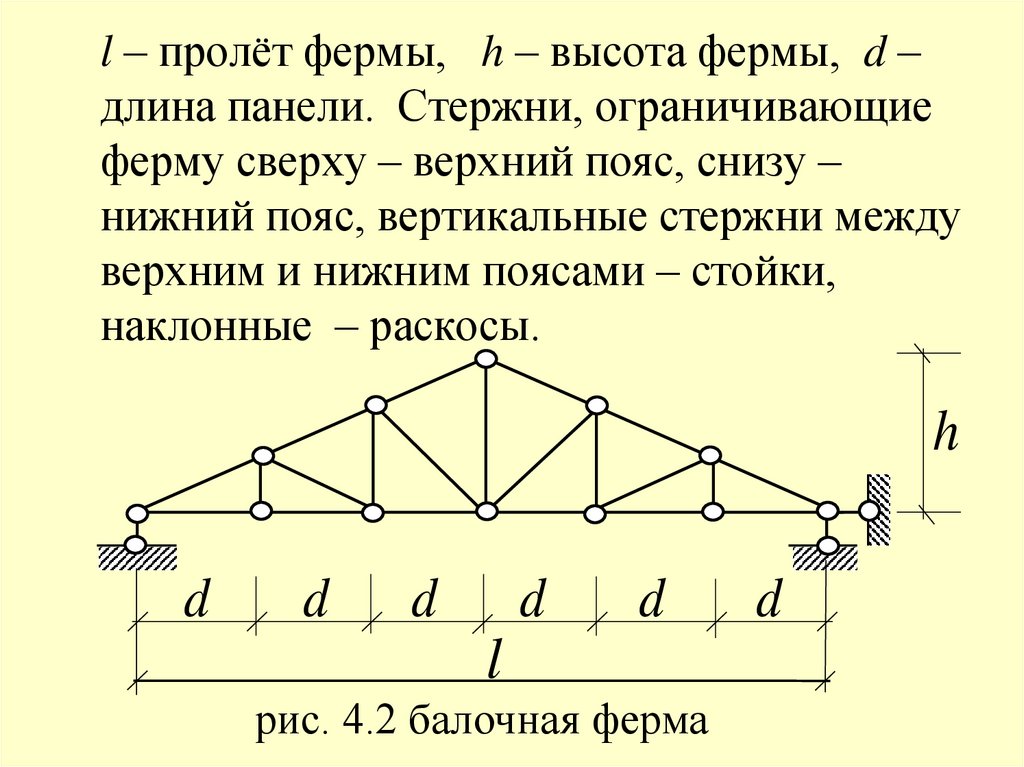
l – пролёт фермы, h – высота фермы, d –длина панели. Стержни, ограничивающие
ферму сверху – верхний пояс, снизу –
нижний пояс, вертикальные стержни между
верхним и нижним поясами – стойки,
наклонные – раскосы.
h
d
d
d
d
d
l
рис. 4.2 балочная ферма
d
120.
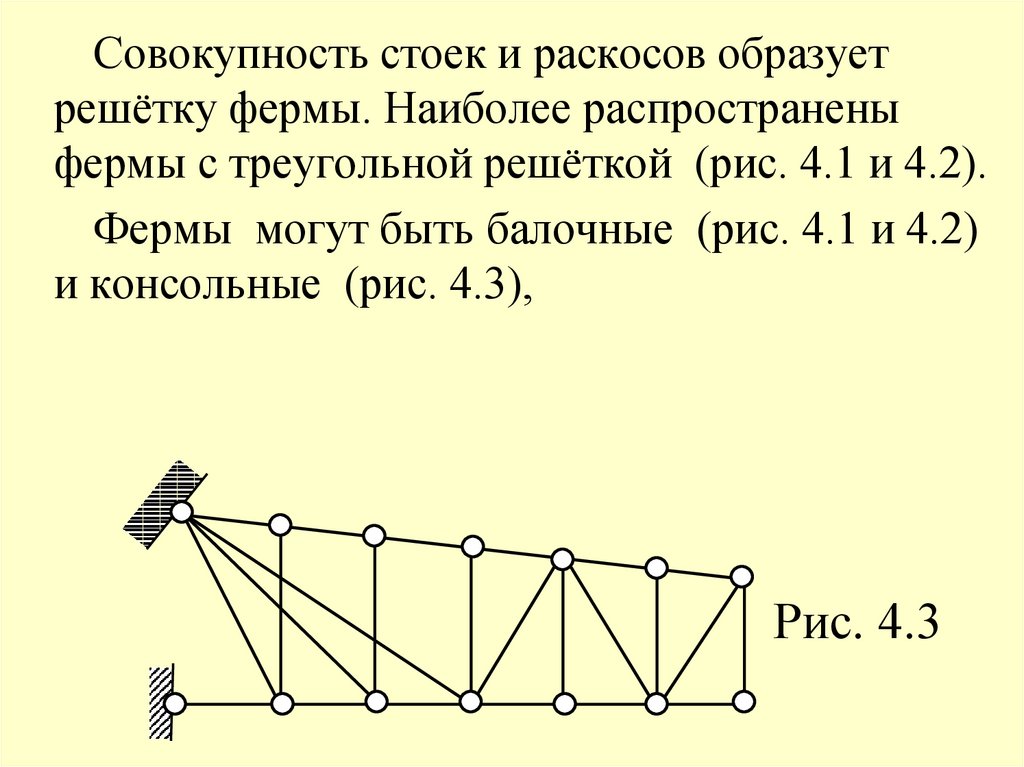
Совокупность стоек и раскосов образуетрешётку фермы. Наиболее распространены
фермы с треугольной решёткой (рис. 4.1 и 4.2).
Фермы могут быть балочные (рис. 4.1 и 4.2)
и консольные (рис. 4.3),
Рис. 4.3
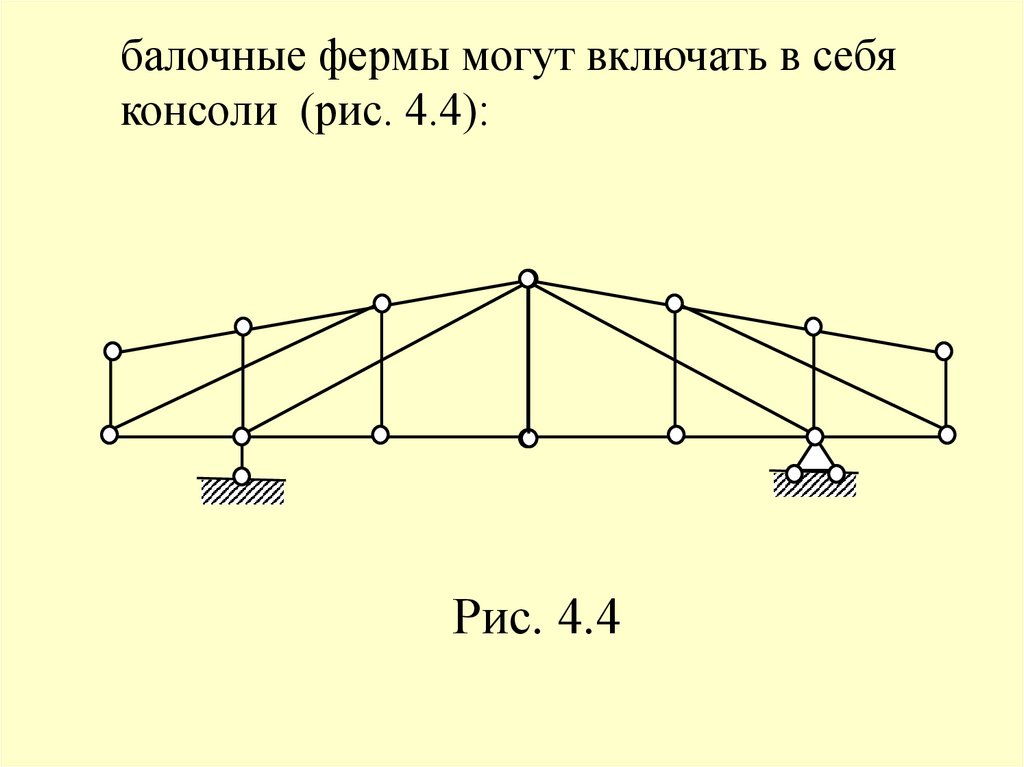
121.
балочные фермы могут включать в себяконсоли (рис. 4.4):
Рис. 4.4
122.
Кинематический анализ фермНеобходимое условие геометрической
неизменяемости: W = nD– nc 0
а) по общей формуле:
Вычисление W:
W = 3D – 2H – C0 – для плоской фермы
5D – 3H – C0 – для пространственной фермы
( D = числу стержней фермы)
б) по специальной формуле для ферм:
2Y – C – C0 – для плоской фермы
W = 3Y – C – C – для пространственной фермы
0
( C – число стержней фермы; Y – количество узлов)















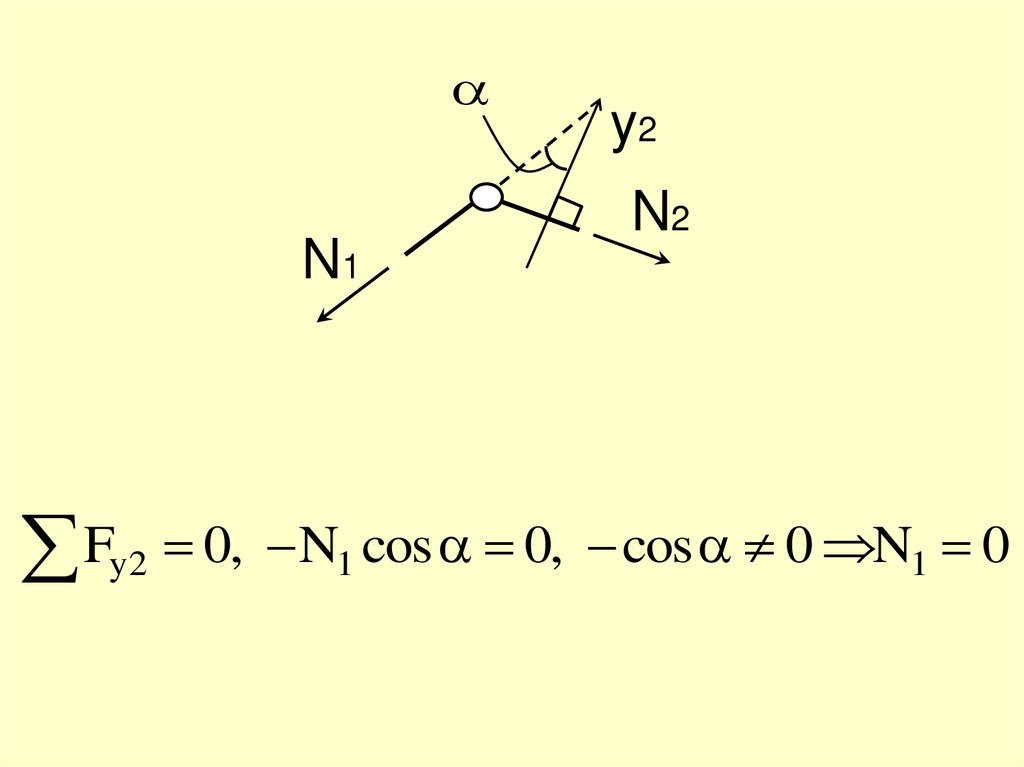



















 Механика
Механика