‫טענות הקשורות‬ ‫להערכה במתמטיקה‬

1.

‫טענות הקשורות‬
‫להערכה במתמטיקה‬

2.

‫טענה ‪1‬‬
‫‪ ‬ללמוד מתמטיקה זה לשלוט במספר מיומנויות מתמטיות בסיסיות‪ .‬לכן‪ ,‬מבחנים‬
‫במתמטיקה צריכים להתמקד בבדיקת השליטה במיומנויות אלה אצל תלמידים‪.‬‬
‫מיומנויות למידה בסיסיות‪ :‬קריאה‪ ,‬הבנת הנקרא‪ ,‬איות‪ ,‬הבעה בכתב‪ ,‬חישוב והבנה מתמטית‪.‬‬
‫התשובה לטענה‪:‬‬
‫מיומנויות עבור המתמטיקה הן מה שסולמות עבור מוסיקה‬
‫או איות עבור כתיבה‪.‬‬
‫אמצעי ללמידה הוא כתיבה‪ ,‬המטרה במוסיקה היא לנגן‪,‬‬
‫המטרה במתמטיקה היא לפתור בעיות – לא רק לשלוט במיומנויות‪.‬‬
‫על תלמיד‪ ,‬מעבר לשליטה במיומנות החישוב‪ ,‬לשלוט במיומנות ההבנה המתמטית‪,‬‬
‫שפירושה שליטה בשימוש בעובדות מתמטיות‪ ,‬פרוצדורות ומושגים מתמטיים‬
‫המובילים בבטחה את התלמיד לפתרון בעיות‪.‬‬
‫כשמטרות הלמידה שלנו משתנות גם כלי ההערכה שלנו חייבים להשתנות‪.‬‬

3.

‫טענה ‪2‬‬
‫‪ ‬תלמידים לומדים רק על ידי חיקוי ושינון‪.‬‬
‫התשובה לטענה‪:‬‬
‫תלמידים משתמשים במה שהם למדו לא רק לרישום ואחסון‪.‬‬
‫תלמיד בונה ידע ומפתח חשיבה מתמטית וזה מאפשר לו לפתור בעיות גם‬
‫אם לא ראה אותן לפני כן‪ .‬למידה נכונה ומובנית מתקיימת באמצעות שאלות חקר‬
‫והעלאת רמות החשיבה משאלה לשאלה‪.‬‬
‫הערכה יעילה כמו גם הוראה יעילה‪ ,‬חייבת לשקף מציאות זו‪.‬‬

4.

‫טענה ‪3‬‬
‫‪ ‬לבעיה מתמטית יש תשובה נכונה אחת‪.‬‬
‫התשובה לטענה‪:‬‬
‫בעיות עם תשובה נכונה אחת נדירות בחיי היום יום‪.‬‬
‫עלינו לחשוף את התלמידים לשאלות‪ ,‬שלהן מספר תשובות אפשריות ואף ללמדם‬
‫להכליל‪.‬‬

5.

‫טענה ‪4‬‬
‫‪ ‬מטרת ההערכה היא לקבוע לאילו תלמידים "יש את זה" ולמי לא ובהתאם לתת‬
‫ציונים ולדרג את התלמידים‪.‬‬
‫התשובה לטענה‪:‬‬
‫בעולם בו מאמינים היום‪ ,‬שכל התלמידים יכולים להצליח ושכולם יכולים וצריכים‬
‫ללמוד מתמטיקה‪ ,‬יש פחות ופחות מקום להערכה מסורתית המדרגת ומתייגת‬
‫תלמידים‪.‬‬
‫בהערכה מסורתית ציון במבחן הוא בעל אותה המשמעות לכל התלמידים ומעריכים בה רק תוצרים‪,‬‬
‫בעיקר באמצעות כלים של "נייר ועיפרון"‪.‬‬
‫היום הצורך הוא במגוון שיטות הערכה‪ ,‬המחוברות להוראה‪.‬‬
‫הערכה המאבחנת והמיידעת‪ ,‬מחזקת הן את המורים והן את התלמידים‪.‬‬

6.

‫טענה ‪5‬‬
‫‪ ‬מבחנים אובייקטיביים רב ברירתיים‪ ,‬הינם הדרך הטובה ביותר למדוד את‬
‫הרעיונות החשובים ביותר במתמטיקה‪.‬‬
‫התשובה לטענה‪:‬‬
‫יש מרכיבים בלמידת מתמטיקה שניתן למדוד אותם רק בדרכים שונות מהמבחנים‬
‫הסטנדרטיים‪.‬‬
‫למשל‪,‬‬
‫האם תלמיד יכול להציג‪ ,‬לסכם ולפרש נתונים?‬
‫האם הוא יכול לפרש ביעילות את התשובה שהמחשב מראה?‬
‫האם הוא יכול לשוחח על הרעיונות המתמטיים שלו?‬
‫האם הוא יכול להתמיד בעבודה על פתרון בעיה?‬
‫האם הוא ימשיך מעבר לבעיה המיידית‪ ,‬ויבדוק "מה יקרה אם…"?‬
‫האם תלמיד יכול להסביר במילים שלו את דרך פתרונו?‬
‫האם יכול לנמק? להכליל?‬

7.

‫טענה ‪6‬‬
‫‪ ‬הציונים של תלמידי הכתה צריכים להראות‬
‫בצורת עקומת פעמון‬
‫(עקומת גאוס‪-‬התפלגות נורמאלית)‪.‬‬
‫התשובה לטענה‪:‬‬
‫המטרה של הוראה יעילה היא לשנות התפלגות כזו ולאפשר‬
‫לתלמידים להגיע להערכה גבוהה ולא ממוצעת‪.‬‬

8.

‫טענה ‪7‬‬
‫‪ ‬דרכים אלטרנטיביות להערכה הינן פחות אובייקטיביות‪ ,‬לעומת הצורות המסורתיות‬
‫של מבחנים‪.‬‬
‫הדרכים החדשות הן שיגעון חולף‪.‬‬
‫התשובה לטענה‪:‬‬
‫מערכת החינוך משתמשת בהערכות חלופיות‪ ,‬המאפשרות לקבל החלטות בהסתמך‬
‫על מרחב גדול ומגוון יותר של נתונים‪.‬‬
‫הערכת תלמיד אפשרית גם על ידי‪:‬‬
‫היכולת לנסח בעיות‪ ,‬להעלות ולבדוק השערות‪ ,‬לפתור בעיות הדורשות זמן‬
‫ומחשבה‪ ,‬עקביות‪ ,‬גמישות‪ ,‬הכללות‪.‬‬

9.

‫הערכה‬
‫תיאור ושפיטה של דברים שונים למטרות שונות‪.‬‬
‫אובייקט ההערכה‪:‬‬
‫הדבר שאותו אנו מעריכים‪.‬‬
‫בעבר היה זה התלמיד בלבד‪.‬‬
‫משנות ה ‪ 60 -‬יש הרחבה לאובייקטים נוספים‪ :‬תכניות לימודים‪ ,‬פרויקטים חינוכיים…‬
‫בשנות ה ‪ 90 -‬נכנסה גם הערכה של המורה‪.‬‬
‫תפקידי ההערכה‪:‬‬
‫למבחן יש השפעה על סוג הלמידה שהוא מעודד‪.‬‬
‫באמצעות המבחן המורה משדר לתלמיד מה חשוב ומה עליו ללמוד‪.‬‬
‫מורה יכול לדבר על חשיבות ההבנה ולתת מבחן עם אוסף של תרגילים טכניים‪.‬‬
‫המסר לתלמידים ברור‪ :‬מה שחשוב זה הטכניקה ולא ההבנה‪.‬‬
‫חבל לבזבז זמן על הבנה כשאפשר לפתור עוד ועוד סוגים של תרגילים ובכך להצליח יותר במבחן‪.‬‬
‫מאמר של דוד נבו‪:‬‬
‫"ההערכה ככלי לשיפור ההוראה והלמידה"‪.‬‬

10.

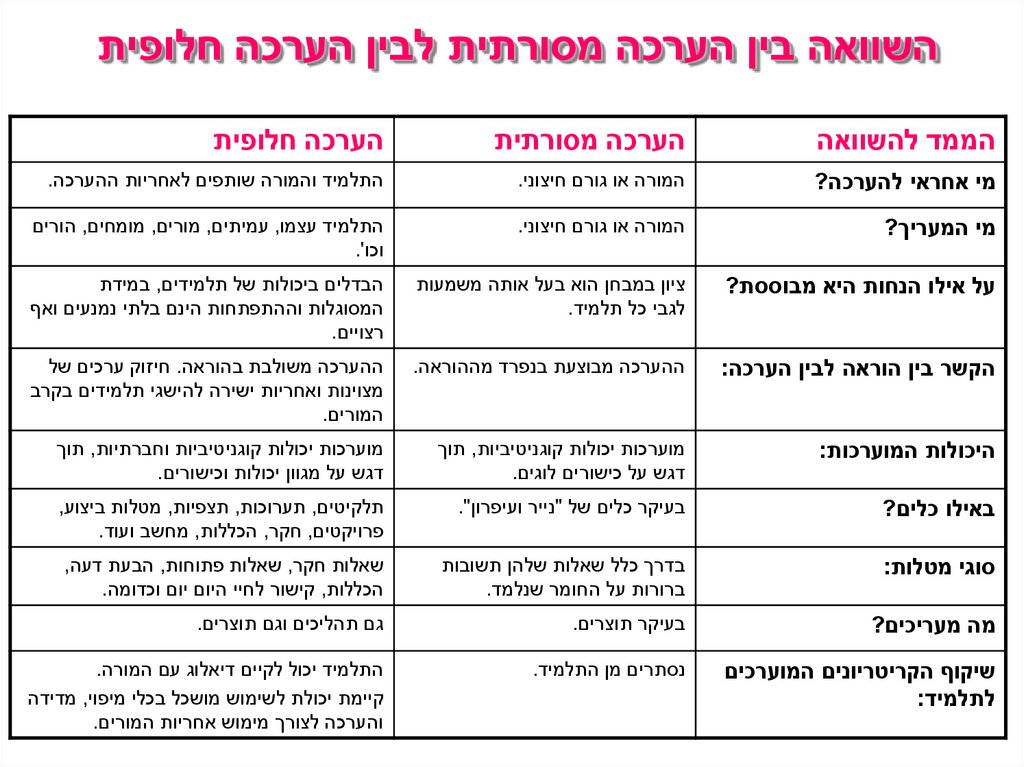
‫השוואה בין הערכה מסורתית לבין הערכה חלופית‬
‫הממד להשוואה‬
‫הערכה מסורתית‬
‫הערכה חלופית‬
‫מי אחראי להערכה?‬
‫המורה או גורם חיצוני‪.‬‬
‫התלמיד והמורה שותפים לאחריות ההערכה‪.‬‬
‫מי המעריך?‬
‫המורה או גורם חיצוני‪.‬‬
‫התלמיד עצמו‪ ,‬עמיתים‪ ,‬מורים‪ ,‬מומחים‪ ,‬הורים‬
‫וכו'‪.‬‬
‫על אילו הנחות היא מבוססת?‬
‫ציון במבחן הוא בעל אותה משמעות‬
‫לגבי כל תלמיד‪.‬‬
‫הבדלים ביכולות של תלמידים‪ ,‬במידת‬
‫המסוגלות וההתפתחות הינם בלתי נמנעים ואף‬
‫רצויים‪.‬‬
‫הקשר בין הוראה לבין הערכה‪:‬‬
‫ההערכה מבוצעת בנפרד מההוראה‪.‬‬
‫ההערכה משולבת בהוראה‪ .‬חיזוק ערכים של‬
‫מצוינות ואחריות ישירה להישגי תלמידים בקרב‬
‫המורים‪.‬‬
‫היכולות המוערכות‪:‬‬
‫מוערכות יכולות קוגניטיביות‪ ,‬תוך‬
‫דגש על כישורים לוגים‪.‬‬
‫מוערכות יכולות קוגניטיביות וחברתיות‪ ,‬תוך‬
‫דגש על מגוון יכולות וכישורים‪.‬‬
‫באילו כלים?‬
‫בעיקר כלים של "נייר ועיפרון"‪.‬‬
‫תלקיטים‪ ,‬תערוכות‪ ,‬תצפיות‪ ,‬מטלות ביצוע‪,‬‬
‫פרויקטים‪ ,‬חקר‪ ,‬הכללות‪ ,‬מחשב ועוד‪.‬‬
‫סוגי מטלות‪:‬‬
‫בדרך כלל שאלות שלהן תשובות‬
‫ברורות על החומר שנלמד‪.‬‬
‫שאלות חקר‪ ,‬שאלות פתוחות‪ ,‬הבעת דעה‪,‬‬
‫הכללות‪ ,‬קישור לחיי היום יום וכדומה‪.‬‬
‫מה מעריכים?‬
‫בעיקר תוצרים‪.‬‬
‫גם תהליכים וגם תוצרים‪.‬‬
‫שיקוף הקריטריונים המוערכים‬
‫לתלמיד‪:‬‬
‫נסתרים מן התלמיד‪.‬‬
‫התלמיד יכול לקיים דיאלוג עם המורה‪.‬‬
‫קיימת יכולת לשימוש מושכל בכלי מיפוי‪ ,‬מדידה‬
‫והערכה לצורך מימוש אחריות המורים‪.‬‬

11.

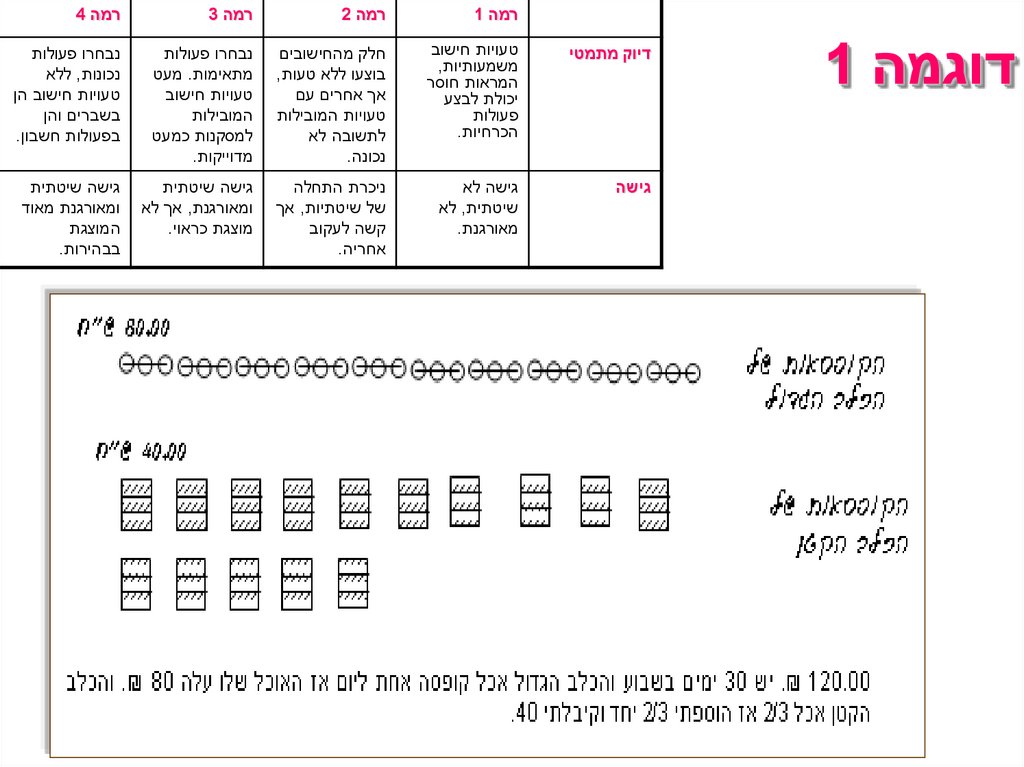
‫‪A collection of performance tasks and rubrics. Upper elementary school. Charlotte Danielson. 1977. p. 84‬‬
‫אוכל לכלבים‬
‫למשפחתו של עומר שני כלבים‪ ,‬נט ושוגי‪.‬‬
‫נט היא כלבה גדולה ואוכלת קופסת מזון שלמה כל יום‪.‬‬
‫שוגי הוא כלב קטן יותר ואוכל רק ‪ 2/3‬הקופסא ליום‪.‬‬
‫מחיר חבילה בה ‪ 3‬קופסאות מזון הוא ‪.₪ 8‬‬
‫כמה יעלה למשפחתו של עומר להאכיל את הכלבים כל חודש?‬
‫נט‬
‫שוגי‬
‫הצג את דרך העבודה שלך (שרטוטים‪ ,‬חישובים‪ ,‬הסברים)‬
‫באופן שתלמיד אחר יוכל להסביר איך הגעת לפתרון שלך‪.‬‬

12.

‫‪ ‬‬
‫‪ ‬‬
‫‪ ‬‬
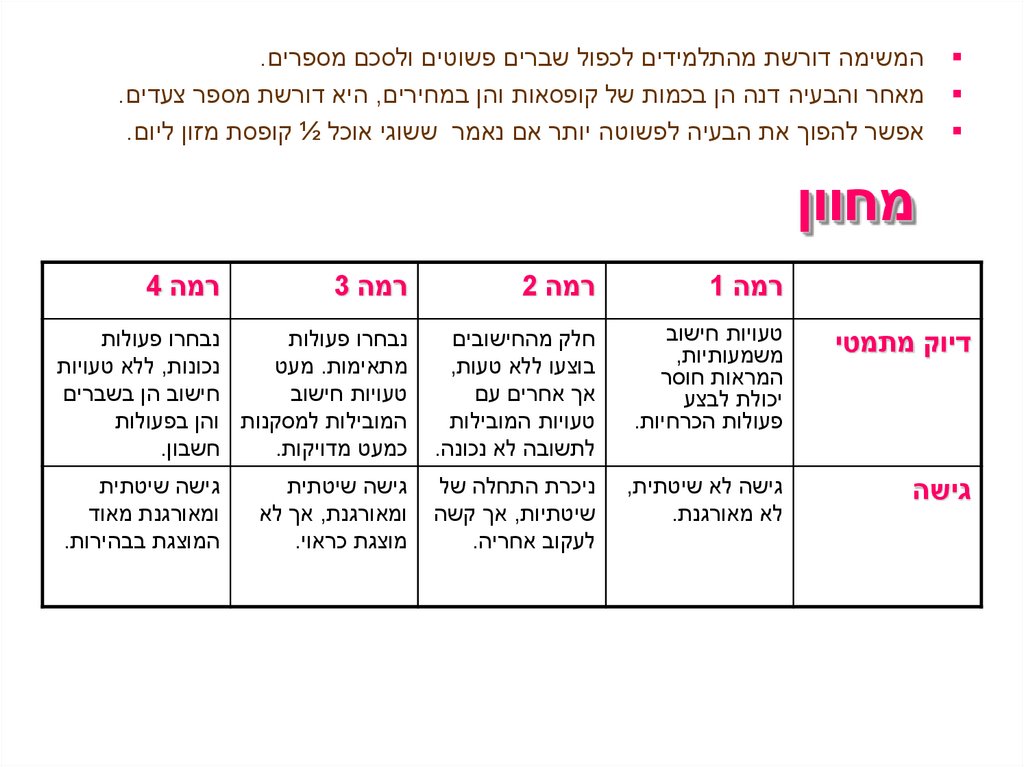
‫המשימה דורשת מהתלמידים לכפול שברים פשוטים ולסכם מספרים‪.‬‬
‫מאחר והבעיה דנה הן בכמות של קופסאות והן במחירים‪ ,‬היא דורשת מספר צעדים‪.‬‬
‫אפשר להפוך את הבעיה לפשוטה יותר אם נאמר ששוגי אוכל ½ קופסת מזון ליום‪.‬‬
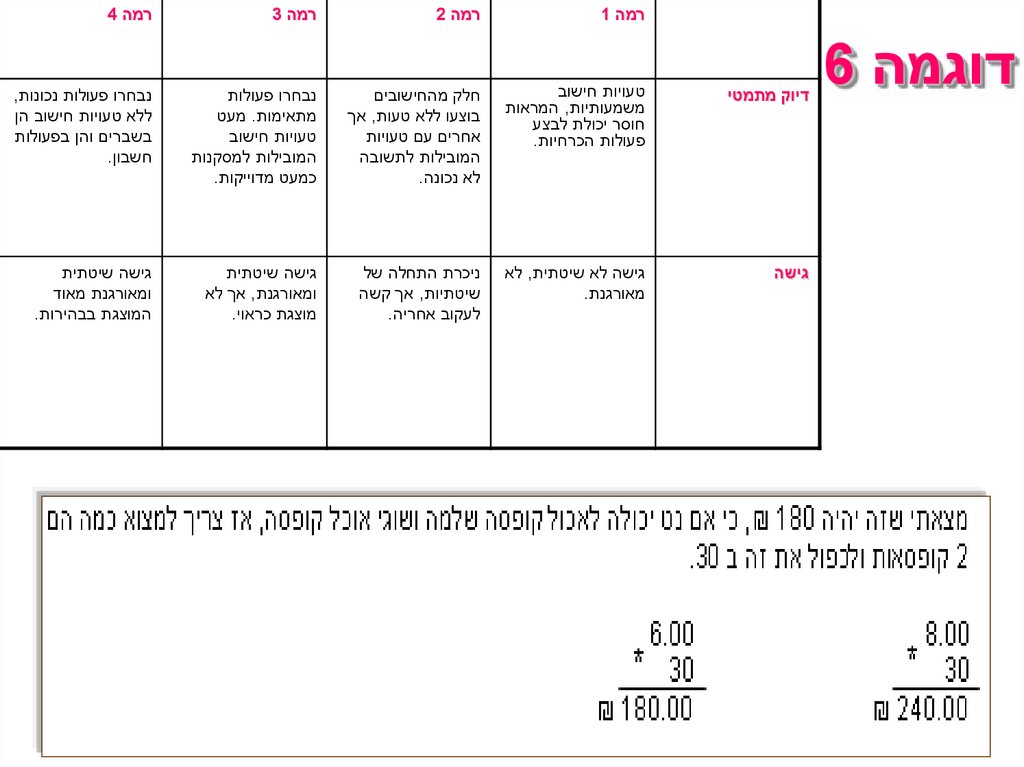
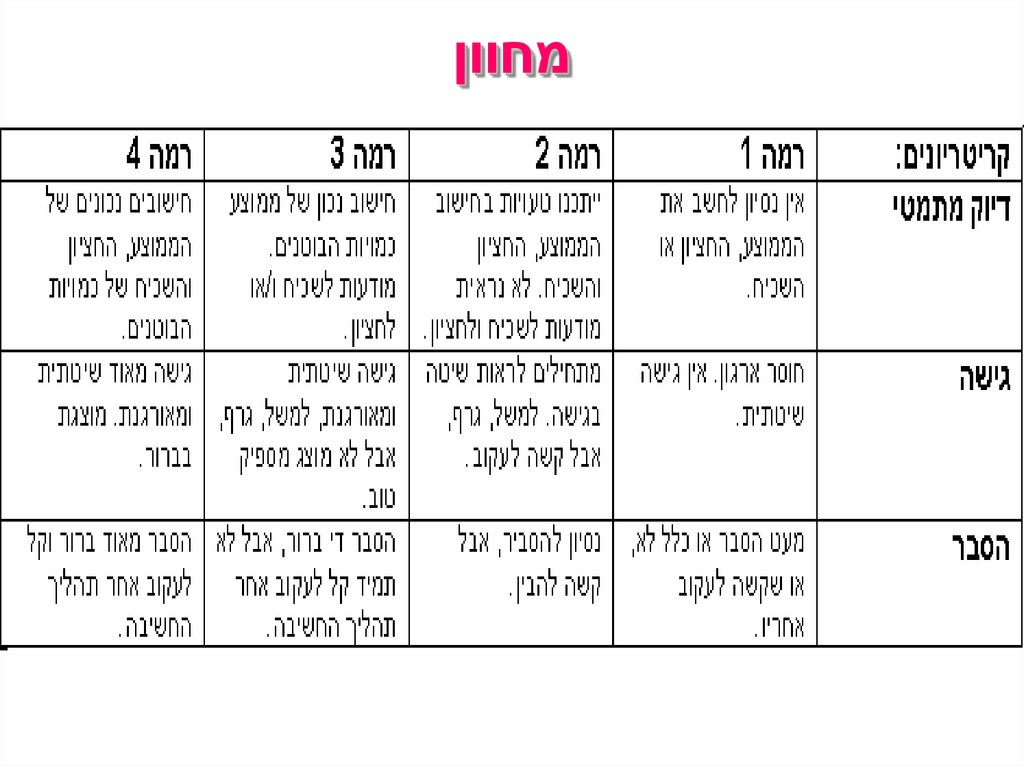
‫מחוון‬
‫רמה ‪1‬‬
‫רמה ‪2‬‬
‫רמה ‪3‬‬
‫דיוק מתמטי‬
‫טעויות חישוב‬
‫משמעותיות‪,‬‬
‫המראות חוסר‬
‫יכולת לבצע‬
‫פעולות הכרחיות‪.‬‬
‫חלק מהחישובים‬
‫בוצעו ללא טעות‪,‬‬
‫אך אחרים עם‬
‫טעויות המובילות‬
‫לתשובה לא נכונה‪.‬‬
‫נבחרו פעולות‬
‫נבחרו פעולות‬
‫נכונות‪ ,‬ללא טעויות‬
‫מתאימות‪ .‬מעט‬
‫חישוב הן בשברים‬
‫טעויות חישוב‬
‫המובילות למסקנות והן בפעולות‬
‫חשבון‪.‬‬
‫כמעט מדויקות‪.‬‬
‫גישה‬
‫גישה לא שיטתית‪,‬‬
‫לא מאורגנת‪.‬‬
‫ניכרת התחלה של‬
‫שיטתיות‪ ,‬אך קשה‬
‫לעקוב אחריה‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת מאוד‬
‫המוצגת בבהירות‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת‪ ,‬אך לא‬
‫מוצגת כראוי‪.‬‬
‫רמה ‪4‬‬

13.

‫דוגמה ‪1‬‬
‫רמה ‪1‬‬
‫רמה ‪2‬‬
‫רמה ‪3‬‬
‫רמה ‪4‬‬
‫דיוק מתמטי‬
‫טעויות חישוב‬
‫משמעותיות‪,‬‬
‫המראות חוסר‬
‫יכולת לבצע‬
‫פעולות‬
‫הכרחיות‪.‬‬
‫חלק מהחישובים‬
‫בוצעו ללא טעות‪,‬‬
‫אך אחרים עם‬
‫טעויות המובילות‬
‫לתשובה לא‬
‫נכונה‪.‬‬
‫נבחרו פעולות‬
‫מתאימות‪ .‬מעט‬
‫טעויות חישוב‬
‫המובילות‬
‫למסקנות כמעט‬
‫מדוייקות‪.‬‬
‫נבחרו פעולות‬
‫נכונות‪ ,‬ללא‬
‫טעויות חישוב הן‬
‫בשברים והן‬
‫בפעולות חשבון‪.‬‬
‫גישה‬
‫גישה לא‬
‫שיטתית‪ ,‬לא‬
‫מאורגנת‪.‬‬
‫ניכרת התחלה‬
‫של שיטתיות‪ ,‬אך‬
‫קשה לעקוב‬
‫אחריה‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת‪ ,‬אך לא‬
‫מוצגת כראוי‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת מאוד‬
‫המוצגת‬
‫בבהירות‪.‬‬

14.

‫רמה ‪1‬‬
‫רמה ‪2‬‬
‫רמה ‪3‬‬
‫רמה ‪4‬‬
‫דוגמה ‪2‬‬
‫דיוק מתמטי‬
‫טעויות חישוב‬
‫משמעותיות‪ ,‬המראות‬
‫חוסר יכולת לבצע‬
‫פעולות הכרחיות‪.‬‬
‫חלק מהחישובים‬
‫בוצעו ללא טעות‪ ,‬אך‬
‫אחרים עם טעויות‬
‫המובילות לתשובה‬
‫לא נכונה‪.‬‬
‫נבחרו פעולות‬
‫מתאימות‪ .‬מעט‬
‫טעויות חישוב‬
‫המובילות למסקנות‬
‫כמעט מדוייקות‪.‬‬
‫נבחרו פעולות נכונות‪,‬‬
‫ללא טעויות חישוב הן‬
‫בשברים והן בפעולות‬
‫חשבון‪.‬‬
‫גישה‬
‫גישה לא שיטתית‪ ,‬לא‬
‫מאורגנת‪.‬‬
‫ניכרת התחלה של‬
‫שיטתיות‪ ,‬אך קשה‬
‫לעקוב אחריה‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת‪ ,‬אך לא‬
‫מוצגת כראוי‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת מאוד‬
‫המוצגת בבהירות‪.‬‬
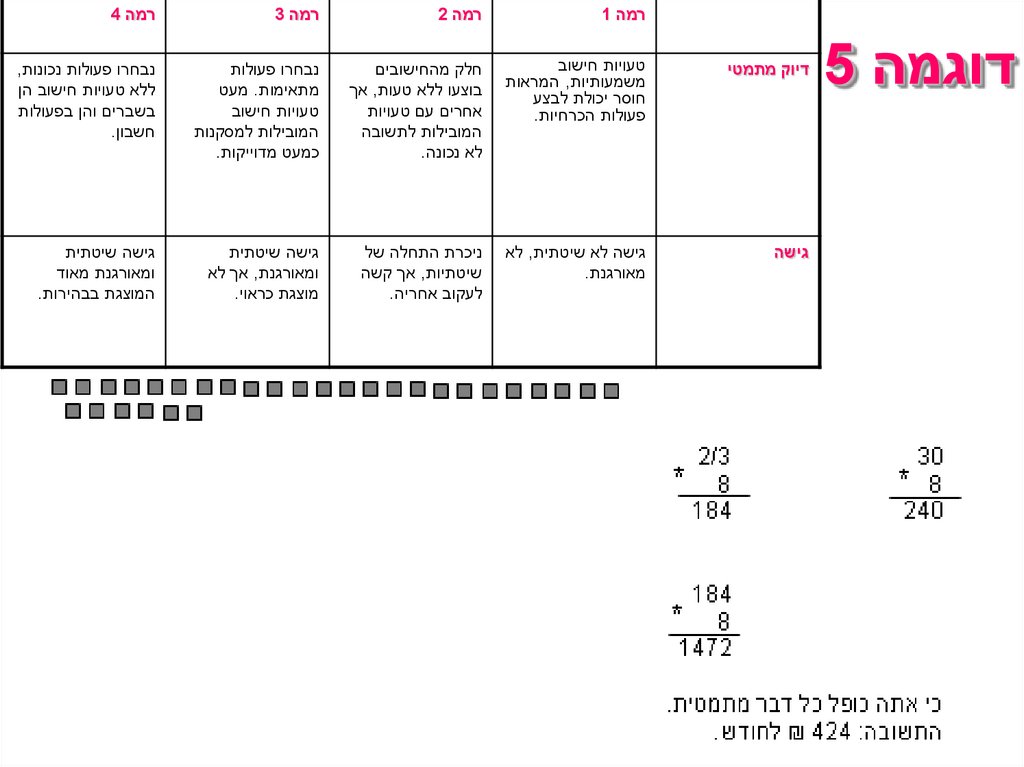
‫• אני חושב שזה ‪ ,₪ 50‬כי ‪ 2/3‬של ‪ 30‬זה ‪.₪ 50 = 30 + 20‬‬

15.

‫דוגמה ‪3‬‬
‫רמה ‪1‬‬
‫רמה ‪2‬‬
‫רמה ‪3‬‬
‫רמה ‪4‬‬
‫דיוק מתמטי‬
‫טעויות חישוב‬
‫משמעותיות‪,‬‬
‫המראות חוסר‬
‫יכולת לבצע פעולות‬
‫הכרחיות‪.‬‬
‫חלק מהחישובים‬
‫בוצעו ללא טעות‪,‬‬
‫אך אחרים עם‬
‫טעויות המובילות‬
‫לתשובה לא נכונה‪.‬‬
‫נבחרו פעולות‬
‫מתאימות‪ .‬מעט‬
‫טעויות חישוב‬
‫המובילות למסקנות‬
‫כמעט מדוייקות‪.‬‬
‫נבחרו פעולות‬
‫נכונות‪ ,‬ללא טעויות‬
‫חישוב הן בשברים‬
‫והן בפעולות חשבון‪.‬‬
‫גישה‬
‫גישה לא שיטתית‪,‬‬
‫לא מאורגנת‪.‬‬
‫ניכרת התחלה של‬
‫שיטתיות‪ ,‬אך קשה‬
‫לעקוב אחריה‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת‪ ,‬אך לא‬
‫מוצגת כראוי‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת מאוד‬
‫המוצגת בבהירות‪.‬‬

16.

‫דוגמה ‪4‬‬
‫רמה ‪1‬‬
‫רמה ‪2‬‬
‫רמה ‪3‬‬
‫רמה ‪4‬‬
‫דיוק מתמטי‬
‫טעויות חישוב‬
‫משמעותיות‪,‬‬
‫המראות חוסר יכולת‬
‫לבצע פעולות‬
‫הכרחיות‪.‬‬
‫חלק מהחישובים‬
‫בוצעו ללא טעות‪ ,‬אך‬
‫אחרים עם טעויות‬
‫המובילות לתשובה‬
‫לא נכונה‪.‬‬
‫נבחרו פעולות‬
‫מתאימות‪ .‬מעט‬
‫טעויות חישוב‬
‫המובילות למסקנות‬
‫כמעט מדוייקות‪.‬‬
‫נבחרו פעולות נכונות‪,‬‬
‫ללא טעויות חישוב הן‬
‫בשברים והן בפעולות‬
‫חשבון‪.‬‬
‫גישה‬
‫גישה לא שיטתית‪,‬‬
‫לא מאורגנת‪.‬‬
‫ניכרת התחלה של‬
‫שיטתיות‪ ,‬אך קשה‬
‫לעקוב אחריה‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת‪ ,‬אך לא‬
‫מוצגת כראוי‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת מאוד‬
‫המוצגת בבהירות‪.‬‬

17.

‫דוגמה ‪5‬‬
‫רמה ‪1‬‬
‫רמה ‪2‬‬
‫רמה ‪3‬‬
‫רמה ‪4‬‬
‫דיוק מתמטי‬
‫טעויות חישוב‬
‫משמעותיות‪ ,‬המראות‬
‫חוסר יכולת לבצע‬
‫פעולות הכרחיות‪.‬‬
‫חלק מהחישובים‬
‫בוצעו ללא טעות‪ ,‬אך‬
‫אחרים עם טעויות‬
‫המובילות לתשובה‬
‫לא נכונה‪.‬‬
‫נבחרו פעולות‬
‫מתאימות‪ .‬מעט‬
‫טעויות חישוב‬
‫המובילות למסקנות‬
‫כמעט מדוייקות‪.‬‬
‫נבחרו פעולות נכונות‪,‬‬
‫ללא טעויות חישוב הן‬
‫בשברים והן בפעולות‬
‫חשבון‪.‬‬
‫גישה‬
‫גישה לא שיטתית‪ ,‬לא‬
‫מאורגנת‪.‬‬
‫ניכרת התחלה של‬
‫שיטתיות‪ ,‬אך קשה‬
‫לעקוב אחריה‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת‪ ,‬אך לא‬
‫מוצגת כראוי‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת מאוד‬
‫המוצגת בבהירות‪.‬‬

18.

‫דוגמה ‪6‬‬
‫רמה ‪1‬‬
‫רמה ‪2‬‬
‫רמה ‪3‬‬
‫רמה ‪4‬‬
‫דיוק מתמטי‬
‫טעויות חישוב‬
‫משמעותיות‪ ,‬המראות‬
‫חוסר יכולת לבצע‬
‫פעולות הכרחיות‪.‬‬
‫חלק מהחישובים‬
‫בוצעו ללא טעות‪ ,‬אך‬
‫אחרים עם טעויות‬
‫המובילות לתשובה‬
‫לא נכונה‪.‬‬
‫נבחרו פעולות‬
‫מתאימות‪ .‬מעט‬
‫טעויות חישוב‬
‫המובילות למסקנות‬
‫כמעט מדוייקות‪.‬‬
‫נבחרו פעולות נכונות‪,‬‬
‫ללא טעויות חישוב הן‬
‫בשברים והן בפעולות‬
‫חשבון‪.‬‬
‫גישה‬
‫גישה לא שיטתית‪ ,‬לא‬
‫מאורגנת‪.‬‬
‫ניכרת התחלה של‬
‫שיטתיות‪ ,‬אך קשה‬
‫לעקוב אחריה‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת‪ ,‬אך לא‬
‫מוצגת כראוי‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת מאוד‬
‫המוצגת בבהירות‪.‬‬

19.

‫רמה ‪1‬‬
‫דוגמה ‪7‬‬
‫רמה ‪2‬‬
‫רמה ‪3‬‬
‫רמה ‪4‬‬
‫דיוק מתמטי‬
‫טעויות חישוב‬
‫משמעותיות‪ ,‬המראות‬
‫חוסר יכולת לבצע‬
‫פעולות הכרחיות‪.‬‬
‫חלק מהחישובים‬
‫בוצעו ללא טעות‪ ,‬אך‬
‫אחרים עם טעויות‬
‫המובילות לתשובה‬
‫לא נכונה‪.‬‬
‫נבחרו פעולות‬
‫מתאימות‪ .‬מעט‬
‫טעויות חישוב‬
‫המובילות למסקנות‬
‫כמעט מדוייקות‪.‬‬
‫נבחרו פעולות נכונות‪,‬‬
‫ללא טעויות חישוב הן‬
‫בשברים והן בפעולות‬
‫חשבון‪.‬‬
‫גישה‬
‫גישה לא שיטתית‪ ,‬לא‬
‫מאורגנת‪.‬‬
‫ניכרת התחלה של‬
‫שיטתיות אך‪ ,‬קשה‬
‫לעקוב אחריה‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת‪ ,‬אך לא‬
‫מוצגת כראוי‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת מאוד‬
‫המוצגת בבהירות‪.‬‬
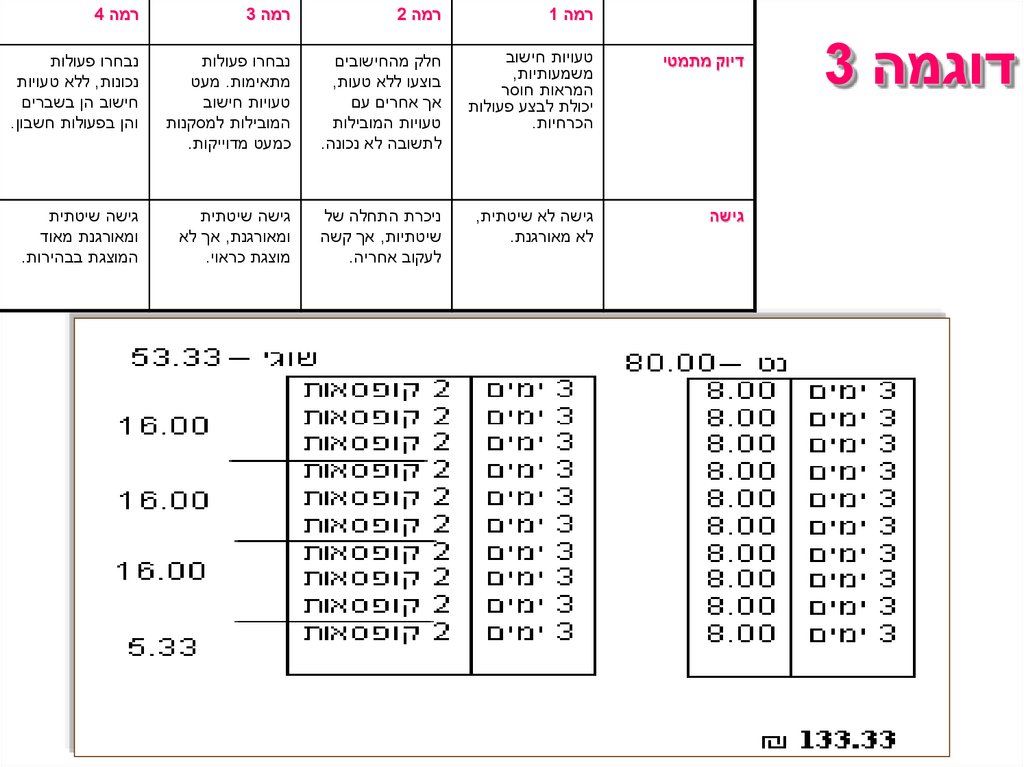
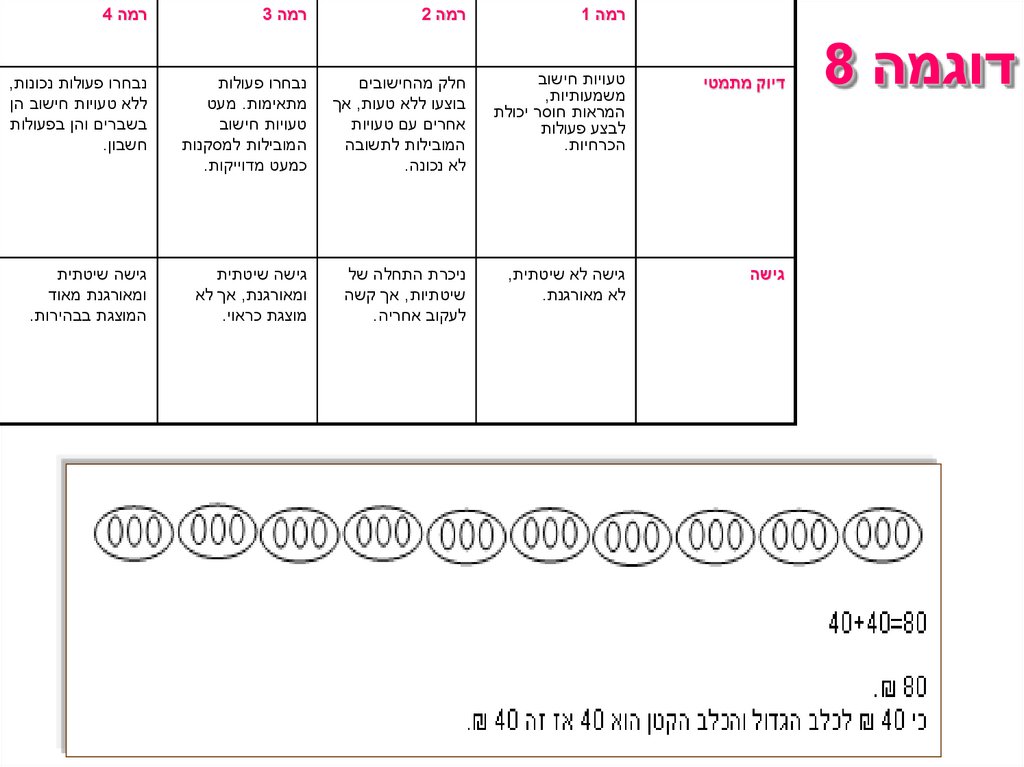
‫‪ ‬שוגי אוכל ‪ 2‬קופסאות כל ‪ 3‬ימים‪.‬‬
‫‪ ‬ונט ‪.3‬‬
‫‪ ‬נט עולה ‪ ₪ 8‬ל ‪ 3‬ימים ושוגי עולה ‪ ,5.32‬אז זה ‪ 13.32‬ל ‪ 3‬ימים‪ ,‬או ‪133.20‬‬
‫לחודש‪.‬‬

20.

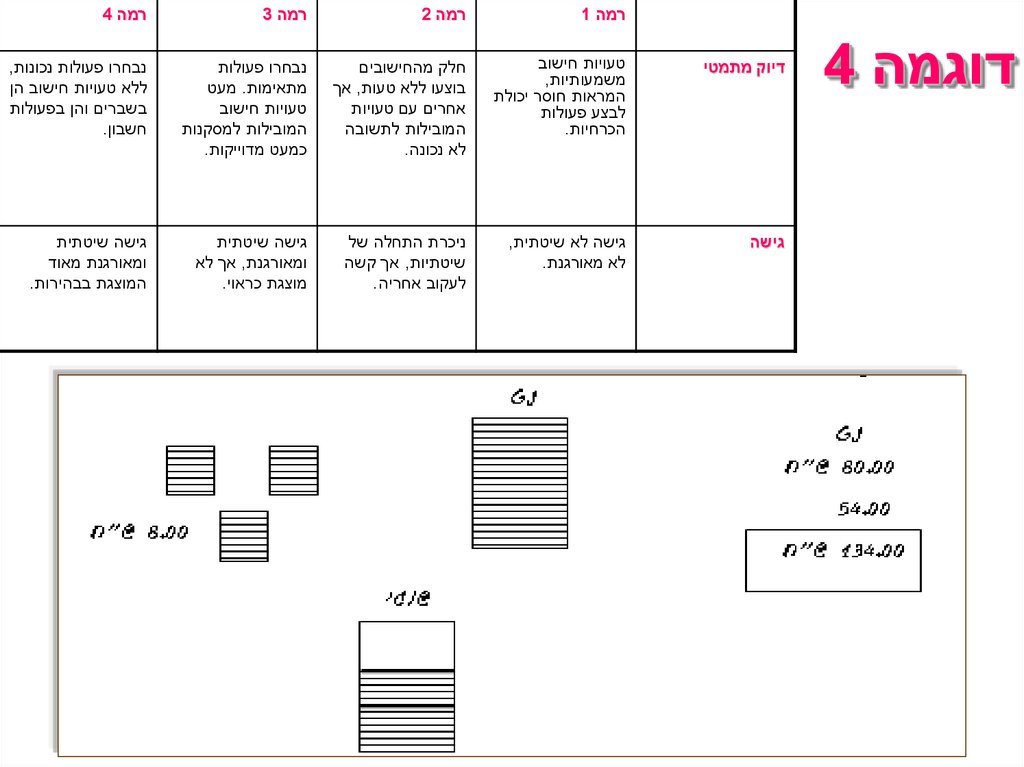
‫דוגמה ‪8‬‬
‫רמה ‪1‬‬
‫רמה ‪2‬‬
‫רמה ‪3‬‬
‫רמה ‪4‬‬
‫דיוק מתמטי‬
‫טעויות חישוב‬
‫משמעותיות‪,‬‬
‫המראות חוסר יכולת‬
‫לבצע פעולות‬
‫הכרחיות‪.‬‬
‫חלק מהחישובים‬
‫בוצעו ללא טעות‪ ,‬אך‬
‫אחרים עם טעויות‬
‫המובילות לתשובה‬
‫לא נכונה‪.‬‬
‫נבחרו פעולות‬
‫מתאימות‪ .‬מעט‬
‫טעויות חישוב‬
‫המובילות למסקנות‬
‫כמעט מדוייקות‪.‬‬
‫נבחרו פעולות נכונות‪,‬‬
‫ללא טעויות חישוב הן‬
‫בשברים והן בפעולות‬
‫חשבון‪.‬‬
‫גישה‬
‫גישה לא שיטתית‪,‬‬
‫לא מאורגנת‪.‬‬
‫ניכרת התחלה של‬
‫שיטתיות‪ ,‬אך קשה‬
‫לעקוב אחריה‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת‪ ,‬אך לא‬
‫מוצגת כראוי‪.‬‬
‫גישה שיטתית‬
‫ומאורגנת מאוד‬
‫המוצגת בבהירות‪.‬‬

21.

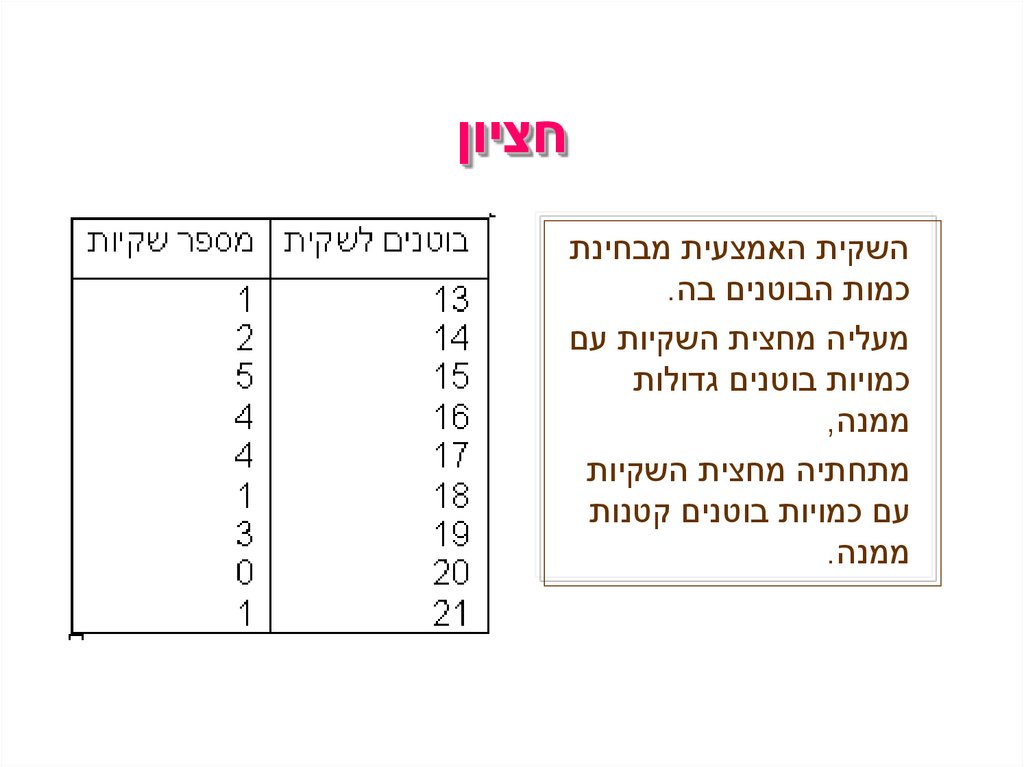
‫בוטנים‬
‫התלמידים בכיתתה של אילנה קנו שקיות בוטנים‪.‬‬
‫כל תלמיד דיווח בכתה על מספר הבוטנים בשקית שלו‪.‬‬
‫לפניכם תוצאות הדיווח‪:‬‬
‫‪ .1‬אם מישהו היה שואל אתכם‪" :‬כמה בוטנים‪ ,‬בערך‪ ,‬יש בשקית?" מה הייתם עונים לו?‬
‫‪ .2‬כמה תשובות אפשריות קיימות?‬
‫‪ .3‬הסבירו את הסיבות לתשובה או לתשובות שלכם‪.‬‬

22.

‫מחוון‬

23.

‫‪ ‬התלמידים יכולים לחשב ממוצע‪ ,‬חציון או שכיח‪ ,‬אבל להצדיק‬
‫כל דרך שהם בוחרים בה‪.‬‬
‫‪ ‬ממוצע הבוטנים לשקית הוא ‪.344/21=16.38‬‬
‫‪ ‬החציון שווה ‪( 16‬יש ‪ 10‬ילדים עם שקיות מתחתיו‪,‬‬
‫ו ‪ 10 -‬ילדים עם שקיות מעליו)‪.‬‬
‫‪ ‬השכיח הוא ‪ ,15‬מאחר ויש ‪ 5‬ילדים עם ‪ 15‬בוטנים לשקית‪.‬‬

24.

‫חציון‬
‫השקית האמצעית מבחינת‬
‫כמות הבוטנים בה‪.‬‬
‫מעליה מחצית השקיות עם‬
‫כמויות בוטנים גדולות‬
‫ממנה‪,‬‬
‫מתחתיה מחצית השקיות‬
‫עם כמויות בוטנים קטנות‬
‫ממנה‪.‬‬

25.

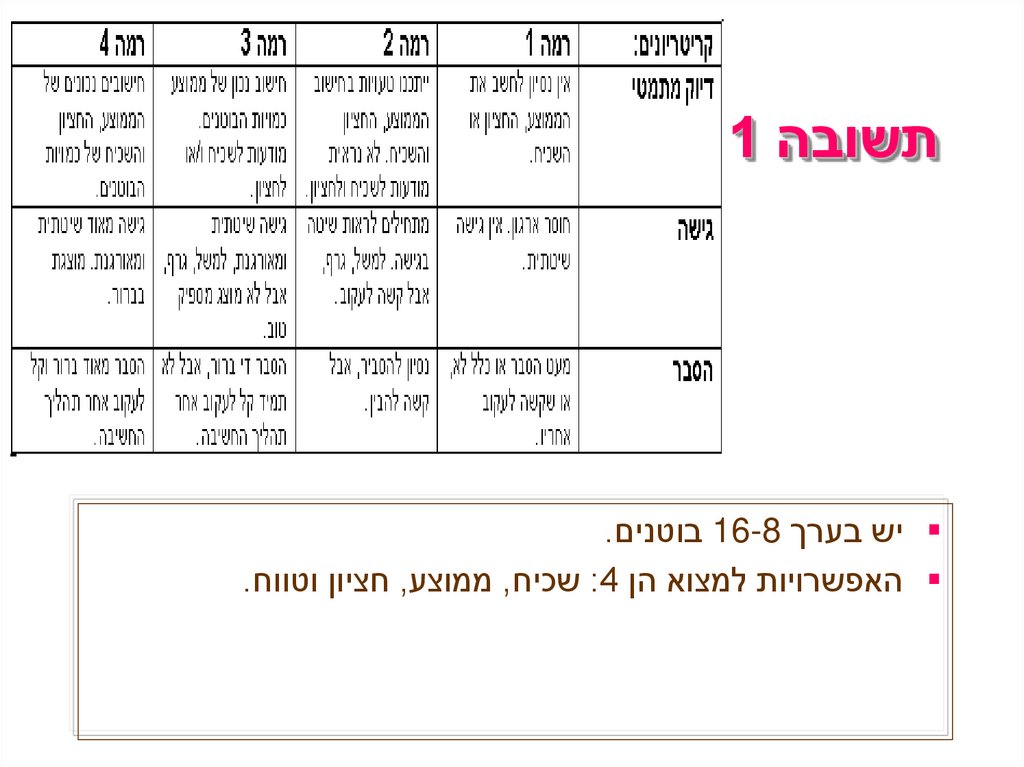
‫תשובה ‪1‬‬
‫‪ ‬יש בערך ‪ 16-8‬בוטנים‪.‬‬
‫‪ ‬האפשרויות למצוא הן ‪ :4‬שכיח‪ ,‬ממוצע‪ ,‬חציון וטווח‪.‬‬

26.

‫תשובה ‪2‬‬
‫‪ ‬יכולות להיות הרבה תשובות‪ .‬אף פעם לא נוכל לדעת כמה בוטנים‬
‫בשקית‪ .‬יכולים להיות ‪ 300 ,200 ,100 ,1000‬ואולי ‪ .900‬אף פעם‬
‫אין אותה כמות‪.‬‬

27.

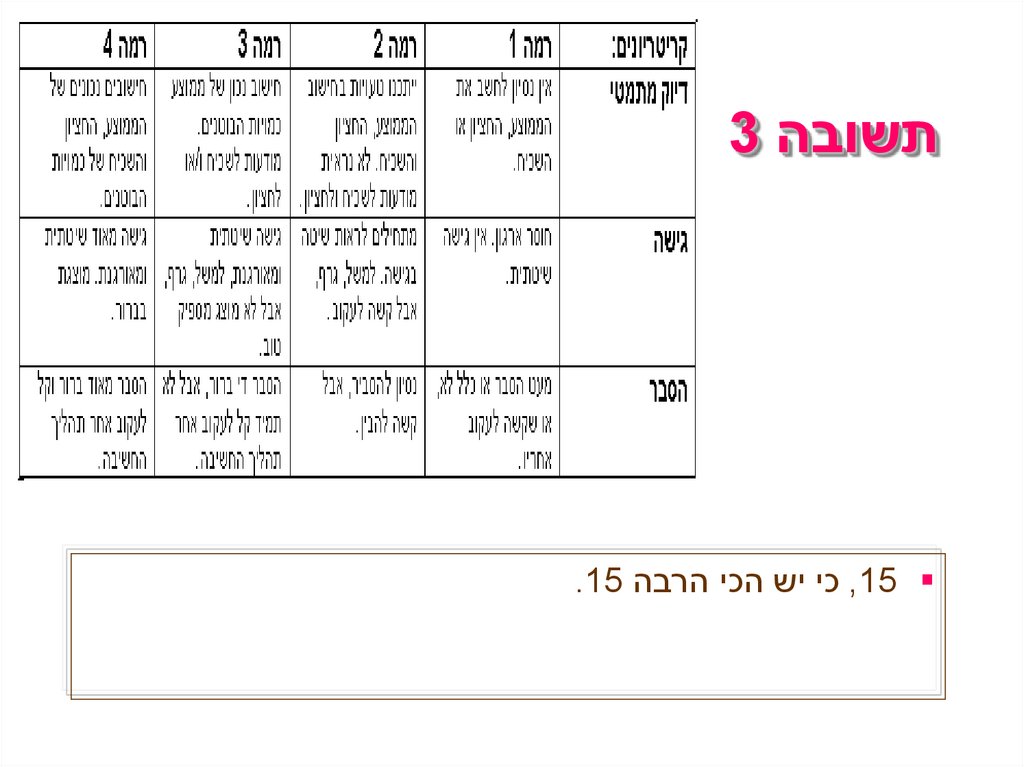
‫תשובה ‪3‬‬
‫‪ ,15 ‬כי יש הכי הרבה ‪.15‬‬

28.

‫תשובה ‪4‬‬
‫‪ ‬בערך ‪ 16‬כי מצאתי את הממוצע‪.‬‬
‫‪ ‬תשובות אחרות הן‪ 15 :‬או ‪ 17‬כי הם מופיעים הרבה‪.‬‬

29.

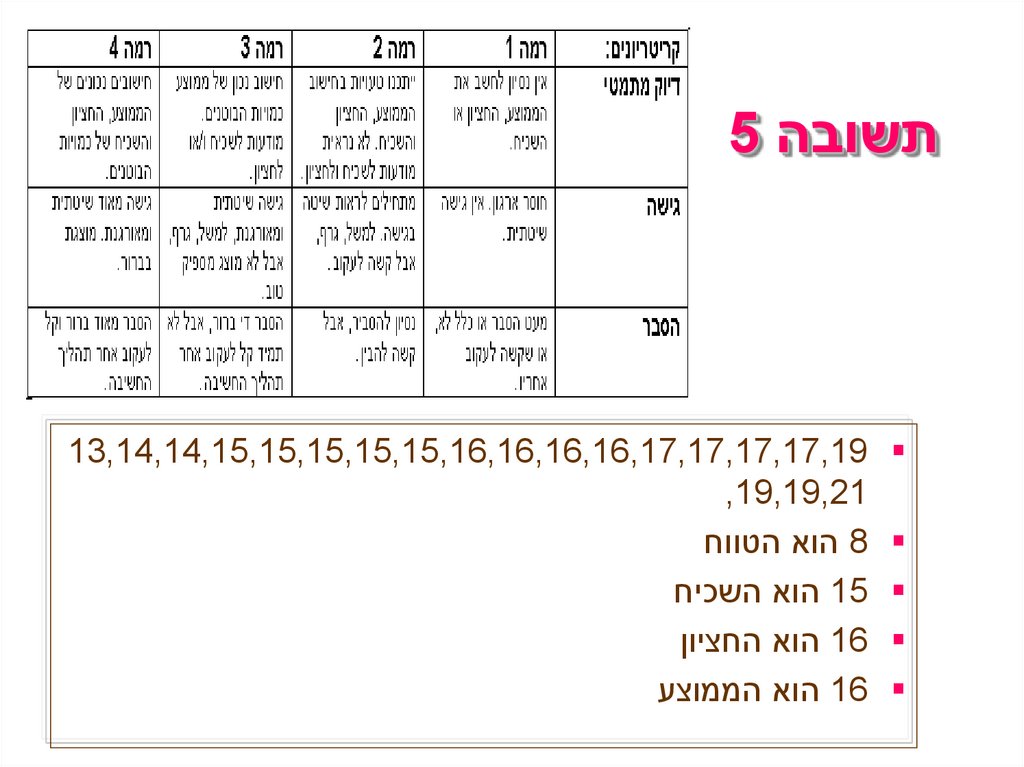
‫תשובה ‪5‬‬
‫‪13,14,14,15,15,15,15,15,16,16,16,16,17,17,17,17,19 ‬‬
‫‪,19,19,21‬‬
‫‪ 8 ‬הוא הטווח‬
‫‪ 15 ‬הוא השכיח‬
‫‪ 16 ‬הוא החציון‬
‫‪ 16 ‬הוא הממוצע‬

30.

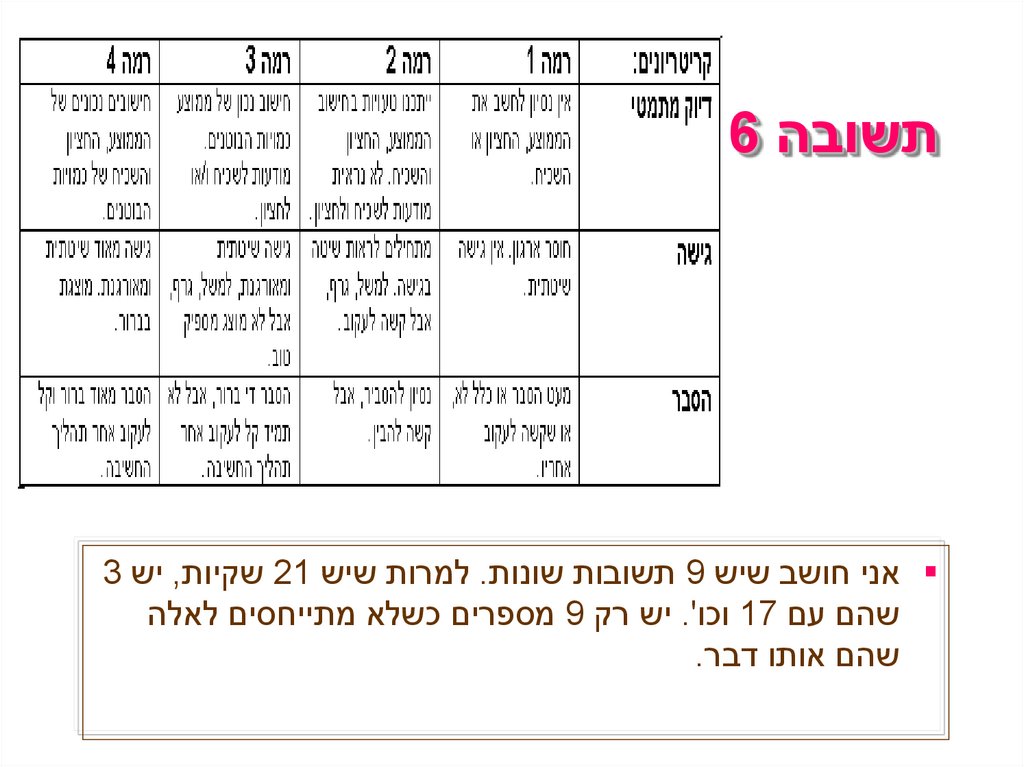
‫תשובה ‪6‬‬
‫‪ ‬אני חושב שיש ‪ 9‬תשובות שונות‪ .‬למרות שיש ‪ 21‬שקיות‪ ,‬יש ‪3‬‬
‫שהם עם ‪ 17‬וכו'‪ .‬יש רק ‪ 9‬מספרים כשלא מתייחסים לאלה‬
‫שהם אותו דבר‪.‬‬

31.

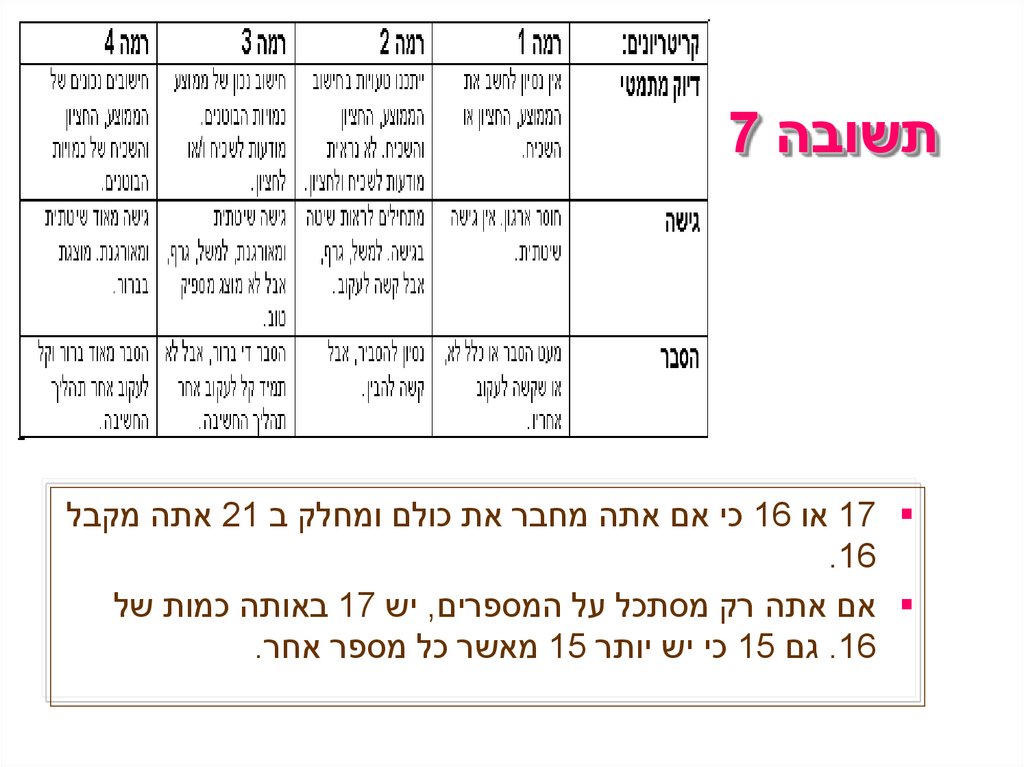
‫תשובה ‪7‬‬
‫‪ 17 ‬או ‪ 16‬כי אם אתה מחבר את כולם ומחלק ב ‪ 21‬אתה מקבל‬
‫‪.16‬‬
‫‪ ‬אם אתה רק מסתכל על המספרים‪ ,‬יש ‪ 17‬באותה כמות של‬
‫‪ .16‬גם ‪ 15‬כי יש יותר ‪ 15‬מאשר כל מספר אחר‪.‬‬

32.

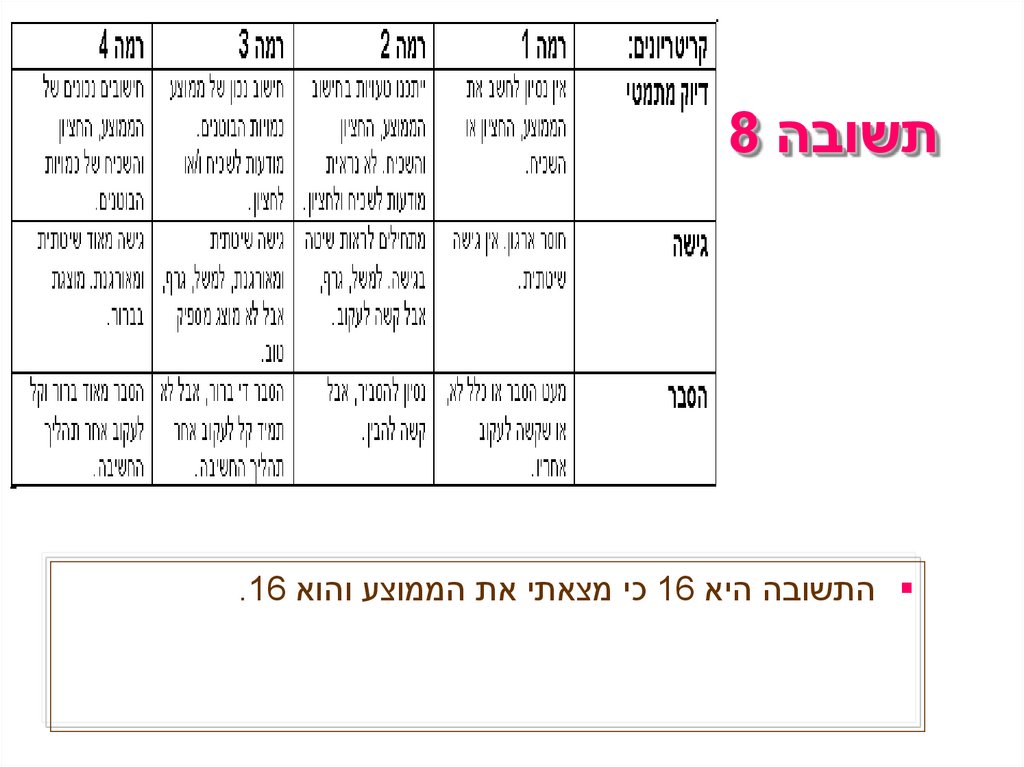
‫תשובה ‪8‬‬
‫‪ ‬התשובה היא ‪ 16‬כי מצאתי את הממוצע והוא ‪.16‬‬