Похожие презентации:
מספרים משולשיים
1.
מספרים משולשיים2.
מספרים משולשיים1
+2
+3
+4
+5
+6
+7
=1
=3
=6
= 10
= 15
= 21
= 28
…
+36 = 666
3.
במשולש פסקל:1
1
1
1
1
1
1
1
1
8
3
5
7
6
15
1
4
10
20
35
56
1
3
10
21
28
2
4
6
1
5
15
35
70
1
1
6
21
56
1
7
28
1
8
1
4.
תכונות פשוטותn n 1
n
2
n n 1 n
2
5.
חידה חשובה אבל קצת מיושנתבכמה דרכים ניתן לבחור שתי משבצות בלוח שח?
(אין חשיבות לסדר)
?
6.
פעולות חשבוןm n m n m n
n2
2
n
2
n 1
mn m n m 1 n 1
mn 1 m n 1 m 1 n
7.
מספרים מצולעיםיש גם ריבועים ,מחומשים ,משושים ...
כל מספר טבעי הוא
סכום של 3משולשים (גאוס)
סכום של 4ריבועים (לגרנז')
סכום של 5מחומשים 6 ,משושים וכו' (קושי)
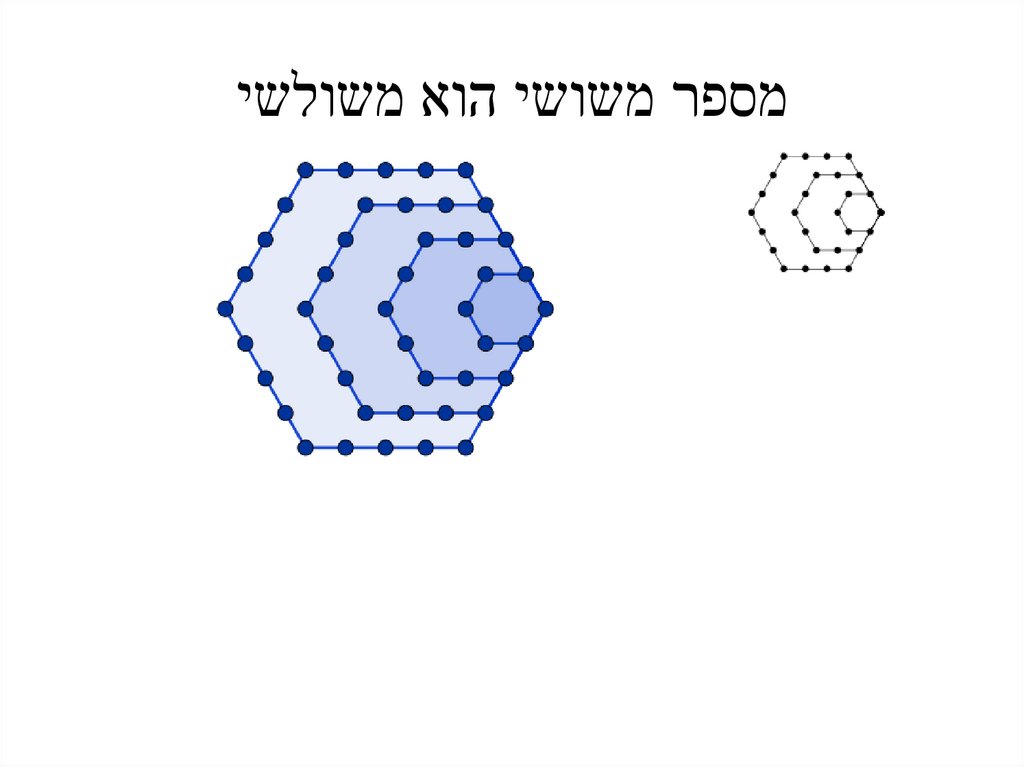
חידה :כל מספר משושי הוא משולשי.
8.
מספר משושי הוא משולשי9.
מספר מחומשי הוא שליש ממשולש10.
?האם יש משולשים שהם ריבועים1 + 2 + … + 8 = 62
?האם יש עוד
1 + 2 + … + 49 = 352
3 8
3 8
n
n
32
3 8 3 8
n
4
?האם יש עוד
2
n
2
3 8 3 8
n
4
2
n
2
11.
אם Tמספר משולשי ...אז גם
9T 1
25T 3
49T 6
משולשים.
מספר 111111בבסיס ,9מספר 333333בבסיס 25משולשיים.
12.
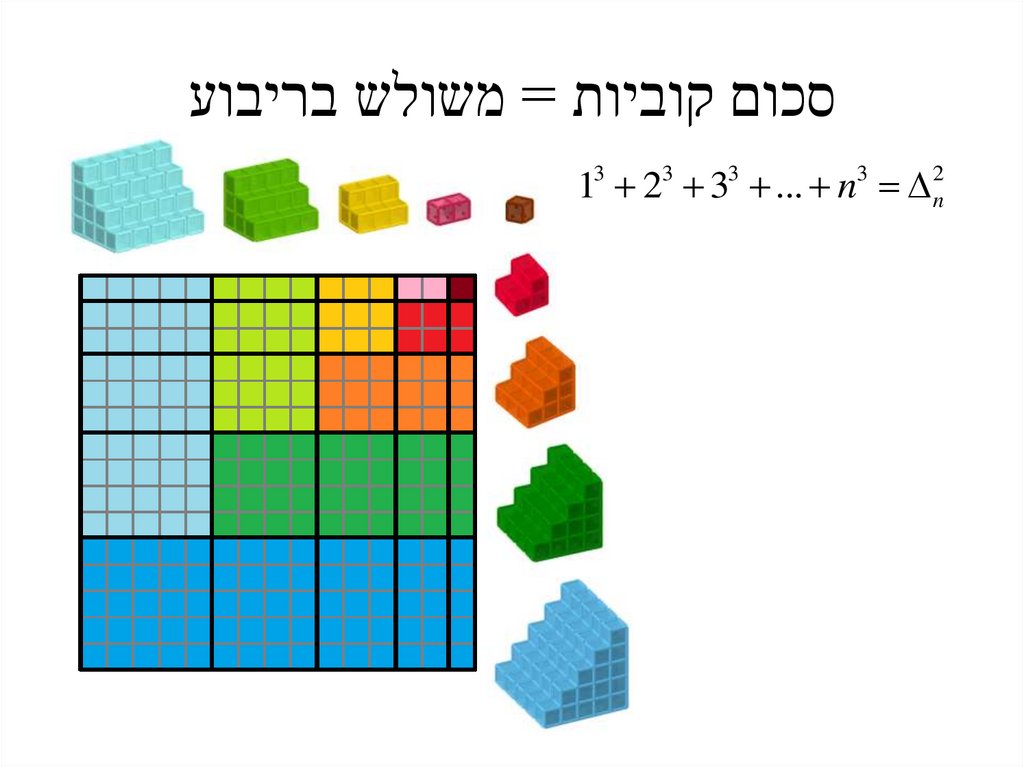
סכום קוביות = משולש בריבוע13 23 33 ... n3 2n
13.
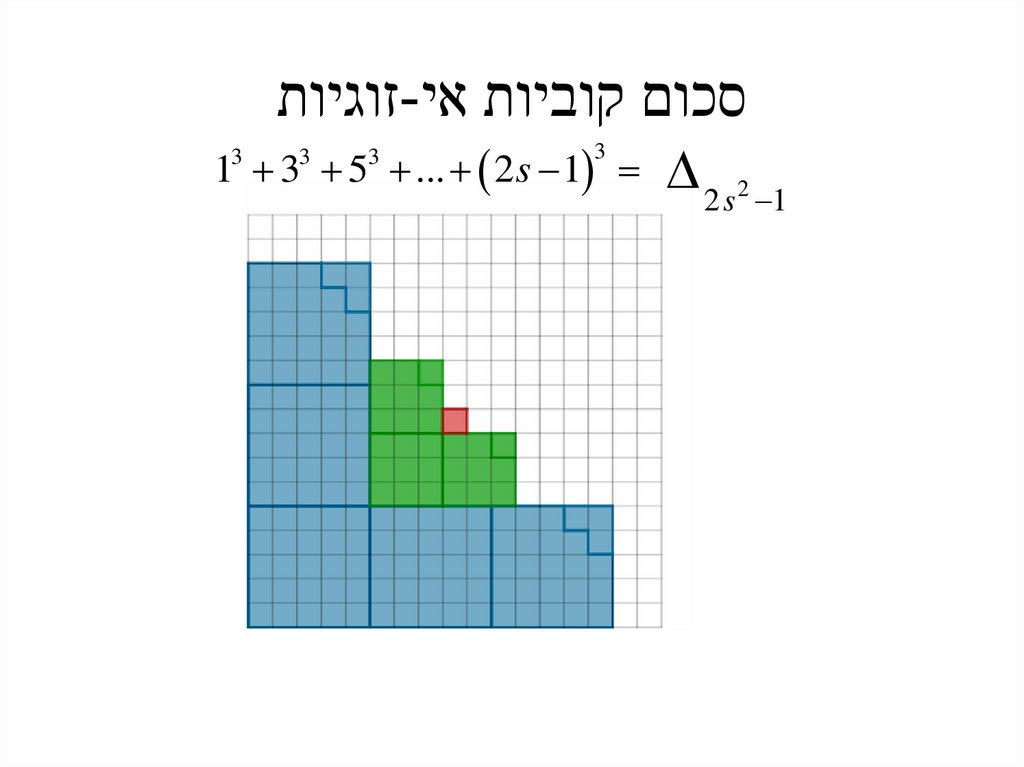
סכום קוביות אי-זוגיות 2 s 2 1
1 3 5 ... 2s 1
3
3
3
3
14.
מספרים מושלמיםמספר נקרא מושלם אם הוא שווה לסכום
של כל המחלקים שלו חוץ מעצמו .למשל:
6 1 2 3
28 1 2 4 7 14
איזה עוד מספרים מושלמים יש?
15.
ראשוני מרסן ()Mersenneמספר ראשוני נקרא ראשוני מרסן אם הוא מהצורה
2 1
np
במקרים אלה nבהכרח ראשוני (למה?)
ולכן מסמנים אותו בp -
דוגמאות:
25 1 31,
23 1 7,
22 1 3,
213 1 8191
211 1 2047 23 89,
27 1 127,
16.
משולש של מרסן נותן מספר מושלםעבור מספר שלם שנתון פירוק שלו לגורמים:
n p1k1 p2k2 p3k3 pmkm
סכום כל המחלקים כולל עצמו שווה ל-
1 p
km
2
p
...
p
m
m
m
... p1k1 1 p2 p22 ... p2k2
1 p p
2
1
1
אם p 1 2 4 ... 2kראשוני,
אז סכום כל המחלקים של p n p 2kשווה ל-
k
k 1
1
2
4
...
2
1
p
p
2
2n
17.
יש גם (חצי) משפט הפוךמשפט .מספר מושלם זוגי הוא מהסוג , n p 2k
כאשר p 2k 1 1ראשוני מרסן.
אנחנו לא יודעים האם יש מספר מושלם אי-זוגי.
נסמן את סכום כל המחלקים של , mכולל עצמו,
על ידי . m
אנחנו נוכיח את המשפט על המושלמים הזוגיים.
18.
הוכחת המשפטניקח מספר מושלם זוגי n 2k sכאשר sאי-זוגי.
2k 1 s 2n n 1 2 ... 2k s 2k 1 1 s
2k 1 s 2k 1 1 s t
כאשר tהוא סכום כל המחלקים של sחוץ מעצמו.
2k 1 s 2k 1 1 s 2k 1 1 t
s 2k 1 1 t
אבל tהוא סכום כל המחלקים ,אז אם יש בסכום זה
יותר ממחלק אחד ,הוא יותר גדול מכל מחלק.
19.
סוף הוכחהלכן t 1ולכן sראשוני.
הזהות s 2k 1 1 tהפכה לזהות , s 2k 1 1
לכן זה ראשוני מרסן.
מסקנה :כל מספר מושלם זוגי (ואולי אפילו כל מספר
מושלם) הוא משולש של ראשוני מרסן.
20.
עוד מסקנה:מספרים מושלמים הם
6
28 13 33
496 1 3 5 7
3
3
3
3
8128 1 3 5 7 9 11 13 15
3
3
3
3
3
3
3
3
33550336 13 33 53 73 93 113 133 ... 127 3
...
2 s2 1 1 3 5 ... 2 s 1
3
3
3
3
הרי


















 Математика
Математика





