Физические основы систем связи

1.

Физические основы систем
связи
Рабчевский Андрей Николаевич
Старший преподаватель кафедры ИБиСС
E-mail: andrey@ranat.ru, +7 (912) 7808729
1

2.

Свойства векторных полей
Вычисление полей с помощью
теоремы Гаусса
Лекция 2
Главы 1.11-1.14
2

3.

Список литературы
• Савельев И.В. Курс общей физики. В 5-и тт. Том 2.
Электричество и магнетизм. ISBN - 978-5-8114-1208-2.
Издательство «Лань». 2021 г.
• Савельев И.В. Курс общей физики. В 5-и тт. Том 4. Волны.
Оптика. ISBN - 978-5-8114-1210-5. Издательство «Лань».
2021 г.
• Иродов, И. Е. Задачи по общей физике : учебное пособие
для вузов / И. Е. Иродов. — 18-е изд., стер. — СанктПетербург : Лань, 2021. — 420 с. — ISBN 978-5-8114-6779-2.
• Перминов, А. В. Общая физика. Задачи с решениями :
задачник / А. В. Перминов, Ю. А. Барков. — Саратов :
Вузовское образование, 2020. — 725 c. — ISBN 978-5-44870603-5. DOI: https://doi.org/10.23682/95156
3

4.

Лекция 2. Основные темы
• Векторный анализ
• Градиент
• Поток вектора
• Дивергенция
• Теорема Остроградского-Гаусса
• Циркуляция
• Ротор
• Теорема Гаусса
• Циркуляция и ротор электростатического поля
• Вычисление полей с помощью теоремы Гаусса
4

5.

Векторный анализ
• Электрическое поле имеет векторный характер
• Для описания векторных явлений используется математический
аппарат, называемый векторным анализом.
• Величины, используемые в векторном анализе имеют
наибольшую наглядность в случае поля вектора скорости текущей
жидкости.
• Мы будем рассматривать течение идеальной несжимаемой
жидкости и распространять полученные результаты на векторные
поля любой природы
5

6.

Градиент
• Градиент используется для характеристики скалярных полей.
• Градиент - это вектор показывающий направление наибольшего
возрастания функции. Модуль вектора градиента показывает скорость
изменения функции.
• Если каждой точке P с координатами x, y, z сопоставляется значение
скалярной величины = (x, y, z), говорят, задано скалярное поле .
• Градиентом величины называется вектор
(1)
grad = =
ex +
ey +
ez .
x
y
z
• Приращение функции на отрезок dl=exdx + eydy + ezdz равно
d =
dx +
dy +
dz
x
y
z
или
d = dl.
(2)
6

7.

Поток вектора
• Пусть течение жидкости охарактеризовано полем вектора
скорости.
• Объем жидкости, протекающей в единицу времени через
некоторую воображаемую поверхность S, называется потоком
жидкости через эту поверхность.
• Чтобы найти поток, разобьём поверхность S
на элементарные участки S.
• Из рис.1 видно, что за время t через
участок S пройдет объём жидкости,
равный
V = S cos t.
Рис.1
7

8.

Поток вектора
• Разделив этот объем на промежуток времени t, найдем поток
через поверхность S:
= V t = S cos .
• Перейдя к дифференциалам, получим, что
(3)
d = cos dS .
• Учитывая, что cos это проекция вектора скорости на нормаль
n к площадке dS, формулу (3) можно записать в виде
(4)
d = n dS
• Если ввести вектор dS, модуль равен площадке dS, а направление
совпадает с направлением нормали к площадке n:
dS =dS n
8

9.

Поток вектора
• Угол в формуле (3) есть угол между векторами v и dS,
следовательно
(5)
d = vdS.
• Просуммировав все потоки через элементарные площадки S
получим поток жидкости через поверхность S:
v = vdS = n dS .
S
(6)
S
• Аналогичное выражение, написанное для произвольного
векторного поля a, т.е. величина
a = adS = an dS .
S
(7)
S
называется потоком вектора а через поверхность S.
9

10.

Поток вектора
• Поток вектора есть алгебраическая величина.
• Знак этой величины зависит от выбора направления нормали к
элементарным площадкам.
• Изменение направления нормали меняет знак формулы (7).
• В случае замкнутых поверхностей принято вычислять поток,
«вытекающий» из охватываемой поверхности наружу.
• То есть, в качестве n будет всегда подразумеваться обращенная
наружу внешняя нормаль (рис.1).
10

11.

Поток вектора
• Представим векторное поле системой линий а, построенных так,
чтобы густота линий в каждом месте была численно равна
модулю вектора а в той же точке поля.
• Найдем число N пересечений линий поля с воображаемой
площадкой S.
• На рис.2 показаны линии вектора а в
окрестности площадки S.
• Число линий, пронизывающих площадку,
равно густоте линий, умноженной на S⊥
• Из рисунка видно, что S⊥= Scos ,
следовательно число пересечений N
Рис.2
N = густота линий S cos .
11

12.

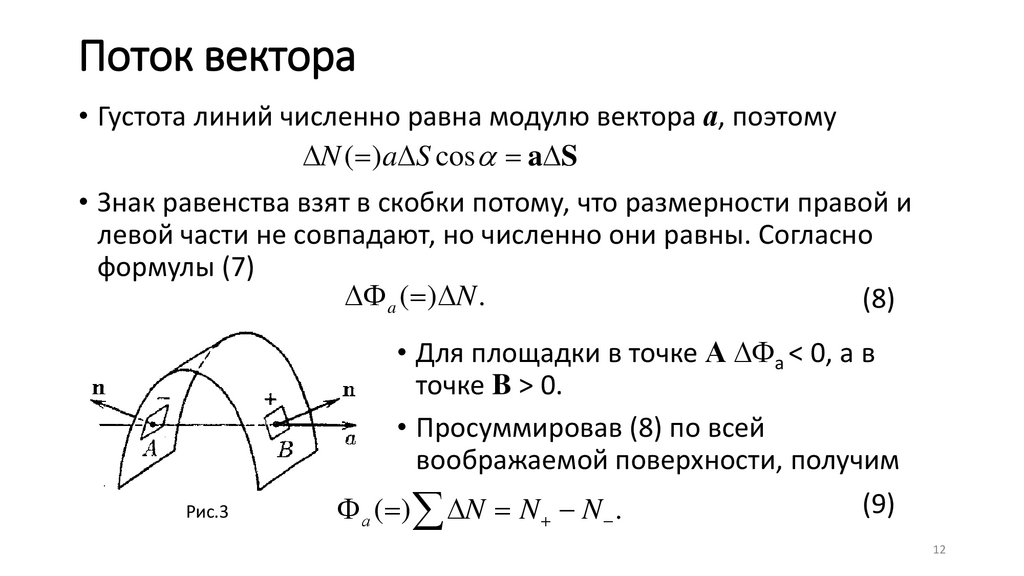
Поток вектора
• Густота линий численно равна модулю вектора а, поэтому
N (=)a S cos = a S
• Знак равенства взят в скобки потому, что размерности правой и
левой части не совпадают, но численно они равны. Согласно
формулы (7)
a (=) N .
(8)
Рис.3
• Для площадки в точке А а < 0, а в
точке B > 0.
• Просуммировав (8) по всей
воображаемой поверхности, получим
(9)
а (=) N = N + − N − .
12

13.

Поток вектора
• Практически подсчитывать число пересечений мы не будем, но
будем использовать это как удобный прием получения формул и
соотношений векторных полей.
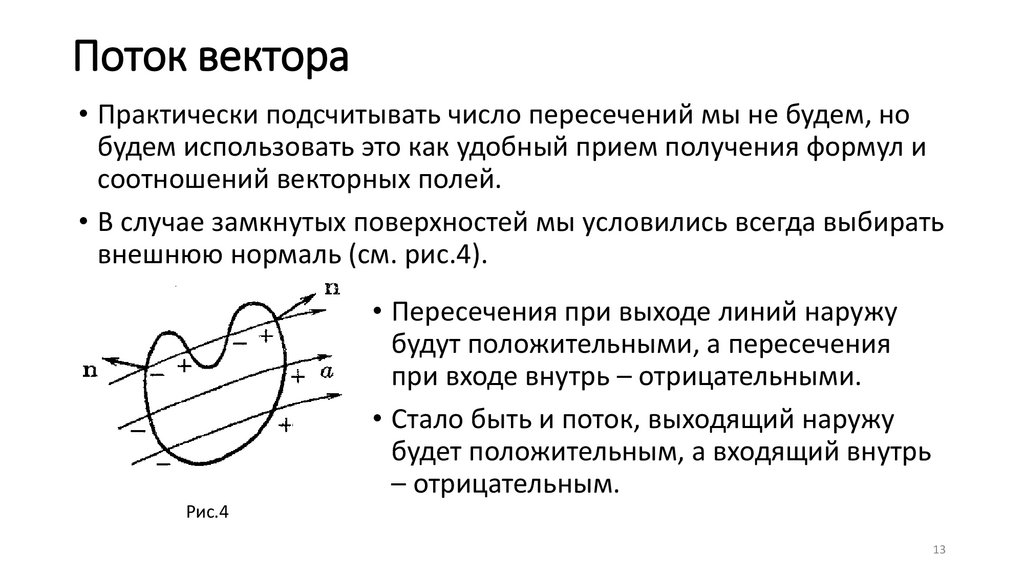
• В случае замкнутых поверхностей мы условились всегда выбирать
внешнюю нормаль (см. рис.4).
• Пересечения при выходе линий наружу
будут положительными, а пересечения
при входе внутрь – отрицательными.
• Стало быть и поток, выходящий наружу
будет положительным, а входящий внутрь
– отрицательным.
Рис.4
13

14.

Поток вектора
Рис.4
• Из рис.4 видно, что в случае, когда лини поля
проходят внутри замкнутой поверхности не
прерываясь, каждая линия пересекая
поверхность входит внутрь и выходит наружу
одинаковое число раз.
• В итоге полное число положительных
пересечений будет равно полному числу
отрицательных пересечений и поток вектора
через поверхность оказывается равной 0.
14

15.

Поток вектора
Рис.5
• Из рис.5 следует, что линия, начинающаяся внутри
замкнутой поверхности, вносит в поток вклад,
равный +1, а линия оканчивающаяся внутри
поверхности, - вклад, равный -1.
• Отсюда заключаем, что поток вектора через
замкнутую поверхность численно равен разности
числа линий, начинающихся внутри поверхности
Nнач, и числа линий, оканчивающихся внутри
поверхности Nоканч
a (=) N нач − N оканч .
(10)
• Линии, начинающиеся и оканчивающиеся внутри
замкнутой поверхности, вклада в поток не вносят.
15

16.

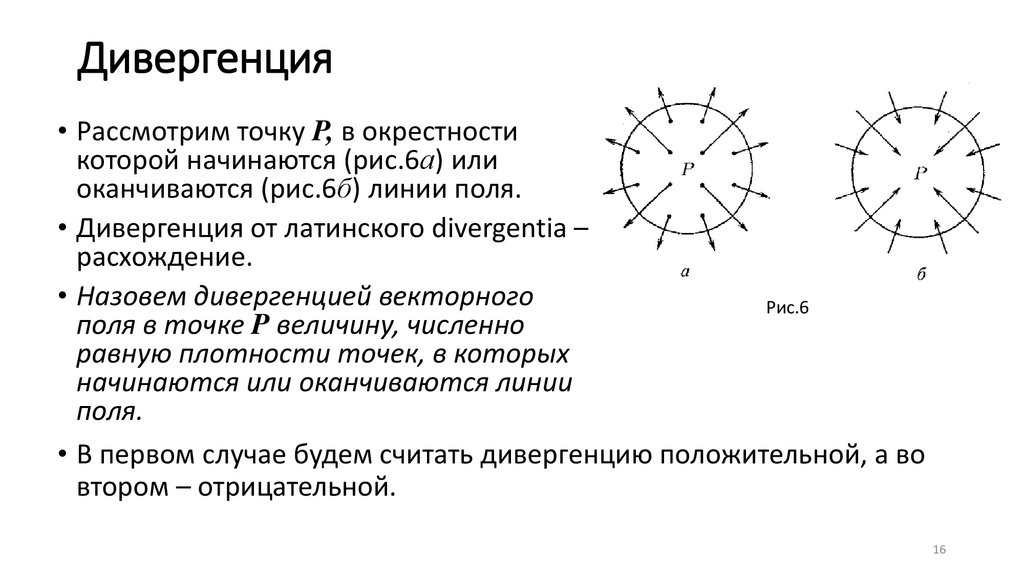
Дивергенция
• Рассмотрим точку P, в окрестности
которой начинаются (рис.6а) или
оканчиваются (рис.6б) линии поля.
• Дивергенция от латинского divergentia –
расхождение.
• Назовем дивергенцией векторного
Рис.6
поля в точке P величину, численно
равную плотности точек, в которых
начинаются или оканчиваются линии
поля.
• В первом случае будем считать дивергенцию положительной, а во
втором – отрицательной.
16

17.

Дивергенция
• Дивергенцию векторного поля a обозначают символом div a либо
a.
• Выделим в окрестности точки P объем V очень малых размеров.
• Если внутрь этого объема попадает Nнач или Nоканч , то
дивергенция будет равна
N нач
diva(=)
в первом случае,
V
(11)
N оканч
diva(=) −
во втором случае
V
17

18.

Дивергенция
• Согласно формуле (10) Nнач в первом случае и -Nоканч во втором
случае численно равны потоку вектора a через поверхность S,
ограничивающую объем V.
• Поэтому оба соотношения (11) можно представить в виде
a
diva =
.
(12)
V
• При неравномерном распределении точек, в которых начинаются
или заканчиваются линии, для получения значения дивергенции
в точке P нужно взять предел выражения (12) при условии, что V
стремится к нулю, стягиваясь в точке P, тогда с учетом (7) получим
1
diva = lim adS
V →0 V
S
(13)
18

19.

Дивергенция
• Дивергенция скалярная величина, которая может быть как
положительной, так и отрицательной.
• Точки, в которых начинаются линии поля, называются источником
поля.
• В этом случае дивергенцию можно трактовать как мощность
источников поля, отнесенную к единице объема.
• Точки, в которых оканчиваются линии поля, называются стоками
поля или источниками с отрицательной мощностью.
• Найдем выражение для дивергенции в декартовой системе
координат.
• Рассмотрим в окрестности точки P(x, y, z) малый объем в виде
параллелепипеда с ребрами, перпендикулярными осям (рис. 7).
19

20.

Дивергенция
• Поток вектора через поверхность
параллелепипеда образуется из потоков,
текущих через каждую из шести граней в
отдельности.
• Найдем поток через пару граней,
перпендикулярных оси x (заштрихованные).
Рис.7
• Внешняя нормаль n2 к грани 2 совпадает с
направлением оси x. Следовательно, для точек
этой грани an2=ax
• Внешняя нормаль n1 к грани 1 имеет направление,
противоположное оси x, поэтому для точек этой грани an1=-ax
20

21.

Дивергенция
• Поток через грань 2 можно записать в виде
ax 2 y z ,
где ax2 – значение ax, усредненное по грани 2.
• Поток через грань 1 равен
−ax1 y z ,
• Суммарный поток через грани 1 и 2 определяется выражением
(14)
( ax 2 − ax1 ) y z.
• Разность ax2 – ax1 представляет собой приращение среднего
значения ax, при смещении вдоль оси x на x.
21

22.

Дивергенция
• Поскольку размеры объема стремятся к нулю, это приращение
можно выразить в виде ( ax x ) x , где значение дроби берется в
точке P, тогда формула (14) переходит в
ax
ax
x y z =
V .
x
x
• Путем аналогичных вычислений можно получить пары потоков,
перпендикулярных осям y и z
a y
az
V и
V .
y
z
22

23.

Дивергенция
• Таким образом, полный поток через всю замкнутую поверхность
определяется выражением
ax a y az
a =
+
+
V .
y
z
x
• Разделив это выражение на V, найдем дивергенцию вектора a в
точке P(x, y, z):
ax a y az
diva =
+
+
.
x
y
z
(15)
23

24.

Теорема Остроградского - Гаусса
• Поток вектора поля а через замкнутую поверхность равен
алгебраической сумме заключенных внутри этой
поверхности точек, в которых начинаются или
заканчиваются линии поля.
a dS = div a dV
S
(16)
V
• В левой части интеграл вычисляется по произвольной
площади.
• В правой части – по объему, ограниченному этой площадью
24

25.

Циркуляция
Рис.8
• Рассмотрим течение идеальной несжимаемой
жидкости.
• Представим себе замкнутую линию – контур Г.
• Предположим, мы заморозили весь объем
жидкости за исключением тонкого канала в
контуре Г.
• В зависимости от характера вектора поля жидкость будет либо
неподвижной, либо будет двигаться вдоль контура (циркулировать)
в одном из двух направлений.
• В качестве меры этого движения возьмем величину, равную
произведению скорости течения жидкости на длину контура Г.
25

26.

Циркуляция
• Эту величину назвали циркуляцией вектора v по контуру Г
циркуляция v по Г = υl
• Взаимодействие между частицами жидкости в канале приводит к
тому, что скорость всех частиц жидкости одинакова.
• Направление вектора скорости l каждой частицы имеет
направление по касательной с контуру.
• С этой скоростью связан импульс dpl, модуль которого для
частицы жидкости, заключенной в отрезке dl, имеет величину
ldl
Где ( - плотность жидкости, - площадь поперечного сечения
канала).
26

27.

Циркуляция
• Следовательно суммарный импульс будет равен
l = l dl ,
Г
где - скорость циркуляции, а l – касательная составляющая
скорости жидкости в объеме dl.
• Сократив на , получим, что
циркуляция v по Г = vl = vl dl.
Г
• Аналогично определяется циркуляция любого вектора a по
произвольному контуру Г:
(17)
циркуляция a по Г = adl = al dl.
Г
Г
27

28.

Циркуляция
Рис.9
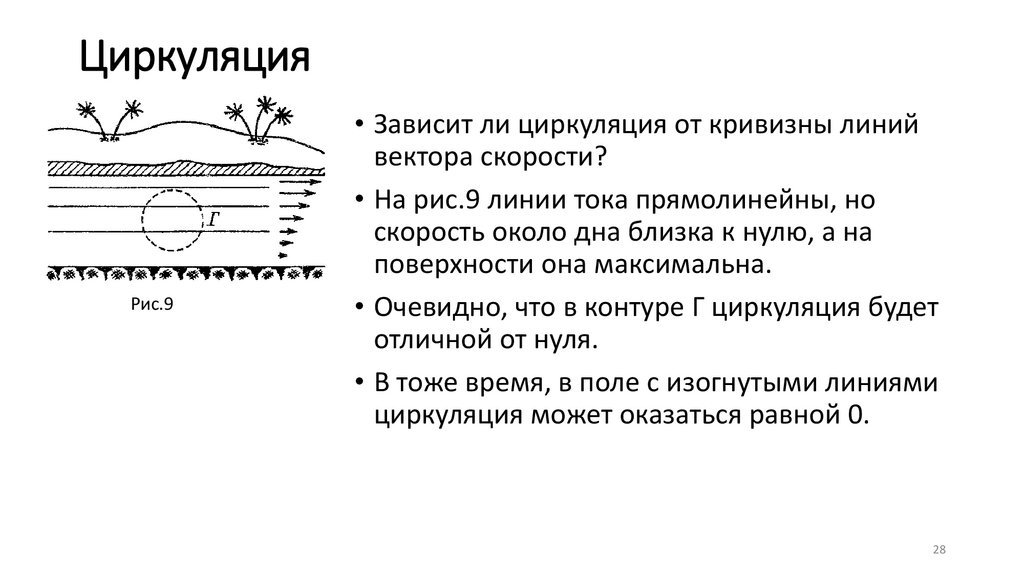
• Зависит ли циркуляция от кривизны линий
вектора скорости?
• На рис.9 линии тока прямолинейны, но
скорость около дна близка к нулю, а на
поверхности она максимальна.
• Очевидно, что в контуре Г циркуляция будет
отличной от нуля.
• В тоже время, в поле с изогнутыми линиями
циркуляция может оказаться равной 0.
28

29.

Циркуляция
Рис.10
• Циркуляция обладает свойством аддитивности.
• То есть, циркуляция по контуру, ограничивающему
несколько смежных поверхностей, равна сумме
циркуляций в каждом контуре.
• Циркуляция C1 по контуру, ограничивающему
поверхность S1, может быть представлена как
сумма интегралов
2
1
C1 = adl = adl + adl.
Г1
1
(I)
(18)
2
( Общ )
• Первый интеграл берется по участку I внешнего контура, второй - по
общей границе поверхностей S1 и S2 в направлении 2-1.
29

30.

Циркуляция
• Аналогично, циркуляция C2 по контуру, ограничивающему
поверхность S2, равна
1
2
C2 = adl = adl + adl.
Г2
2
(19)
1
( Общ )
( II )
• Первый интеграл берется по участку II внешнего контура, второй –
по общей границе поверхностей S1 и S2 в направлении 1 – 2.
• Циркуляция по контуру, ограничивающему суммарную
поверхность S , может быть представлена в виде
2
1
C = adl = adl + adl.
Г
1
2
(I)
( II )
(20)
30

31.

Циркуляция
• Вторые слагаемые в формулах (18) и (19) различаются только
знаком, поэтому
(21)
C = C1 + C2
• Это соотношение не зависит от формы поверхностей и
справедливо при любом числе слагаемых.
Рис.11
• Тогда, если разбить произвольную поверхность
S на большое число элементарных
поверхностей S (см. рис.11), то общая
циркуляция будет равна сумме элементарных
циркуляций
(22)
С = С.
31

32.

Ротор
• Из свойств аддитивности вытекает, что элементарная циркуляция
пропорциональна не длине контура, а поверхности элементарной
площадки.
• Это дает основание утверждать, что циркуляция порождается на
поверхности.
• Тогда можно ввести понятие плотности порождения циркуляции,
т.е. циркуляции, порождаемой бесконечно малым участком
поверхности в расчете на единицу площади это участка:
C
плотность порождения циркуляции = lim
.
S →0 S
(23)
32

33.

Ротор
• Величина (23), вычисленная для некоторой точки P , будет
зависеть не только от свойств поля в этой точке, но также и от
ориентации в пространстве площадки S.
• Эта ориентация может быть задана направлением
положительной нормали n к плоскости контура (положительная
нормаль получается при обходе контура по правилу правого
винта).
• В одной и той же точке P значение (23) для разных направлений
будет различным.
• Выясним зависимости между этими значениями.
33

34.

Ротор
• В однородном поле циркуляция по любому контуру равна нулю.
• В этом случае постоянный вектор a можно вынести за знак
интеграла:
adl = a dl,
а интеграл dl, очевидно, равен нулю.
• Плотность порождения циркуляции однородного поля также
равна нулю.
• Рассмотрим простейшее неоднородное поле, определяемое как
a = axe x = kye x ,
где k – константа.
(24)
34

35.

Ротор
• У этого поля отлична от нуля только компонента ax, которая
пропорциональна координате y.
• Представим себе в этом поле очень малый квадратный контур со
стороной 2b (см. рис.12).
• На рис.12а и 12б контур лежит в
плоскости xy.
• Положительная нормаль n и
фиксированный орт er
направлены на чертеж.
• Цифры в скобках – номера углов
квадратов, расположенных за
углами (цифры без скобок).
Рис.12
35

36.

Ротор
• При такой ориентации контура циркуляция равна
2
k ( y + b ) 2b − k ( y − b ) 2b = 4kb = kS ,
• Соответственно плотность порождения циркуляции равна k.
• Для случая 12в циркуляция равна
k ( y + b cos ) 2b − k ( y − b cos ) 2b = 4kb 2 cos = kS cos ,
• Где - угол между нормалью к контуру и фиксированным ортом er.
• Соответственно плотность порождения циркуляции будет равна
k cos .
• Таким образом, плотность порождения циркуляции ведет себя при
вращении контура как проекция вектора ker на нормаль к контуру.
36

37.

Ротор
• Этот вектор называют ротором векторного поля и обозначают
символом rot a либо [ a].
• Модуль ротора равен наибольшему положительному значению
плотности порождения циркуляции из всех значений,
соответствующих различным ориентациям контура в
пространстве.
• Итак, плотность порождения циркуляции равна проекции
характеризующего поле вектора rot a на положительную нормаль
к контуру:
C
1
= lim
adl.
(25)
( rot a )n = lim
S →0 S
S →0 S
• Эта формула справедлива для любого векторного поля.
37

38.

Ротор
Рис.13
• Наглядное представление о роторе v можно
получить, если мысленно поместить легкую
крыльчатку в текущую жидкость (рис.13).
• В тех местах, где ротор отличен от нуля,
крыльчатка будет вращаться.
• Скорость будет тем выше, чем больше значение
ротора на ось крыльчатки.
• Выражение (25) определяет вектор rot a в самом общем виде, вне
зависимости от системы координат.
• Определим выражения для проекций вектора rot a в декартовой
системе координат.
38

39.

Ротор
Рис.14
• Для этого нужно определить значения
величины (25) для таких ориентаций
площадки S, при которых нормаль n к
площадке совпадает с одной из осей x, y, z.
• Если направить n по оси x, то (25) превратится
в (rot a)x. Контур Г в этом случае будет
расположен в плоскости yz.
• Возьмем этот контур в виде прямоугольника со сторонами y и z
(рис.14), ось направлена на нас, направление обхода по правилу
правого винта.
• Участок 1 контура противоположен по направлению оси z, поэтому
на этом участке al равен – az.
39

40.

Ротор
• Соответственно al на участках 2, 3 и 4 равна aу, az и -aу.
• Следовательно, циркуляцию можно представить в виде
( az 3 − az1 ) z − ( a y 4 − a y 2 ) y,
(26)
• где az3 и az1 – средние значения az на участках 3 и 1, а ay4 и ay2 –
средние значения ay на участках 4 и 2.
• Разность az3 - az1 представляет собой приращение среднего
значения az на отрезке z при смещении этого отрезка в
направлении оси y на y.
• Ввиду малости y и z это приращение можно представить в
виде ( az y ) y , а разность ay4 - ay2 –в виде ( a y z ) z .
40

41.

Ротор
• Подставив эти выражения в формулу (26), получим выражение
для циркуляции
az a y
az a y
y − z y z = y − z S ,
• где S – площадь контура. Разделив циркуляцию на площадь
контура, найдем выражение для проекции rot a на ось x:
az a y
(27)
( rot a ) x = − .
y
z
ax az
(28)
( rot a ) y = − .
• Аналогично
z
x
a y ax
(29)
( rot a ) z = − .
x y
41

42.

Ротор
• Легко убедиться, что любое из этих выражений (27-29) может
быть получено из предыдущего путем циклической перестановки
координат по схеме
• Итак, ротор вектора a определяется в декартовой системе
координат следующим выражением:
az a y
a y ax
ax az
rot a = e x
−
+ ey
−
−
.
+ ez
z
x
z
y
x y
(30)
42

43.

Теорема Стокса
• Зная ротор вектора a в каждой точке некоторой поверхности S,
можно вычислить циркуляцию этого вектора по контуру Г,
ограничивающему S.
• Для этого разобьем поверхность на очень малые элементы S.
• Ввиду их малости эти элементы можно считать плоскими.
• Поэтому в соответствии с (25) циркуляция вектора a по контуру,
ограничивающему S, может быть представлена в виде
(31)
C ( rot a )n S = rot a S ,
• Где n – положительная нормаль к элементу поверхности S.
• Просуммируем (31) по всем S и получим
C = C rot a S .
43

44.

Теорема Стокса
• Осуществив предельный переход S → 0 , придем к формуле
adl = rot a dS.
Г
(32)
S
• Соотношение (32) носит название теоремы Стокса.
• Ее смысл в том, что циркуляция вектора а по произвольному
контуру Г равна потоку вектора rot a через произвольную
поверхность S, ограниченную данным контуром.
• Из теоремы Стокса следует, что ротор соотносится с циркуляцией
подобно тому, как дивергенция соотносится с потоком:
дивергенция порождает поток, ротор порождает циркуляцию.
44

45.

Циркуляция и Ротор электростатического поля
• Ранее мы выяснили, что силы, действующие на заряд q в
электростатическом поле, являются консервативными, то есть
работа этих сил на любом замкнутом контуре Г равна нулю:
A = qEdl = 0.
Г
• Сократив на q, получим соотношение
Edl = 0
(33)
Г
• Интеграл, стоящий в левой части, представляет собой
циркуляцию вектора E по контуру Г.
45

46.

Циркуляция и Ротор электростатического поля
• Таким образом, циркуляция вектора напряженности для
электростатического поля по любому замкнутому контуру
равна нулю.
• Возьмем произвольную поверхность S,
опирающуюся на контур Г, для которого
вычисляется циркуляция (рис.15).
• Согласно теореме Стокса интеграл ротора E,
взятый по поверхности, равен циркуляции
вектора E по контуру Г:
(34)
Рис.15
E dS = Edl.
S
Г
46

47.

Циркуляция и Ротор электростатического поля
• Поскольку циркуляция равна нулю, мы приходим к выводу, что
E dS = 0.
S
• Это возможно лишь в том случае, если ротор вектора E в каждой
точке поля равен нулю:
(35)
E = 0.
Рис.16
• По аналогии с крыльчаткой представим
себе «электрическую крыльчатку» в виде
легкой втулки со спицами, на концах
которых помещаются одинаковые по
величине положительные заряды q.
47

48.

Циркуляция и Ротор электростатического поля
• Она должна вращаться в тех местах, где ротор E отличен от нуля,
с тем большим ускорением, чем больше ротор.
• В случае электростатического поля такое устройство не пришло
бы во вращение при любой ориентации его оси.
• То есть электрическое поле – это безвихревое поле.
• Из необходимости соблюдения (34), можно
заключить что существование
электростатического поля, показанного на
рис.17, невозможно.
• Действительно, циркуляция для такого поля
Рис.17
по штриховому контуру будет отлична от
нуля.
48

49.

Циркуляция и Ротор электростатического поля
• Точно также невозможно, чтобы поле, отличное от нуля в
ограниченном объеме, было во всем этом объеме однородным
(рис.18).
• В этом случае циркуляция по штриховому
контуру была бы отличной от нуля.
Рис.18
49

50.

Теорема Гаусса
• Рассмотрим точечный заряд q и вычислим поток
вектора E через замкнутую поверхность S,
заключающую в себе заряд.
• Количество линий вектора E, начинающихся или
заканчивающихся на точечном заряде q численно
равно произведению плотности линий на
площадь поверхности точечного заряда.
1
q
2
E S =
4
r
4 0 r 2
• Таким образом, количество линий напряженности поля E будет
равно
q
0
50

51.

Теорема Гаусса
• Из векторного анализа известно, что поток вектора E
через любую замкнутую поверхность равен числу
линий, начинающихся или заканчивающихся на
заряде
• Тогда можно записать, что поток вектора E равен
E =
q
0
(36)
51

52.

Теорема Гаусса
• Допустим, что внутри замкнутой поверхности S находится
система из N точечных зарядов q1, q2, …, qN
• Напряженность поля системы зарядов равна
E = Ei
• Исходя из формулы (1) потока вектора получаем
E = EdS = Ei dS = Ei dS
i S
S
S i
52

53.

Теорема Гаусса
• Каждый из интегралов под знаком суммы равен
Ei =
qi
0
• Следовательно, cумма потоков векторов от каждого
заряда будет
N
ФE = E dS =
S
1
q
0 i =1
i
(37)
• Теорема Гаусса: Поток вектора напряженности
электрического поля через замкнутую поверхность
равен алгебраической сумме заключенных внутри
этой поверхности зарядов, деленной на 0.
53

54.

Теорема Гаусса
• Для макрозарядов уходят от дискретной структуры зарядов и
считают, что заряд распределен в пространстве непрерывно с
конечной плотностью.
• Объемная плотность заряда определяется как
dq
=
dV
(38)
• Объемная плотность это отношение заряда dq к физически
бесконечно малому объему, в котором заключен этот заряд
54

55.

Теорема Гаусса
• Зная плотность в каждой точке пространства, можно найти
суммарный заряд, заключенный внутри замкнутой поверхности S.
q = dV
i
V
• Подставим это выражение в формулу (7) и получим
E = EdS =
S
1 N
1
q = dV
0 i =1
i
(39)
0 V
55

56.

Теорема Гаусса
• Согласно теореме Остроградского-Гаусса можно заменить
интеграл по поверхности на интеграл по объему
a
dS
=
a
dV
• Тогда получаем
S
V
1
E dV = dV
0V
V
• То есть, дивергенция поля E связана с плотностью заряда
E =
1
0
(40)
56

57.

Вычисление полей с помощью теоремы
Гаусса
• Если заряд сосредоточен в тонком поверхностном слое
заряженного тела, то используют поверхностную
плотность заряда
dq
=
dS
(41)
• Если заряд распределен по объему или поверхности
цилиндрического тела, используется линейная
плотность
dq
=
dl
(42)
57

58.

Поле бесконечной однородно заряженной
плоскости
• Пусть поверхностная плотность заряда однородна
и равна
• Все линии напряженности поля перпендикулярны
плоскости S
• Напряженность поля в симметричных точках
одинакова по модулю и различна по направлению
• Суммарный поток через поверхность равен 2E S
• Внутри поверхности заключен заряд S . По
теореме Гаусса 2 E S = S / 0 , тогда
E=
2 0
(43)
58

59.

Поле бесконечной однородно заряженной
плоскости
• Для бесконечной плоскости, поскольку
плотность линий не изменяется, то
напряженность поля не зависит от расстояния.
• Если плоскость имеет конечные размеры, то чем
ближе к краю, тем поле сильнее отличается от
поля бесконечной плоскости.
• На больших расстояниях, значительно
превышающих размеры плоскости, создаваемое
ею поле можно рассматривать как поле
точечного заряда.
59

60.

Поле двух разноименно заряженных
плоскостей
• Поле двух параллельных бесконечных
плоскостей с одинаковой по величине
поверхностной плотностью заряда это
суперпозиция полей, создаваемых каждой
плоскостью.
• В области между пластинами напряженность
E = E+ + E− =
+
E=
2 0 2 0
0
(44)
• Вне объема, ограниченного плоскостями, поля
имеют противоположные направления и
значит напряженность будет равна 0.
60

61.

Поле двух разноименно заряженных
плоскостей
• Таким образом, поле сосредоточено между
плоскостями.
• Для плоскостей конечных размеров это также
справедливо, если расстояние между плоскостями
много меньше размеров самой плоскости.
• Это свойство используется в плоских конденсаторах.
61

62.

Поле бесконечного заряженного цилиндра
• Пусть поле создается бесконечной цилиндрической
поверхностью R, заряженной с постоянной
поверхностной плотностью λ
• Модуль напряженности поля E зависит от
расстояния от r от оси цилиндра
• Представим коаксиальную замкнутую
цилиндрическую поверхность радиуса r и высотой h
• В основаниях цилиндра поле En=0
• Для боковой поверхности En=E(r)
62

63.

Поле бесконечного заряженного цилиндра
• Поток вектора E через рассматриваемую поверхность равен
E (r ) 2 rh
• Если r > R, внутрь поверхности попадает заряд q= h , то по
теореме Гаусса
h
1
E ( r ) 2 rh = =
E (r ) =
0 0
2 0 r
q
(45)
• Внутри равномерно заряженной цилиндрической поверхности
бесконечной длины поле отсутствует.
• Вне поверхности поле определяется линейной плотностью и
расстоянием от оси цилиндра
63

64.

Поле бесконечного заряженного цилиндра
• Чем меньше r, тем выше напряженность поля
• Линейный заряд можно представить как
= 2 R
• Тогда в непосредственной близости (при r=R)
1 2 R
E ( R) =
=
=
2 0 R 2 0 R
0
• То есть поле бесконечного заряженного цилиндра вблизи
поверхности равно
1
E ( R) =
0
(46)
64

65.

Поле бесконечного заряженного цилиндра
• С помощью принципа суперпозиции полей
легко найти поле двух коаксиальных
цилиндрических поверхностей, заряженных
одинаковыми разноименными зарядами
• Внутри меньшего и вне большего цилиндров
поле отсутствует.
• В зазоре поле определяется формулой (45).
• Это справедливо и для цилиндров конечной
длины, если расстояние между поверхностями
много меньше размеров цилиндра
65

66.

Поле заряженной сферы
• Поле, создаваемое сферической поверхностью радиуса R,
заряженной с постоянной поверхностной плотностью
• Для концентрической сферы радиуса r от центра сферы En=E(r)
• Если r > R, внутрь поверхности сферы попадает весь заряд q,
значит поле сферы будет равно
E ( r ) 4 r =
2
q
0
• Тогда напряженность поля, создаваемая поверхностью
заряженной сферы равна
1
q
E (r ) =
(r R )
2
4 0 r
(47)
66

67.

Поле заряженной сферы
• Внутри поверхностно заряженной сферы поле отсутствует
• Вне сферы поле тождественно с полем точечного заряда той же
величины, помещенного в центр сферы
• Согласно принципа суперпозиции, поле двух концентрических
поверхностей, заряженных одинаковыми по модулю
разноименными зарядами, сконцентрировано в зазоре между
поверхностями.
• Модуль напряженности определяется формулой (47).
67

68.

Поле объемно-заряженного шара
• Шар радиуса R заряжен с постоянной объемной плотностью
• Для поля вне шара поле будет таким же как и для заряженной
сферы.
• Внутри шара все иначе.
• Сферическая поверхность радиуса r (r<R) заключает в себе заряд,
равный
4 3
q = r
3
68

69.

Поле объемно-заряженного шара
• Теорема Гаусса запишется в такой форме, тогда
q
1 4 3
2
E ( r ) 4 r = = r
0 0 3
1 q 4 3
q
2
r
• Заменим на =
и получим E ( r ) 4 r =
4
4
3 3
3
0
R
R
3
3
• Следовательно
1
q
E (r ) =
r , (r R )
3
4 0 R
(48)
• Внутри шара напряженность растет линейно с расстоянием от
центра, а вне шара убывает как у точечного заряда.
69