Вычисление простейших тригонометрических выражений (1)

1.

ВЫЧИСЛЕНИЕ
ПРОСТЕЙШИХ
ТРИГОНОМЕТРИЧЕСКИХ
ВЫРАЖЕНИЙ

2.

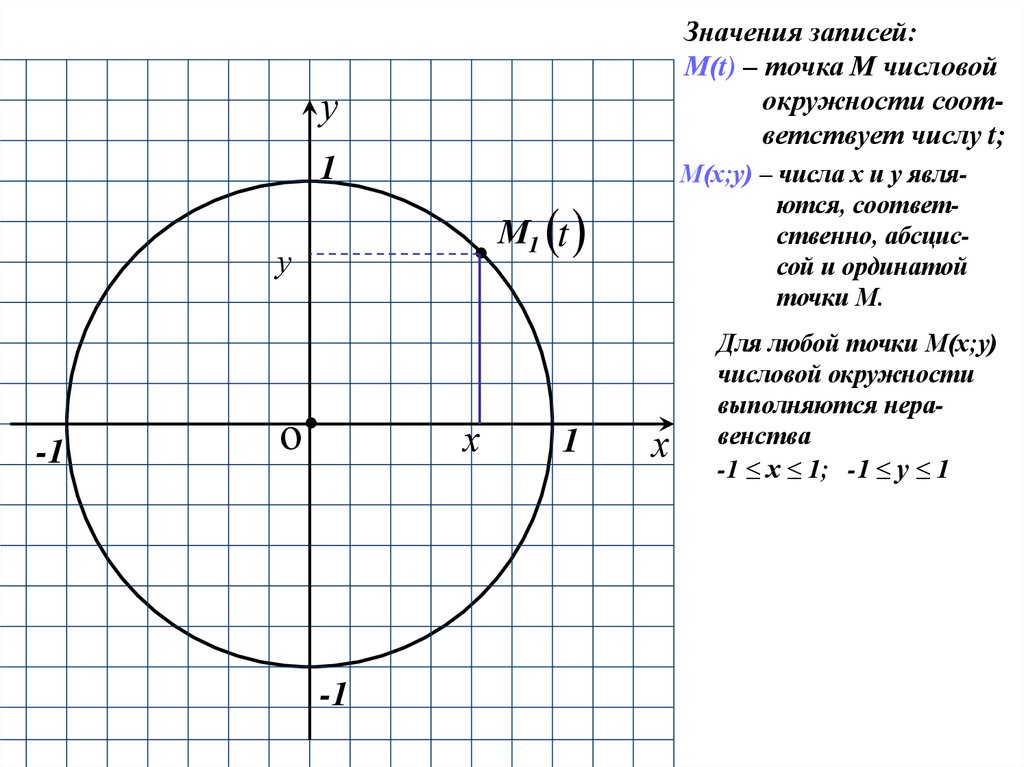
Значения записей:
М(t) – точка М числовой
окружности соответствует числу t;
у
1
у
-1
о
х
М(х;у) – числа х и у являются, соответственно, абсциссой и ординатой
точки М.
М1 t
1
х
1
-1
Для любой точки М(х;у)
числовой окружности
выполняются неравенства
-1 ≤ х ≤ 1; -1 ≤ ху ≤ 1

3.

у
1
2
2
-1
о
М
1 4
2
2
1
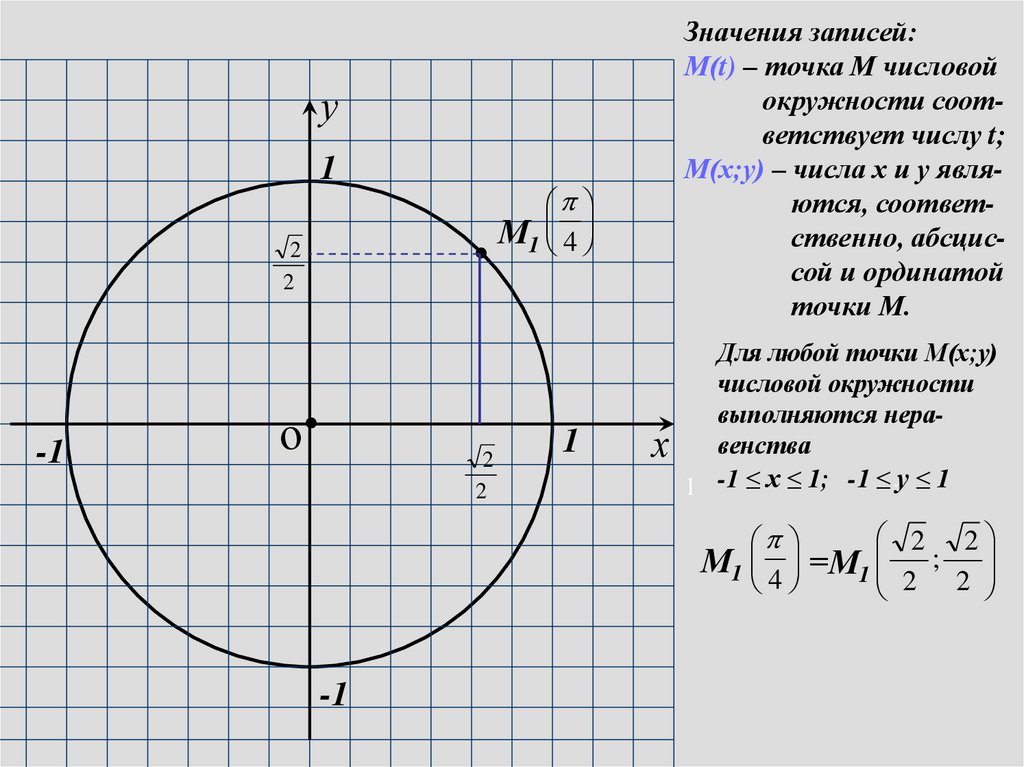
Значения записей:
М(t) – точка М числовой
окружности соответствует числу t;
М(х;у) – числа х и у являются, соответственно, абсциссой и ординатой
точки М.
Для любой точки М(х;у)
числовой окружности
выполняются нерах венства
1 -1 ≤ х ≤ 1; -1 ≤ ху ≤ 1
2 2
М1 4 =М1 ;
2 2
-1

4.

у
3
-1
2
3
3
3
1
3
2
5
6
7
6
5
4
●
4
1
2
1
2
2
2
3
2
-1
3
2
5
3
1
7
4
11
6
3
3
3
х
2
2
2
3
2
6
3
● ●
2
31
1
2
4
● ● ●
-1 3 2 1
2
3
3
● 3
2
2
2
3

4
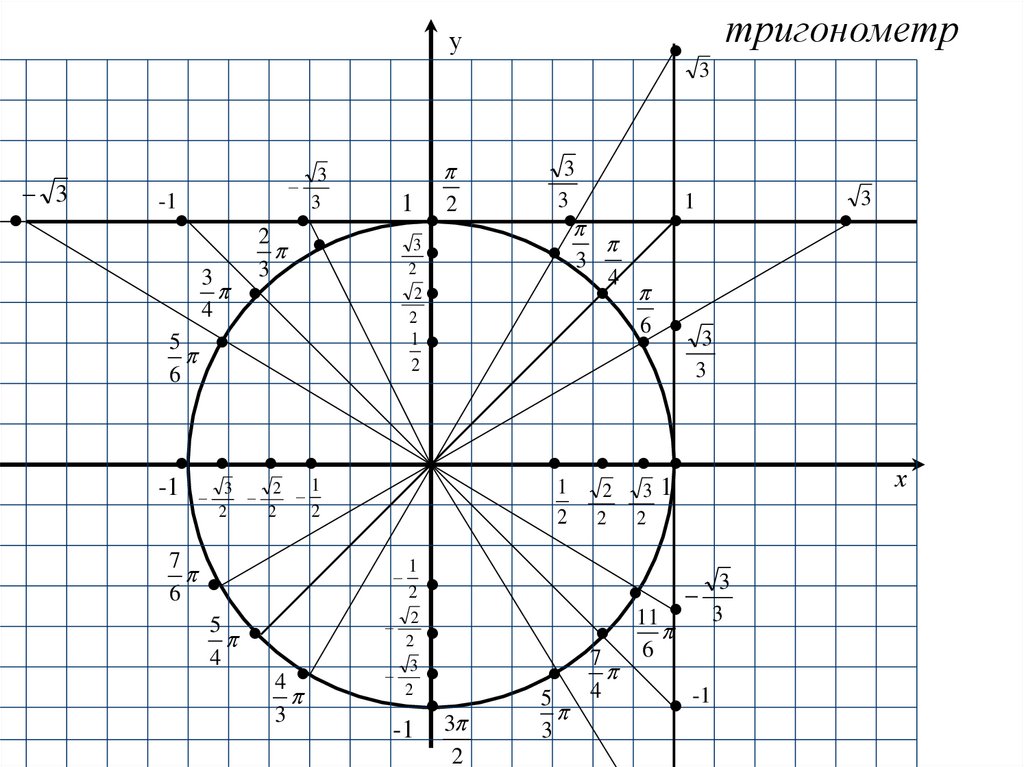
тригонометр
● -1
3
3

5.

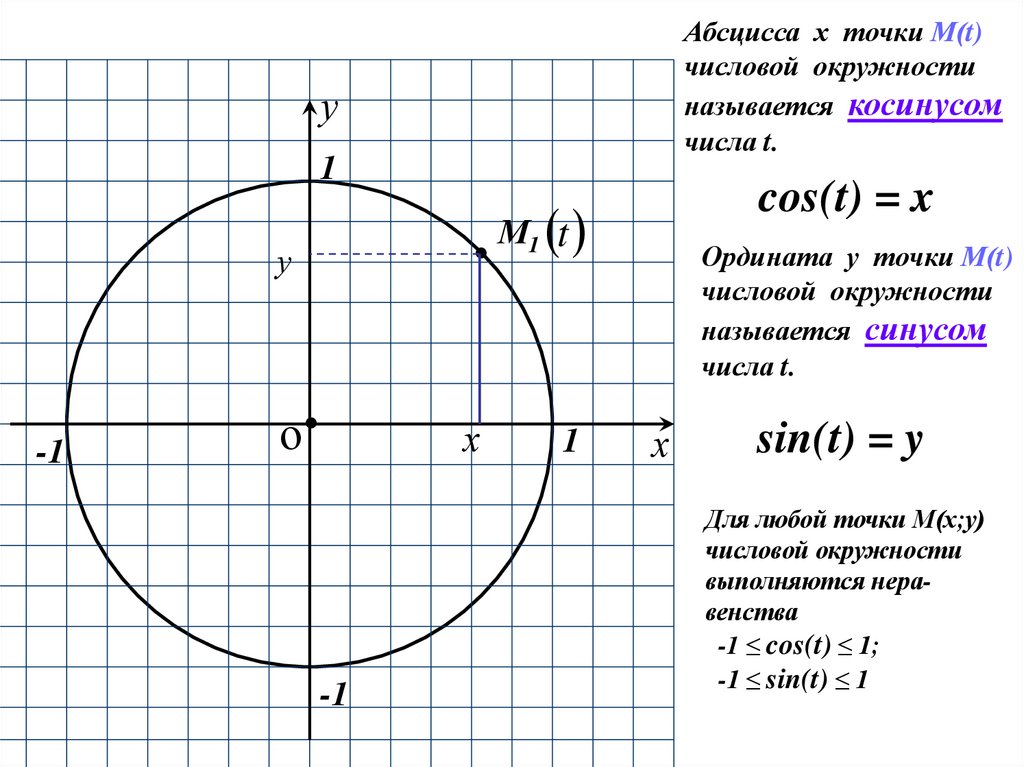
Абсцисса х точки М(t)
числовой окружности
называется косинусом
числа t.
у
1
у
-1
о
М1 t
х
1
cos(t) = x
Ордината у точки М(t)
числовой окружности
называется синусом
числа t.
sin(t) = y
х
1
-1
х
Для любой точки М(х;у)
числовой окружности
выполняются неравенства
-1 ≤ cos(t) ≤ 1;
-1 ≤ sin(t) ≤ 1

6.

Отношение синуса числа t к косинусу того же числа
называют тангенсом числа t и обозначают
Отношение косинуса числа t к синусу того же числа
называют котангенсом числа t и обозначают

7.

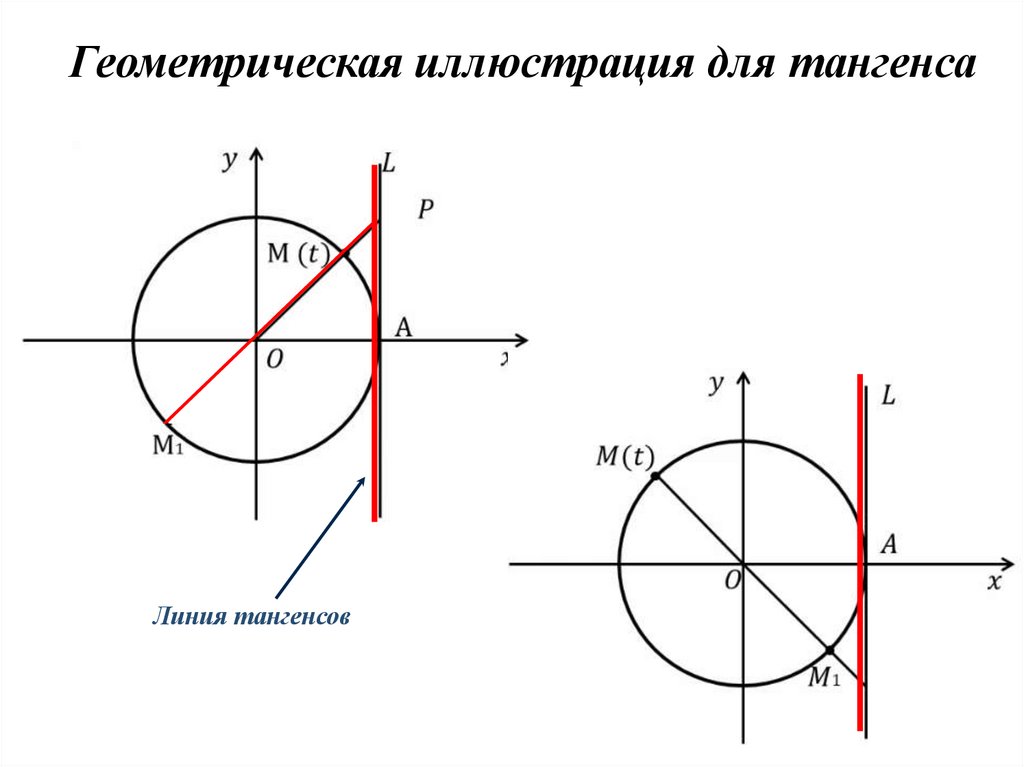
Геометрическая иллюстрация для тангенса
Линия тангенсов

8.

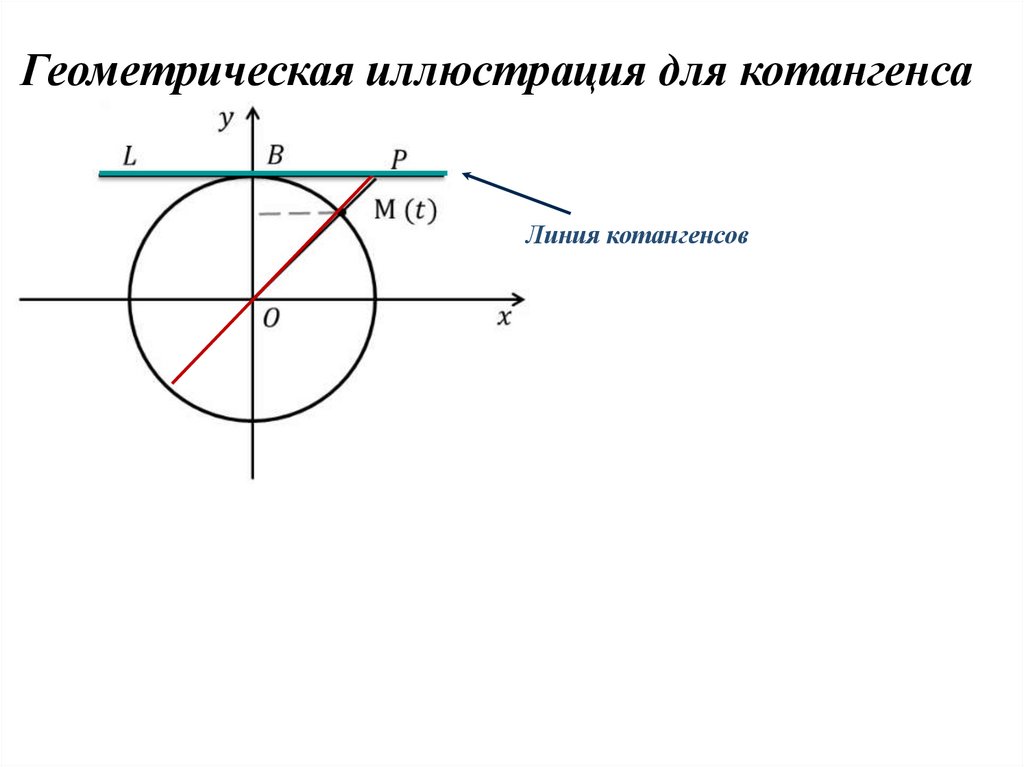
Геометрическая иллюстрация для котангенса
Линия котангенсов