Тригонометрический круг

1.

у
1
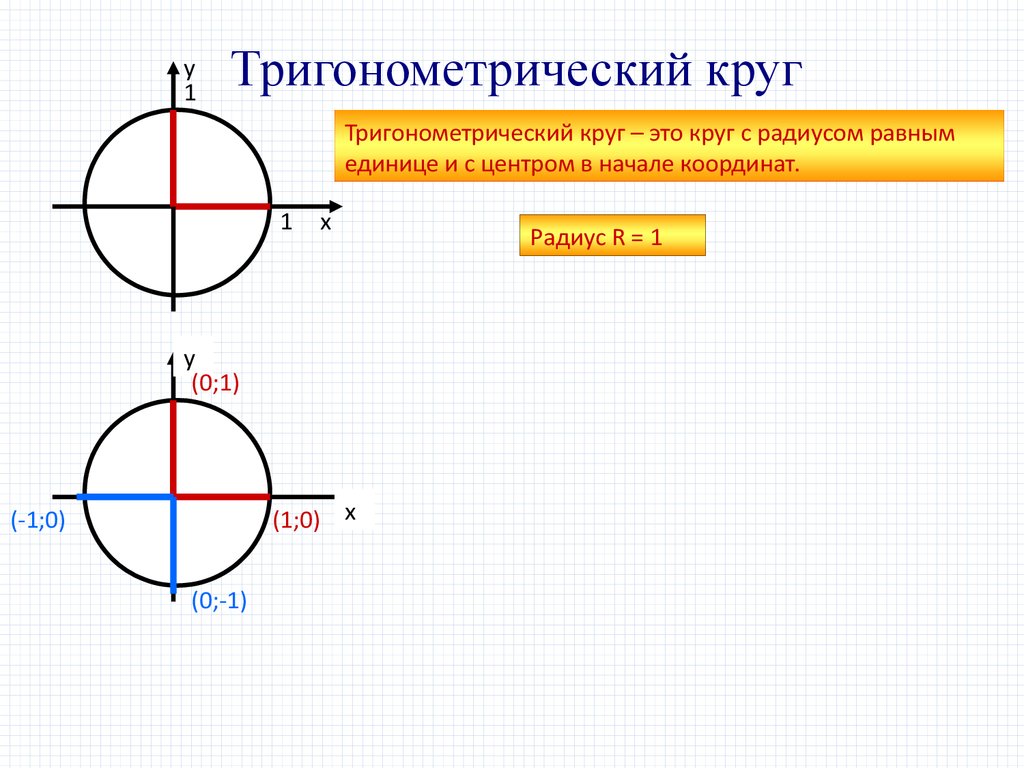
Тригонометрический круг
Тригонометрический круг – это круг с радиусом равным
единице и с центром в начале координат.
1
х
у
(0;1)
(1;0) х
(-1;0)
(0;-1)
Радиус R = 1

2.

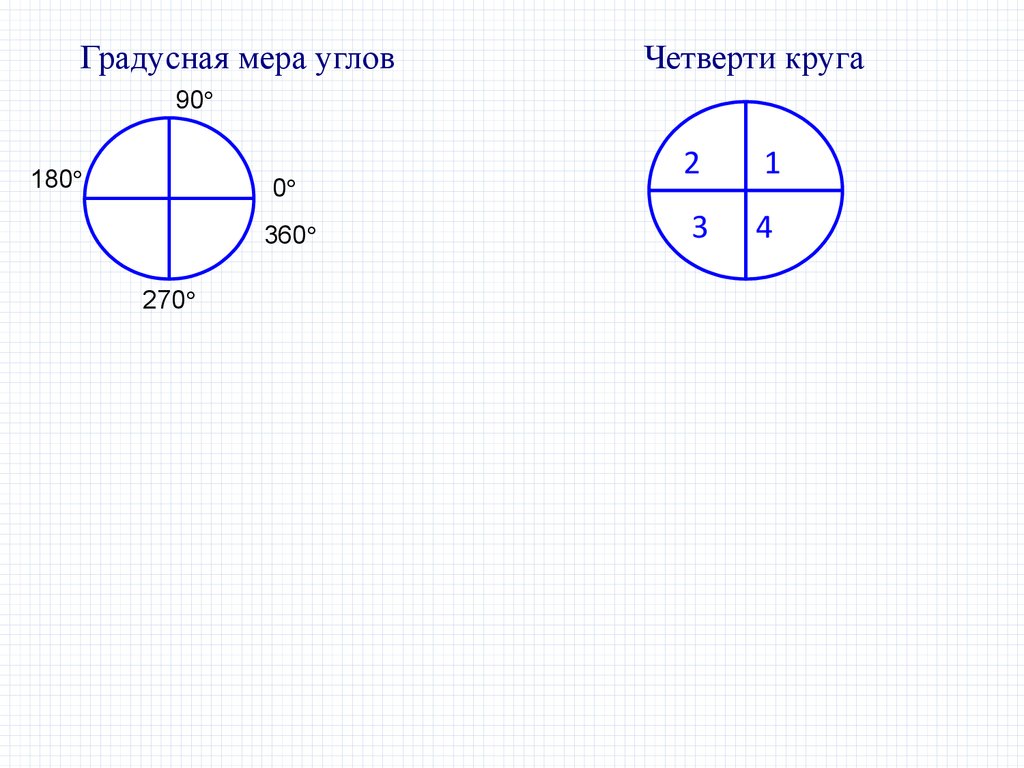
Градусная мера углов
Четверти круга
90
180
0
360
270
2
1
3
4

3.

Углы
на тригонометрическом круге
у
Угол на круге определяется поворотом радиуса
+
х
-
За нулевое положение радиуса принято его положение на
положительном направлении оси Х.
Угол поворота радиуса отсчитывается от положительного направления оси Х: с
плюсом - против часовой стрелки, с минусом - по часовой стрелке.
у
у
х
х

4.

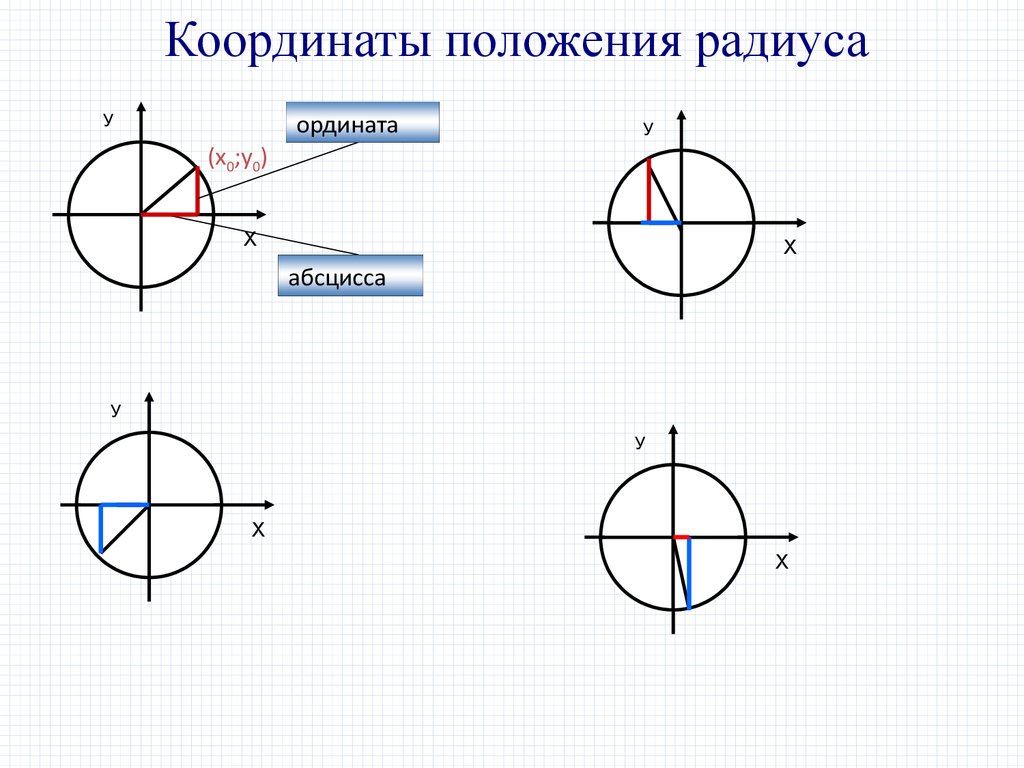
Координаты положения радиуса
У
ордината
У
(х0;у0)
Х
Х
абсцисса
У
У
Х
Х

5.

Радианная мера угла
Один радиан – это центральный угол, опирающийся на дугу равную радиусу
Длина окружности 2πR
В окружности 2πR : R = 2π радиан
2π соответствуют 360°
2π --------------- 360°
90° = 180° /2 = π /2
π --------------- 180°
270° = 90°· 3 = 3π /2
Радианная мера углов в круге
1,57
π /2
π
0
Так как π = 3,14…, то
3,14
0
6,28
2π
3π /2
4,71

6.

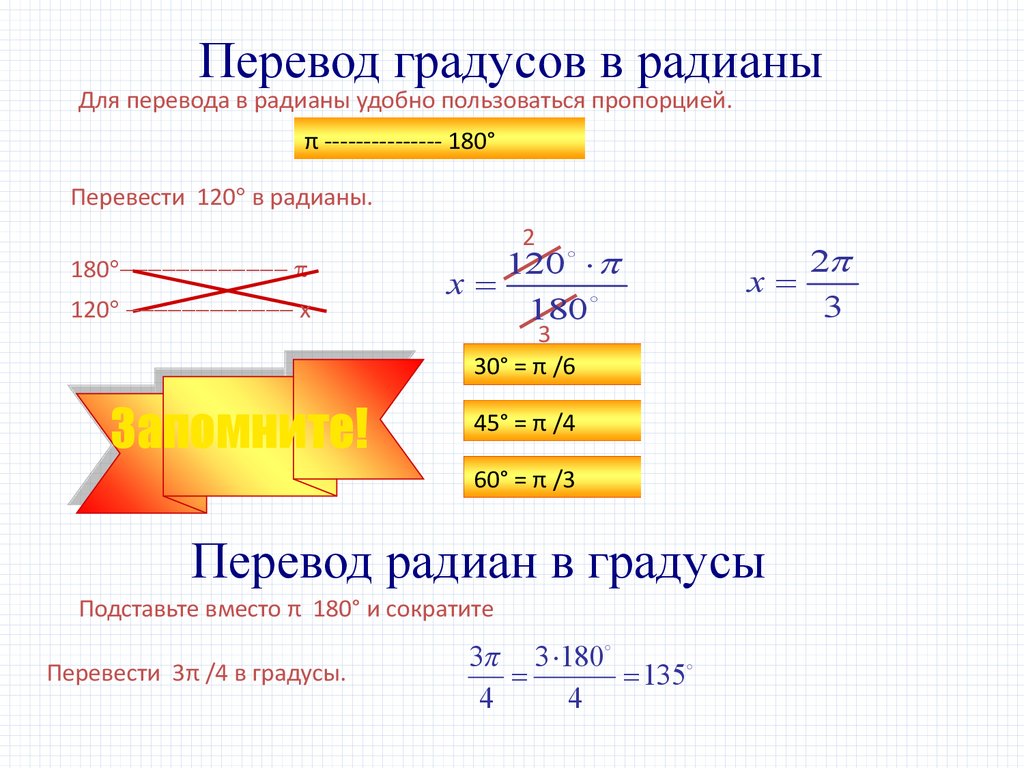
Перевод градусов в радианы
Для перевода в радианы удобно пользоваться пропорцией.
π --------------- 180°
Перевести 120 в радианы.
180
120 х
Запомните!
2
120
x
180
3
30° = π /6
2
x
3
45° = π /4
60° = π /3
Перевод радиан в градусы
Подставьте вместо π 180° и сократите
Перевести 3π /4 в градусы.
3 3 180
135
4
4

7.

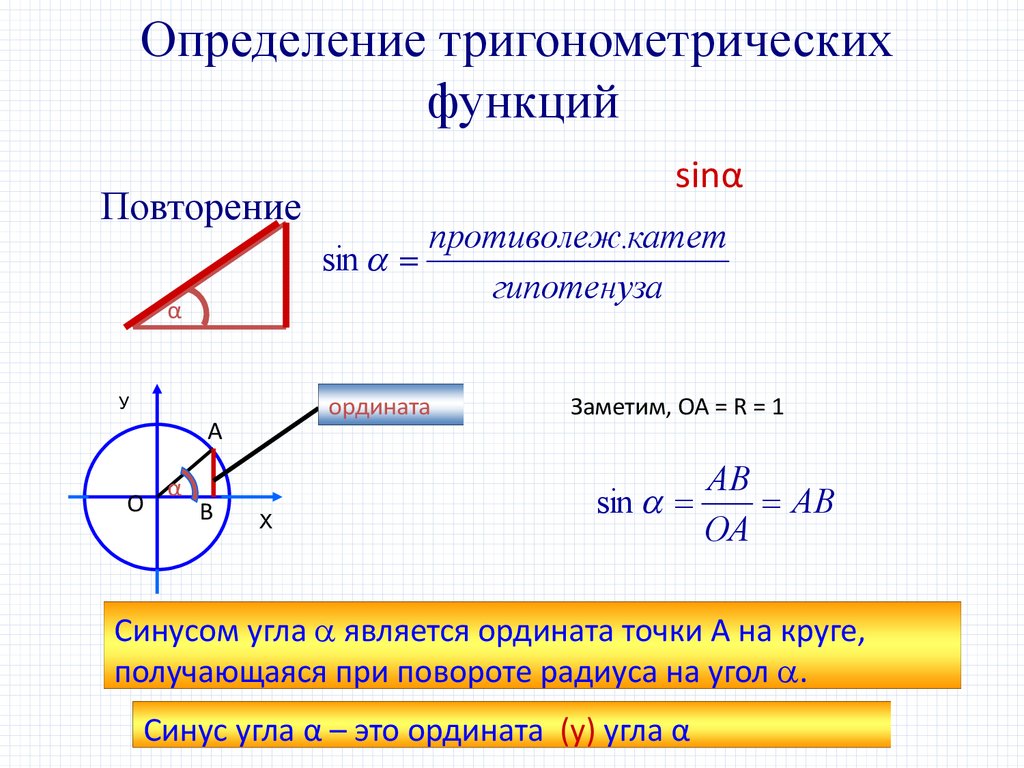
Определение тригонометрических
функций
Повторение
α
У
α
В
противолеж.катет
sin
гипотенуза
ордината
А
О
sinα
Х
Заметим, ОА = R = 1
AB
sin
AB
OA
Синусом угла является ордината точки А на круге,
получающаяся при повороте радиуса на угол .
Синус угла α – это ордината (у) угла α

8.

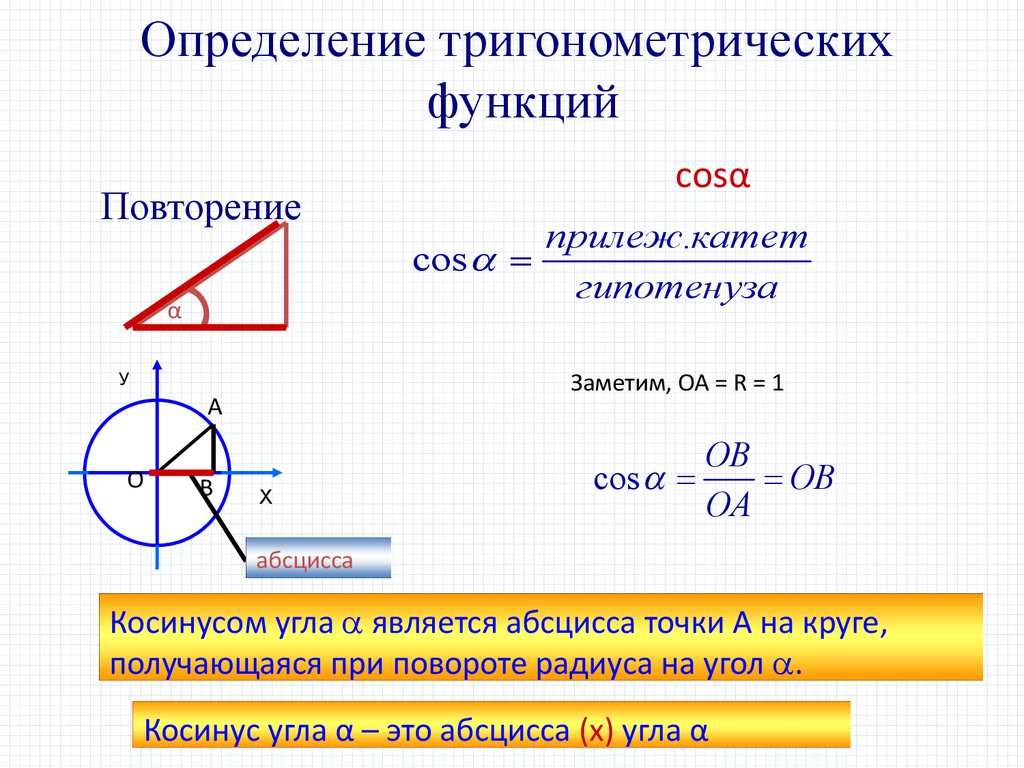
Определение тригонометрических
функций
Повторение
α
У
В
прилеж.катет
cos
гипотенуза
Заметим, ОА = R = 1
А
О
cosα
Х
OB
cos
OB
OA
абсцисса
Косинусом угла является абсцисса точки А на круге,
получающаяся при повороте радиуса на угол .
Косинус угла α – это абсцисса (х) угла α

9.

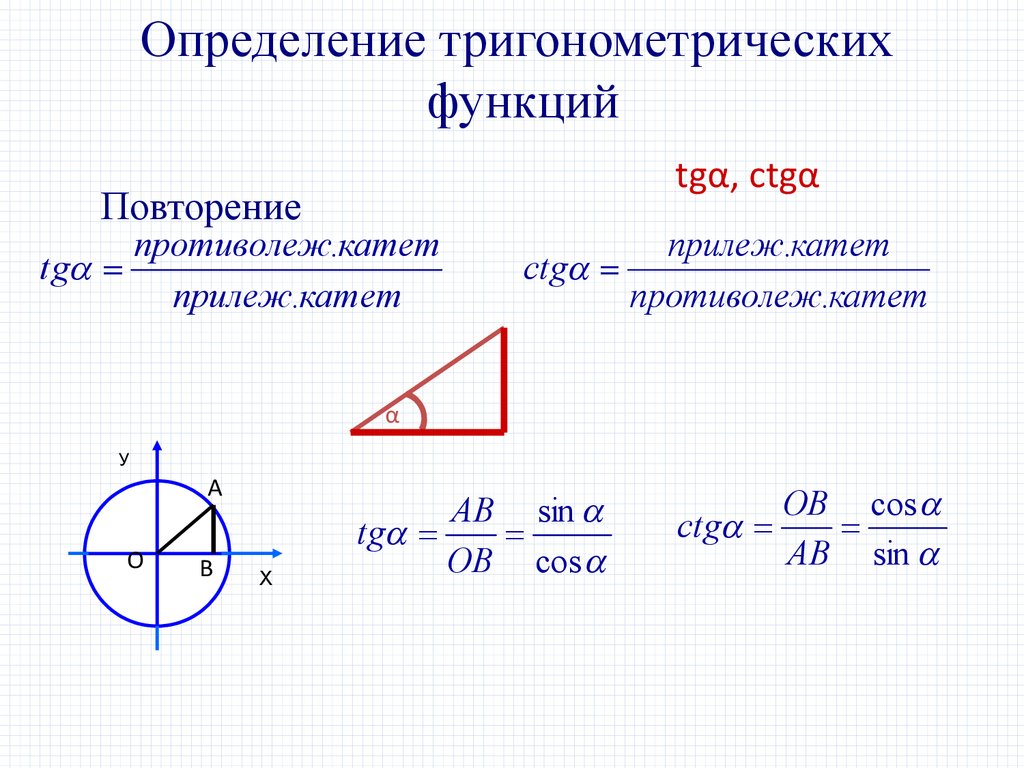
Определение тригонометрических
функций
tgα, ctgα
Повторение
противолеж.катет
tg
прилеж.катет
прилеж.катет
ctg
противолеж.катет
α
У
А
О
В
Х
AB sin
tg
OB cos
OB cos
сtg
AB sin

10.

У
М
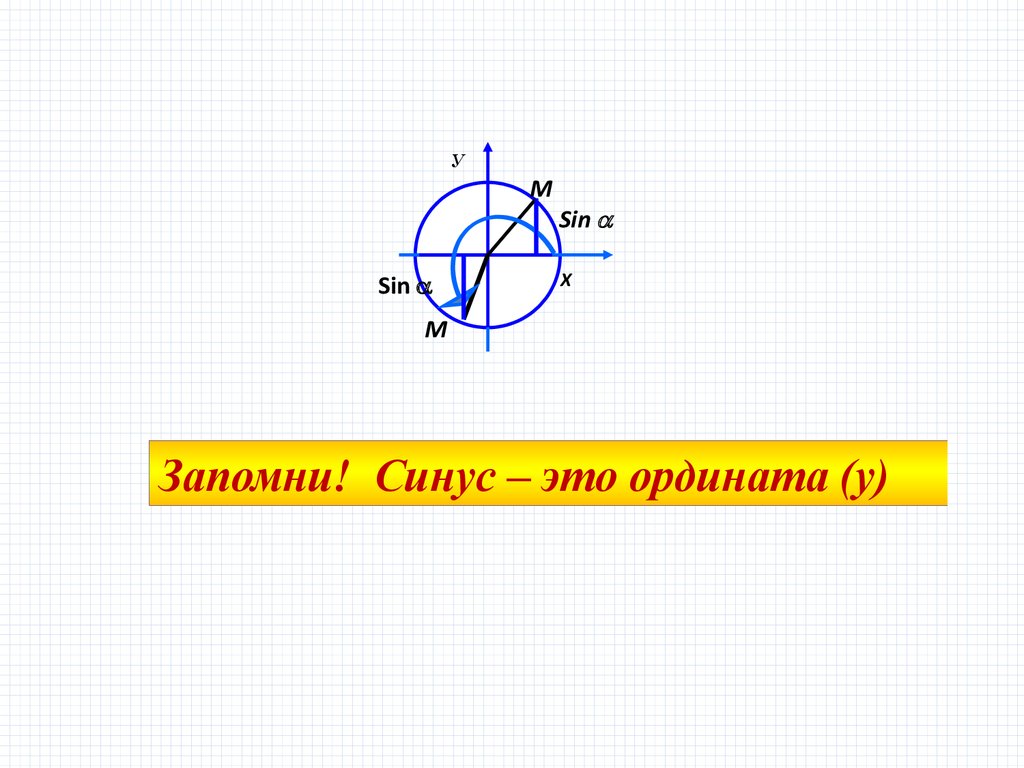
Sin
Sin
Х
M
Запомни! Синус – это ордината (y)

11.

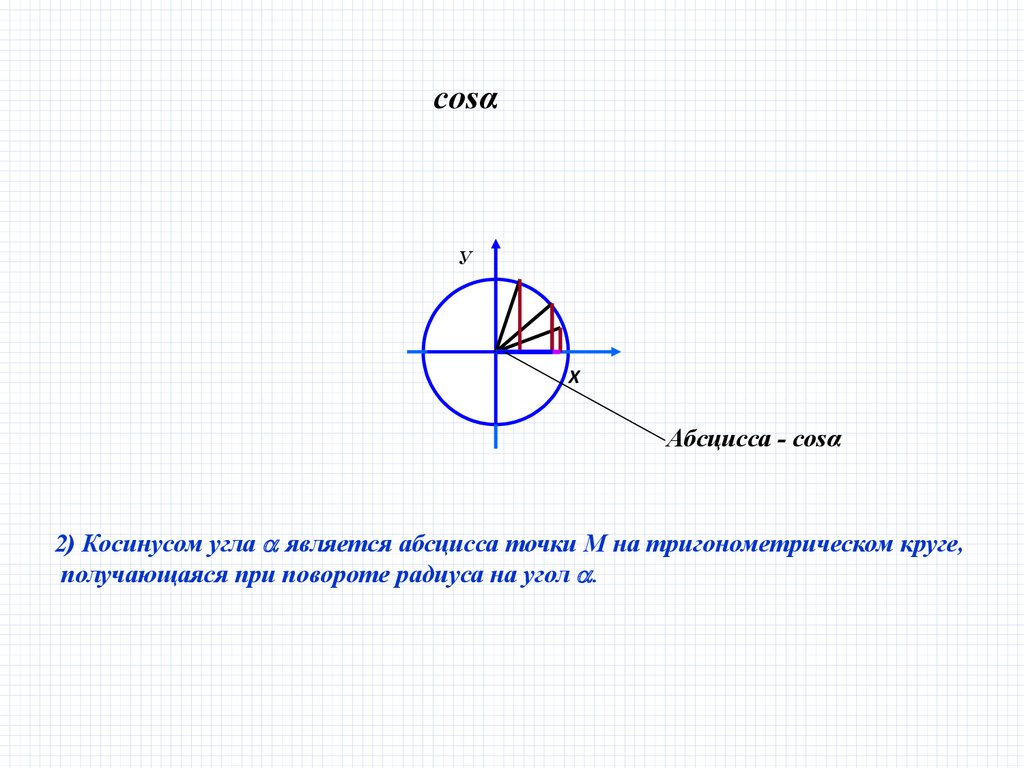
cosα
У
Х
Абсцисса - cosα
2) Косинусом угла является абсцисса точки М на тригонометрическом круге,
получающаяся при повороте радиуса на угол .

12.

У
М
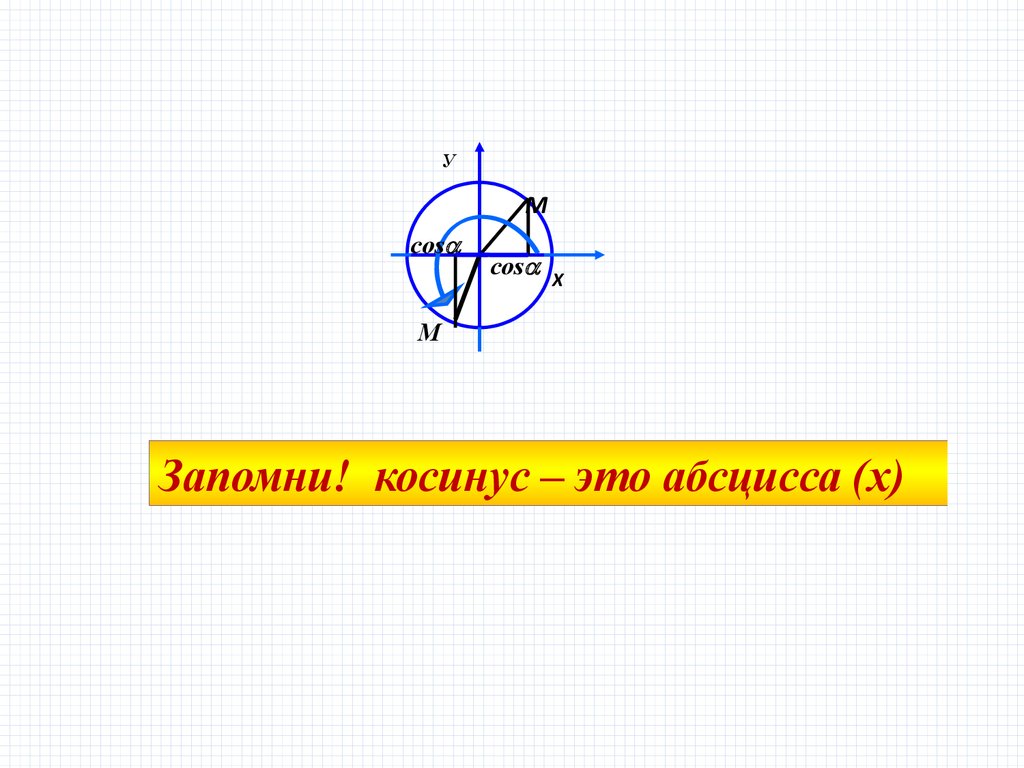
cos
cos
Х
M
Запомни! косинус – это абсцисса (x)

13.

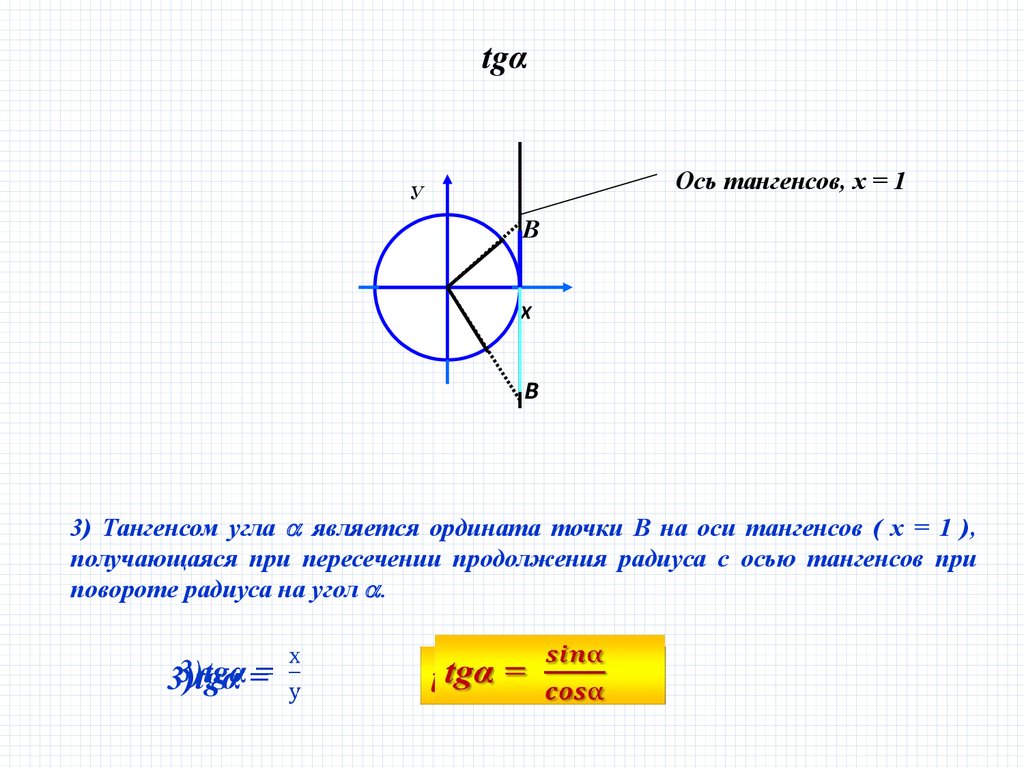
tgα
Ось тангенсов, х = 1
У
В
Х
В
3) Тангенсом угла является ордината точки В на оси тангенсов ( х = 1 ),
получающаяся при пересечении продолжения радиуса с осью тангенсов при
повороте радиуса на угол .
3)tgα =
tgα =

14.

сtgα
В
У
В
Ось котангенсов, у = 1
Х
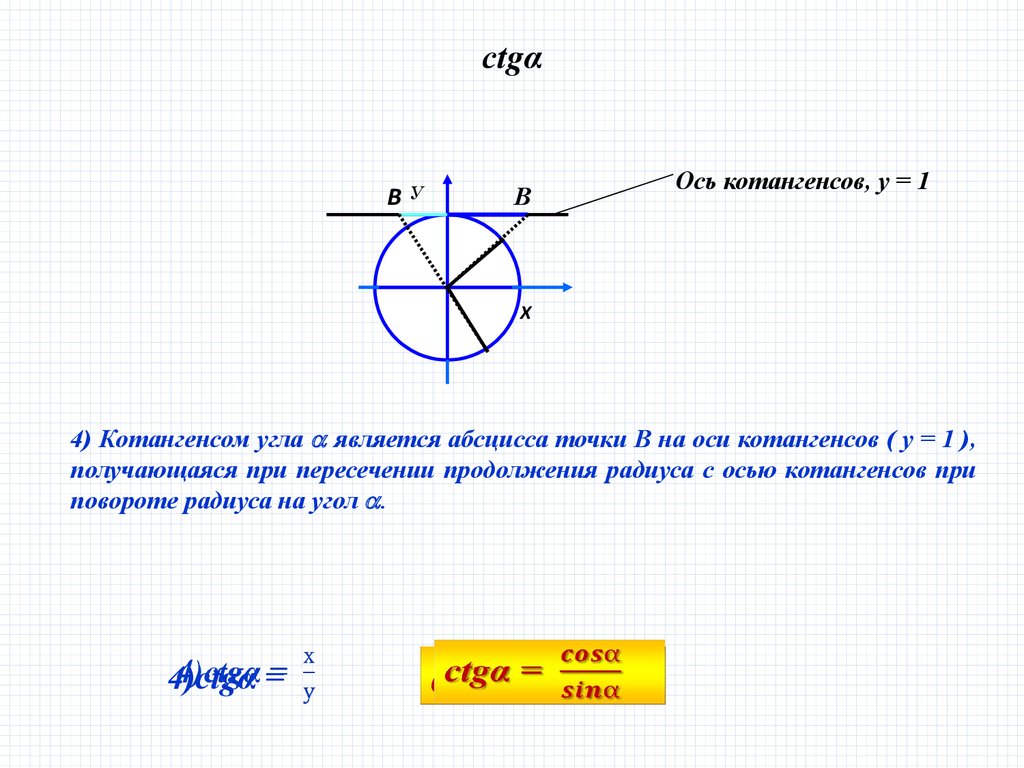
4) Котангенсом угла является абсцисса точки В на оси котангенсов ( у = 1 ),
получающаяся при пересечении продолжения радиуса с осью котангенсов при
повороте радиуса на угол .
4)ctgα =
ctgα =

15.

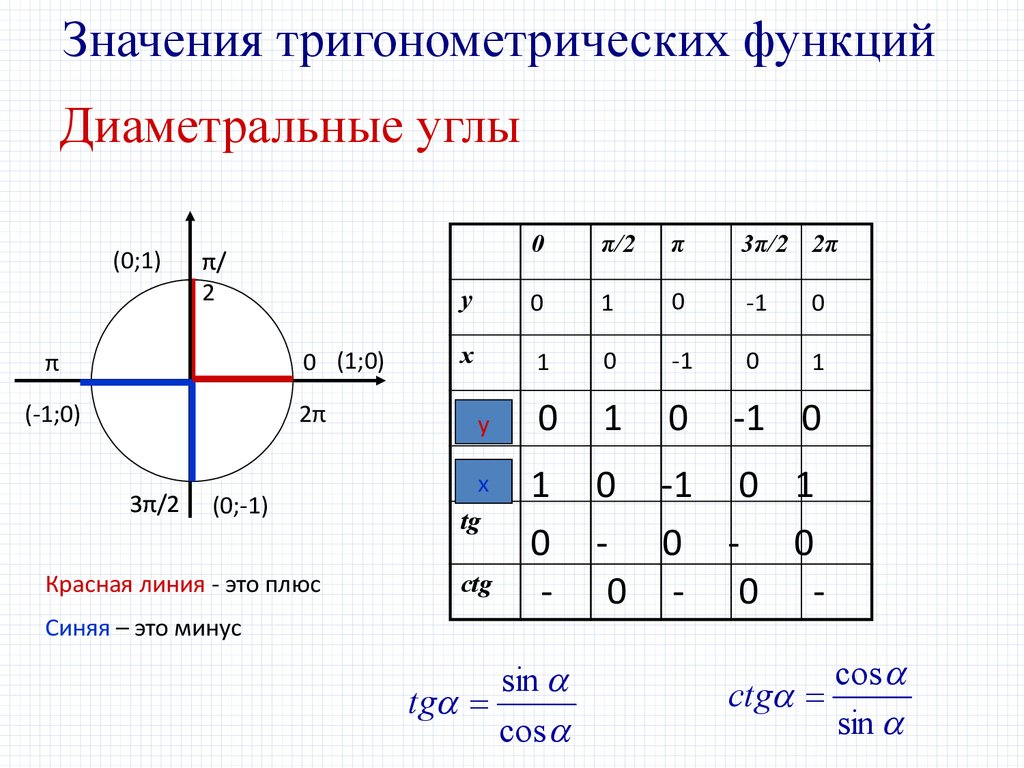
Значения тригонометрических функций
Диаметральные углы
(0;1)
π
(-1;0)
3π/2
0
π/2
π
3π/2 2π
у
0
1
0
-1
0
0 (1;0)
х
1
0
-1
0
1
2π
sin
y
0
1
0
cos
x
tg
1
0
-
0 -1 0 1
- 0 - 0
0 - 0 -
π/
2
(0;-1)
Красная линия - это плюс
Синяя – это минус
сtg
sin
tg
cos
-1 0
cos
сtg
sin

16.

Значения тригонометрических функций
π/6
π/4
π/3
1
2
2
2
3
2
π/6
sin
2
2
3
2
cos
3
2
3
3
2
2
1
2
3
3
сtg
1
2
π/4
2
2
π/3
3
3
1
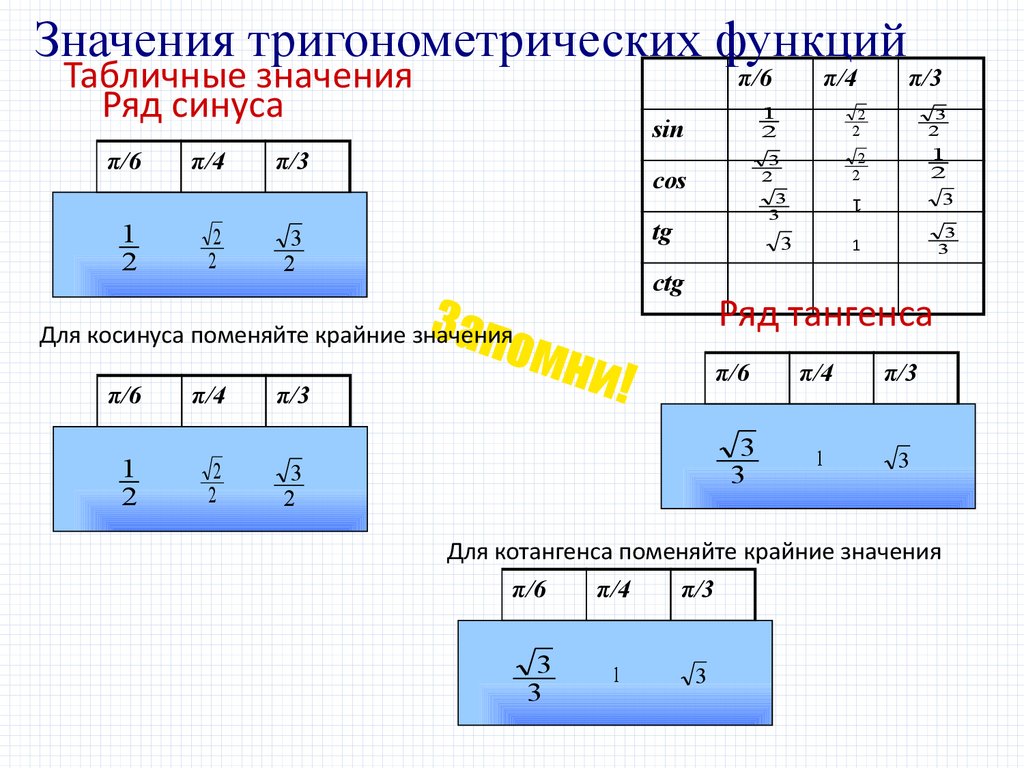
Ряд тангенса
Для косинуса поменяйте крайние значения
π/6
π/3
1
2
tg
Зап
омн
и!
π/4
1
Табличные значения
Ряд синуса
π/6
3
3
3
2
π/4
π/3
1
3
Для котангенса поменяйте крайние значения
π/6
π/4
π/3
3
3
1
3

17.

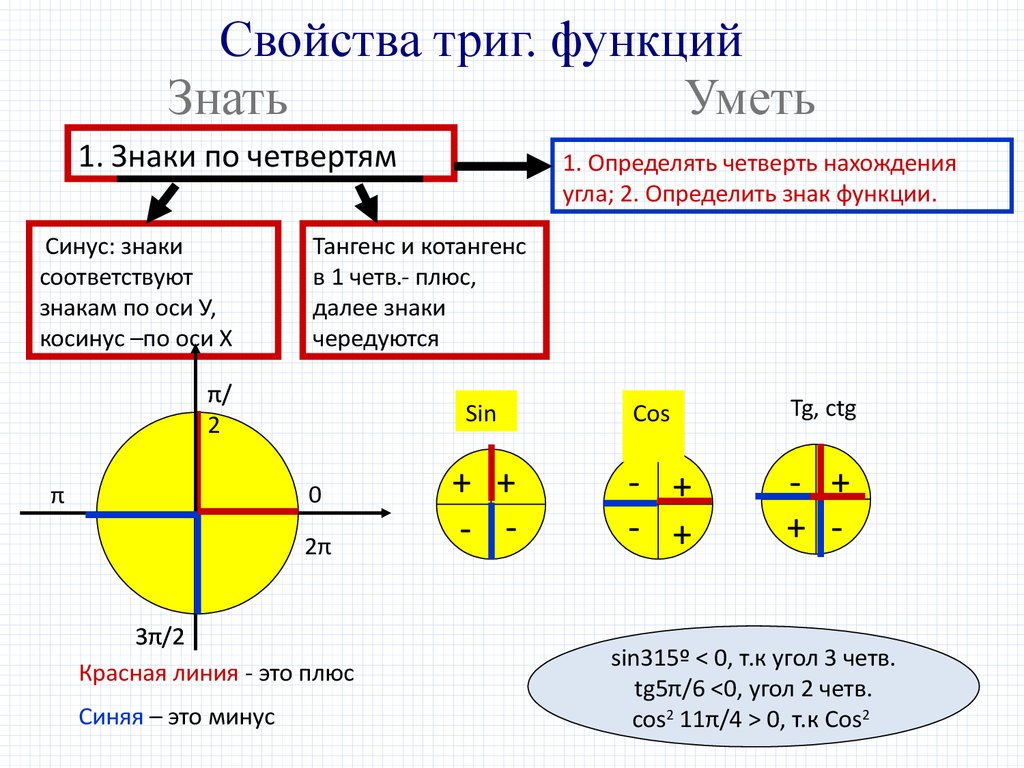
Свойства триг. функций
Знать
Уметь
1. Знаки по четвертям
Синус: знаки
соответствуют
знакам по оси У,
косинус –по оси Х
Тангенс и котангенс
в 1 четв.- плюс,
далее знаки
чередуются
π/
2
Sin
0
π
2π
3π/2
Красная линия - это плюс
Синяя – это минус
1. Определять четверть нахождения
угла; 2. Определить знак функции.
+ +
- -
Cos
Tg, ctg
- +
- +
- +
+ -
sin315º < 0, т.к угол 3 четв.
tg5π/6 <0, угол 2 четв.
cos2 11π/4 > 0, т.к Cos2

18.

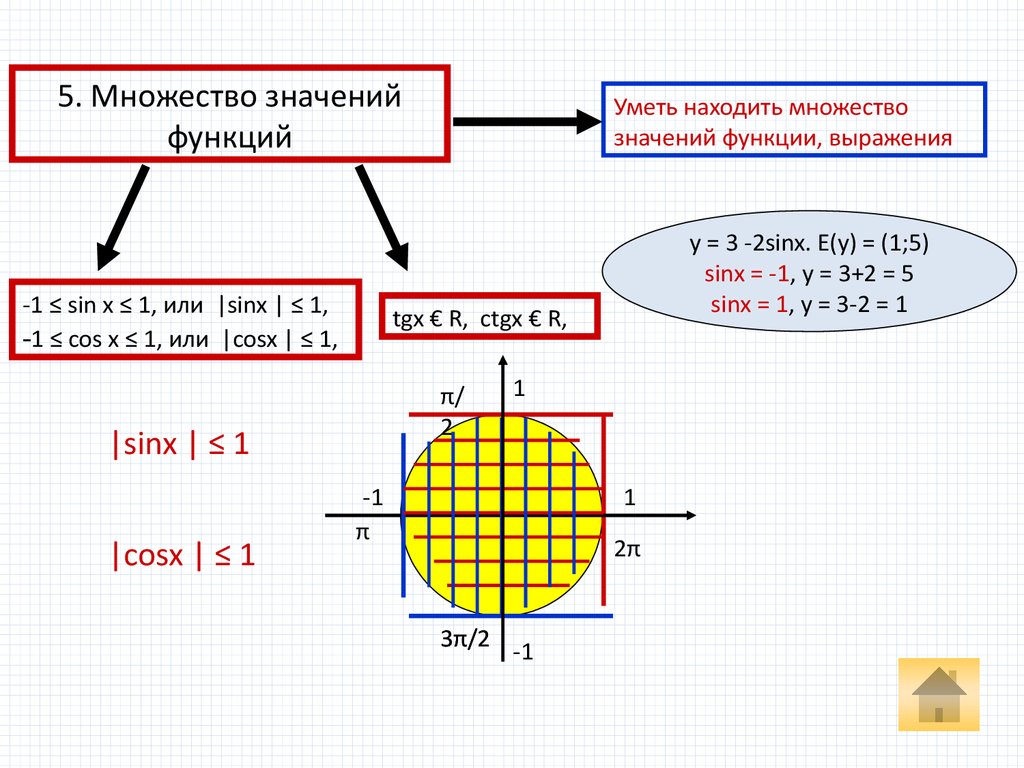
5. Множество значений
функций
-1 ≤ sin х ≤ 1, или |sinx | ≤ 1,
-1 ≤ cos х ≤ 1, или |cosx | ≤ 1,
y = 3 -2sinx. E(y) = (1;5)
sinx = -1, y = 3+2 = 5
sinx = 1, y = 3-2 = 1
tgx € R, ctgx € R,
π/
2
|sinx | ≤ 1
|cosx | ≤ 1
Уметь находить множество
значений функции, выражения
1
-1
π
1
2π
3π/2
-1

19.

Период
Период
– это число, при прибавлении которого к
аргументу значение функции не изменяется.
f(x +Т) = f(x)
Если Т – период, то Tn для n € Z тоже период. Считается Т –
наименьший период
Так как f(x
sin, cos
+Тn) = f(x), то Tn можно опустить
Т = 2π
tg, ctg
Примеры
1. sin 390º = sin (360º + 30º) = sin 30º = ½
2. sin 790º = sin (2·360º + 30º) = sin 30º = ½
3
3. tg 210º = tg (180º + 30º) = tg 30º = 3
4. cos 7π/3= cos (2π + π/3) = cos π/3 = ½
5. cos (2π – β) = cos (-β) = cos β
6. sin (6π – 2α) = sin (-2α) = - sin 2α
Т=π

20.

Четность, нечетность
Синус, тангенс, котангенс – функции
нечетные.
Минус у угла можно вынести за знак функции
Косинус – функция
четная.
Минус у угла можно опустить
Примеры
1. sin ( – х) = - sin х
2. sin ( π/4 – х) = - sin ( х - π/4 )
3. tg (- π/6) = - tg π/6 = -
3
3
4. cos (-7π/3)= cos 7π/3 = cos (2π + π/3) = cos π/3 = ½
5. cos (-β) = cos β
6. ctg ( 2α - π/2) = - ctg (π/2 - 2α )

21.

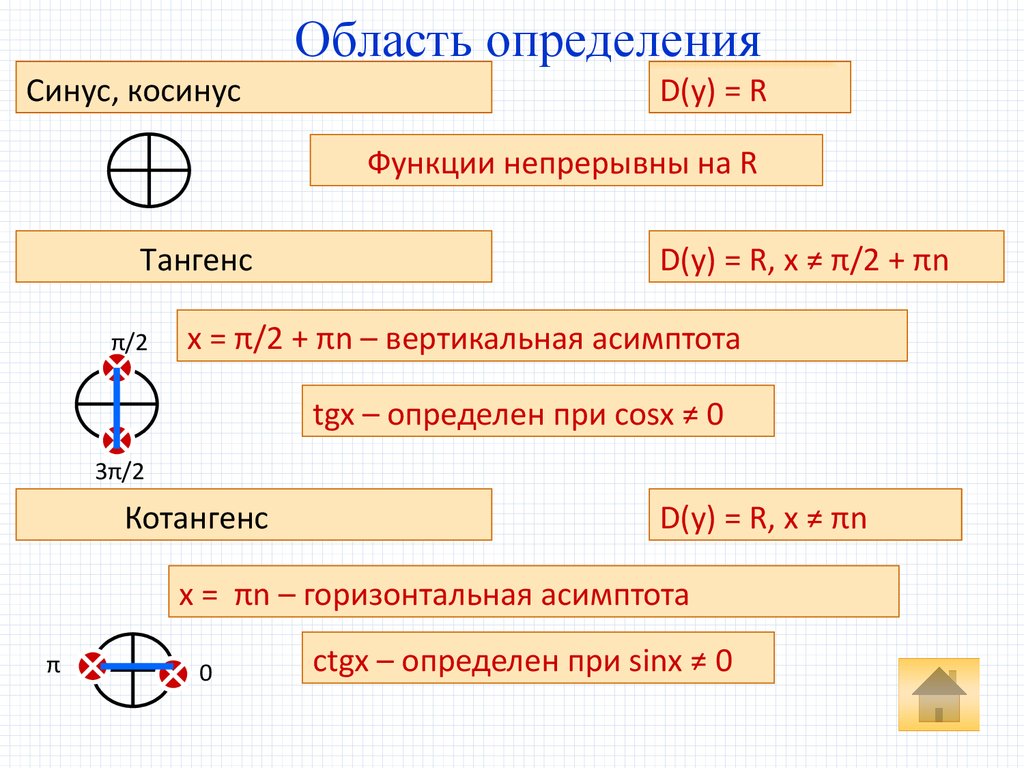
Область определения
Синус, косинус
D(y) = R
Функции непрерывны на R
Tангенс
π/2
D(y) = R, x ≠ π/2 + πn
x = π/2 + πn – вертикальная асимптота
tgx – определен при cosx ≠ 0
3π/2
Котангенс
D(y) = R, x ≠ πn
x = πn – горизонтальная асимптота
π
0
ctgx – определен при sinx ≠ 0