Лекция_5_2к_3с_Электромагнетизм_Электростатика

1.

Физика. 2 курс. 3 семестр
2025-2026 учебный год
Лекция 5 Электромагнетизм
Раздел 1: Электростатика
- Локальное поле в диэлектрике
- Сегнетоэлектрик
В.И. Читайкин
кандидат физико-математических наук
доцент

2.

План лекции
Наименование раздела
Номер слайда
Введение
3
Раздел 1. Локальное электрическое поле в диэлектрике
4
1.1. Определение
5
1.2. Расчёт локального поля
6
1.3. Связь макро- и микро-характеристик диэлектрика
7
а). Формула Клаузиуса-Мосотти
7
б). Формула Дебая-Ланжевена
8
в). Формула Лоренц-Лоренца
9
г). Дополнительные полезные соотношения
10
1.4. Экспериментальное определение поляризуемостей и дипольных электрических
моментов молекул
11
1.4.1. Экспериментальное определение поляризуемостей и дипольных электрических
моментов молекул. Таблицы значений
12
Раздел 2. Сегнетоэлектрик
13
2.1. Определение и основное свойство: гистерезис
14
2.2. Причина гистерезиса (факультативно)
15
2.3. Другие свойства сегнетоэлектрика
17
2

3.

Введение
В 5-ой лекции завершается рассмотрение вопросов по теме «Диэлектрики».
Раздел 1 лекции посвящён довольно тонкому и практически важному вопросу: расчёту локального
поля в диэлектрике, действующего на так называемый «одиночный» диполь («одиночную» молекулу).
Это локальное поле наряду со средним макроскопическим полем (см. предыдущие лекции) полностью
определяют электрические свойства диэлектрика. Напомню, любая молекула (изначально полярная или
неполярная) во внешнем поле является диполем, т.е. частицей с двумя полюсами («+» и «-»).
В этом же разделе 1 лекции приведены формулы, устанавливающие связь между
макроскопическими характеристиками диэлектрика в целом и микроскопическими характеристиками
молекул (диполей), из которых этот диэлектрик состоит.
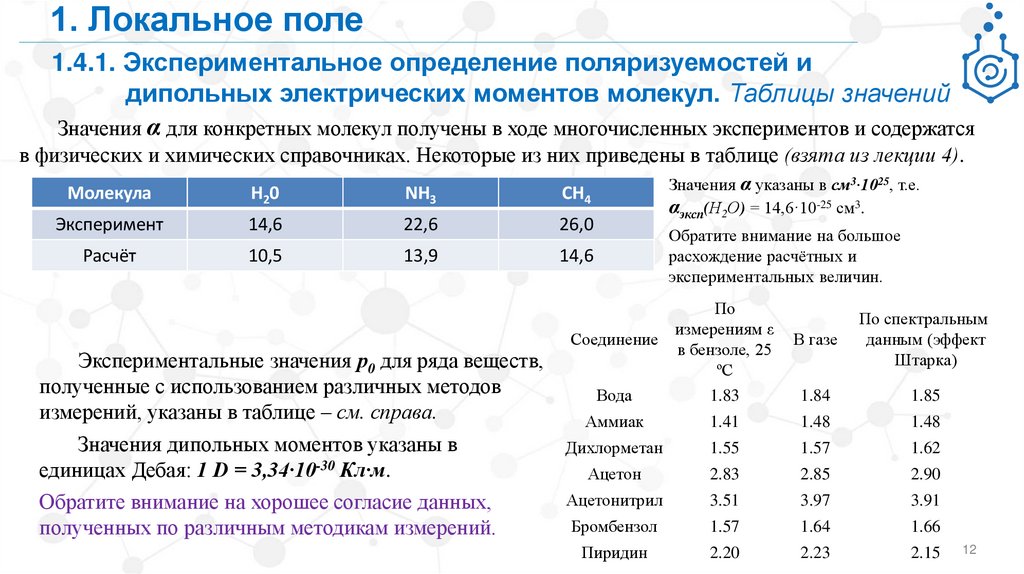
В заключении раздела 1 лекции дан краткий обзор экспериментальных методов определения
микроскопических характеристик молекул, приведены значения этих характеристик для ряда веществ.
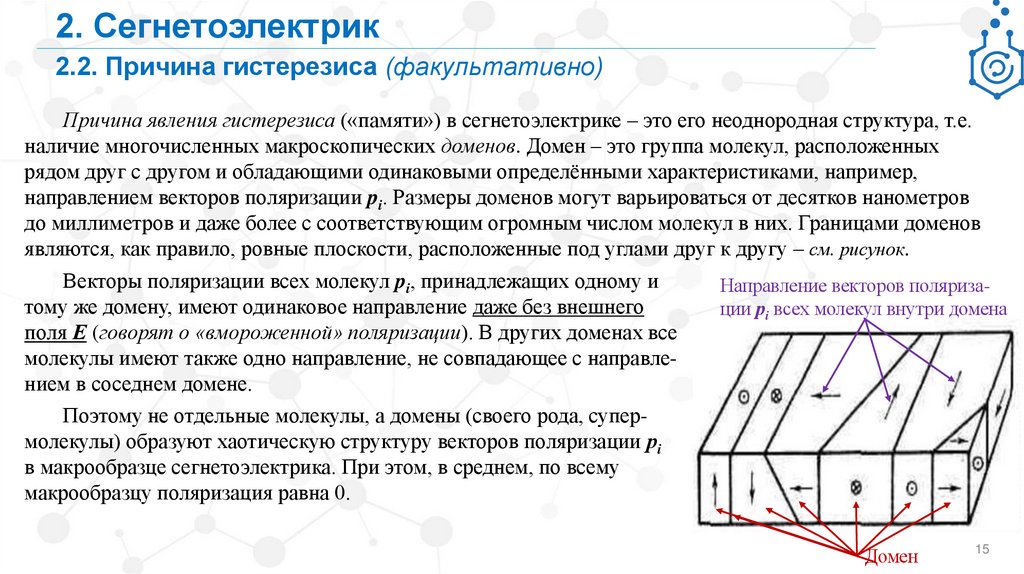
В разделе 2 лекции изложены основные понятия специфической разновидности диэлектрика –
сегнетоэлектрика. Свойства сегнетоэлектрика имеют ряд важных и интересных отличий от свойств
«классического» диэлектрика, основное из них – это своеобразная «память».
3

4.

Раздел 1. Локальное электрическое поле в диэлектрике
4

5.

1. Локальное поле
1.1. Определение
Определение: локальное электрическое поле в диэлектрике ЕЛОК – это поле, действующее на одиночный
диполь (или – одиночную молекулу), расположенный в произвольной точке внутри этого диэлектрика.
Точка А на рисунке – место расположения одиночного диполя (молекулы),
в котором надо рассчитать локальное поле ЕЛОК – рис. справа, вверху.
Локальное поле ЕЛОК следует отличать от среднего макроскопического поля Е,
которое также присутствует внутри диэлектрика.
•А
Важно: локальной поле как и среднее макроскопическое поле возникают
только при наличии внешнего поля.
Напоминание (по материалам лекций 3 и 4):
Среднее макроскопическое поле Е направлено в ту же сторону, что и внешнее поле Е0,
но меньше его в ε раз:
Е = Е0 / ε,
ε – диэлектрическая проницаемость среды, ε > 1
Е0
На рисунке (справа, внизу) схематично показаны поля:
- внешнее Е0, образованное внешними заряженными пластинами (пластины не показаны);
- поле Е1, образованное поверхностными зарядами на наружных поверхностях
диэлектрика, эти заряды появились в результате его поляризации во внешнем поле;
- среднее макроскопическое поле Е = Е0 – Е1.
-
Е1 +
+
Е +
5

6.

1. Локальное поле
Е0
1.2. Расчёт локального поля
Вырежем в диэлектрике вокруг точки А сферу (т.н. сферу Лоренца).
Сфера Лоренца
В центре сферы размещён одиночный диполь (молекула), сфера пуста.
ЕЛОК
А
Диполи диэлектрика на внешней поверхности сферы, как и во всём
r
диэлектрике, будут ориентированы «по макрополю Е». Тогда слева на
поверхности сферы окажутся положительные заряды диполей (молекул),
Е – среднее макрополе в диэлектрике,
справа – отрицательные.
Р – поляризованность,
Поле в точке А от этих зарядов ЕПОВ.СФ (имеет специальное название: ЕЛОК – локальное поле,
поле Лоренца) рассчитывается интегрированием по сфере при стремлении Е0 – внешнее поле.
Не показаны:
её радиуса r к нулю. В результате получим (без вывода):
- поле Е1, покажите самостоятельно,
ЕПОВ.СФ = Р / (3ε0).
- внешние заряженные пластины.
Тогда: ЕЛОК = Е + ЕПОВ.СФ = Е + Р / (3ε0).
Т.к. Р = χ·ε0·Е, то ЕЛОК = Е + (1/3)·χ·Е .
После простейших алгебраических преобразований получим:
ЕЛОК
Рисунок для
ЕЛОК = (1/3)·(ε+2)·Е
или
ЕЛОК = (1/3)·(3+χ)·Е
А
самостояВыполните эти преобразования сами с учётом, что χ=ε-1.
Важно: векторы полей Е, ЕПОВ.СФ и ЕЛОК сонаправлены.
Покажите (нарисуйте) эти векторы на рисунке справа.
тельного
вывода
формулы
для ЕПОВ.СФ
Сфера Лоренца
6

7.

1. Локальное поле
1.3. Связь макро- и микро-характеристик диэлектрика
Очевидно, что должна существовать однозначная связь между характеристиками диэлектрика как
вещества в целом (диэлектрические проницаемость ε, восприимчивость χ, ряд других, т.е. макрохарактеристик) и характеристиками молекул, из которых этот диэлектрик состоит (поляризуемость
молекул α, элементарный дипольный момент р, т.е. микро-характеристик).
Такая связь была установлена на рубеже XIX-XX веков различными учёными, именами которых
названы формулы.
а). Формула Клаузиуса-Мосотти устанавливает связь диэлектрической проницаемости ε с
поляризуемостью неполярных молекул α. Напомню, у таких молекул в отсутствии внешнего
электрического поля (Е0 = 0) дипольный момент равен нулю (р = 0).
n – концентрация частиц в единице объёма
n = (ρ/M)·NA, М – молярная масса
Можно легко получить другой вид этой формулы:
Проделайте это сами. Потом перепишите оба уравнения, вспомнив, что ε – 1 = χ.
7

8.

1. Локальное поле
1.3. Связь макро- и микро-характеристик диэлектрика
б). Формула Дебая-Ланжевена
Формула Дебая-Ланжевена устанавливает связь макро- и микро-характеристик для
полярного диэлектрика, у молекул которого изначально есть постоянный дипольный момент р0,
т.е. такие молекулы поляризованы даже в отсутствие электрического поля.
р0 – дипольный момент полярной молекулы при
отсутствии внешнего поля Е0
k – постоянная Больцмана
Т - температура
n – концентрация частиц в единице объёма
Используя соотношение n = (ρ/M)·NA, М – молярная масса, можно легко получить другой
вид этой формулы – по аналогии с формулой Клаузиуса-Мосотти (проделайте это сами; а потом
перепишите уравнения с учётом того, что ε – 1 = χ).
8

9.

1. Локальное поле
1.3. Связь макро- и микро-характеристик диэлектрика
в). Формула Лоренц-Лоренца
Формула Лоренц-Лоренца устанавливает связь оптических макро-характеристик
диэлектрика (показатель преломления n) с микро-характеристиками – с поляризуемостью
неполярных молекул α, у которых в отсутствие электрического поля дипольный момент р=0.