lec24

1.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Lecture 24: Cicular Convolution
Mark Hasegawa-Johnson
All content CC-SA 4.0 unless otherwise specified.
ECE 401: Signal and Image Analysis, Fall 2022
Summary

2.

Review
Periodic in Time
Circular Convolution
1
Review: DTFT and DFT
2
Sampled in Frequency ↔ Periodic in Time
3
Circular Convolution
4
Zero-Padding
5
Summary
Zero-Padding
Summary

3.

Review
Periodic in Time
Circular Convolution
Outline
1
Review: DTFT and DFT
2
Sampled in Frequency ↔ Periodic in Time
3
Circular Convolution
4
Zero-Padding
5
Summary
Zero-Padding
Summary

4.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Summary
Review: DTFT
The DTFT (discrete time Fourier transform) of any signal is X (ω),
given by
X (ω) =
∞
X
x[n]e −jωn
n=−∞
1
x[n] =
2π
Z π
X (ω)e jωn dω
−π
Particular useful examples include:
f [n] = δ[n] ↔ F (ω) = 1
g [n] = δ[n − n0 ] ↔ G (ω) = e −jωn0

5.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Properties of the DTFT
Properties worth knowing include:
0
Periodicity: X (ω + 2π) = X (ω)
1
Linearity:
z[n] = ax[n] + by [n] ↔ Z (ω) = aX (ω) + bY (ω)
2
Time Shift: x[n − n0 ] ↔ e −jωn0 X (ω)
3
Frequency Shift: e jω0 n x[n] ↔ X (ω − ω0 )
4
Filtering is Convolution:
y [n] = h[n] ∗ x[n] ↔ Y (ω) = H(ω)X (ω)
Summary

6.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Review: DFT
The DFT (discrete Fourier transform) of any signal is X [k], given
by
X [k] =
x[n] =
N−1
X
2πkn
x[n]e −j N
n=0
N−1
X
1
N
2πkn
X [k]e j N
0
Particular useful examples include:
f [n] = δ[n] ↔ F [k] = 1
g [n] = δ [((n − n0 ))N ] ↔ G [k] = e −j
2πkn0
N
Summary

7.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Properties of the DTFT
Properties worth knowing include:
0
Periodicity: X [k + N] = X [k]
1
Linearity:
z[n] = ax[n] + by [n] ↔ Z [k] = aX [k] + bY [k]
2
Circular Time Shift: x [((n − n0 ))N ] ↔ e −j
2πk n
j N0
2πkn0
N
X (ω)
x[n] ↔ X [k − k0 ]
3
Frequency Shift: e
4
Filtering is Circular Convolution:
y [n] = h[n] ~ x[n] ↔ Y [k] = H[k]X [k],
Summary

8.

Review
Periodic in Time
Circular Convolution
Outline
1
Review: DTFT and DFT
2
Sampled in Frequency ↔ Periodic in Time
3
Circular Convolution
4
Zero-Padding
5
Summary
Zero-Padding
Summary

9.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Summary
Two different ways to think about the DFT
1. x[n] is finite length; DFT is samples of DTFT
x[n] = 0, n < 0 or n ≥ N
↔
X [k] = X (ω)|ω= 2πk
N
2. x[n] is periodic; DFT is scaled version of Fourier series
x[n] = x[n + N]
↔
X [k] = NXk

10.

Review
Periodic in Time
Circular Convolution
Zero-Padding
1. x[n] finite length, DFT is samples of DTFT
If x[n] is nonzero only for 0 ≤ n ≤ N − 1, then
X (ω) =
∞
X
n=−∞
x[n]e
−jωn
=
N−1
X
n=0
and
X [k] = X (ω)|ω= 2πk
N
x[n]e −jωn ,
Summary

11.

Review
Periodic in Time
Circular Convolution
Zero-Padding
2. x[n] periodic, X [k] = NXk
If x[n] = x[n + N], then its Fourier series is
N−1
Xk =
x[n] =
2πkn
1 X
x[n]e −j N
N
n=1
N−1
X
2πkn
Xk e j N ,
k=0
and its DFT is
X [k] =
x[n] =
N−1
X
n=1
N−1
X
1
N
2πkn
x[n]e −j N
k=0
2πkn
X [k]e j N
Summary

12.

Review
Periodic in Time
Circular Convolution
Zero-Padding
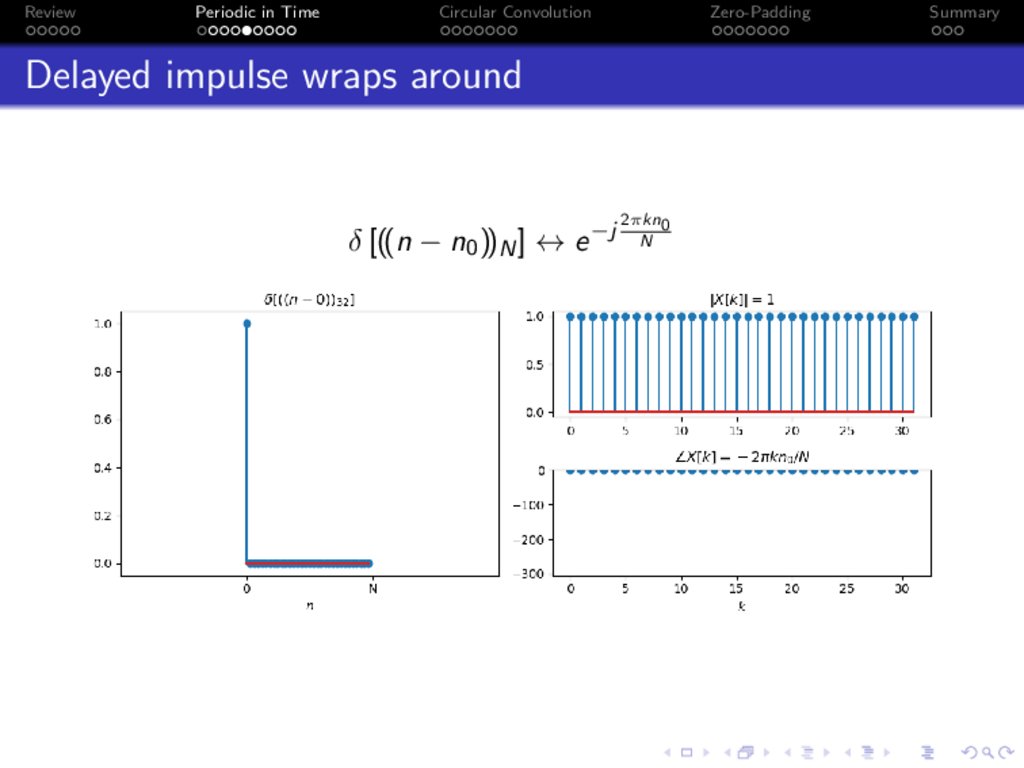
Delayed impulse wraps around
δ [((n − n0 ))N ] ↔ e −j
2πkn0
N
Summary

13.

Review
Periodic in Time
Circular Convolution
Zero-Padding
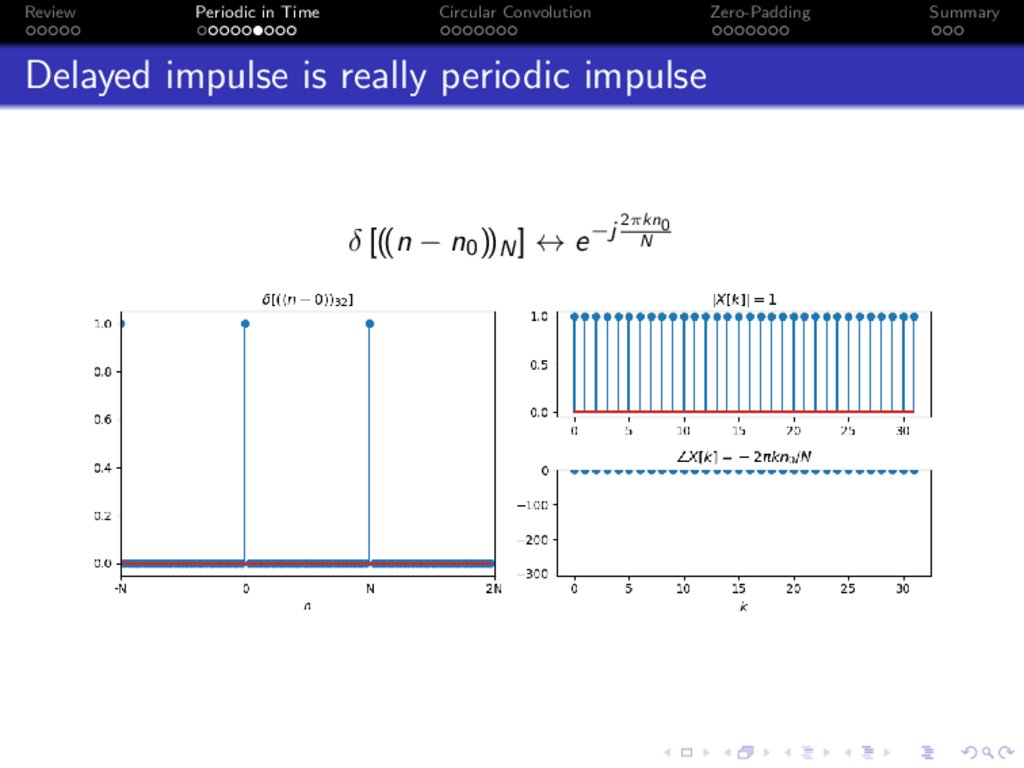
Delayed impulse is really periodic impulse
δ [((n − n0 ))N ] ↔ e −j
2πkn0
N
Summary

14.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Summary
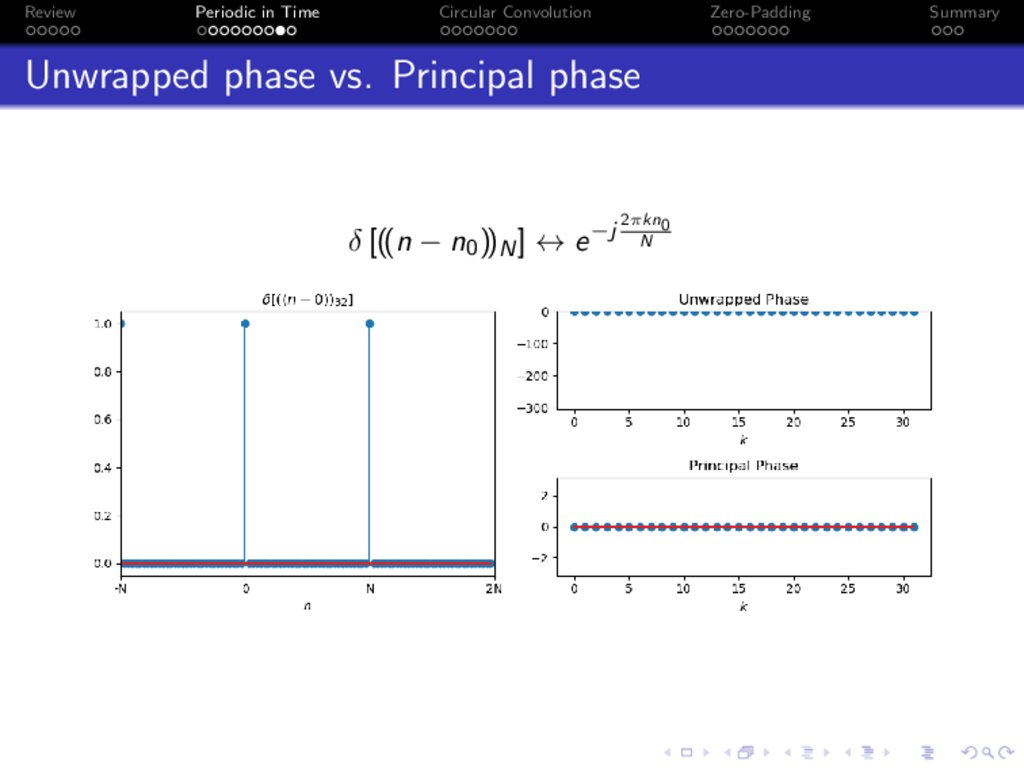
Principal Phase
Something weird going on: how can the phase keep getting
bigger and bigger, but the signal wraps around?
It’s because the phase wraps around too!
∠X [k] = −ωk (N + n) = −ωk n,
because ωk =
2πk
N
Principal phase = add ±2π to the phase, as necessary, so
that −π < ∠X [k] ≤ π
Unwrapped phase = let the phase be as large as necessary
so that it is plotted as a smooth function of ω

15.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Unwrapped phase vs. Principal phase
δ [((n − n0 ))N ] ↔ e −j
2πkn0
N
Summary

16.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Summary
Summary: Two different ways to think about the DFT
1. x[n] is finite length; DFT is samples of DTFT
x[n] = 0, n < 0 or n ≥ N
↔
X [k] = X (ω)|ω= 2πk
N
2. x[n] is periodic; DFT is scaled version of Fourier series
x[n] = x[n + N]
↔
X [k] = NXk

17.

Review
Periodic in Time
Circular Convolution
Outline
1
Review: DTFT and DFT
2
Sampled in Frequency ↔ Periodic in Time
3
Circular Convolution
4
Zero-Padding
5
Summary
Zero-Padding
Summary

18.

Review
Periodic in Time
Circular Convolution
Zero-Padding
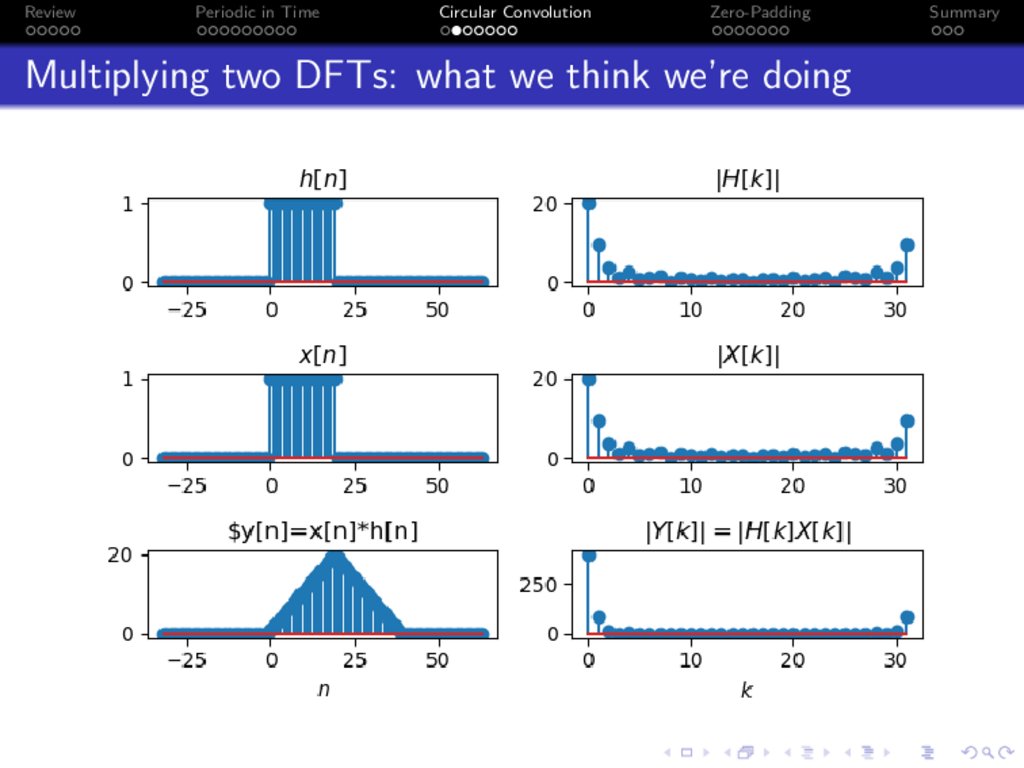
Multiplying two DFTs: what we think we’re doing
Summary

19.

Review
Periodic in Time
Circular Convolution
Zero-Padding
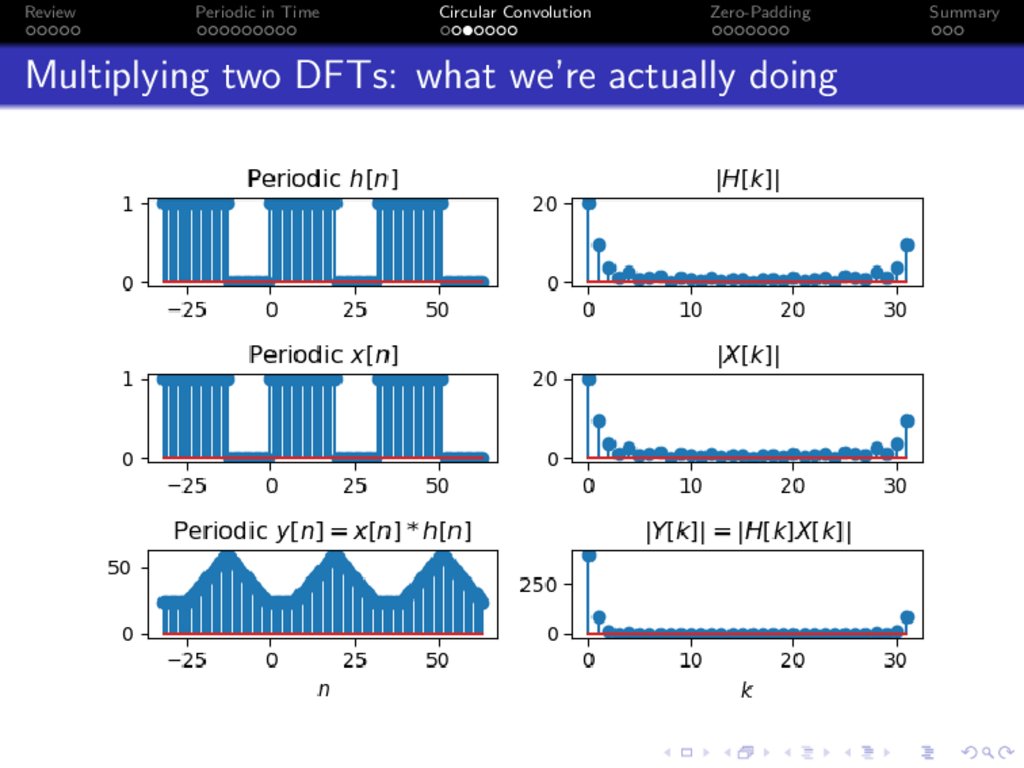
Multiplying two DFTs: what we’re actually doing
Summary

20.

Review
Periodic in Time
Circular Convolution
Zero-Padding
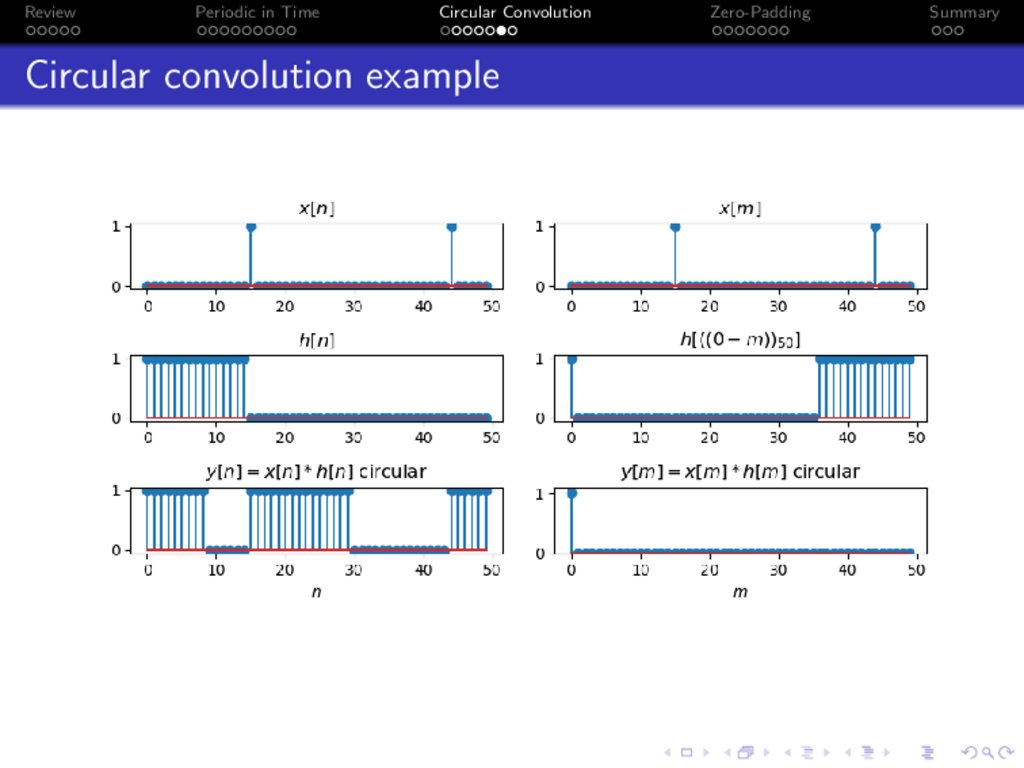
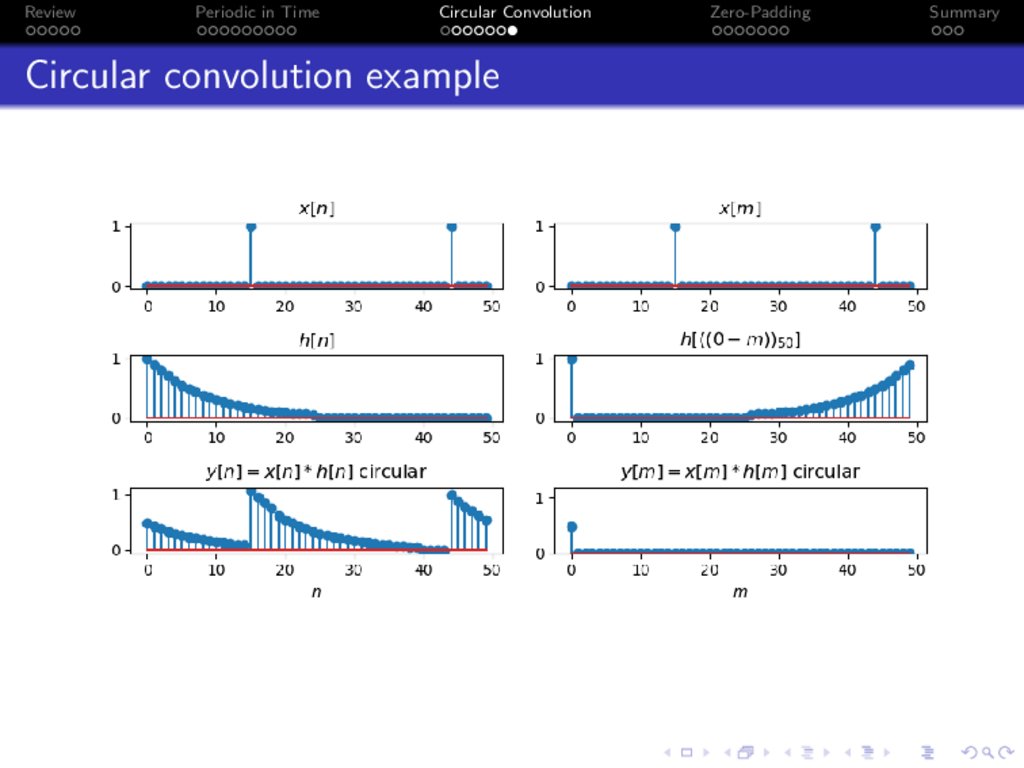
Circular convolution
Suppose Y [k] = H[k]X [k], then
N−1
y [n] =
2πkn
1 X
H[k]X [k]e j N
N
1
=
N
=
k=0
N−1
X
k=0
N−1
X
x[m]
m=0
=
H[k]
N−1
X
N−1
X
!
x[m]e
−j 2πkm
N
2πkn
ej N
m=0
N−1
2πk(n−m)
1 X
H[k]e −j N
N
k=0
x[m]h [((n − m))N ]
m=0
N
The last line is because 2πk(n−m)
= 2πk((n−m))
.
N
N
!
Summary

21.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Circular convolution
Multiplying the DFT means circular convolution of the
time-domain signals:
y [n] = h[n] ~ x[n] ↔ Y [k] = H[k]X [k],
Circular convolution (h[n] ~ x[n]) is defined like this:
h[n] ~ x[n] =
N−1
X
m=0
x[m]h [((n − m))N ] =
N−1
X
m=0
h[m]x [((n − m))N ]
Summary

22.

Review
Periodic in Time
Circular Convolution
Circular convolution example
Zero-Padding
Summary

23.

Review
Periodic in Time
Circular Convolution
Circular convolution example
Zero-Padding
Summary

24.

Review
Periodic in Time
Circular Convolution
Outline
1
Review: DTFT and DFT
2
Sampled in Frequency ↔ Periodic in Time
3
Circular Convolution
4
Zero-Padding
5
Summary
Zero-Padding
Summary

25.

Review
Periodic in Time
Circular Convolution
Zero-Padding
How long is h[n] ∗ x[n]?
If x[n] is M samples long, and h[n] is L samples long, then their
linear convolution, y [n] = x[n] ∗ h[n], is M + L − 1 samples long.
Summary

26.

Review
Periodic in Time
Circular Convolution
Zero-Padding
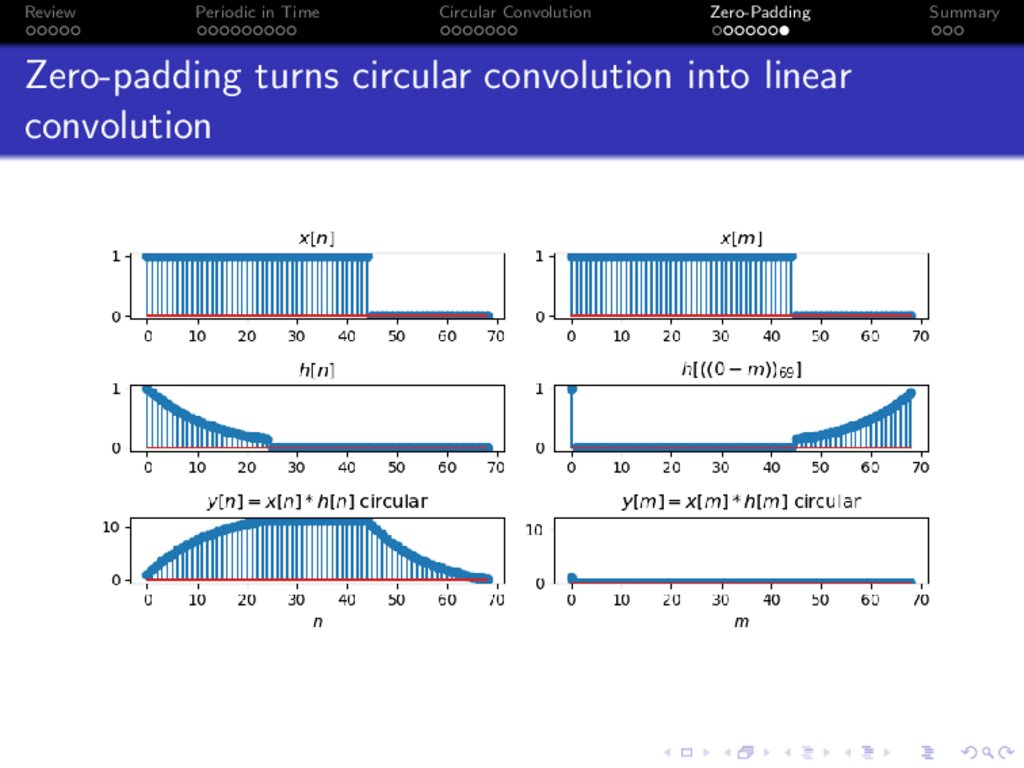
Zero-padding turns circular convolution into linear
convolution
How it works:
h[n] is length-L
x[n] is length-M
As long as they are both zero-padded to length
N ≥ L + M − 1, then
y [n] = h[n] ~ x[n] is the same as h[n] ∗ x[n].
Summary

27.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Zero-padding turns circular convolution into linear
convolution
Why it works: Either. . .
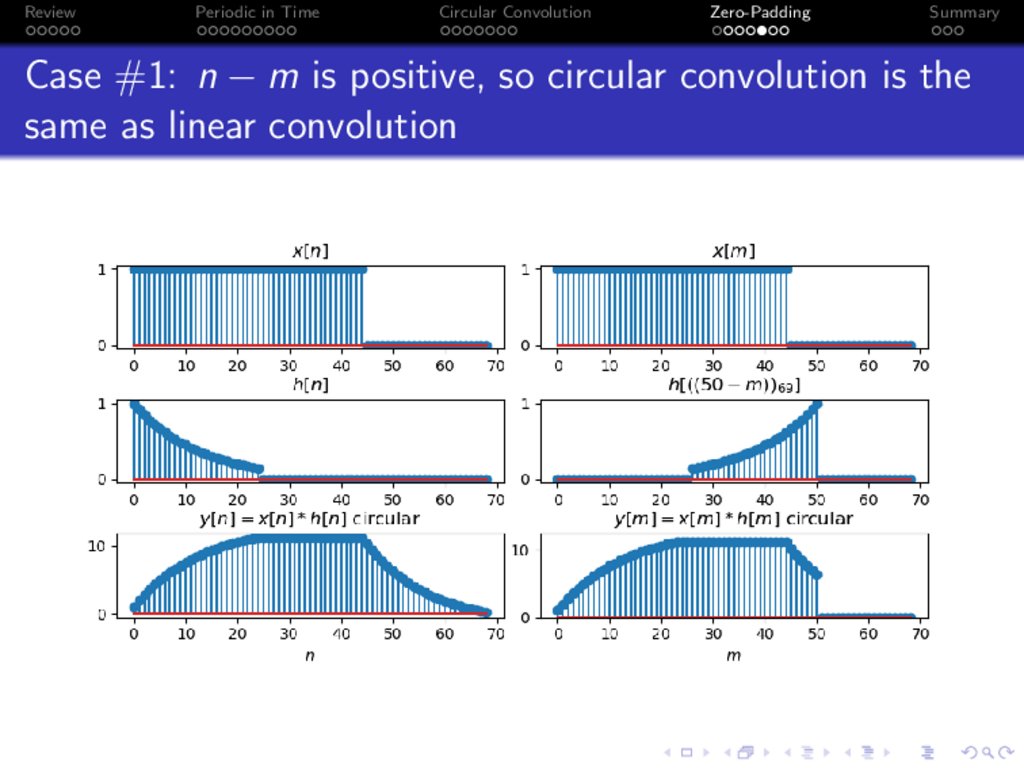
n − m is a positive number, between 0 and N − 1. Then
((n − m))N = n − m, and therefore
x[m]h [((n − m))N ] = x[m]h[n − m]
n − m is a negative number, between 0 and −(L − 1). Then
((n − m))N = N + n − m ≥ N − (L − 1) > M − 1, so
x[m]h [((n − m))N ] = 0
Summary

28.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Summary
Case #1: n − m is positive, so circular convolution is the
same as linear convolution

29.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Summary
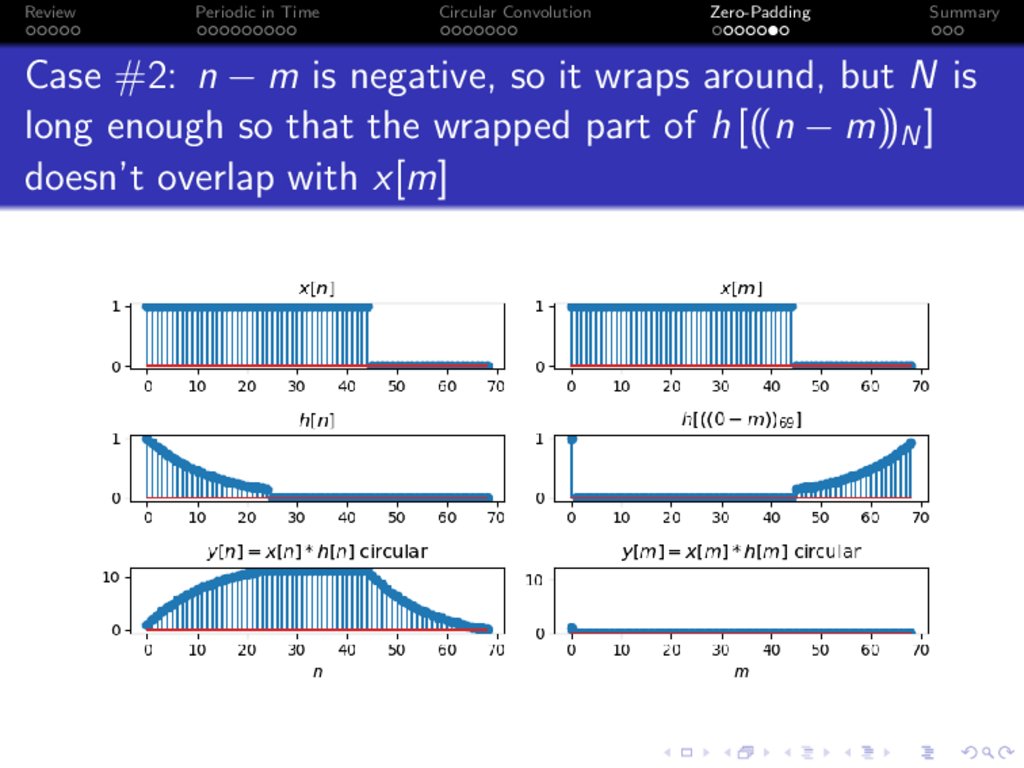
Case #2: n − m is negative, so it wraps around, but N is
long enough so that the wrapped part of h [((n − m))N ]
doesn’t overlap with x[m]

30.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Zero-padding turns circular convolution into linear
convolution
Summary

31.

Review
Periodic in Time
Circular Convolution
Outline
1
Review: DTFT and DFT
2
Sampled in Frequency ↔ Periodic in Time
3
Circular Convolution
4
Zero-Padding
5
Summary
Zero-Padding
Summary

32.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Summary
Summary: Two different ways to think about the DFT
1. x[n] is finite length; DFT is samples of DTFT
x[n] = 0, n < 0 or n ≥ N
↔
X [k] = X (ω)|ω= 2πk
N
2. x[n] is periodic; DFT is scaled version of Fourier series
x[n] = x[n + N]
↔
X [k] = NXk

33.

Review
Periodic in Time
Circular Convolution
Zero-Padding
Summary
Circular convolution
Multiplying the DFT means circular convolution of the
time-domain signals:
y [n] = h[n] ~ x[n] ↔ Y [k] = H[k]X [k],
Circular convolution (h[n] ~ x[n]) is defined like this:
h[n] ~ x[n] =
N−1
X
m=0
x[m]h [((n − m))N ] =
N−1
X
h[m]x [((n − m))N ]
m=0
Circular convolution is the same as linear convolution if and only if
N ≥ L + M − 1.