L_9

1.

Плоскость
Поверхностью называют геометрическое место точек M(x;y;z),
координаты которых удовлетворяют уравнению
F(x,y,z) = 0,
где F(x,y,z) – многочлен степени n.
1. Общее уравнение плоскости
Опр. Плоскостью называется геометрическое место точек,
координаты которых удовлетворяют уравнению
Ax + By + Cz+D = 0

2.

ЗАДАЧА 1. Записать уравнение плоскости, проходящей через
точку M0(x0;y0;z0), перпендикулярно вектору N̄ = {A; B; C}.
Вектор N̄ = {A; B; C}, перпендикулярный плоскости, называют
нормальным вектором этой плоскости.
пропустить 25 клеточек

3.

ВЫВОДЫ:
1) Плоскость – это поверхность первого порядка.
2) Коэффициенты A, B, C не обращаются в ноль одновременно,
так как с геометрической точки зрения это координаты
вектора, перпендикулярного плоскости.
Если в уравнении Ax+By+Cz+D = 0 все коэффициенты A,B,C
и D отличны от нуля, то уравнение называют полным; если
хотя бы один из коэффициентов равен нулю – неполным.

4. Уравнение плоскости в отрезках

Рассмотрим уравнение
пропустить 15 клеточек
Ax + By + Cz + D = 0

5.

Исследование общего уравнения плоскости Ax + By + Cz + D = 0
Параметры
Уравнение
График
z
A≠0, B ≠0, C ≠0, а D = 0
Ax+By +Cz = 0
Такая плоскость проходит через
начало координат O(0;0;0)
A, B или C – нулевой,
а D 0.
1
y
O
x
2
а) Ax+By+D = 0
б) Ax+Cz+D = 0
Оставить место
для трех рисунков
в) By+Cz+D = 0
Вывод: (2 строчки)
два из коэфф. A, B или
C – нулевые, а D 0.
а) Ax+D = 0
б) By+D = 0
в) Cz+D = 0
Вывод: (3 строчки)
Оставить место
для трех рисунков

6.

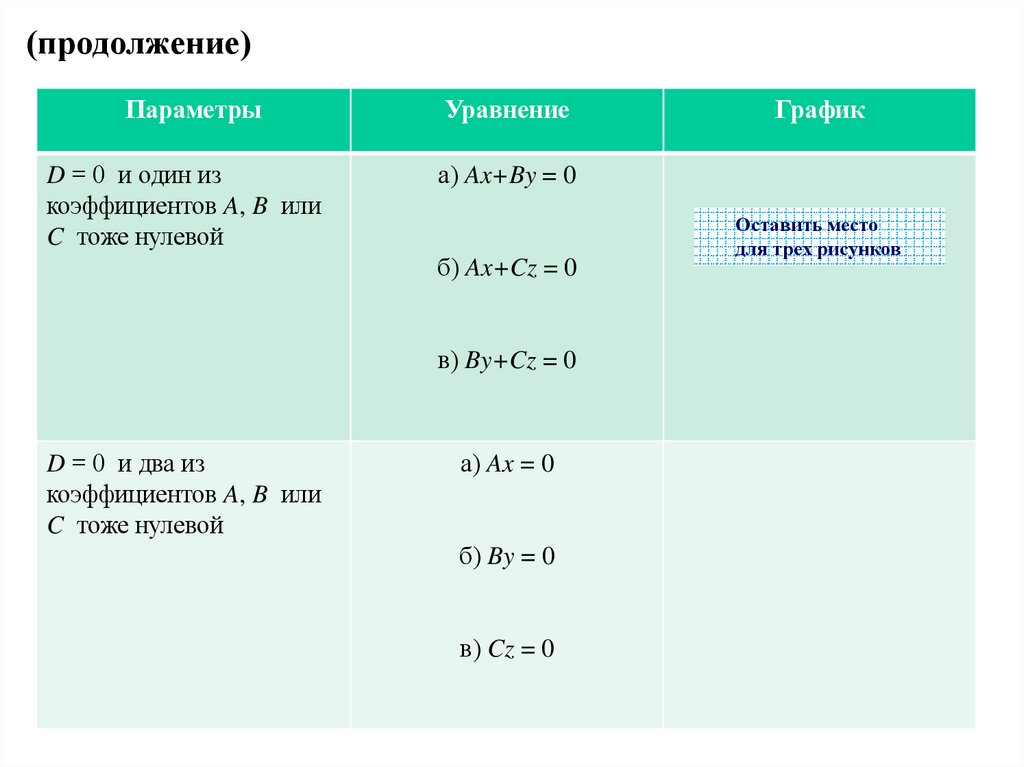
(продолжение)
Параметры
Уравнение
D = 0 и один из
коэффициентов A, B или
C тоже нулевой
а) Ax+By = 0
б) Ax+Cz = 0
в) By+Cz = 0
D = 0 и два из
коэффициентов A, B или
C тоже нулевой
а) Ax = 0
б) By = 0
в) Cz = 0
График
Оставить место
для трех рисунков

7. 2. Другие формы записи уравнения плоскости

Уравнение плоскости, проходящей через точку параллельно
двум неколлинеарным векторам
ЗАДАЧА 2. Записать уравнение плоскости, проходящей через
точку M0(x0;y0;z0), параллельно неколлинеарным векторам
1 {m1; n1; p1}
и 2 {m2 ; n2 ; p2 } .
пропустить 20 клеточек

8.

Уравнение плоскости, проходящей через три точки, не
лежащие на одной прямой – частный случай уравнения (4)
Дано M1(x1;y1;z1), M2(x2;y2;z2) и M3(x3;y3;z3) , не лежащие на
одной прямой.
пропустить 1.0 страницу

9. 3. Взаимное расположение плоскостей

В пространстве две плоскости могут:
а) быть параллельны,
б) пересекаться.
Рассмотрим плоскости L1 и L2 :
L1: A1x + B1y + C1z + D1 = 0 N̄1 = {A1; B1; C1} – нормаль к L1
L2: A2x + B2y + C2z + D2 = 0
N̄2 = {A2; B2; C2} – нормаль к
L2.
N1
1) Плоскости параллельны
L1
N2
L2
Плоскости L1 и L2 параллельны N1 || N 2
A1
A2
B1
B2
C1
C2

10.

2) Пусть плоскости пересекаются
1
2
1