НГ лекции 3, 4 (1)

1.

Использование способа замены
плоскостей проекций для решения
задач

2. Пример. Определить угол наклона плоскости α (fՈh) к плоскости П1.

ШИИ
f2
12
h2
А2
Х12
А1
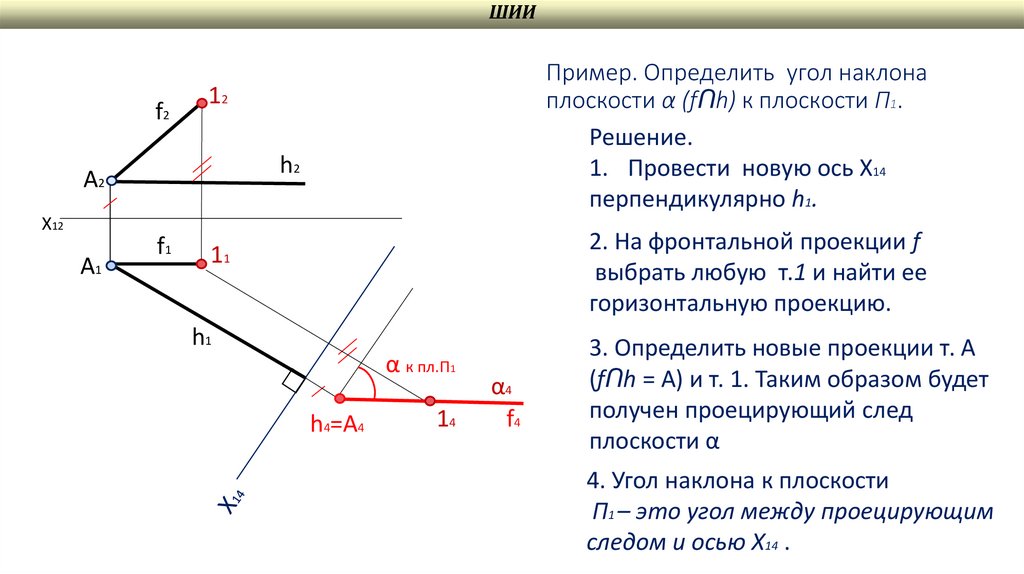
Пример. Определить угол наклона
плоскости α (fՈh) к плоскости П1.
Решение.
1. Провести новую ось Х14
перпендикулярно h1.
f1
2. На фронтальной проекции f
выбрать любую т.1 и найти ее
горизонтальную проекцию.
11
h1
α к пл.П1
h4=А4
14
α4
f4
3. Определить новые проекции т. А
(fՈh = А) и т. 1. Таким образом будет
получен проецирующий след
плоскости α
4. Угол наклона к плоскости
П1 – это угол между проецирующим
следом и осью Х14 .

3. Пример. Определить длину отрезка АВ и угол наклона его к плоскости П1.

ШИИ
А2
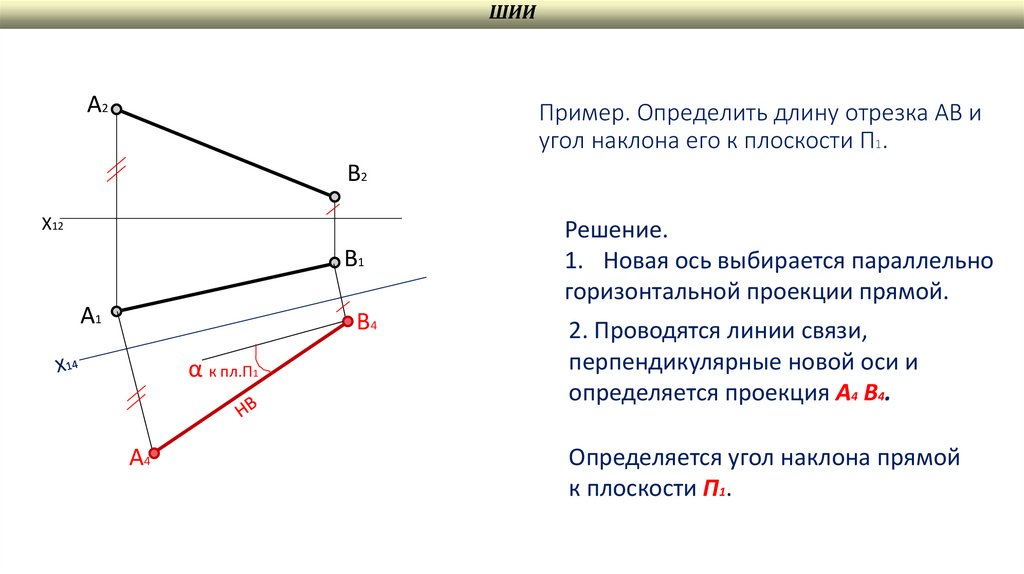
Пример. Определить длину отрезка АВ и
угол наклона его к плоскости П1.
В2
Х12
В1
А1
В4
α к пл.П1
А4
Решение.
1. Новая ось выбирается параллельно
горизонтальной проекции прямой.
2. Проводятся линии связи,
перпендикулярные новой оси и
определяется проекция А4 В4.
Определяется угол наклона прямой
к плоскости П1.

4. Пример. Определить натуральную величину треугольника АВС и угол наклона его к плоскости П1.

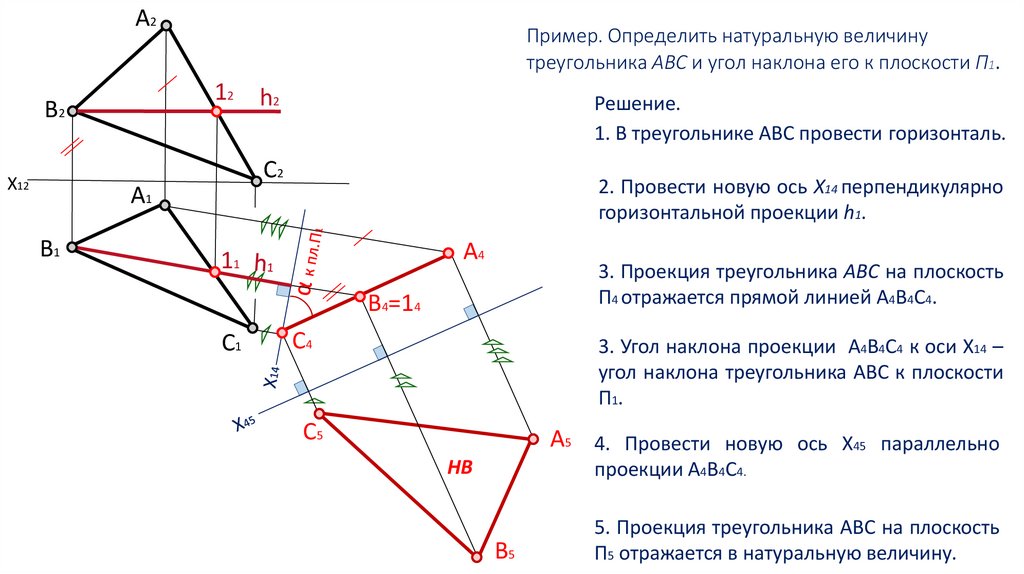
А2
Пример. Определить натуральную величину
треугольника АВС и угол наклона его к плоскости П1.
12
В2
h2
Решение.
1. В треугольнике АВС провести горизонталь.
С2
Х12
2. Провести новую ось Х14 перпендикулярно
горизонтальной проекции h1.
А1
В1
А4
11
3. Проекция треугольника АВС на плоскость
П4 отражается прямой линией А4В4С4.
В4=14
C1
C4
3. Угол наклона проекции А4В4С4 к оси Х14 –
угол наклона треугольника АВС к плоскости
П1 .
C5
А5 4. Провести новую ось Х45 параллельно
НВ
проекции А4В4С4.
В5
5. Проекция треугольника АВС на плоскость
П5 отражается в натуральную величину.

5.

ШИИ
Пересечение прямой линии с поверхностями
Общий способ построения точек пересечения прямой линии с поверхностью заключается в
следующем:
- через прямую проводят вспомогательную плоскость;
- строят линию пересечения этой плоскости с поверхностью;
- точки пересечения заданной прямой и построенной линии пересечения будут искомыми
точками пересечения прямой с поверхностью;
- затем определяют видимость прямой линии на проекциях.
Вспомогательные плоскости таком образом, чтобы они пересекали заданные поверхности по
окружностям или прямым линиям.
Вспомогательная плоскость может быть проецирующей, уровня или плоскостью оющего
положения.
Рассмотрим пример.

6.

ШИИ
α2
12
(K2)
22
L2 32
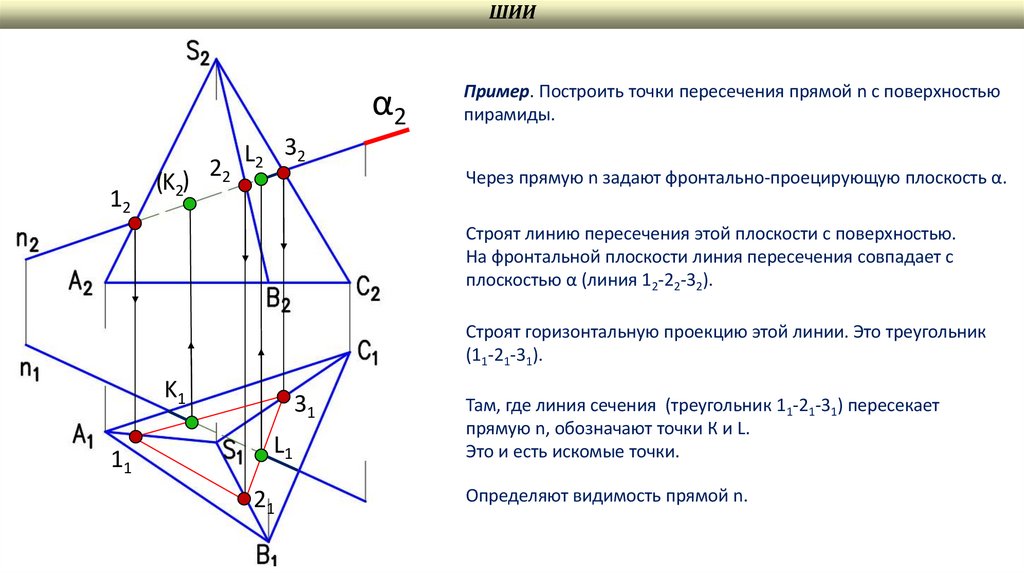
Пример. Построить точки пересечения прямой n с поверхностью
пирамиды.
Через прямую n задают фронтально-проецирующую плоскость α.
Строят линию пересечения этой плоскости с поверхностью.
На фронтальной плоскости линия пересечения совпадает с
плоскостью α (линия 12-22-32).
Строят горизонтальную проекцию этой линии. Это треугольник
(11-21-31).
K1
11
31
L1
21
Там, где линия сечения (треугольник 11-21-31) пересекает
прямую n, обозначают точки К и L.
Это и есть искомые точки.
Определяют видимость прямой n.

7.

ШИИ
Сечение поверхностей плоскостью
При пересечении поверхности плоскостью образуется линия сечения.
Линия сечения – это замкнутая плоская кривая или ломаная линия.
Часть секущей плоскости, ограниченная линией сечения, называется фигурой сечения или просто
сечением.
Часть поверхности, заключенная между основанием и плоскостью сечения, называется усеченной.
Общий способ построения линии сечения заключается в построении точек пересечения
отдельных линий заданной поверхности или отдельных граней поверхности с секущей плоскостью.
Фигура сечения многогранника плоскостью представляет собой замкнутый плоский
многоугольник.
Построение линии сечения кривых поверхностей плоскостью сводится к построению точек
пересечения образующих или других линий на поверхности с секущей плоскостью.
Начинают построение с определения характерных точек сечения:
- точек пересечения очерковых линий с секущей плоскостью;
- высшей и низшей точек;
- точек видимости (граница видимости).

8.

ШИИ
2
12
32=42
2
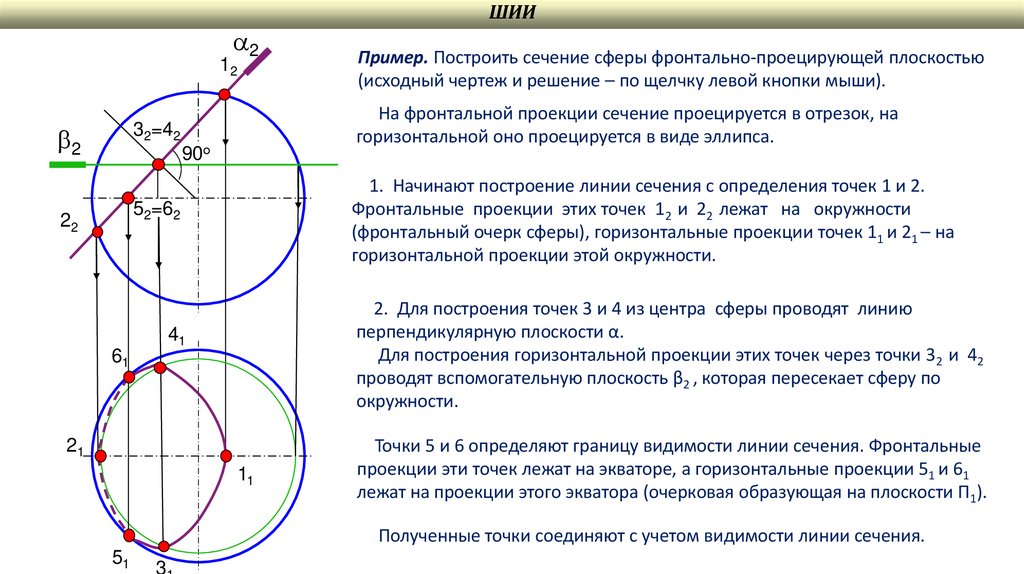
На фронтальной проекции сечение проецируется в отрезок, на
горизонтальной оно проецируется в виде эллипса.
90о
1. Начинают построение линии сечения с определения точек 1 и 2.
Фронтальные проекции этих точек 12 и 22 лежат на окружности
(фронтальный очерк сферы), горизонтальные проекции точек 11 и 21 – на
горизонтальной проекции этой окружности.
52=62
22
Пример. Построить сечение сферы фронтально-проецирующей плоскостью
(исходный чертеж и решение – по щелчку левой кнопки мыши).
2. Для построения точек 3 и 4 из центра сферы проводят линию
перпендикулярную плоскости α.
Для построения горизонтальной проекции этих точек через точки 32 и 42
проводят вспомогательную плоскость β2 , которая пересекает сферу по
окружности.
41
61
21
11
Точки 5 и 6 определяют границу видимости линии сечения. Фронтальные
проекции эти точек лежат на экваторе, а горизонтальные проекции 51 и 61
лежат на проекции этого экватора (очерковая образующая на плоскости П1).
Полученные точки соединяют с учетом видимости линии сечения.
51
3

9.

ШИИ
Взаимное пересечение поверхностей
В технике при создании сложных технических форм приходится строить линии пересечения
отдельных элементарных форм, из которых составлены сложные формы.
Линии пересечения поверхностей – это линии, общие для обеих поверхностей. Они могут быть
плоскими или пространственными, замкнутыми или разомкнутыми кривыми или ломаными
линиями.
Для построения линии пересечения поверхностей используют вспомогательные плоскости
(посредники). Их задают таким образом, чтобы они пересекали данные поверхности по наиболее
простым линиям.
Далее строят линии пересечения вспомогательных плоскостей с каждой поверхностью и
отмечают точки пересечения границ сечений. Эти точки принадлежит искомой линии сечения.
При пересечении поверхностей может иметь место проницание одной поверхности другою и
врезание (неполное пересечение).
При проницании получаются две замкнутые линии пересечения (плоские или пространственные).
При врезании получается одна замкнутая пространственная линия пересечения.
Рассмотрим несколько примеров.

10.

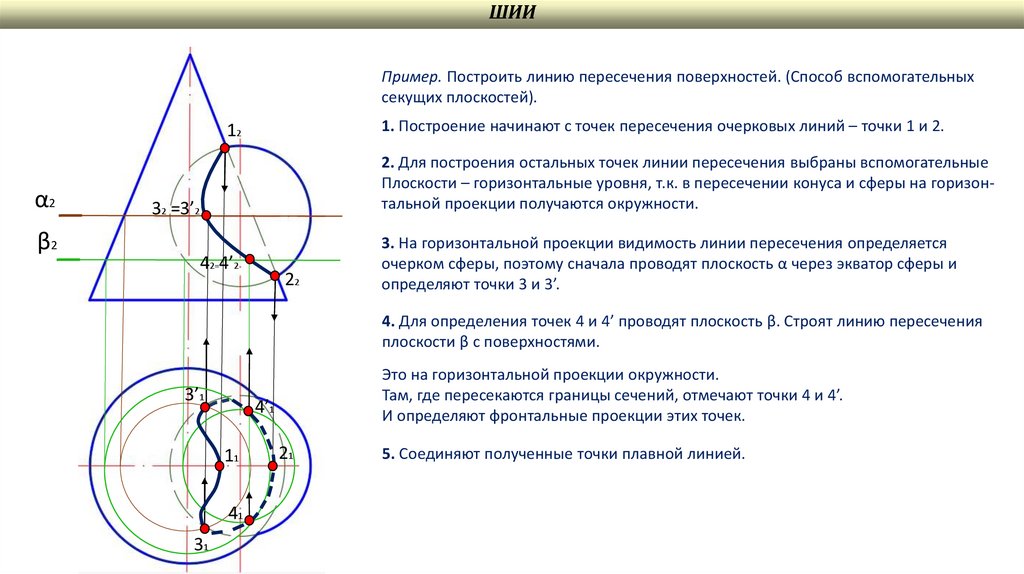
ШИИ
Пример. Построить линию пересечения поверхностей. (Способ вспомогательных
секущих плоскостей).
1. Построение начинают с точек пересечения очерковых линий – точки 1 и 2.
12
α2
β2
2. Для построения остальных точек линии пересечения выбраны вспомогательные
Плоскости – горизонтальные уровня, т.к. в пересечении конуса и сферы на горизонтальной проекции получаются окружности.
32 =3’2
42=4’2
22
3. На горизонтальной проекции видимость линии пересечения определяется
очерком сферы, поэтому сначала проводят плоскость α через экватор сферы и
определяют точки 3 и 3’.
4. Для определения точек 4 и 4’ проводят плоскость β. Строят линию пересечения
плоскости β с поверхностями.
3’1
4’1
11
41
31
Это на горизонтальной проекции окружности.
Там, где пересекаются границы сечений, отмечают точки 4 и 4’.
И определяют фронтальные проекции этих точек.
21
5. Соединяют полученные точки плавной линией.

11.

ШИИ
2
S2
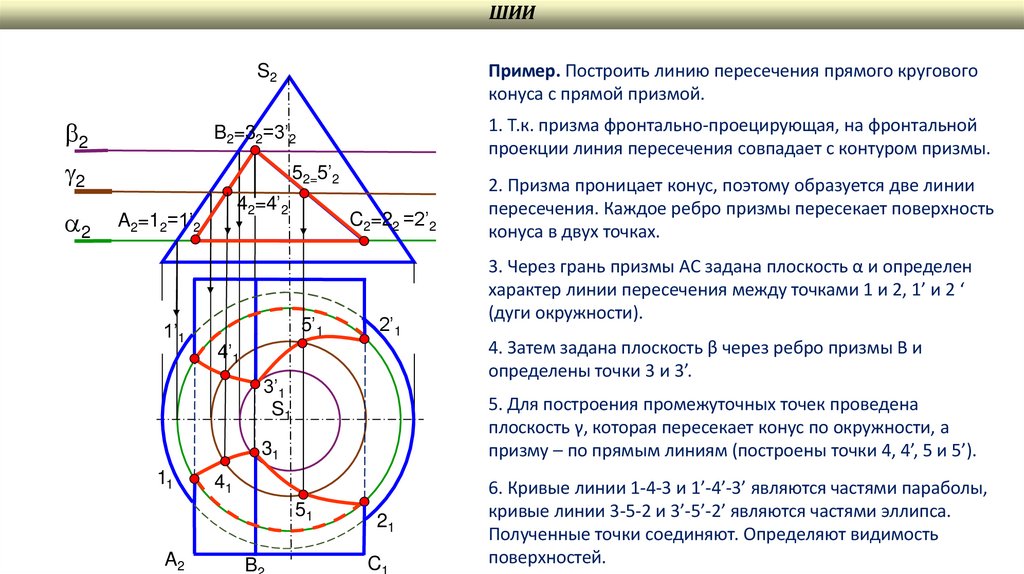
Пример. Построить линию пересечения прямого кругового
конуса с прямой призмой.
B2=32=3’2
1. Т.к. призма фронтально-проецирующая, на фронтальной
проекции линия пересечения совпадает с контуром призмы.
2
2
52=5’2
42=4’2
A2=12=1’2
1’1
C2=22 =2’2
5’1
2’1
5. Для построения промежуточных точек проведена
плоскость γ, которая пересекает конус по окружности, а
призму – по прямым линиям (построены точки 4, 4’, 5 и 5’).
31
41
51
A2
B
3. Через грань призмы АC задана плоскость α и определен
характер линии пересечения между точками 1 и 2, 1’ и 2 ‘
(дуги окружности).
4. Затем задана плоскость β через ребро призмы В и
определены точки 3 и 3’.
4’1
3’1
S1
11
2. Призма проницает конус, поэтому образуется две линии
пересечения. Каждое ребро призмы пересекает поверхность
конуса в двух точках.
21
C1
6. Кривые линии 1-4-3 и 1’-4’-3’ являются частями параболы,
кривые линии 3-5-2 и 3’-5’-2’ являются частями эллипса.
Полученные точки соединяют. Определяют видимость
поверхностей.