Похожие презентации:
Конструктивная геометрия. Решение задач способом замены плоскостей проекции
1.
Дальневосточный государственный университетпутей сообщения
Кафедра «Вычислительная техника и компьютерная
графика»
Практические занятия 9
2.
План практических занятий1
Расстояние от точки до прямой
2
Расстояние между параллельными
прямыми линиями
5
Расстояние между
скрещивающимися прямыми
4
Расстояние от точки до плоскости
5
Угол между пересекающимися и
скрещивающимися прямыми
6
Угол между прямой и плоскостью,
между двумя плоскостями
1
3.
ВступлениеВ предыдущей лекции отмечено, что
метрические задачи - это задачи
связанные с измерением, а именно,на
определение натуральной величины
размеров заданных фигур: расстояний
(длин), углов, контуров плоских
геометрических форм
2
4.
ВступлениеИз свойств ортогонального проецирования отметили,
если прямая параллельна плоскости проекций
(прямая уровня), то её отрезок на эту плоскость
проекций изображается в натуральную величину.
Аналогичное свойство имеет плоская фигура,
расположенная в плоскости уровня.
Таким образом, результат решения задачи имеет
место, когда прямая и плоскость занимают частное
положение относительно плоскостей проекций
2
5.
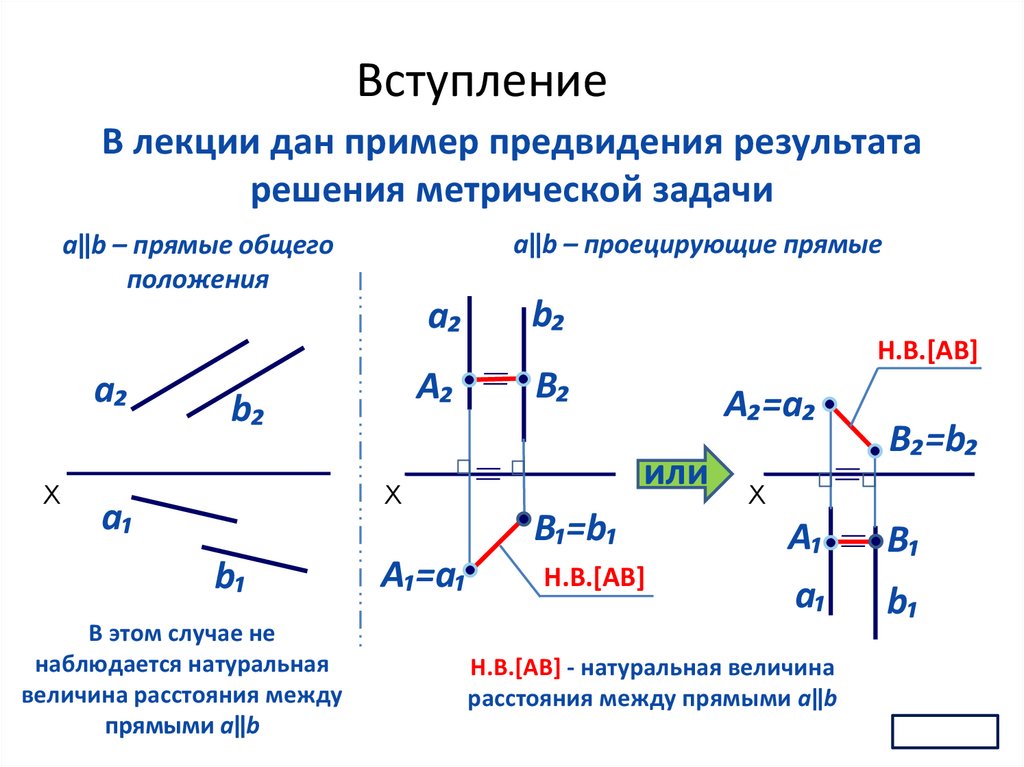
ВступлениеВ лекции дан пример предвидения результата
решения метрической задачи
aǁb – проецирующие прямые
aǁb – прямые общего
положения
a₂
X
b₂
a₂
b₂
A₂
B₂
Н.В.[AB]
или
X
a₁
A₂=a₂
B₁=b₁
b₁
В этом случае не
наблюдается натуральная
величина расстояния между
прямыми aǁb
A₁=a₁
Н.В.[AB]
B₂=b₂
X
A₁
a₁
Н.В.[AB] - натуральная величина
расстояния между прямыми aǁb
B₁
b₁
6.
ВступлениеОтмечено положение: решение метрических задач
значительно облегчается, когда заданные
геометрические объекты занимают частные
положения, т.е. параллельны и/или
перпендикулярны относительно плоскостей
проекций. В связи с этим, во многих решаемых
задачах возникает необходимость преобразования
комплексного чертежа, при котором заданные
геометрические объекты переводятся из общего
положения в частное
2
7.
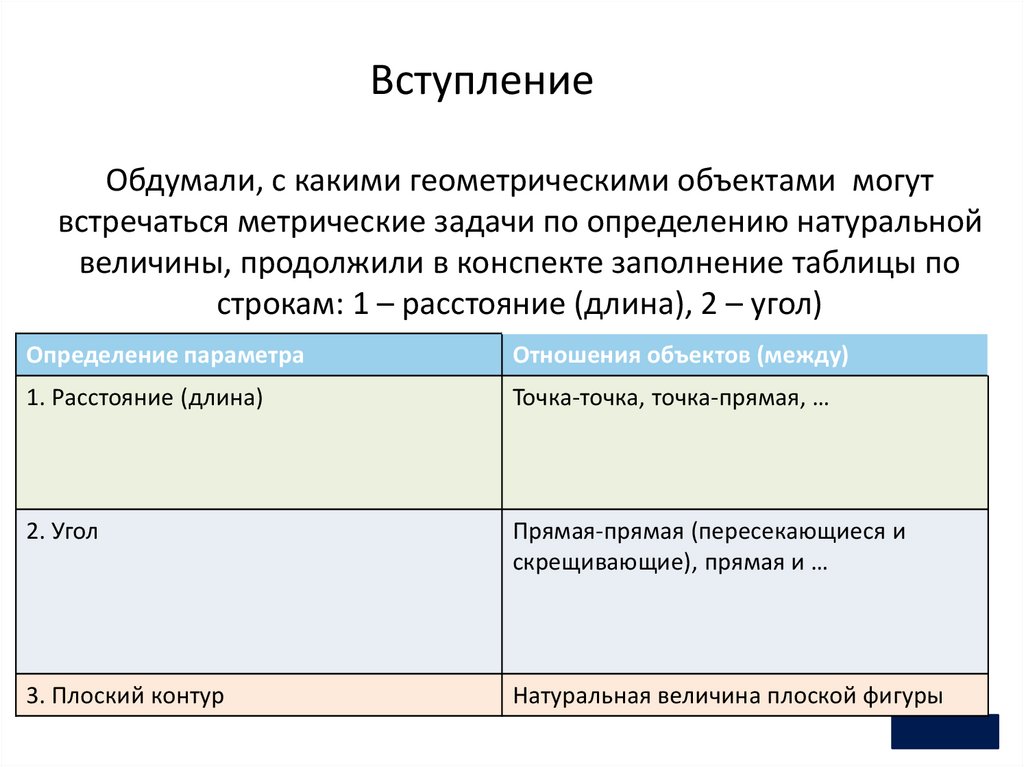
ВступлениеОбдумали, с какими геометрическими объектами могут
встречаться метрические задачи по определению натуральной
величины, продолжили в конспекте заполнение таблицы по
строкам: 1 – расстояние (длина), 2 – угол)
Определение параметра
Отношения объектов (между)
1. Расстояние (длина)
Точка-точка, точка-прямая, …
2. Угол
Прямая-прямая (пересекающиеся и
скрещивающие), прямая и …
3. Плоский контур
Натуральная величина плоской фигуры
2
8.
ВступлениеВ лекции отмечено, что метрические задачи, решаются
посредством определенного способа преобразования на
основе реализации четырех основных задач :
1) преобразование прямой общего положения в прямую
уровня;
2) преобразование прямой уровня в прямую
проецирующую;
3) преобразование плоскости общего положения в
плоскость проецирующую;
4) преобразование проецирующей плоскости в
плоскость уровня.
Необходимо запомнить формулировку четырех основных задач
2
9.
Четыре основные задачиПримеры 1-й и 2-й основных задач (1оз и 2оз), которые
предусматривают преобразования прямой линии
1оз можно трактовать и так: преобразовать чертеж так,
чтобы прямая общего положения стала прямой уровня
X
X
2оз - преобразовать чертеж так, чтобы прямая уровня
заняла положение прямой проецирующей;
X
X
S
Условные обозначения проекций не указаны, так
как могут быть различные положения относительно
квадрантов (знак S указывает на какой
проекции будет Н.В.)
2
10.
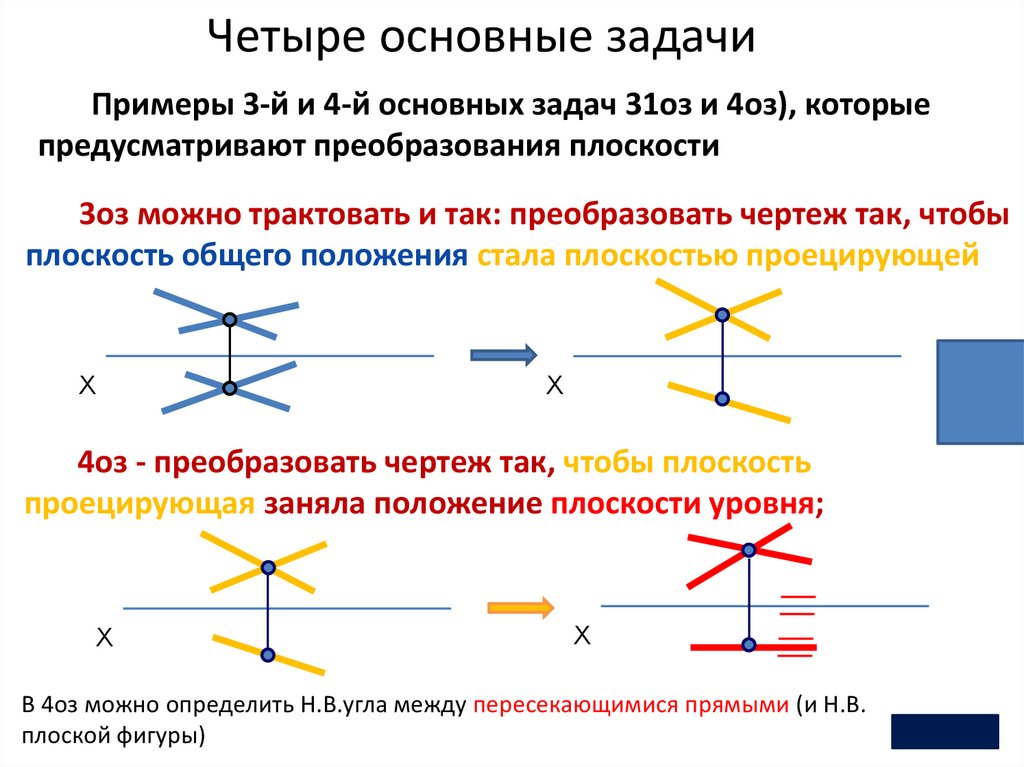
Четыре основные задачиПримеры 3-й и 4-й основных задач 31оз и 4оз), которые
предусматривают преобразования плоскости
3оз можно трактовать и так: преобразовать чертеж так, чтобы
плоскость общего положения стала плоскостью проецирующей
X
X
4оз - преобразовать чертеж так, чтобы плоскость
проецирующая заняла положение плоскости уровня;
X
X
В 4оз можно определить Н.В.угла между пересекающимися прямыми (и Н.В.
плоской фигуры)
2
11.
Метрические задачи.Основные положения (три важных аспекта)
Таким образом, рассмотрим три очень важных аспекта, без знаний
которых требуемую метрическую задачу не решить:
1 аспект – необходимо предвидеть конечный результат решаемой задачи
(казалось бы мы не знаем как ещё решать, но в соответствии с
представленными выше примерами, их необходимо обобщить на остальные
задачи в составленной Вами таблице (решаемые задачи);
2 аспект – для решения конкретной задачи необходимо освоить четыре
основные задачи, как «подзадачи», применение которых позволит выполнить
решение конкретной задачи. При этом, возможно нужно будет применить
только одну основную задачу, или последовательно за ней и следующую;
3 аспект – поставленная задача решается одним из способов
преобразования комплексного чертежа (т.е. ортогональных проекций). В
конструктивной (начертательной) геометрии таких способов несколько,
поэтому следующие слайды посвящены способам преобразования и решению
основных задач с примерами.
2
12.
Метрические задачи.Основные положения (способы преобразования)
В соответствии с решением метрических задач можно подразделить
такие способы преобразования, при которых геометрический объект(ы),
при решении поставленной задачи, остаются фиксированными
(неизменными) относительно системы плоскостей проекций, в другом
преобразовании – геометрические объекты меняют своё положение
относительно плоскостей проекций.
Любой из этих способов преобразования однозначно приводит к
решению поставленной задачи, при условии, что Вами, во-первых, в общем
виде реализуется предвиденье результата решения задачи, это –
выполнение первого аспекта, во-вторых, Вы обоснованно применили
реализацию основной(ных) задач – это второй аспект.
В результате этих преобразований будет получен чертёж, облегчающий
дальнейшее решение задачи, либо на выполняемом чертеже будет
получено готовое решение задачи.
2
13.
Способ замены плоскостей проекцийИз лекции известно, что способ замены плоскостей проекций
заключается в замене одной из плоскостей проекций на другую (новую)
плоскость проекций, на которой задача решается проще или будет
получен готовый результат решения.
Геометрическая фигура относительно исходной системы
плоскостей проекций П₁, П₂, П₃ своего положения не меняет!
При этом должны быть обязательно выдержаны два условия:
1. Новая плоскость проекций по отношению к оставшейся плоскости
проекций должна быть перпендикулярна (но таких новых плоскостей
может быть множество, тогда необходимо второе условие:
2. Новая плоскость проекций ориентируется в соответствии с
применяемой основной задачи
3
14.
Проекции и натуральная величина расстояния от точки N допрямой АВ
N2
А2
П2
X₁₂ П1
В2
K2
N1
П2
П4
X14
1оз: X12
П1
П1
П₄⟘П₁; П4 || (AB)
X14 || (А1B1 )
В1
K1
А1
A5=B
=K55
A55=B
K4
2оз: X14
П5 П4; П5 (AB)
В4
А4
П4
П4
X 45
П1
П5
N5
X₄₅⟘A₄B₄
N₅K₅=н.в.[NK]
N4
N₁K₁, N₂K₂ - проекции расстояния от точки N до прямой АВ
7
15.
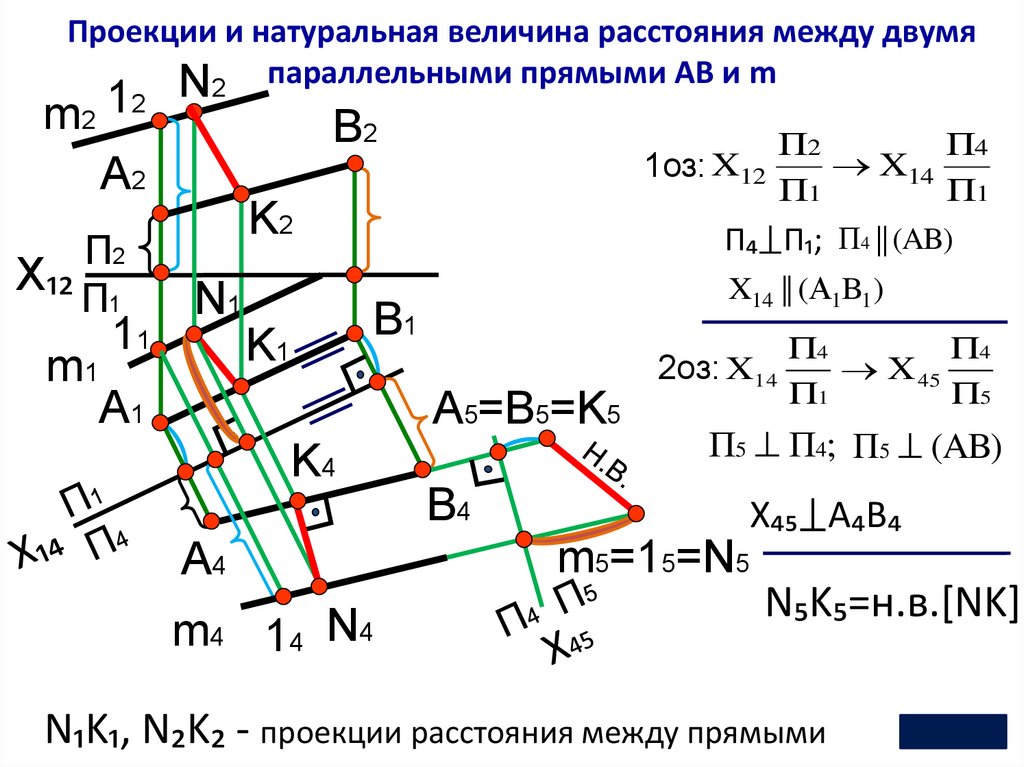
Проекции и натуральная величина расстояния между двумяN2 параллельными прямыми АВ и m
m2 12
А2
П2
X₁₂ П1
m1
11
В2
П2
П4
X14
1оз: X12
П1
П1
П₄⟘П₁; П4 || (AB)
K2
N1
X14 || (А1B1 )
В1
K1
А1
A5=B5=K5
K4
В4
2оз: X14
П4
П4
X 45
П1
П5
П5 П4; П5 (AB)
X₄₅⟘A₄B₄
А4
m5=15=N5
N₅K₅=н.в.[NK]
m4 14 N4
N₁K₁, N₂K₂ - проекции расстояния между прямыми
7
16.
Проекции и натуральная величина расстояния междускрещивающимися прямыми АВ и m
m₂
А2
C2
T2
В2
ZА=ZВ
K2
П2
Так как прямая АВ является прямой
уровня (горизонталь), то сразу
приступаем реализовывать вторую
основную задачу (2оз)
П2
П4
X12
X14
П1
П1
П4 П1
2ο3 П4 AB
X₁₂ П1
А1
m₁
T1
K1
X14 А1В1
В1
ZА=ZВ
А4=В4
C1
K4
T4=А4=В4
m₄
9
C4
T₄K₄⟘m₄
T₄K₄ - Н.В.[KT]
17.
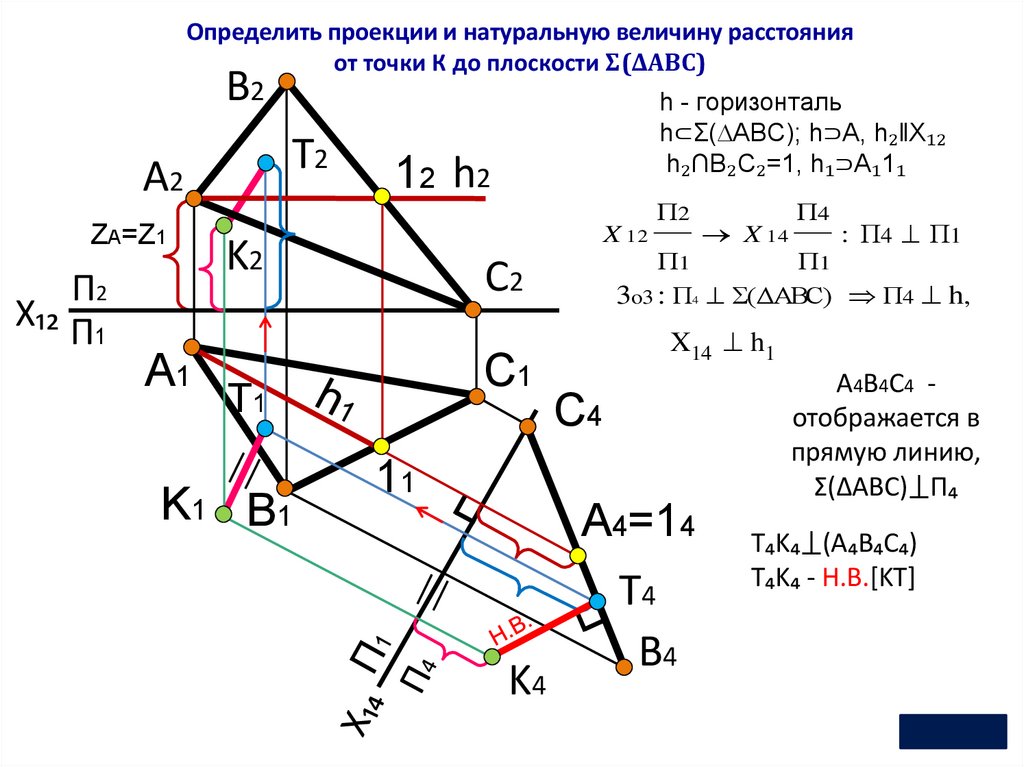
Определить проекции и натуральную величину расстоянияот точки К до плоскости Σ(ΔАВС)
В2
T2
А2
ZА=Z1
П2
X₁₂ П1
А1
12 h2
П2
X 12
K2
С1
11
K4
13
X 14
П4
: П4 П1
П1
П1
3o3 : П4 Σ(ΔABC) П4 h,
С2
T1
K1 В1
h - горизонталь
h⊂Σ( ABC); h⊃A, h₂ǁX₁₂
h₂∩B₂C₂=1, h₁⊃A₁1₁
X14 h1
С4
А4=14
T4
В4
A4B4C4 отображается в
прямую линию,
Σ(ΔАВС)⟘П₄
T₄K₄⟘(A₄B₄C₄)
T₄K₄ - Н.В.[KT]
18.
Определить натуральную величину угла ϕмежду пересекающимися прямыми a и b
П2
X₁₂ П1
a₂
b₂
1₂
2₂
h₂
Двумя пересекающимися прямыми a и b
(как и любой плоской фигурой Σ,
например, треугольником) может быть
задана плоскость. Достраиваем эти
прямые до треугольника (Δ123)с
помощью горизонтали h: h⊂Σ(a∩b );
h₂=X₁₂.
Определив натуральную величину Δ123,
отмечаем угол ϕ
3₂
1₁ a₁
2₁
h₁
3₁ a₄=b₄
b₁
h₄= 2₄=3₄
1₄
3₅
2₅
Н.В. (ϕ)= ∠(a₅^b₅)
a₅
h₅
13
b₅
Σ(Δ123) – плоскость общего
положения, поэтому решаем
последовательно 3оз и 4оз:
3оз: П₄⟘П₁, П₄⟘Σ₁, Х₁₄⟘h₁;
4оз: П₅⟘П₄, П₅ǁΣ₁,
Х₄₅ǁ(a₄=b₄);
1₅
19.
Определить натуральную величину угла ϕмежду скрещивающимися прямыми a и b
b₂
П2
X₁₂ П1
a′₂ a₂
a′₁ a₁
b₁
Эта задача решается по
предварительной подготовке:
например, прямая а переносится
параллельно самой себе до
пересечения с прямой b.
Далее задача решается как по
определению угла между
пересекающимися прямыми а’ и b
(см. предыдущий слайд)
20.
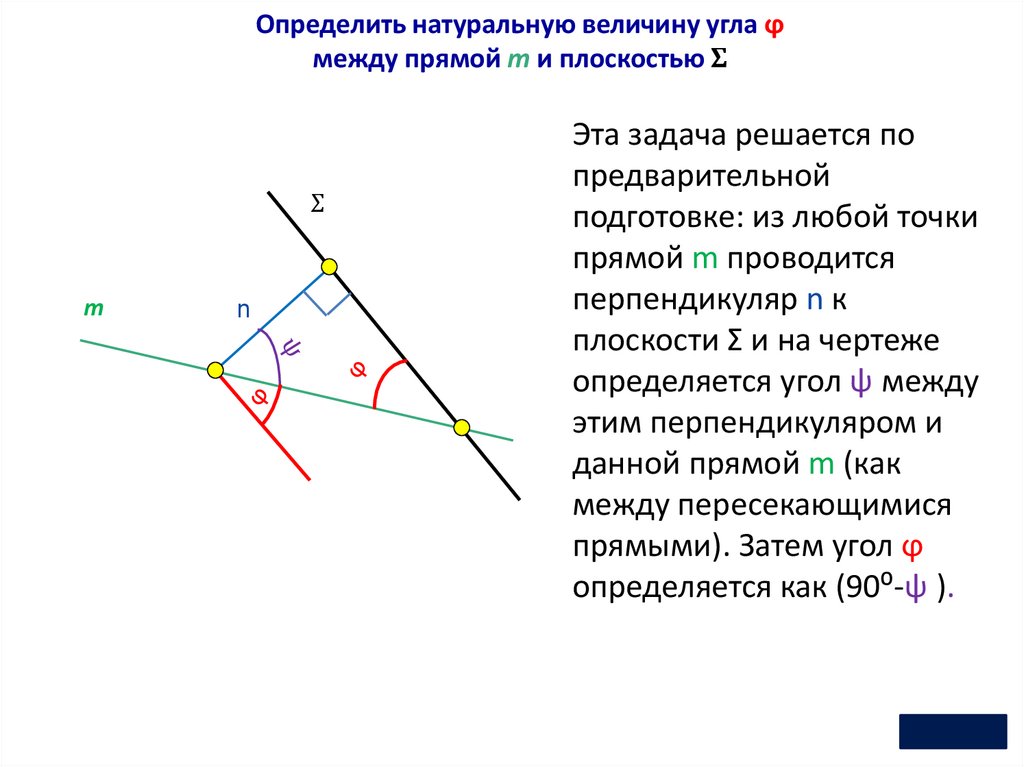
Определить натуральную величину угла ϕмежду прямой m и плоскостью Σ
Σ
m
n
Эта задача решается по
предварительной
подготовке: из любой точки
прямой m проводится
перпендикуляр n к
плоскости Σ и на чертеже
определяется угол ψ между
этим перпендикуляром и
данной прямой m (как
между пересекающимися
прямыми). Затем угол ϕ
определяется как (90⁰-ψ ).
21.
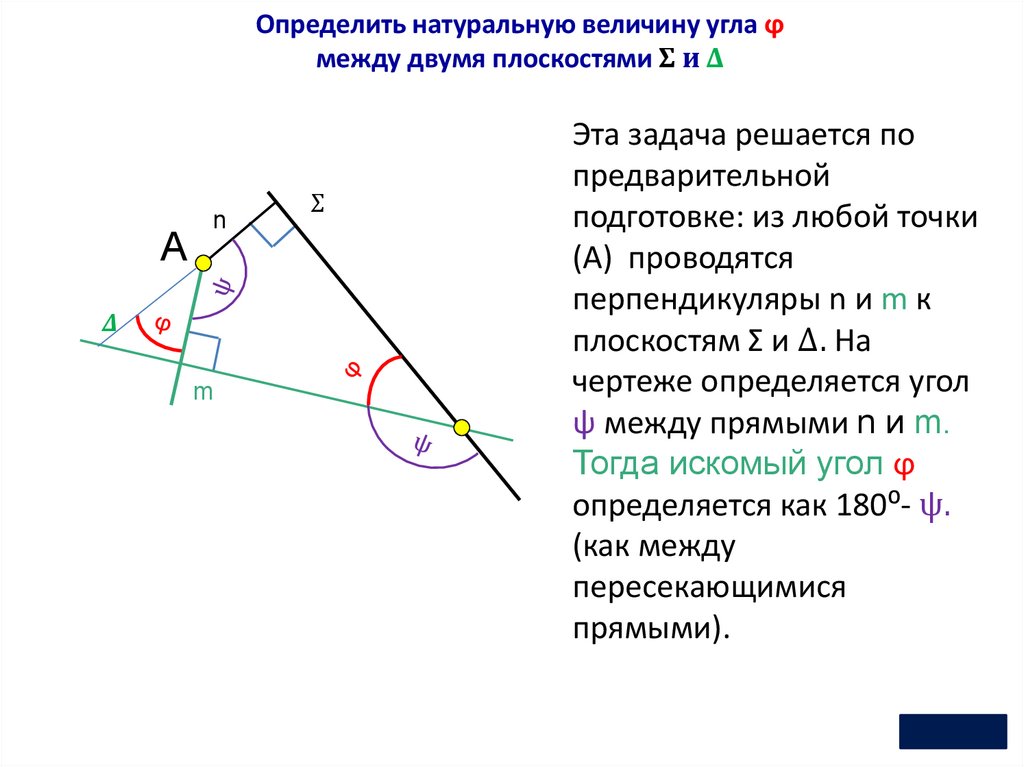
Определить натуральную величину угла ϕмежду двумя плоскостями Σ и Δ
А
n
Δ
m
Σ
Эта задача решается по
предварительной
подготовке: из любой точки
(А) проводятся
перпендикуляры n и m к
плоскостям Σ и Δ. На
чертеже определяется угол
ψ между прямыми n и m.
Тогда искомый угол ϕ
определяется как 180⁰- ψ.
(как между
пересекающимися
прямыми).













 Математика
Математика Инженерная графика
Инженерная графика








