Колебания

1. Колебания и волны

Колебания – движение или процессы, которые обладают определенной повторяемостью
во времени. Колебания бывают свободными (собственными), если они совершаются за
счет первоначально сообщенной энергии без дальнейшего внешнего воздействия.
Колебания вынужденные, если они происходят под действием периодически
изменяющиеся внешней силы.
Гармонические колебания – колебания, при которых физическая величина изменяется
по закону синуса или косинуса.
Основное уравнение колебаний:
S (t ) A cos( t )
А - амплитуда колебаний.
ω – круговая (циклическая) частота.
φ – начальная фаза колебаний в момент времени t=0.
(ωt+φ) - фаза колебаний в момент времени t.
Частота – число полных колебаний в единицу времени.
n
1
T 2

2.

Дифференциальное уравнение гармонических колебаний:
2
d 2S
2
S
S 0
S
0
dt 2
Решение этого уравнения:
S (t ) A cos( t )
Метод векторных диаграмм

3.

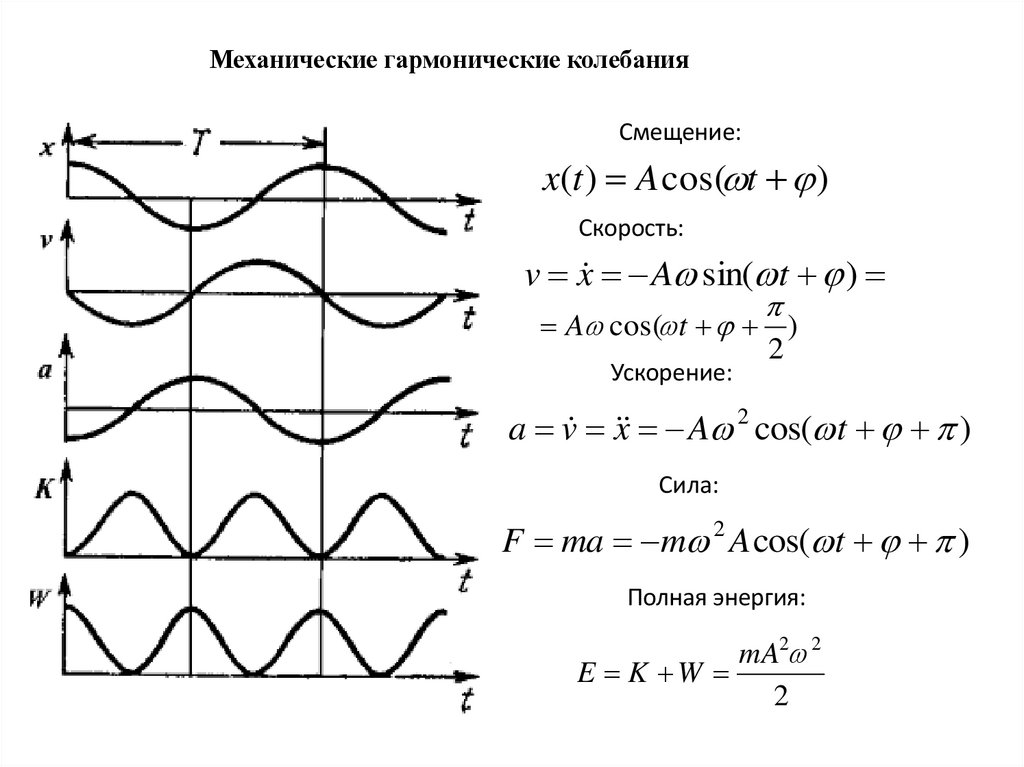
Механические гармонические колебания
Смещение:
x(t ) A cos( t )
Скорость:
v x A sin( t )
A cos( t )
2
Ускорение:
a v x A 2 cos( t )
Сила:
F ma m 2 A cos( t )
Полная энергия:
mA2 2
E K W
2

4.

Пружинный маятник груз массой m, подвешенный на абсолютно упругой пружине и совершающий
гармонические колебания под действием упругой силы.
F kx
m x kx
k
x x 0
m
k
m
m
T 2
k
m 2 x 2 kx 2
W
2
2
Если есть трение:
r
k
x x x 0
m
m

5.

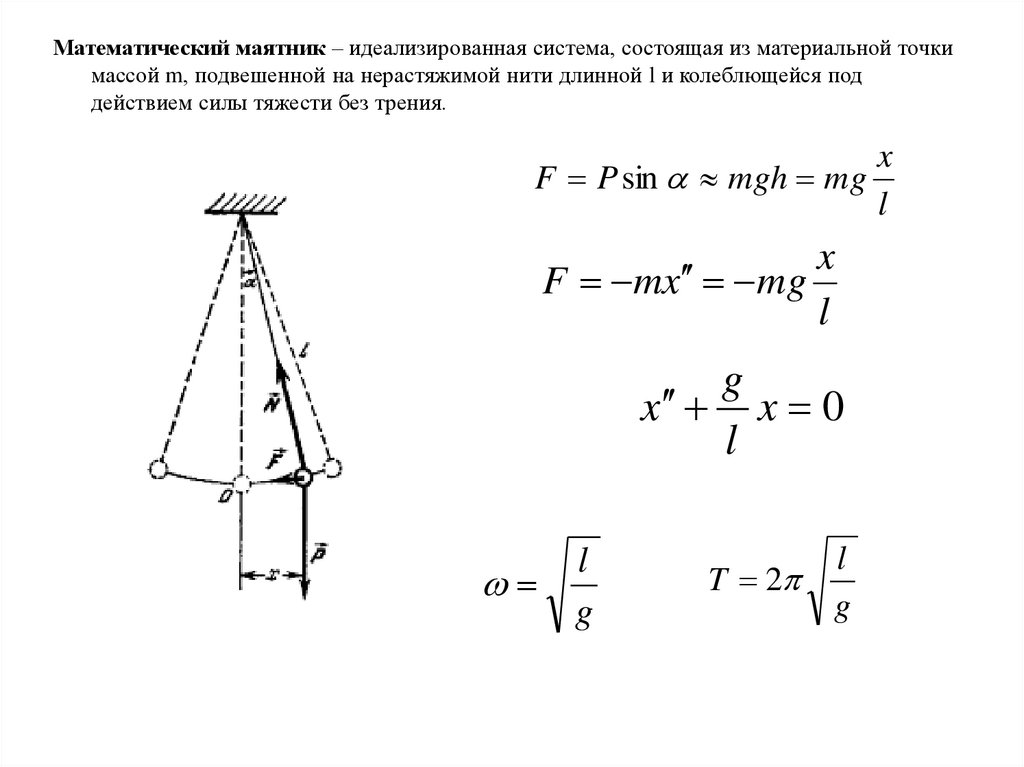
Математический маятник – идеализированная система, состоящая из материальной точки
массой m, подвешенной на нерастяжимой нити длинной l и колеблющейся под
действием силы тяжести без трения.
x
F P sin mgh mg
l
x
F mx mg
l
g
x x 0
l
l
g
T 2
l
g

6.

Физический маятник – твердое тело, совершающее под действием силы тяжести
колебания вокруг горизонтальной оси подвеса, не проходящий через центр масс тел.
M I I
M Fl mgl sin mgl
I mgl 0
mgl
I
L
T 2
q
L – приведенная длина физического
маятника.
Приведенная длина физического маятника — это длина такого математического
маятника, который имеет такой же период колебаний, что и данный физический
маятник.

7.

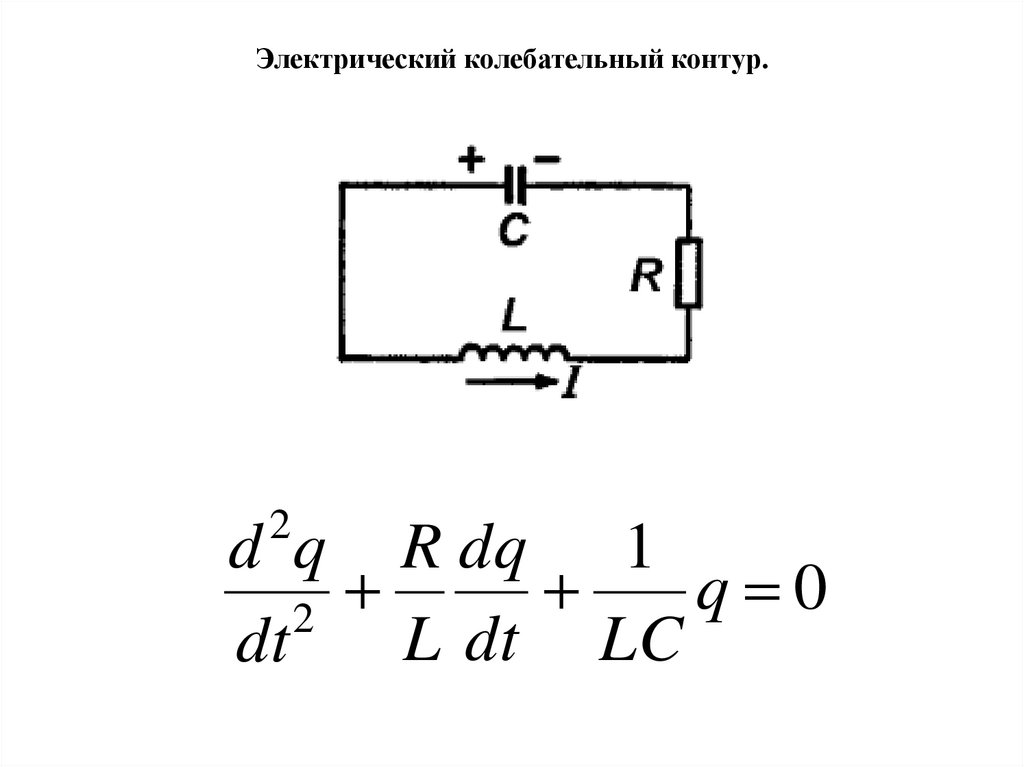
Электрический колебательный контур.
2
d q R dq 1
q
0
2
L dt LC
dt

8.

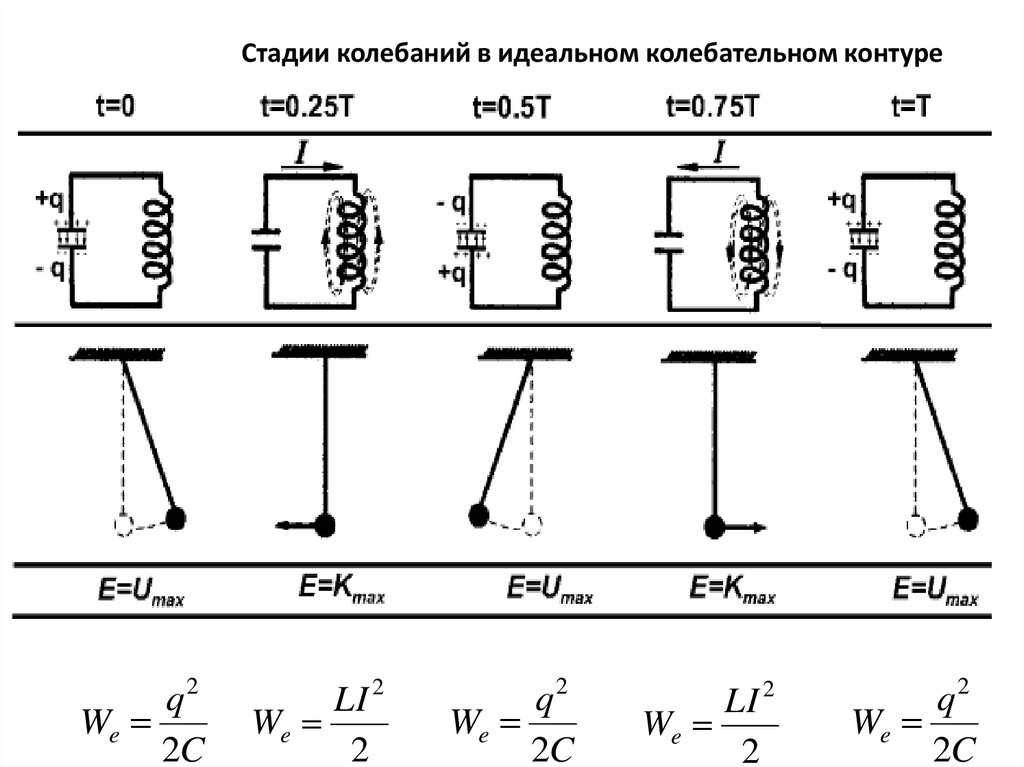
Стадии колебаний в идеальном колебательном контуре
q2
We
2C
LI 2
We
2
q2
We
2C
LI
We
2
2
q2
We
2C

9.

Из сравнения электрических колебаний с механическими
колебаниями, следует, что:
— энергия электрического поля конденсатора аналогична
потенциальной энергии маятника,
— энергия магнитного поля катушки аналогична кинетической
энергии маятника,
— сила тока в контуре аналогична скорости движения
маятника,
— индуктивность L выполняет функцию массы,
— сопротивление R играет роль силы трения, действующей
на маятник.

10.

Свободные гармонические колебания в колебательном контуре
d 2q 1
q 0
2
LC
dt
q q0 cos( t )
q 2 q 0
1
LC
T 2 LC
dq
I
q0 sin( t ) I max cos t
dt
2
Ток в колебательном контуре опережает колебания заряда на
2

11.

Разность потенциалов на конденсаторе изменяется по гармоническому закону и
совпадает по фазе с зарядом
q qm cos( t )
U
C
C
q m - Амплитуда разности потенциалов
U
C
I max U max
C
L
C
L
- Волновое сопротивление колебательного контура

12. Сложение гармонических колебаний.

x1 A1 cos( t 1 )
x2 A2 cos( t 2 )
2
A
2
2
A1 A2 2 A1 A2 cos( 2
A1 sin 1 A2 sin 2
tg
A1 cos 1 A2 cos
1 )
Сумма двух гармонических колебаний одного направления и одинаковой частоты
есть гармоническое колебание в том же направлении и с той же частотой, что и
складываемые колебания.

13.

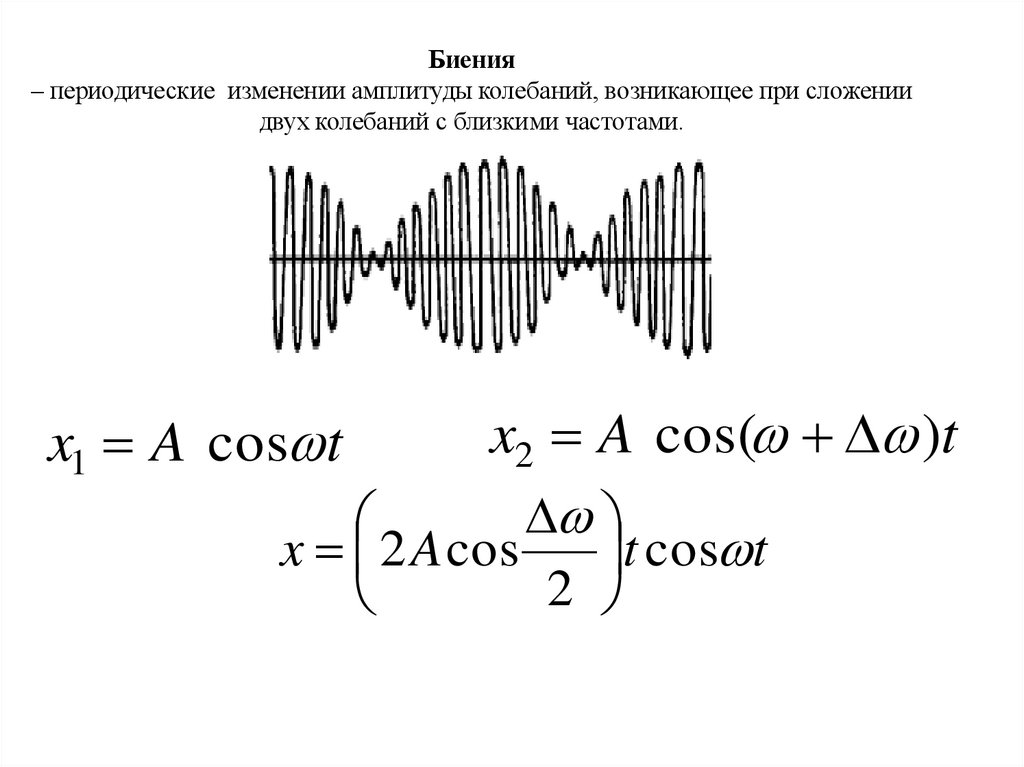
Биения
– периодические изменении амплитуды колебаний, возникающее при сложении
двух колебаний с близкими частотами.
x2 A cos( )t
x 2 A cos
t cos t
x1 A cos t
2

14.

Сложение взаимно перпендикулярных гармонических
колебаний одинаковой частоты.
x A cos t y B cos( t )
x 2 2 xy
y2
cos 2 sin 2
A AB
B

15.

Линейно поляризованные колебания
m
(m 0, 1, 2...)
B
y x
A

16.

Циркулярно поляризованные колебания
(2m 1)
2
2
(m 0, 1, 2...)
2
x
y
1
2
2
A
B

17.

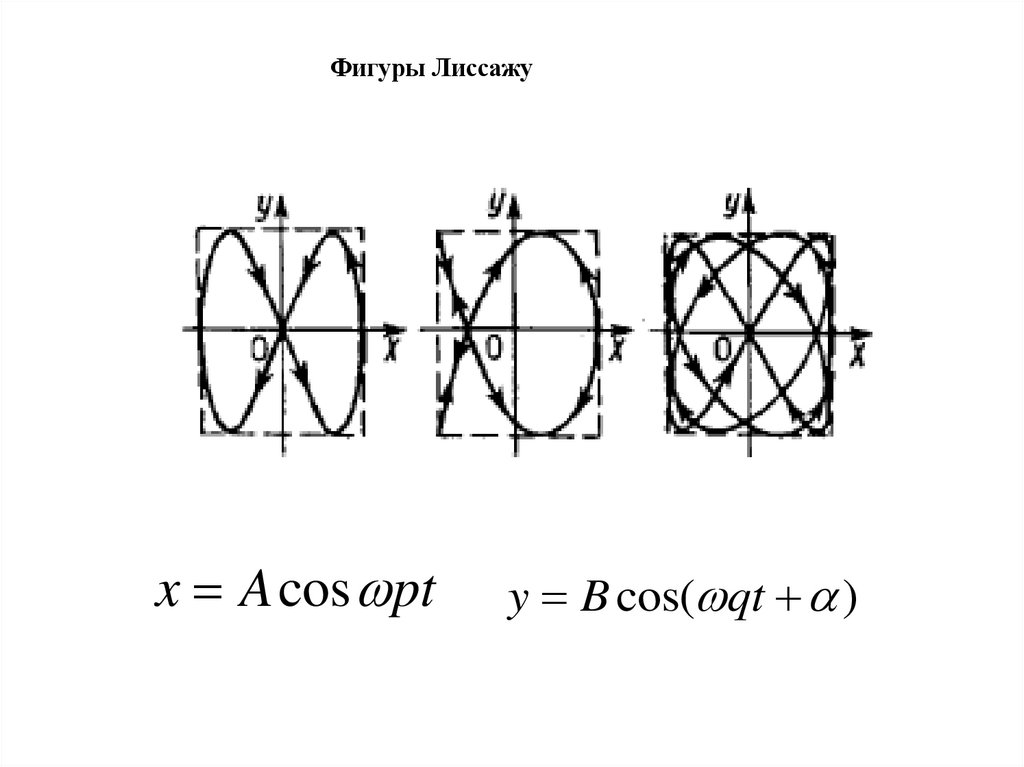
Фигуры Лиссажу
x A cos pt
y B cos( qt )

18. Затухающие и вынужденные колебания.

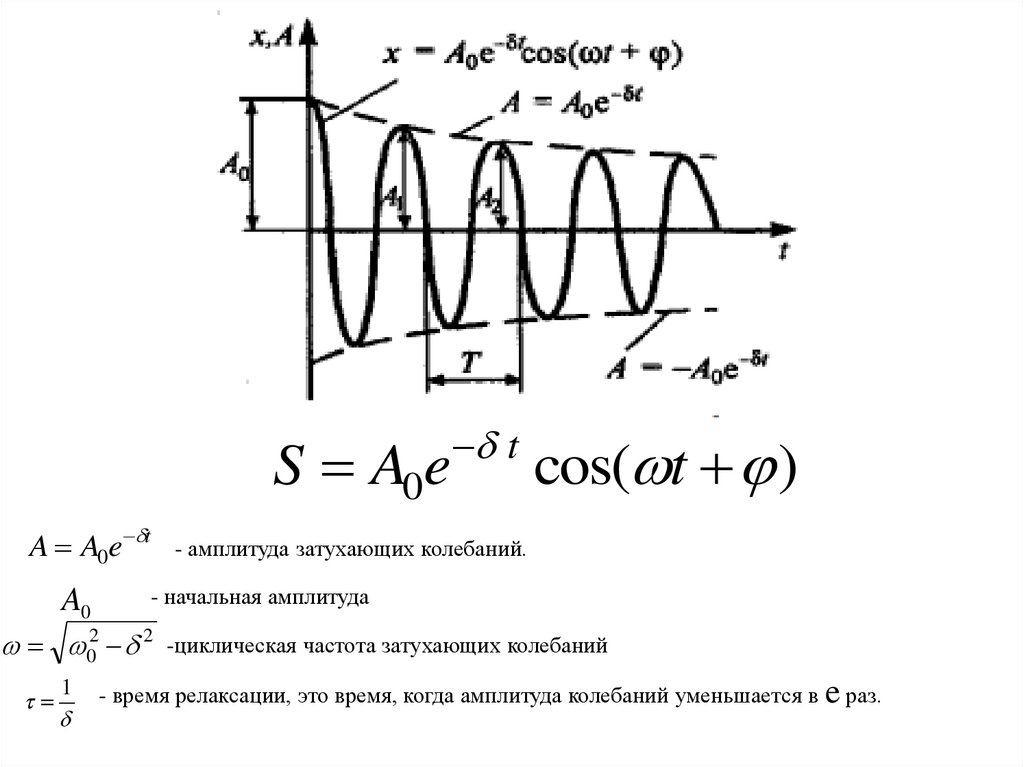
Затухающим колебанием называется постепенное ослабление колебаний с течением времени.
Система называется линейной, если параметры, характеризующие те физические свойства
системы, которые существенны для рассматриваемого процесса не изменяется в ходе
процесса.
Линейные системы описываются линейным дифференциальным уравнением:
2
d S
dS
2
2
0 S 0
2
dt
dt
S – колеблющиеся величина;
- коэффициент затухания;
0 - циклическая частота не затухающих колебаний.

19.

S A0e
A A0e t
A0
t
cos( t )
- амплитуда затухающих колебаний.
- начальная амплитуда
02 2 -циклическая частота затухающих колебаний
1
- время релаксации, это время, когда амплитуда колебаний уменьшается в e раз.

20.

Если затухание мало, то можно условно пользоваться понятием периода затухающих
колебаний.
T
2
2
02 2
Декремент затухания:
A(t )
e T
A(t T )
ln
A(t )
T 1
T
A(t T )
N
- логарифмический декремент затухания.
N – число колебаний, совершаемых за время уменьшения амплитуды.
Добротность колебаний – называется безразмерная величина Q равная произведению
W (t )
A2 (t )
2
2
Q 2
2 2
W (t ) W (t T )
A (t ) A2 (t T ) 1 e 2 T 1 e 2
Q 1
Q
N 0
2

21.

Примеры свободных затухающих колебаний
x 2 x 2 x 0
S A0e t cos( t )

22.

Вынужденные колебания.
В случае механического колебания для пружинного маятника
вынуждающая сила:
F (t ) F0 cos t
mx kx rx F0 cos t
В случае электрического колебательного контура переменное
или ЭДС
U (t ) U m cos t
2
S 2 S 0 S x0 cos t
напряжение

23.

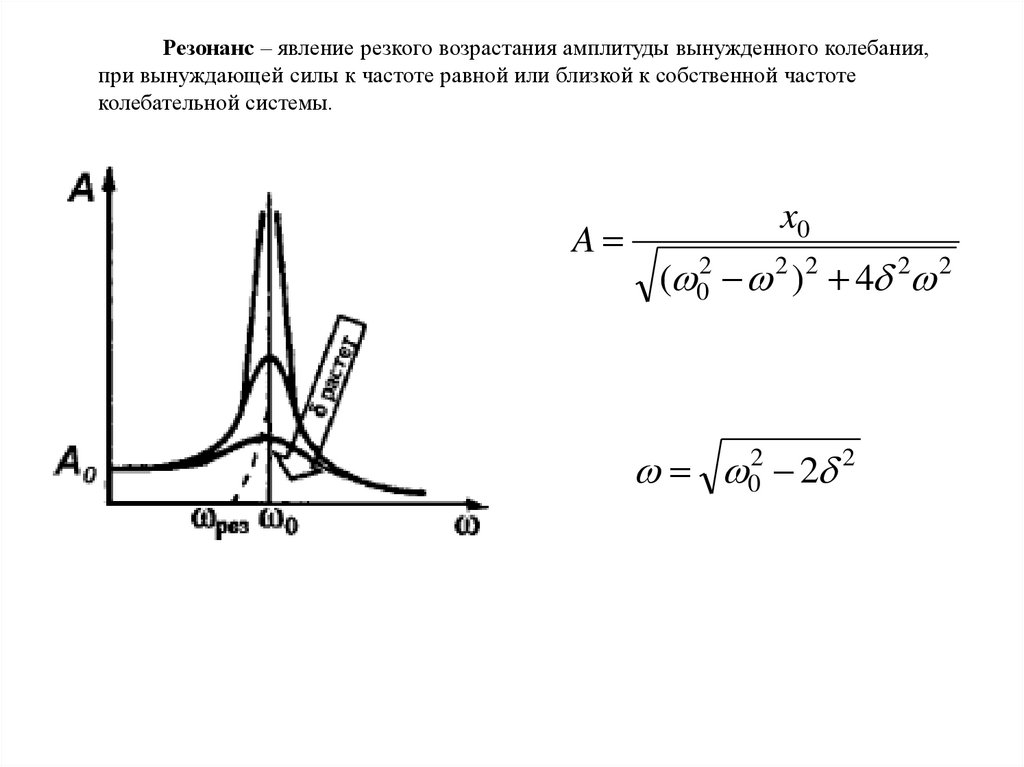
Резонанс – явление резкого возрастания амплитуды вынужденного колебания,
при вынуждающей силы к частоте равной или близкой к собственной частоте
колебательной системы.
A
x0
( 02 2 ) 2 4 2 2
02 2 2

24. Переменный ток.

Переменным током называются вынужденные колебания тока в цепи, совпадающие
с частотой вынуждающей силы.
U U m cos t
На участке цепи, имеющем сопротивление R, емкость С и индуктивность L закон
Ома:
q
Um
R
1
q
q
cos t
L
LC
L

25.

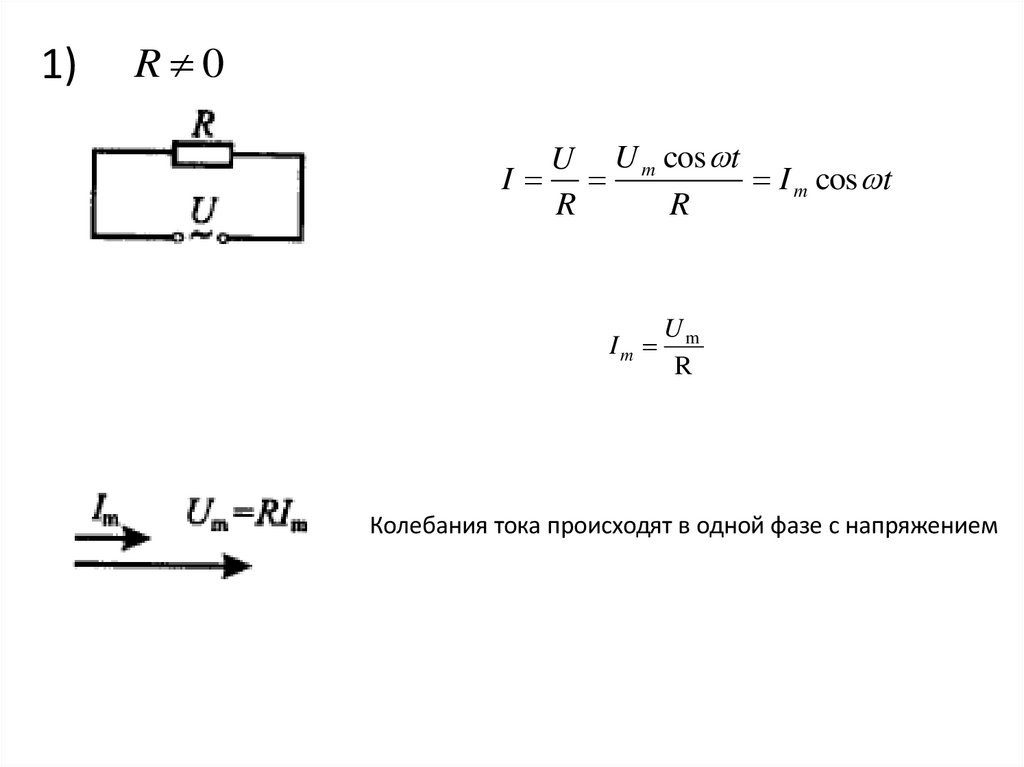
1)
R 0
U U m cos t
I
I m cos t
R
R
Im
Um
R
Колебания тока происходят в одной фазе с напряжением

26.

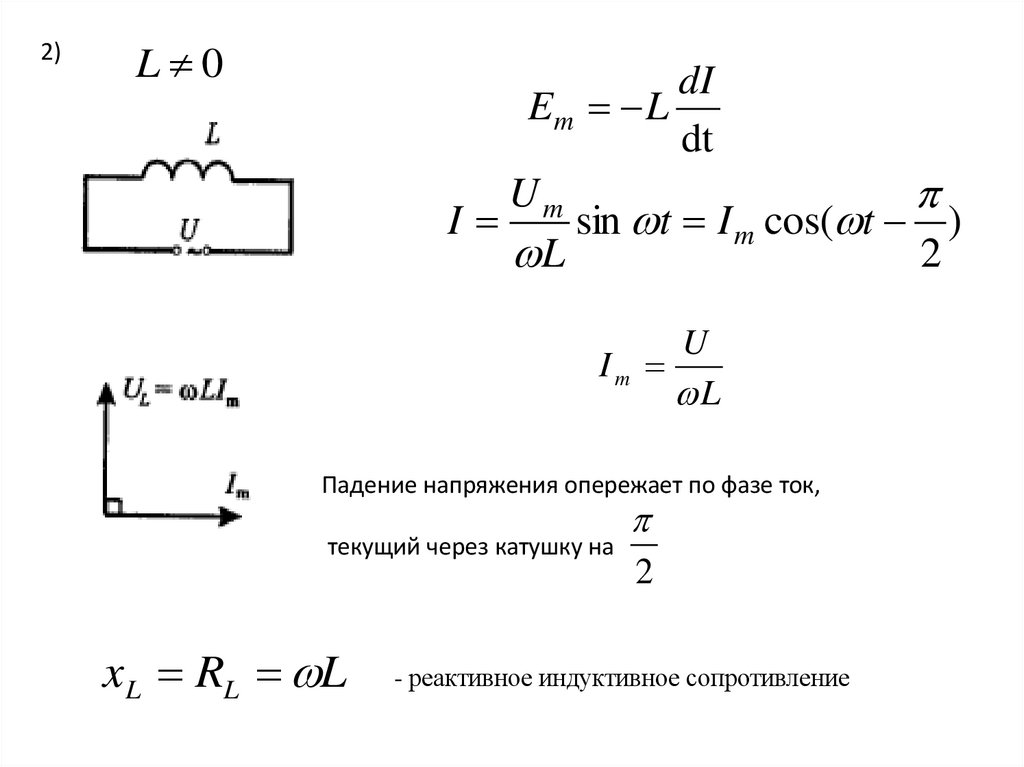
2)
L 0
dI
Em L
dt
Um
I
sin t I m cos( t )
L
2
U
Im
L
Падение напряжения опережает по фазе ток,
текущий через катушку на
2
xL RL L
- реактивное индуктивное сопротивление

27.

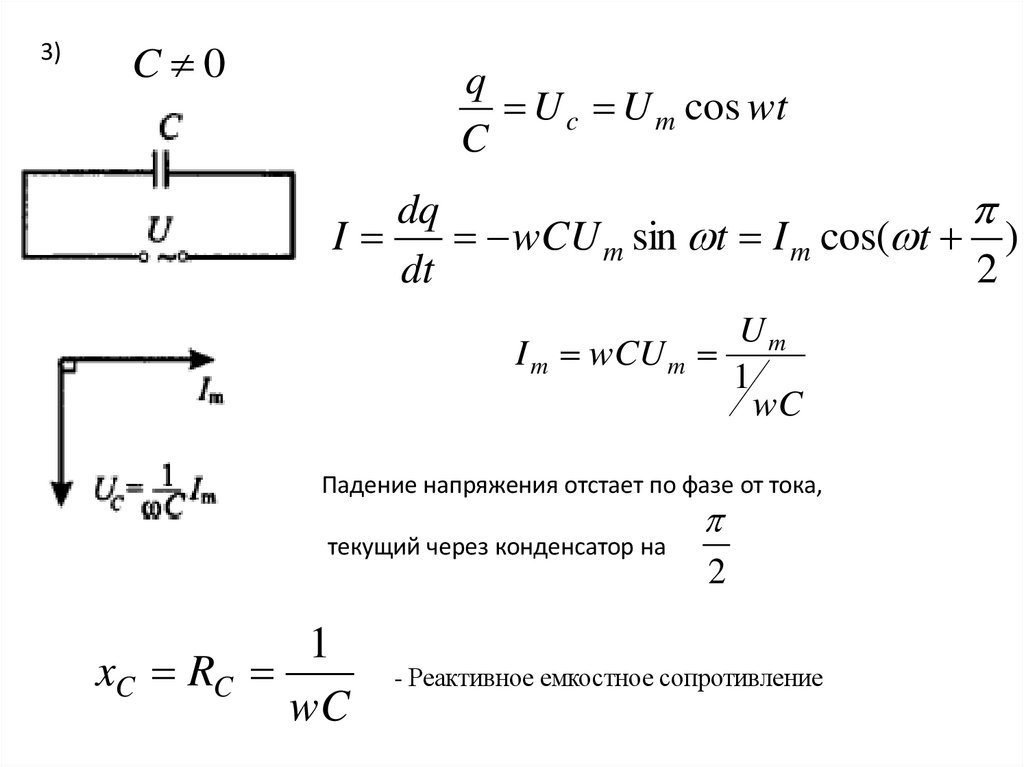
3)
C 0
q
U c U m cos wt
C
dq
I
wCU m sin t I m cos( t )
dt
2
Um
I m wCU m
1
wC
Падение напряжения отстает по фазе от тока,
текущий через конденсатор на
1
xC RC
wC
2
- Реактивное емкостное сопротивление

28.

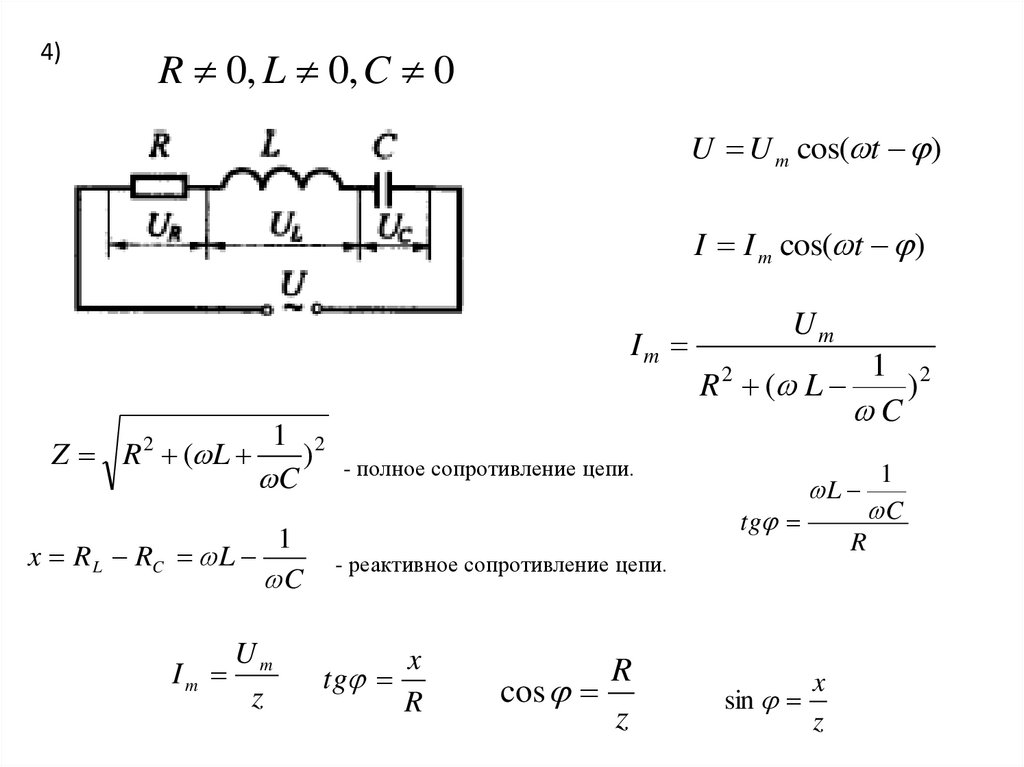
4)
R 0, L 0, C 0
U U m cos( t )
I I m cos( t )
Im
Z R 2 ( L
R 2 ( L
1 2
) - полное сопротивление цепи.
C
1
x R L RC L
C
Im
Um
Um
z
tg
L
R
- реактивное сопротивление цепи.
tg
x
R
R
cos
z
sin
1 2
)
C
x
z
1
C

29. Резонанс напряжения.

Если
L
1
C
, то
0
и изменение тока и напряжение происходит синфазно, z=R и ток определяется только
активным сопротивлением и достигает максимального возможного значения.
Падение напряжения на конденсаторе одинаковы по амплитуде и противоположны по
фазе. Это явление называется резонансом напряжений.
рез
1
LC

30.

Резонанс токов
U U m cos( t )
Um
I m1
1
wC
U
I m2
L
Токи в ветвях 1С2 1L2противоположны по фазам.
1
I m I m1 I m 2 U m wC
wL
1
w w рез
, I m1 I m 2 I m 0
LC
Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей
параллельно включенные конденсатор и катушку индуктивности, при приближении
частоты w приложенного напряжения к резонансной частоте называется
резонансом тонов (параллельным резонансом).

31.

Действующее значение переменного тока.
Действующим или эффективным значением переменного тока
I I 0 cos t
называется среднее квадратичное значение силы тока за период Т его изменения:
T
I эф
I
1
I 2 (t )dt 0
T
2
0
U0
U эф
2