Л1 Векторная алгебра

1.

2. Векторная алгебра

Основные понятия

3. Основные понятия

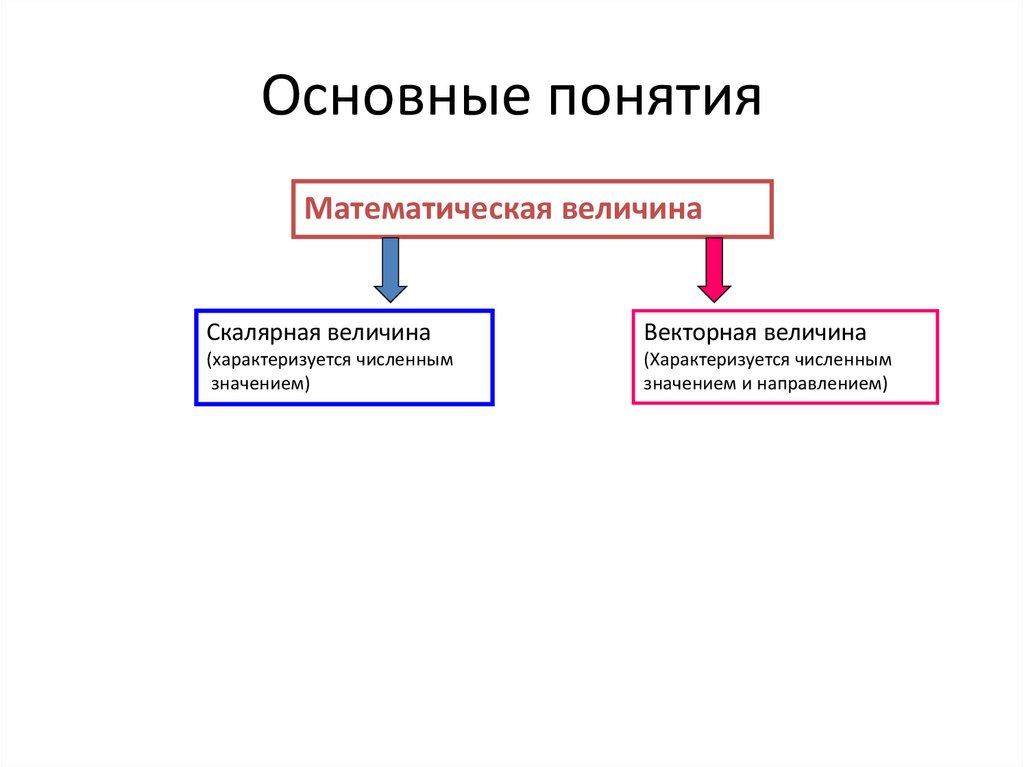
Математическая величина
Скалярная величина
Векторная величина
(характеризуется численным
значением)
(Характеризуется численным
значением и направлением)

4. Основные понятия

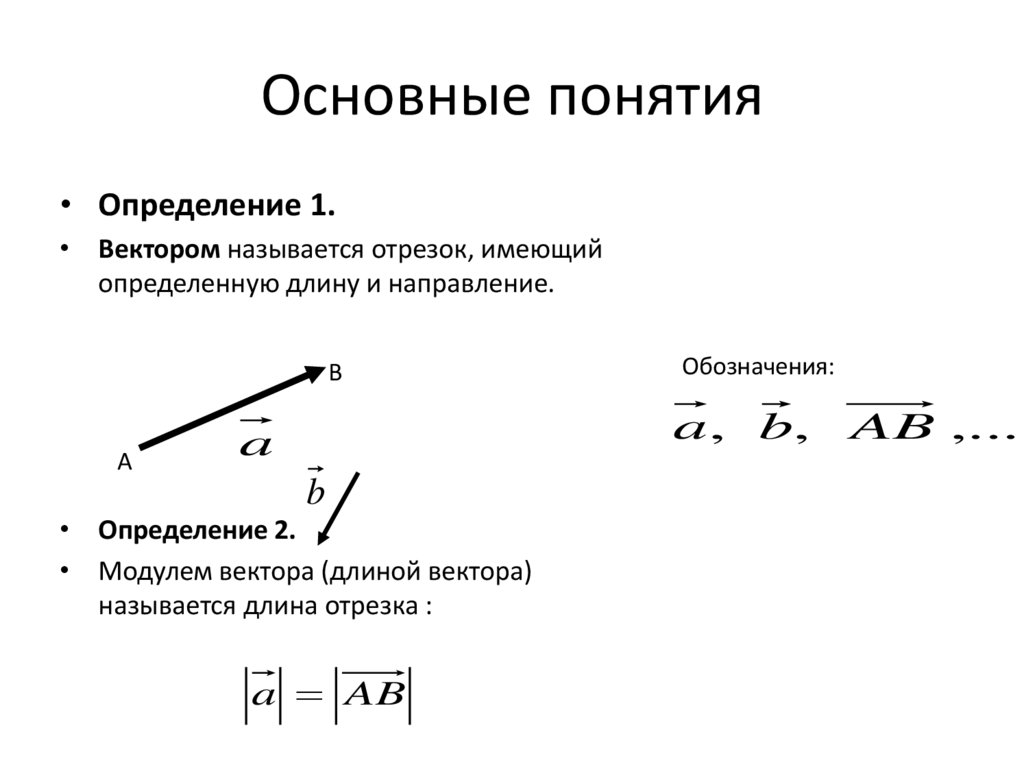
• Определение 1.
• Вектором называется отрезок, имеющий
определенную длину и направление.
В
А
Обозначения:
a, b,
a
b
• Определение 2.
• Модулем вектора (длиной вектора)
называется длина отрезка :
a AB
AB ,...

5. Основные понятия

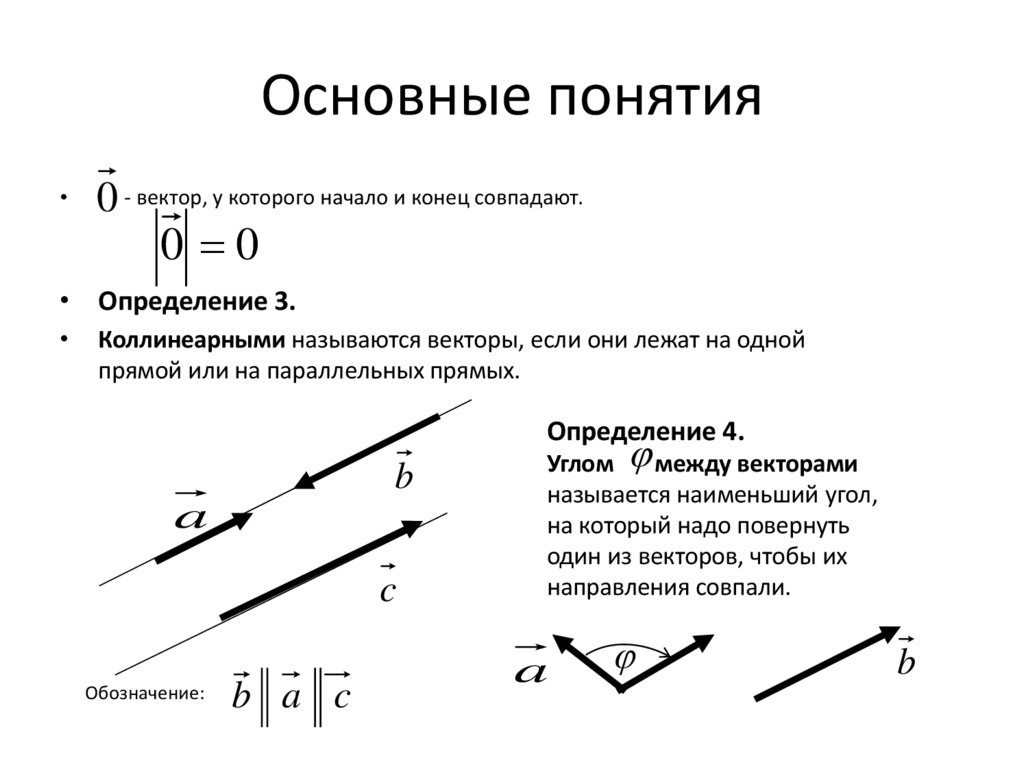
0 - вектор, у которого начало и конец совпадают.
0 0
• Определение 3.
Коллинеарными называются векторы, если они лежат на одной
прямой или на параллельных прямых.
Определение 4.
b
a
c
Обозначение:
b a c
Углом между векторами
называется наименьший угол,
на который надо повернуть
один из векторов, чтобы их
направления совпали.
a
b

6. Основные понятия

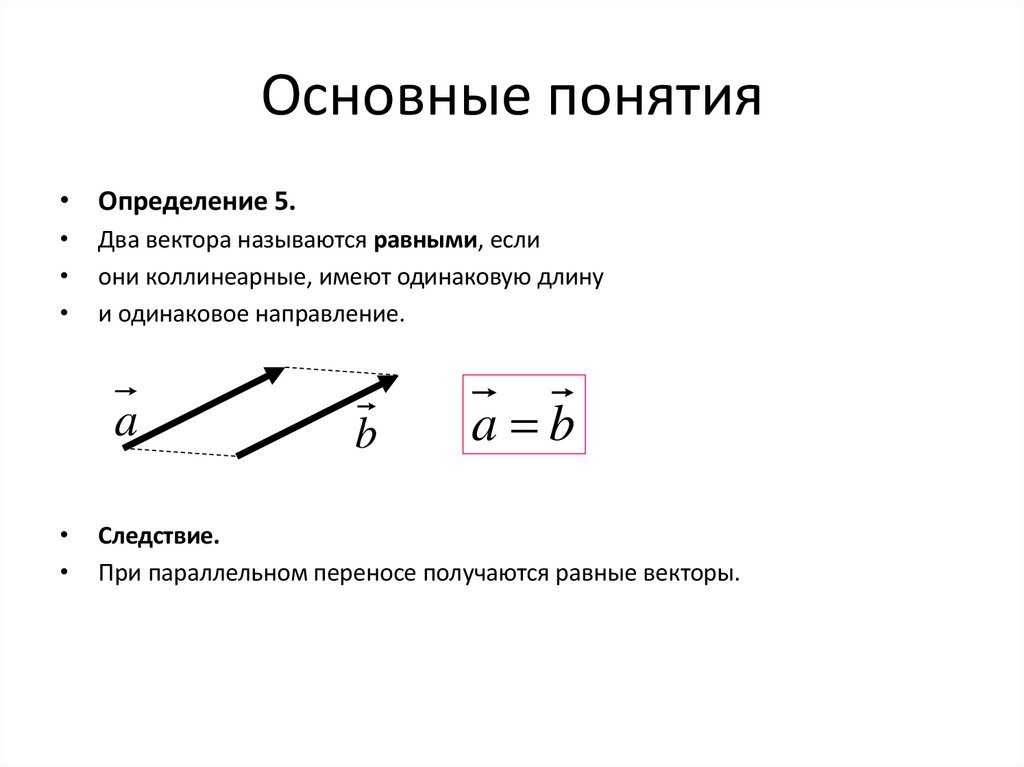
• Определение 5.
Два вектора называются равными, если
они коллинеарные, имеют одинаковую длину
и одинаковое направление.
a
b
a b
Следствие.
При параллельном переносе получаются равные векторы.

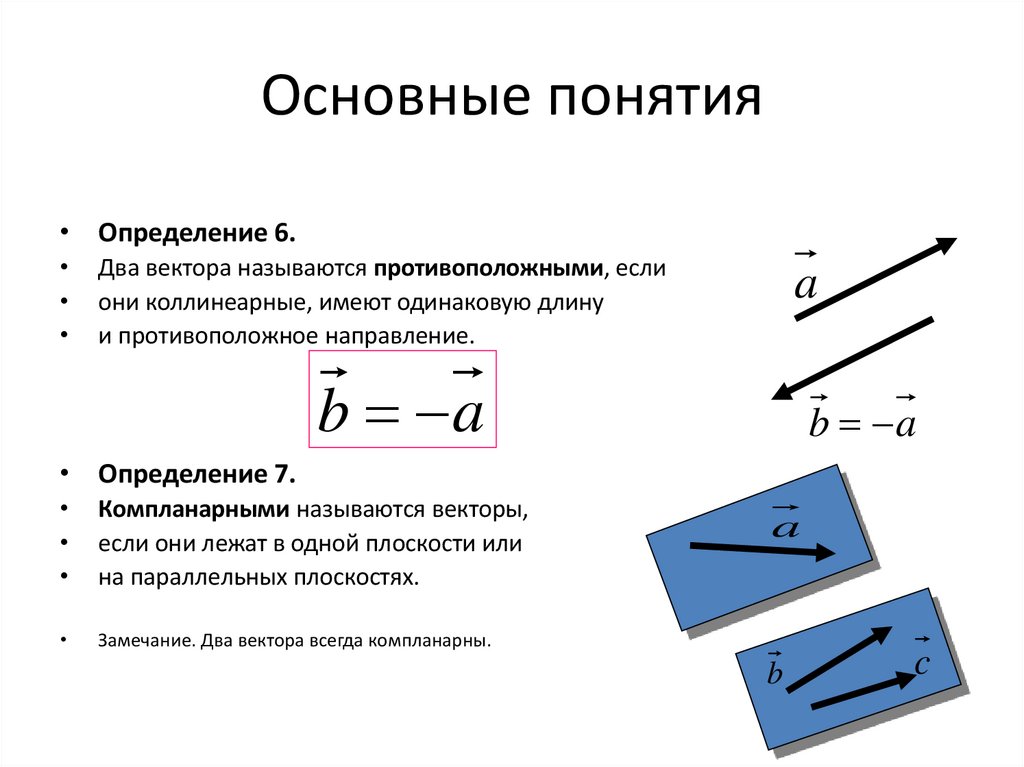
7. Основные понятия

• Определение 6.
Два вектора называются противоположными, если
они коллинеарные, имеют одинаковую длину
и противоположное направление.
a
b a
b a
• Определение 7.
Компланарными называются векторы,
если они лежат в одной плоскости или
на параллельных плоскостях.
Замечание. Два вектора всегда компланарны.
a
b
c

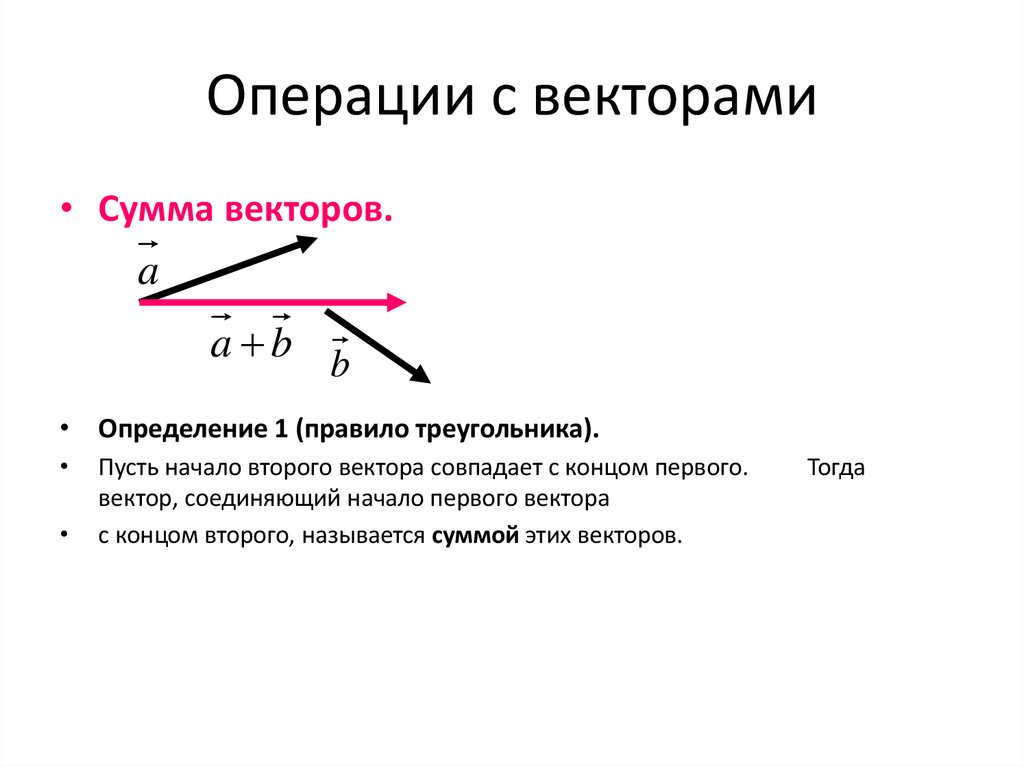
8. Операции с векторами

• Сумма векторов.
a
a b b
• Определение 1 (правило треугольника).
Пусть начало второго вектора совпадает с концом первого.
вектор, соединяющий начало первого вектора
с концом второго, называется суммой этих векторов.
Тогда

9.

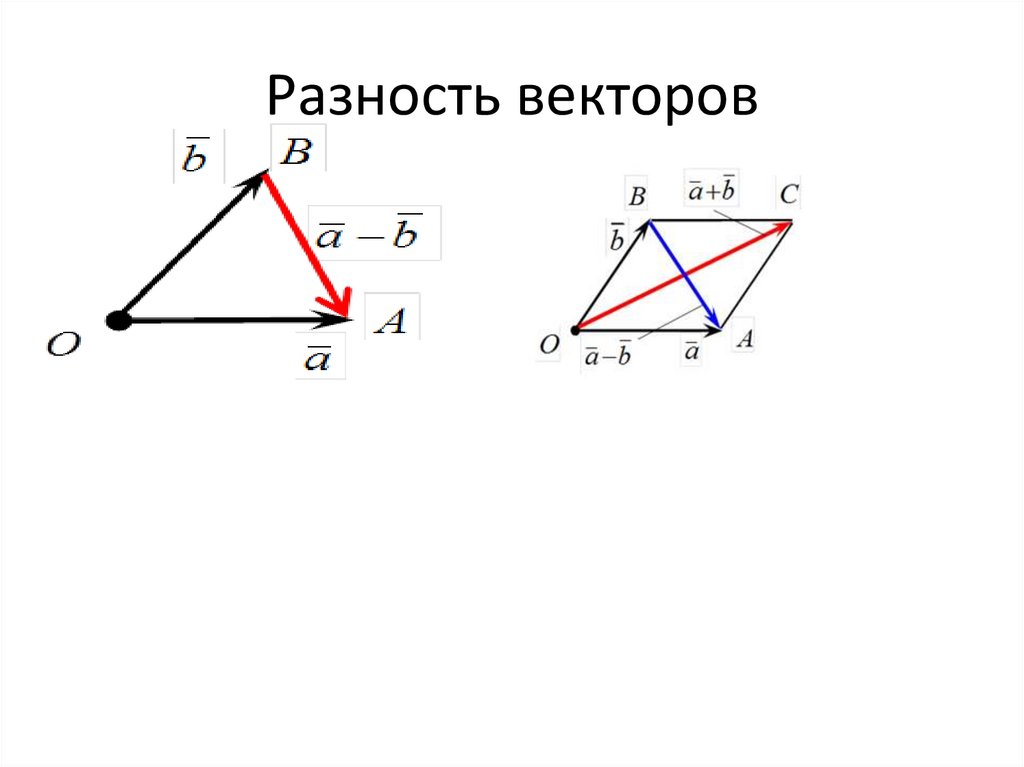
10. Разность векторов

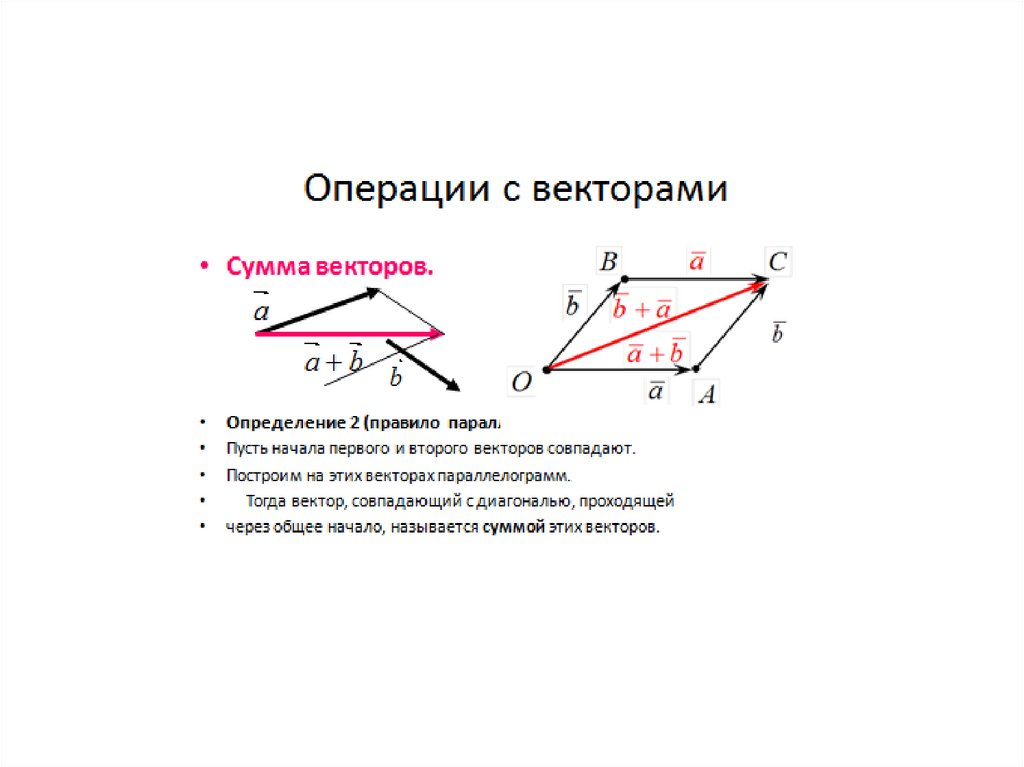
11. Операции с векторами

• Произведение вектора на число.
• Определение.
a• Произведением вектора на число
• вектор
a , a
a
• коллинеарный вектору
,
называется
равный по модулю
, a
направленный при 0
в ту же сторону, что и
и в противоположную сторону, если
.
0
,
a

12. Операции с векторами

• Пример.
Задан вектор
Построение :
1
1
2a, a, a .
2
2
a. Построить векторы
2a
a
a
1
a
2
a
1
a
2
• Теорема.
b и a коллинеарны тогда и только тогда,
Пусть a 0 . Векторы
когда найдется такая постоянная
, что
b a b a
b a

13. Основные свойства операций

• 1. a b b a
• 2. ( a b) c a (b c)
• 3. a ( a ) 0
• 4. ( a b) a b
• 5. ( 1 2 )a 1 a 2 a
• 6. ( 1 2 )a 1 ( 2 a)

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

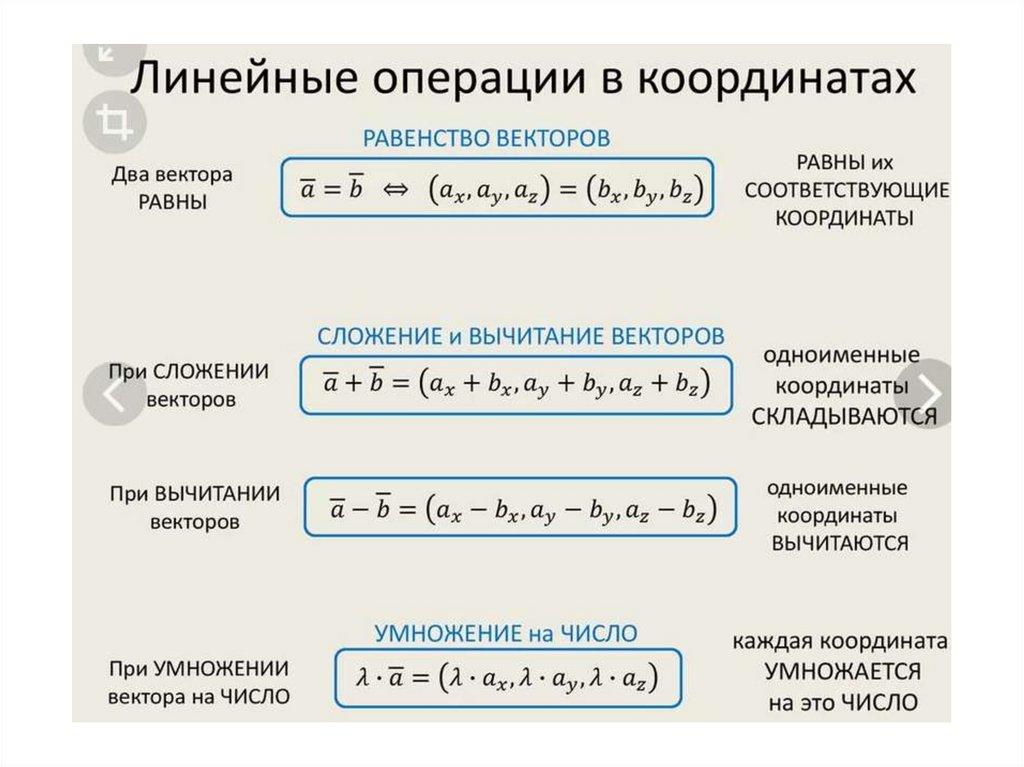
25. Действия с векторами в координатной форме

Необходимое и достаточное условие коллинеарности
векторов, заданных в координатной форме.
Два ненулевых вектора коллинеарны
тогда и только тогда, когда
соответствующие координаты пропорциональны.
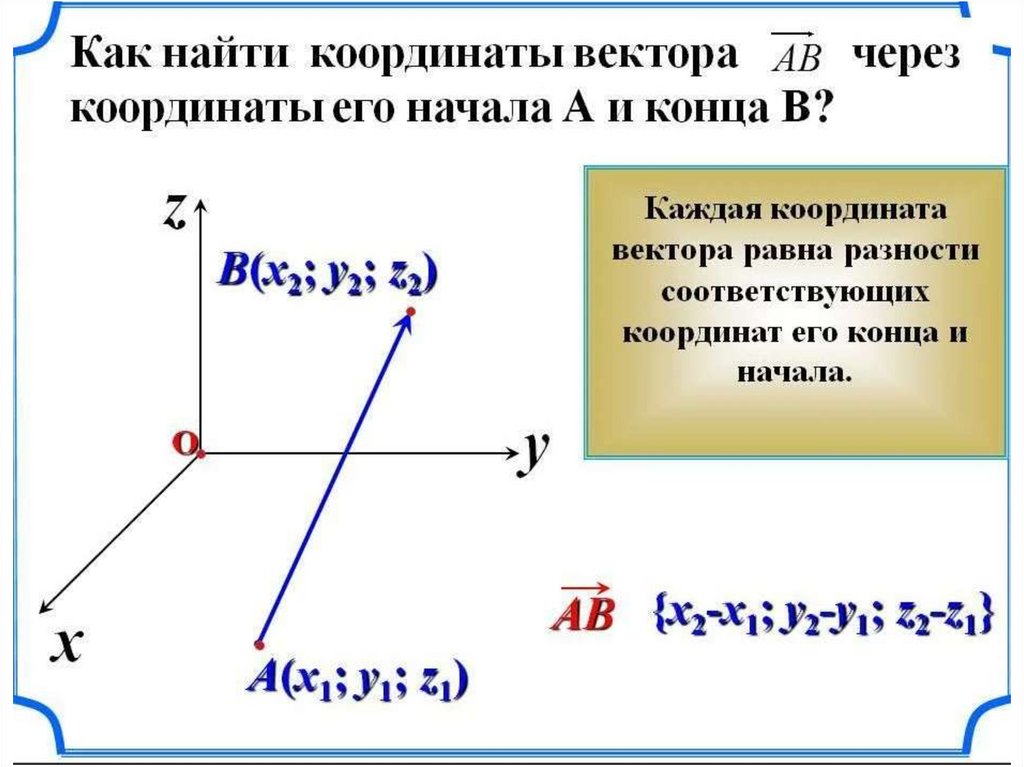
Пусть
a x1 , y1 , z1 и b x2 , y2 , z 2
Тогда
x1
y1
z1
a b
x2
y2
z2
Доказательство.
x1
y1
z1
x1 x2
a b a b y1 y2
x
y
z
z
z
2
2
2
2
1