Лекция 7. Векторная алгебра ч.2

1.

ВЕКТОРНАЯ АЛГЕБРА
(произведения векторов, проекция
векторов, разложение вектора по
базису)
ЛЕКЦИЯ 7

2. ВСПОМИНАЕМ ИЗУЧЕННЫЙ МАТЕРИАЛ

Чем множество отрезков на плоскости отличается от свободного вектора,
выходящего из нескольких точек?
Если вектор a задан точками A и B (то есть это вектор AB), то как,
используя эти же точки A и B, задать вектор -a?
Дан вектор AB, где A(1, 2, 3) и B(4, 6, 9). Как найти координаты точки C,
если известно, что вектор AC в два раза длиннее вектора AB и направлен
в противоположную сторону?
Почему в физике при описании движения тела на плоскости (например,
по столу) нам достаточно двух неколлинеарных векторов (базиса), а для
описания движения в комнате (в пространстве) уже нужны три
некомпланарных? Приведите пример из жизни.

3.

Скалярное
произведение векторов

4.

5.

6.

Скалярное произведение векторов в
координатах

7.

Формула косинуса между векторами,
заданными координатами

8.

Проекция
вектора на
вектор

9.

Проекция вектора
на вектор

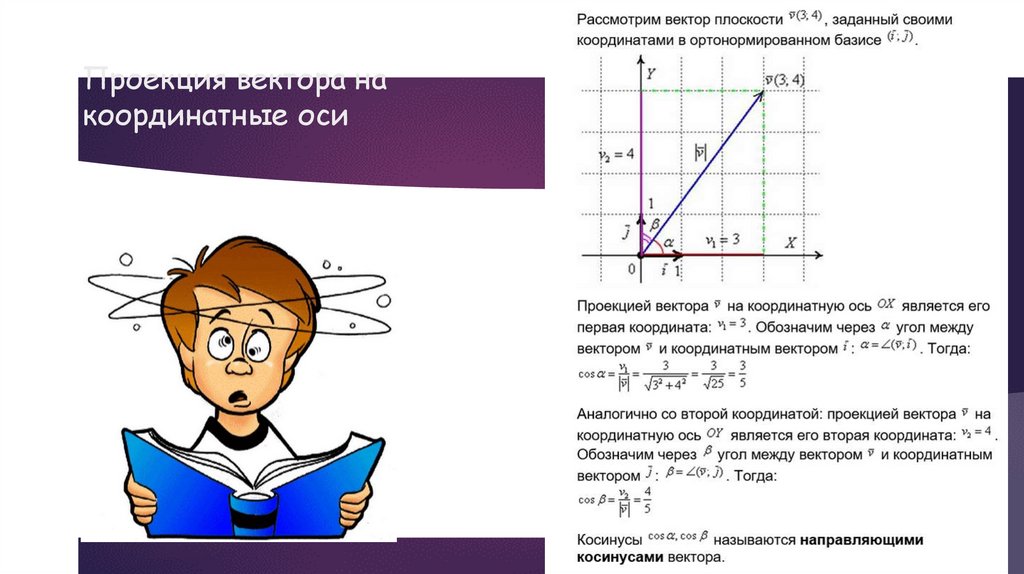
10.

Проекция вектора на
координатные оси

11.

Линейная
зависимость
векторов
Линейная зависимость векторов
означает, что хотя бы один вектор из
системы можно представить как
линейную комбинацию остальных, то
есть выразить через них с помощью
сложения и умножения на число.
Другими словами, это значит, что
существует ненулевая линейная
комбинация векторов, равная
нулевому вектору.

12.

Два вектора плоскости линейно зависимы тогда и
только тогда, когда они коллинеарны.

13.

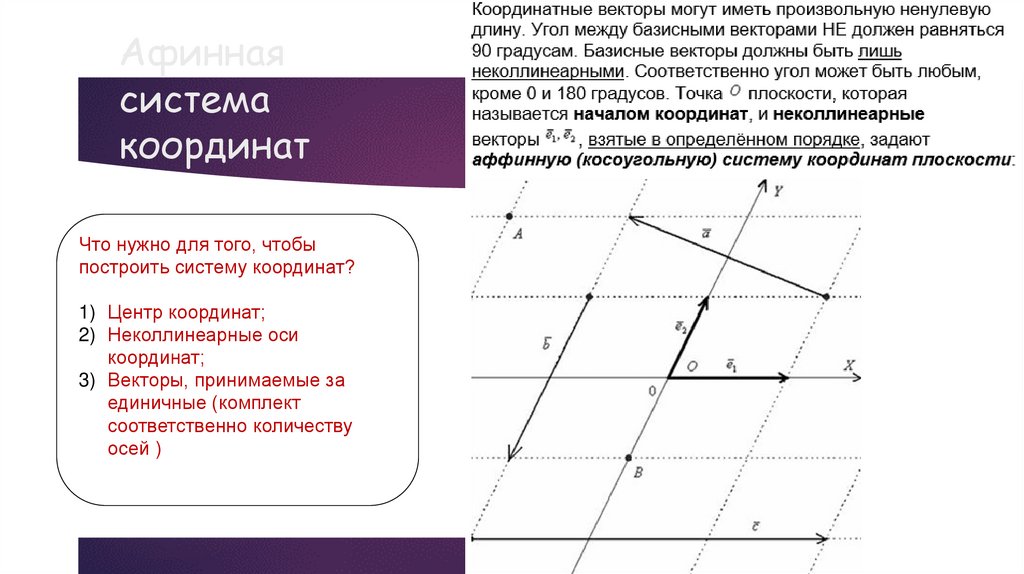
Афинная
система
координат
Что нужно для того, чтобы
построить систему координат?
1) Центр координат;
2) Неколлинеарные оси
координат;
3) Векторы, принимаемые за
единичные (комплект
соответственно количеству
осей )

14.

Коллинеарность векторов на плоскости

15.

Определитель из
координат
И наоборот: если определитель не равен нулю, векторы
НЕ коллинеарны.

16.

ВЫВОД:

17.

Векторы пространства

18.

Векторы пространства
Частный случай:

19.

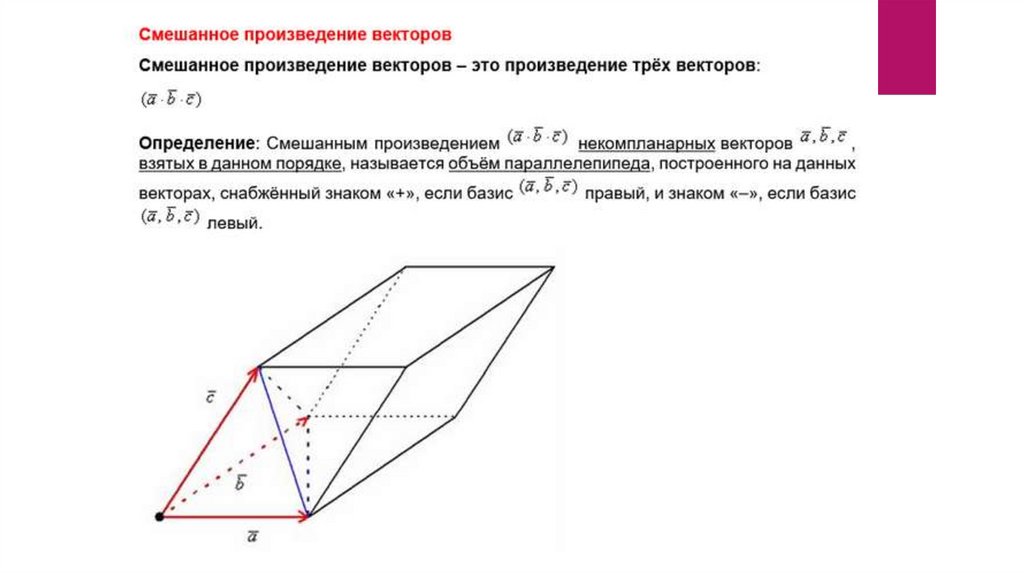
Векторное и смешанное
произведения векторов.

20.

21.

22.

23.

24.

25.

26.

27.

Пример
ПРИМЕР

28.

29.

30.

31.

Пример

32. РАЗЛОЖЕНИЕ ВЕКТОРА ПО БАЗИСУ

Базис — это набор независимых векторов, которые позволяют однозначно
описать любой вектор в пространстве. На плоскости базис состоит из двух
неколлинеарных векторов. В пространстве базис состоит из трех
некомпланарных векторов.
Разложить вектор по базису — значит представить его в виде суммы
базисных векторов, умноженных на некоторые числа.
a=x·i+y·j+z·k
Где: a — наш вектор;
i, j, k — базисные векторы;
x, y, z — координаты (или коэффициенты разложения) вектора a в этом
базисе.
Координаты вектора — это не что иное, как коэффициенты его разложения
по выбранному базису. Меняете базис — меняются координаты, но сам
вектор (как геометрический объект) остается тем же.

33. РАЗЛОЖЕНИЕ ВЕКТОРА ПО БАЗИСУ

Дан вектор с координатами и 3 вектора, которые возможно
составляют базис. Разложить заданных вектор в базисе.
Алгоритм решения:
Доказать, что векторы составляют базис, составив матрицу из координат указанных векторов,
располагая их в СТОЛБЦАХ, и рассчитав определитель. Если определитель не равен нулю, векторы
составляют базис.
Если соблюдается условие из п.1., то составляем СЛАУ, где координаты исходных векторов попрежнему СТОЛБЦЫ, а координаты нового вектора становятся «правыми частями».
Решаем СЛАУ любым доступным способом. Найденные неизвестные – это и будет ответ, сколько раз
нужно взять исходные векторы, чтобы найти местоположение нового вектора в их базисе.

34.

Пример

35.

Пример