Похожие презентации:
урок 3. площадь криволинейной трапеции без интеграла
1.
Площадькриволинейной
трапеции
2. Вставьте вместо *
3 21) 3 x ( *x )
2
Вставьте вместо *
( * 3)x )
3) 3 cos 3 x (sin
1
1
1
4) 2 ( * )
2) Sin 5 x ( * )cos
5x
x
x
5
Определение первообразной:
F ( x) первообразная для f ( x),
если F ( x) f ( x)
© Комаров Р.А.
3. Будут ли первообразными следующие функции
3x3
x
1) y 5 x 2 ; 2) y 10 x 2 ;
3
3
x3
x3
2
3) y 7 ;
4) y x 25.
3
3
для функции y x 2 2 x.
© Комаров Р.А.
4. Определение: фигура, ограниченная графиком непрерывной и не меняющей своего знака на отрезке [a; b] функции, прямыми x=a, x=b и
отрезком [a; b]называется криволинейной трапецией.
© Комаров Р.А.
5. Рассмотрим следующие чертежи
yy
а
0
0
а
b
x
x
b
y
y
0
0
а
а
b
x
b x
© Комаров Р.А.
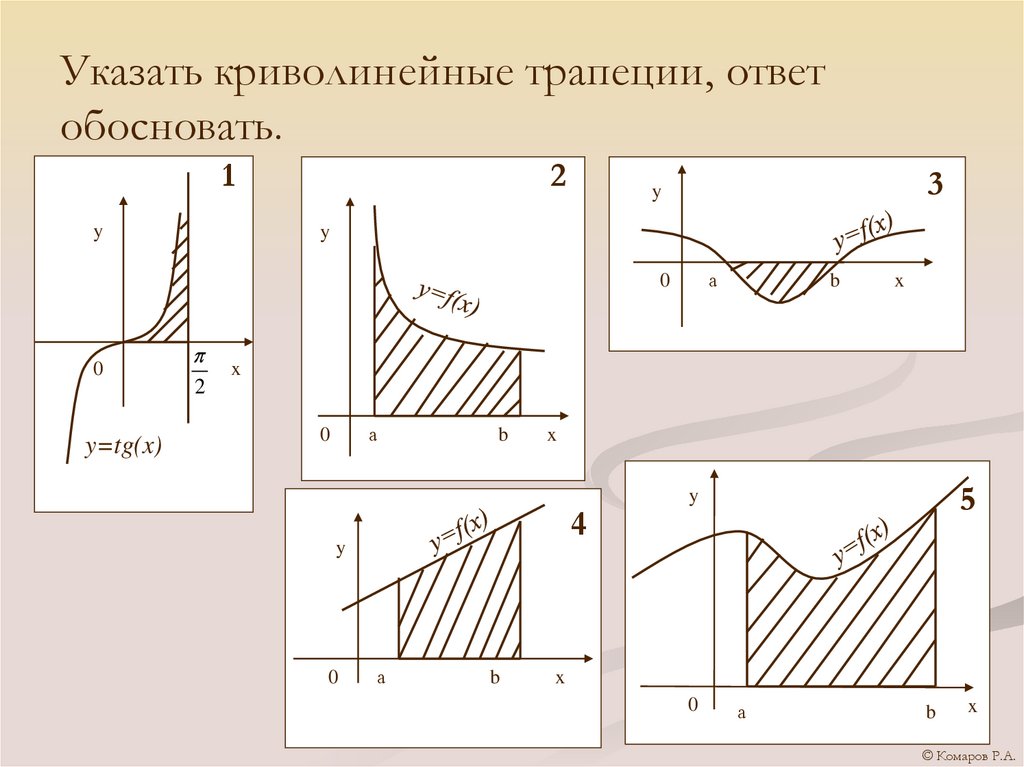
6. Указать криволинейные трапеции, ответ обосновать.
1y
2
3
y
y
а
0
0
y=tg(x)
2
b
x
x
а
0
b
x
4
y
0
а
b
5
y
x
0
а
b
x
© Комаров Р.А.
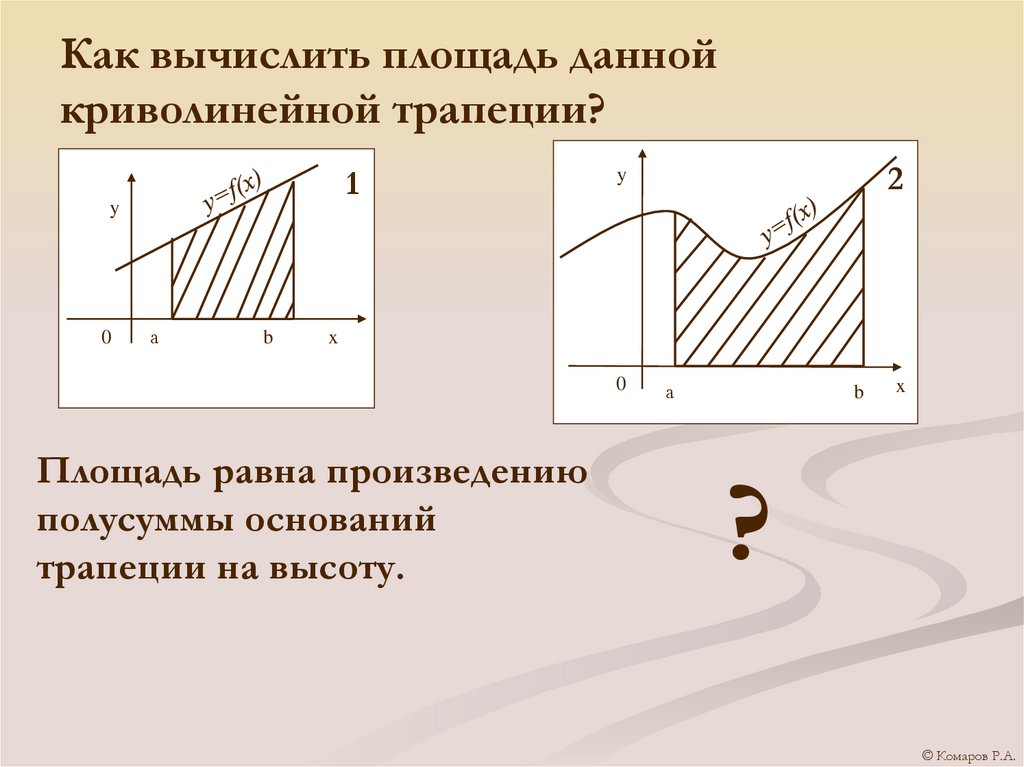
7. Как вычислить площадь данной криволинейной трапеции?
1y
0
а
b
2
y
x
0
Площадь равна произведению
полусуммы оснований
трапеции на высоту.
а
b
x
?
© Комаров Р.А.
8. Вычислите площадь криволинейной трапеции 2-мя способами
1) Используя формулу площадитрапеции из геометрии, получим:
5 3
S
2 8
2
2) Найдите F(x) и вычислите
S по формуле S=F(b)-F(a)
у
3
1
О
2
x
F ( x) 2 x
2
f ( x) x 2
5
1
3
х
F (b) F (3) 10,5
F (a) F (1) 2,5
S 10,5 2,5 8
© Комаров Р.А.
9. Теорема: Если f – непрерывная и неотрицательная на отрезке [a; b] функция, а F – ее первообразная на этом отрезке, то площадь S
соответствующейкриволинейной трапеции равна приращению
первообразной на отрезке [a; b], т.е. S=F(b)-F(a).
Дано: f – функция непрерывная,
неотрицательная на отрезке [a; b]
y
криволинейная трапеция
0
Док-ть: S=F(b)-F(a)
а
b
x
© Комаров Р.А.
10.
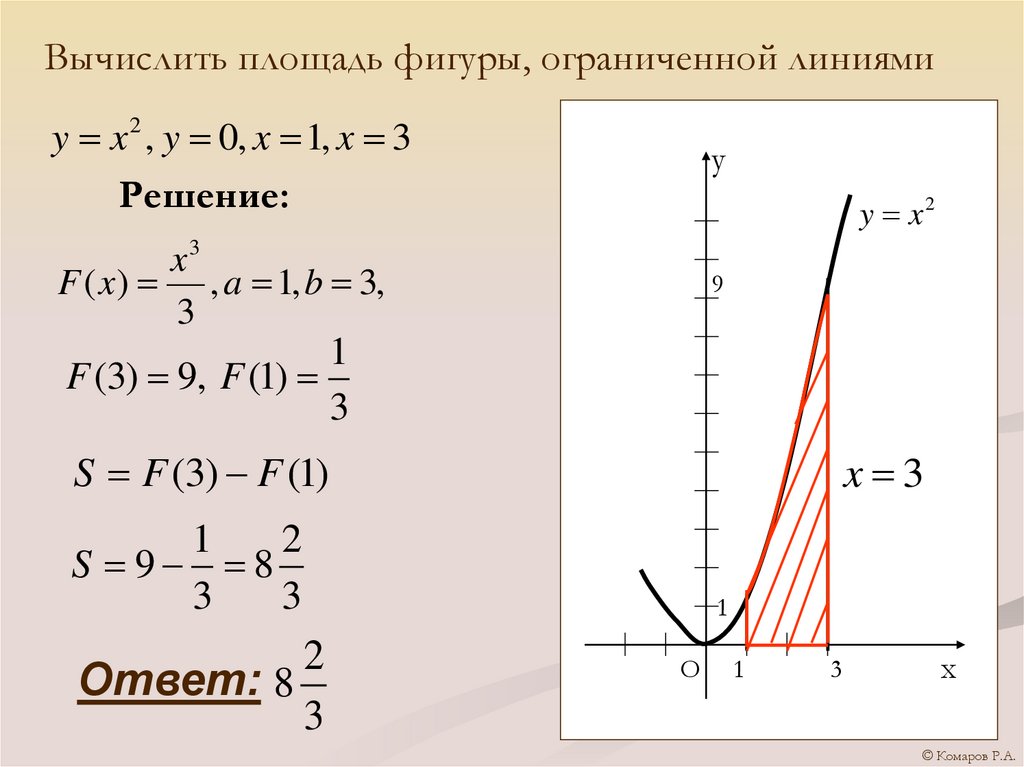
Вычислить площадь фигуры, ограниченной линиямиy x 2 , y 0, x 1, x 3
у
Решение:
y x2
x3
F ( x) , a 1, b 3,
3
9
1
F (3) 9, F (1)
3
x 3
S F (3) F (1)
1
2
S 9 8
3
3
2
Ответ: 8
3
1
О
1
3
х
© Комаров Р.А.
11.
Алгоритм нахождения площадикриволинейной трапеции:
1. Изобразить чертеж и убедится, является ли
данная фигура криволинейной трапецией
2. Найти первообразную F(x)
3. Применить формулу S=F(b)-F(a)
© Комаров Р.А.
12. Формулы для нахождения площади различных фигур
y1. Если криволинейная трапеция
a
b
расположена ниже оси Ох (f(x)<0),
0
то её площадь берут со знаком «-»
x
2. Если фигура ограничена кривыми
F(x)
y=f(x) и y=g(x), прямыми x=a, x=b
y
(при условии f ( x) g ( x) ),
g(x)
то из площади одной фигуры
f(x)
вычитают площадь другой фигуры
0
a
b x
3. При вычислении площади
криволинейной трапеции площадь
y
той части, которая расположена
выше оси Ох, берут со знаком «+», а
S3
той части, которая расположена
S1
x
ниже оси Ох, со знаком «-».
a
S2
b
13.
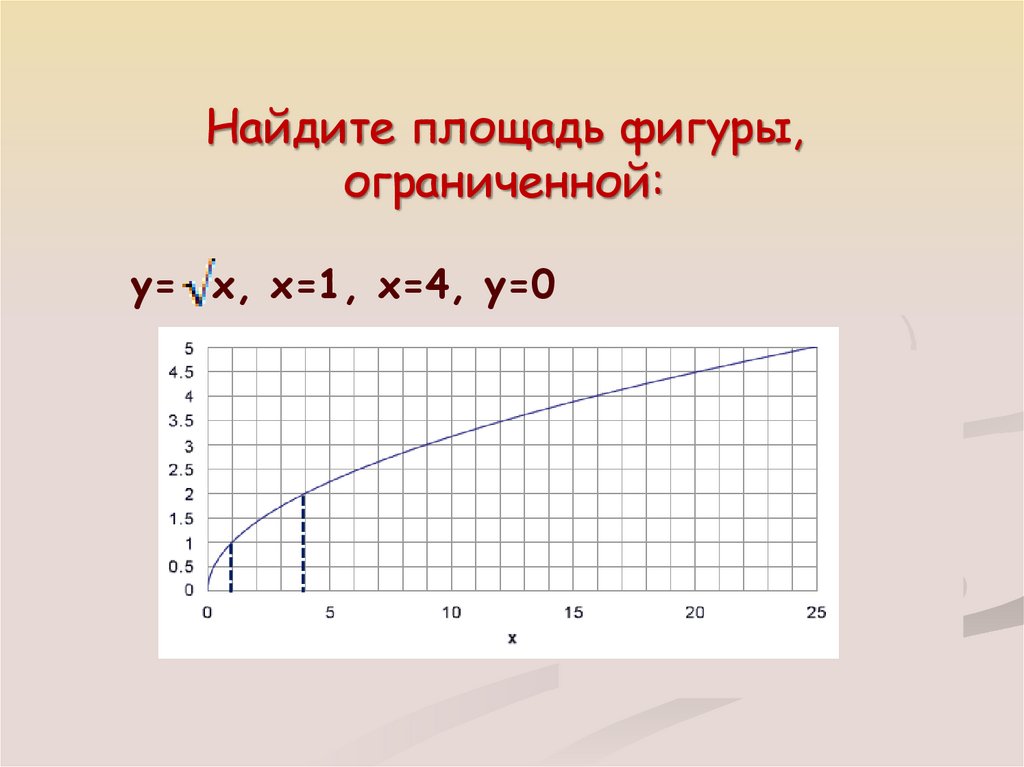
Найдите площадь фигуры,ограниченной:
y= x, x=1, x=4, y=0



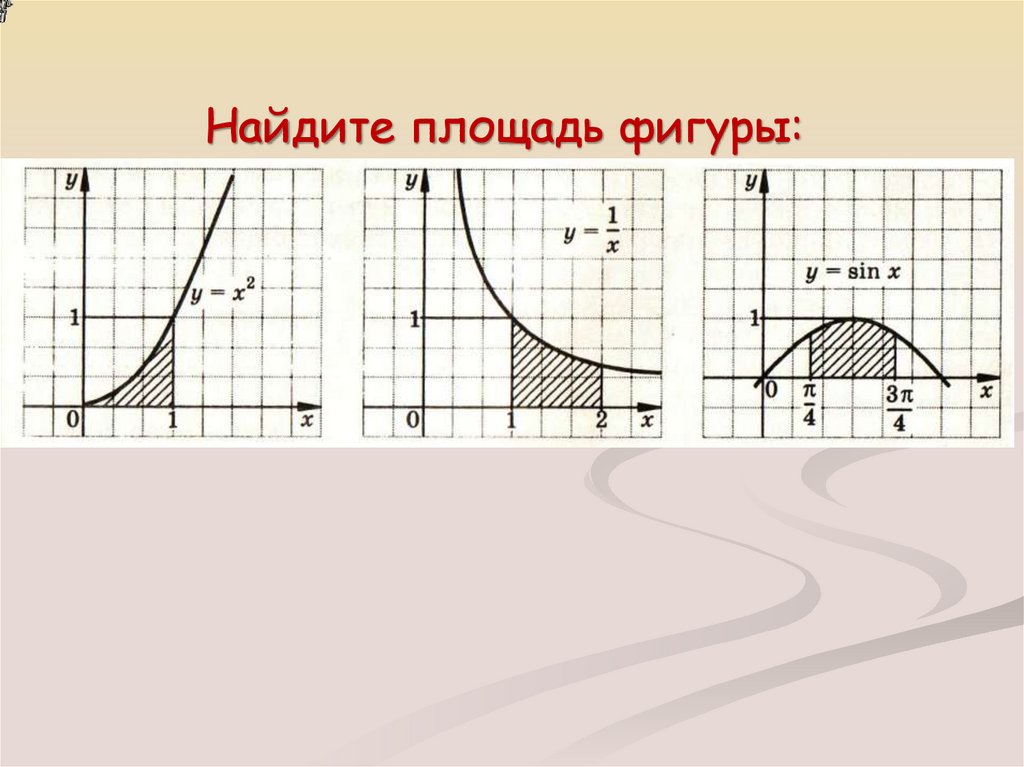
![Определение: фигура, ограниченная графиком непрерывной и не меняющей своего знака на отрезке [a; b] функции, прямыми x=a, x=b и Определение: фигура, ограниченная графиком непрерывной и не меняющей своего знака на отрезке [a; b] функции, прямыми x=a, x=b и](https://cf5.ppt-online.org/files5/slide/w/wkqW6V05LCZNlMGF9ptgsjhHyx4Ua7dm2IBE8r/slide-3.jpg)


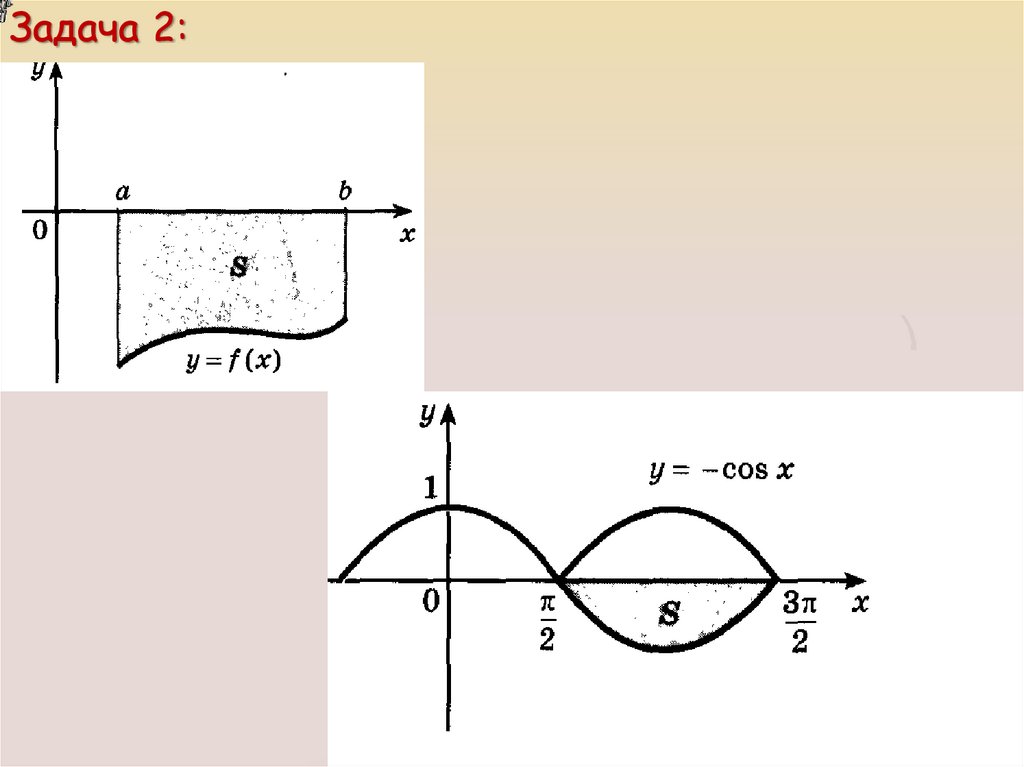
![Теорема: Если f – непрерывная и неотрицательная на отрезке [a; b] функция, а F – ее первообразная на этом отрезке, то площадь S Теорема: Если f – непрерывная и неотрицательная на отрезке [a; b] функция, а F – ее первообразная на этом отрезке, то площадь S](https://cf5.ppt-online.org/files5/slide/w/wkqW6V05LCZNlMGF9ptgsjhHyx4Ua7dm2IBE8r/slide-8.jpg)


 Математика
Математика








