Площадь криволинейной трапеции

1.

Площадь
криволинейной
трапеции
© Комаров Р.А.

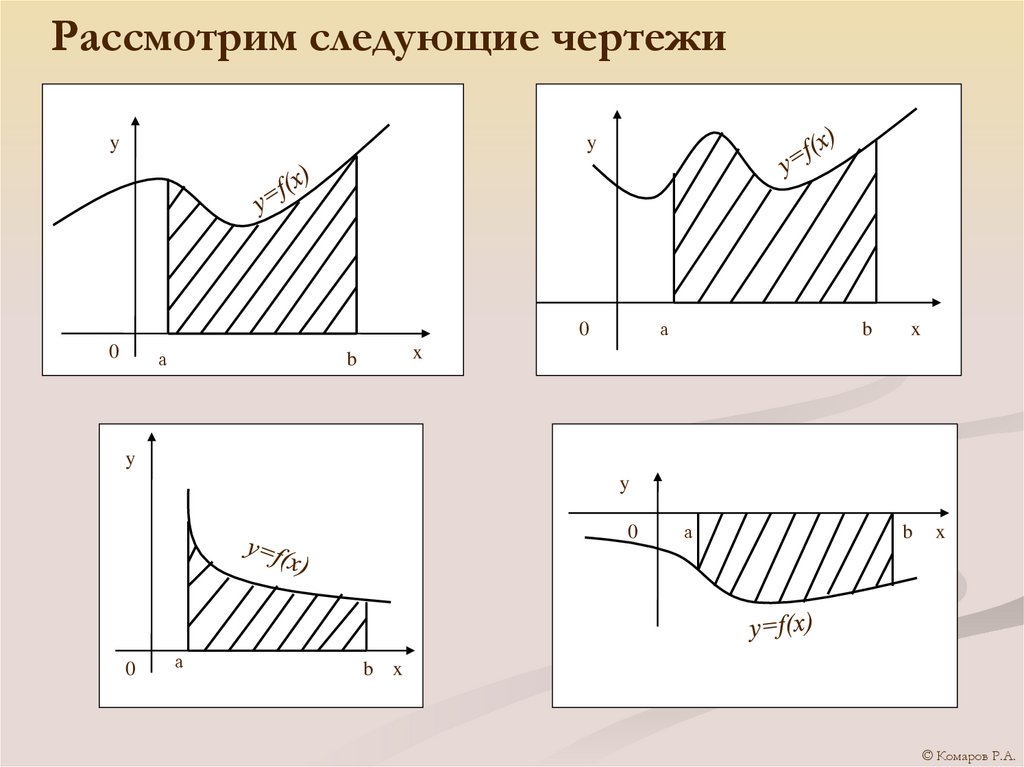
2. Рассмотрим следующие чертежи

y
y
а
0
0
а
b
x
x
b
y
y
0
0
а
а
b
x
b x
© Комаров Р.А.

3. Определение: фигура, ограниченная графиком непрерывной и не меняющей своего знака на отрезке [a; b] функции, прямыми x=a, x=b и

отрезком [a; b]
называется криволинейной трапецией.
© Комаров Р.А.

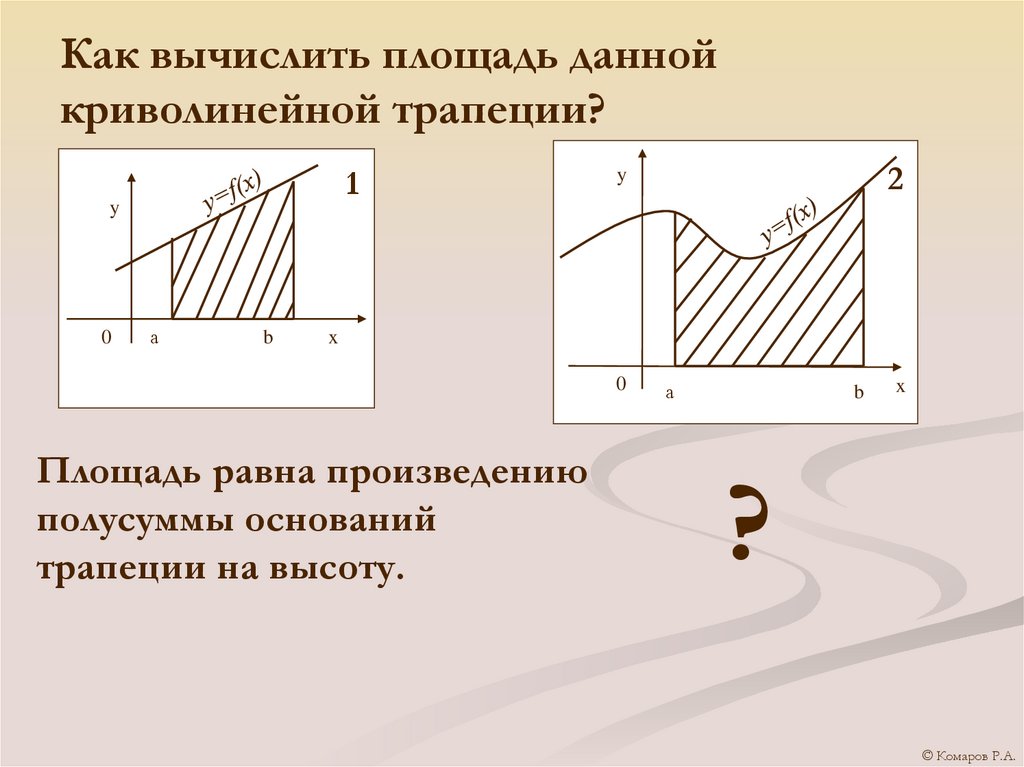
4. Как вычислить площадь данной криволинейной трапеции?

1
y
0
а
b
2
y
x
0
Площадь равна произведению
полусуммы оснований
трапеции на высоту.
а
b
x
?
© Комаров Р.А.

5. Вычислите площадь криволинейной трапеции 2-мя способами

1) Используя формулу площади
трапеции из геометрии, получим:
5 3
S
2 8
2
2) Найдите F(x) и вычислите
S по формуле S=F(b)-F(a)
у
3
1
О
2
x
F ( x) 2 x
2
f ( x) x 2
5
1
3
х
F (b) F (3) 10,5
F (a) F (1) 2,5
S 10,5 2,5 8
© Комаров Р.А.

6.

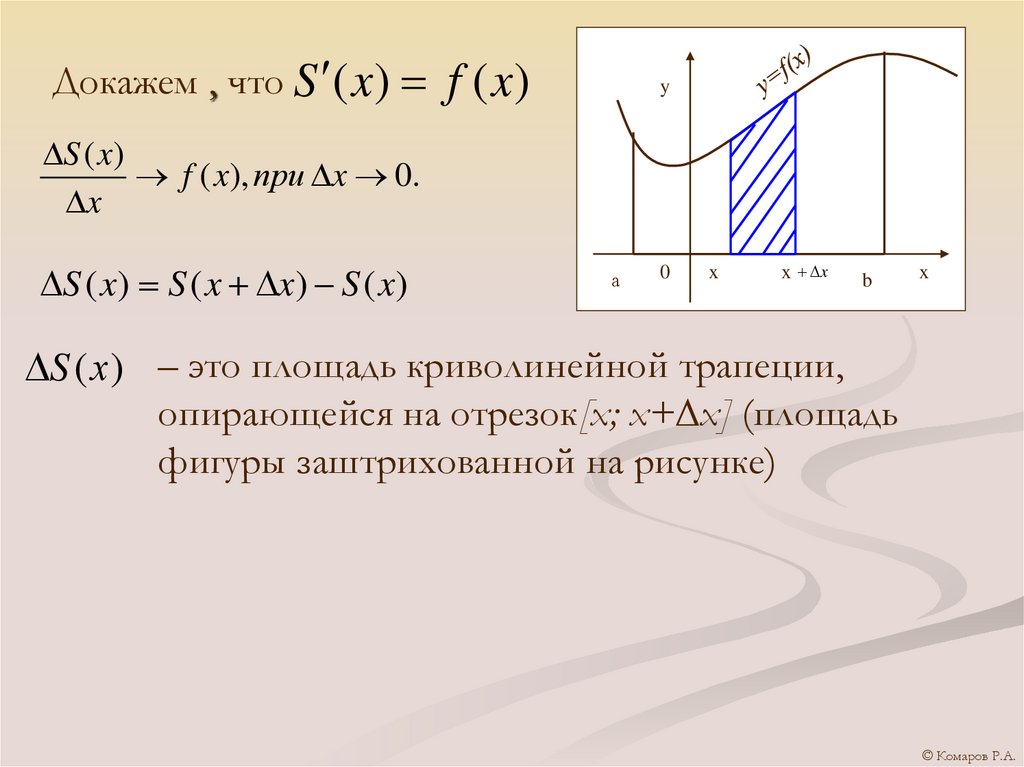
Докажем , что S ( x ) f ( x )
y
S ( x )
f ( x), при x 0.
x
S ( x) S ( x x) S ( x)
а
0
x
x x
b
x
S (х) – это площадь криволинейной трапеции,
опирающейся на отрезок[x; x+∆x] (площадь
фигуры заштрихованной на рисунке)
© Комаров Р.А.

7.

S ( x) F ( х) C Найдем С:
при x b, S S (b), S (b) F (b) C
при x a, S (a ) F (a ) C , но S (a ) 0,
получаем С F (a )
Тогда
S ( x) F ( x) F (a ), поскольку S S (b),
получим S S (b) F (b) F (a )
Таким образом, мы доказали теорему и в
дальнейшем площадь криволинейной трапеции
будем вычислять по формуле
S=F(b)-F(a)
© Комаров Р.А.

8.

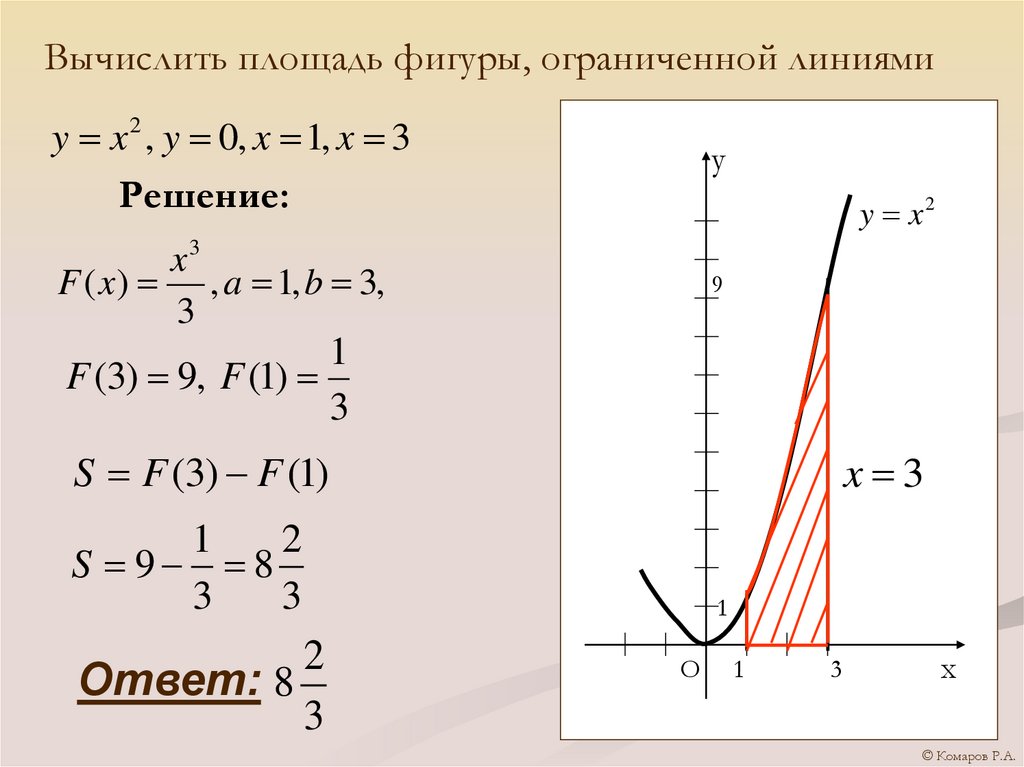
Вычислить площадь фигуры, ограниченной линиями
y x 2 , y 0, x 1, x 3
у
Решение:
y x2
x3
F ( x) , a 1, b 3,
3
9
1
F (3) 9, F (1)
3
x 3
S F (3) F (1)
1
2
S 9 8
3
3
2
Ответ: 8
3
1
О
1
3
х
© Комаров Р.А.

9.

Алгоритм нахождения площади
криволинейной трапеции:
1. Изобразить чертеж и убедится, является ли
данная фигура криволинейной трапецией
2. Найти первообразную F(x)
3. Применить формулу S=F(b)-F(a)
© Комаров Р.А.