1. Линейная алгебра

1. Линейная алгебра

1
Линейная алгебра

2.

1. Определение матрицы. Виды матриц
Матрицей размера m×n называется таблица чисел,
содержащая m строк и n столбцов. Числа, составляющие
матрицу, называются элементами матрицы. Место
каждого элемента однозначно определяется номером
строки и столбца, на пересечении которых он находится.
Элементы матрицы обозначаются aij, где i - номер
строки, а j - номер столбца.
a11
a21
Обозначение: A
...
a m1
a12
a 22
...
am 2
...
...
...
...
a1n
a2 n
или A aij m n .
...
a mn

3.

Матрица может состоять как из одной строки, так и
из одного столбца. Вообще говоря, матрица может
состоять даже из одного элемента.
Матрицу, имеющую только одну строку, называют
матрицей-строкой.
(a11 a12 ... a1n ) - матрица-строка.
Матрицу, имеющую только один столбец, называют
матрицей-столбцом.
a11
a12
... - матрица-столбец.
an1
Будем считать две матрицы равными, если эти
матрицы имеют одинаковые порядки и все их
соответствующие элементы совпадают.

4.

Если число столбцов матрицы равно числу строк (m =
n), то матрица называется квадратной, а число n
называется порядком квадратной матрицы.
a11 a12 a1n
a21 a22 a2 n
(1)
- квадратная матрица.
an1 an 2 ann
В случае квадратной матрицы вводятся понятия
главной и побочной диагоналей.
Главной диагональю матрицы (1) называется
диагональ а11 а12 … ann идущая из левого верхнего угла
этой матрицы в правый нижний ее угол.
Побочной диагональю матрицы (1) называется
диагональ аn1 а(n-1)2 … a1n , идущая из левого нижнего
угла в правый верхний угол.

5.

Если все недиагональные элементы квадратной матрицы
равны нулю, то матрица называется диагональной:
a11 0 ... 0
0 a22 ... 0
... ... ... 0 .
0 ... ann
0
Квадратная матрица называется скалярной, если на
главной диагонали стоит одно и то же число k, а все
элементы вне этой диагонали равны нулю:
k 0 ... 0
0 k ... 0
... ... ... 0
0 0 ... k

6.

Если у диагональной матрицы n-го порядка все
диагональные элементы равны единице, то матрица
называется единичной матрицей n-го порядка и
обозначается буквой Е:
1 0 ... 0
0 1 ... 0
Е=
.
... ... ... ...
0 0 ... 1
Матрица любого размера называется нулевой, или нульматрицей, если все её элементы равны нулю:
0 0 ... 0
0 0 ... 0
O
.
... ... ... ...
0 0 ... 0

7.

2.Операции над матрицами
Сложение и вычитание матриц определены только для
матриц одинакового размера.
Пусть A aij m n и B bij m n .
Суммой (разностью) матриц А и В является матрица
C cij m n (С = А ± В), элементами которой являются
соответственно сумма (разность) элементов исходных
матриц, т.е. cij aij bij , i 1, m, j 1, n.
1 2
2 3
Пример 1. Найти А+В, если A
и B
.
4 3
4 5
1 2 2 3 1 2 2 3 3 5
A B
.
4 3 4 5 4 4 3 5 8 8

8.

Операция умножения (деления) матрицы любого
размера на произвольное число сводится к умножению
(делению) каждого элемента матрицы на это число:
a11
a 21
A
...
a m1
a12
a 22
...
a m 2
... a1n
... a 2 n
.
...
...
... a mn
1
Пример 2. Найти 5*А, если A
3
1
5 A 5
3
2
.
4
2 5 1 5 2 5 10
.
4 5 3 5 4 15 20

9.

Произведение двух матриц определено, когда число
столбцов первой матрицы равно числу строк второй.
Пусть A aij m k и B bij k n .
Произведением матриц А и В называется матрица C cij m n
(С=АВ), элементы которой
cij ai1b1 j ai 2 b2 j ... aik bkj , i 1, m, j 1, n.
4 6
2 3 1
Пример 3. Найти АВ, если A
и B 5 4 .
3 2 1
6 5
4 6
2 3 1
A B
5 4
3 2 1
6 5
2 4 3 5 1 6 2 6 3 4 1 5 29 29
.
3 4 2 5 1 6 3 6 2 4 1 5 28 31

10.

10
Пример.

11.

Свойства матричных операций
1) А+В=В+А (коммутативный закон)
2) (А+В)+С=А+(В+С) (ассоциативный закон)
3) А+О=О+А=А
(закон поглощения нуля)
4) 1А=А1=А
5) 0А=А0=О; λО=Оλ=О
6) λ(μА)=(λμ)А (ассоциативность)
7) (λ+μ)А=λА+μА (дистрибутивность относительно сложения чисел)
8) λ(А+В)=λА+λВ (дистрибутивность относительно сложения матриц)
9) λ(АВ)=(λА)В

12.

Свойства матричных операций
10)
(А+В)С=АС+ВС (дистрибутивность)
11)
А(В+С)=АВ+АС
12)
А(ВС)=(АВ)С =АВС (ассоциативность)
13)
АЕ=ЕА=А
(дистрибутивность)
14)
Если произведение АВ существует, то ВА может и не
существовать.
15)
Если даже АВ и ВА существуют, то они могут быть
матрицами разных размеров.
16)
В случае, когда АВ и ВА существуют и оба – матрицы
одинакового размера, вообще говоря, АВ ВА.
17)
Из того, что АВ=0, не следует, что А=0, или В=0.

13.

Транспонирование матрицы
a11 a12 ... a1n
a21 a22 ... a2 n
Рассмотрим матрицу A
.
... ... ... ...
as1 as 2 ... asn
Транспонированной матрицей к матрице А называется
T
матрица A , получающаяся из А заменой строк столбцами:
a11 a 21 ... a s1
a12 a 22 ... a s 2
T
A
... ... ... ...
.
a
1n a 2 n ... a sn

14.

Пример 4.
Найти
транспонированную
2 3 1
относительно матрицы A
.
3 2 1
2 3
T
A 3 2 .
1 1
матрицу

15.

Свойства операции транспонирования
1)
(АТ)Т = А
2)
(λА)Т = λАТ
Т
Т
Т
3)
(А+В) = А +В
4)
(АВ)Т = ВТАТ

16.

Определитель квадратной матрицы
Пусть А – квадратная матрица порядка п с числовыми
элементами:
a11
a21
A
...
an1
a12
a22
...
an 2
... a1n
... a2 n
.
... ...
... ann
Определитель (детерминант) квадратной матрицы А – это
число, которое ставится в соответствие матрице и вычисляется
по ее элементам согласно определённому правилу.
Определитель матрицы А обозначается как:
det(A), |А| или Δ(A).

17.

Определителем матрицы A (a11 ) порядка n 1 называется
единственный элемент этой матрицы:
det A | a11 | a11 .
Определитель 2-го порядка можно вычислить по формуле:
a11
| A |
a21
a12
a11a22 a12 a21.
a22
1 2
Пример 1. Пусть A
, тогда
3 4
1 2
det A A
1 4 2 3 4 6 2 .
3 4

18.

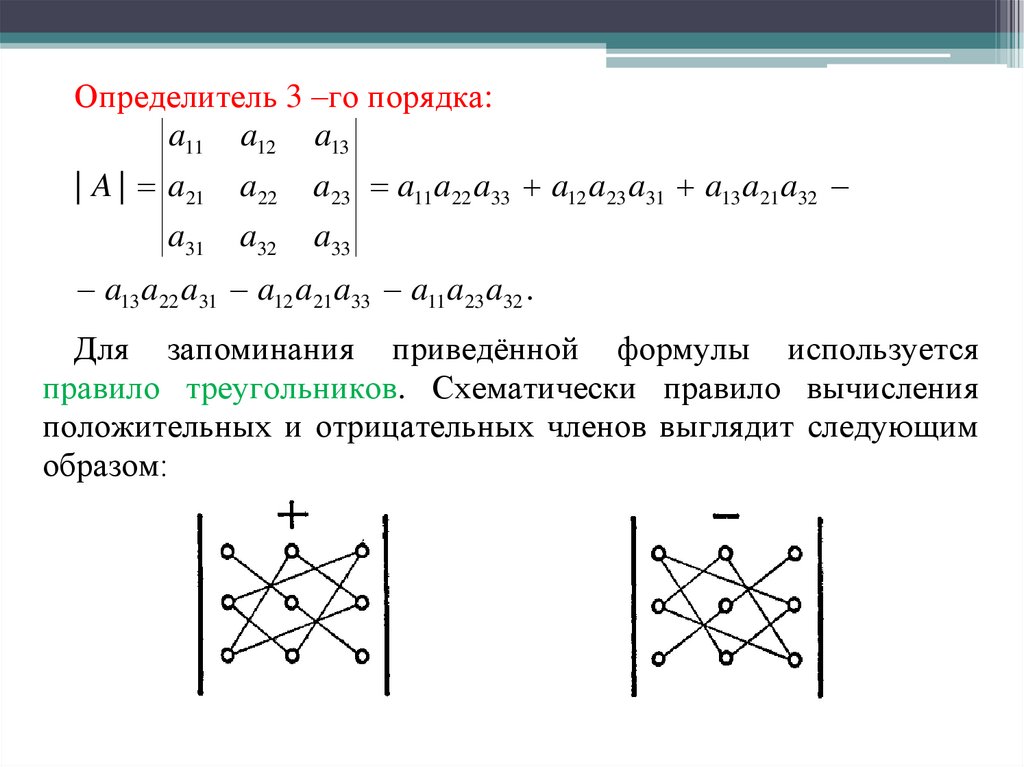
Определитель 3 –го порядка:
a11 a12 a13
| A | a21 a22 a23 a11a22 a33 a12 a23 a31 a13 a21a32
a31 a32 a33
a13 a22 a31 a12 a21a33 a11a23 a32 .
Для запоминания приведённой формулы используется
правило треугольников. Схематически правило вычисления
положительных и отрицательных членов выглядит следующим
образом:

19.

Можно также воспользоваться правилом Саррюса:
к матрице приписать справа первый и второй столбцы,
вычислить произведения элементов, стоящих на каждой из
указанных шести прямых, а затем найти алгебраическую сумму
этих произведений, при этом произведение элементов на
прямых, параллельных главной диагонали, берутся со знаком
плюс, а произведение элементов на прямых, параллельных
побочной диагонали – со знаком минус:

20.

Пример 2.
2 3 1
Найти A , если A 2 4 3 .
1 2 3
2 3 1
det A A 2 4 3 2 4 3 3 3 1 1 2 2 1 4 1 2 3 2 3 2 3
1 2 3
24 9 4 4 12 18 3.

21.

Свойства определителей
Свойство 1. Определитель
транспонировании.
не
меняется
при
Замечание. Из свойства 1 вытекает, что всякое утверждение
о строках определителя справедливо и для его столбцов и
обратно, т.е. что в определителе строки и столбцы равноправны.
Свойство 2. Если одна из строк определителя состоит из
нулей, то определитель равен нулю.
Свойство 3. Если в определителе поменять две какие-либо
строки местами, то определитель лишь изменит знак на
противоположный.

22.

Свойство 4. Определитель, содержащий две одинаковые
стоки, равен нулю.
Свойство 5. Если все элементы некоторой строки
определителя умножить на некоторое число k, сам определитель
умножится на k. Отсюда следует, что если все элементы какойнибудь строки определителя имеют общий множитель, то его
можно вынести за знак определителя.
Свойство 6. Определитель,
содержащий
пропорциональные строки, равен нулю.
две

23.

Свойство 7. Если все элементы i-ой строки определителя nго порядка представлены в виде суммы двух слагаемых
aij b j c j , j 1,..., n , то определитель равен сумме двух
определителей, у которых все строки, кроме i-ой – такие же, как
и в заданном определителе, а i-ая строка в одном из слагаемых
состоит из элементов b j , а в другом – из элементов c j .
Свойство 8. Если одна из строк определителя есть
линейная комбинация его других строк, то определитель равен
нулю.
Свойство 9. Определитель не меняется, если к элементам
одной из его строк прибавляются соответственные элементы
другой строки, умноженные на одно и то же число.

24.

Миноры и алгебраические дополнения
a11
a 21
A
...
Пусть
a
n1
a12
a 22
...
an2
... a1n
... a 2 n
... ...
квадратная матрица n-го порядка.
... a nn
Минором Mij элемента aij
определителя n-го порядка
называется определитель (n-1)-го порядка, получающийся после
вычеркивания из определителя n-го порядка i-ой строки и j-го
столбца.
Алгебраическим дополнением Aij элемента aij определителя nго порядка называется минор Mij элемента aij , взятый со знаком
(-1)i+j:
Aij ( 1)
i j
M ij .

25.

Пример 3.
2 3 1
Пусть. A 2 4 3
1 2 3
2 3 1
A 2 4 3
1 2 3
Тогда минор M 23 элемента a23 :
2 3
M 23
4 3 1.
1 2
Алгебраическое дополнение элемента a23 :
3
2 3
52
A23 ( 1) M 23 ( 1)
(4 3) 1.
1 2

26.

Теорема о разложении определителя
по строке (столбцу)
Определитель n-го порядка d равен сумме произведений
всех элементов произвольной его строки (столбца) на их
алгебраические дополнения.
Т. е. имеет место следующее разложение определителя d по
i-ой строке:
d ai1 Ai1 ai 2 Ai 2 ... ain Ain .
Аналогичное разложение определителя можно получить по
любому его столбцу.

27.

1
1
Пример 4. Вычислить определитель
0
1
2
3
1
1
0
0
2
1
1
2
.
3
0
Разложим определитель по первой строке:
a11 A11 a12 A12 a13 A13 a14 A14 =
3 0 2
1 0 2
1 3 2
1 ( 1)1 1 1 2 3 2 ( 1)1 2 0 2 3 0 ( 1)1 3 0 1 3
1 1 0
1 1 0
1 1 0
1 3 0
1 ( 1)1 4 0 1 2 (0 0 2 4 0 9) 2 (0 0 0 4 0 3)
1 1 1
0 (1 6 0 0 0 2) 11 2 ( 7) 5 11 14 5 2.

28.

Определитель, у которого все элементы, находящиеся выше
или ниже главной диагонали, равны нулю, называется
определителем треугольного вида.
Используя свойства определителей всякий определитель п-го
порядка можно привести к треугольному виду.
Теорема. Если все элементы определителя, расположенные
по одну сторону от главной диагонали равны нулю, то этот
определитель равен произведению элементов, стоящих на
главной диагонали.
a11 a12 ... a1n
0 a 22 ... a 2n
0
0
...
a
nn
верхняя треугольная матрица
a11 0 ... 0
a 21 a 22 ... 0
a
a
...
a
n1
n2
nn
нижняя треугольная матрица

29.

Обратная матрица и её свойства
Квадратная матрица называется вырожденной (или
особенной), если её определитель равен нулю, и
невырожденной (или неособенной) – в противоположном
случае, т.е.
det A 0
Обратной матрицей к квадратной матрице А называется
-1
-1
-1
такая матрица А , что А А=АА = Е.

30.

Теорема. Квадратная матрица А n-го порядка имеет
обратную матрицу А-1 , причем единственную, тогда и
только тогда, когда матрица А невырожденная.
В этом случае обратная матрица
следующей формуле:
A11
1 A12
1
A
det A ...
A1n
A21
A22
...
A2 n
вычисляется по
... An1
... An 2
,
... ...
... Ann
где Аij – алгебраическое дополнение элемента aij матрицы
А.

31.

31
A
1
П
det A
Для составления матрицы П следует заменить
элементы матрицы соответствующими
алгебраическими дополнениями и
транспонировать полученную матрицу.
A11
A12
П
A
1n
A21 ... An1
A22 ... An 2
A2n ... Ann

32.

Для невырожденных матриц выполняются следующие
свойства:
1.
(А-1)-1 = А
2.
(АВ)-1 = В-1А-1
3.
(А-1)Т = (АТ)-1
4.
det(A-1) = (detA)-1.

33.

33
Пример.

34.

Матричные уравнения
1) Рассмотрим матричное уравнение
A X B ,
(1)
где A – квадратная невырожденная (det A ≠ 0) матрица
порядка n, B – матрица размера n × m и X – неизвестная матрица.
Умножим обе части уравнения слева на матрицу A−1:
A 1 ( A X ) A 1 B .
Ввиду ассоциативности умножения матриц, имеем:
( A 1 A) X A 1 B E X A 1 B X A 1 B
Таким образом, искомое решение матричного уравнения (1)
определяется формулой
X A 1 B .

35.

2) Рассмотрим матричное уравнение
Y A B,
(2)
где A – квадратная невырожденная (det A ≠ 0) матрица
порядка n, B – матрица размера m × n и Y – неизвестная
матрица.
Умножим обе части уравнения справа на матрицу A−1 . По
определению обратной матрицы и используя свойство
ассоциативности умножения матриц, получим:
(Y A) A 1 B Y 1 Y ( A A 1 ) B Y 1
Y E B Y 1 Y B Y 1
Таким образом, искомое решение матричного уравнения (2):
Y B Y 1 .

36.

Системы линейных алгебраических
уравнений (СЛАУ) и их решения
Пусть дана система из т линейных уравнений с n неизвестными:
a11 x1 a12 x2 .. a1n xn b1
a x a x .. a x b
21 1
22 2
2n n
2
(*)
..........................................
am1 x1 am 2 x2 .. amn xn bm
Здесь x1 , x 2 , ..., x n – неизвестные, a11, a12 , ...,a mn – коэффициенты
системы и b1 , b2 , ...,bm – свободные члены (предполагаются
известными). Индексы коэффициентов a ij системы обозначают
номера уравнения i и неизвестного j, при котором стоит этот
коэффициент, соответственно.

37.

Решением системы (*) называется упорядоченная система
( 1 , 2 ,..., n ) из n чисел, удовлетворяющих этой системе.
Эти числа при подстановке на место соответствующих
переменных обращают все уравнения системы в числовые
равенства.
Если система имеет хотя бы одно решение, то она
называется совместной. Если не имеет ни одного решения, то
она называется несовместной.
Совместная система называется определенной, если система
имеет одно решение. Если совместная система имеет больше
одного решения, то она называется неопределенной.

38.

Однородная система линейных
уравнений
Система линейных алгебраических уравнений, у которой
все свободные члены равны нулю, называется однородной
системой:
a11 x1 a12 x2 .. a1n xn 0
a x a x .. a x 0
21 1
22 2
2n n
.
..........................................
a s1 x1 a s 2 x2 .. a sn xn 0
Эта система всегда совместна, т.к. x1 x2 ... xn 0
является (нулевым) решением.

39.

Метод Крамера для решения СЛАУ
При определенных условиях решить систему можно с
помощью правила Крамера.
Теорема.
Пусть дана система
a11 x1 a12 x2 .. a1n xn b1
a x a x .. a x b
21 1
22 2
2n n
2
.
..........................................
an1 x1 an 2 x2 .. ann xn bn

40.

Если
a11
определитель
a12 ... a1n
матрицы
системы
a21 a22 ... a2 n
0 , то система имеет одно
... ... ... ...
an1 an 2 ... ann
единственное решение, определяемое следующими
формулами (формулами Крамера):
xj
x j
, j 1,..., n , где - определитель матрицы
системы, а x j - определитель матрицы, полученной из
заменой j-го столбца столбцом свободных членов.

41.

Пример 1. Решить систему с помощью формул
Крамера:
x1 x2 x3 1
x1 2 x2 x3 2 .
3x x x 3
1 2 3
Выпишем определитель матрицы коэффициентов
системы:
1 1 1
1 2 1 2 1 3 6 1 1 2 0 , следовательно,
3 1 1
система имеет одно единственное решение, которое
можно найти по формулам Крамера.

42.

Имеем:
1 1 1
x1 2 2 1 2 2 3 6 2 1 2 ;
3 1 1
1 1 1
x2 1 2 1 2 3 3 6 3 1 2 ;
3 3 1
1 1 1
x3 1 2 2 6 6 1 6 2 3 2 .
3 1 3
Тогда,
x3
x1
x3
2
1.
2
x1 2
1,
2
x2
x2 2
1,
2

43.

Если, при решении системы линейных уравнений с помощью
правила Крамера, мы приходим к тому, что определитель
системы равен нулю, буквально правило Крамера применить
нельзя. Однако можно точно сказать о совместности системы.
При выводе правила Крамера мы переходим от данных
уравнений к уравнениям:
x1 x1 , x2 x2 , ……...., xn xn ,
являющимся их следствиями.
Отсюда видно, что если ∆ = 0, а хотя бы один из
определителей x1 , x 2 ,…, x n не равен нулю, то данная система
уравнений несовместна (противоречива) и если все
определители x1 , x 2 ,…, x n равны нулю, то система
неопределенна, т.е. имеет множество решений.

44.

Пример 2.
Решить систему уравнений:
2 x y 3z 9
3x 5 y z 4 .
4x 7 y z 5
Здесь мы имеем тот особый случай, когда определитель
системы равен нулю:
2 1 3
∆ = 3 5 1 = 2∙(–5)∙1 + (–7)∙3∙3 + 1∙(–1) ∙4 –
4 7 1
– 4∙(–5)∙3 – 3∙(–1) ∙1 – (–7)∙1∙2 = –10 – 63 – 4 + 60 + 3 + 14 = 0.

45.

Поэтому правило Крамера применить нельзя. Однако,
подсчитав определитель x1:
9 1 3
x1 = 4 5 1 = 9∙(–5) ∙1 + (–7) ∙(–4) ∙3 + (–1) ∙1∙5 –
5 7 1
– 3∙(–5) ∙5 – (–4) ∙(–1) ∙1 – (–7) ∙1∙9 = –45 + 84 – 5+75–4+63 = –
168,
видим, что он отличен от нуля. Откуда сразу можно
заключить, что система несовместна.

46.

Матричный метод решения СЛАУ
Матричный метод также применим к решению
систем уравнений, где число уравнений равно числу
неизвестных.
Пусть дана система уравнений:
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1
22 2
2n n
2
...............................................
an1 x1 an 2 x2 ... ann xn bn

47.

Составим матрицы:
a11
a21
A=
...
an1
a12
a22
...
an 2
... a1n
... a2 n
;
... ...
... ann
x1
x2
X = ;
...
xn
b1
b2
B = .
...
bn
Систему уравнений можно записать в виде
матричного уравнения:
A X = B.
Решая его, получим: A-1 A X = A-1 B, т.к. А-1 А = Е,
то Е Х = А-1 В и
Х = А-1 В.

48.

Пример 3.
Решить систему матричным способом:
x1 x2 2 x3 5,
2 x1 x2 2 x3 3,
4 x x 4 x 9.
1
2
3
Выпишем матрицы:
1 1 2
x1
5
A 2 1 2 , X x2 , B 3 .
4 1 4
x
9
3
Решение системы запишется в виде X A 1 B .

49.

6 2 4
1
1
Имеем, A 0 4 2 , тогда
6
6
3
3
6 2 4 5
30 6 36
1
1
1
X A B 0 4 2 3 12 18
6
9 6 30 9 27
6
3
3
0 0
1
6 1 , откуда x1 0 , x2 1, x3 2 .
6
12 2

50.

Эквивалентные системы
Пусть даны системы:
a11 x1 a12 x 2 .. a1n x n b1
a x a x .. a x b
21 1
22 2
2n n
2
..........................................
a s1 x1 a s 2 x 2 .. a sn x n bs
a'11 x1 a'12 x2 .. a'1n xn b'1
a' x a' x .. a' x b'
21 1
22 2
2n n
2
..........................................
и
a' s1 x1 a' s 2 x2 .. a' sn x n b' s
(1)
(2)
Две системы (1) и (2) с одинаковым количеством
переменных называются эквивалентными (равносильными),
если обе системы несовместны или обе совместны и обладают
одними и теми же решениями.

51.

Элементарные преобразования
систем
1. Перемена мест двух уравнений в системе;
2. Умножение обеих частей уравнения на число, отличное от 0;
3. Прибавление к частям какого-нибудь уравнения
соответствующих частей другого уравнения, предварительно
умноженных на какое-нибудь число;
4. Выбрасывание уравнения вида 0=0;
5. Перемена мест двух слагаемых во всех уравнениях системы.
Теорема. При элементарных преобразованиях система
приводится к эквивалентной системе.

52.

Ступенчатая система
Система называется ступенчатой, если каждое
уравнение имеет хотя бы 1 отличный от 0 коэффициент
или свободный член и, начиная со 2-го уравнения, 1-ое
отличное от 0 слагаемое расположено правее 1-го
отличного от 0 слагаемого предыдущего уравнения:
a11 x1 a12 x2 ............ a1n xn b1 ,
a22 x2 ........... a2 n xn b2 ,
..................................
a ss xs ... a sn xn bs
Теорема. Всякая система линейных уравнений при
помощи элементарных преобразований приводится к
равносильной ступенчатой системе.

53.

Метод Гаусса для решения СЛАУ
Метод Гаусса может быть применен к системам
линейных уравнений с произвольным числом уравнений и
неизвестных.
Суть метода заключается в последовательном
исключении неизвестных, когда с помощью элементарных
преобразований система уравнений приводится к
равносильной системе ступенчатого (или треугольного)
вида, из которой последовательно, начиная с последних (по
номеру)
переменных,
находятся
все
остальные
переменные.

54.

Рассмотрим систему линейных уравнений:
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
21 1
22 2
2n n
2
...............................................
am1 x1 am 2 x2 ... amn xn bm
(*)
Разделим обе части 1–го уравнения на a11 0, затем:
1) умножим на а21 и вычтем из второго уравнения;
2) умножим на а31 и вычтем из третьего уравнения и т.д.

55.

Получим:
x1 d12 x2 ... d1n xn d1
d x d x ... d x d
22 2
23 3
2n n
2
,
..............................................
d m 2 x2 d m3 ... d mn xn d m
где d1j = a1j /a11, j = 2, 3, …,n+1;
dij = aij – ai1d1j , i = 2, 3, … , n;
j = 2, 3, … , n+1.
Далее повторяем эти же действия для второго уравнения
системы, потом – для третьего и т.д., пока не получим
равносильную систему ступенчатого (или треугольного) вида.

56.

При этом система будет несовместной, если в процессе
преобразований мы получим уравнение, в котором
коэффициенты при всех неизвестных равны нулю, а
свободный член отличен от нуля, в противном случае
система будет совместной.
Совместная система уравнений будет определённой,
если она приводится к треугольному виду, и
неопределённой, если приводится к трапецоидальному
виду, в котором число уравнений меньше числа
неизвестных.

57.

Пример. Решить систему линейных уравнений методом
Гаусса:
2 x1 x2 x3 5
x1 2 x2 3x3 3
7 x x x 10 .
1
2
3
Решение. Составим расширенную матрицу системы:
2 1 1 5
A = 1 2 3 3
7 1 1 10
и приведём её к ступенчатому виду.

58.

Для этого поменяем местами первую и вторую строки, затем
от второй строки вычтем первую, умноженную на 2, а от
третьей строки вычтем первую, умноженную на 7. В
полученной матрице от третьей строки отнимем вторую,
умноженную на 3. Получим:
2 1 1 5 1 2 3 3
A = 1 2 3 3 ~ 2 1 1 5 ~
7 1 1 10 7 1 1 10
3
3 1 2 3 3
1 2
~ 0 5
7 11 ~ 0 5 7 11
0 15 22 31 0 0 1 2 .

59.

Таким образом,
представлена в виде:
исходная
система
x1 2 x2 3x3 3
5 x2 7 x3 11
,
x 2
3
откуда получаем: x3 = 2, x2 = 5, x1 = 1.
может
быть