Мех. колебания (2) (1)

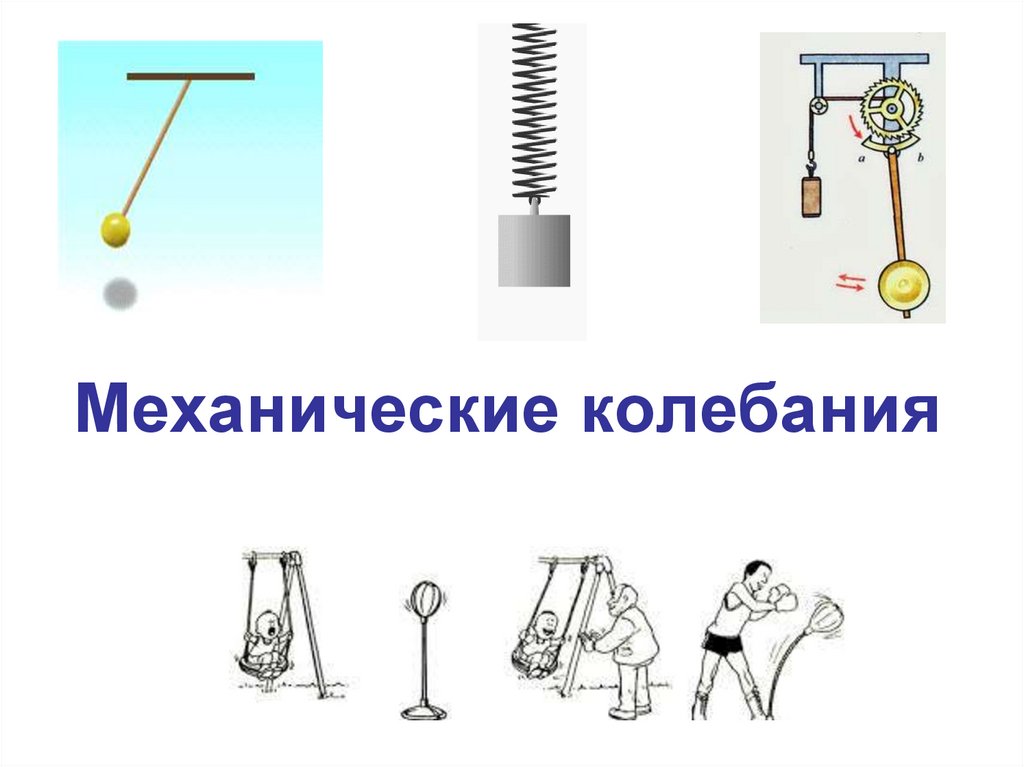
1. Механические колебания

2.

Колебания – это движения или процессы, которые
характеризуются определенной повторяемостью во
времени.
Механические колебания – движения, которые
периодически или почти периодически повторяются
через определенные интервалы времени.

3. Свободные колебания

В природе, и особенно в технике, чрезвычайно большую роль
играют тела и устройства, которые сами по себе способны
совершать периодические движения. «Сами по себе» —
это значит: не будучи принуждаемы к этому действием
периодических внешних сил. Такие колебания называют
поэтому свободными колебаниями в отличие
отвынужденных, протекающих под действием
периодически меняющихся внешних сил.
Свободные колебания – колебания, происходящие в
системе только под действием внутренних сил системы.

4.

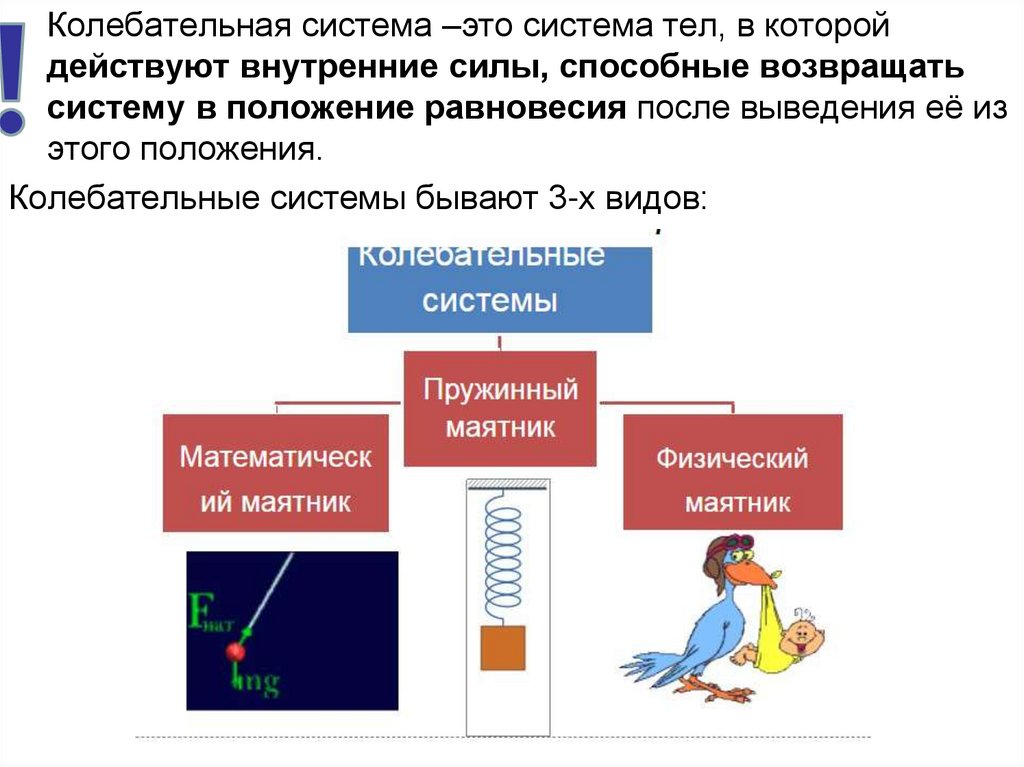
Колебательная система –это система тел, в которой
действуют внутренние силы, способные возвращать
систему в положение равновесия после выведения её из
этого положения.
Колебательные системы бывают 3-х видов:

5. Пружинный маятник

Пружинный маятник представляет собой небольшой грузик,
который соединён с пружиной и может совершать колебания
из стороны в сторону:
Колебания происходят под действием внутренней силы
системы – силы упругости деформированной пружины,
которая стремиться вернуть систему в положение
равновесия. Но грузик каждый раз проходит это положение по
инерции и отклоняется в другую сторону от положения
равновесия.

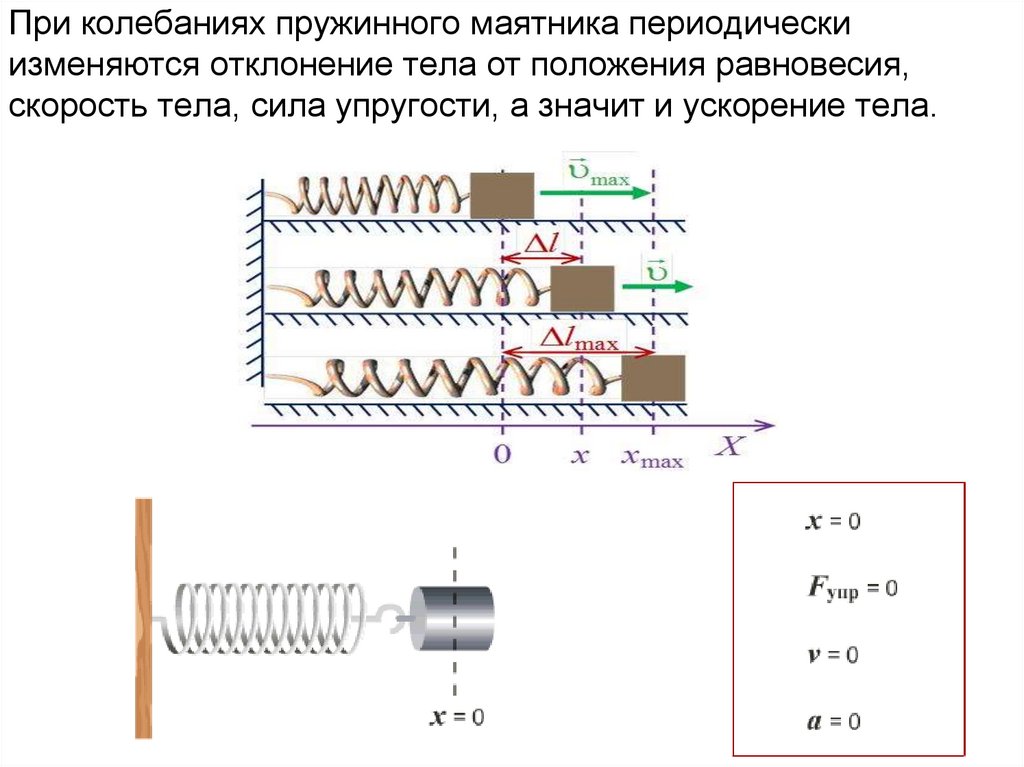
6. При колебаниях пружинного маятника периодически изменяются отклонение тела от положения равновесия, скорость тела, сила

упругости, а значит и ускорение тела.

7. Математический маятник

Математическим маятником называют тело
небольших размеров, подвешенное на тонкой
нерастяжимой нити, масса которой пренебрежимо мала по
сравнению с массой тела.
В положении равновесия, когда
маятник висит по отвесу, сила
тяжести тела уравновешивается
силой натяжения нити.
При отклонении маятника от
положения равновесия на угол
появляется равнодействующая
этих сил, отличная от нуля.
Именно она стремится вернуть
маятник в положение равновесия.

8.

Физические величины,
характеризующие механические
колебания
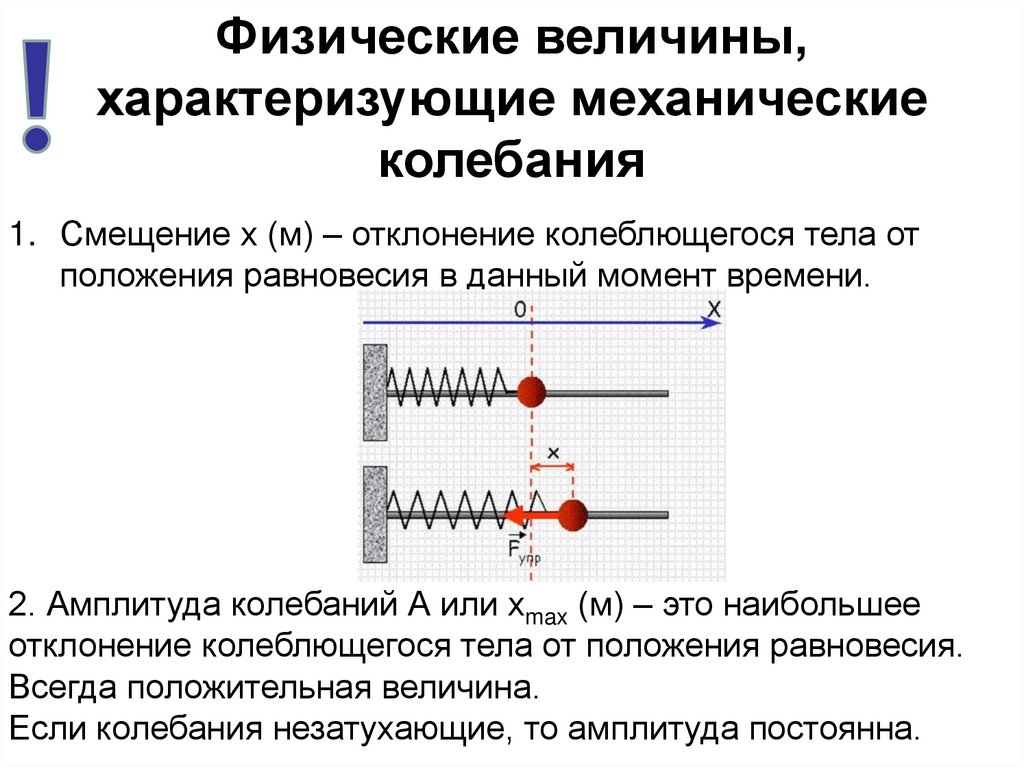
1. Смещение х (м) – отклонение колеблющегося тела от
положения равновесия в данный момент времени.
2. Амплитуда колебаний А или хmax (м) – это наибольшее
отклонение колеблющегося тела от положения равновесия.
Всегда положительная величина.
Если колебания незатухающие, то амплитуда постоянна.

9.

Колебания называются периодическими, если значения
физических величин, изменяющихся в процессе
колебаний, повторяются через равные промежутки
времени. (В противном случае колебания называются
апериодическими).
Период Т (с) – промежуток времени, в течение которого
совершается 1 полное колебание.
Частота ν (Гц или с -1) – число полных колебаний,
совершённых телом за 1с.

10.

Циклическая частота ω (1 рад/с) - число полных колебаний,
совершённых за 2π секунд.
=
Фаза колебаний φ (рад) - физическая величина,
определяющая смещение x в данный момент времени.

11.

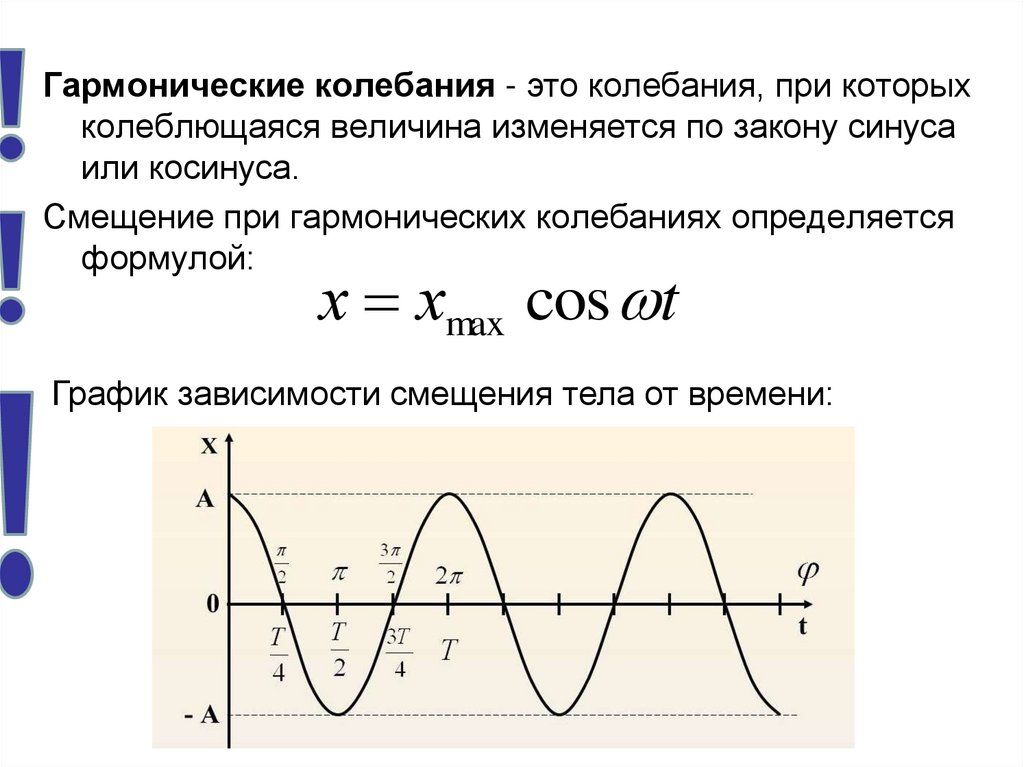
Гармонические колебания - это колебания, при которых
колеблющаяся величина изменяется по закону синуса
или косинуса.
Смещение при гармонических колебаниях определяется
формулой:
х хmax cos t
График зависимости смещения тела от времени:

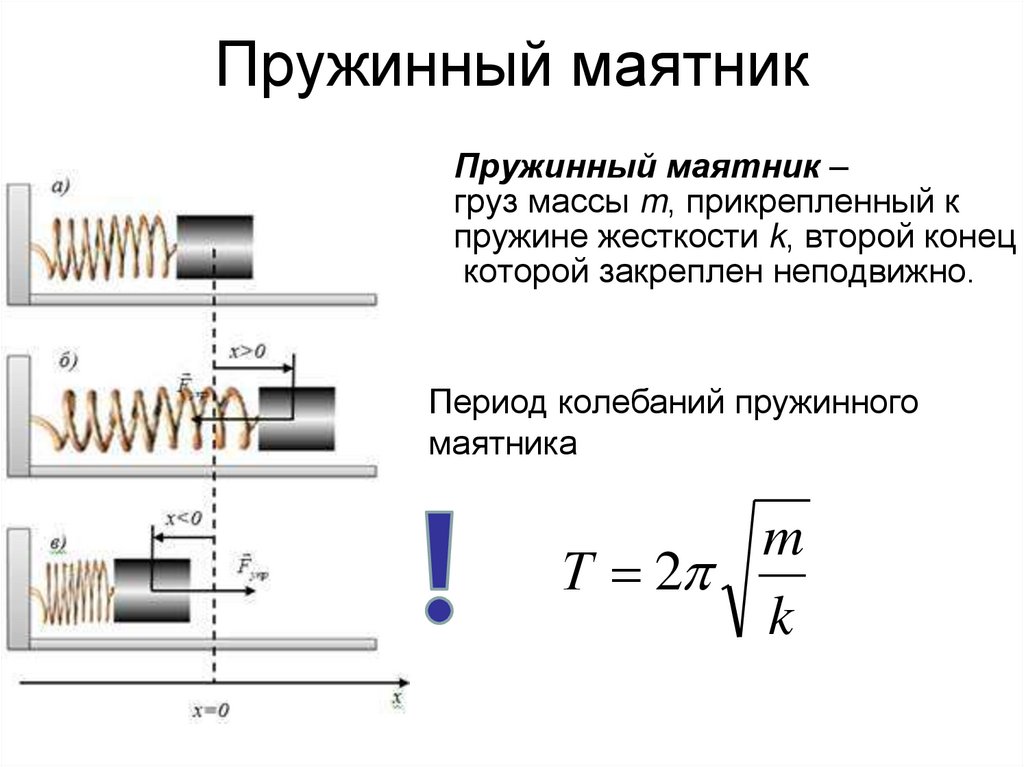
12. Пружинный маятник

Пружинный маятник –
груз массы m, прикрепленный к
пружине жесткости k, второй конец
которой закреплен неподвижно.
Период колебаний пружинного
маятника
m
Т 2
k

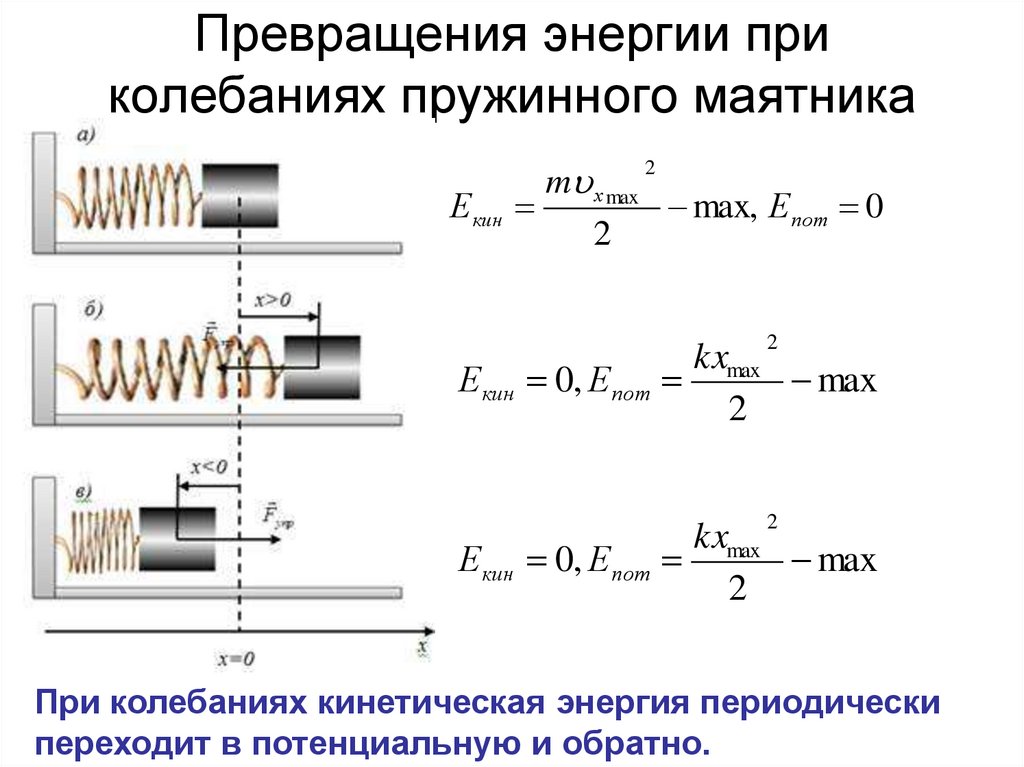
13. Превращения энергии при колебаниях пружинного маятника

m х max
Екин
max, Епот 0
2
2
2
kxmax
Екин 0, Епот
max
2
2
kxmax
Екин 0, Епот
max
2
При колебаниях кинетическая энергия периодически
переходит в потенциальную и обратно.

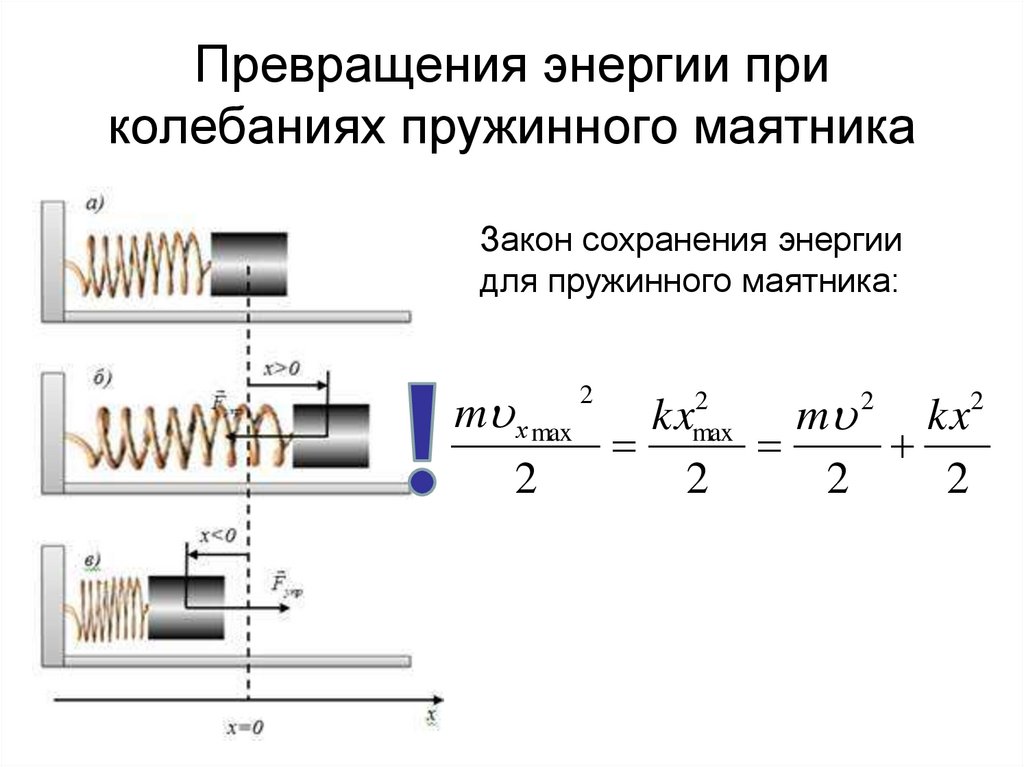
14. Превращения энергии при колебаниях пружинного маятника

Закон сохранения энергии
для пружинного маятника:
m х max
kx
2
2
2
2
max
m
kx
2
2
2
2

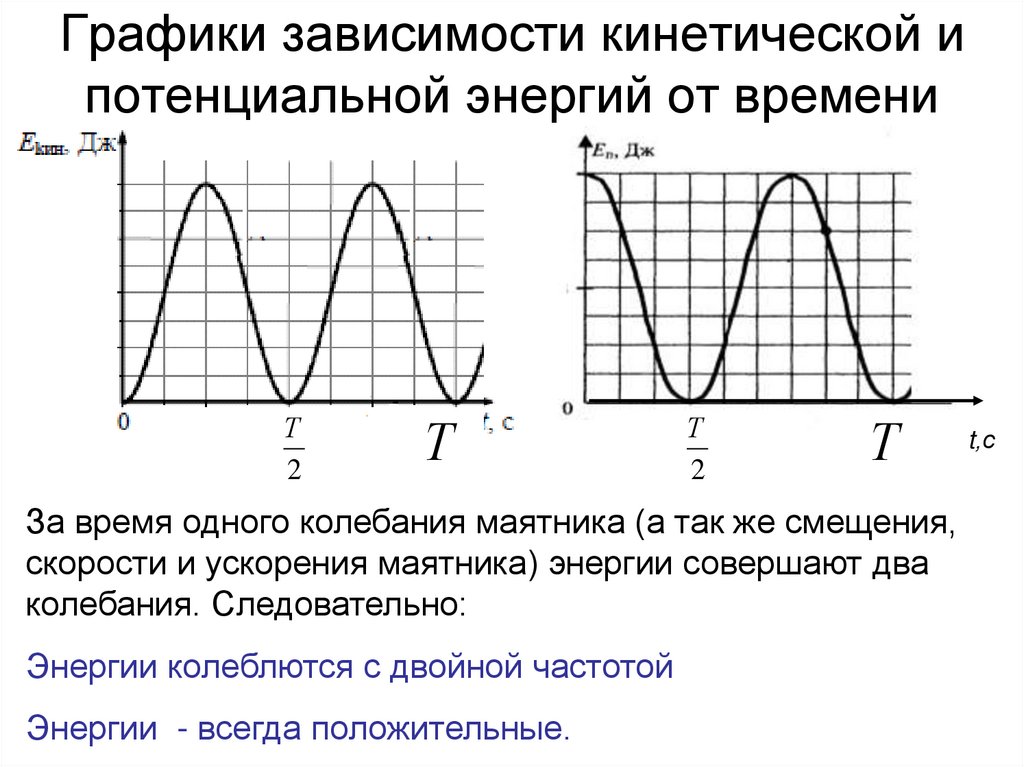
15. Графики зависимости кинетической и потенциальной энергий от времени

Т
2
Т
Т
2
Т
За время одного колебания маятника (а так же смещения,
скорости и ускорения маятника) энергии совершают два
колебания. Следовательно:
Энергии колеблются с двойной частотой
Энергии - всегда положительные.
t,с

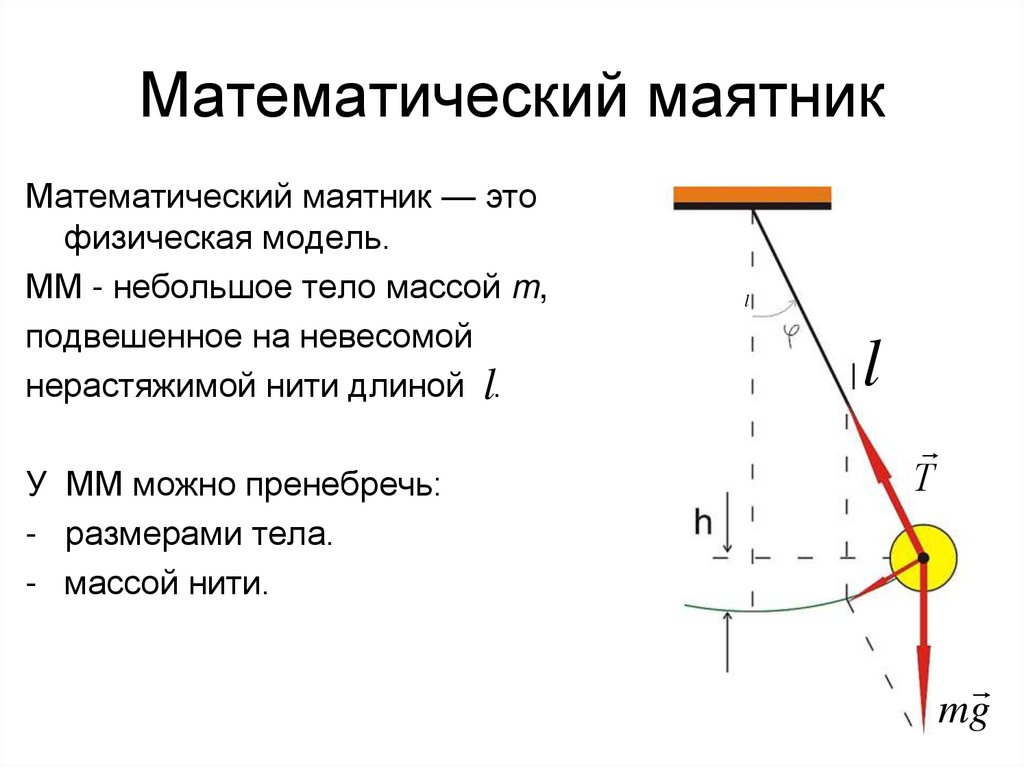
16. Математический маятник

Математический маятник — это
физическая модель.
ММ - небольшое тело массой m,
подвешенное на невесомой
нерастяжимой нити длиной l.
У ММ можно пренебречь:
- размерами тела.
- массой нити.
l
l
Т
mg

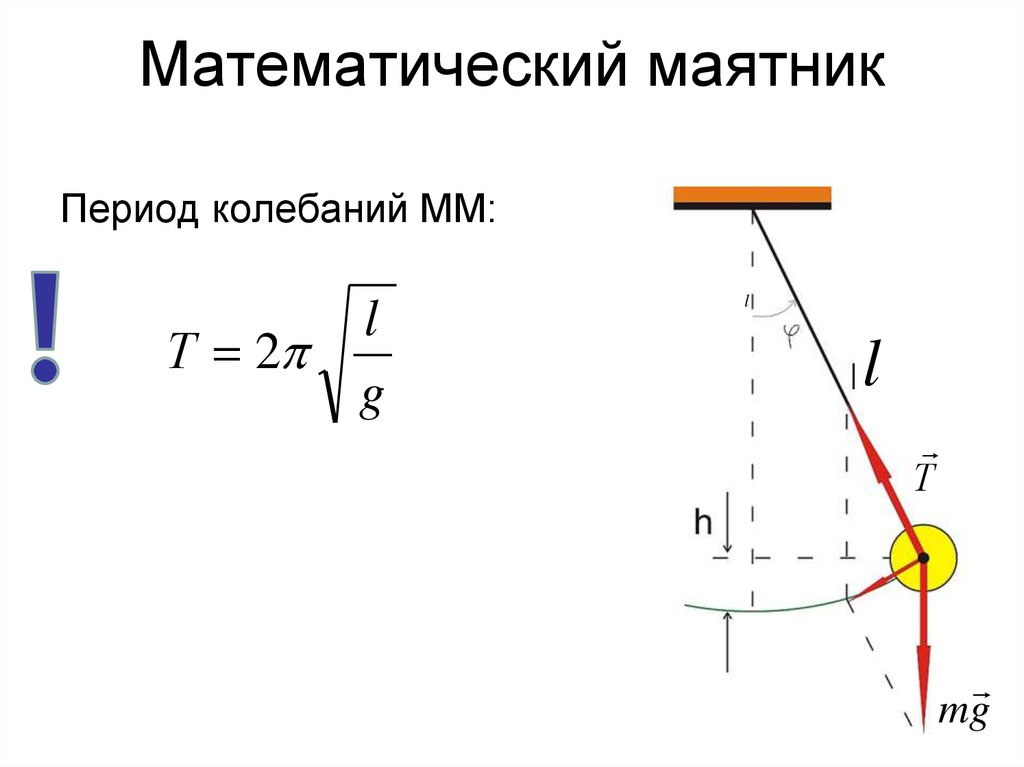
17. Математический маятник

Период колебаний ММ:
l
Т 2
g
l
l
Т
mg

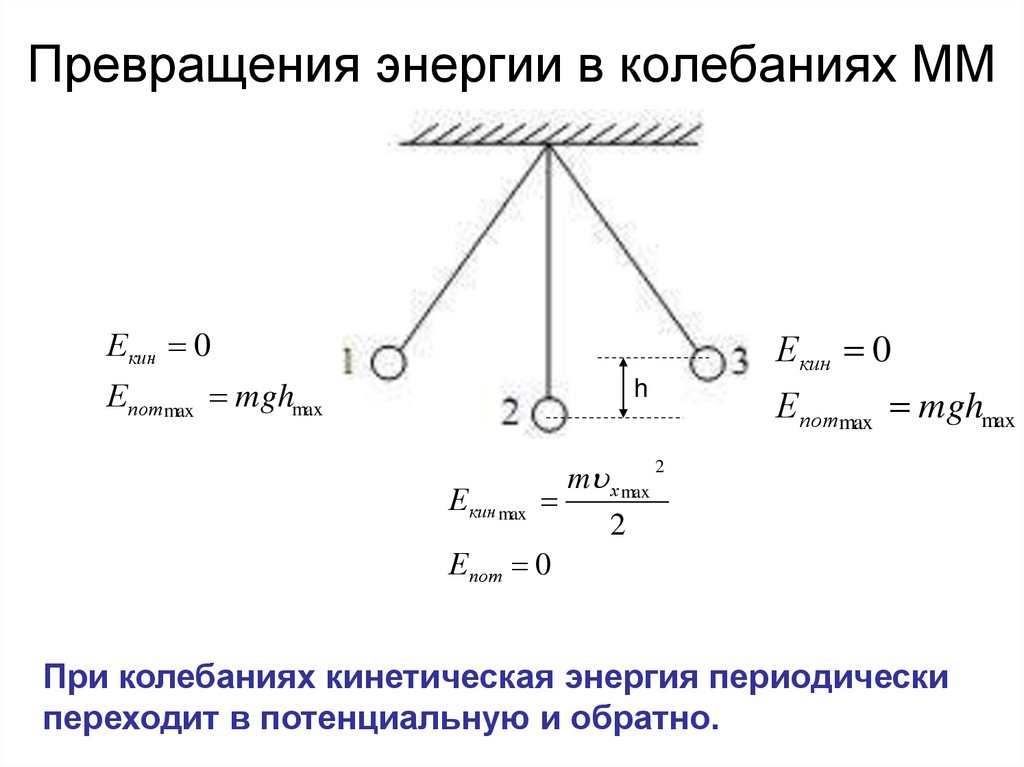
18. Превращения энергии в колебаниях ММ

Екин 0
Епотmax mghmax
Екин 0
h
m х max
Екин max
2
Епот 0
Епотmax mghmax
2
При колебаниях кинетическая энергия периодически
переходит в потенциальную и обратно.

19. Превращения энергии в колебаниях ММ

Закон сохранения энергии для математического маятника:
2
m х max
m
mghmax
mgh
2
2
2