Похожие презентации:
Физические основы высоких технологий
1. ФИЗИЧЕСКИЕ ОСНОВЫ ВЫСОКИХ ТЕХНОЛОГИЙ (ЧАСТЬ 3)
(Колебания и волны)2. Колебания
КолебанияОсциллятор
Гармонические колебания
Пружинный маятник
Математический маятник
Энергия гармонического колебания
3. Колебания
Колебаниями (колебательные движения) называются движения илипроцессы, отличающиеся той или иной степенью повторяемости.
маятник часов
звуковые колебания
пульсары
колебания молекул
…
4. Колебания
Физическая природа колебаний может быть различнойМеханические колебания
Электромагнитные колебания
Звуковые колебания
и т.д.
Различные колебательные процессы описываются одинаковыми
характеристиками и одинаковыми уравнениями.
Единый подход к изучению колебаний различной физической
природы.
5. Колебания
В зависимости от характера воздействия на колеблющуюся системуразличают свободные (или собственные) колебания и вынужденные
колебания.
Свободными называют такие колебания, которые происходят в
системе, предоставленной самой себе при отсутствие внешних
воздействий после того, как ей был сообщен толчок либо она была
выведена из положения равновесия.
Вынужденными называют такие колебания, в процессе которых
колеблющаяся система подвергается воздействию внешней
периодически изменяющейся силы.
Простейшим примером по характеру описания являются
гармонические колебания – колебания, при которых колеблющаяся
величина изменяется со временем по закону синуса или косинуса.
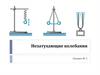
6. Вертикальный пружинный маятник
Простейшим примером системы, где возникают свободныегармонические колебания, является движение тела под действием
силы упругости пружины:
Fx kx
(1.1)
Константа k всегда положительна (размерность – Н/м).
Примером такой системы является тело массы m, подвешенное к
пружине жесткостью k.
7. Вертикальный пружинный маятник
В положение равновесия сила тяжести уравновешивается упругойсилой:
(1.2)
mg k l
здесь ∆l – статическое удлинение пружины.
Направим ось x вниз и начало координат выберем в точке,
соответствующей положению равновесия тела. Если тело сместить
из положения равновесия на расстояния x, то результирующая сила,
действующая на тело, будет равна:
F mg k ( l x )
или с учетом (1.2)
F kx
(1.3)
где х – растяжение пружины (смещение тела из положения равновесия).
8. Вертикальный пружинный маятник
Если силы видаFx kx
имеют другую природу (т.е. не являются силами упругости) то их
называют квазиупругими. В этом случае k – коэффициент
квазиупругой силы.
Запишем второй закон Ньютона, в проекции на ось х, для
пружинного маятника
d 2x
Fx m w x m 2 kx
dt
(1.4)
Дифференциальное уравнение, описывающее колебания данной
системы имеет вид:
mx kx
или
где
x 02 x 0
02
k
m
(1.5)
(1.6)
9. Гармонические колебания
Решение уравнения гармонических колебаний (1.5) имеет вид:Закон движения для
гармонических колебаний
x(t ) A cos( 0t )
(1.7)
где A и φ произвольные постоянные, которые определяются из
начальных условий.
Величина A наибольшего отклонения системы от положения
равновесия называется амплитудой колебаний.
Амплитуда А – постоянная положительная величина.
Величина 0t стоящая под знаком косинуса, называется фазой
колебания.
Угол φ – начальная фаза колебаний, определяется смещением
колеблющейся величины от положения равновесия в начальный
момент.
ω0 – круговая (циклическая) частота гармонических колебаний
10. Гармонические колебания
Промежуток времени Т (одного цикла), в течение которогопроисходит одно полное колебание и за которое фаза колебаний
изменяется на 2π, называется периодом колебания. Период
определяется из следующего условия
( 0 (t T ) ) ( 0t ) 2
T
2
(1.8)
0
Число колебаний в единицу времени называется частотой колебания ν
1
(1.9)
T
Частота ν измеряется в Герцах (1 Гц = 1/с)
1 Гц – частота периодического процесса, при которой за 1 с совершается
один цикл процесса.
11. Гармонические колебания
Циклическая (круговая) частота колебаний ω – это число колебаний,происходящих за 2π секунд.
Циклическая частота колебаний ω связана с частотой v и периодом
колебаний Т соотношениями:
2
T
Единица циклической частоты – радиан в секунду (рад/с).
0 2 v
(1.10)
12. Период пружинного маятника
Вспомним, что длясоотношение (1.6)
пружинного
02
С другой стороны (1.8)
T
маятника
было
получено
k
m
2
0
Сравнивая эти два выражения, получаем период собственных
колебаний пружинного маятника
m
(1.11)
T 2
k
Данная формула справедлива для упругих колебаний в пределах, в
которых выполняется закон Гука, т.е. когда масса пружины мала по
сравнению с массой тела.
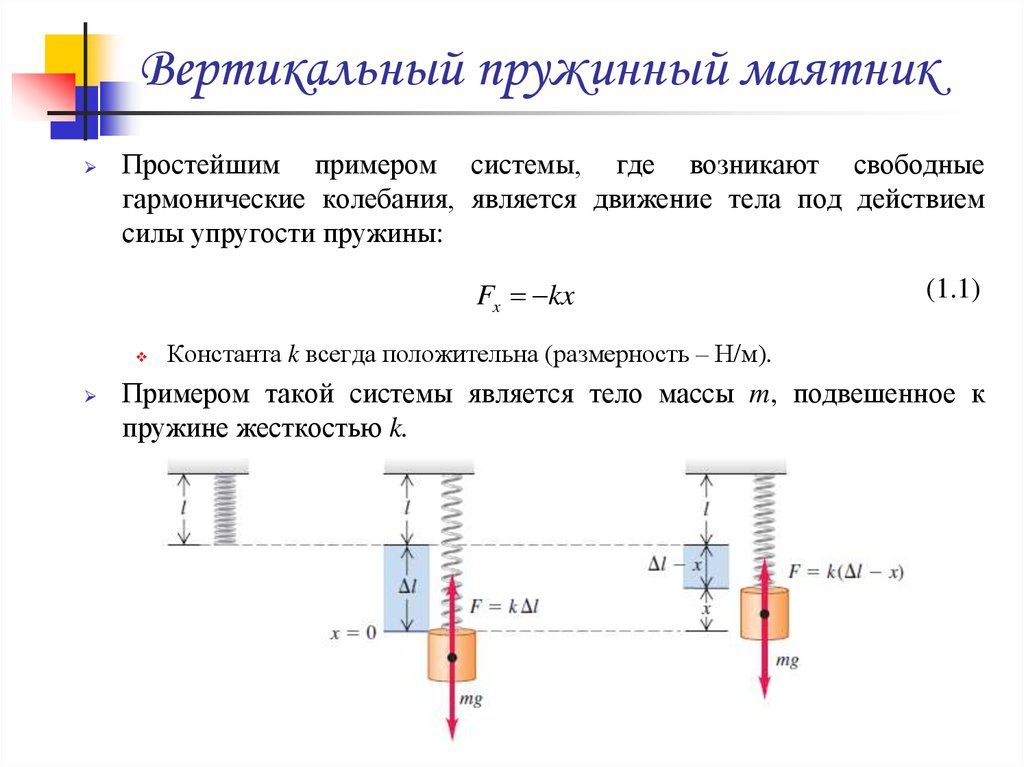
13. Период пружинного маятника
Масса m увеличивается от 1 до 3.При увеличение массы период
увеличивается.
Константа k увеличивается от 1
до 3. При увеличение k период
уменьшается.
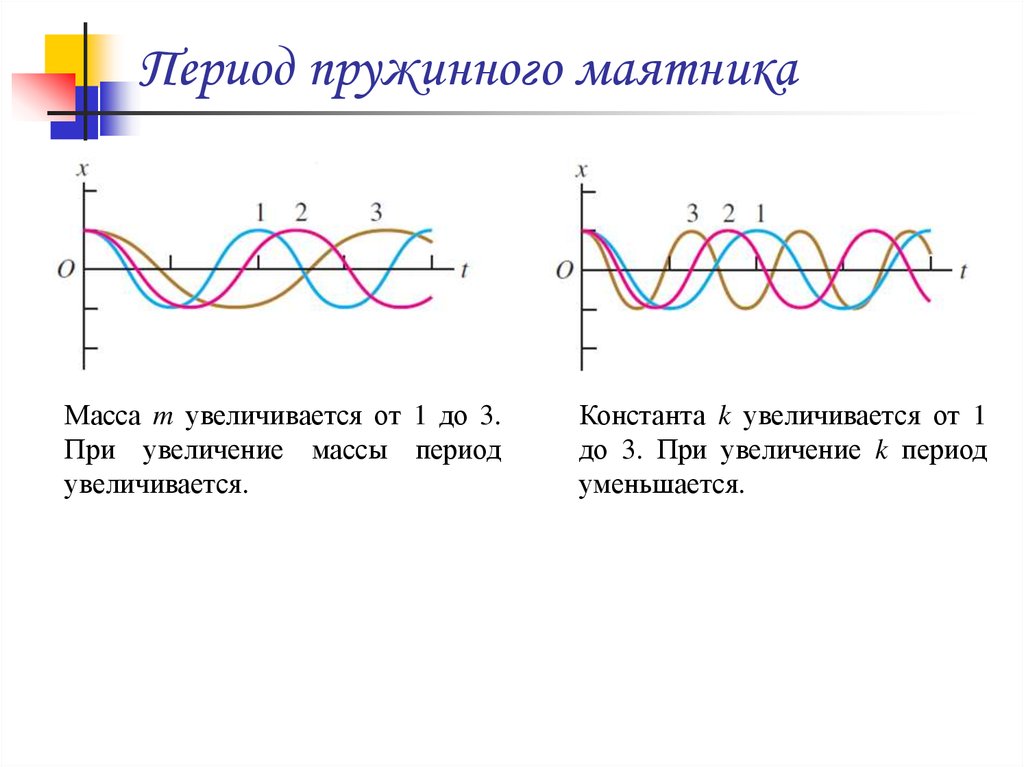
14. Графики гармонического колебания
График гармонических колебанийИзменение амплитуды не влияет на
период
Период и амплитуда при разных
начальных фазах колебаний
15. Скорость , ускорение
x(t ) A cos( 0t )Продифференцировав зависимость смещения от времени x(t) получим
выражение для зависимости скорости от времени. Взяв вторую
производную, получим зависимость ускорения от времени:
dx
A 0 sin( 0 t ) A 0 cos( 0 t )
dt
2
d 2x
w x x= 2 A 02 cos( 0 t ) A 02 cos( 0 t )
dt
v x x=
(1.12)
(1.13)
Видно, что скорость и ускорение также изменяются по
гармоническому закону.
Как следует из этих соотношений ускорение и смещение находятся в
противофазе, т.е. в тот момент, когда смещение достигает
наибольшего положительного значения, ускорение достигает
наибольшего отрицательно значения, и наоборот.
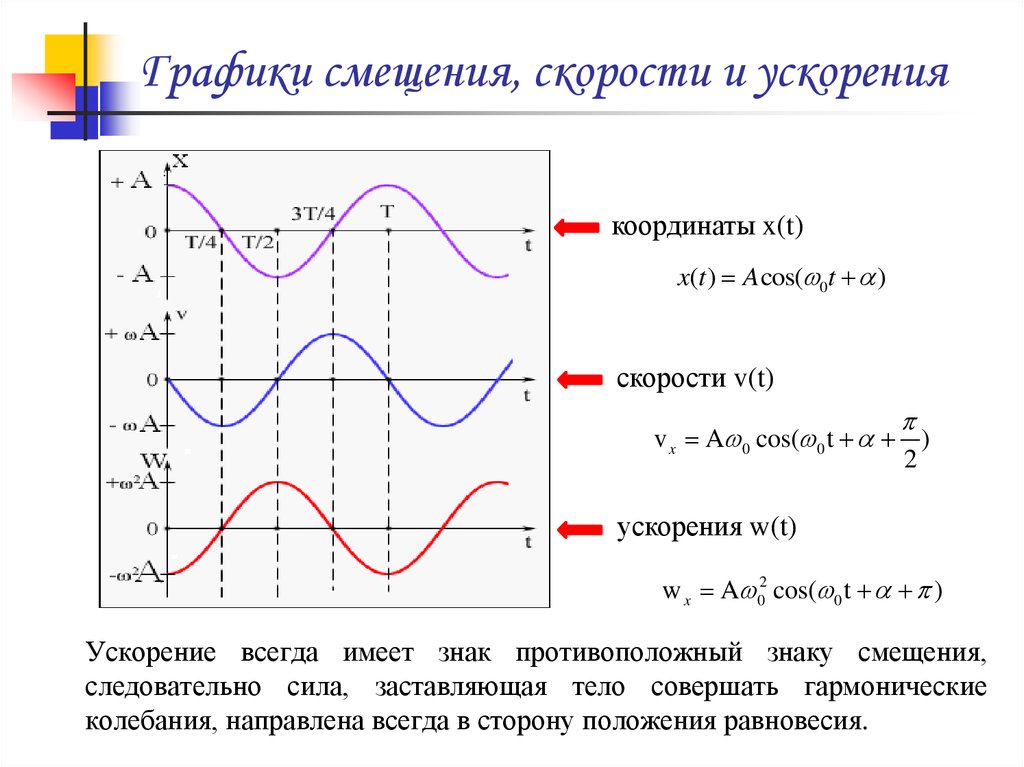
16. Графики смещения, скорости и ускорения
координаты x(t)x(t ) A cos( 0t )
скорости v(t)
v x A 0 cos( 0 t )
2
ускорения w(t)
w x A 02 cos( 0 t )
Ускорение всегда имеет знак противоположный знаку смещения,
следовательно сила, заставляющая тело совершать гармонические
колебания, направлена всегда в сторону положения равновесия.
17. Энергия гармонического колебания
При гармонических колебаниях смещение x изменяется по закону:x(t ) A cos( 0t )
Кинетическая энергия тела, совершающие гармонические колебания
тогда с учетом скорости
или
m v 2 mx 2
T
2
2
mA2 o2
T
sin 2 ( 0t )
2
(1.14)
mA2 o2
T
(1 cos 2( 0t ))
2
Видно, что кинетическая энергия меняется от максимального
значения Тmax до 0 с частотой в 2 раза большей обычных
амплитудных колебаний.
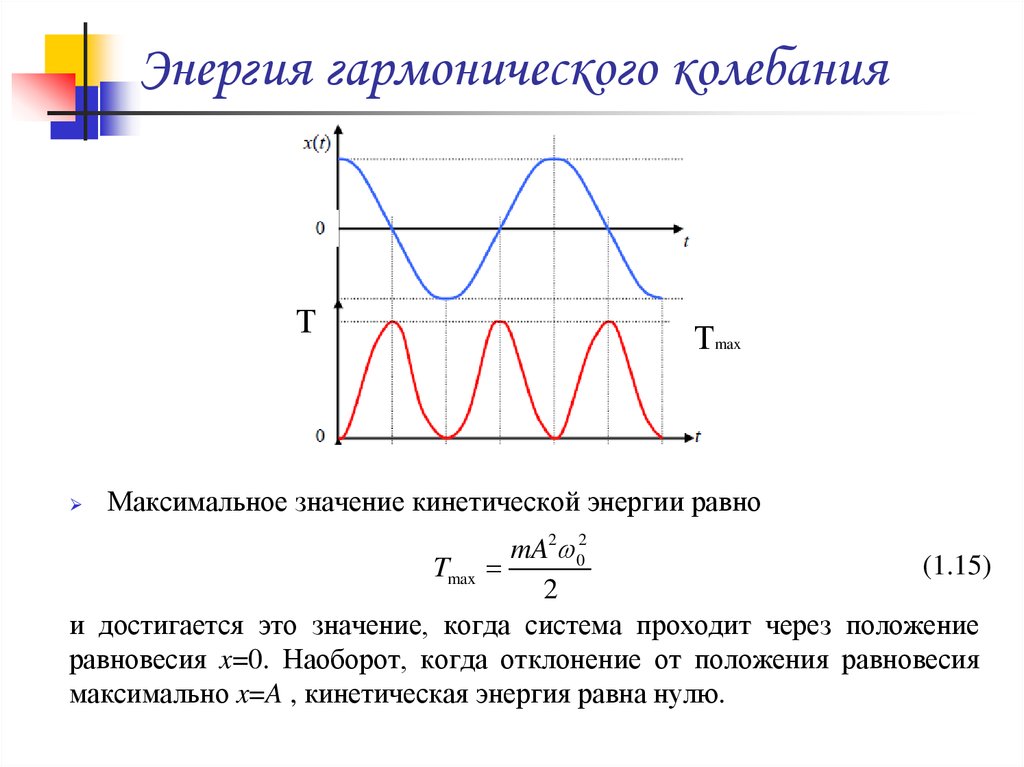
18. Энергия гармонического колебания
ТТmax
Максимальное значение кинетической энергии равно
mA2 02
(1.15)
Tmax
2
и достигается это значение, когда система проходит через положение
равновесия x=0. Наоборот, когда отклонение от положения равновесия
максимально x=A , кинетическая энергия равна нулю.
19. Энергия гармонического колебания
Потенциальная энергия тела, совершающиеколебания под действием упругой силы:
гармонические
kx 2
U Fdx
const
(1.16)
2
Будем отсчитывать потенциальную энергию от положения
равновесия, т.е. при x = 0 имеем U = 0, следовательно, постоянная
также равна нулю (const = 0), т.о.
kx 2
U
2
(1.17)
или
Учитывая, что
kA2
U
cos 2 ( 0t )
2
k 02 m
(1.18)
20. Энергия гармонического колебания
получаемmA2 02
U
cos 2 ( 0t )
2
или
mA2 02
U
(1 cos 2( 0t )
2
Видно, что максимальное значение потенциальной энергии совпадает
с максимальным значением кинетической энергии по величине:
Tmax U max
(1.19)
mA2 02
2
(1.20)
Однако во времени колебания потенциальной энергии происходят в
противофазе по отношению к колебаниям кинетической энергии.
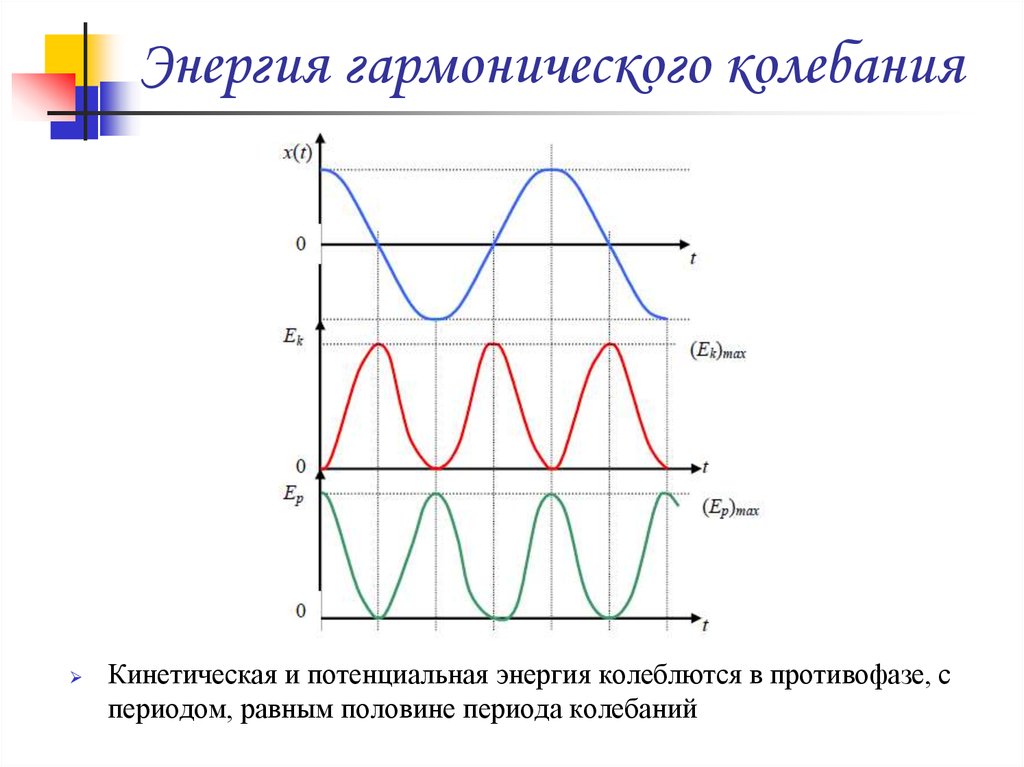
21. Энергия гармонического колебания
Кинетическая и потенциальная энергия колеблются в противофазе, спериодом, равным половине периода колебаний
22. Энергия гармонического колебания
Сложив вместе кинетическую и потенциальную энергии, получимформулу для полной энергии:
1
E T U mA2 02 sin 2 ( 0t ) cos 2 ( 0t )
2
1
E T U mA2 02 const
2
(1.21)
Итак, имеем следующие утверждения:
Максимальные значения кинетической и потенциальной энергий
совпадают, но достигают эти значения в разные моменты времени.
Полная энергия остается постоянной и равной амплитудному значению
кинетической или потенциальной энергий. Во время колебаний
происходит «перекачка» кинетической энергии в потенциальную и
наоборот.
Средняя кинетическая энергия равна его средней потенциальной энергии.
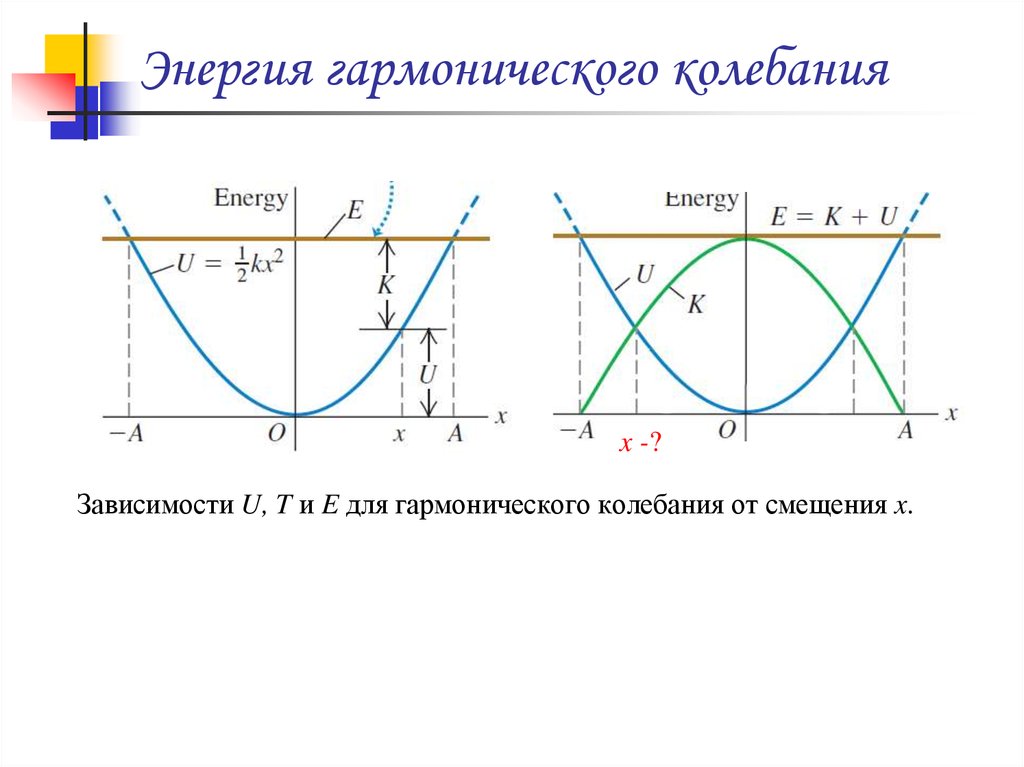
23. Энергия гармонического колебания
x -?Зависимости U, T и E для гармонического колебания от смещения x.
24. Математический маятник
Математическим маятником называют идеализированную систему,состоящую из легкой и нерастяжимой нити, на которой подвешена
масса, сосредоточенная в одной точке.
Достаточно хорошим приближением к математическому маятнику
служит небольшой шарик, подвешенный на длинной тонкой нити.
Отклонение маятника от положения равновесия
характеризуется углом φ.
При отклонении маятника от положения
равновесия возникает вращательный момент N,
равный по величине
mgl sin
Он имеет такое направление, что стремится
вернуть маятник в положение равновесия.
Следовательно выражение для вращательного
момента имеет вид
N mgl sin
(1.22)
25. Математический маятник
Напишемдвижения
для
маятника
уравнение
динамики
вращательного
I N
(1.23)
где I=ml2 – момент инерции маятника относительно точки подвеса l.
Учитывая соотношение (1.22) уравнение (1.23) запишется как
ml 2 mgl sin
Перепишем его в виде
g
sin 0
l
Рассматривая малые колебания можно положить sin .
Пример:
0,1рад
sin 0,0998
различие в 0,2%
(1.24)
26. Математический маятник
Ограничиваясь рассмотрением малых колебаний, уравнение (1.24)принимает вид
02 0
(1.25)
где 0 – частота собственных колебаний математического маятника
0 g / l
Период колебаний математического маятника
T
2
0
2
l
g
(1.26)
Период математического маятника не зависит от его массы, а
определяется лишь длиной нити и ускорением свободного падения в
том месте, где находится маятник.
27. Физический маятник
Физическим маятником называется твердое тело, способноесовершать колебания вокруг неподвижной точки, не совпадающей с
его центром инерции.
При отклонении маятника от положения равновесия на угол φ
возникает вращательный момент N, стремящийся вернуть маятник в
положение равновесия
N mgl sin
I - момент инерции маятника относительно
точки подвеса
I mgl sin
В случае малых колебаний
mgl
I
По теореме Штейнера момент инерции I можно выразить
через момент инерции IC относительно оси, проходящей через центр масс C
маятника и параллельной оси вращения:
I I c ml 2
02 0
02
28. Физический маятник
Период колебания физического маятникаT 2
I
mgl
Сопоставляя данную формулу с формулой периода математического
маятника получается, что математический маятник с длиной
lпр
I
ml
будет иметь такой период колебаний, как и данный физический маятник.
Данную величину называют приведенной длиной физического маятника.
T 2
lпр
g
29. Гармонический осциллятор
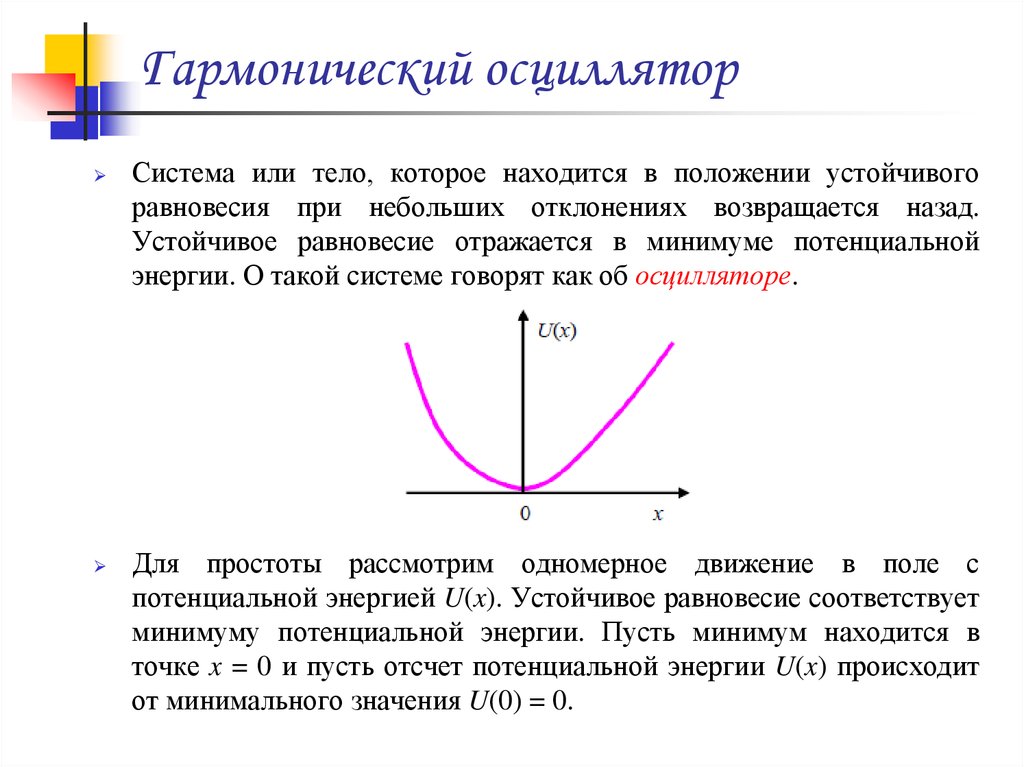
Система или тело, которое находится в положении устойчивогоравновесия при небольших отклонениях возвращается назад.
Устойчивое равновесие отражается в минимуме потенциальной
энергии. О такой системе говорят как об осцилляторе.
Для простоты рассмотрим одномерное движение в поле с
потенциальной энергией U(x). Устойчивое равновесие соответствует
минимуму потенциальной энергии. Пусть минимум находится в
точке x = 0 и пусть отсчет потенциальной энергии U(x) происходит
от минимального значения U(0) = 0.
30. Гармонический осциллятор
Вблизи точки x потенциальную энергию U(x) можно разложить вряд Тейлора по степеням x – отклонения от положения равновесия:
Рассматривая малые отклонения от положения равновесия,
пренебрегаем высшими степенями x3, x4,...
Поскольку в точке x = 0 имеем минимум потенциальной энергии, то
при этом получаем:
31. Гармонический осциллятор
Введем следующее обозначение для значения второй производной внуле:
Тогда потенциальная энергия вблизи положения равновесия имеет
вид:
Сила связана с потенциальной энергией, и для одномерного
движения получаем:
Это сила носит название упругой или квазиупругой силы независимо
от ее природы. Знак минус показывает, что эта сила направлена
всегда к положению равновесия, т.е. к точке x = 0.
32. Гармонический осциллятор
Ограничиваясь потенциальной энергией вида представленной вышеили силой, можно записать одномерное уравнение Ньютона:
Вводя обычные обозначения
перепишем его в виде:
для
производных
по
времени,
Окончательно уравнение для нахождения функции x(t) представим в
виде:
Колебания, описываемые данным уравнением, называются
гармоническим осциллятором.
Следовательно, гармонический осциллятор представляет собой
систему, которая совершает гармонические колебания около
положения равновесия.
33. Гармонический осциллятор
Примеры гармонического осциллятора:математический маятник
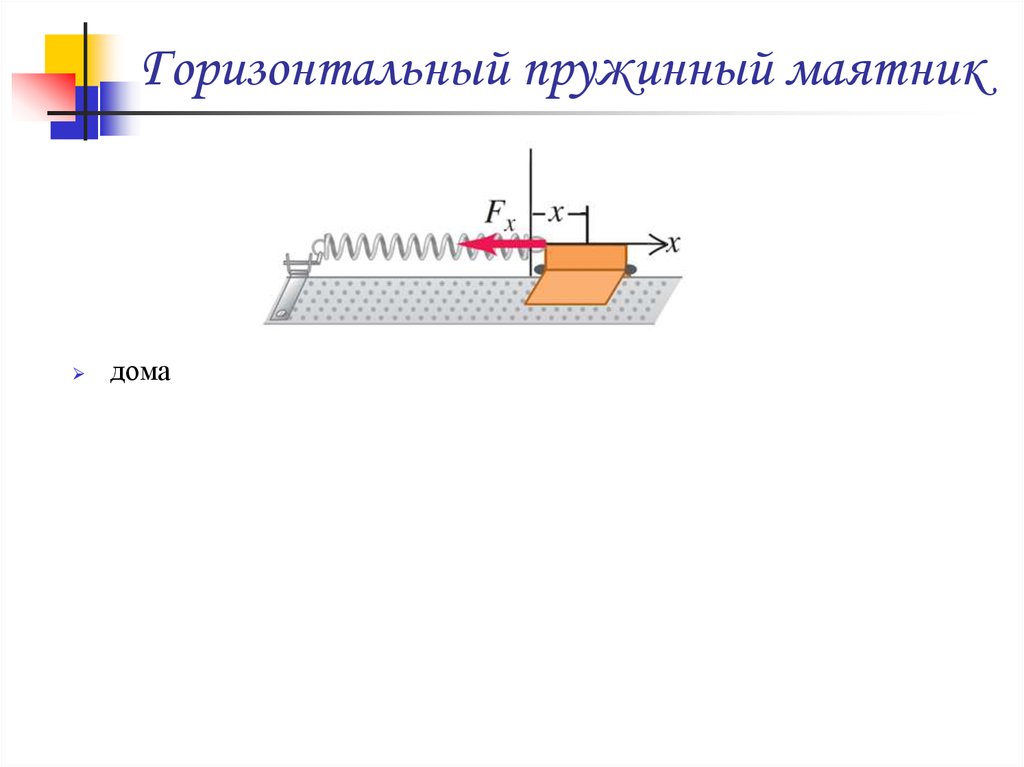
пружинный маятник
крутильный маятник
колебательный контур
в квантовой механике являются колебания атомов в твердых телах,
молекулах и т.д.
и…

























 Физика
Физика