Похожие презентации:
f11f4561b230426eabfba32ba1f4d1a0
1.
2.
3.
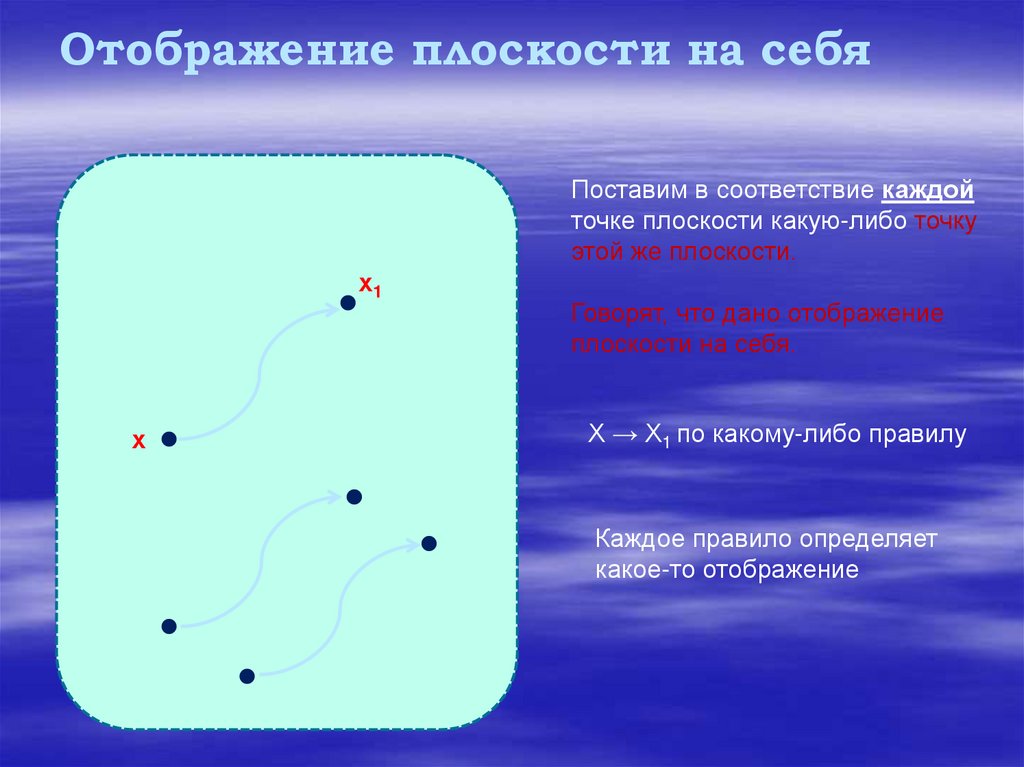
Отображение плоскости на себяПоставим в соответствие каждой
точке плоскости какую-либо точку
этой же плоскости.
х1
х
Говорят, что дано отображение
плоскости на себя.
Х → Х1 по какому-либо правилу
Каждое правило определяет
какое-то отображение
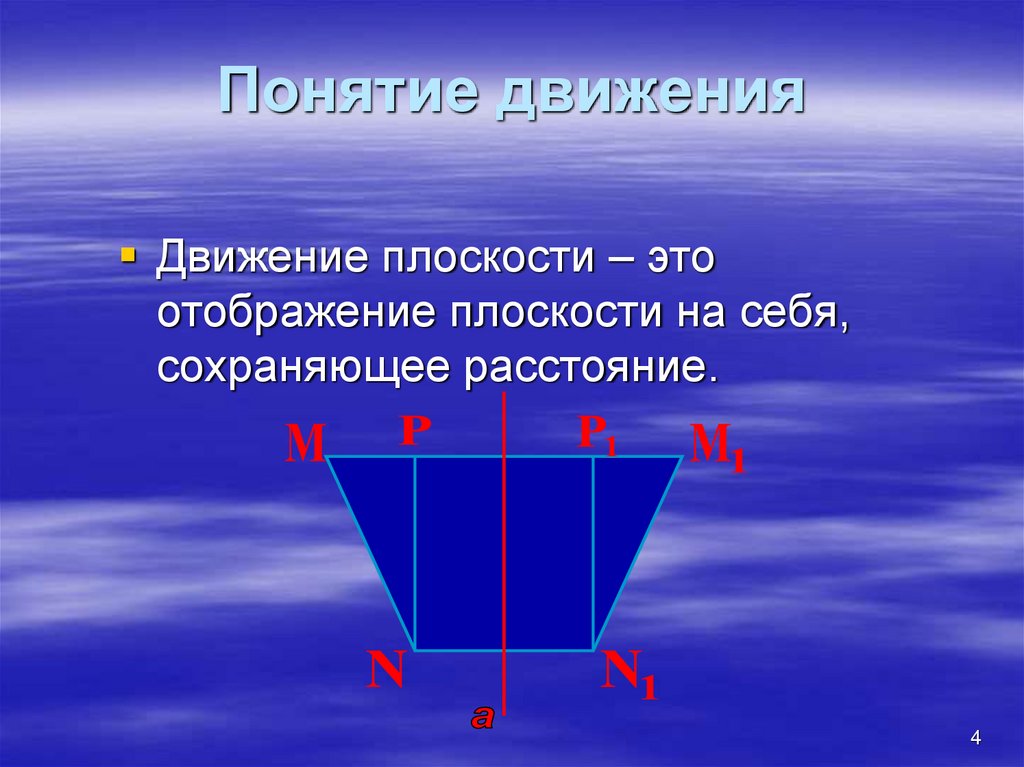
4. Понятие движения
Движение плоскости – этоотображение плоскости на себя,
сохраняющее расстояние.
4
5. Теорема. При движении отрезок отображается на отрезок.
Следствие:При движении
треугольник
отображается на
равный ему
треугольник.
5
6.
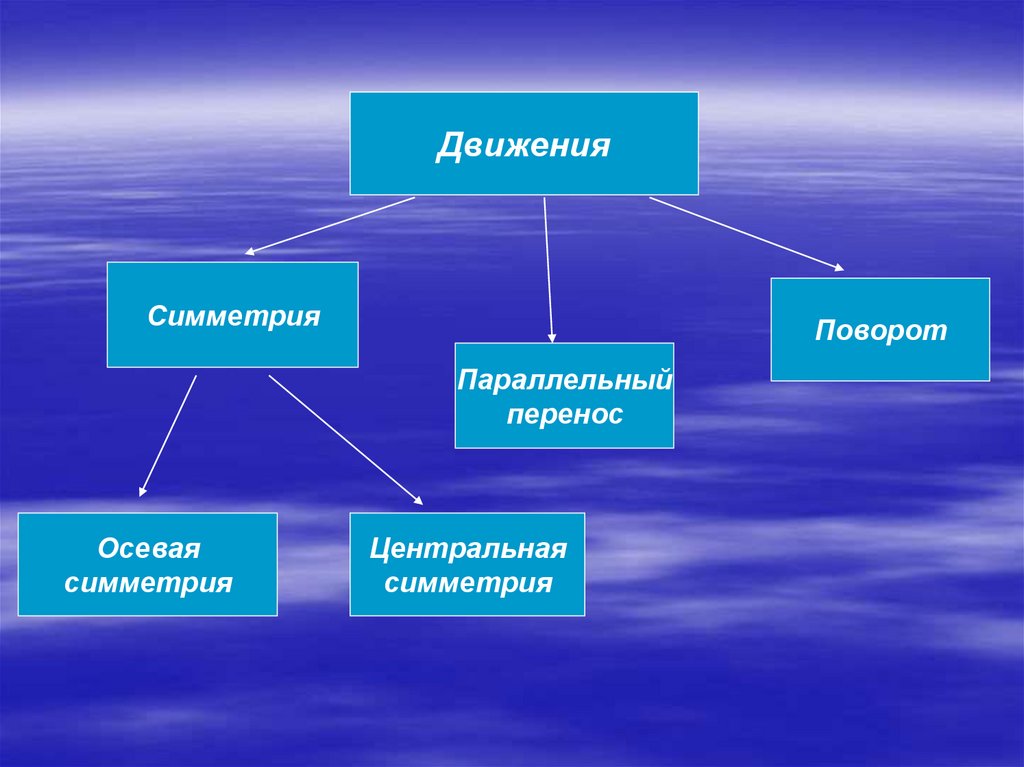
ДвиженияСимметрия
Поворот
Параллельный
перенос
Осевая
симметрия
Центральная
симметрия
7. Осевая симметрия
ОпределениеОсевая симметрия –это
отображение плоскости на
себя, при котором каждая
точка М отображается в
такую точку М1, что отрезок
ММ1 перпендикулярен прямой
а (оси симметрии ) и отрезок
МР равен отрезку РМ1.
8. Построение
Пусть а – ось симметрии.∆АВС – произвольный. Проведем
перпендикуляр ВР к прямой а.
Отложим на прямой ВР отрезок
РВ1 , равный по длине отрезку
ВР. Точка В1 искомая.
Аналогично строим точки А1 и
С1. ∆А1В1С 1 симметричен
∆АВС относительно прямой а.
9.
10.
11. Задача
Сколько осей симметрии имеетравносторонний треугольник?
Сколько осей симметрии имеет
квадрат?
Сколько осей симметрии имеет ромб,
не являющийся квадратом?
Начертите и убедитесь в
правильности своего ответа
12. Центральная симметрия
ОпределениеЦентральная симметрия
–это отображение
плоскости на себя , при
котором каждая точка М
отображается в такую
точку М1,что отрезок ОМ
равен отрезку ОМ 1
(точка О - центр
симметрии).
13. Построение
Пусть точка О – центрсимметрии. ∆АВС произвольный. Проведём луч
ВО. Отложим отрезок ОВ1 ,
равный отрезку ОВ. Точка В1
искомая. Аналогично строим
точки А 1 и С1 . ∆А1В1С1
симметричен ∆АВС
относительно точки О.
14.
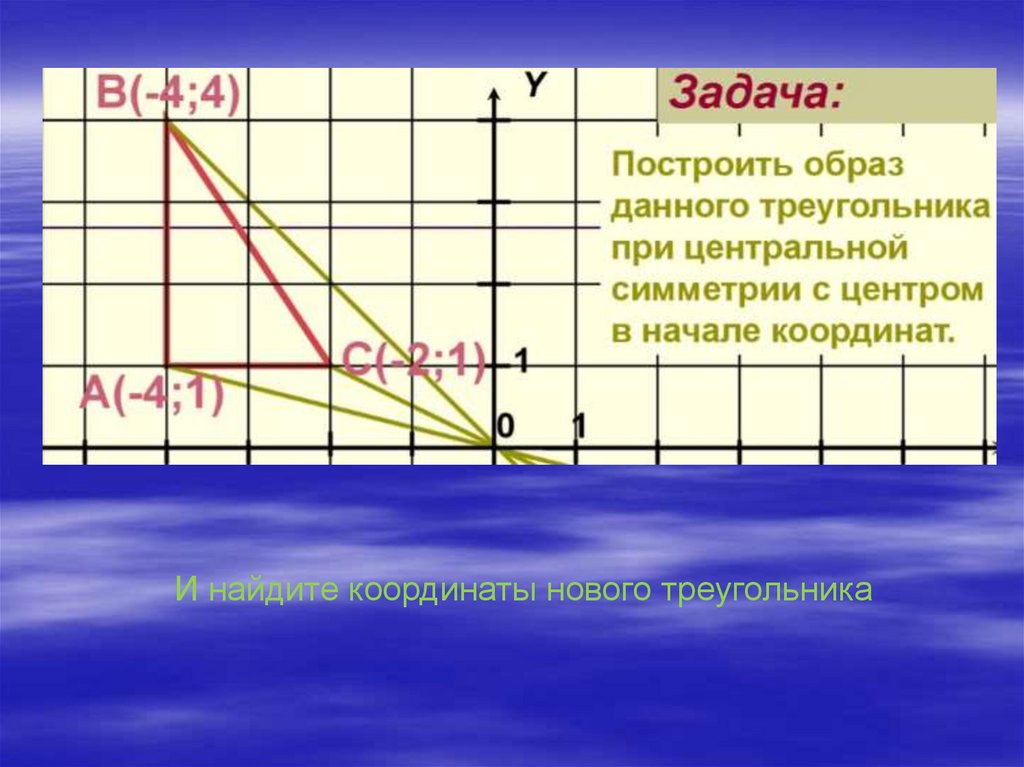
И найдите координаты нового треугольника15.
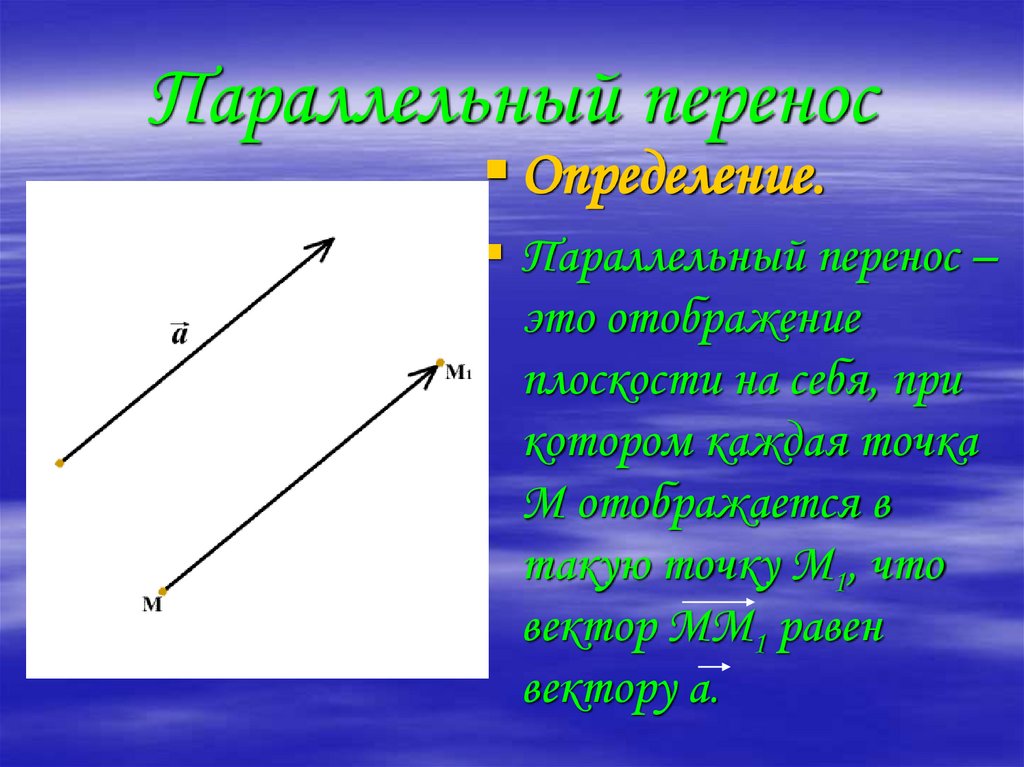
16. Параллельный перенос
Определение.Параллельный перенос –
это отображение
плоскости на себя, при
котором каждая точка
М отображается в
такую точку М1, что
вектор ММ1 равен
вектору а.
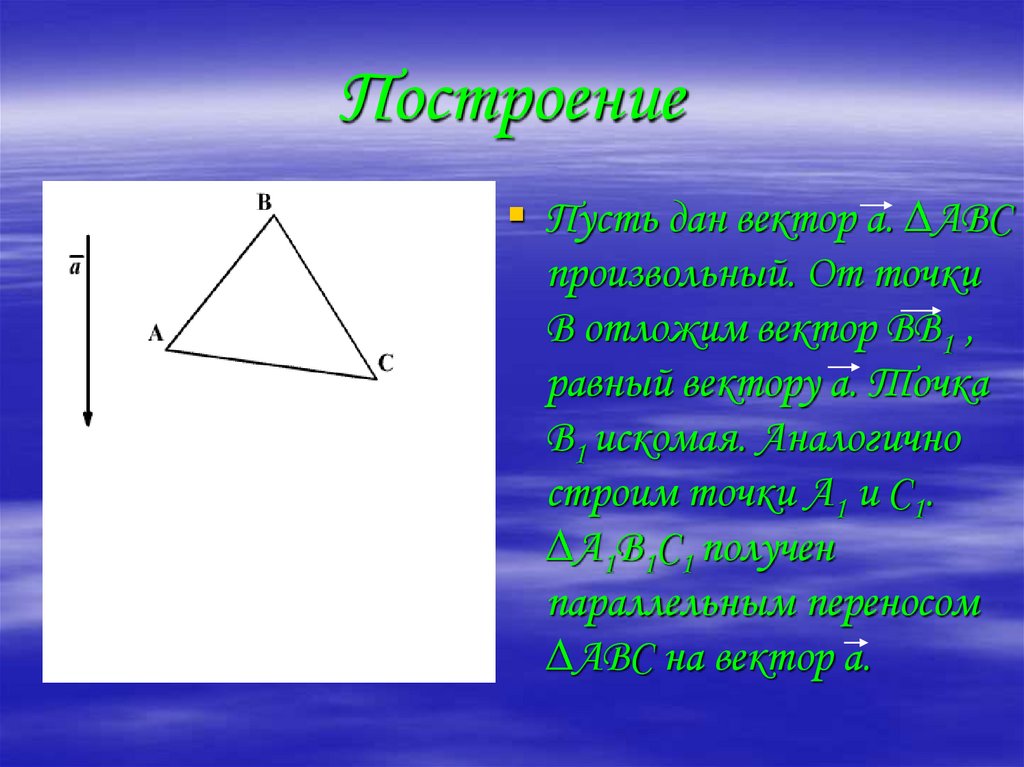
17. Построение
Пусть дан вектор а. ∆АВСпроизвольный. От точки
В отложим вектор ВВ1 ,
равный вектору а. Точка
В1 искомая. Аналогично
строим точки А1 и С1.
∆А1В1С1 получен
параллельным переносом
∆АВС на вектор а.
18.
19.
Задача:Построить образ трапеции с координатами
А(-4;1), В(-5,3), С(0;3) и D(-1;1) при
повороте на 90 градусов по часовой
стрелке. Записать координаты новой
трапеции
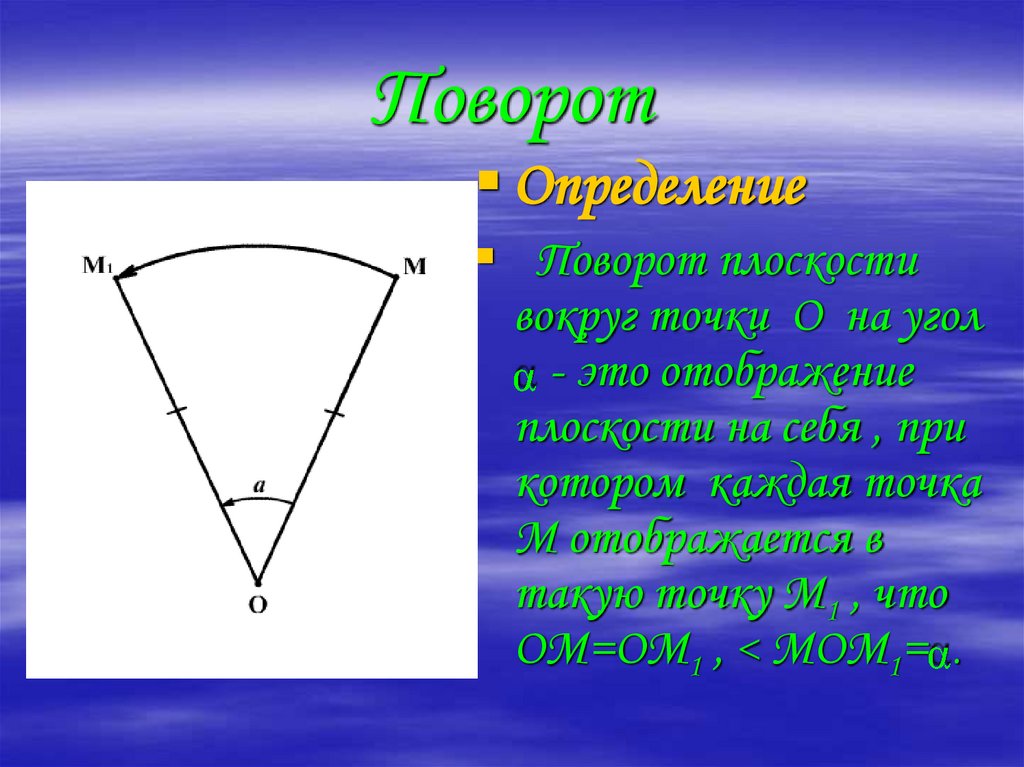
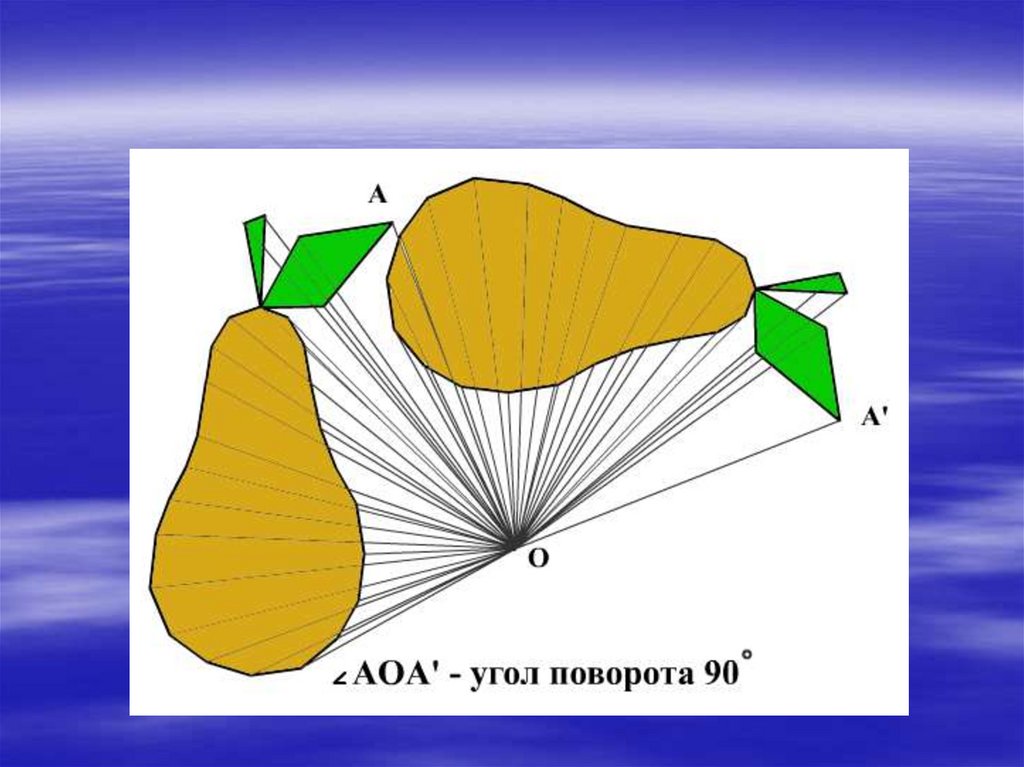
20. Поворот
ОпределениеПоворот плоскости
вокруг точки О на угол
- это отображение
плоскости на себя , при
котором каждая точка
М отображается в
такую точку М1 , что
ОМ=ОМ1 , < МОМ1= .
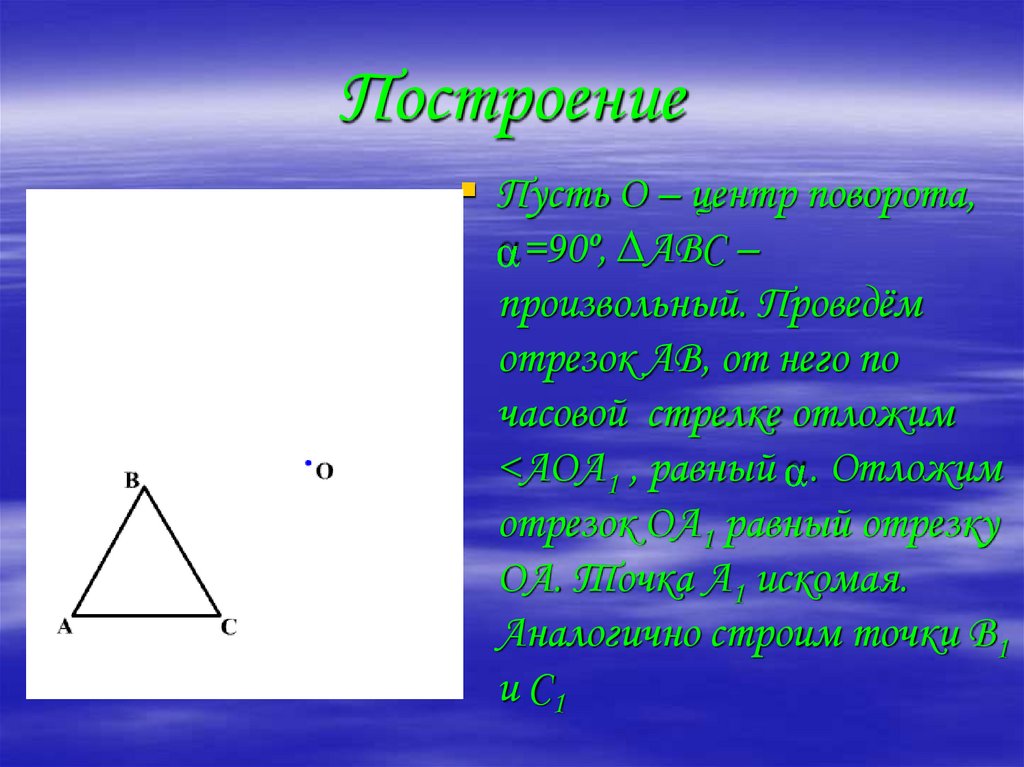
21. Построение
Пусть О – центр поворота,=90º, ∆АВС –
произвольный. Проведём
отрезок АВ, от него по
часовой стрелке отложим
<АОА1 , равный . Отложим
отрезок ОА1 равный отрезку
ОА. Точка А1 искомая.
Аналогично строим точки В1
и С1
22.
23.
24. Вопросы
Определить видсимметрии.
Что вам приходилось
встречать в природе
из известных видов
симметрии?
25. Симметрия в природе
26.
27.
28. Симметрия в архитектуре
29.
30. Какие из данных графиков можно отнести к движению?
А)Г)
Б)
В)
Д)
31. Наложение
Наложение- этоотображение
плоскости н себя.
31
32. Теорема. Любое движение является наложением.
Следствие:При движении любая
фигура отображается
на равную ей фигуру.
Фигуры называются равными,
если существует движение,
отображающее одну из них на другую.
32
33. Подобие фигур
Преобразование фигуры F в фигуру F' называетсяпреобразованием подобия, если при этом
преобразовании расстояния между точками
изменяются в одно и то же число раз.
число k называется коэффициентом подобия.
Х Х'
Х'Y' = k ХY
Y Y'
Y
Две фигуры F и F'
называются
Х
подобными, если одна
из них переводится
в другую подобием.
Х'
F'
F
Y'
34.
Подобие в жизни(карты местности)
35. Гомотетия
OХ
Фигуры F и F´ называются
гомотетичными.
Х'
Преобразование фигуры F, при котором каждая ее
Зафиксируем
точкув точку
O и положительное
точка Х переходит
Х' , построеннуючисло k.
Каждой
точке
Х плоскости,
от O
указанным
способом,
называется отличной
гомотетией
сопоставим
точку
Х' наO.
луче OХ так, что OХ' = k OХ.
относительно
центра
Точке O сопоставим ее саму.
Число k называется коэффициентом гомотетии.
36.
Задача:О
А
А´
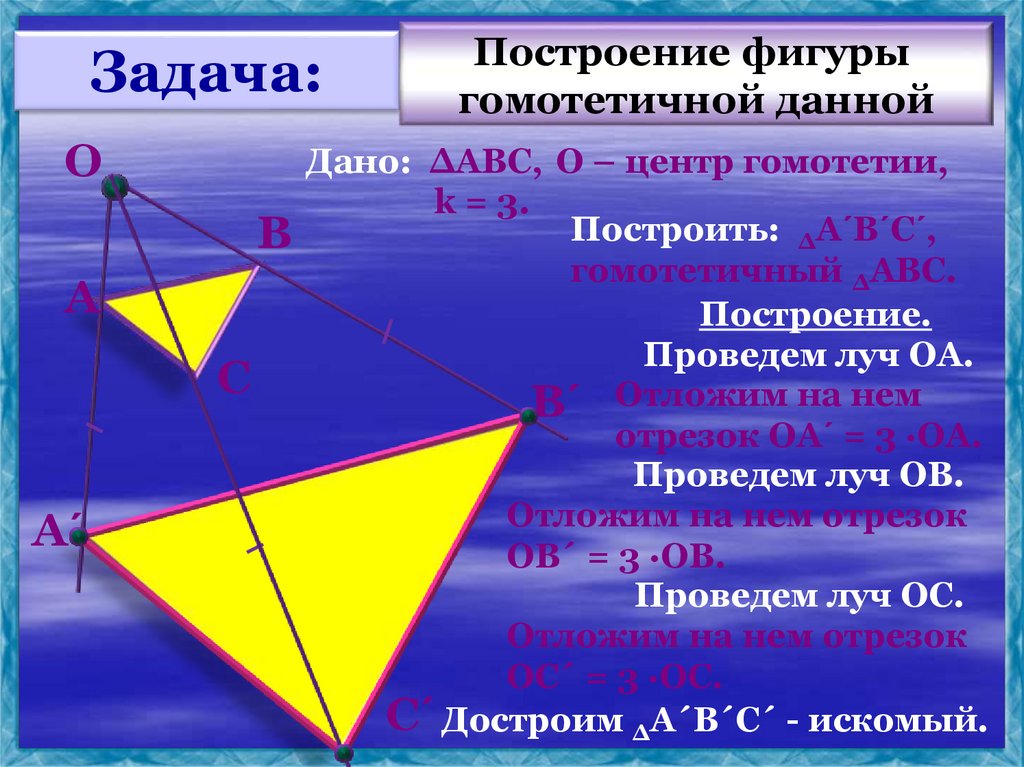
Построение фигуры
гомотетичной данной
Дано: ∆АВС, О – центр гомотетии,
k = 3.
Построить: ∆А´В´С´,
В
гомотетичный ∆АВС.
Построение.
Проведем луч ОА.
С
В´ Отложим на нем
отрезок ОА´ = 3 ∙ОА.
Проведем луч ОВ.
Отложим на нем отрезок
ОВ´ = 3 ∙ОВ.
Проведем луч ОС.
Отложим на нем отрезок
ОС´ = 3 ∙ОС.
С´ Достроим ∆А´В´С´ - искомый.























 Математика
Математика








