intro-fuzzy

1. Fuzzy logic

2. References

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
• L. Zadah, “Fuzzy sets as a basis of
possibility” Fuzzy Sets Systems,
Vol. 1, pp3-28, 1978.
• T. J. Ross, “Fuzzy Logic with
Engineering Applications”,
McGraw-Hill, 1995.
• K. M. Passino, S. Yurkovich,
"Fuzzy Control" Addison Wesley,
1998.
Fuzzy Logic
2

3. Introduction

Boolean logic uses sharp distinctions. It forces
us to draw lines between members of a class and
non- members. For instance, we may say, Tom is
tall because his height is 181 cm. If we drew a
line at 180 cm, we would find that David, who is
179 cm, is small. Is David really a small man or
we have just drawn an arbitrary line in the
sand?
Fuzzy logic reflects how people think. It
attempts to model our sense of words, our
decision making and our common sense. As a
result, it is leading to new, more human,
intelligent systems.

4. Introduction

Fuzzy, or multi-valued logic was introduced in the
1930s by Jan Lukasiewicz , a Polish philosopher.
While classical logic operates with only two values
1 (true) and 0 (false), Lukasiewicz introduced
logic that extended the range of truth values to all
real numbers in the interval between 0 and 1. He
used a number in this interval to represent the
possibility that a given statement was true or
false. For
example, the possibility that a man
181 cm tall is really tall might be set to a value of
0.86. It is
likely that the man is tall. This work
led to an
inexact reasoning technique often
called possibility theory.

5. Introduction

In 1965 Lotfi Zadeh, published his famous paper
“Fuzzy sets”. Zadeh extended the work on
possibility theory into a formal system of
mathematical logic, and introduced a new
concept for applying natural language terms.
This new
logic for representing and
manipulating fuzzy terms was called fuzzy logic.

6. Introduction

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
• Fuzzy logic:
• A way to represent variation or imprecision in logic
• A way to make use of natural language in logic
• Approximate reasoning
• Humans say things like "If it is sunny and
warm today, I will drive fast"
• Linguistic variables:
• Temp: {freezing, cool, warm, hot}
• Cloud Cover: {overcast, partly cloudy, sunny}
• Speed: {slow, fast}
Summary
2/9/2004
Fuzzy Logic
6

7. Introduction

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
• Fuzzy logic:
• A way to represent variation or imprecision in logic
• A way to make use of natural language in logic
• Approximate reasoning
• Humans say things like "If it is sunny and
warm today, I will drive fast"
• Linguistic variables:
• Temp: {freezing, cool, warm, hot}
• Cloud Cover: {overcast, partly cloudy, sunny}
• Speed: {slow, fast}
Summary
2/9/2004
Fuzzy Logic
7

8.

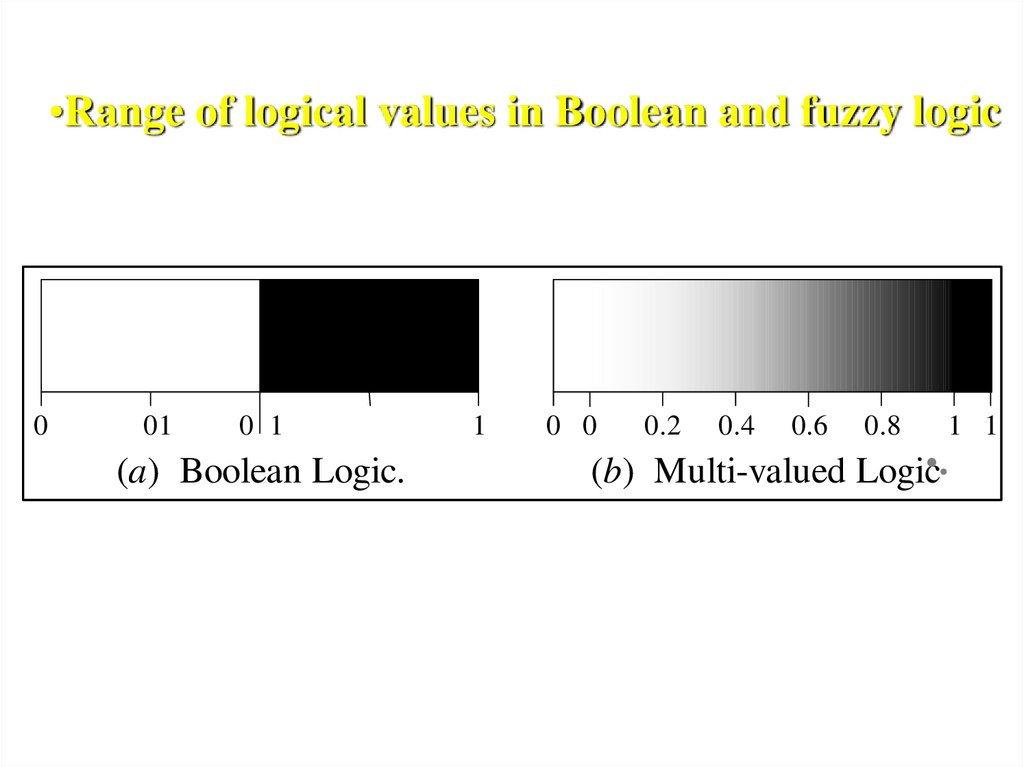
•Range of logical values in Boolean and fuzzy logic
0
01
0 1
(a) Boolean Logic.
1
0 0
0.2
0.4
0.6
0.8
1 1
(b) Multi-valued Logic•.

9.

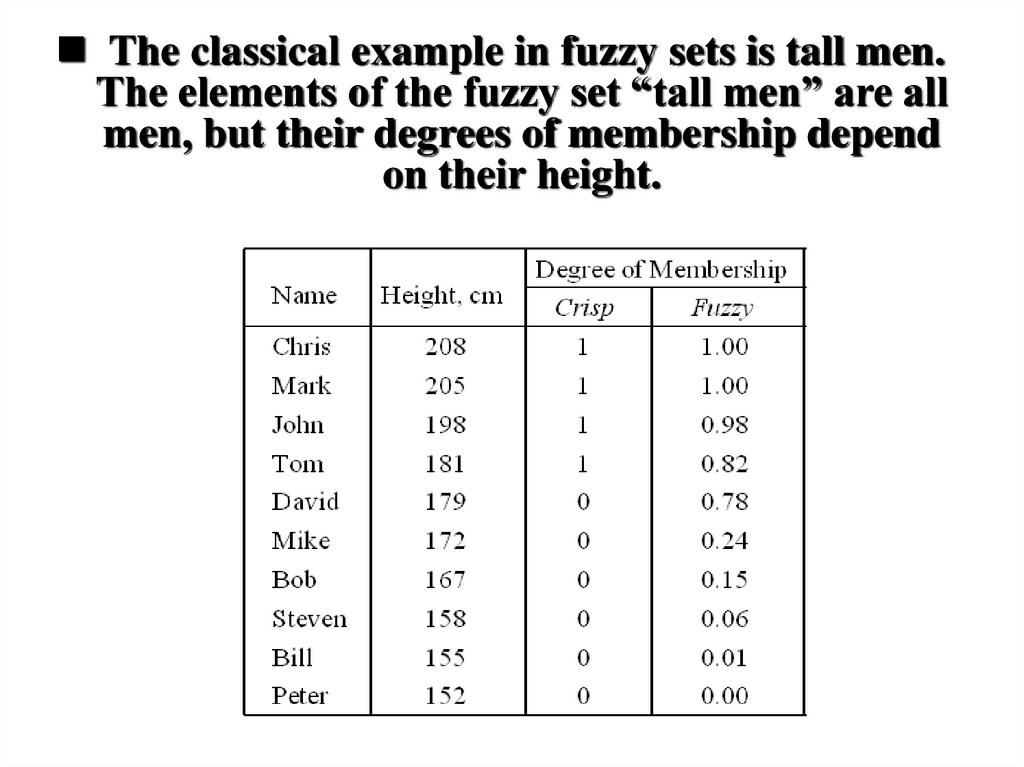
The classical example in fuzzy sets is tall men.
The elements of the fuzzy set “tall men” are all
men, but their degrees of membership depend
on their height.

10.

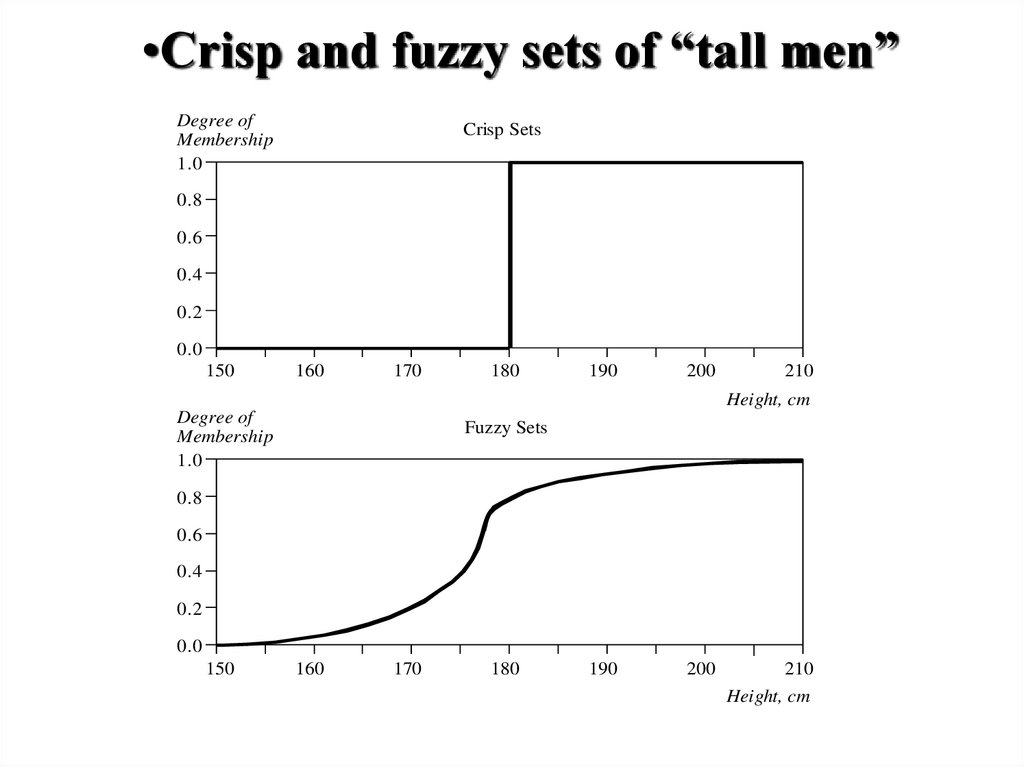
•Crisp and fuzzy sets of “tall men”
Degree of
Membership
1.0
Crisp Sets
0.8
0.6
0.4
0.2
0.0
150
160
170
180
190
200
210
Height, cm
Degree of
Membership
1.0
Fuzzy Sets
0.8
0.6
0.4
0.2
0.0
150
160
170
180
190
200
210
Height, cm

11. Crisp (Traditional) Variables

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
• Crisp variables represent precise
quantities:
• x = 3.1415296
• A {0,1}
• A proposition is either True or False
• A B C
• King(Richard) Greedy(Richard)
Evil(Richard)
• Richard is either greedy or he isn't:
• Greedy(Richard) {0,1}
Fuzzy Logic
11

12. Fuzzy Sets

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
• What if Richard is only somewhat
greedy?
• Fuzzy Sets can represent the degree
to which a quality is possessed.
• Fuzzy Sets (Simple Fuzzy Variables)
have values in the range of [0,1]
• Greedy(Richard) = 0.7
• Question: How evil is Richard?
Fuzzy Logic
12

13. Fuzzy Linguistic Variables

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
• Fuzzy Linguistic Variables are used to
represent qualities spanning a particular
spectrum
• Temp: {Freezing, Cool, Warm, Hot}
• Membership Function
• Question: What is the temperature?
• Answer: It is warm.
• Question: How warm is it?
Summary
2/9/2004
Fuzzy Logic
13

14. Membership Functions

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
1
Freezing
Cool
Warm
Hot
30
50
70
90
Fuzzy OR
Fuzzy AND
Example
Fuzzy Control
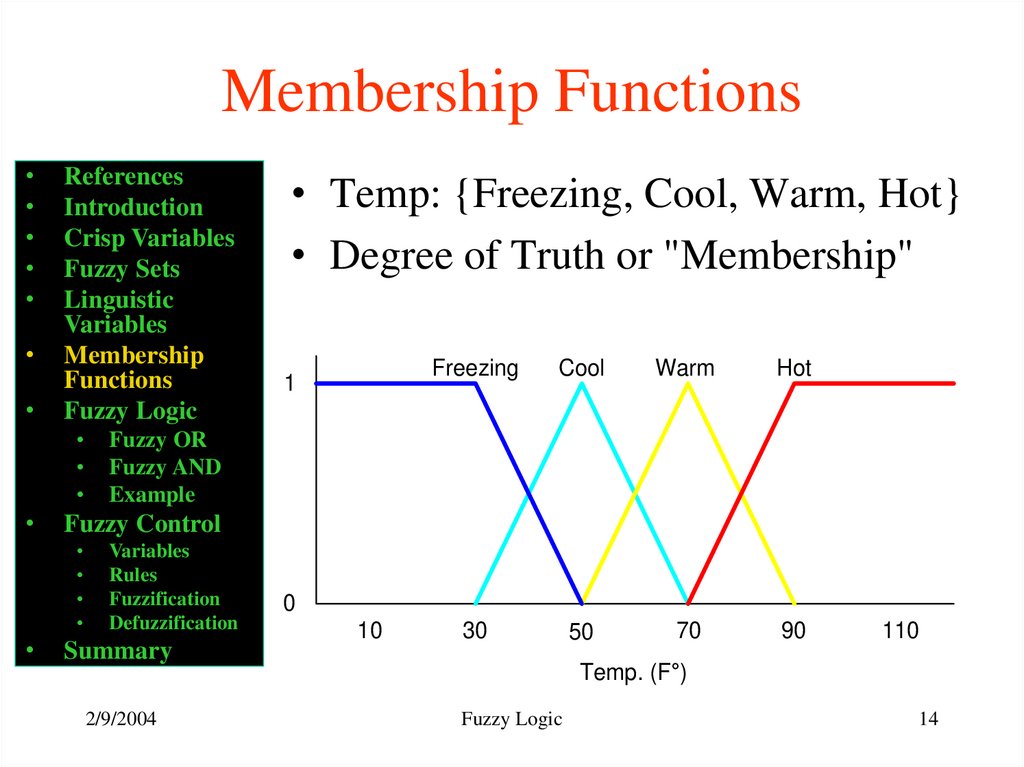
• Temp: {Freezing, Cool, Warm, Hot}
• Degree of Truth or "Membership"
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
0
10
110
Temp. (F°)
Fuzzy Logic
14

15. Membership Functions

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
1
Freezing
Cool
Warm
Hot
30
50
70
90
Fuzzy OR
Fuzzy AND
Example
Fuzzy Control
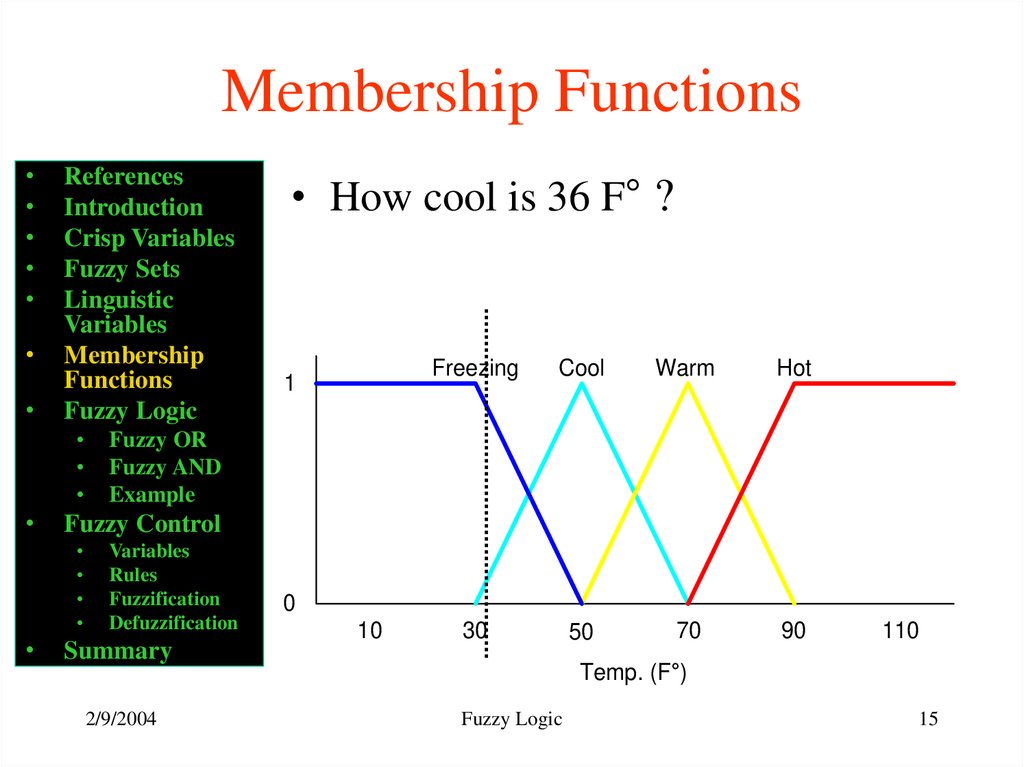
• How cool is 36 F° ?
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
0
10
110
Temp. (F°)
Fuzzy Logic
15

16. Membership Functions

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
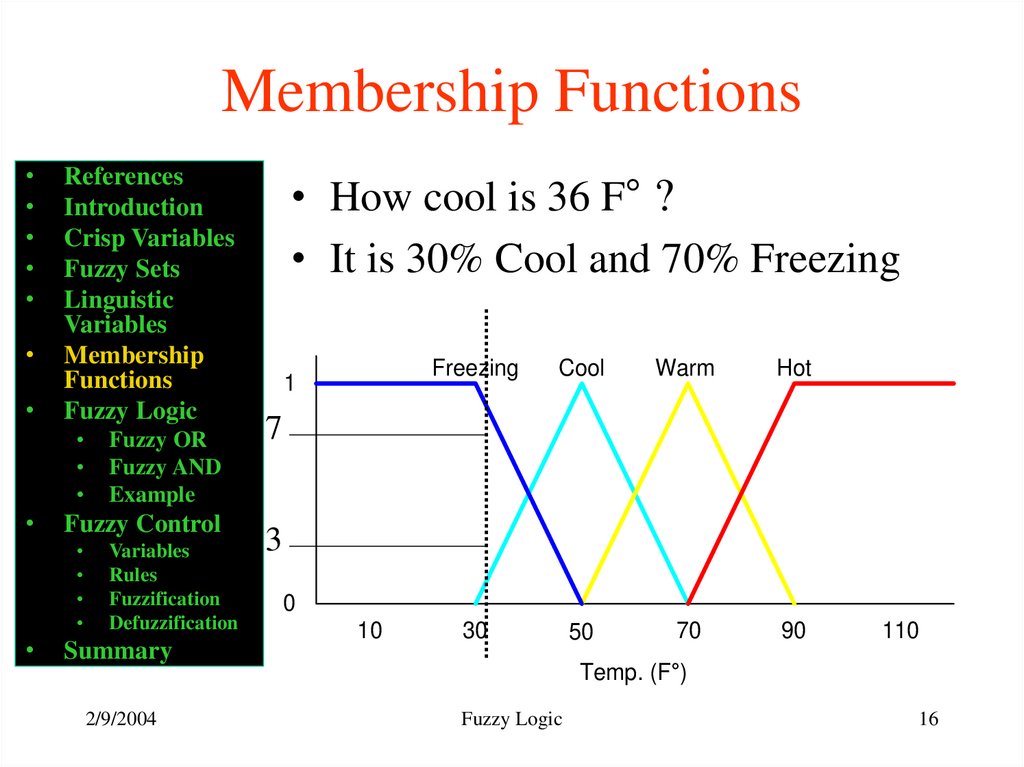
• How cool is 36 F° ?
• It is 30% Cool and 70% Freezing
1
Freezing
Cool
Warm
Hot
30
50
70
90
0.7
0.3
0
10
110
Temp. (F°)
Fuzzy Logic
16

17. Fuzzy Logic

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
• How do we use fuzzy membership
functions in predicate logic?
• Fuzzy logic Connectives:
• Fuzzy Conjunction,
• Fuzzy Disjunction,
• Operate on degrees of membership
in fuzzy sets
Summary
2/9/2004
Fuzzy Logic
17

18. Fuzzy Disjunction

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
B
A
1
1
Fuzzy OR
Fuzzy AND
Example
Fuzzy Control
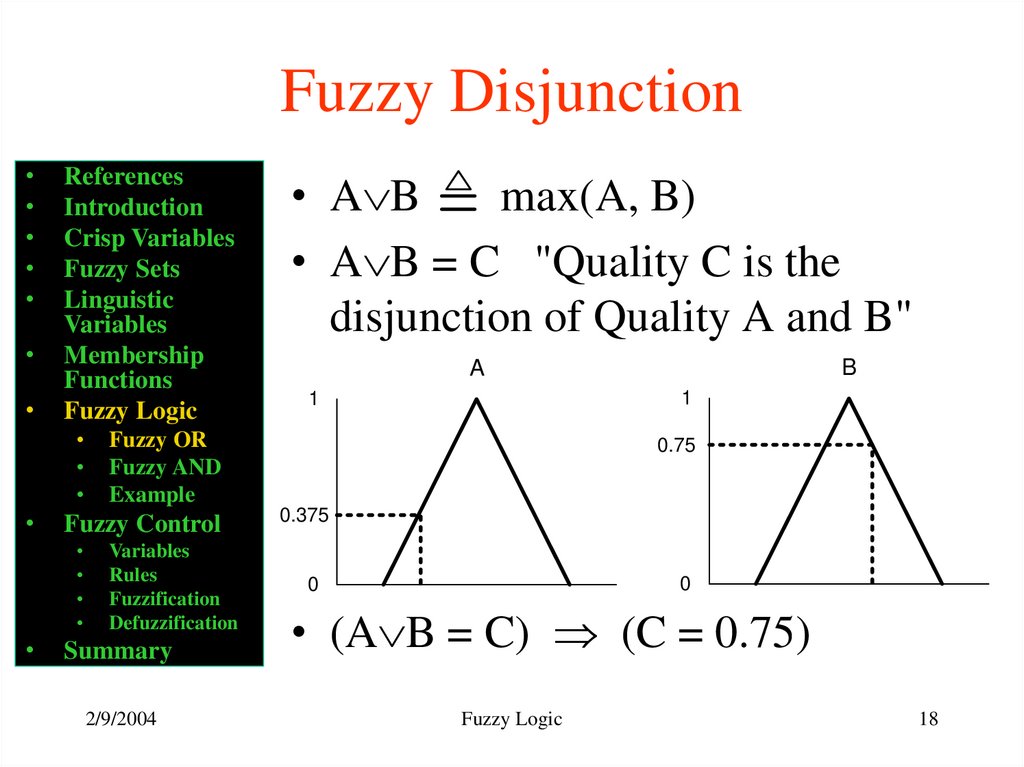
• A B
max(A, B)
• A B = C "Quality C is the
disjunction of Quality A and B"
0.75
0.375
0
0
• (A B = C) (C = 0.75)
Fuzzy Logic
18

19. Fuzzy Conjunction

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
B
A
1
1
Fuzzy OR
Fuzzy AND
Example
Fuzzy Control
• A B
min(A, B)
• A B = C "Quality C is the
conjunction of Quality A and B"
0.75
0.375
0
0
• (A B = C) (C = 0.375)
Fuzzy Logic
19

20. Example: Fuzzy Conjunction

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
B
A
1
1
0
.1 .2 .3 .4 .5 .6 .7 .8 .9
0
1 5 10 15 20 25 30 35 40
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
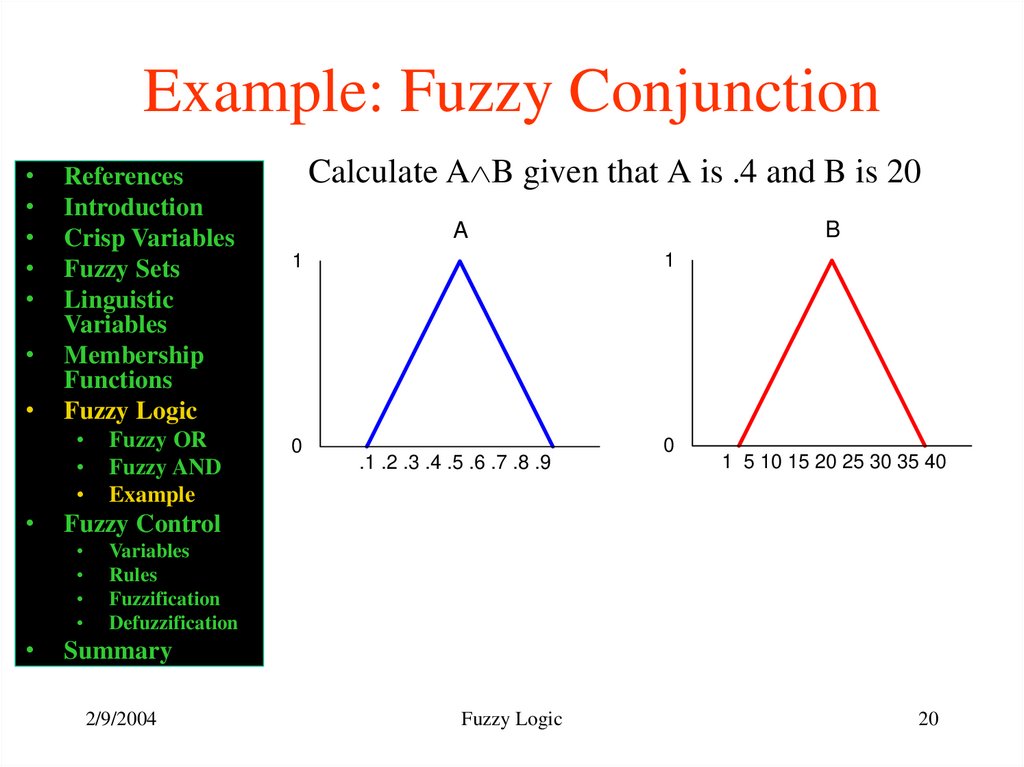
Calculate A B given that A is .4 and B is 20
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
Fuzzy Logic
20

21. Example: Fuzzy Conjunction

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
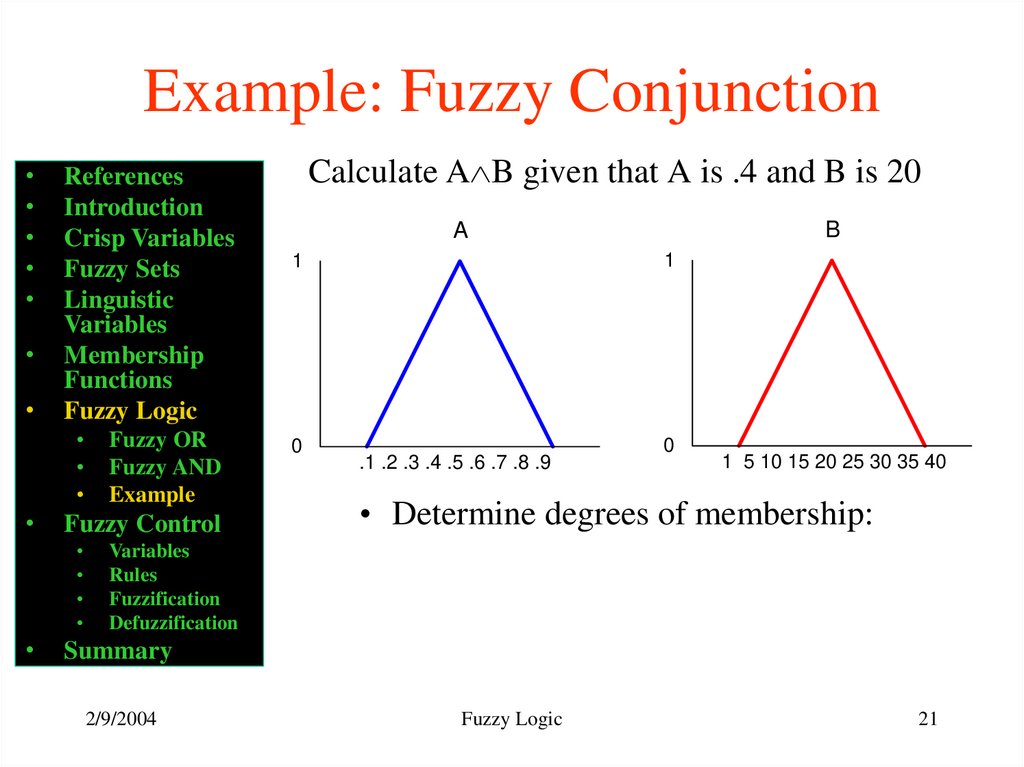
Calculate A B given that A is .4 and B is 20
B
A
1
1
0
.1 .2 .3 .4 .5 .6 .7 .8 .9
0
1 5 10 15 20 25 30 35 40
• Determine degrees of membership:
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
Fuzzy Logic
21

22. Example: Fuzzy Conjunction

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
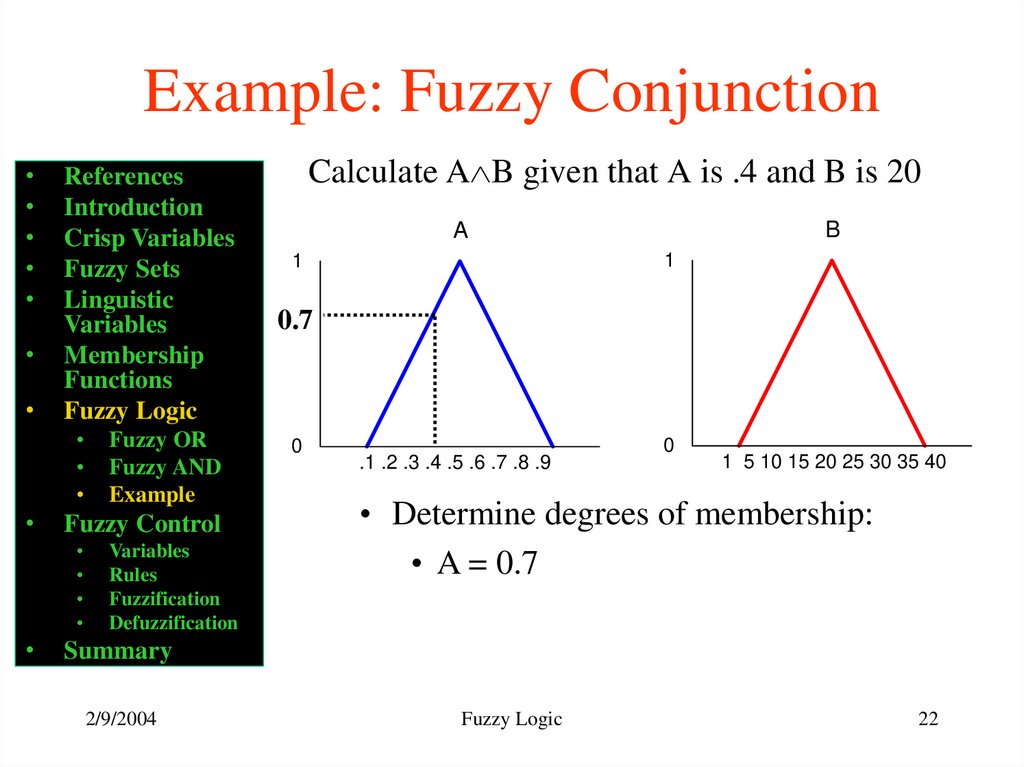
Calculate A B given that A is .4 and B is 20
B
A
1
1
0.7
0
.1 .2 .3 .4 .5 .6 .7 .8 .9
0
1 5 10 15 20 25 30 35 40
• Determine degrees of membership:
• A = 0.7
Summary
2/9/2004
Fuzzy Logic
22

23. Example: Fuzzy Conjunction

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
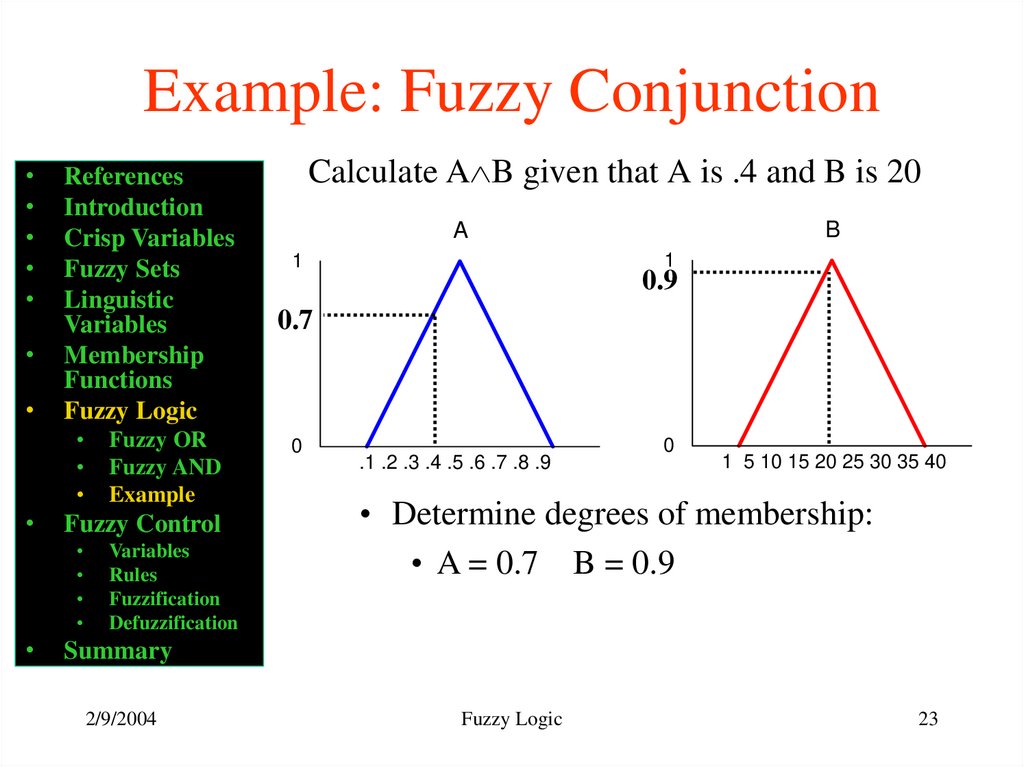
Calculate A B given that A is .4 and B is 20
B
A
1
1
0.9
0.7
0
.1 .2 .3 .4 .5 .6 .7 .8 .9
0
1 5 10 15 20 25 30 35 40
• Determine degrees of membership:
• A = 0.7 B = 0.9
Summary
2/9/2004
Fuzzy Logic
23

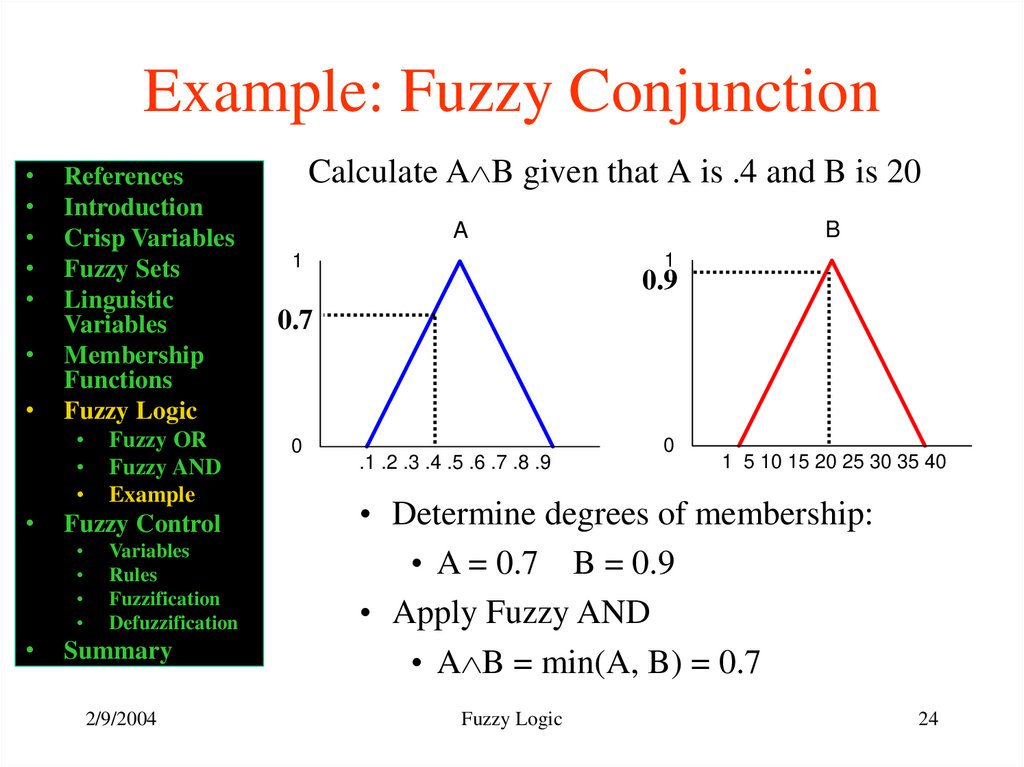
24. Example: Fuzzy Conjunction

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
Calculate A B given that A is .4 and B is 20
B
A
1
1
0.9
0.7
0
.1 .2 .3 .4 .5 .6 .7 .8 .9
0
1 5 10 15 20 25 30 35 40
• Determine degrees of membership:
• A = 0.7 B = 0.9
• Apply Fuzzy AND
• A B = min(A, B) = 0.7
Fuzzy Logic
24

25. Fuzzy Control

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
• Fuzzy Control combines the use of
fuzzy linguistic variables with fuzzy
logic
• Example: Speed Control
• How fast am I going to drive today?
• It depends on the weather.
• Disjunction of Conjunctions
Summary
2/9/2004
Fuzzy Logic
25

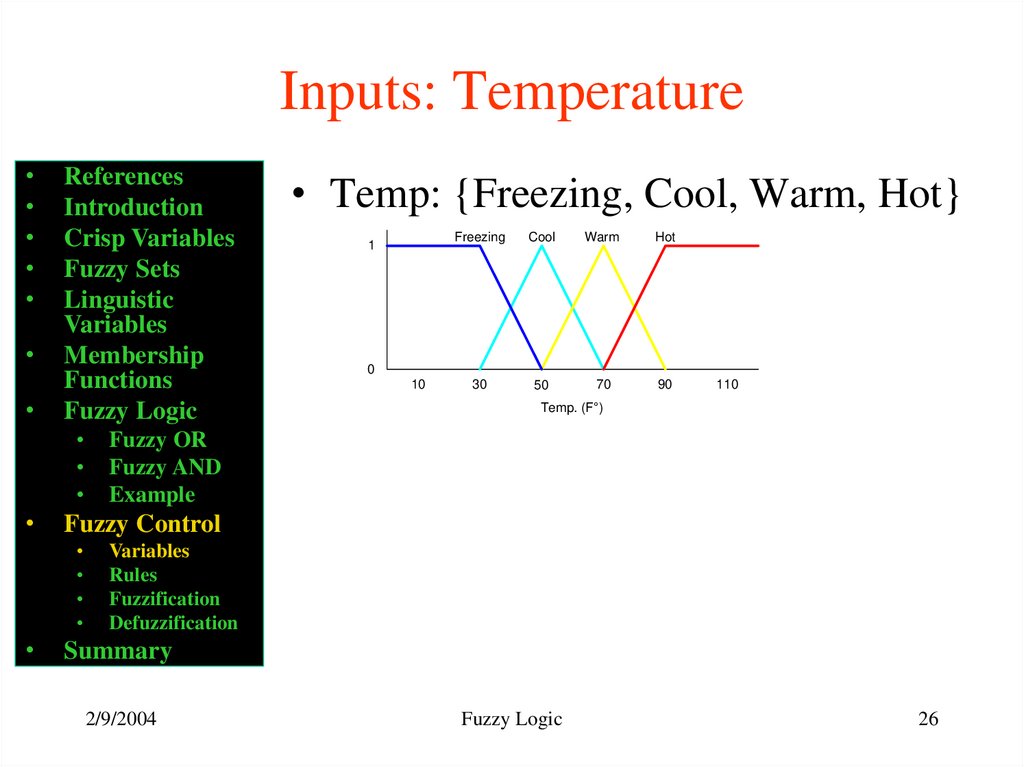
26. Inputs: Temperature

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
1
Freezing
Cool
Warm
Hot
30
50
70
90
0
10
110
Temp. (F°)
Fuzzy OR
Fuzzy AND
Example
Fuzzy Control
• Temp: {Freezing, Cool, Warm, Hot}
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
Fuzzy Logic
26

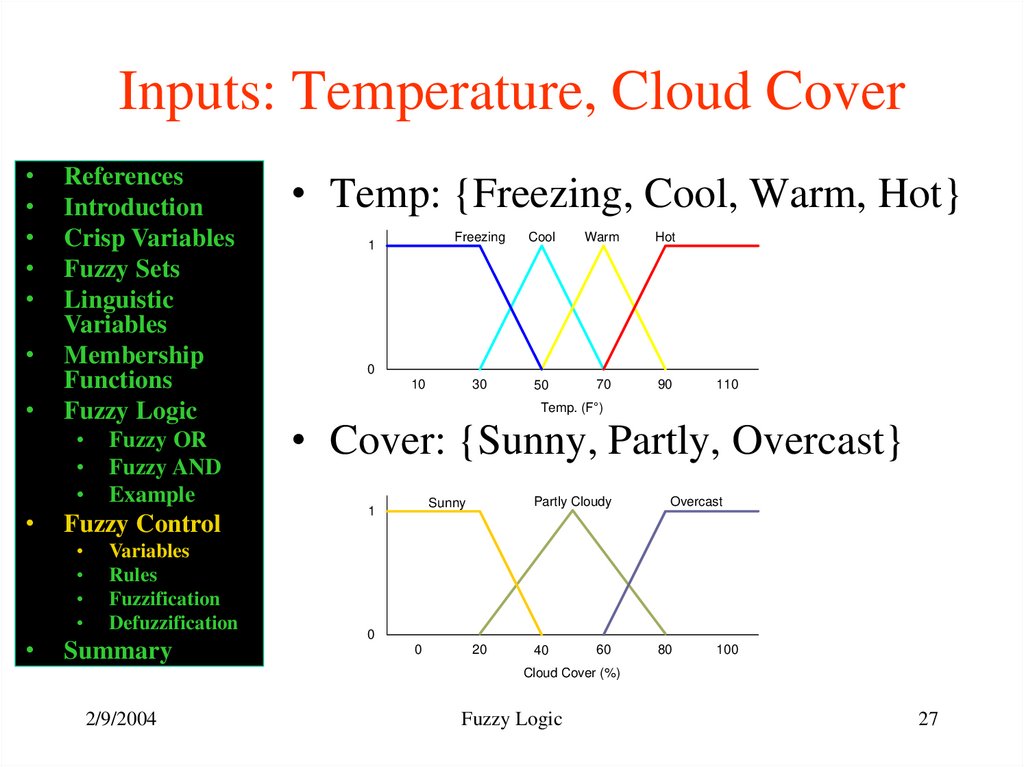
27. Inputs: Temperature, Cloud Cover

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
Summary
• Temp: {Freezing, Cool, Warm, Hot}
1
Freezing
Cool
Warm
Hot
30
50
70
90
0
10
110
Temp. (F°)
• Cover: {Sunny, Partly, Overcast}
Partly Cloudy
Sunny
1
Overcast
0
0
20
40
60
80
100
Cloud Cover (%)
2/9/2004
Fuzzy Logic
27

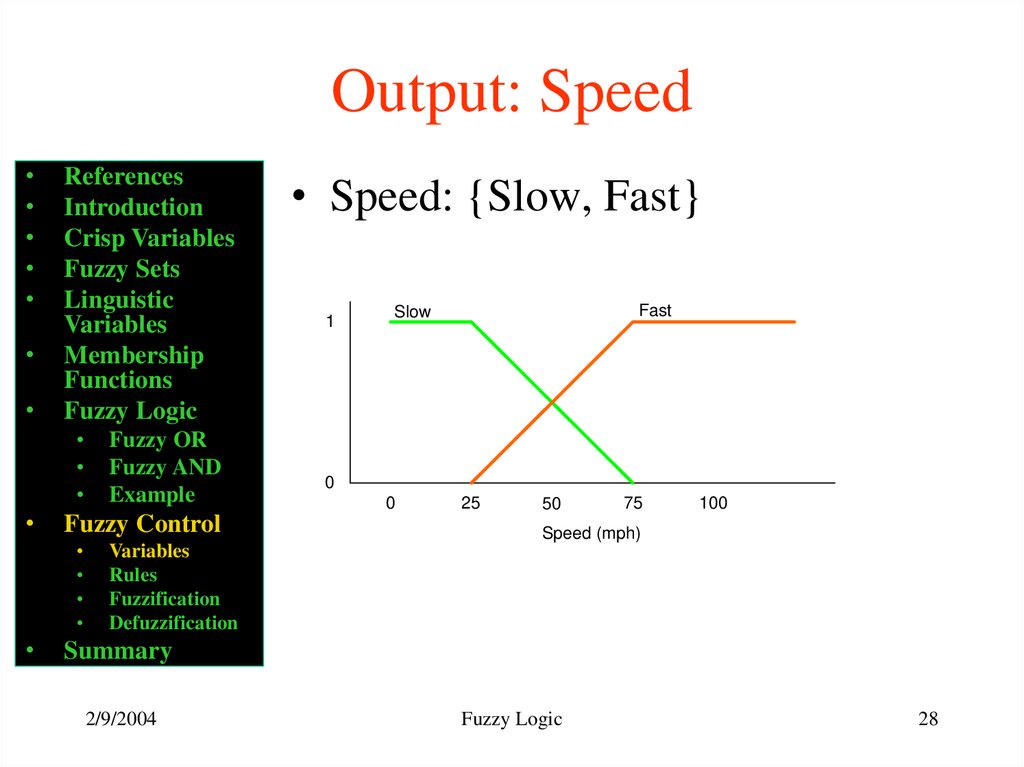
28. Output: Speed

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
• Speed: {Slow, Fast}
1
Fast
Slow
0
0
25
50
75
100
Speed (mph)
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
Fuzzy Logic
28

29. Rules

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
• If it's Sunny and Warm, drive Fast
Sunny(Cover) Warm(Temp) Fast(Speed)
• If it's Cloudy and Cool, drive Slow
Cloudy(Cover) Cool(Temp) Slow(Speed)
• Driving Speed is the combination of
output of these rules...
Summary
2/9/2004
Fuzzy Logic
29

30. Example Speed Calculation

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
• 65 F°
• 25 % Cloud Cover ?
Fuzzy OR
Fuzzy AND
Example
Fuzzy Control
• How fast will I go if it is
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
Fuzzy Logic
30

31. Fuzzification: Calculate Input Membership Levels

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
1
Freezing
Cool
Warm
Hot
30
50
70
90
0
10
110
Temp. (F°)
Fuzzy OR
Fuzzy AND
Example
Fuzzy Control
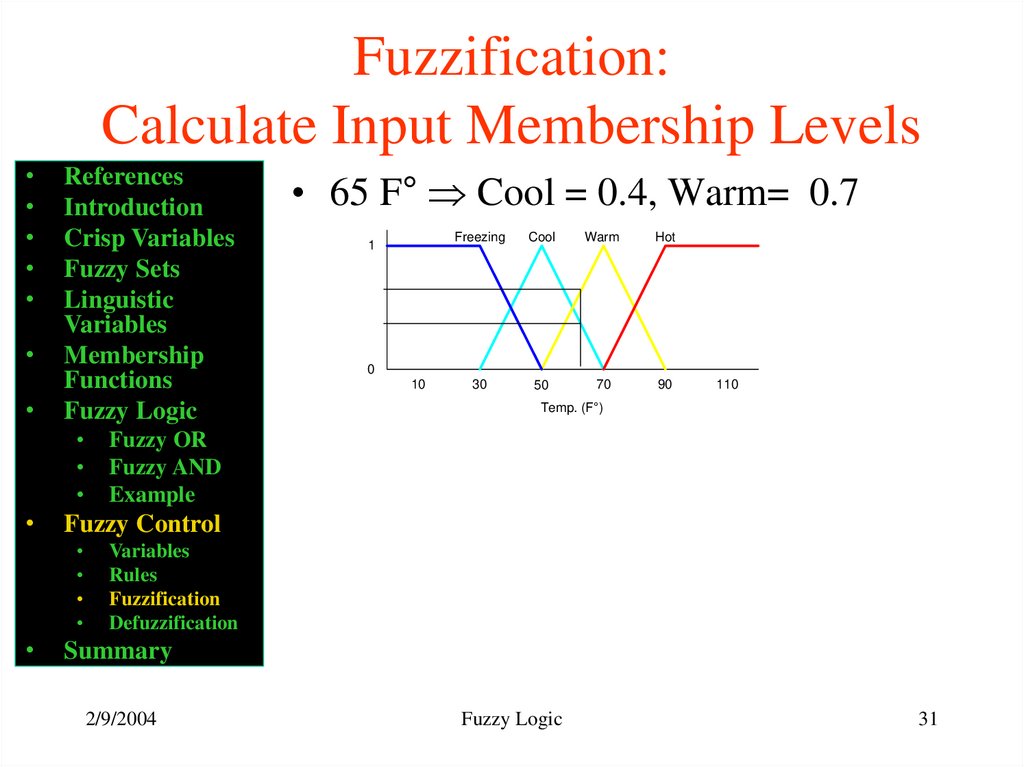
• 65 F° Cool = 0.4, Warm= 0.7
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
Fuzzy Logic
31

32. Fuzzification: Calculate Input Membership Levels

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
Summary
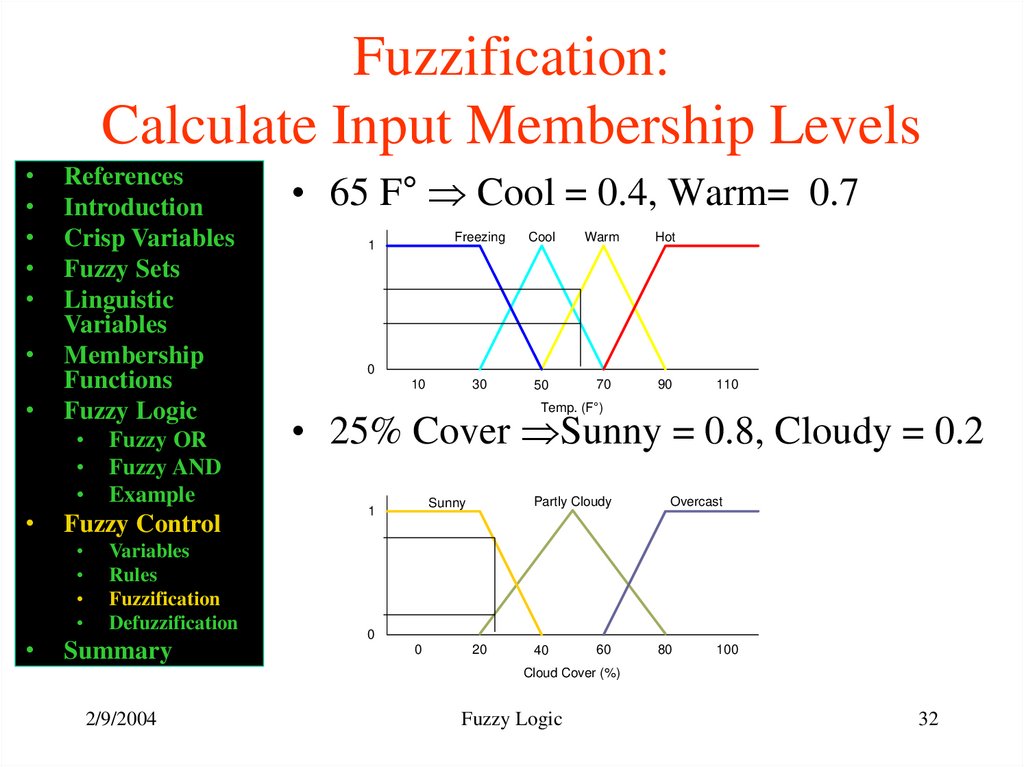
• 65 F° Cool = 0.4, Warm= 0.7
1
Freezing
Cool
Warm
Hot
30
50
70
90
0
10
110
Temp. (F°)
• 25% Cover Sunny = 0.8, Cloudy = 0.2
Partly Cloudy
Sunny
1
Overcast
0
0
20
40
60
80
100
Cloud Cover (%)
2/9/2004
Fuzzy Logic
32

33. ...Calculating...

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
• If it's Sunny and Warm, drive Fast
Sunny(Cover) Warm(Temp) Fast(Speed)
0.8 0.7 = 0.7
Fast = 0.7
• If it's Cloudy and Cool, drive Slow
Cloudy(Cover) Cool(Temp) Slow(Speed)
0.2 0.4 = 0.2
Slow = 0.2
Fuzzy Logic
33

34. Defuzzification: Constructing the Output

Defuzzification:
Constructing the Output
References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
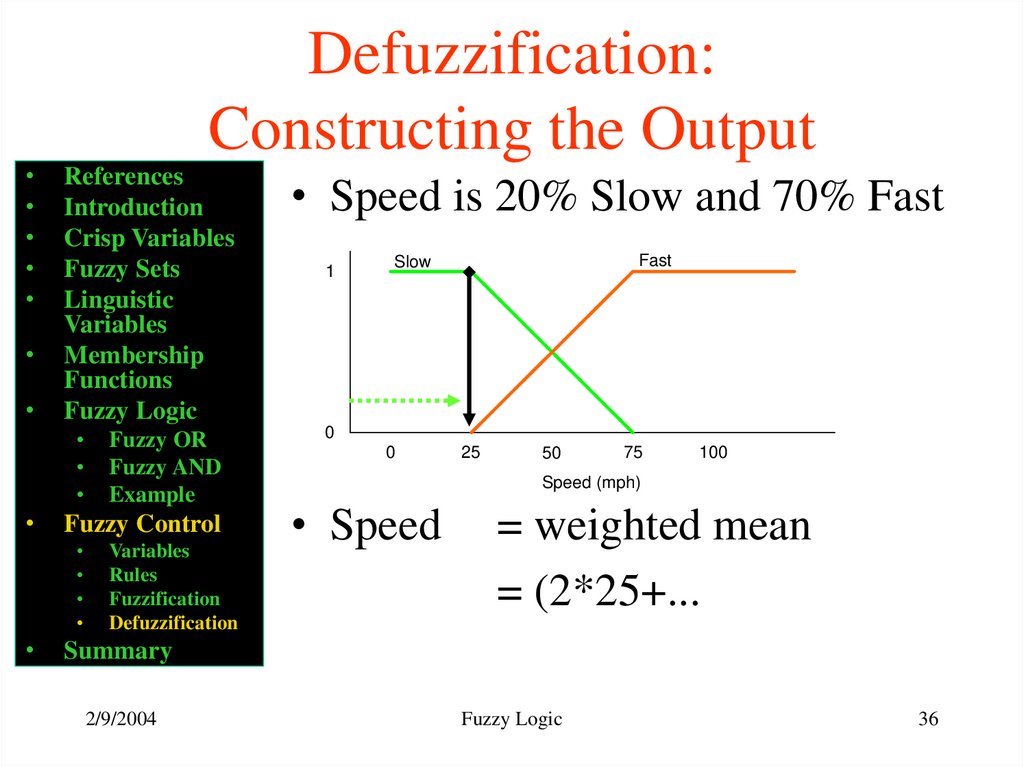
• Speed is 20% Slow and 70% Fast
1
Fast
Slow
0
0
25
50
75
100
Speed (mph)
• Find centroids: Location where
membership is 100%
Summary
2/9/2004
Fuzzy Logic
34

35. Defuzzification: Constructing the Output

Defuzzification:
Constructing the Output
References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
• Speed is 20% Slow and 70% Fast
1
Fast
Slow
0
0
25
50
75
100
Speed (mph)
• Find centroids: Location where
membership is 100%
Summary
2/9/2004
Fuzzy Logic
35

36. Defuzzification: Constructing the Output

Defuzzification:
Constructing the Output
References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
• Speed is 20% Slow and 70% Fast
1
Fast
Slow
0
0
25
50
75
100
Speed (mph)
• Speed
= weighted mean
= (2*25+...
Summary
2/9/2004
Fuzzy Logic
36

37. Defuzzification: Constructing the Output

Defuzzification:
Constructing the Output
References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
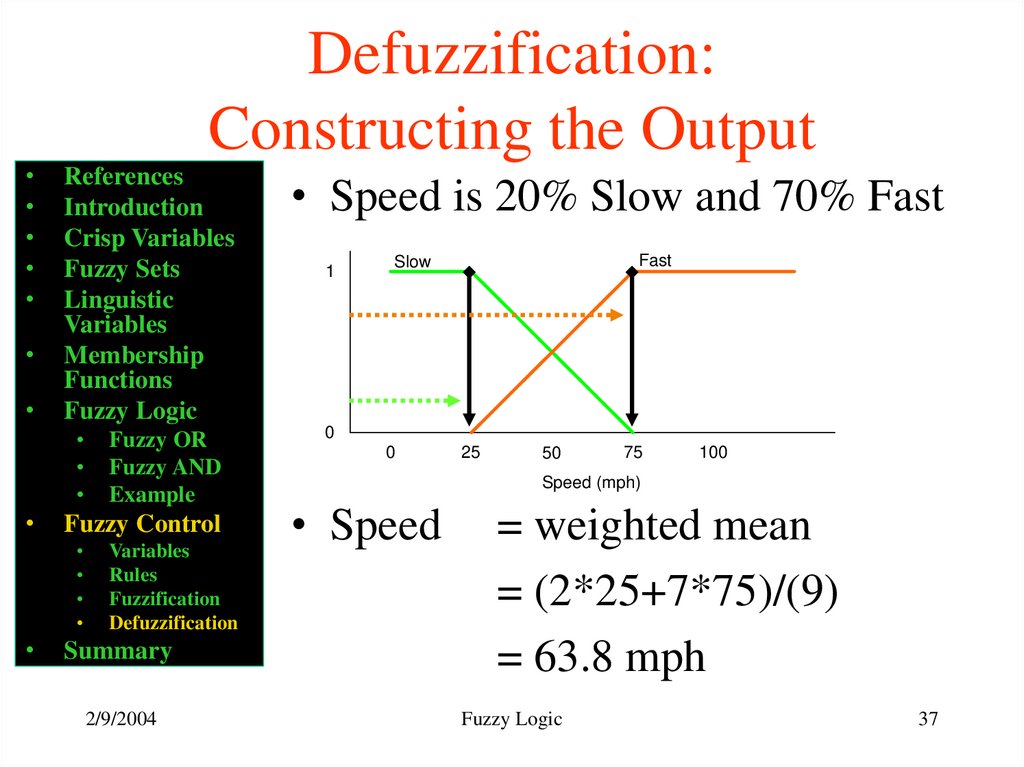
• Speed is 20% Slow and 70% Fast
1
Fast
Slow
0
0
25
50
75
100
Speed (mph)
• Speed
= weighted mean
= (2*25+7*75)/(9)
= 63.8 mph
Fuzzy Logic
37

38. Notes: Follow-up Points

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
• Fuzzy Logic Control allows for the
smooth interpolation between
variable centroids with relatively
few rules
• This does not work with crisp
(traditional Boolean) logic
• Provides a natural way to model
some types of human expertise in a
computer program
Fuzzy Logic
38

39. Notes: Drawbacks to Fuzzy logic

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
• Requires tuning of membership
functions
• Fuzzy Logic control may not scale
well to large or complex problems
• Deals with imprecision but not
uncertainty
Variables
Rules
Fuzzification
Defuzzification
Summary
2/9/2004
Fuzzy Logic
39

40.

Fuzzy Set Theory
An object has a numeric “degree of membership”
Normally, between 0 and 1 (inclusive)
0 membership means the object is not in the set
1 membership means the object is fully inside the set
In between means the object is partially in the set
40

41.

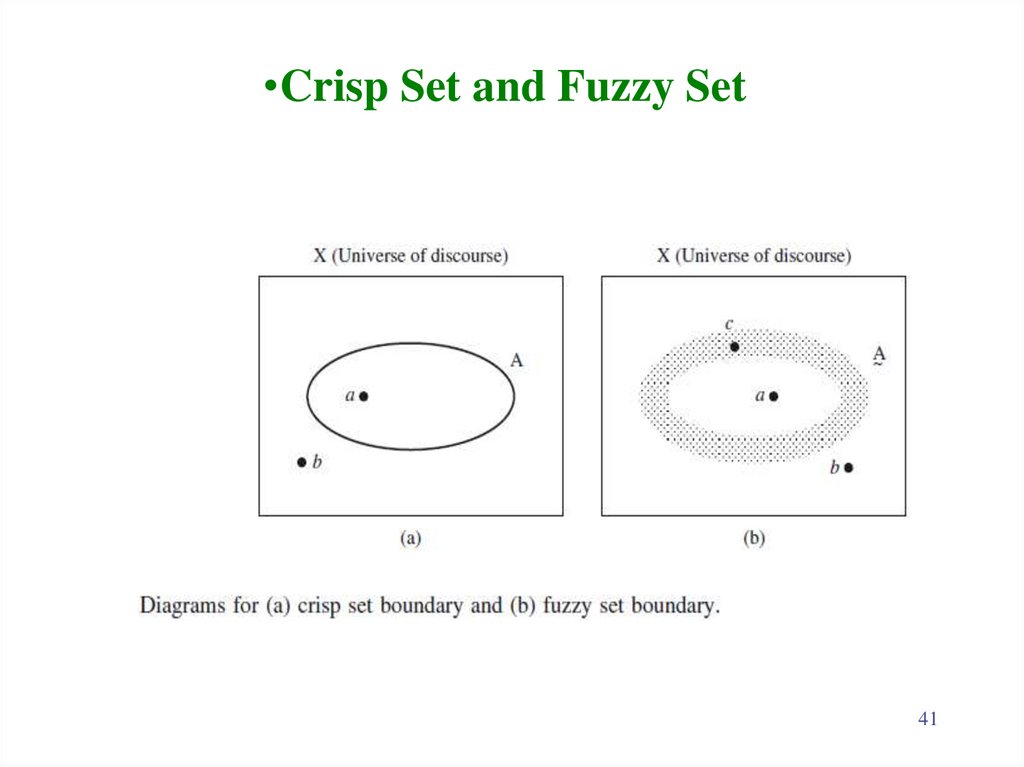
•Crisp Set and Fuzzy Set
41

42.

If U is a collection of objects denoted generically by x, then a
fuzzy set A in U is defined as a set of ordered pairs:
membership
function
U : universe of
discourse.
42

43.

•Fuzzy Sets
•Characteristic function X, indicating the
belongingness of x to the set A
X(x) = 1 x A
0 x A
•or called membership
•Hence,
•A B XA B(x)
= XA(x) XB(x)
= max(XA(x),XB(x))
•Note: Some books use + for , but still it is not
ordinary addition!
43

44.

•Fuzzy Sets
•A B XA B(x)
= XA(x) XB(x)
= min(XA(x),XB(x))
•A’ XA’(x)
• = 1 – XA(x)
•A’’ = A
44

45.

•Fuzzy Set Operations
• A B(x) = A(x) B(x)
= max( A(x), B(x))
• A B(x) = A(x) B(x)
= min( A(x), B(x))
• A’(x) = 1 - A(x)
•De Morgan’s Law also holds:
(A B)’ = A’ B’
(A B)’ = A’ B’
•But, in general
A A’ X
A A’
45

46.

•Fuzzy Set Operations
•Union of fuzzy sets A
and B
•.
∼
•Intersection of fuzzy sets
Aand B
•.
∼
46

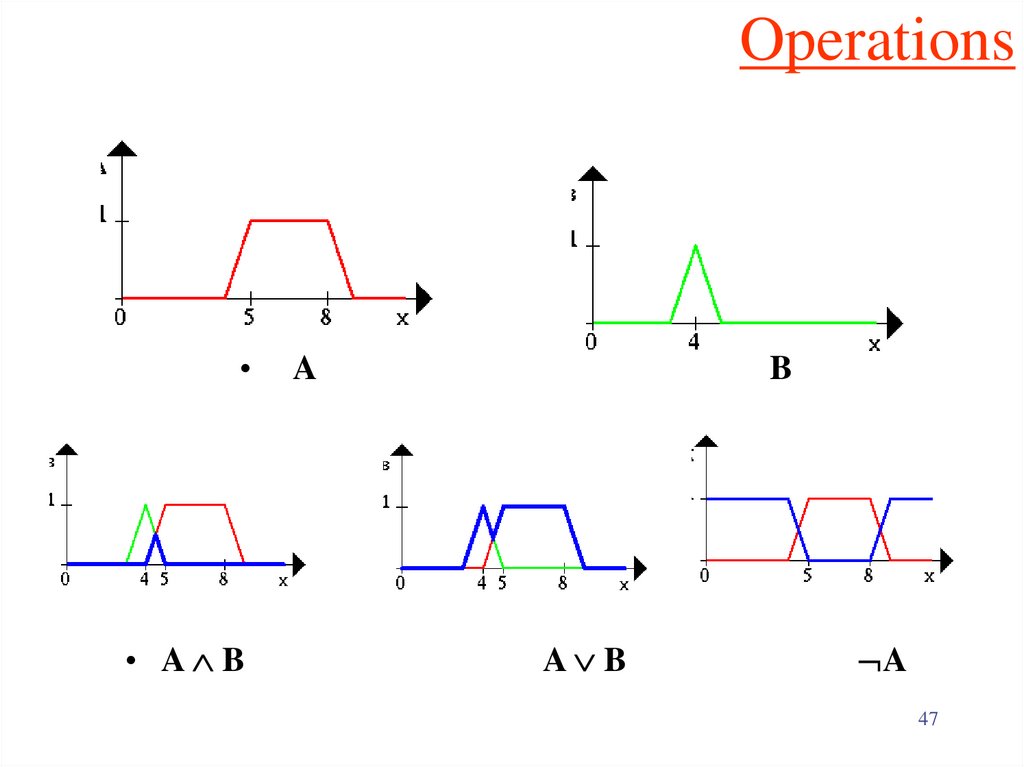
47. Operations

• A B
A
B
A B
A
47

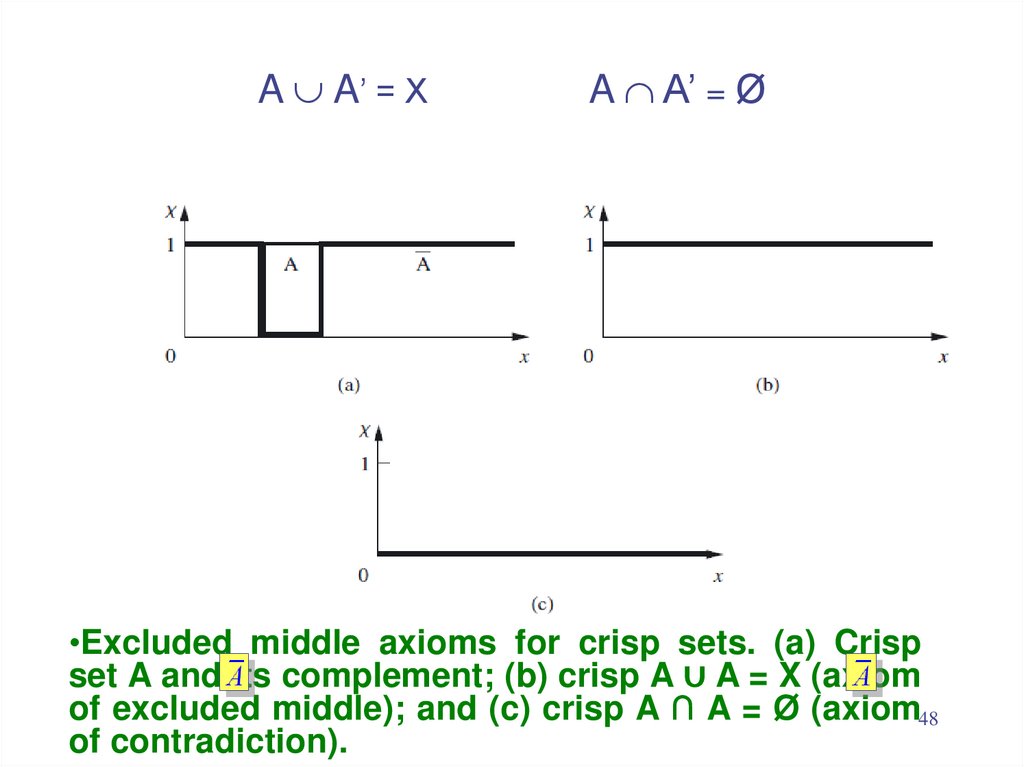
48. A  A’ = X A  A’ = Ø

A A’ = X
A A’ = Ø
•Excluded middle axioms for crisp sets. (a) Crisp
set A and its complement; (b) crisp A ∪ A = X (axiom
of excluded middle); and (c) crisp A ∩ A = Ø (axiom48
of contradiction).

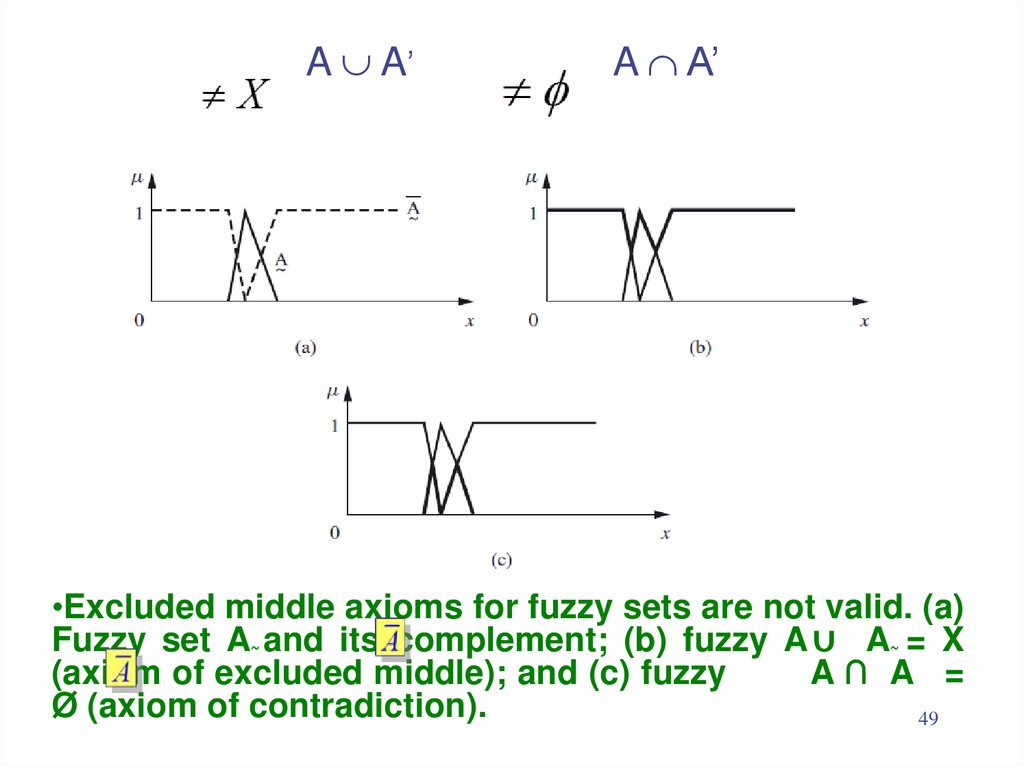
49. A  A’ A  A’

A A’
A A’
•Excluded middle axioms for fuzzy sets are not valid. (a)
Fuzzy set A and its complement; (b) fuzzy A ∪ A = X
(axiom of excluded middle); and (c) fuzzy
A∩ A =
Ø (axiom of contradiction).
49
∼
∼

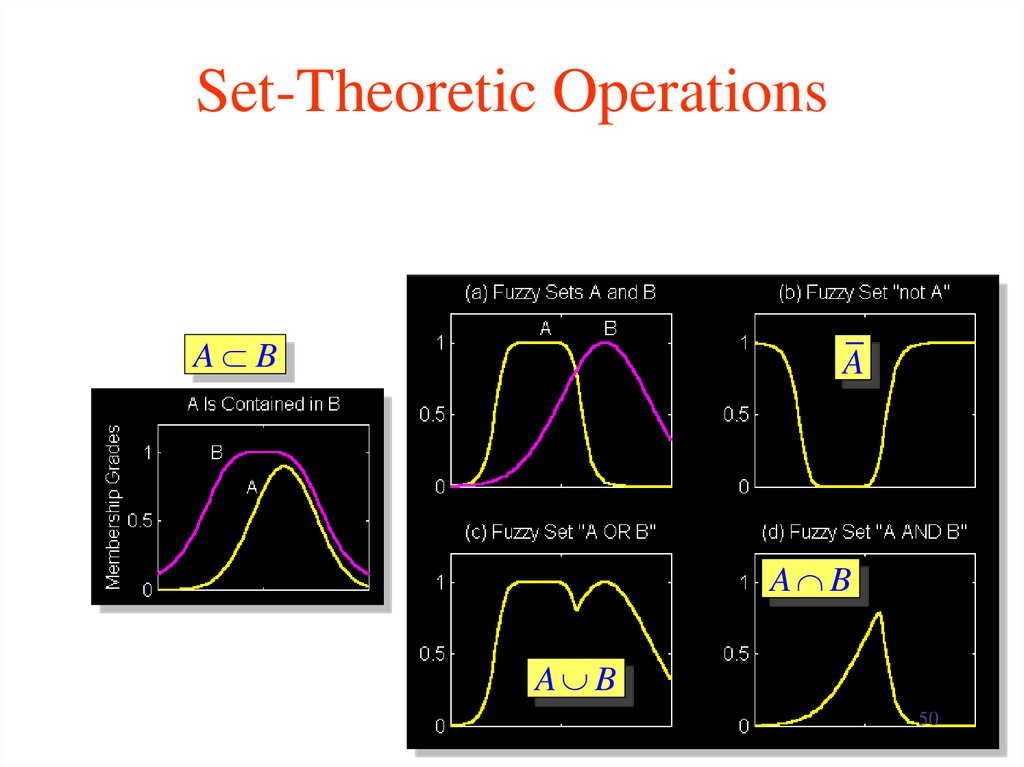
50. Set-Theoretic Operations

A B
A
A B
A B
50

51. Examples of Fuzzy Set Operations

• Fuzzy union ( ): the union of two fuzzy sets is the
maximum (MAX) of each element from two sets.
• E.g.
• A = {1.0, 0.20, 0.75}
• B = {0.2, 0.45, 0.50}
• A B = {MAX(1.0, 0.2), MAX(0.20, 0.45), MAX(0.75,
0.50)} = {1.0, 0.45, 0.75}
51

52. Examples of Fuzzy Set Operations

• Fuzzy intersection ( ): the intersection
of two fuzzy sets is just the MIN of each
element from the two sets.
• E.g.
• A B = {MIN(1.0, 0.2), MIN(0.20,
0.45), MIN(0.75, 0.50)} = {0.2, 0.20,
0.50}
52

53. Examples of Fuzzy Set Operations

53

54.

•Properties of Fuzzy Sets
•A B = B A
•A B = B A
•A (B C) = (A B) C
•A (B C) = (A B) C
•A (B C) = (A B) (A C)
•A (B C) = (A B) (A C)
•A A = A
•A X = X
•A = A
A A=A
A X=A
A =
•If A B C, then A C
•A’’ = A
54

55.

•Fuzzy Sets
•Note (x) [0,1]
not {0,1} like Crisp set
•A = { A(x1) / x1 + A(x2) / x2 + …}
= { A(xi) / xi}
•Note:‘+’ add
‘/ ’ divide
•Only for representing
membership.
element
and
its
•Also some books use (x) for Crisp Sets too.
55

56. Example (Discrete Universe)

•# courses a
student may
take in a
(1, 0.1) (2, 0.3) (3, 0.8) (4,1) semester.
•appropriat
A
e
(5,
0.9)
(6,
0.5)
(7,
0.2)
(8,
0.1)
•# courses
taken
U {1, 2,3, 4,5, 6, 7,8}
•1
A ( x)
•0.5
•0
•2
•4
•6
•8
•x : # courses
56

57. Example (Discrete Universe)

•# courses a
student may
take in a
(1, 0.1) (2, 0.3) (3, 0.8) (4,1) semester.
•appropriat
A
e
(5,
0.9)
(6,
0.5)
(7,
0.2)
(8,
0.1)
•# courses
taken
•Alternative Representation:
U {1, 2,3, 4,5, 6, 7,8}
A 0.1/ 1 0.3/ 2 0.8/ 3 1.0/ 4 0.9/ 5 0.5/ 6 0.2/ 7 0.1/ 8
57

58. Example (Continuous Universe)

•U : the set of positive real numbers
•possible
ages
B ( x, B ( x)) x U
B ( x)
•1
about 50 years old
x 50
1
5
4
1.2
1
•Alternative
Representation:
B
B ( x)
0.8
0.6
0.4
0.2
1
R 1 x 550
4
x
0
0
20
40
60
•x : age
80
58
100

59. Alternative Notation

A ( x, A ( x)) x U
•U : discrete universe
A A ( xi ) / xi
xi U
•U : continuous universe
A A ( x) / x
U
•Note that and integral signs stand for the union of
membership grades; “ / ” stands for a marker and does not
imply division.
59

60. Fuzzy Disjunction

• A B
max(A, B)
• A B = C "Quality C is the
disjunction of Quality A and B"
B
A
1
1
0.75
0.375
0
0
• (A B = C) (C = 0.75)
60

61. Fuzzy Conjunction

• A B
min(A, B)
• A B = C "Quality C is the
conjunction of Quality A and B"
B
A
1
1
0.75
0.375
0
0
• (A B = C) (C = 0.375)
61

62. Example: Fuzzy Conjunction

Calculate A B given that A is .4 and B is 20
B
A
1
1
0
.1 .2 .3 .4 .5 .6 .7 .8 .9
0
1 5 10 15 20 25 30 35 40
62

63. Example: Fuzzy Conjunction

Calculate A B given that A is .4 and B is 20
B
A
1
1
0
.1 .2 .3 .4 .5 .6 .7 .8 .9
0
1 5 10 15 20 25 30 35 40
• Determine degrees of membership:
63

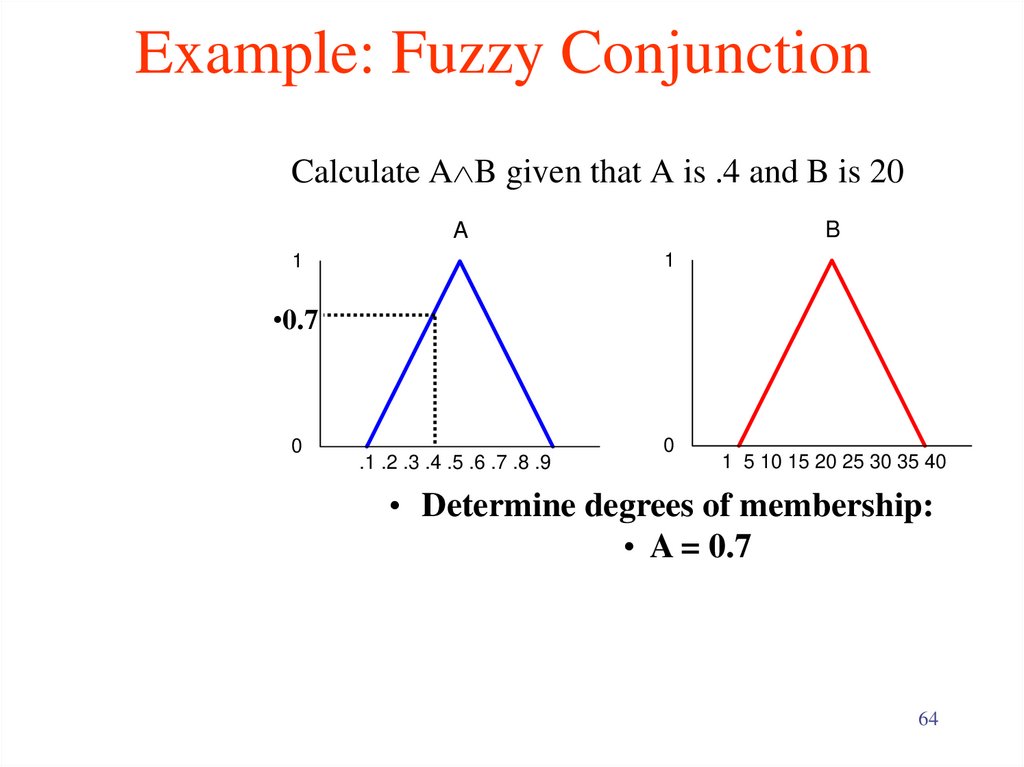
64. Example: Fuzzy Conjunction

Calculate A B given that A is .4 and B is 20
B
A
1
1
•0.7
0
.1 .2 .3 .4 .5 .6 .7 .8 .9
0
1 5 10 15 20 25 30 35 40
• Determine degrees of membership:
• A = 0.7
64

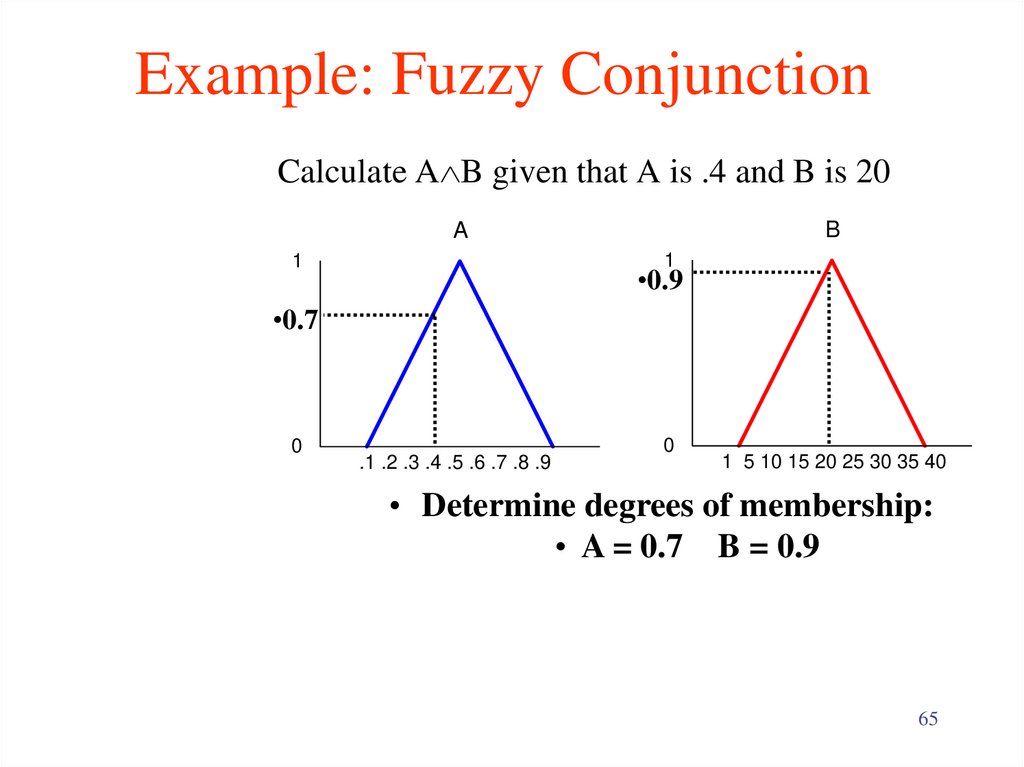
65. Example: Fuzzy Conjunction

Calculate A B given that A is .4 and B is 20
B
A
1
1
•0.9
•0.7
0
.1 .2 .3 .4 .5 .6 .7 .8 .9
0
1 5 10 15 20 25 30 35 40
• Determine degrees of membership:
• A = 0.7 B = 0.9
65

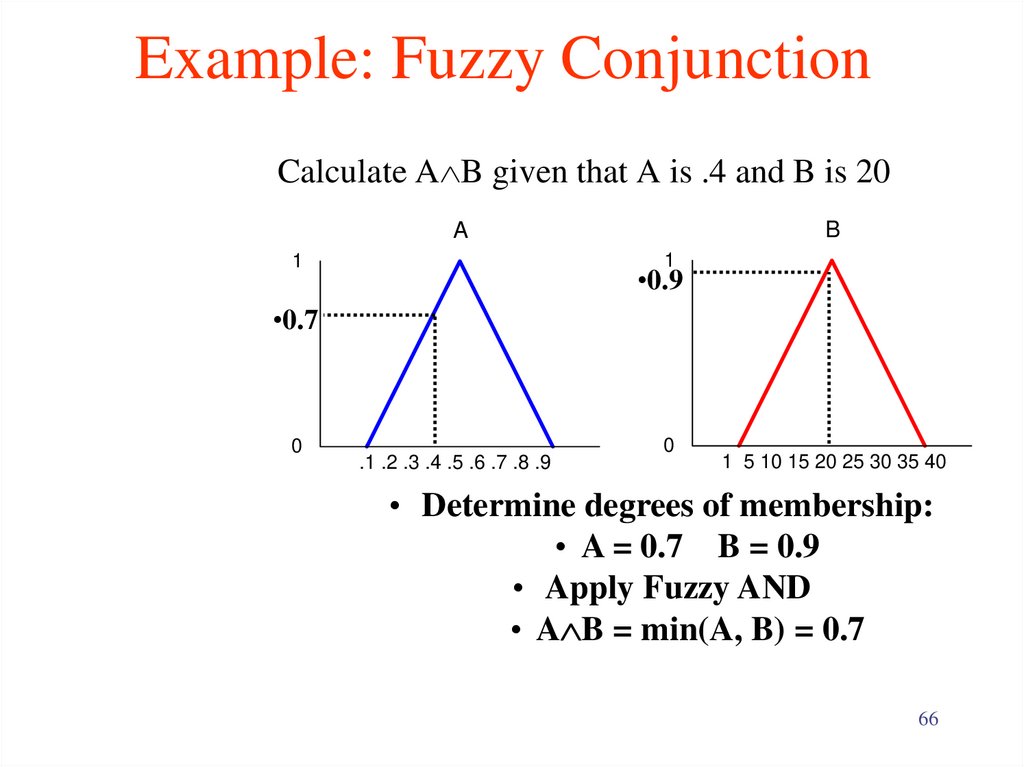
66. Example: Fuzzy Conjunction

Calculate A B given that A is .4 and B is 20
B
A
1
1
•0.9
•0.7
0
.1 .2 .3 .4 .5 .6 .7 .8 .9
0
1 5 10 15 20 25 30 35 40
• Determine degrees of membership:
• A = 0.7 B = 0.9
• Apply Fuzzy AND
• A B = min(A, B) = 0.7
66

67. Generalized Union/Intersection

• Generalized Union
•t-norm
triangular norm.
Or called
• Generalized Intersection
•t-conorm
Or called s-norm.
67

68. T-norms and S-norms

And/OR definitions are called T-norms (S-norms)
Duals of one another
A definition of one defines the other implicitly
Many different ones have been proposed
Min/Max, Product/Bounded-Sum, etc.
Tons of theoretical literature
We will not go into this.
68

69. Examples: T-Norm & T-Conorm

Examples: T-Norm & T-Conorm
• Minimum/Maximum:
T (a, b) min(a, b) a b
S (a, b) max(a, b) a b
• Lukasiewicz:
T (a, b) max(a b 1, 0) LAND(a, b)
S (a, b) min(a b,1) LOR(a, b)
69

70. Summary

References
Introduction
Crisp Variables
Fuzzy Sets
Linguistic
Variables
Membership
Functions
Fuzzy Logic
Fuzzy Control
Fuzzy OR
Fuzzy AND
Example
Variables
Rules
Fuzzification
Defuzzification
• Fuzzy Logic provides way to calculate
with imprecision and vagueness
• Fuzzy Logic can be used to represent
some kinds of human expertise
• Fuzzy Membership Sets
• Fuzzy Linguistic Variables
• Fuzzy AND and OR
• Fuzzy Control
Summary
2/9/2004
Fuzzy Logic
70