ТИК Лекц 1

1.

ТЕОРИЯ
ИНФОРМАЦИИ И
КОДИРОВАНИЯ
Семес- Трудоемтр
кость,
кр.
1
3
Общий
объем
курса,
час.
Лекции,
час.
108
24
Практич. Лаборат. СРС,
Форма
занятия, работы, час. контроля,
час.
час.
Экз./зачет
8
16
24
36
Экзамен
Дисциплина для групп: М*-502, М*-512, М*-522,
М*-532, М*-В01
Автор: доцент, к.т.н. Березкин Евгений Феофанович

2.

Содержание курса
Математические модели
детерминированных
периодических сигналов
2. Математические модели детерминированных
непериодических сигналов
3. Математические модели случайных сигналов
1.
Элементы теории дискретизации
непрерывных функций
5. Элементы теории оптимального приема
и статистических решений
4.
2010
Изд. 1
«НИЯУ
МИФИ»
2018
Изд. 2
«ЛАНЬ»
2019
Изд. 3
«ЛАНЬ»
6. Измерение информации
Кодирование сообщений дискретного
множества
8. Дискретные источники информации
2023
9. Дискретные каналы связи
10. Помехоустойчивое кодирование
2025
7.
Изд. 4
«ЛАНЬ»
Изд. 5
«ЛАНЬ»

3.

Содержание
курса
ТИК
по
существу
является
теоретическим базисом для специализированных курсов,
связанных с восприятием, обработкой и передачей информации.
Это
позволяет
рассчитывать
на
долговременную
актуальность учебного материала в быстроменяющемся мире
информационных технологий.
Более того, структура курса соответствует учебным
программам многих специальностей, по которым проводится
подготовка IT-специалистов в технических Вузах.
Курс ТИК базируется на сочетании теоретической и
практической подготовки студентов.

4.

Электронный образовательный ресурс
Практическая
поддержка
процесса
обучения
обеспечивается за счет использования ИКТ в условиях
ограниченных ресурсов и аудиторных часов без снижения
качества обучения.
Ссылка на дистрибутив КУ ОТИК 4.19, хранящийся в
облаке:
https://cloud.mail.ru/public/isH1/c3rVaZkDR
Режим использования электронного образовательного
ресурса ‒ Off-line.
Ссылка на онлайн-аудиторию:
https://ivaedu.mephi.ru/#join:te9dc0348-b532-42a9- 9d92-166b9dfd2c8e
Почта:
efberezkin@mephi.ru

5.

6.

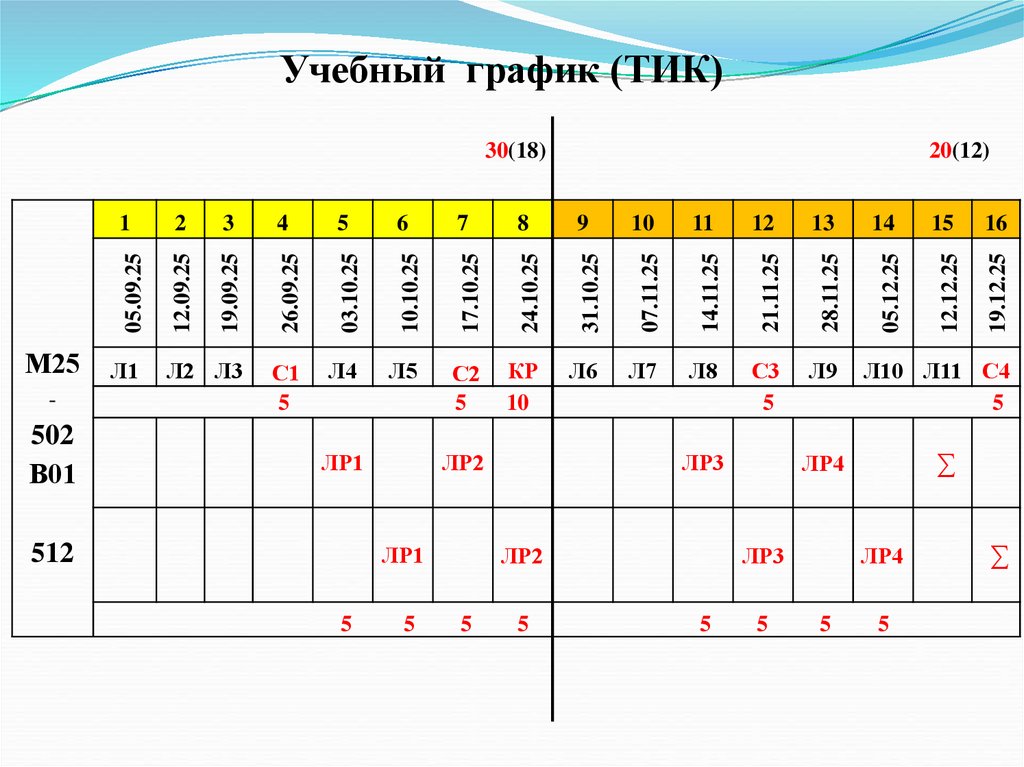
Учебный график (ТИК)
31.10.25
07.11.25
14.11.25
Л2 Л3
С1
5
Л4
Л5
С2
5
КР
10
Л6
Л7
Л8
ЛР2
ЛР1
512
5
8
5
9
10
11
5
13
15
16
Л9
Л10 Л11 С4
5
ЛР4
∑
ЛР3
5
14
С3
5
ЛР3
ЛР2
5
12
19.12.25
24.10.25
Л1
ЛР1
7
12.12.25
17.10.25
6
05.12.25
10.10.25
5
28.11.25
03.10.25
4
21.11.25
502
В01
26.09.25
-
3
19.09.25
М25
2
12.09.25
1
20(12)
05.09.25
30(18)
5
ЛР4
5
5
∑

7.

ВВЕДЕНИЕ
Создание и внедрение информационно-управляющих систем
(ИУС) позволяет успешно решать задачи управления объектами,
технологическими процессами, координации работ и планирования
производства, что, в конечном счете, ускоряет научно-технический
прогресс.
В состав сложной ИУС могут входить отдельные самостоятельные автоматизированные комплексы.
Неотъемлемыми элементами таких комплексов являются системы восприятия и передачи информации, в которых, в свою
очередь, находят применение:
датчики, предназначенные для представления входной информации в виде эквивалентного электрического сигнала;
анализаторы случайных процессов, предназначенные для
получения обобщенных характеристик источника информации;
каналы связи, различаемые по используемым линиям связи
и по физической природе сигналов.

8.

Теоретической основой техники восприятия и передачи информации является статистическая теория связи, которая определяет принципы и основные пути построения оптимальных систем
передачи информации.
Основными проблемами теории связи являются проблемы эффективности и достоверности.
Проблема эффективности состоит в определении возможных
путей, обеспечивающих передачу наибольшего количества информации наиболее экономным способом.
Проблема достоверности состоит в определении путей, обеспечивающих при наличии помех максимальное соответствие принятых сообщений переданным.

9.

При таких видах связи, как телефония и телеграфия, информация воспринимается непосредственно человеком и благодаря свойственной человеческому языку избыточности небольшие искажения передаваемого текста не приводят к нарушению достоверности
принятых сообщений.
Совершенно иначе обстоит дело при передаче данных, где даже
незначительное количество ошибок может полностью исказить
результаты обработки информации в ЭВМ.
Вопрос о международных нормах на допустимое количество
ошибок для различных систем передачи находится в стадии изучения. Однако уже сейчас ясно, что речь может идти о вероятности
искажения одного элемента порядка 10 5 10 9 .
Для обеспечения высокой эффективности и достоверности применяются системы передачи данных, использующие специальные
методы кодирования, и виды модуляции.

10.

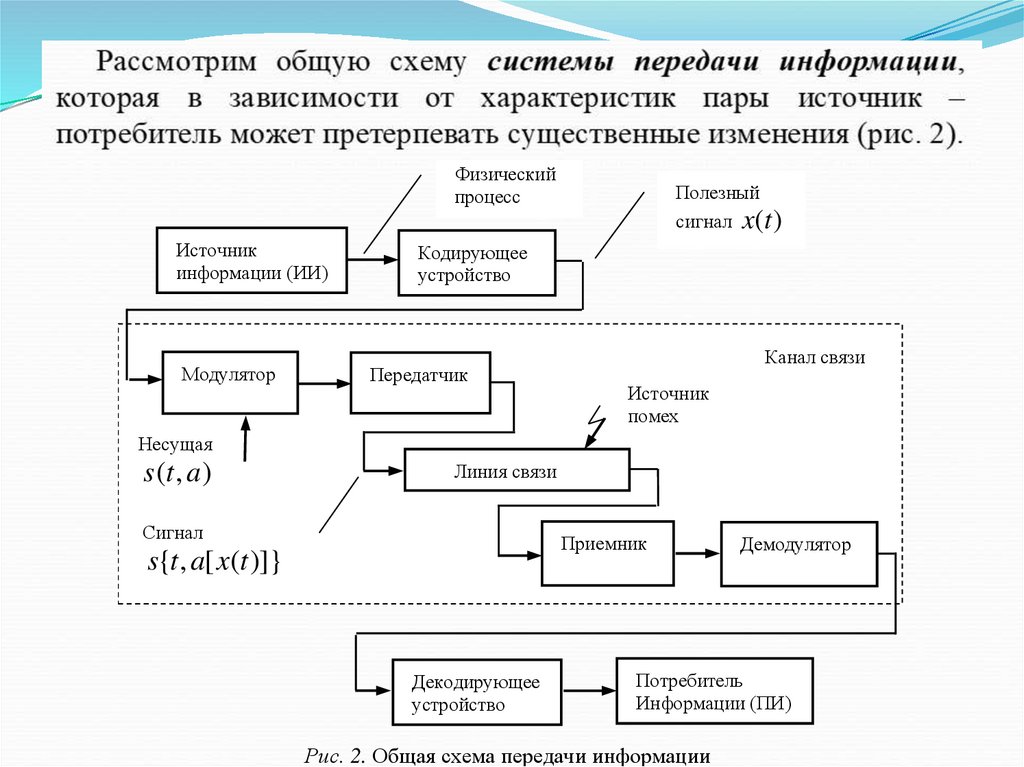
Итак, задачей системы связи является передача сообщения о
каком-либо событии на расстоянии. Расстояние разделяет отправителя и адресата, датчик команд и исполнительное устройство, исследуемый процесс и измерительный механизм, источник излучения и регистрирующий прибор, различные блоки ЭВМ – словом,
источник и потребителя информации (рис. 1).
Рис.1. Информационный процесс
Расстояние, на которое передается сигнал, может быть очень
незначительным (передача команд в ЭВМ) или огромным (космическая связь). Передача сообщений осуществляется с помощью
проводных, кабельных, волноводных линий или в свободном пространстве. Естественно, что для передачи сигналов целесообразно использовать те физические процессы, которые имеют свойство
перемещаться в пространстве без существенного затухания. К числу таких процессов относятся применяемые в радиотехнике и радиолокации, например, электромагнитные колебания.

11.

Физический
процесс
Источник
информации (ИИ)
Модулятор
Полезный
сигнал x (t )
Кодирующее
устройство
Передатчик
Канал связи
Источник
помех
Несущая
s (t , a )
Линия связи
Сигнал
Приемник
s{t , a[ x(t )]}
Декодирующее
устройство
Демодулятор
Потребитель
Информации (ПИ)
Рис. 2. Общая схема передачи информации

12.

Источник
информации
представляет собой некоторый
физический
процесс.
Источник информации представляет
собой некоторый
физиФизическому
процессу
ческий процесс. Физическому процессу
необходимо
поставить в
необходимо
поставить
соответствие эквивалентный электрический
сигнал. эквивалентный
соответствие
Целью кодирования, как правило,
является согласование
источэлектрический
сигнал.
ника информации с каналом связи, обеспечивающее
либо максиЦелью кодирования,
как
мально возможную скорость передачи
либо заданправило,информации,
является согласование
ную помехоустойчивость.
источника информации с каналом
Канал
связи, комплекс
технических
средств,
обеспечивающий
связи,
обеспечивающее
либо
максимально
возможную
скорость
передачу
ИИзаданную
к ПИ.
передачи информации
информации,от
либо
помехоустойчивость.
Под сигналом понимается изменяющаяся физическая величина,
отображающая физический
физическийпроцесс.
процесс.Другими
Другими
словами
сигнал
–
словами
сигнал
– это
это
материальный
переносчик
информации.
материальный
переносчик
информации.
Линией связи называется физическая среда и совокупность
аппаратных средств, используемых для передачи сигналов от
передатчика к приемнику. В системах проводной связи это, прежде
всего, кабель или волновод, в системах радиосвязи – область
пространства, в котором распространяются электромагнитные
волны от передатчика к приемнику.

13.

Для передачи исследуемого физического процесса необходимо
применять тот материальный носитель, который способен эффективно распространяться по используемой в системе линии связи. Например, по проводной линии связи наиболее легко проходят
постоянный ток и переменные токи невысоких частот (не более
нескольких десятков килогерц). По радиолинии эффективно распространяются только электромагнитные колебания высоких частот (до десятков тысяч мегагерц).
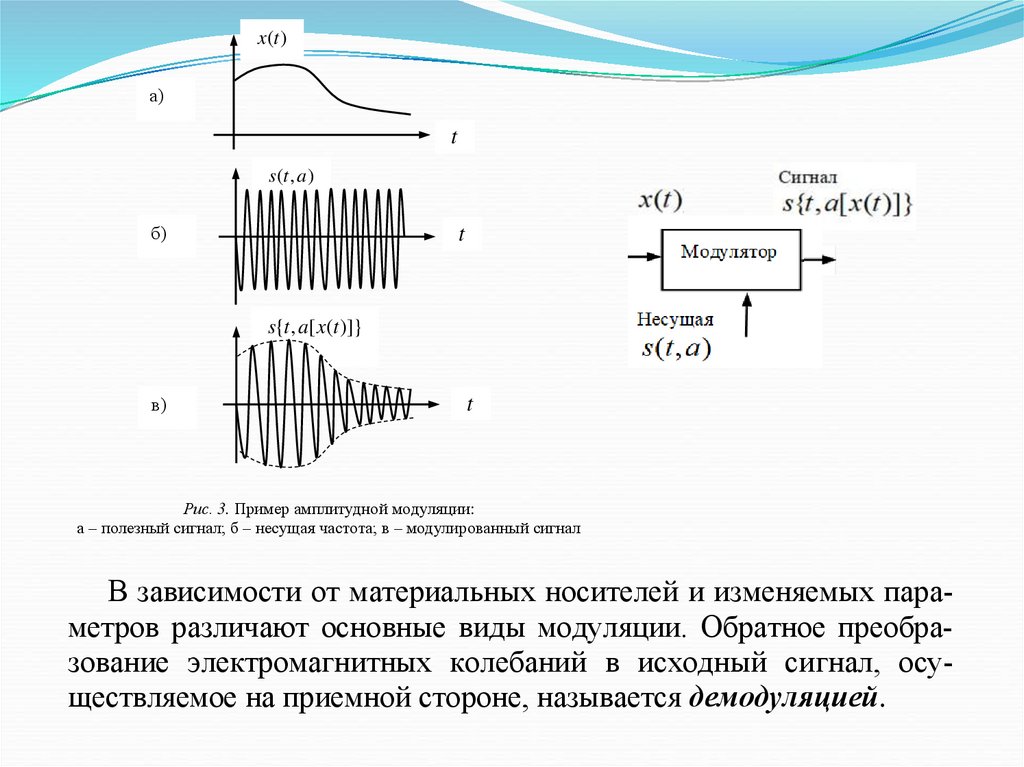
Процесс модуляции заключается в том, что высокочастотное
колебание s (t , a ) , способное распространяться на большие расстояния, наделяются признаками, характеризующими полезное колебание x(t ) . Таким образом, s{t , a[ x (t )]} используется как переносчик сообщения, подлежащего передаче. Для этого один из параметров высокочастотного колебания изменяются по закону, совпадающему с законом изменения передаваемого сообщения (рис.
3).

14.

x(t )
а)
t
s (t , a )
б)
t
s{t , a[ x(t )]}
в)
t
Рис. 3. Пример амплитудной модуляции:
а – полезный сигнал; б – несущая частота; в – модулированный сигнал
В зависимости от материальных носителей и изменяемых параметров различают основные виды модуляции. Обратное преобразование электромагнитных колебаний в исходный сигнал, осуществляемое на приемной стороне, называется демодуляцией.

15.

Модулятор, выполняя функции генератора несущей частоты,
Модулятор, выполняя функции генератора несущей частоты,
начинает
процесс преобразования полезного сигнала в
начинает процесс преобразования полезного сигнала в высокочавысокочастотный
сигнал. завершает
Передатчикпроцесс
завершает
процесс
стотный сигнал. Передатчик
преобразования,
преобразования,
например,
выполняя
усилительные
например, выполняя
усилительные
функции.
Приемник,функции.
демодуПриемник,
демодулятор устройство
и декодирующее
устройство
реализуют
лятор и декодирующее
реализуют
процесс
восстапроцесс
восстановления, источником
сформированного
источником
новления сформированного
физического процесса
по
физического
процесса по принятому сигналу.
принятому сигналу.
При передаче по каналу сигнал, может искажаться и на него могут
воздействовать помехи. Приемное устройство обрабатывает
принятый сигнал, представляющий собой сумму пришедшего
искаженного сигнала и помехи, и восстанавливает по нему сигнал,
который с некоторой погрешностью отображает полезный сигнал.
Другими словами, приемник должен на основе анализа принятого
сигнала определить, какой из возможных полезных сигналов
передавался. Поэтому приемное устройство является одним из
наиболее ответственных и сложных элементов системы связи.

16.

Принято различать две группы относительно самостоятельных
устройств: кодеки и модемы. Кодеком называется совокупность
кодера и декодера, которые при двухсторонней связи
конструктивно объединены в одно устройство. Модемом
называется конструктивно совмещенная совокупность модулятора
и демодулятора.
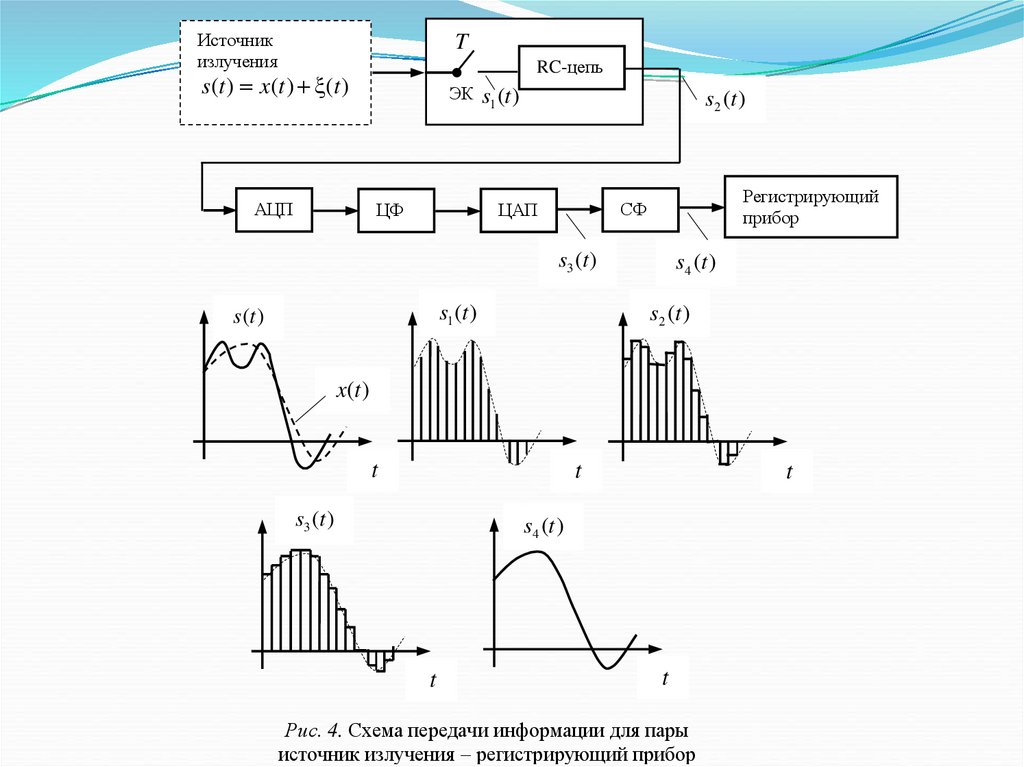
Для пары источник излучения – регистрирующий прибор схема
Для пары источник излучения – регистрирующий прибор схема
передачи информации может вырождаться в набор технических
передачи информации может вырождаться в набор технических
средств и сигналов, представленных на рис. 4.
средств и сигналов, представленных на рис. 4.
Входной сигнал s (t ) подвергается сначала дискретизации по
Входной сигнал s (t ) подвергается сначала дискретизации по
времени с помощью электронного ключа (ЭК), работающего с
времени с помощью электронного ключа (ЭК), работающего с
шагом T . Дискретизированный сигнал s1 (t ) имеет вид последовашагом T . Дискретизированный сигнал s1 (t ) имеет вид
тельности равноотстоящих коротких импульсов, являющихся отпоследовательности
равноотстоящих
коротких
импульсов,
счетами сигнала s (t ) . Каждый из отсчетов запоминается в интеявляющихся отсчетами сигнала s (t ) . Каждый из отсчетов
грирующей RC-цепи на время, необходимое для срабатывания
запоминается в интегрирующей RC-цепи на время, необходимое
аналого-цифрового преобразователя (АЦП). В результате, на выдля срабатывания аналого-цифрового преобразователя (АЦП). В
s2 (t ) . колебание
ходе
RC-цепи
ступенчатое
колебание
результате,
на получается
выходе RC-цепи
получается
ступенчатое

17.

Источник
излучения
T
RC-цепь
s(t ) x(t ) (t )
АЦП
ЭК s1 (t )
ЦФ
s2 (t )
Регистрирующий
прибор
СФ
ЦАП
s3 (t )
s1 (t )
s (t )
s4 (t )
s2 (t )
x(t )
t
t
s3 (t )
t
s4 (t )
t
t
Рис. 4. Схема передачи информации для пары
источник излучения – регистрирующий прибор

18.

В АЦП каждый отсчет квантуется по уровню и преобразуется в
кодовое слово:
Последовательность кодовых слов обрабатывается в цифровом
фильтре (ЦФ).
Цифро-аналоговый преобразователь (ЦАП) осуществляет суммирование эталонных напряжений ( s3 (t ) ), соответствующих каждому кодовому слов:
Наконец, синтезирующий фильтр (СФ) формирует выходной
сигнал s4 (t ) максимально похожий на x(t ) .

19.

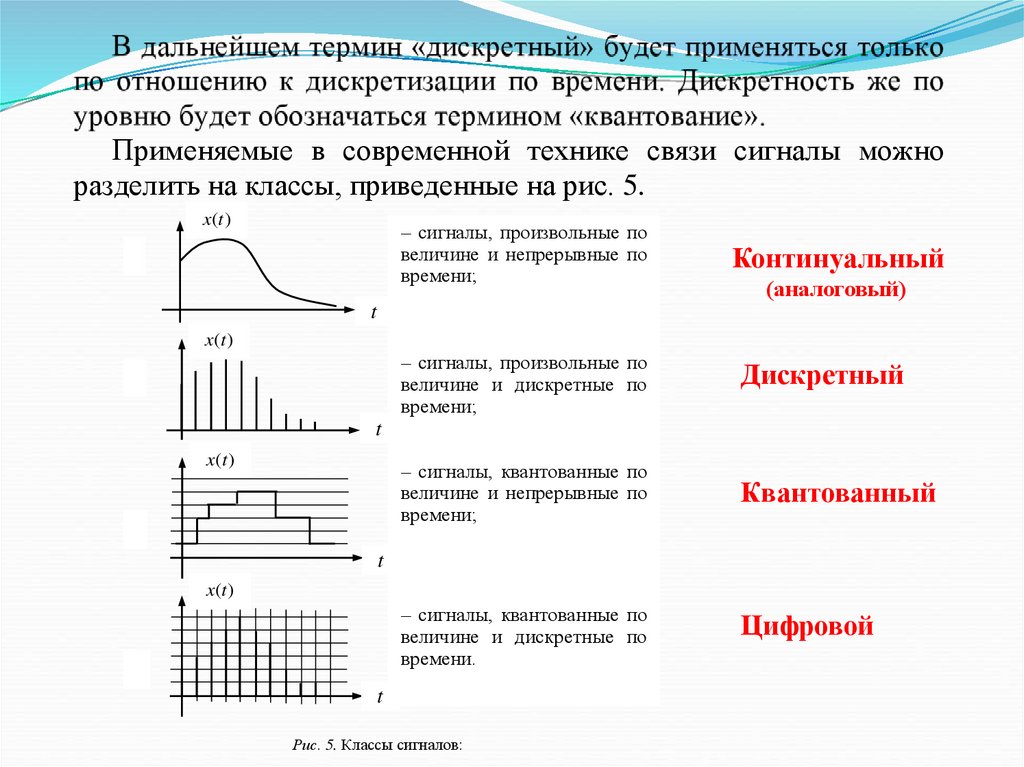
Применяемые в современной технике связи сигналы можно
разделить на классы, приведенные на рис. 5.
x(t )
– сигналы, произвольные по
величине и непрерывные по
времени;
а)
Континуальный
(аналоговый)
t
x(t )
– сигналы, произвольные по
величине и дискретные по
времени;
б)
Дискретный
t
x(t )
– сигналы, квантованные по
величине и непрерывные по
времени;
в)
Квантованный
t
x(t )
– сигналы, квантованные по
величине и дискретные по
времени.
г)
t
Рис. 5. Классы сигналов:
а – континуальный; б – дискретный; в – квантованный; г – цифровой
Цифровой

20.

В дальнейшем термин «дискретный» будет применяться только
по отношению к дискретизации по времени. Дискретность же по
уровню
«квантование».
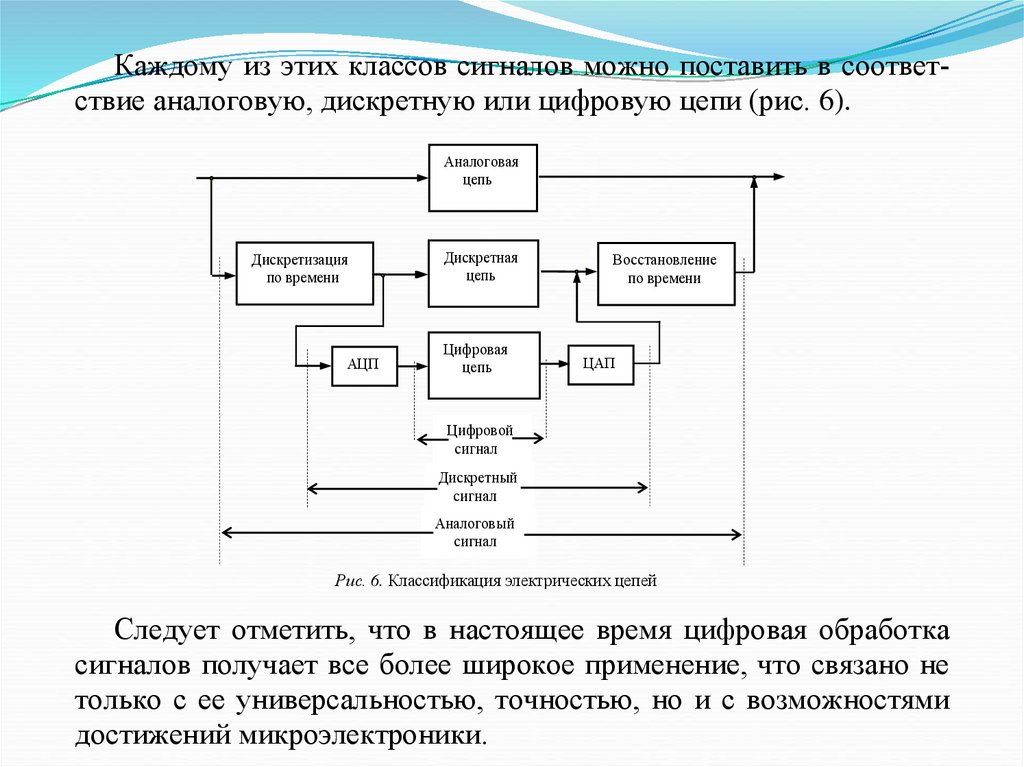
Каждому
избудет
этихобозначаться
классовтермином
сигналов
можно поставить в соответКаждому из этих классов сигналов можно поставить в
ствие аналоговую,
дискретную
или цифровую
цепи
(рис.
соответствие аналоговую,
дискретную
или цифровую цепи
(рис.
6). 6).
Аналоговая
цепь
Дискретизация
по времени
АЦП
Дискретная
цепь
Цифровая
цепь
Восстановление
по времени
ЦАП
Цифровой
сигнал
Дискретный
сигнал
Аналоговый
сигнал
Рис. 6. Классификация электрических цепей
Следует отметить, что в настоящее время цифровая обработка
сигналов получает все более широкое применение, что связано не
только с ее универсальностью, точностью, но и с возможностями
достижений микроэлектроники.

21.

Основными параметрами сигналов являются длительность сигнала Tc, динамический диапазон Dc и ширина спектра ΔFc. Всякий
сигнал, рассматриваемый как временной процесс, имеет начало и
конец.
Длительность сигнала Tc является естественным его параметром, определяющим интервал времени, в пределах которого сигнал
существует.
Динамический диапазон Dc – это отношение наибольшей
мгновенной мощности сигнала к той наименьшей мощности, которая необходима для обеспечения заданного качества передачи. Он
выражается в децибелах [дБ]:
Pc max
Dc 10 lg
.
Pc min
Ширина спектра ΔFc – этот параметр дает представление о
скорости изменения сигнала внутри интервала его существования.
Спектр сигнала, в принципе, может быть неограниченным. Однако
для любого сигнала можно указать диапазон частот, в пределах
которого сосредоточена его основная энергия. Этим диапазоном и
определяется ширина спектра сигнала.

22.

Как отмечалось, сигнал – изменяющаяся физическая величина,
обеспечивающая передачу информации по линии связи. В технических системах используются в большинстве случаев электрические сигналы.
Все многообразие сигналов можно по своим особенностям разделить на две группы: детерминированные и случайные сигналы.
Детерминированные сигналы характеризуются тем, что в любые
моменты времени их значения являются известными величинами, а
случайные – тем, что их значения в любые моменты времени –
случайные величины.
Деление сигналов на детерминированные и случайные условно,
так как детерминированных сигналов в точном их понимании в
природе нет. На практике нельзя точно предсказать значение сигнала в любые моменты времени, в противном случае сигнал не нес
бы полезной информации. Кроме того, любой реальный сигнал
случаен в силу воздействия на него многочисленных случайных
факторов.

23.

Несмотря на это, исследование детерминированных сигналов
весьма важно, так как выводы, полученные в результате анализа
математических моделей именно таких сигналов, во многих случаях
можно использовать для исследования и анализа случайных
сигналов.
Детерминированные сигналы можно подразделить на
периодические и непериодические. В реальных условиях
периодические сигналы не существуют, так как идеальный
периодический сигнал бесконечен во времени, в то время как всякий
реальный сигнал имеет начало и конец. Однако во многих случаях
конечностью времени действия сигнала можно пренебречь и для его
анализа допустимо использовать аппарат, пригодный для
идеальных периодических сигналов.
Случайный процесс носит двойственный характер. С одной
стороны, в каждом конкретном эксперименте он представлен
своей реализацией – неслучайной функцией времени. С другой
стороны, случайный процесс описывается совокупностью
случайных функций времени.

24.

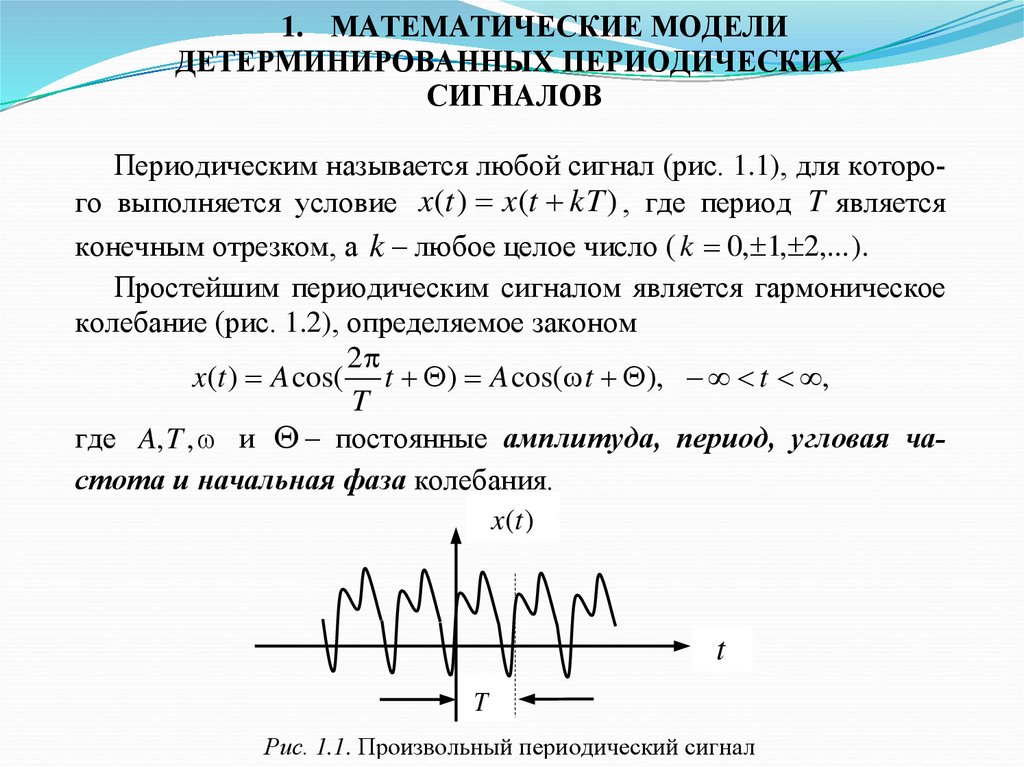
1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ
ДЕТЕРМИНИРОВАННЫХ ПЕРИОДИЧЕСКИХ
СИГНАЛОВ
Периодическим называется любой сигнал (рис. 1.1), для которого выполняется условие x(t ) x(t kT ) , где период T является
конечным отрезком, а k – любое целое число ( k 0, 1, 2,... ).
Простейшим периодическим сигналом является гармоническое
колебание (рис. 1.2), определяемое законом
2
x(t ) A cos( t ) A cos( t ), t ,
T
где A,T , и – постоянные амплитуда, период, угловая частота и начальная фаза колебания.
x(t )
t
T
Рис. 1.1. Произвольный периодический сигнал

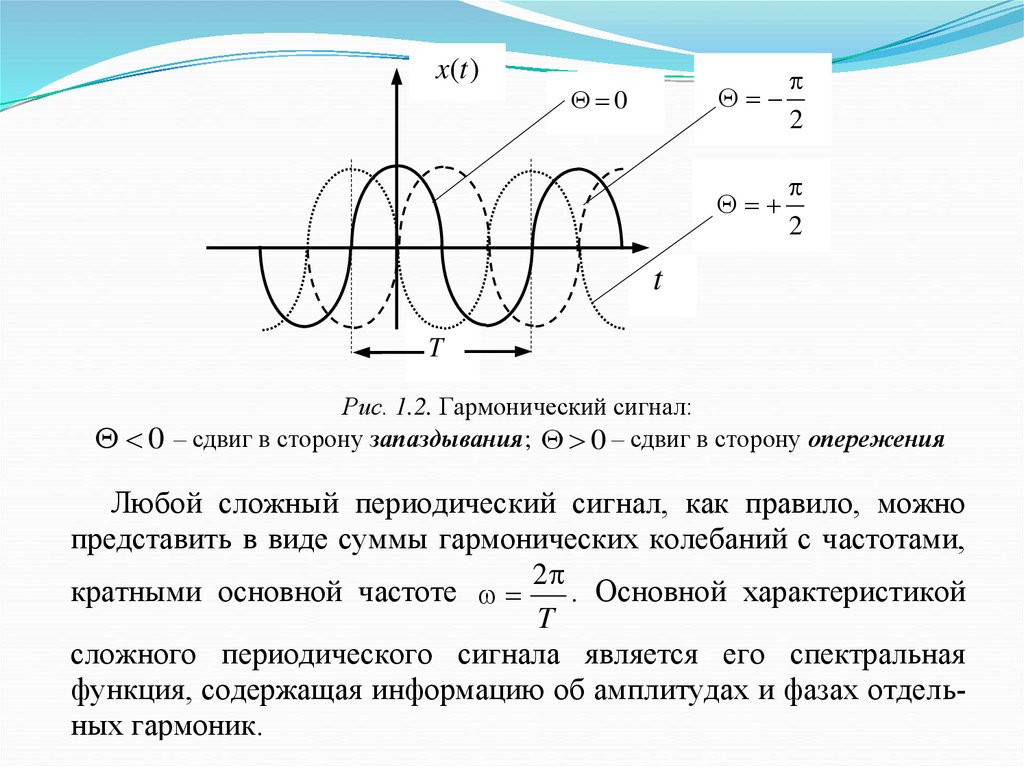
25.

x(t )
2
0
2
t
T
Рис. 1.2. Гармонический сигнал:
0 – сдвиг в сторону запаздывания; 0 – сдвиг в сторону опережения
Любой сложный периодический сигнал, как правило, можно
представить в виде суммы гармонических колебаний с частотами,
2
кратными основной частоте
. Основной характеристикой
T
сложного периодического сигнала является его спектральная
функция, содержащая информацию об амплитудах и фазах отдельных гармоник.

26.

1.1. РАЗЛОЖЕНИЕ ПРОИЗВОЛЬНОГО СИГНАЛА ПО ЗАДАННОЙ
СИСТЕМЕ ФУНКЦИЙ
Для техники формирования и обработки сигналов особое значение имеет разложение заданной функции по разным ортогональным системам функций. Напомним основные определения,
относящиеся к свойствам ортогональных систем.
Бесконечная система действительных непрерывных функций
0 ( x), 1 ( x), 2 ( x),..., k ( x),..., m ( x),...
называется ортогональной на отрезке a, b , если
b
( x) ( x)dx 0 при k m .
k
m
(1.1)
a
Отрезок a, b , на котором выполняется это условие, называется
интервалом ортогональности.
b
При этом предполагается, что
2
k ( x)dx 0 , т.е. никакая из
a
функций рассматриваемой системы не равна тождественно нулю.

27.

Условие (1.1) выражает попарную ортогональность функций.
b
k ( x)
Величина
2
k ( x)dx
называется нормой функции
a
k (x) .
Функция
k (x) ,
для
которой
выполняется
условие
b
k ( x) 2k ( x)dx 1 , называется нормированной функцией, а
2
a
система нормированных функций 0 ( x), 1 ( x), 2 ( x),... , в которой две различные функции взаимно ортогональны, называется
ортонормированной системой.
В математике доказывается, что если функции k (x) непрерывны, то произвольная кусочно-непрерывная функция, заданная в
промежутке a, b , для которой выполняется условие
b
f ( x) dx ,
a
(1.2)

28.

может быть формально представлена в виде ряда
f ( x) Ck k ( x) C0 0 ( x) C1 1 ( x) ...
(1.3)
k 0
Умножим обе части уравнения (1.3) на k (x) и проинтегриру-
ем в пределах a, b :
b
b
f ( x) ( x)dx C ( x)dx C
k
2
k
k
a
k
2
k
.
a
Откуда следует важное соотношение
Ck
b
1
k
2
f ( x) ( x)dx .
k
(1.4)
a
Ряд (1.3), в котором коэффициенты Ck определены по формуле
(1.4), называется обобщенным рядом Фурье по данной системе
k (x) , а сами Ck – коэффициентами Фурье.

29.

может быть формально представлена в виде ряда
f ( x) Ck k ( x) C0 0 ( x) C1 1 ( x) ...
(1.3)
k 0
Умножим обе части уравнения (1.3) на k (x) и проинтегриру-
ем в пределах a, b :
b
b
f ( x) ( x)dx C ( x)dx C
k
2
k
k
a
k
2
k
.
a
Откуда следует важное соотношение
Ck
b
1
k
2
f ( x) ( x)dx .
k
(1.4)
a
Ряд (1.3), в котором коэффициенты Ck определены по формуле
(1.4), называется обобщенным рядом Фурье по данной системе
k (x) , а сами Ck – коэффициентами Фурье.

30.

Правую часть выражения (1.3) называют суммой ряда Фурье и
обозначают S ( x ) .
Более строго ряд Фурье функции f (x ) будет сходиться и его
сумма S ( x ) будет равна f (x ) , если только сделать некоторые
ограничительные предположения относительно функции f (x ) .
ТЕОРЕМА (Дирихле). Пусть функция f (x ) определена на
отрезке [−π; π ] и удовлетворяет на нём условиям:
1) f (x ) непрерывна или имеет конечное число точек разрыва
первого рода (т.е. кусочно-непрерывна);
2) f (x ) монотонна или имеет конечное число точек
экстремумов (т.е. кусочно-монотонна).
Тогда f (x ) разлагается на отрезке [−π; π ] в ряд Фурье. Т.е. ряд
Фурье функции f (x ) сходится на отрезке [−π; π ] и его суммой
является функция S ( x ) , определенная на этом отрезке следующим
образом:

31.

1. S ( x ) f ( x ) во всех точках x ; в которых f ( x ) – непрерывна.
f ( xk 0) f ( xk 0)
, если xk ; и x k – точка
2
разрыва первого рода функции f ( x ) . Т.е. в точках разрыва функции
f ( x ) функция S ( x ) равна среднему арифметическому односторонних
пределов f ( x ) в этой точке.
2. S ( xk )
f ( 0) f ( 0)
3. S ( ) S ( )
. Т.е. на границах отрезка
2
; функция S ( x ) равна среднему арифметическому левого предела функции f ( x ) в точке x и правого предела функции f ( x ) в
точке x .

32.

Условия 1) и 2) теоремы Дирихле называются условиями Дирихле.
Функцию f ( x ) произвольного периода T 0 , удовлетворяющую условиям Дирихле, можно свести к функции периода 2 пу-
T
t . Тогда изменению x на T будет
тем замены переменных x
2
соответствовать изменение t на 2 .

33.

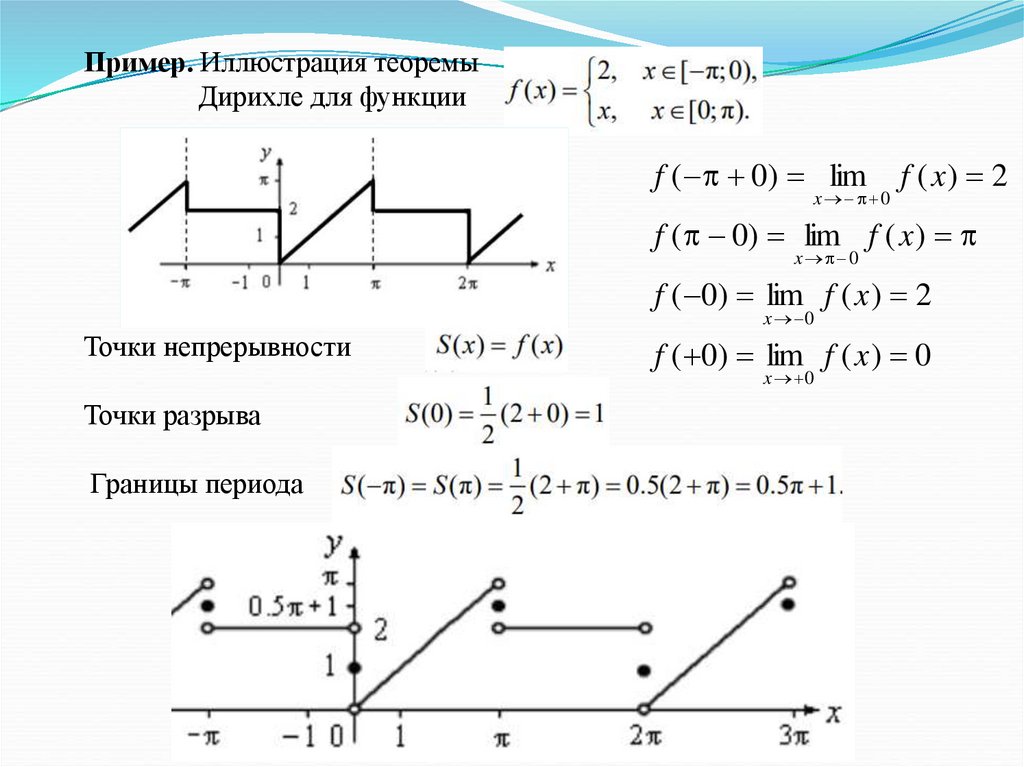
Пример. Иллюстрация теоремы
Дирихле для функции
f ( 0) lim
x 0
f ( x) 2
f ( 0) lim f ( x )
x 0
f ( 0) lim f ( x ) 2
x 0
Точки непрерывности
f ( 0) lim f ( x ) 0
x 0
Точки разрыва
Границы периода