лекция 4 Положение плоскостей

1.

Лекция 4
Взаимное положение прямых,
плоскостей в Пространстве

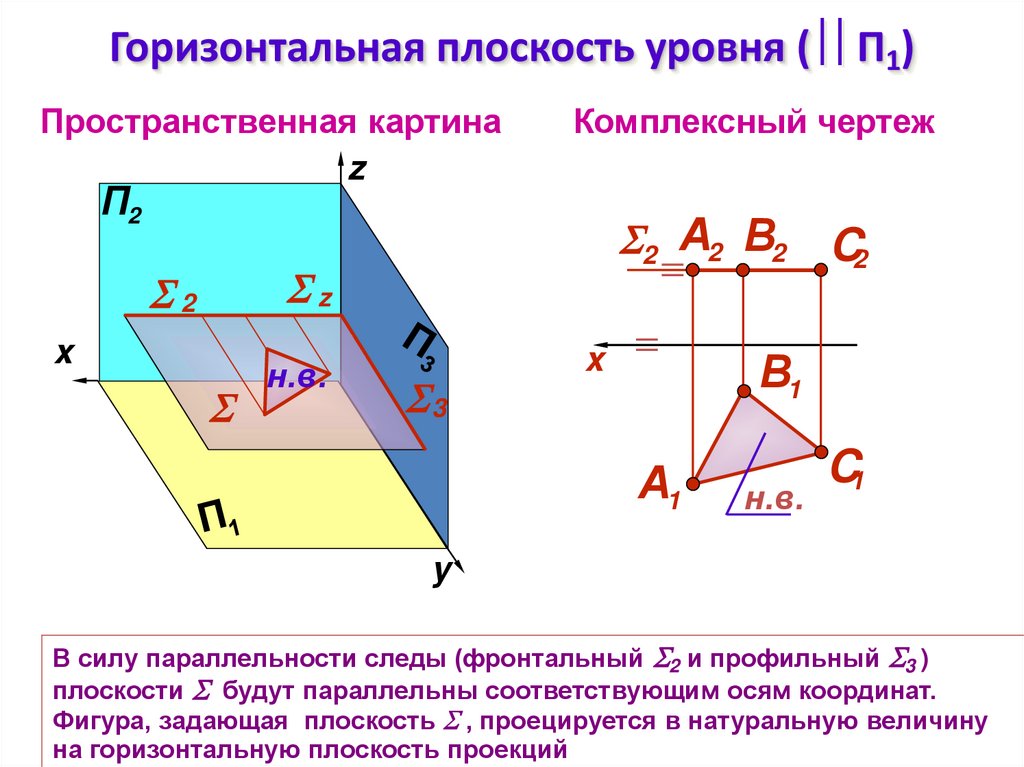
2. Горизонтальная плоскость уровня ( П1)

Горизонтальная плоскость уровня ( П1)
Пространственная картина
z
Комплексный чертеж
П2
2 А2 В2
z
2
x
н.в.
3
x
C2
В1
А1
н.в.
C1
y
В силу параллельности следы (фронтальный 2 и профильный 3 )
плоскости будут параллельны соответствующим осям координат.
Фигура, задающая плоскость , проецируется в натуральную величину
на горизонтальную плоскость проекций

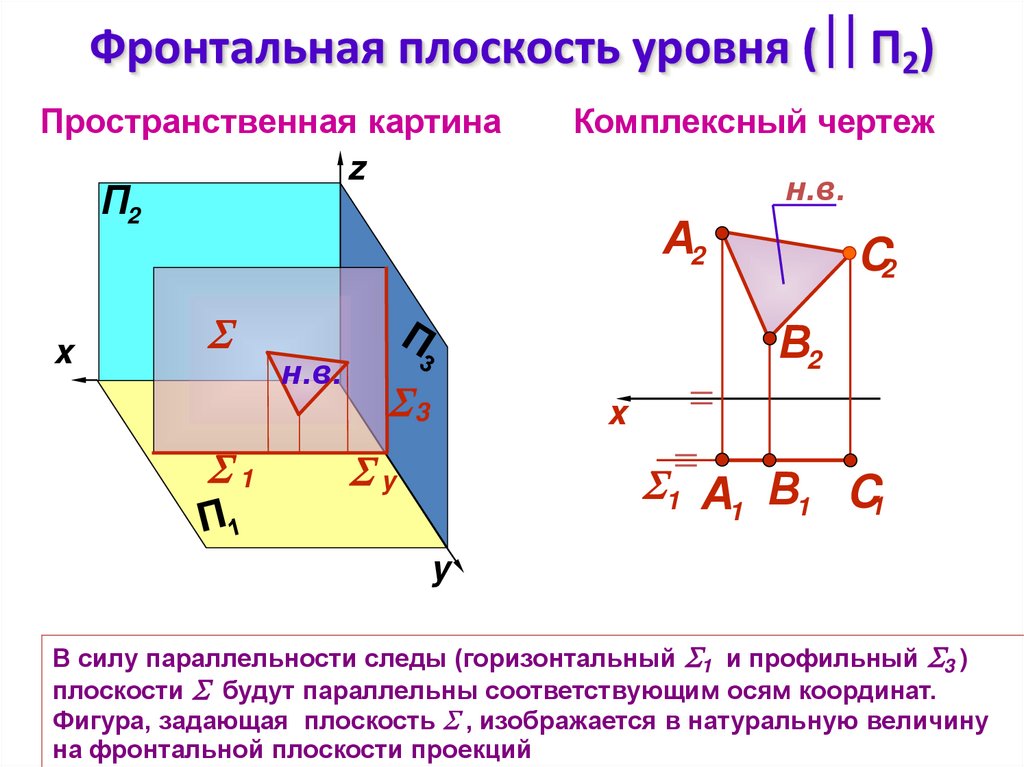
3. Фронтальная плоскость уровня ( П2)

Фронтальная плоскость уровня ( П2)
Пространственная картина
z
Комплексный чертеж
н.в.
П2
x
А2
1
н.в.
C2
В2
3
x
y
1 А В1 C1
1
y
В силу параллельности следы (горизонтальный 1 и профильный 3 )
плоскости будут параллельны соответствующим осям координат.
Фигура, задающая плоскость , изображается в натуральную величину
на фронтальной плоскости проекций

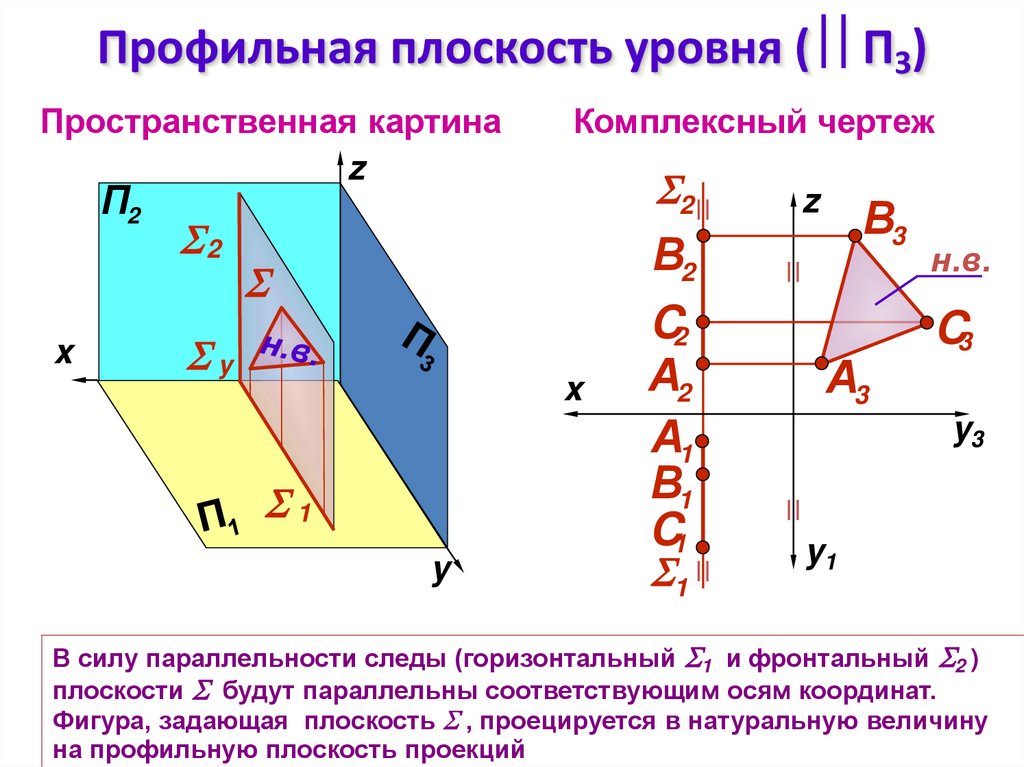
4. Профильная плоскость уровня ( П3)

Профильная плоскость уровня ( П3)
Пространственная картина
z
П2
x
2
Комплексный чертеж
2
y
x
1
y
В2
C2
А2
А1
В1
C1
1
z
В3
А3
н.в.
C3
y3
y1
В силу параллельности следы (горизонтальный 1 и фронтальный 2 )
плоскости будут параллельны соответствующим осям координат.
Фигура, задающая плоскость , проецируется в натуральную величину
на профильную плоскость проекций

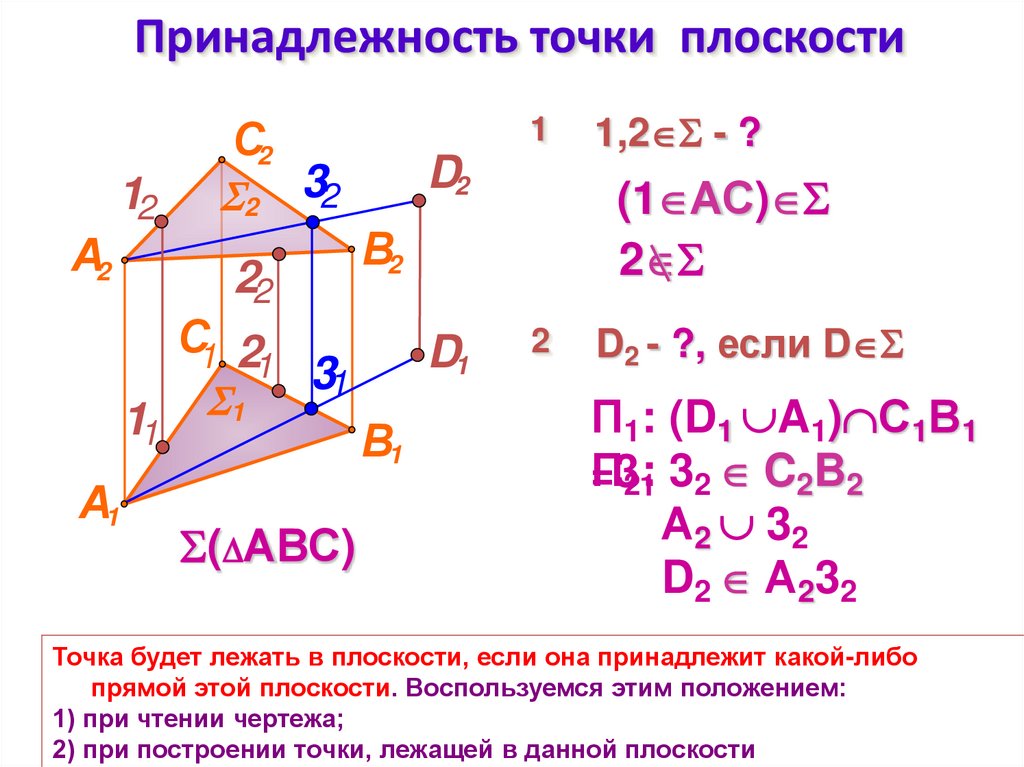
5. Принадлежность точки плоскости

С2
12
А2
2
11
1
1
D2
32
D1
31
( АВС)
В1
1,2 - ?
(1 АС)
2
В2
22
С1 2
А1
1
2
D2 - ?, если D
П1: (D1 A1) С1В1
П321: 32 C2B2
=
А2 32
D2 А232
Точка будет лежать в плоскости, если она принадлежит какой-либо
прямой этой плоскости. Воспользуемся этим положением:
1) при чтении чертежа;
2) при построении точки, лежащей в данной плоскости

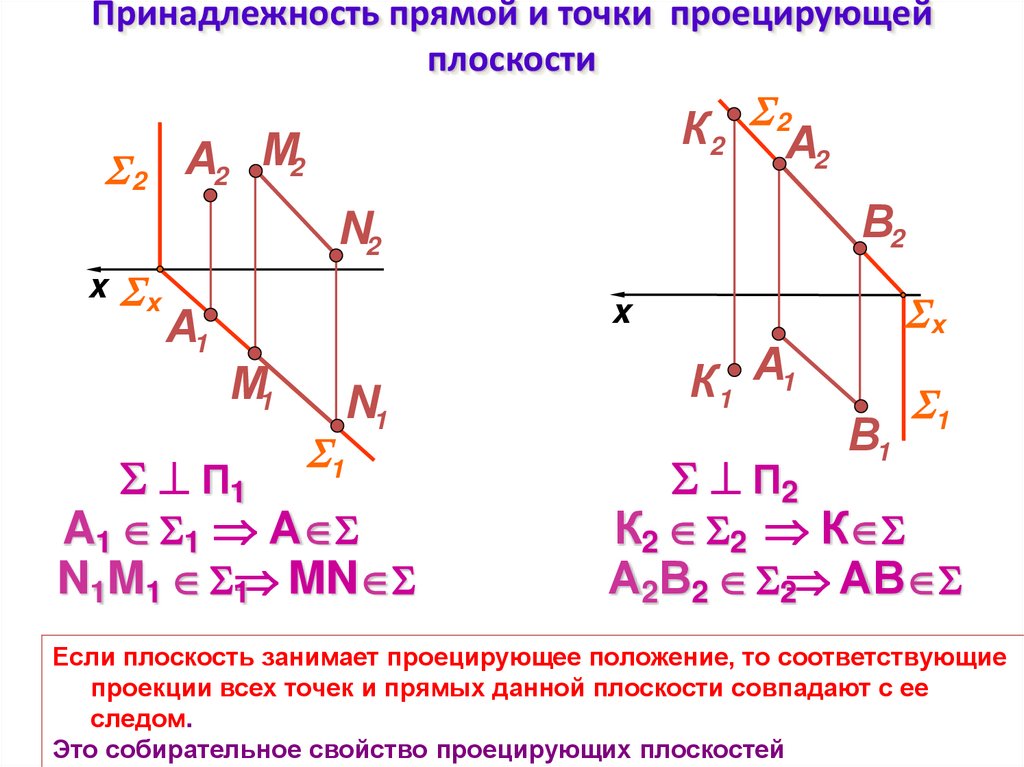
6. Принадлежность прямой и точки проецирующей плоскости

К2 2А
2 А2 М2
2
В2
N2
x х
А1
х
x
М1
1
N1
П1
A1 1 А
N1M1 1 MN
К1 А1
В1
1
П2
К2 2 К
А2В2 2 АВ
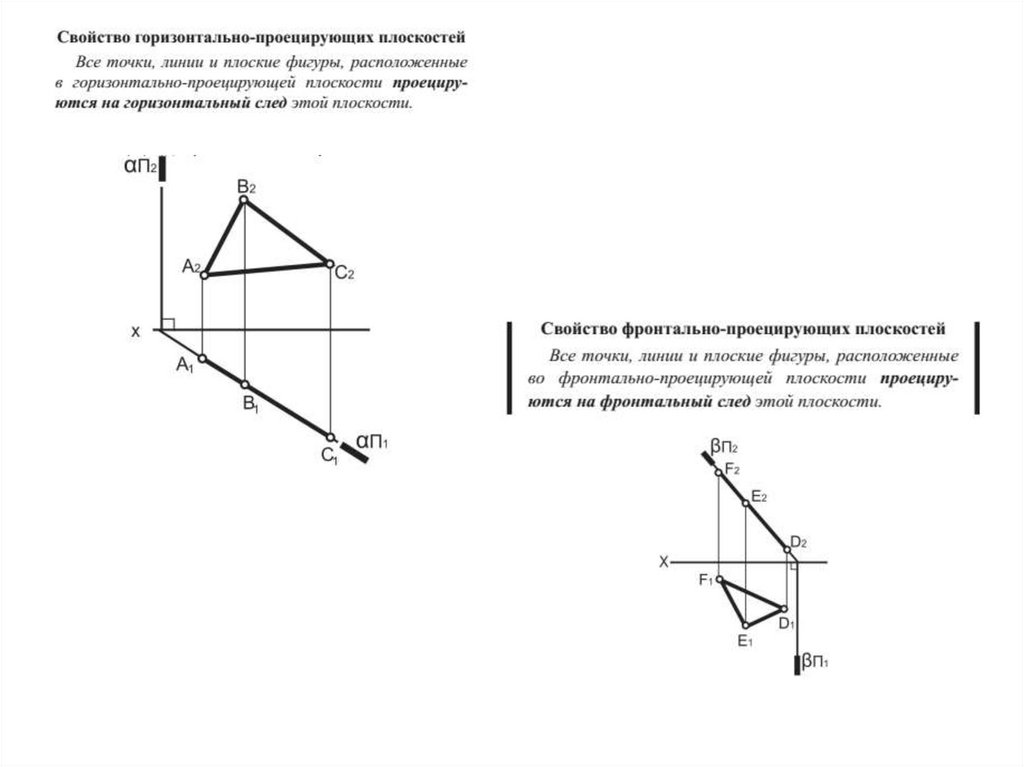
Если плоскость занимает проецирующее положение, то соответствующие
проекции всех точек и прямых данной плоскости совпадают с ее
следом.
Это собирательное свойство проецирующих плоскостей

7. Принадлежность плоскости плоской фигуры

• Фигура называется плоской, если все
точки этой фигуры лежат в одной
плоскости
• Плоские фигуры принадлежат плоскости,
если все точки этой фигуры лежат в
указанной плоскости

8.

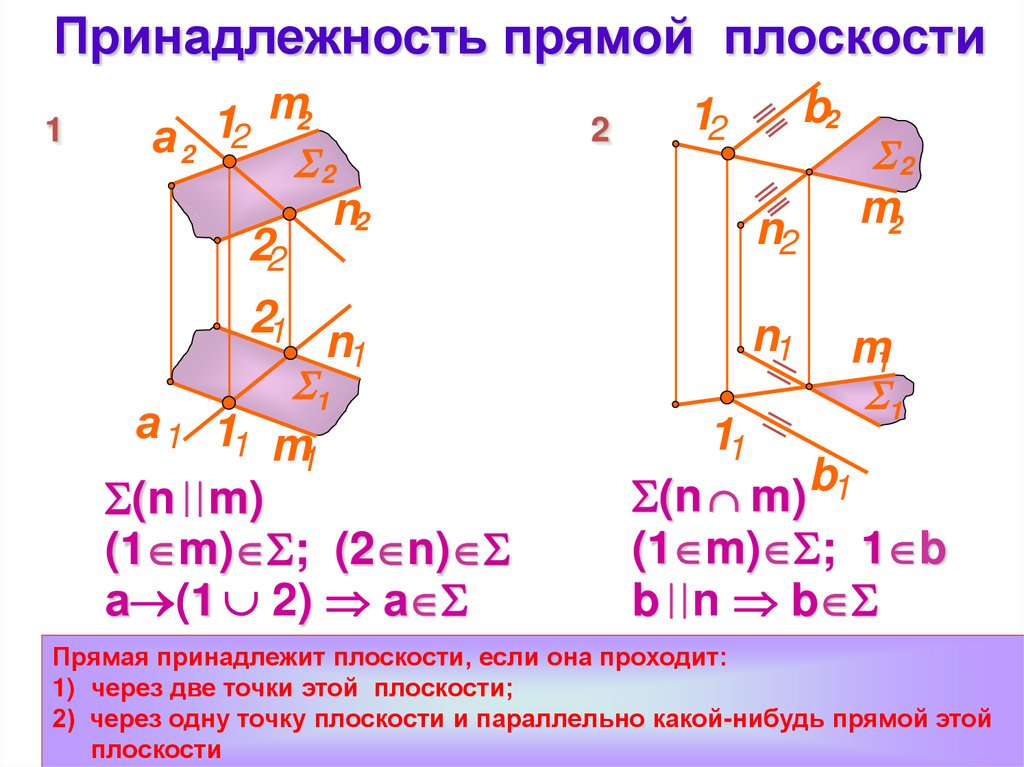
Принадлежность прямой плоскости
1
m2
1
а2 2
2
n2
m2
n1
n1
m1
1
а 1 11 m
1
2
n2
22
21
2
b2
12
(n m)
(1 m) ; (2 n)
а (1 2) а
11
1
(n m) b1
(1 m) ; 1 b
b n b
Прямая принадлежит плоскости, если она проходит:
1) через две точки этой плоскости;
2) через одну точку плоскости и параллельно какой-нибудь прямой этой
плоскости

9.

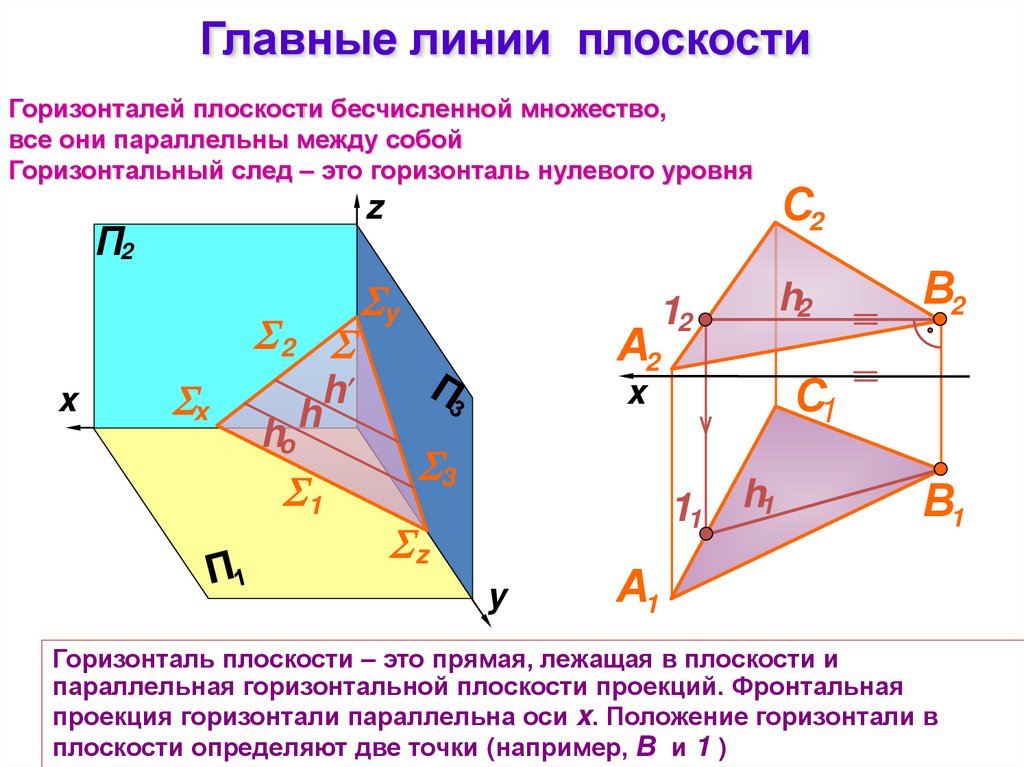
Главные линии плоскости
Горизонталей плоскости бесчисленной множество,
все они параллельны между собой
Горизонтальный след – это горизонталь нулевого уровня
П2
2
x
х
hh
z
С2
y
h2
А2
h
o
1
12
С1
x
3
11 h1
z
y
В2
В1
А1
Горизонталь плоскости – это прямая, лежащая в плоскости и
параллельная горизонтальной плоскости проекций. Фронтальная
проекция горизонтали параллельна оси x. Положение горизонтали в
плоскости определяют две точки (например, В и 1 )

10.

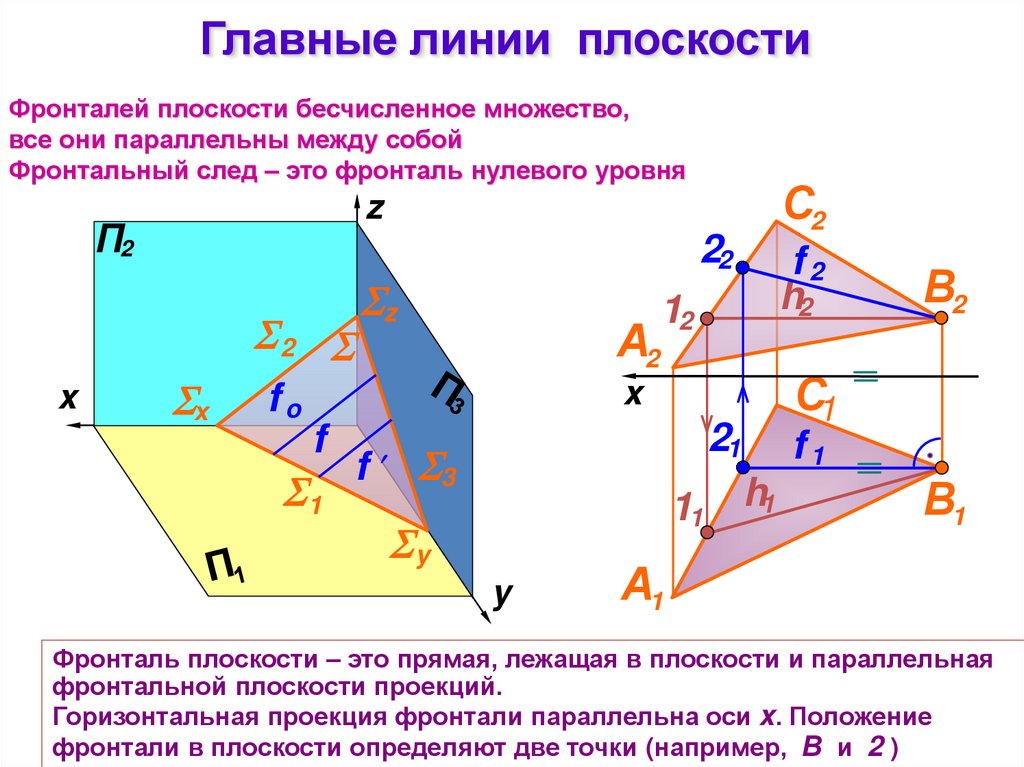
Главные линии плоскости
Фронталей плоскости бесчисленное множество,
все они параллельны между собой
Фронтальный след – это фронталь нулевого уровня
z
П2
2
x
х
22
z
А2
12
x
fo
f
1
f
21
3
11 h1
y
y
С2
f2
h2
В2
С1
f1
В1
А1
Фронталь плоскости – это прямая, лежащая в плоскости и параллельная
фронтальной плоскости проекций.
Горизонтальная проекция фронтали параллельна оси x. Положение
фронтали в плоскости определяют две точки (например, В и 2 )

11. Взаимное положение прямой и плоскости, двух плоскостей

Прямая и плоскость:
• Прямая принадлежит плоскости: все точки прямой
являются точками плоскости
• Прямая параллельна плоскости: общих собственных
точек нет
• Прямая пересекает плоскость: одна общая точка
Две плоскости:
• Плоскости параллельны: общих собственных
прямых нет
• Плоскости пересекаются: одна общая прямая
Рассмотрим все возможные случаи взаимного положения прямой и
плоскости и двух плоскостей

12.

Параллельность прямой и плоскости
b
А
n
Признак параллельности:
Прямая параллельна
плоскости, если она
параллельна какой-ли
прямой, лежащей в
этой плоскости
b n b
Через точку А в пространстве можно провести бесчисленное множество
прямых линий, параллельных данной плоскости . Для однозначного
решения проведем в плоскости прямую n

13. Взаимное расположение плоскостей

• Плоскости в пространстве могут быть
расположены параллельно друг другу или
пересекаться
• Плоскости являются параллельными, если
две пересекающиеся прямые, лежащие в
одной плоскости, параллельны двум
пересекающимся прямым, лежащим в
другой плоскости

14.

Параллельность двух плоскостей
n
a
b
П2
m
а m
b n
2
x
х
2
х
1
1
1 1
2 2
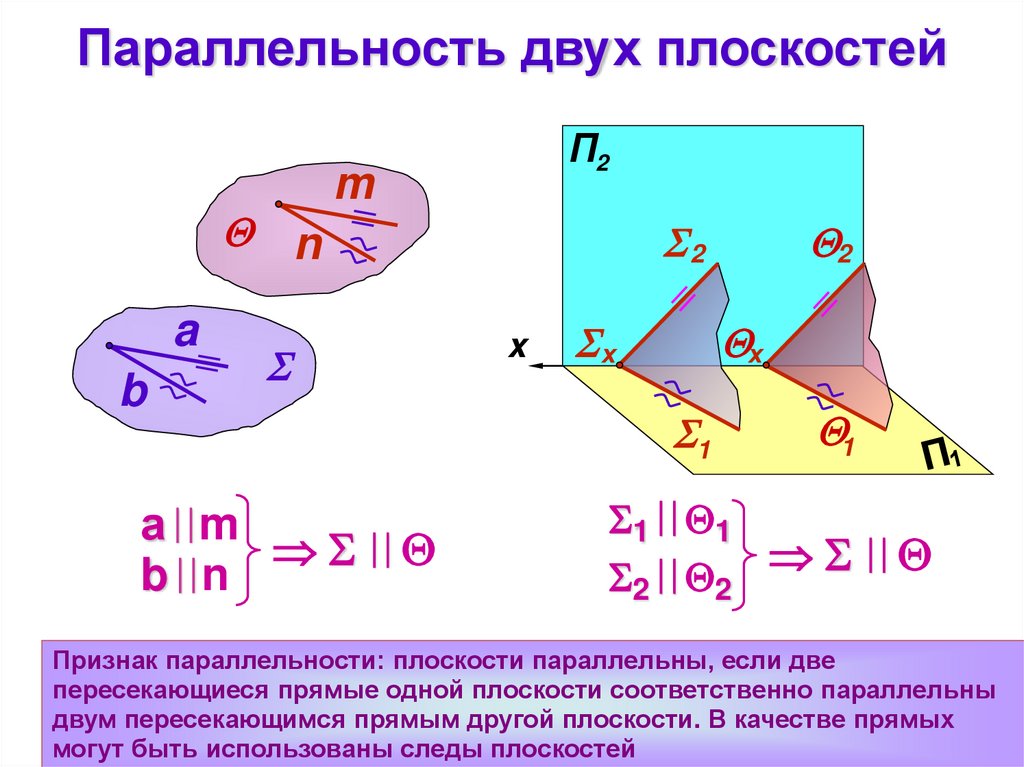
Признак параллельности: плоскости параллельны, если две
пересекающиеся прямые одной плоскости соответственно параллельны
двум пересекающимся прямым другой плоскости. В качестве прямых
могут быть использованы следы плоскостей

15.

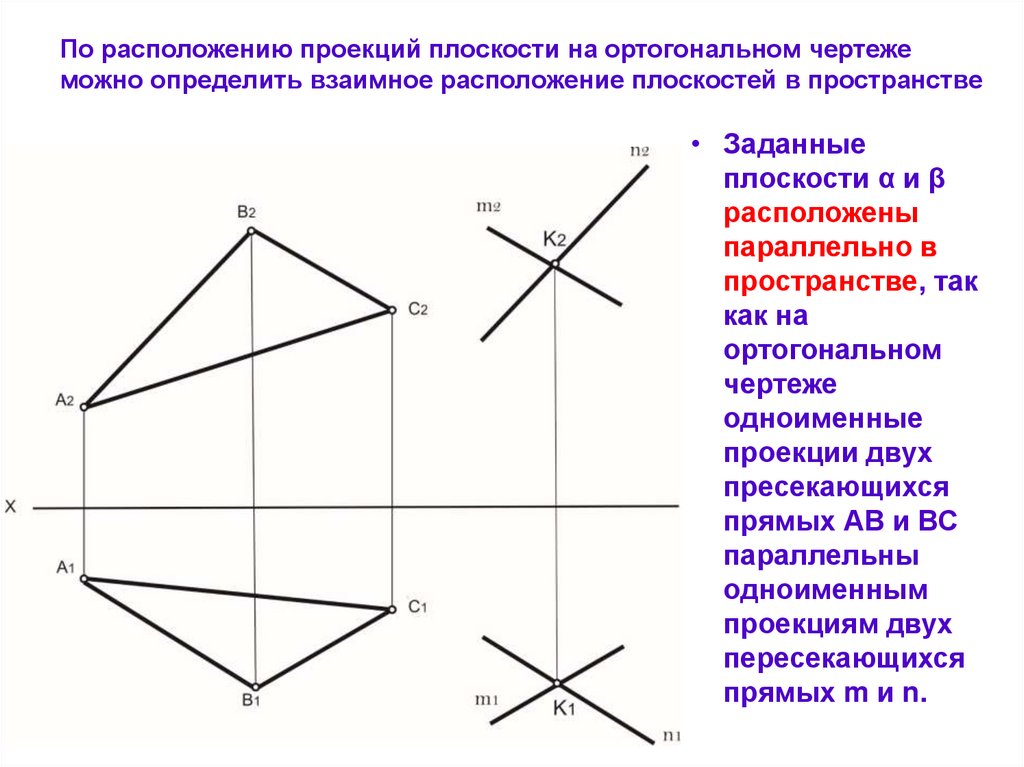
По расположению проекций плоскости на ортогональном чертеже
можно определить взаимное расположение плоскостей в пространстве
• Заданные
плоскости α и β
расположены
параллельно в
пространстве, так
как на
ортогональном
чертеже
одноименные
проекции двух
пресекающихся
прямых АВ и ВС
параллельны
одноименным
проекциям двух
пересекающихся
прямых m и n.

16.

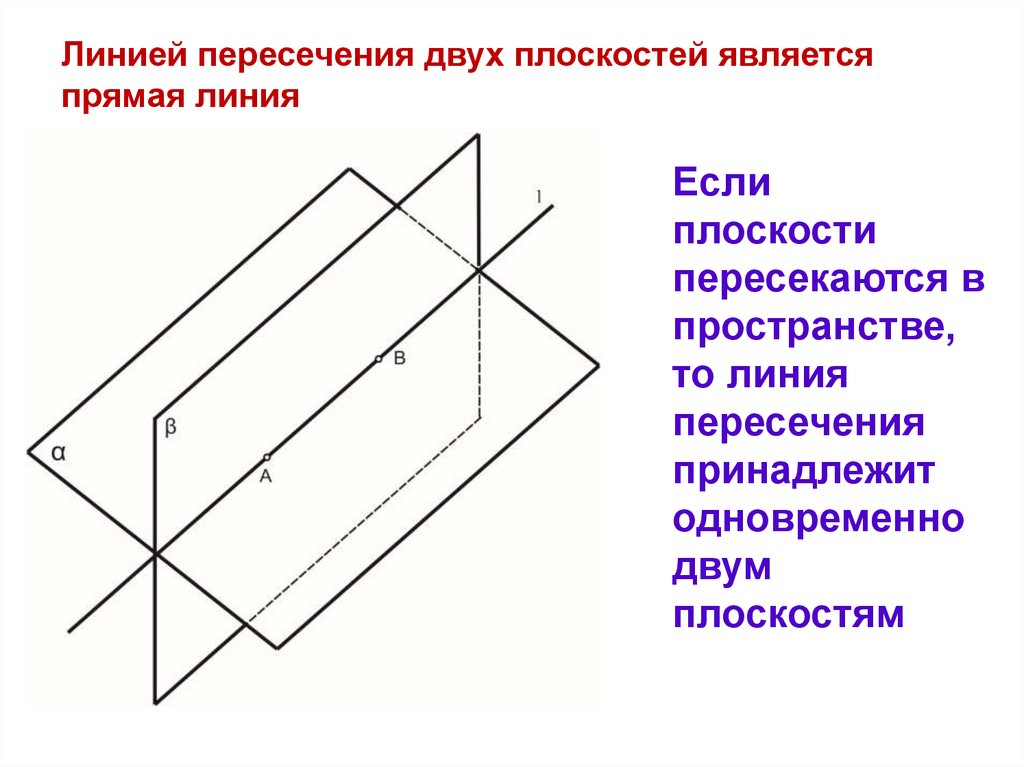
Линией пересечения двух плоскостей является
прямая линия
Если
плоскости
пересекаются в
пространстве,
то линия
пересечения
принадлежит
одновременно
двум
плоскостям

17.

Пересечение прямой с проецирующей
плоскостью
2
П2
2
x
х
1
2
n
2
n 1
n 11
1
1 n
2
x х
1
2
n
11 1
1
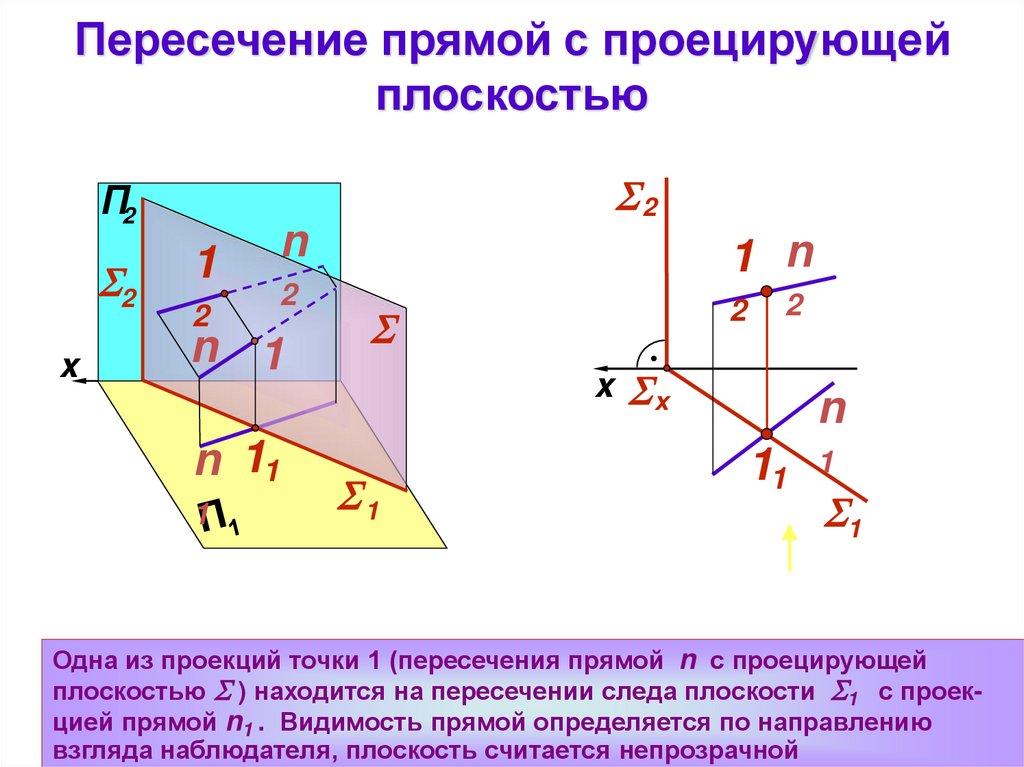
Одна из проекций точки 1 (пересечения прямой n с проецирующей
плоскостью ) находится на пересечении следа плоскости 1 с проекцией прямой n1 . Видимость прямой определяется по направлению
взгляда наблюдателя, плоскость считается непрозрачной

18.

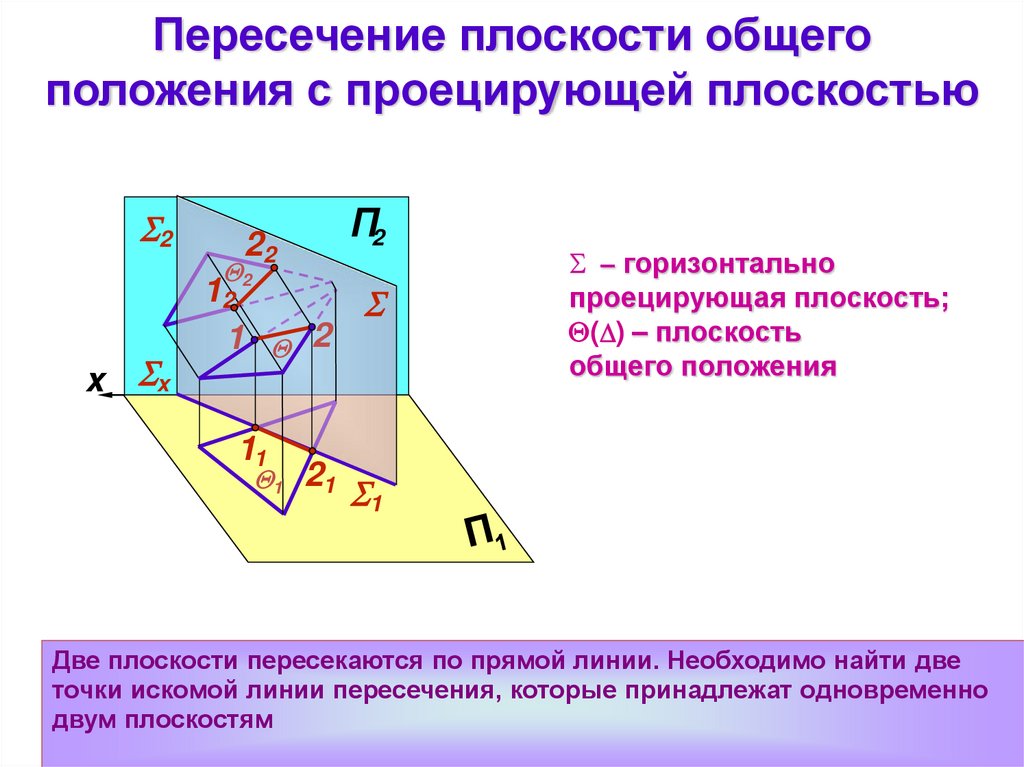
Пересечение плоскости общего
положения с проецирующей плоскостью
2
П2
22
2
x х
12
1
2
1
21
11
– горизонтально
проецирующая плоскость;
( ) – плоскость
общего положения
1
Две плоскости пересекаются по прямой линии. Необходимо найти две
точки искомой линии пересечения, которые принадлежат одновременно
двум плоскостям

19.

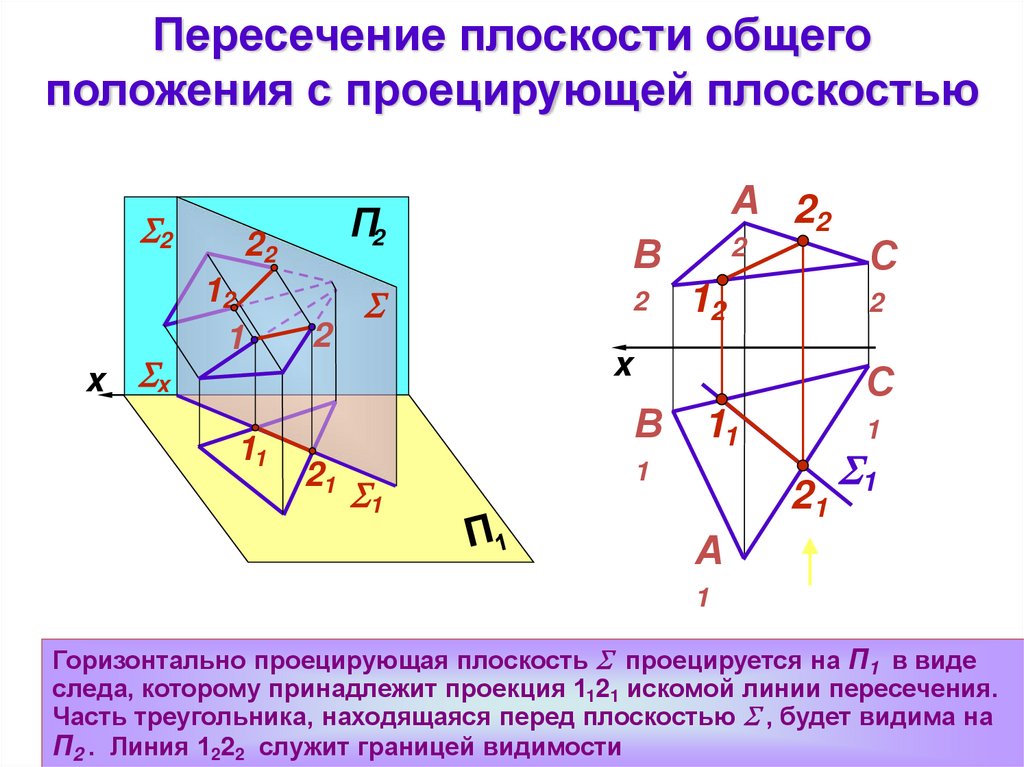
Пересечение плоскости общего
положения с проецирующей плоскостью
2
x х
П2
22
12
1
11
2
В
2
2
12
1
С
2
x
В
21
А 22
С
11
1
1
21
1
А
1
Горизонтально проецирующая плоскость проецируется на П1 в виде
следа, которому принадлежит проекция 1121 искомой линии пересечения.
Часть треугольника, находящаяся перед плоскостью , будет видима на
П2 . Линия 1222 служит границей видимости