лекция 3 проекции плоскости

1.

Лекция 3
Проекции плоскости

2. Ортогональная проекция плоскости

• Плоскость является простейшей
поверхностью, не имеющей кривизы
• Положение плоскости в пространстве
однозначно определяется тремя
различными точками, не
принадлежащими одной прямой

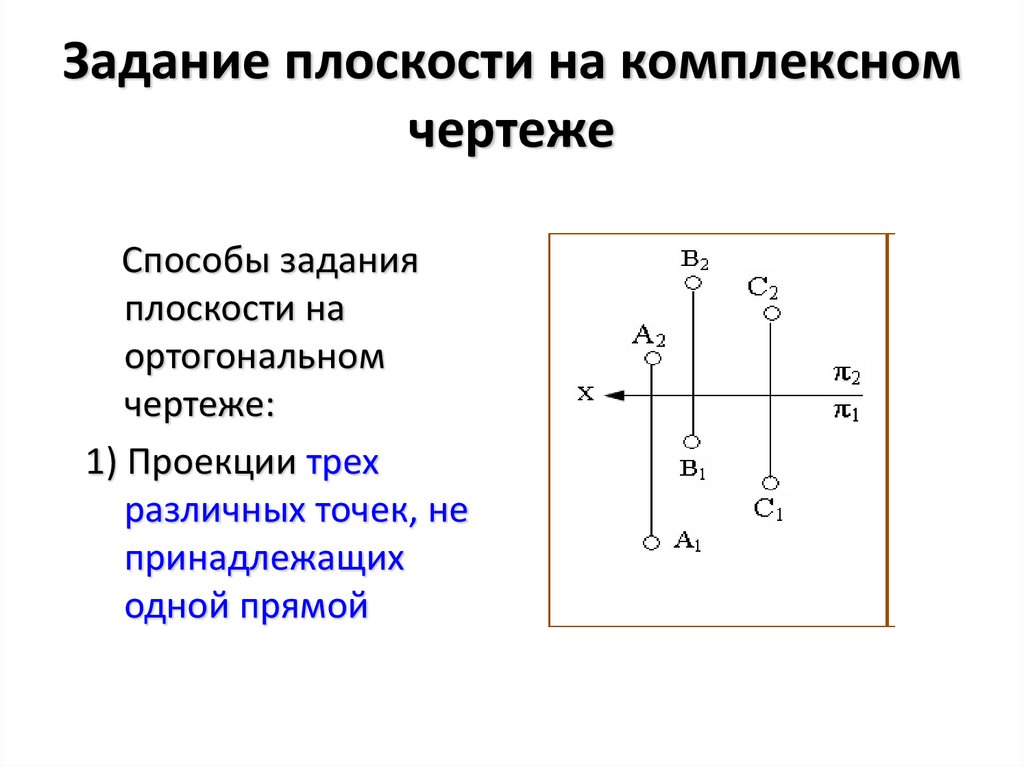
3. Задание плоскости на комплексном чертеже

Способы задания
плоскости на
ортогональном
чертеже:
1) Проекции трех
различных точек, не
принадлежащих
одной прямой

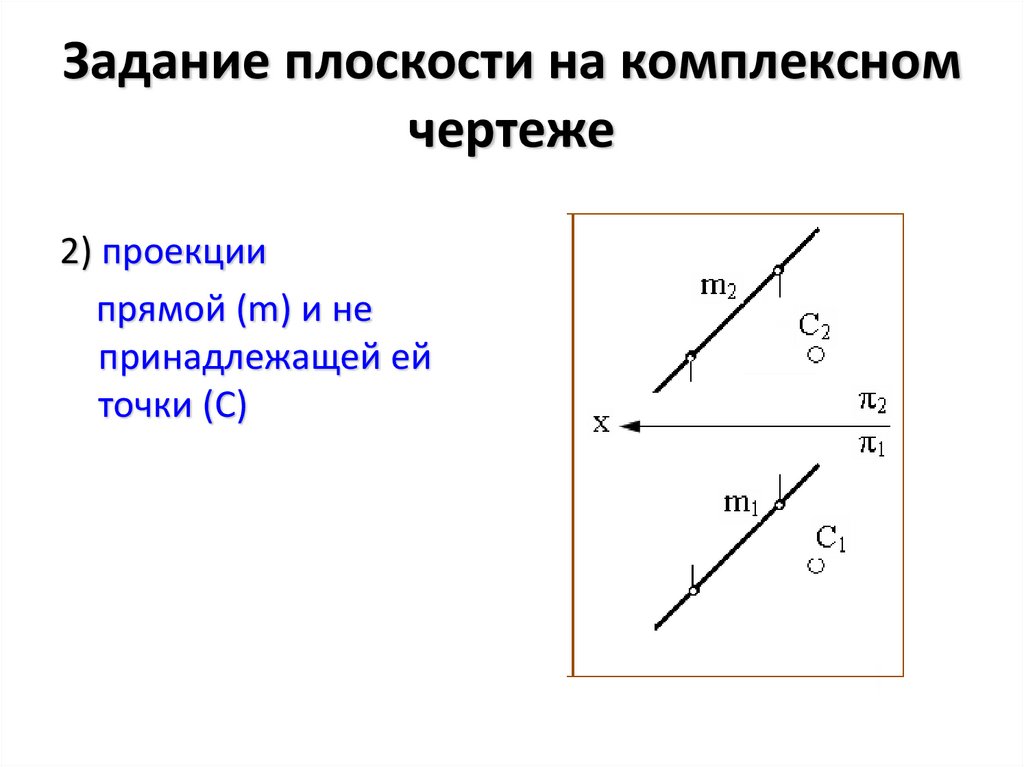
4. Задание плоскости на комплексном чертеже

2) проекции
прямой (m) и не
принадлежащей ей
точки (C)

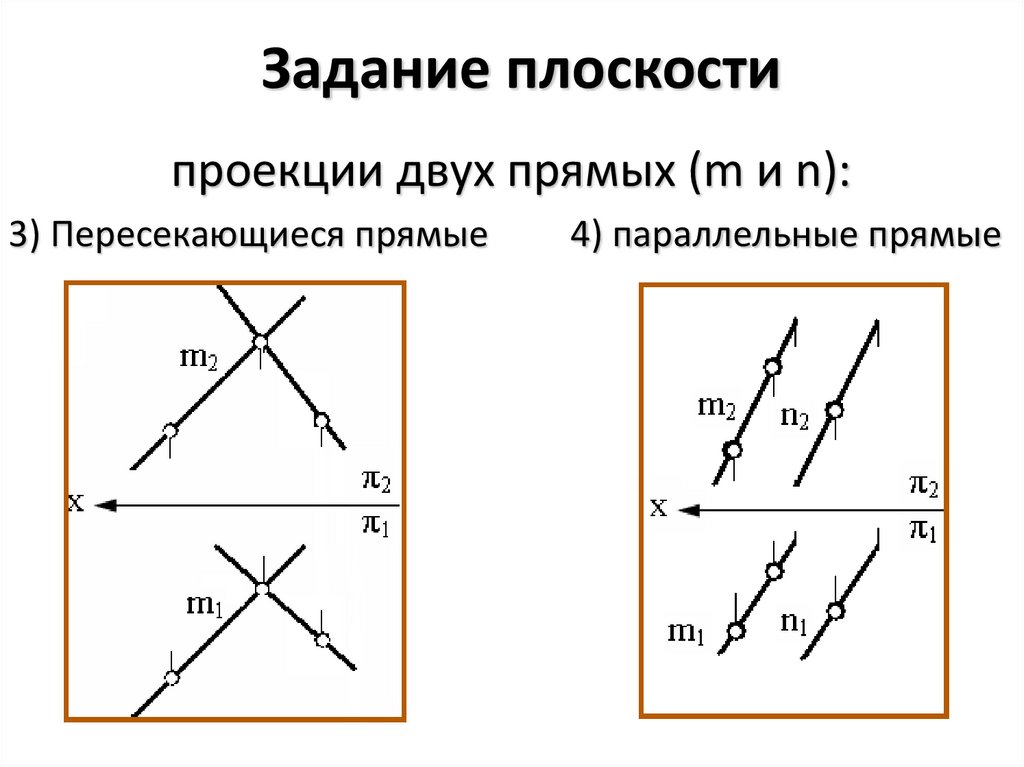
5. Задание плоскости

проекции двух прямых (m и n):
3) Пересекающиеся прямые
4) параллельные прямые

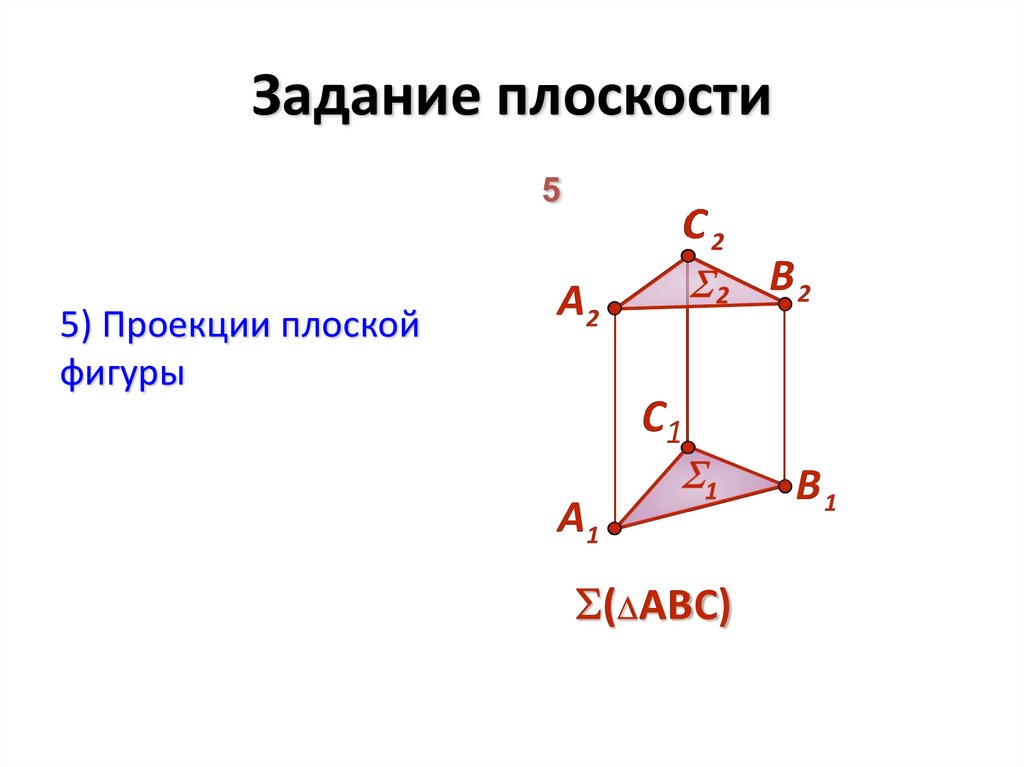
6. Задание плоскости

5) Проекции плоской
фигуры

7. Задание плоскости

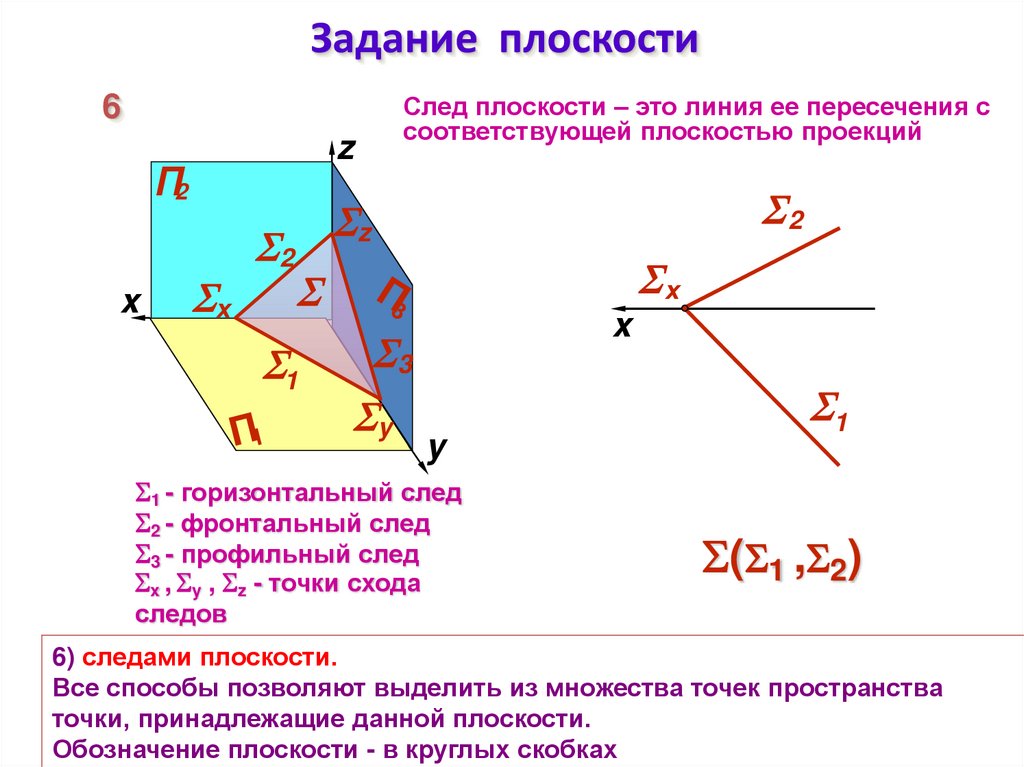
След плоскости – это линия ее пересечения с
соответствующей плоскостью проекций
6
z
П2
x
х
2
2
z
х
1
x
3
y
y
1 - горизонтальный след
2 - фронтальный след
3 - профильный след
x , y , z - точки схода
следов
1
( 1 , 2)
6) следами плоскости.
Все способы позволяют выделить из множества точек пространства
точки, принадлежащие данной плоскости.
Обозначение плоскости - в круглых скобках

8. Положение плоскости относительно плоскостей проекций

Плоскость общего положения наклонена ко всем
плоскостям проекций
Плоскость частного положения перпендикулярна
или параллельна одной из плоскостей проекций
Плоскость, перпендикулярная одной из плоскостей
проекций, называется проецирующей плоскостью:
Горизонтально проецирующая плоскость
П1
Фронтально проецирующая плоскость
П2
Профильно
проецирующая
П3
Плоскость,
параллельная
плоскостиплоскость
проекций, назы-
вается плоскостью уровня (дважды проецирующей):
Горизонтальная плоскость П1
Фронтальная плоскость
П2
Профильная плоскость
П3

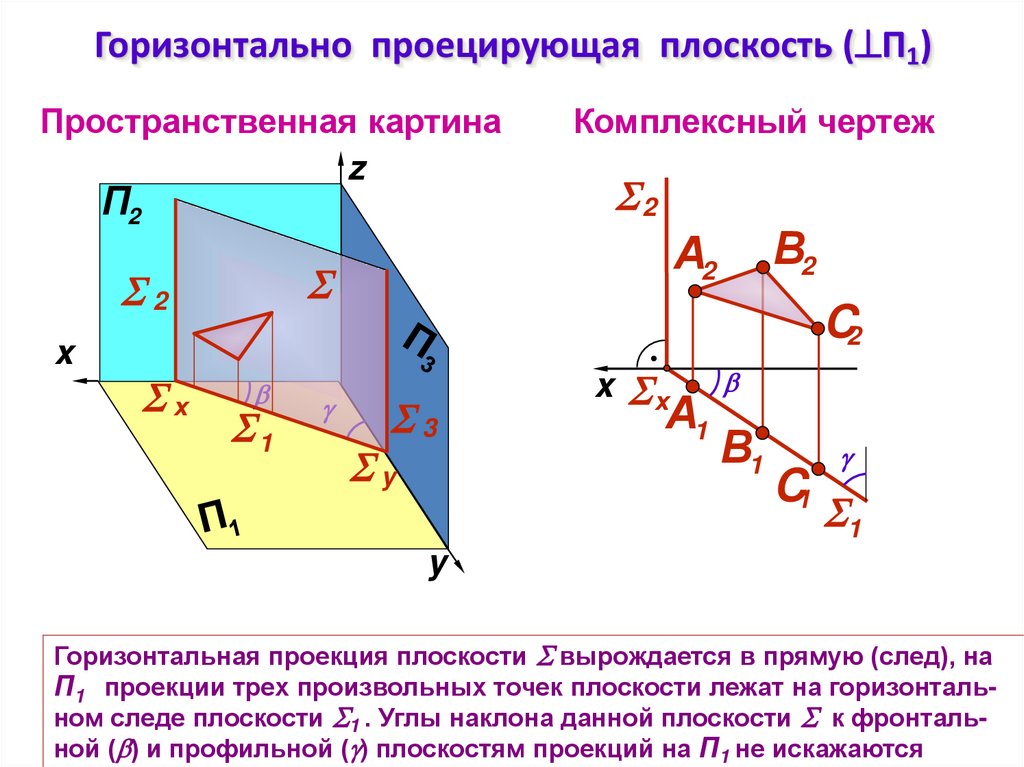
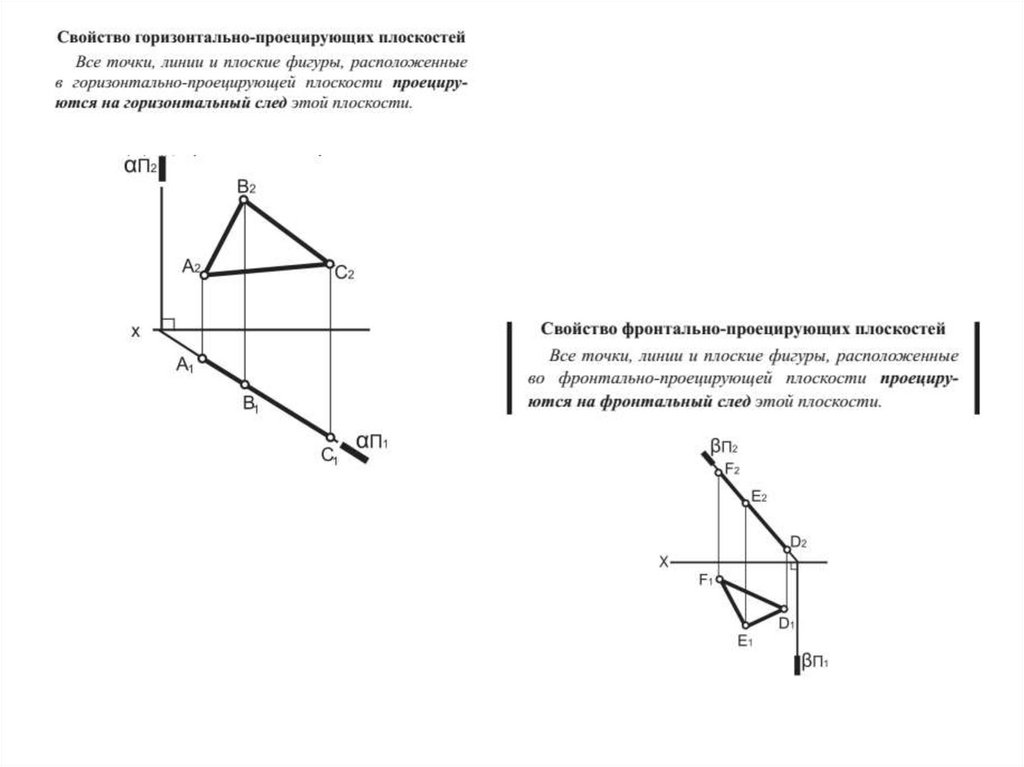
9. Горизонтально проецирующая плоскость (П1)

Горизонтально проецирующая плоскость ( П1)
Пространственная картина
z
П2
х
2
1
В2
А2
2
x
Комплексный чертеж
C2
3
y
x х
А1
В1
C1
1
y
Горизонтальная проекция плоскости вырождается в прямую (след), на
П1 проекции трех произвольных точек плоскости лежат на горизонтальном следе плоскости 1 . Углы наклона данной плоскости к фронтальной ( ) и профильной ( ) плоскостям проекций на П1 не искажаются

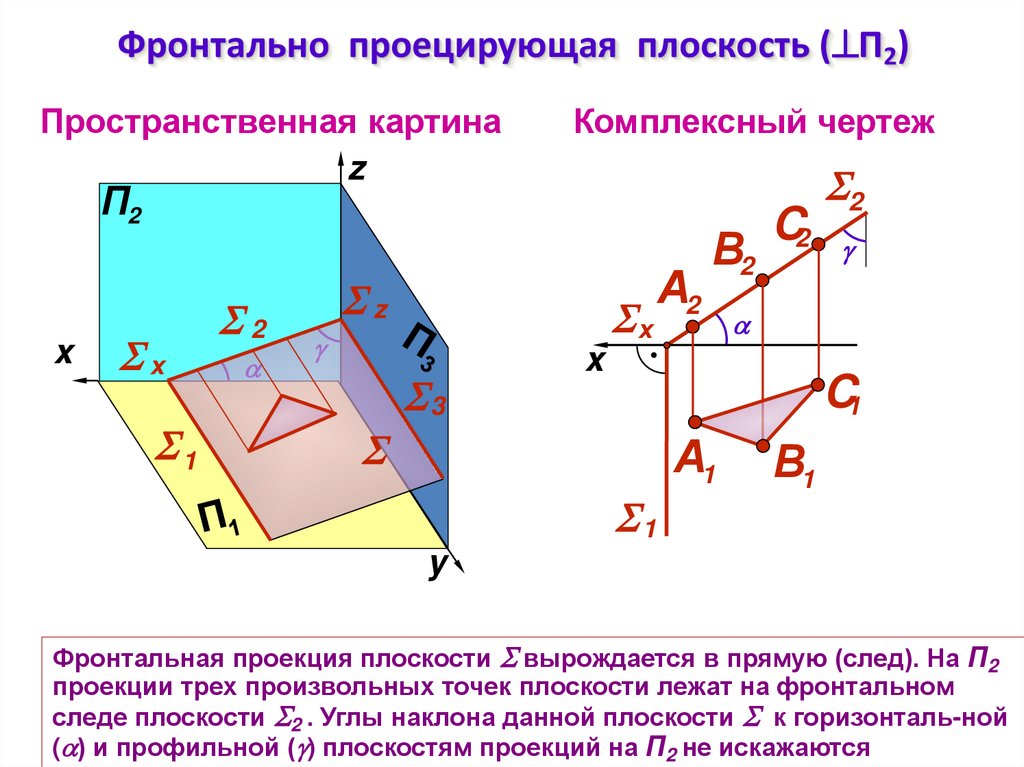
10. Фронтально проецирующая плоскость (П2)

Фронтально проецирующая плоскость ( П2)
Пространственная картина
z
Комплексный чертеж
П2
x
х
1
2
z
х
3
А2
В2
C2
2
x
C1
А1
1
В1
y
Фронтальная проекция плоскости вырождается в прямую (след). На П2
проекции трех произвольных точек плоскости лежат на фронтальном
следе плоскости 2 . Углы наклона данной плоскости к горизонталь-ной
( ) и профильной ( ) плоскостям проекций на П2 не искажаются

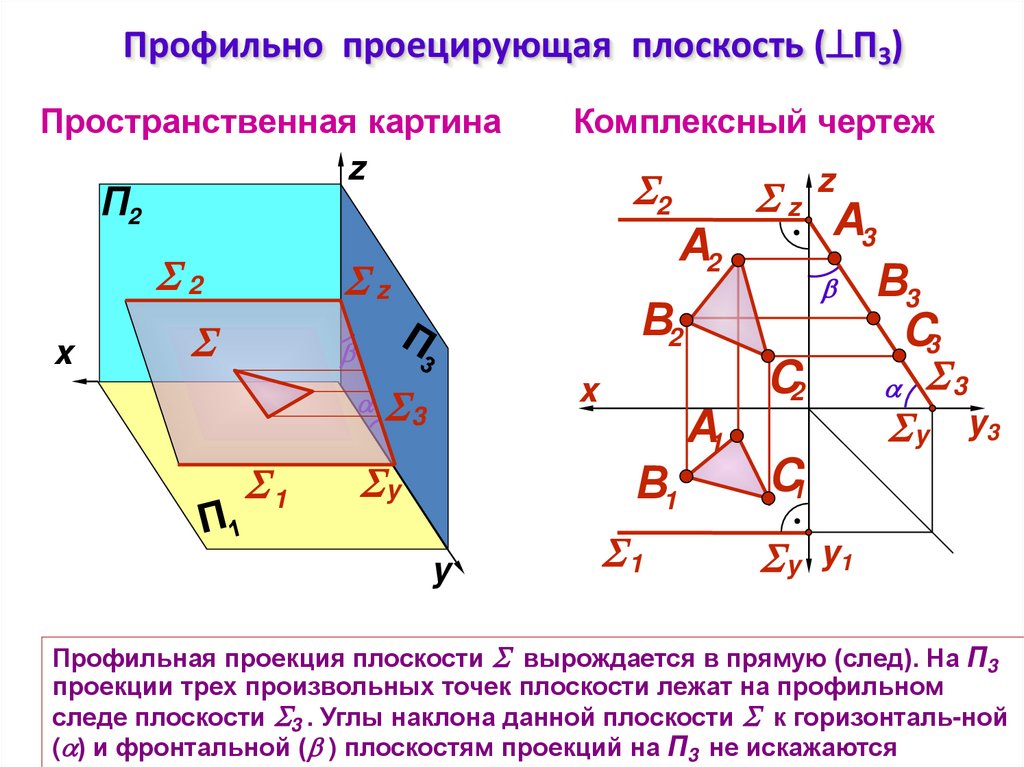
11. Профильно проецирующая плоскость (П3)

Профильно проецирующая плоскость ( П3)
Пространственная картина
z
Комплексный чертеж
2
П2
2
x
z
x
3
y
А1
В1
y
1
А3
В2
1
А2
z
z
C2
В3
C3
3
y y3
C1
y y1
Профильная проекция плоскости вырождается в прямую (след). На П3
проекции трех произвольных точек плоскости лежат на профильном
следе плоскости 3 . Углы наклона данной плоскости к горизонталь-ной
( ) и фронтальной ( ) плоскостям проекций на П3 не искажаются

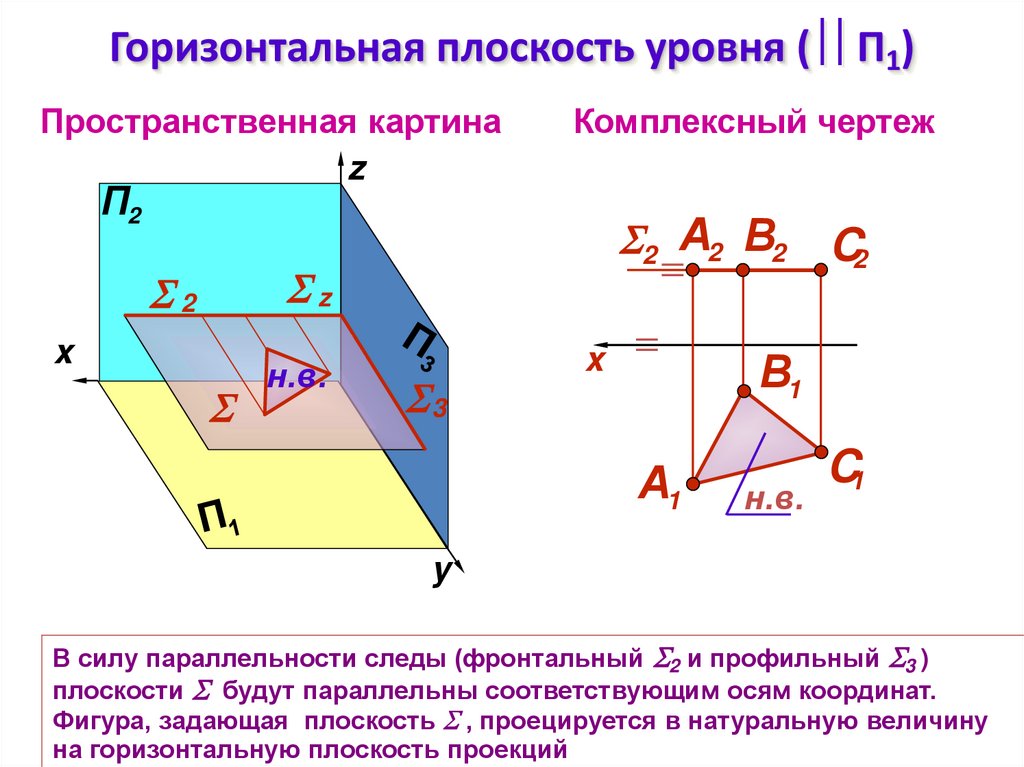
12. Горизонтальная плоскость уровня ( П1)

Горизонтальная плоскость уровня ( П1)
Пространственная картина
z
Комплексный чертеж
П2
2 А2 В2
z
2
x
н.в.
3
x
C2
В1
А1
н.в.
C1
y
В силу параллельности следы (фронтальный 2 и профильный 3 )
плоскости будут параллельны соответствующим осям координат.
Фигура, задающая плоскость , проецируется в натуральную величину
на горизонтальную плоскость проекций

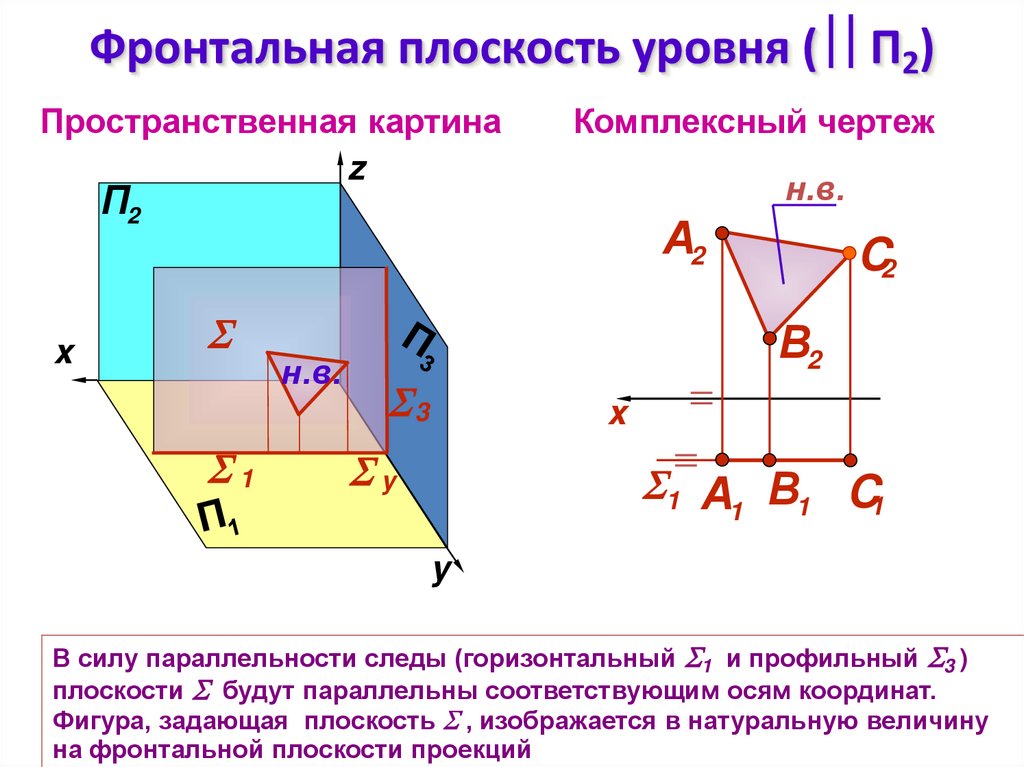
13. Фронтальная плоскость уровня ( П2)

Фронтальная плоскость уровня ( П2)
Пространственная картина
z
Комплексный чертеж
н.в.
П2
x
А2
1
н.в.
C2
В2
3
x
y
1 А В1 C1
1
y
В силу параллельности следы (горизонтальный 1 и профильный 3 )
плоскости будут параллельны соответствующим осям координат.
Фигура, задающая плоскость , изображается в натуральную величину
на фронтальной плоскости проекций

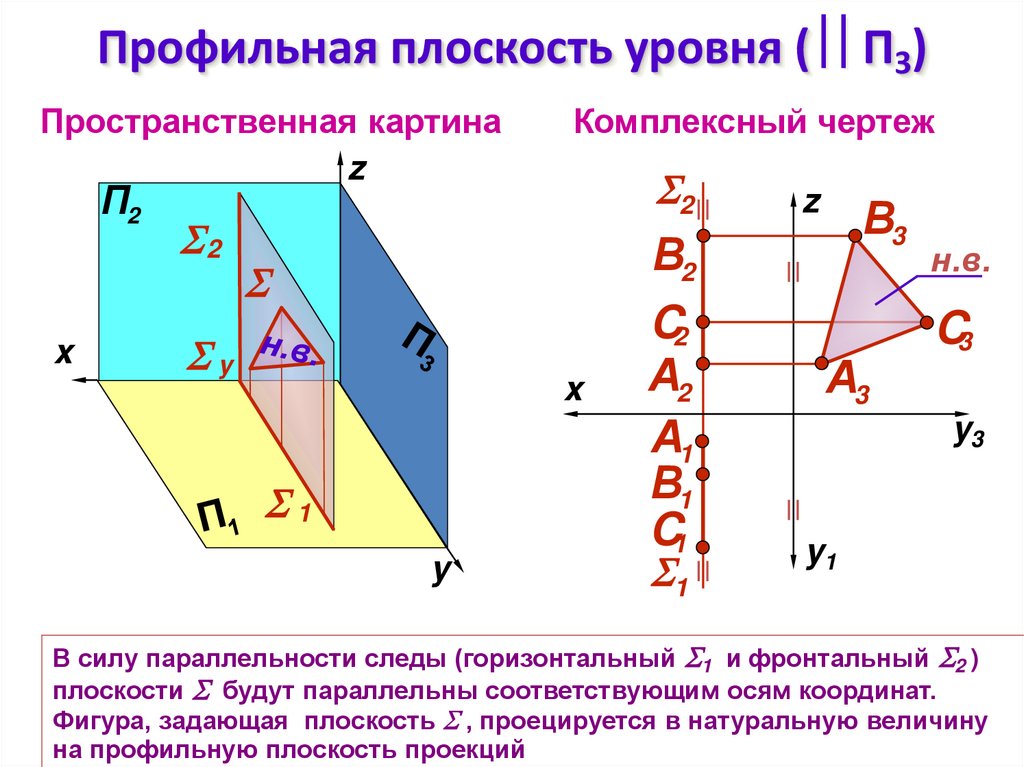
14. Профильная плоскость уровня ( П3)

Профильная плоскость уровня ( П3)
Пространственная картина
z
П2
x
2
Комплексный чертеж
2
y
x
1
y
В2
C2
А2
А1
В1
C1
1
z
В3
А3
н.в.
C3
y3
y1
В силу параллельности следы (горизонтальный 1 и фронтальный 2 )
плоскости будут параллельны соответствующим осям координат.
Фигура, задающая плоскость , проецируется в натуральную величину
на профильную плоскость проекций

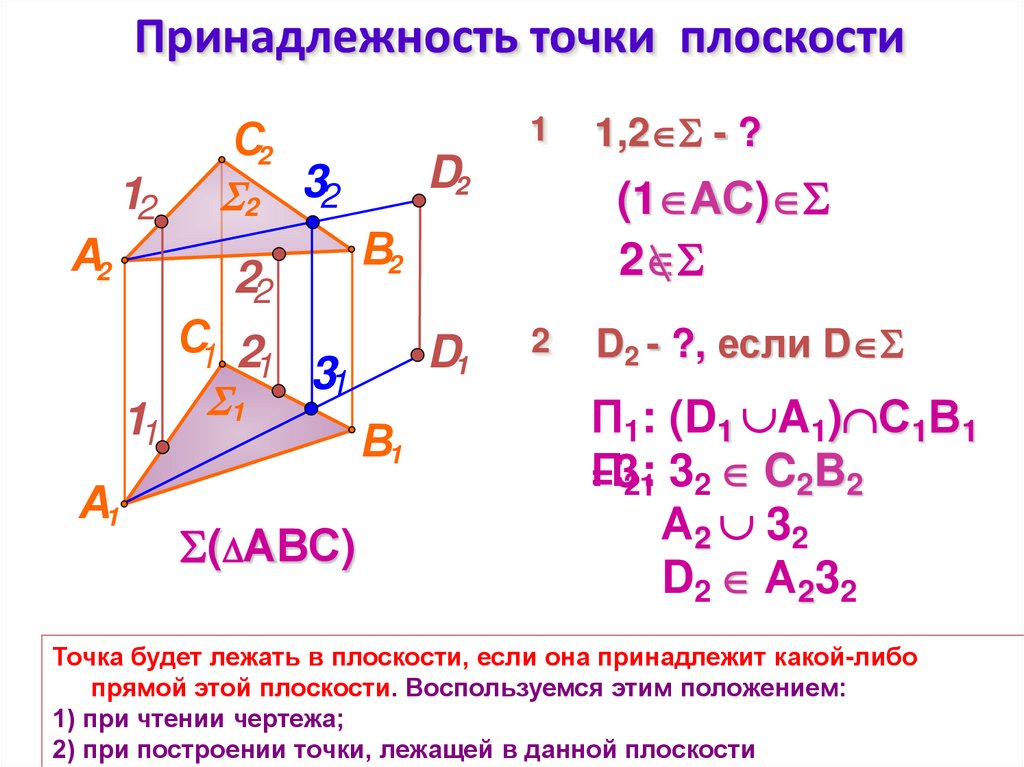
15. Принадлежность точки плоскости

С2
12
А2
2
11
1
1
D2
32
D1
31
( АВС)
В1
1,2 - ?
(1 АС)
2
В2
22
С1 2
А1
1
2
D2 - ?, если D
П1: (D1 A1) С1В1
П321: 32 C2B2
=
А2 32
D2 А232
Точка будет лежать в плоскости, если она принадлежит какой-либо
прямой этой плоскости. Воспользуемся этим положением:
1) при чтении чертежа;
2) при построении точки, лежащей в данной плоскости

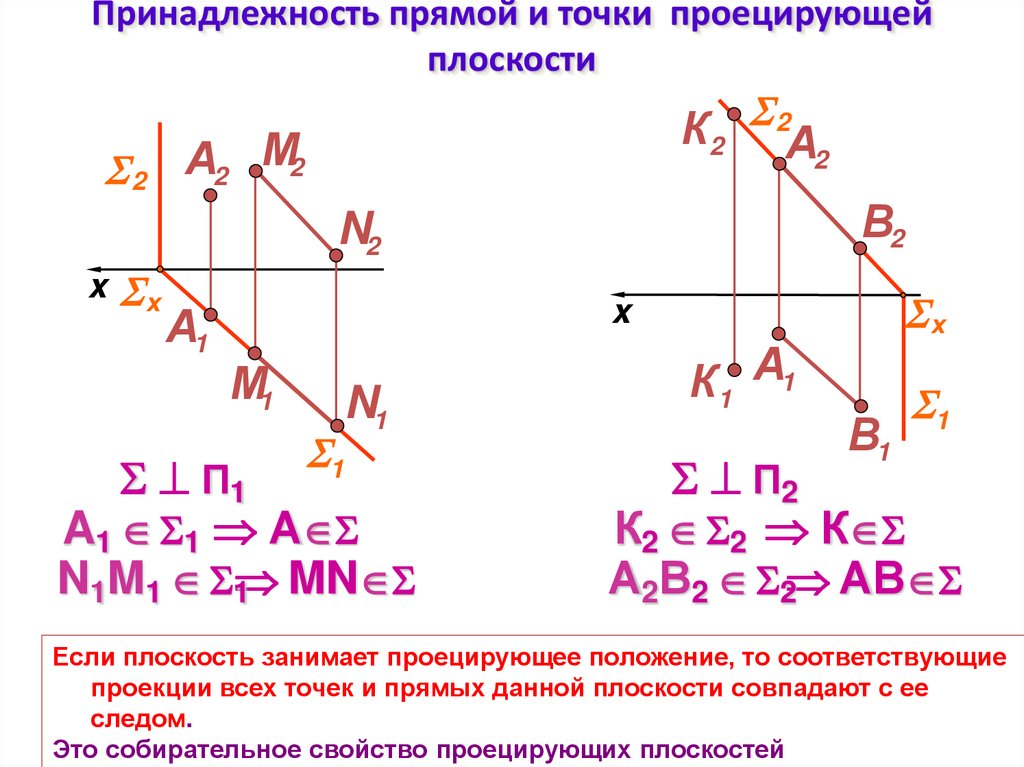
16. Принадлежность прямой и точки проецирующей плоскости

К2 2А
2 А2 М2
2
В2
N2
x х
А1
х
x
М1
1
N1
П1
A1 1 А
N1M1 1 MN
К1 А1
В1
1
П2
К2 2 К
А2В2 2 АВ
Если плоскость занимает проецирующее положение, то соответствующие
проекции всех точек и прямых данной плоскости совпадают с ее
следом.
Это собирательное свойство проецирующих плоскостей

17. Принадлежность плоскости плоской фигуры

• Фигура называется плоской, если все
точки этой фигуры лежат в одной
плоскости
• Плоские фигуры принадлежат плоскости,
если все точки этой фигуры лежат в
указанной плоскости

18.

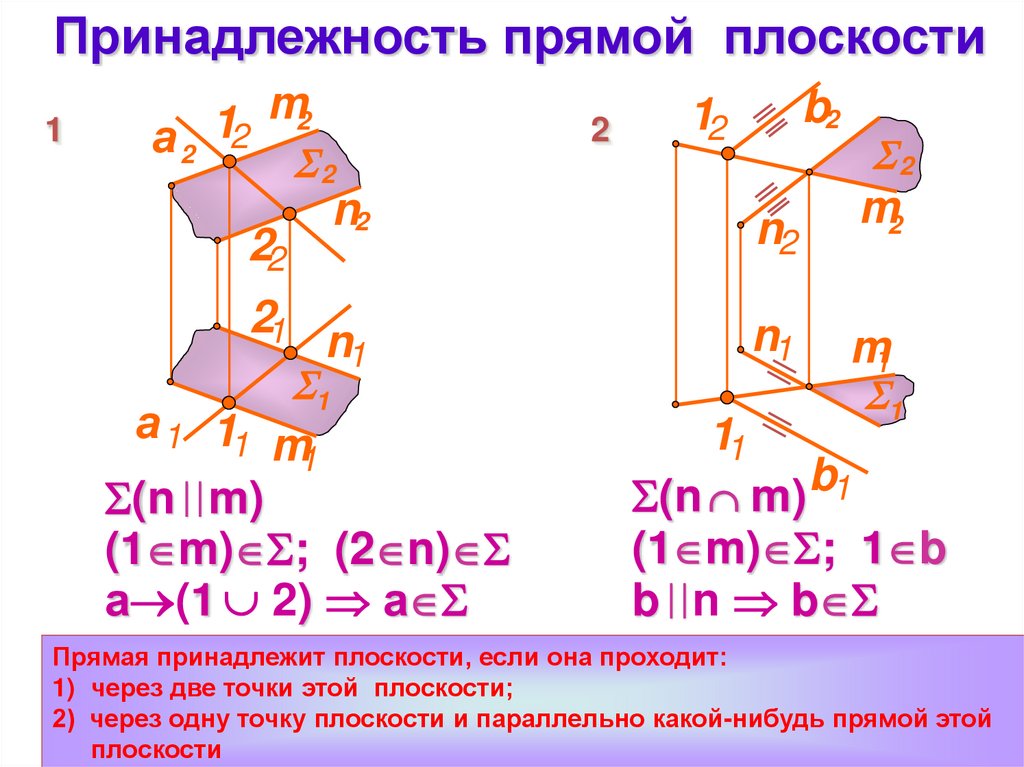
Принадлежность прямой плоскости
1
m2
1
а2 2
2
n2
m2
n1
n1
m1
1
а 1 11 m
1
2
n2
22
21
2
b2
12
(n m)
(1 m) ; (2 n)
а (1 2) а
11
1
(n m) b1
(1 m) ; 1 b
b n b
Прямая принадлежит плоскости, если она проходит:
1) через две точки этой плоскости;
2) через одну точку плоскости и параллельно какой-нибудь прямой этой
плоскости

19.

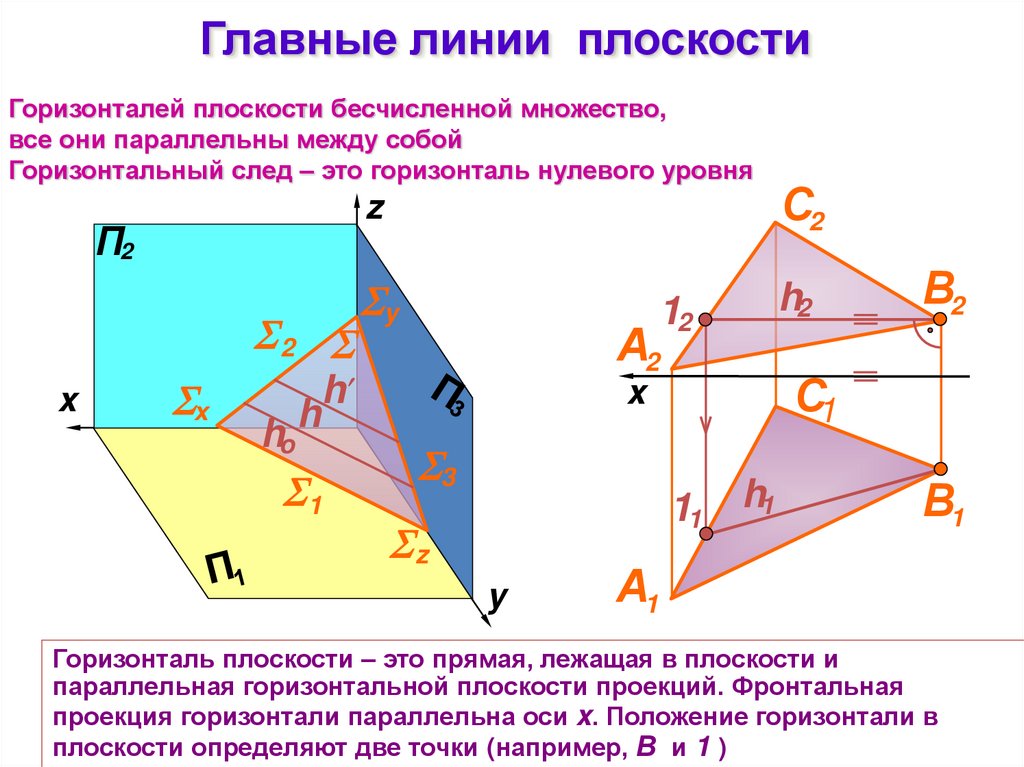
Главные линии плоскости
Горизонталей плоскости бесчисленной множество,
все они параллельны между собой
Горизонтальный след – это горизонталь нулевого уровня
П2
2
x
х
hh
z
С2
y
h2
А2
h
o
1
12
С1
x
3
11 h1
z
y
В2
В1
А1
Горизонталь плоскости – это прямая, лежащая в плоскости и
параллельная горизонтальной плоскости проекций. Фронтальная
проекция горизонтали параллельна оси x. Положение горизонтали в
плоскости определяют две точки (например, В и 1 )

20.

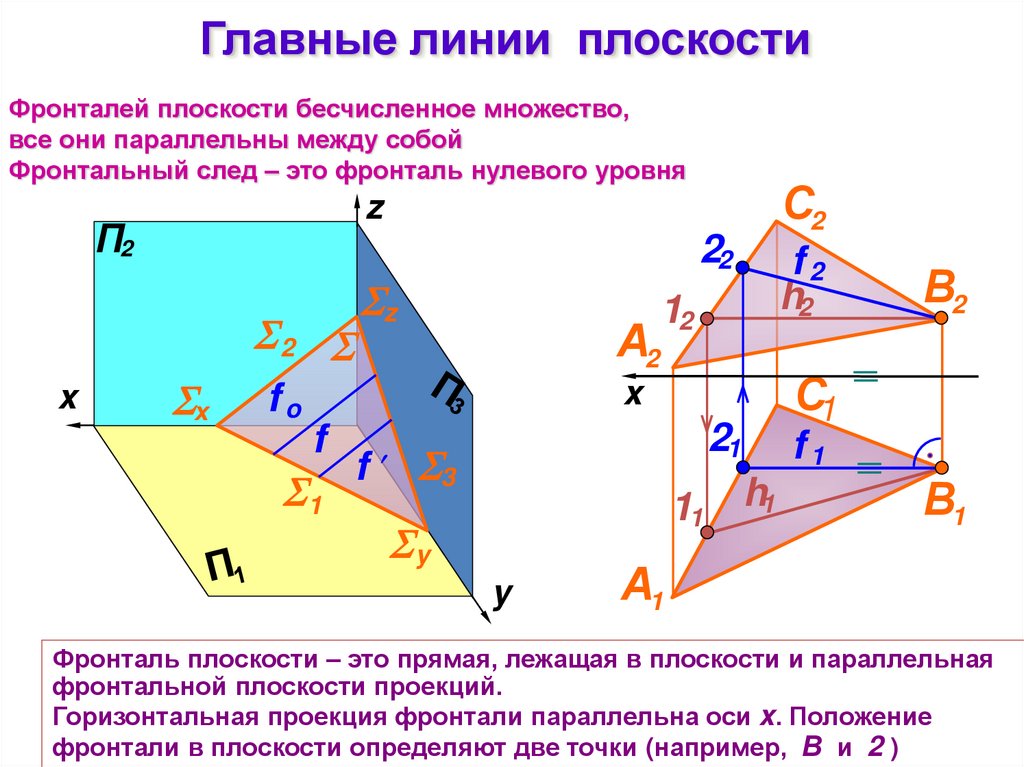
Главные линии плоскости
Фронталей плоскости бесчисленное множество,
все они параллельны между собой
Фронтальный след – это фронталь нулевого уровня
z
П2
2
x
х
22
z
А2
12
x
fo
f
1
f
21
3
11 h1
y
y
С2
f2
h2
В2
С1
f1
В1
А1
Фронталь плоскости – это прямая, лежащая в плоскости и параллельная
фронтальной плоскости проекций.
Горизонтальная проекция фронтали параллельна оси x. Положение
фронтали в плоскости определяют две точки (например, В и 2 )

21. Взаимное положение прямой и плоскости, двух плоскостей

Прямая и плоскость:
• Прямая принадлежит плоскости: все точки прямой
являются точками плоскости
• Прямая параллельна плоскости: общих собственных
точек нет
• Прямая пересекает плоскость: одна общая точка
Две плоскости:
• Плоскости параллельны: общих собственных
прямых нет
• Плоскости пересекаются: одна общая прямая
Рассмотрим все возможные случаи взаимного положения прямой и
плоскости и двух плоскостей

22.

Параллельность прямой и плоскости
b
А
n
Признак параллельности:
Прямая параллельна
плоскости, если она
параллельна какой-ли
прямой, лежащей в
этой плоскости
b n b
Через точку А в пространстве можно провести бесчисленное множество
прямых линий, параллельных данной плоскости . Для однозначного
решения проведем в плоскости прямую n

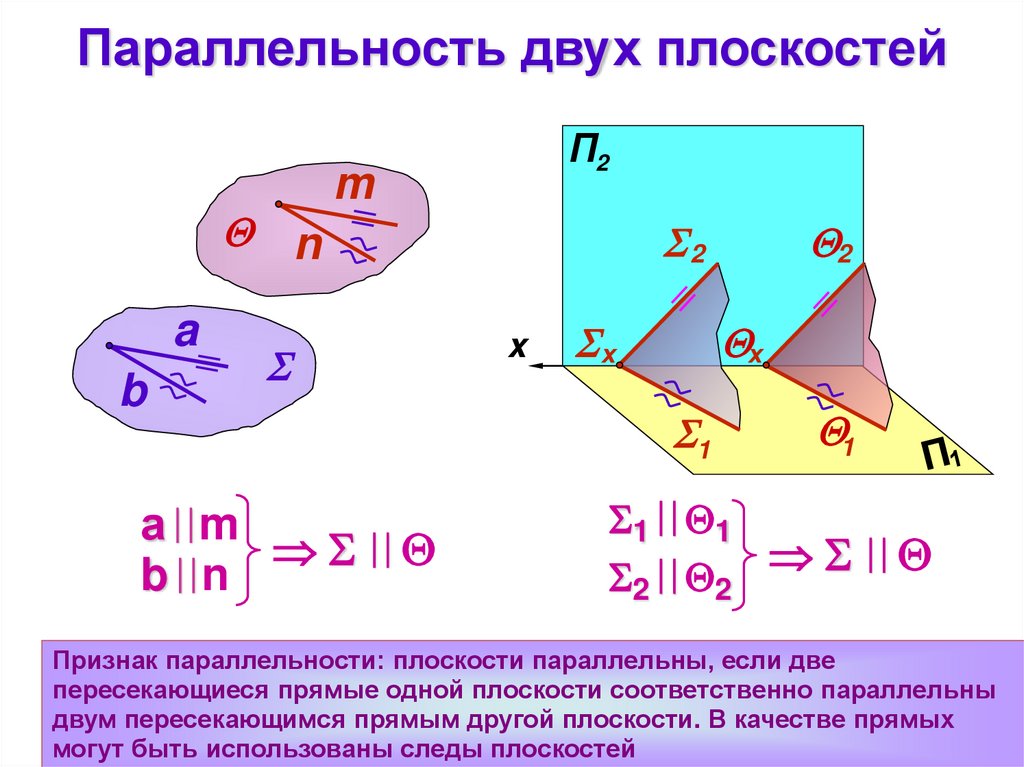
23. Взаимное расположение плоскостей

• Плоскости в пространстве могут быть
расположены параллельно друг другу или
пересекаться
• Плоскости являются параллельными, если
две пересекающиеся прямые, лежащие в
одной плоскости, параллельны двум
пересекающимся прямым, лежащим в
другой плоскости

24.

Параллельность двух плоскостей
n
a
b
П2
m
а m
b n
2
x
х
2
х
1
1
1 1
2 2
Признак параллельности: плоскости параллельны, если две
пересекающиеся прямые одной плоскости соответственно параллельны
двум пересекающимся прямым другой плоскости. В качестве прямых
могут быть использованы следы плоскостей

25.

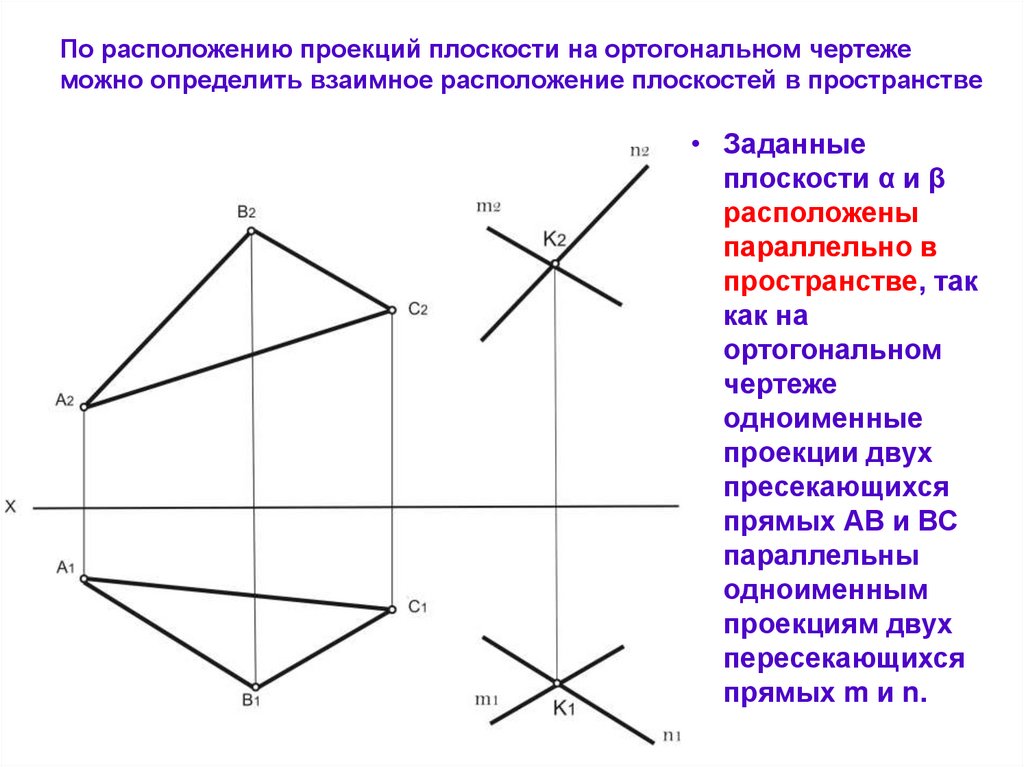
По расположению проекций плоскости на ортогональном чертеже
можно определить взаимное расположение плоскостей в пространстве
• Заданные
плоскости α и β
расположены
параллельно в
пространстве, так
как на
ортогональном
чертеже
одноименные
проекции двух
пресекающихся
прямых АВ и ВС
параллельны
одноименным
проекциям двух
пересекающихся
прямых m и n.

26.

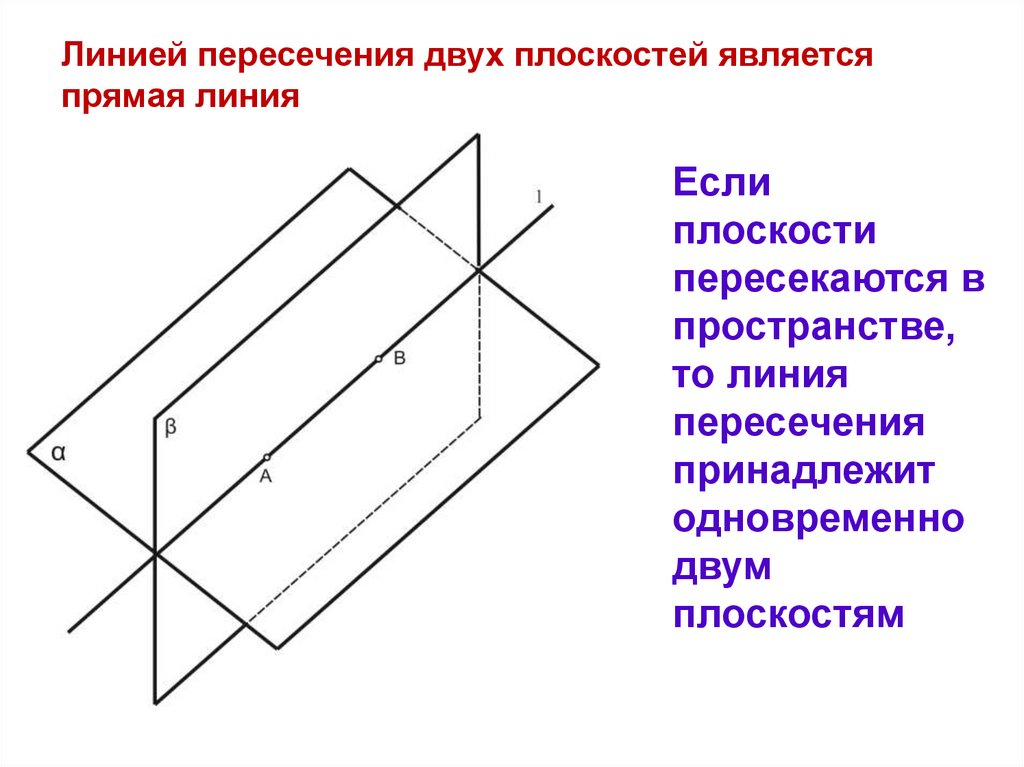
Линией пересечения двух плоскостей является
прямая линия
Если
плоскости
пересекаются в
пространстве,
то линия
пересечения
принадлежит
одновременно
двум
плоскостям

27.

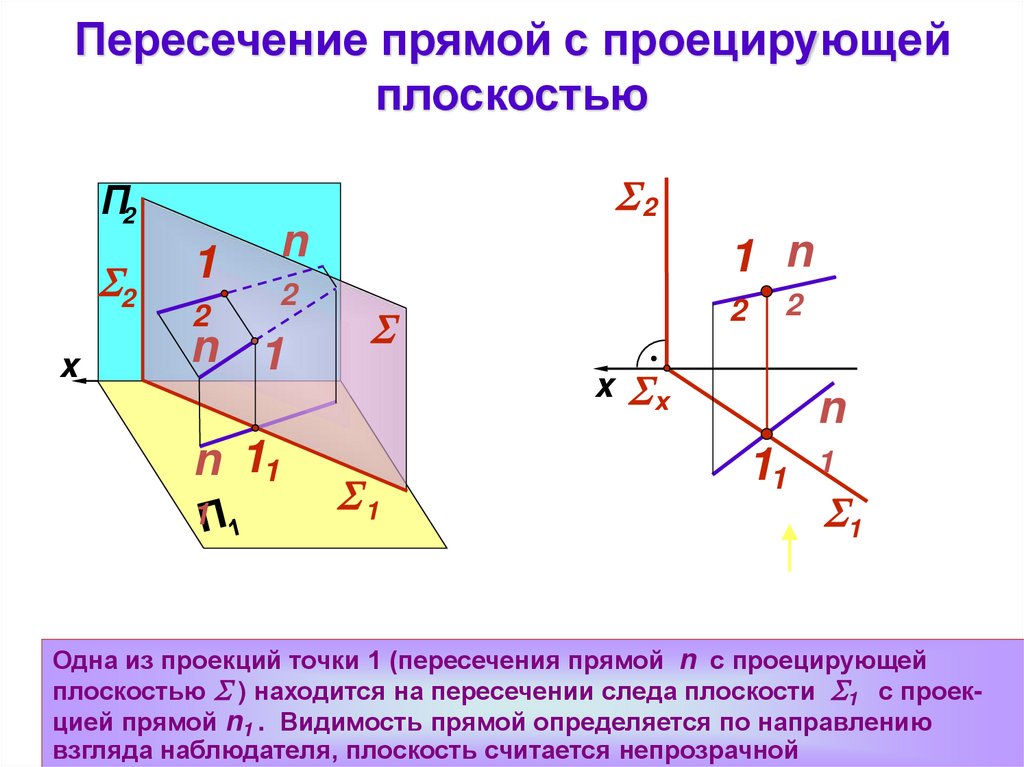
Пересечение прямой с проецирующей
плоскостью
2
П2
2
x
х
1
2
n
2
n 1
n 11
1
1 n
2
x х
1
2
n
11 1
1
Одна из проекций точки 1 (пересечения прямой n с проецирующей
плоскостью ) находится на пересечении следа плоскости 1 с проекцией прямой n1 . Видимость прямой определяется по направлению
взгляда наблюдателя, плоскость считается непрозрачной

28.

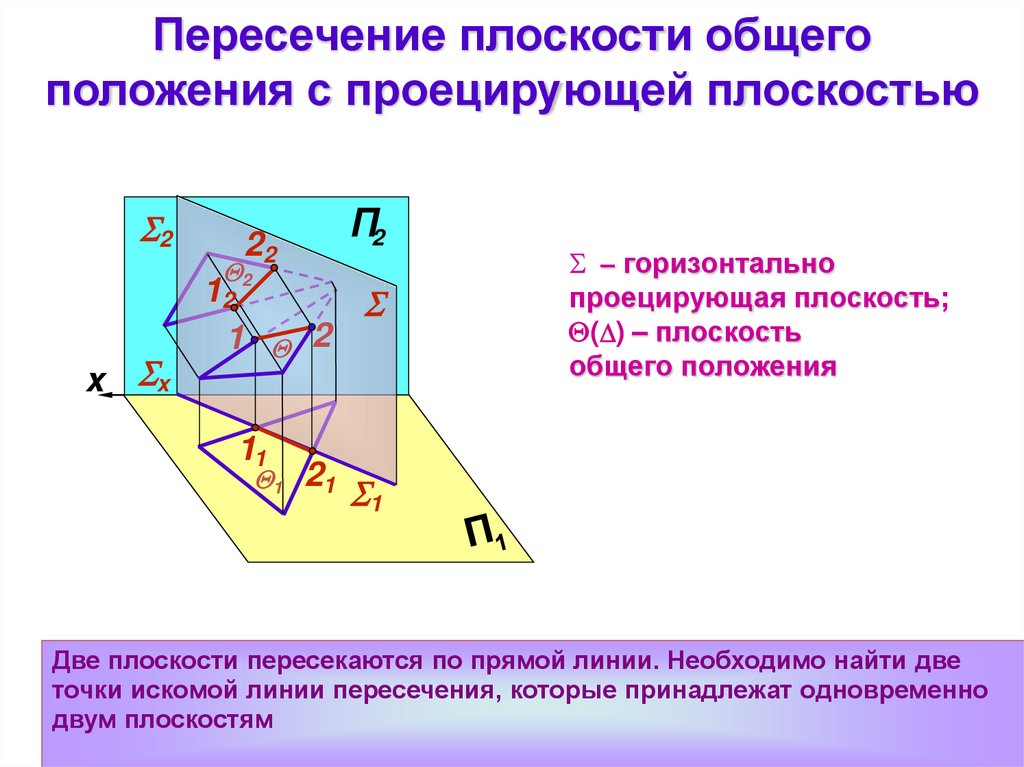
Пересечение плоскости общего
положения с проецирующей плоскостью
2
П2
22
2
x х
12
1
2
1
21
11
– горизонтально
проецирующая плоскость;
( ) – плоскость
общего положения
1
Две плоскости пересекаются по прямой линии. Необходимо найти две
точки искомой линии пересечения, которые принадлежат одновременно
двум плоскостям

29.

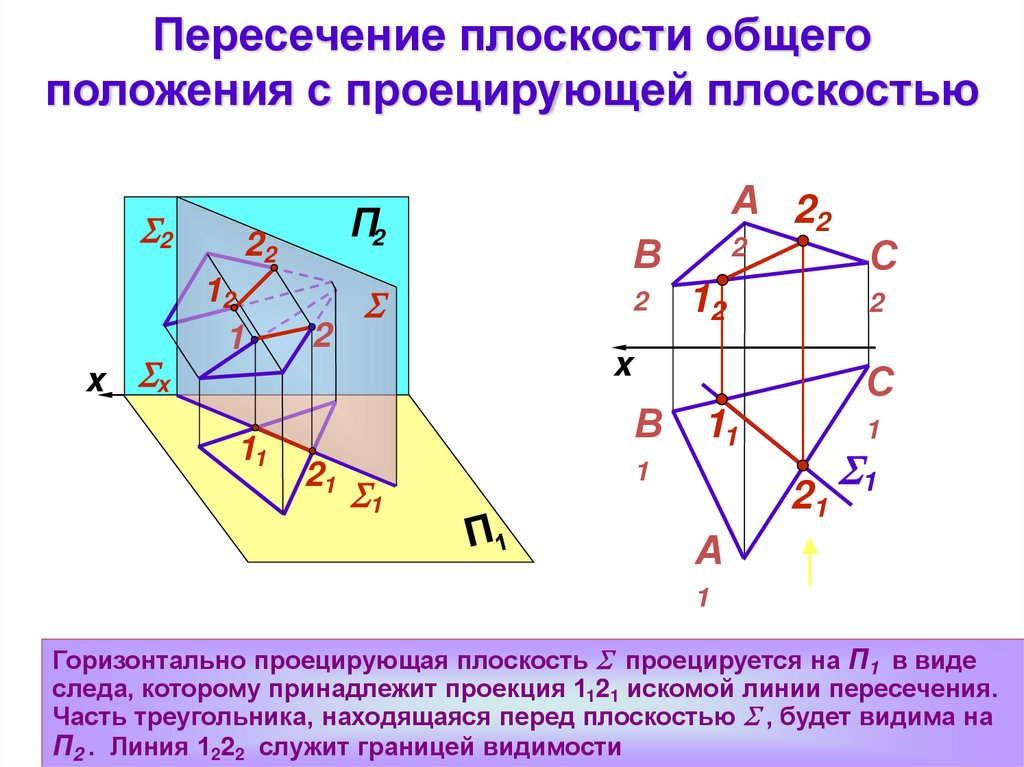
Пересечение плоскости общего
положения с проецирующей плоскостью
2
x х
П2
22
12
1
11
2
В
2
2
12
1
С
2
x
В
21
А 22
С
11
1
1
21
1
А
1
Горизонтально проецирующая плоскость проецируется на П1 в виде
следа, которому принадлежит проекция 1121 искомой линии пересечения.
Часть треугольника, находящаяся перед плоскостью , будет видима на
П2 . Линия 1222 служит границей видимости