Похожие презентации:
Лекция 05. Основные понятия проективной геометрии
1.
Основные понятияпроективной геометрии
2.
1. Понятиегруппы
преобразований
2
3.
Умножение преобразованийНекоторые преобразования можно составить
из нескольких других.
3
4.
Умножение преобразованийНекоторые преобразования можно составить
из нескольких других.
Пример. Винтовые движения составляются из
поворотов вокруг оси и сдвигов вдоль оси.
4
5.
Умножение преобразованийНекоторые преобразования можно составить
из нескольких других.
Пример. Винтовые движения составляются из
поворотов вокруг оси и сдвигов вдоль оси.
Процесс составления новых преобразований
из заданных и есть
умножение преобразований.
5
6.
Пусть есть некоторая совокупностьпреобразований с операцией умножения.
Она обладает такими свойствами:
6
7.
Пусть есть некоторая совокупностьпреобразований с операцией умножения.
Она обладает такими свойствами:
1. Произведение двух преобразований,
принадлежащих совокупности, само
принадлежит этой совокупности.
7
8.
Пусть есть некоторая совокупностьпреобразований с операцией умножения.
Она обладает такими свойствами:
1. Произведение двух преобразований,
принадлежащих совокупности, само
принадлежит этой совокупности.
2. Произведение преобразований
ассоциативно.
8
9.
Пусть есть некоторая совокупностьпреобразований с операцией умножения.
Она обладает такими свойствами:
1. Произведение двух преобразований,
принадлежащих совокупности, само
принадлежит этой совокупности.
2. Произведение преобразований
ассоциативно.
3. Тождественное преобразование
принадлежит совокупности.
9
10.
Пусть есть некоторая совокупностьпреобразований с операцией умножения.
Она обладает такими свойствами:
1. Произведение двух преобразований,
принадлежащих совокупности, само
принадлежит этой совокупности.
2. Произведение преобразований
ассоциативно.
3. Тождественное преобразование
принадлежит совокупности.
4. Если преобразование принадлежит
совокупности, то обратное преобразование
также принадлежит этой совокупности.
10
11.
Таким образом, всякая совокупностьвзаимно однозначных
преобразований множества М,
обладающая этими свойствами,
называется
группой преобразований множества М.
11
12.
Таким образом, всякая совокупностьвзаимно однозначных
преобразований множества М,
обладающая этими свойствами,
называется
группой преобразований множества М.
Группа преобразований
не обязательно коммутативна.
То есть, группа преобразований
может не быть абелевой.
12
13.
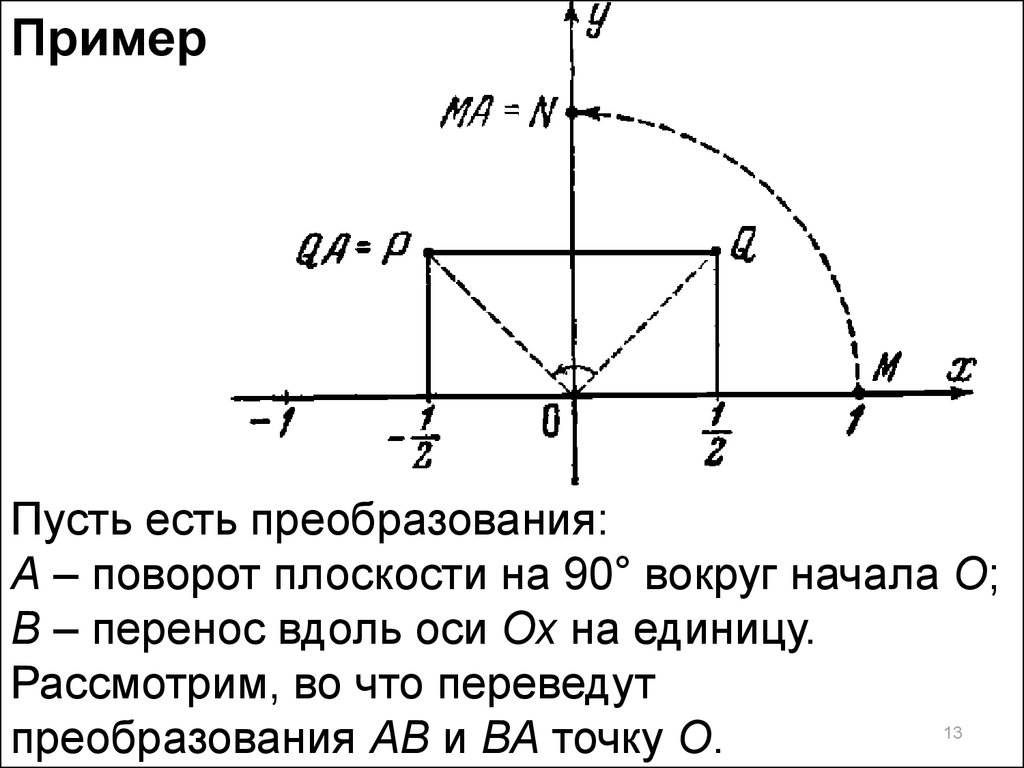
ПримерПусть есть преобразования:
А – поворот плоскости на 90° вокруг начала О;
В – перенос вдоль оси Ох на единицу.
Рассмотрим, во что переведут
преобразования АВ и ВА точку О.
13
14.
ПримерА – пово
В – пере
По определению, имеем:
O(AB) = (OA)B = OB = M
14
15.
ПримерА – пово
В – пере
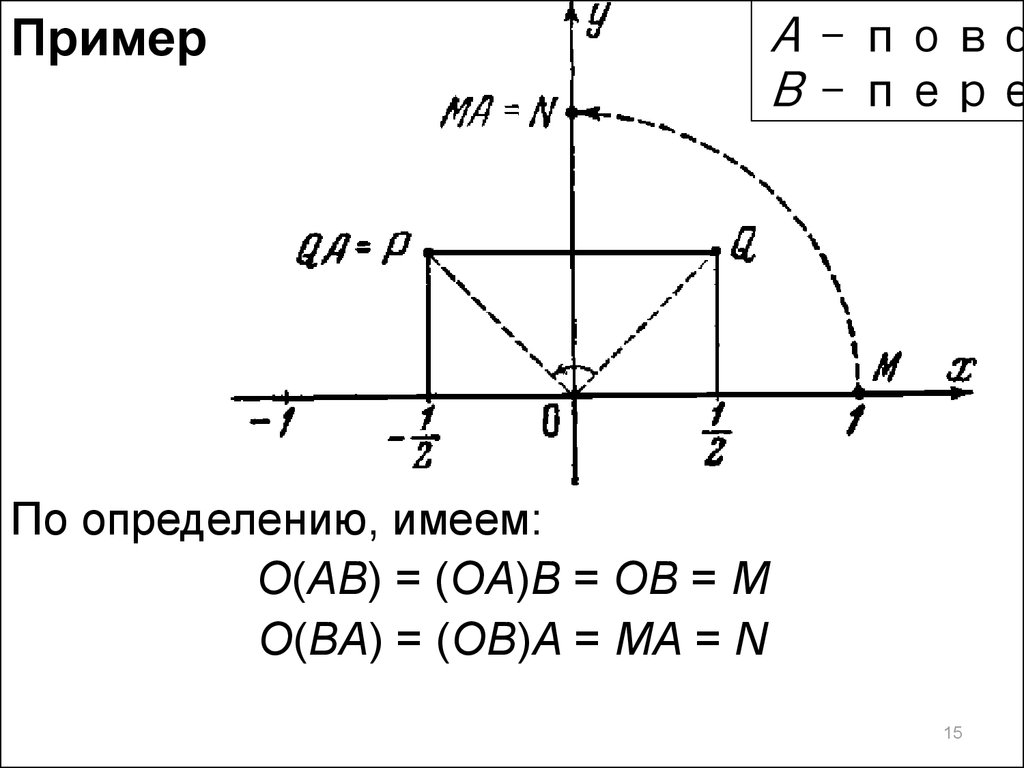
По определению, имеем:
O(AB) = (OA)B = OB = M
O(BA) = (OB)A = MA = N
15
16.
ПримерА – пово
В – пере
По определению, имеем:
O(AB) = (OA)B = OB = M
O(BA) = (OB)A = MA = N
Следовательно, AB ≠ BA.
16
17.
ПримерА – пово
В – пере
O(BA) = N
O(AB) = M
Выясним геометрическую природу ВА.
Рассмотрим точку Р. Имеем:
P(BA) = (PB)A = QA = P
Точка Р неподвижна. Значит, ВА есть поворот
плоскости на 90° вокруг точки Р.
17
18.
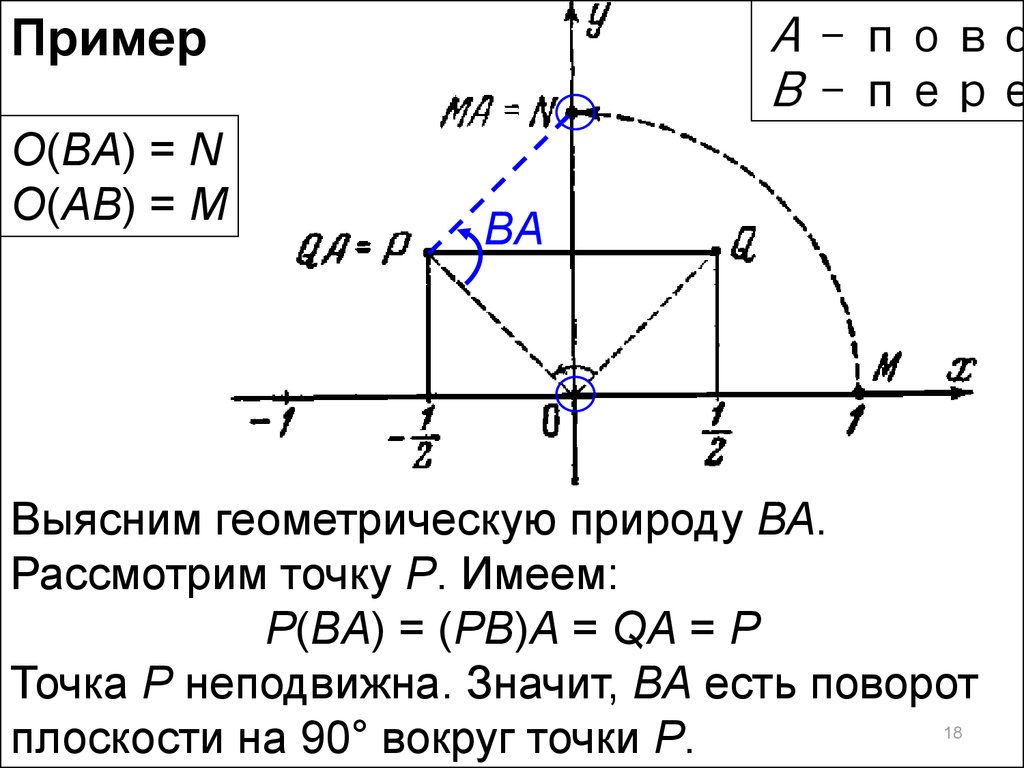
ПримерO(BA) = N
O(AB) = M
А – пово
В – пере
BA
Выясним геометрическую природу ВА.
Рассмотрим точку Р. Имеем:
P(BA) = (PB)A = QA = P
Точка Р неподвижна. Значит, ВА есть поворот
плоскости на 90° вокруг точки Р.
18
19.
ПримерА – пово
В – пере
O(BA) = N
O(AB) = M
Аналогично исследуем АВ.
Рассмотрим точку Q. Имеем:
Q(AB) = (QA)B = PB = Q
Точка Q неподвижна. Значит, АB есть поворот
плоскости на 90° вокруг точки Q.
19
20.
ПримерА – пово
В – пере
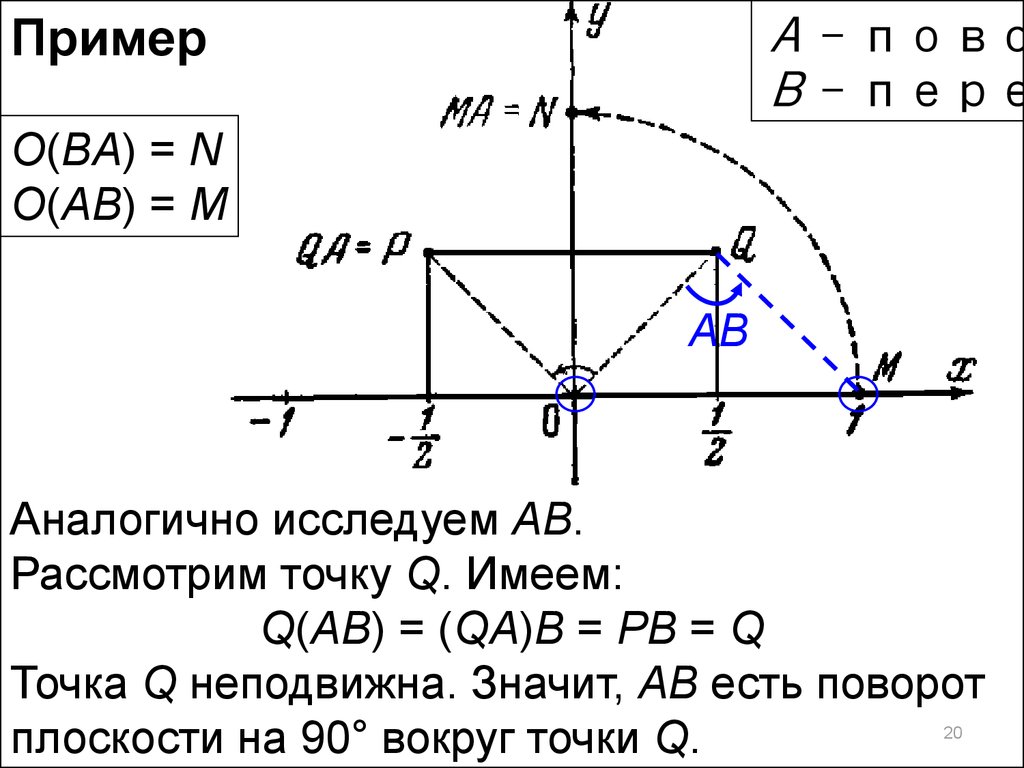
O(BA) = N
O(AB) = M
AB
Аналогично исследуем АВ.
Рассмотрим точку Q. Имеем:
Q(AB) = (QA)B = PB = Q
Точка Q неподвижна. Значит, АB есть поворот
плоскости на 90° вокруг точки Q.
20
21.
2. Группапроективных
преобразований
21
22.
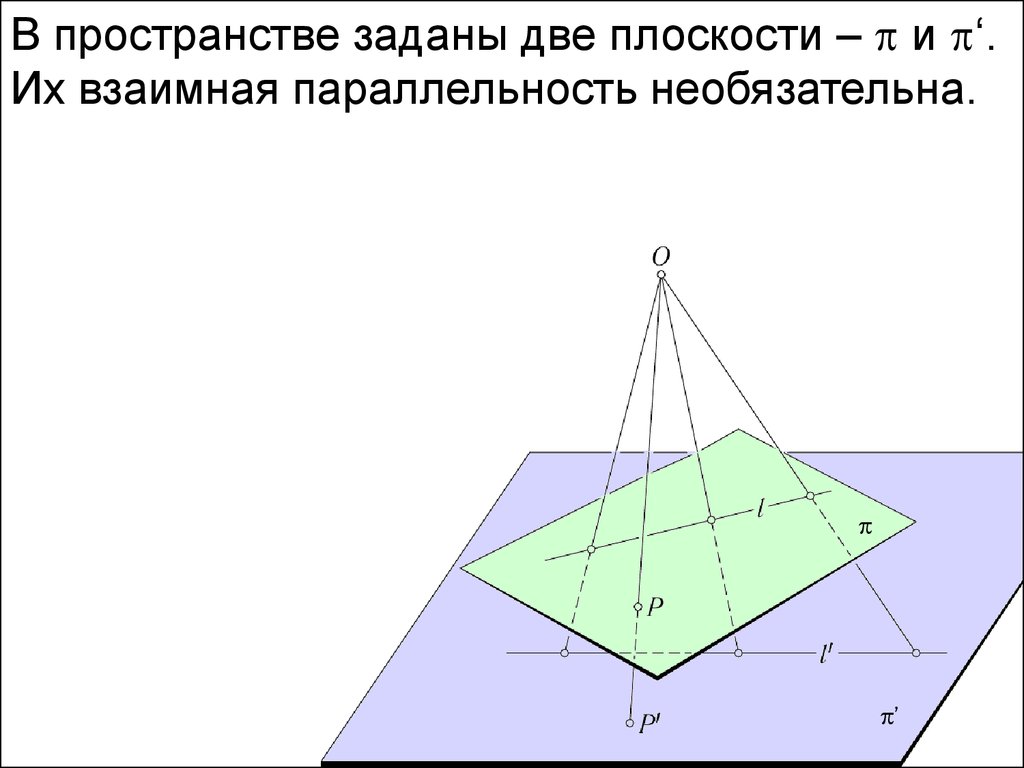
В пространстве заданы две плоскости – и ‘.Их взаимная параллельность необязательна.
'
22
23.
В пространстве заданы две плоскости – и '.Их взаимная параллельность необязательна.
Выполним центральную проекцию на '
с данным центром O, лежащим вне и '.
'
23
24.
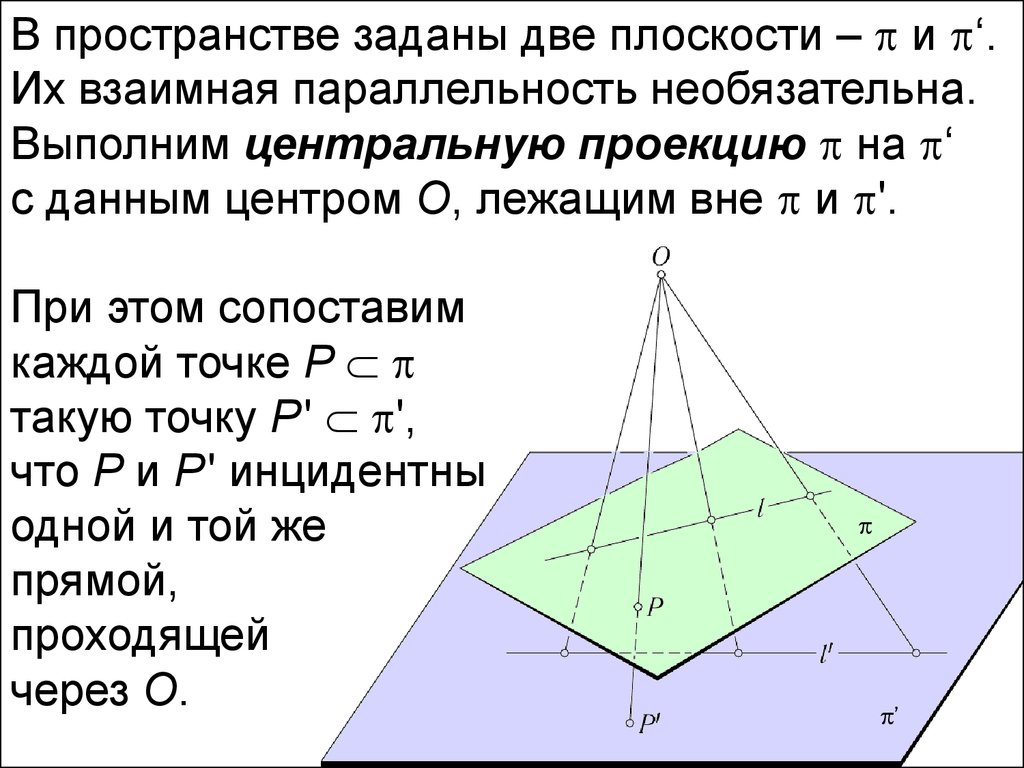
В пространстве заданы две плоскости – и ‘.Их взаимная параллельность необязательна.
Выполним центральную проекцию на ‘
с данным центром O, лежащим вне и '.
При этом сопоставим
каждой точке P
такую точку P' ',
что P и P' инцидентны
одной и той же
прямой,
проходящей
через O.
'
24
25.
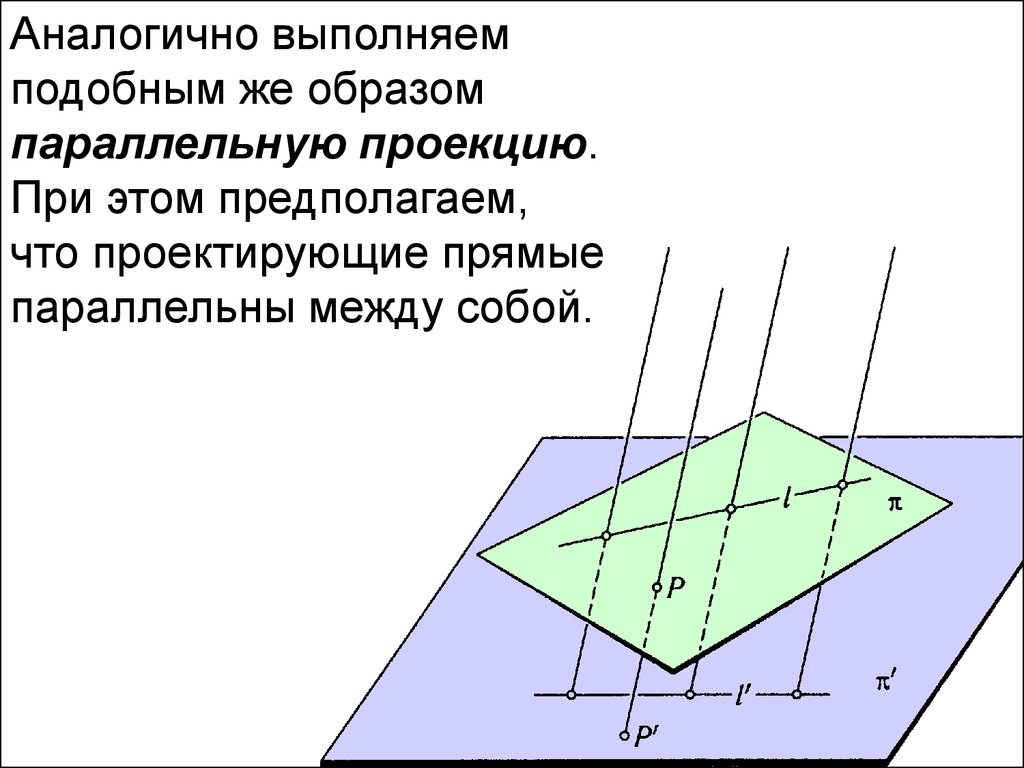
Аналогично выполняемподобным же образом
параллельную проекцию.
При этом предполагаем,
что проектирующие прямые
параллельны между собой.
25
26.
Точно так же определяетсяпроекция прямой или кривой линии l
в плоскости
на некоторую линию l'
в плоскости '.
Причём и в этом случае проекция
может быть
центральной или параллельной.
26
27.
Всякое отображениеодной фигуры на другую,
которое получается
посредством проектирования
(центрального или параллельного)
или же посредством
конечной последовательности
таких проектирований,
называется
проективным преобразованием.
27
28.
ЗамечаниеЕсли две фигуры связаны только одним
проектированием, то говорят,
что они перспективны.
28
29.
ЗамечаниеЕсли две фигуры связаны только одним
проектированием, то говорят,
что они перспективны.
Таким образом, если фигура F
в результате проективного преобразования
переходит в фигуру F', то это значит,
что или фигуры F и F' перспективны,
29
30.
ЗамечаниеЕсли две фигуры связаны только одним
проектированием, то говорят,
что они перспективны.
Таким образом, если фигура F
в результате проективного преобразования
переходит в фигуру F', то это значит,
что или фигуры F и F' перспективны,
или же можно указать последовательность
таких фигур F, F1, F2, ..., Fn, F',
что любые две рядом стоящие в ней фигуры
перспективны.
30
31.
Проективная геометрияплоскости или прямой
составляется из системы
геометрических теорем,
сохраняющихся при произвольных
проективных преобразованиях
соответствующих фигур.
31
32.
Проективной геометриипротивопоставляется
метрическая геометрия,
которая понимается
как система теорем,
устанавливающих связи
между величинами
в рассматриваемых фигурах,
инвариантные
только
относительно класса движений.
32
33.
Cформулируемнекоторые проективные свойства.
33
34.
Точка проектируется в точку.34
35.
Точка проектируется в точку.Прямая линия проектируется в прямую.
35
36.
Точка проектируется в точку.Прямая линия проектируется в прямую.
Покажем это.
36
37.
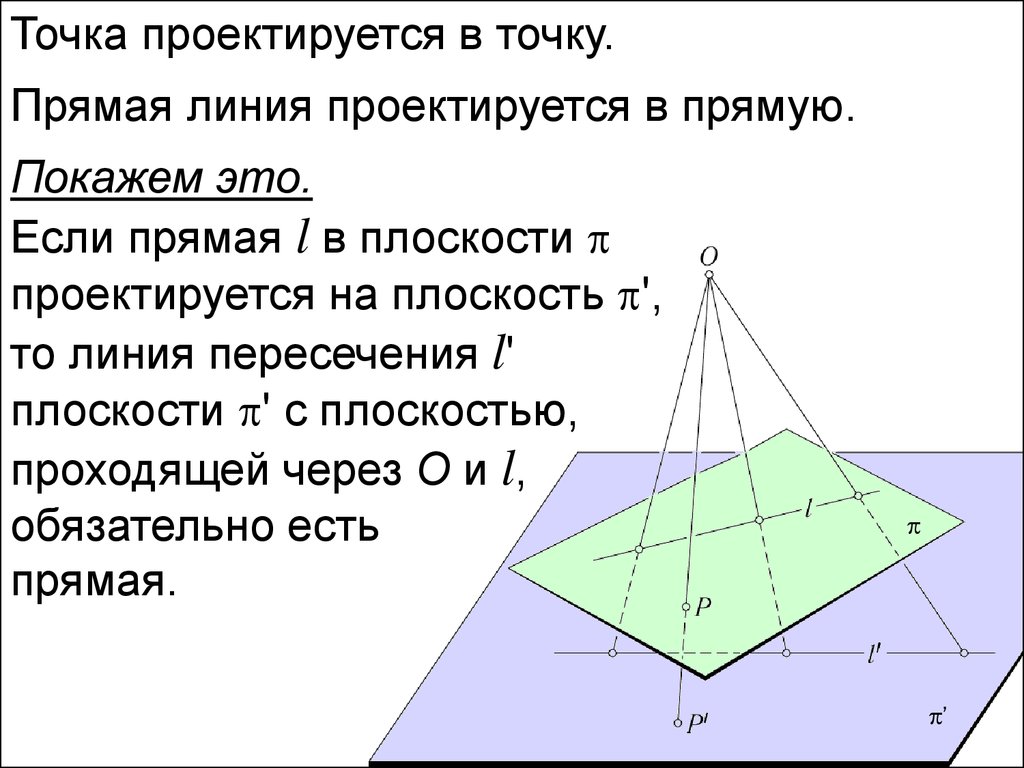
Точка проектируется в точку.Прямая линия проектируется в прямую.
Покажем это.
Если прямая l в плоскости
проектируется на плоскость ',
то линия пересечения l'
плоскости ' с плоскостью,
проходящей через O и l,
обязательно есть
прямая.
'
37
38.
Если точка A и прямая lинцидентны,
то точка A' и прямая l',
возникающие из них
при проективном преобразовании,
также инцидентны.
38
39.
Если точка A и прямая lинцидентны,
то точка A' и прямая l',
возникающие из них
при проективном преобразовании,
также инцидентны.
Другими словами,
инцидентность точки и прямой
есть свойство, инвариантное
относительно группы
проективных преобразований.
39
40.
Следствия.40
41.
Если три точки (или более) коллинеарны,т.е. инцидентны с одной и той же прямой,
то их отображения также коллинеарны.
41
42.
Если три точки (или более) коллинеарны,т.е. инцидентны с одной и той же прямой,
то их отображения также коллинеарны.
Если в плоскости три прямые (или более)
конкуррентны, т.е. инцидентны
с одной и той же точкой,
то их отображения – также
конкуррентные прямые.
42
43.
Если три точки (или более) коллинеарны,т.е. инцидентны с одной и той же прямой,
то их отображения также коллинеарны.
Если в плоскости три прямые (или более)
конкуррентны, т.е. инцидентны
с одной и той же точкой,
то их отображения – также
конкуррентные прямые.
concurrere (лат.) – бежать вместе
43
44.
Итак,инцидентность,
коллинеарность,
конкуррентность
являются проективными свойствами
(инвариантными относительно
проективных преобразований).
44
45.
Итак,инцидентность,
коллинеарность,
конкуррентность
являются проективными свойствами
(инвариантными относительно
проективных преобразований).
Величины отрезков и углов,
а также отношения этих величин
в общем случае
изменяются при проектировании.
45
46.
Пример46
47.
Равнобедренные или равносторонниетреугольники
могут спроектироваться
на треугольники
с тремя различными сторонами.
47
48.
Равнобедренные или равносторонниетреугольники
могут спроектироваться
на треугольники
с тремя различными сторонами.
Следовательно,
хотя понятие «треугольник» и принадлежит
проективной геометрии,
понятие «равносторонний треугольник»
ей не принадлежит,
а принадлежит только
метрической геометрии.
48








































 Математика
Математика








