2 признак подобия треугольников

1. Второй и третий признаки подобия треугольников

2.

B
А
С
B1
С1
А1
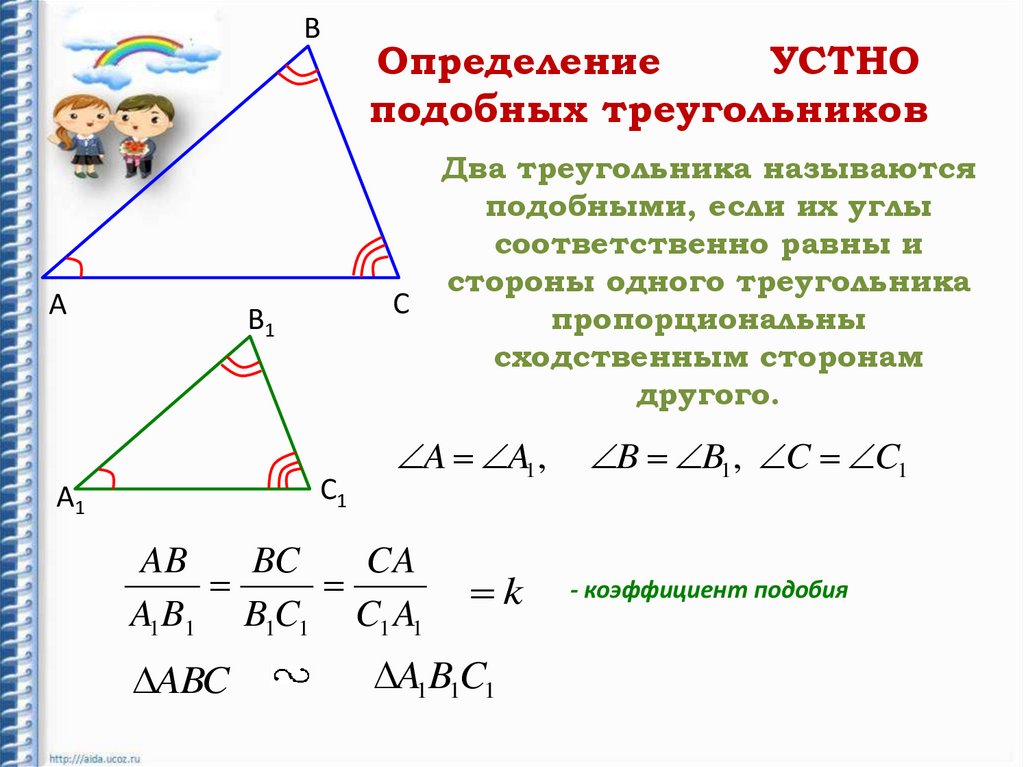
Определение
УСТНО
подобных треугольников
A A1 ,
AB
BC
CA
A1 B1 B1C1 C1 A1
ABC
Два треугольника называются
подобными, если их углы
соответственно равны и
стороны одного треугольника
пропорциональны
сходственным сторонам
другого.
k
A1B1C1
B B1 , C C1
- коэффициент подобия

3.

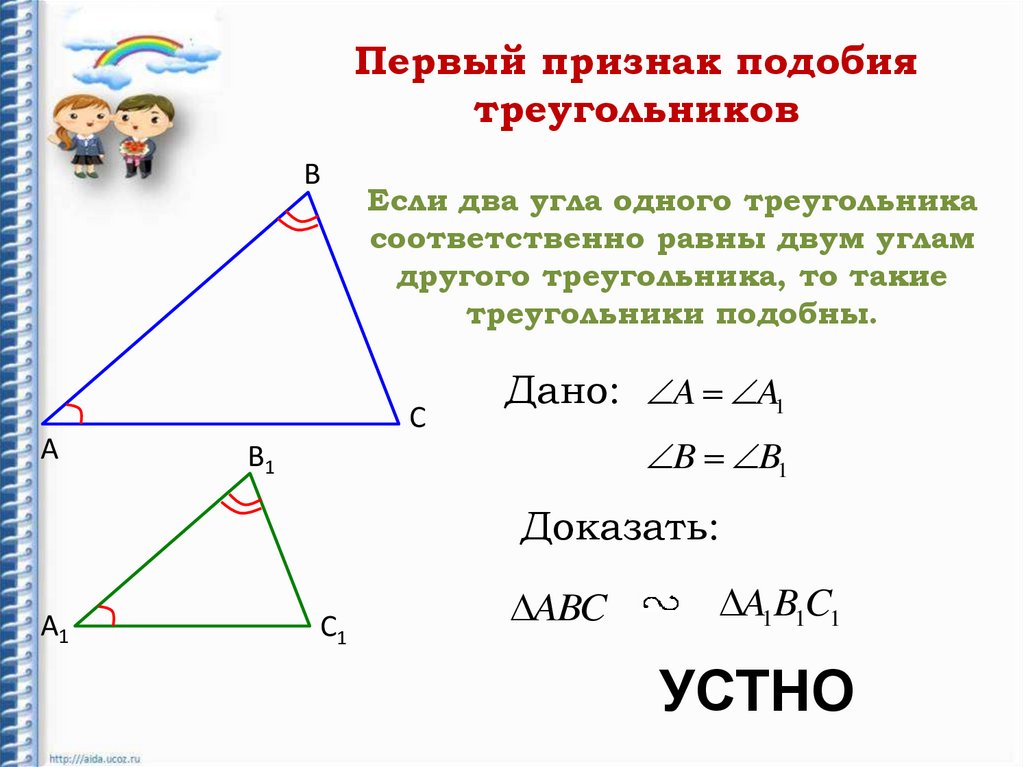
Первый признак подобия
треугольников
B
Если два угла одного треугольника
соответственно равны двум углам
другого треугольника, то такие
треугольники подобны.
С
А
Дано: A A1
B B1
B1
Доказать:
А1
С1
ABC
A1B1C1
УСТНО

4.

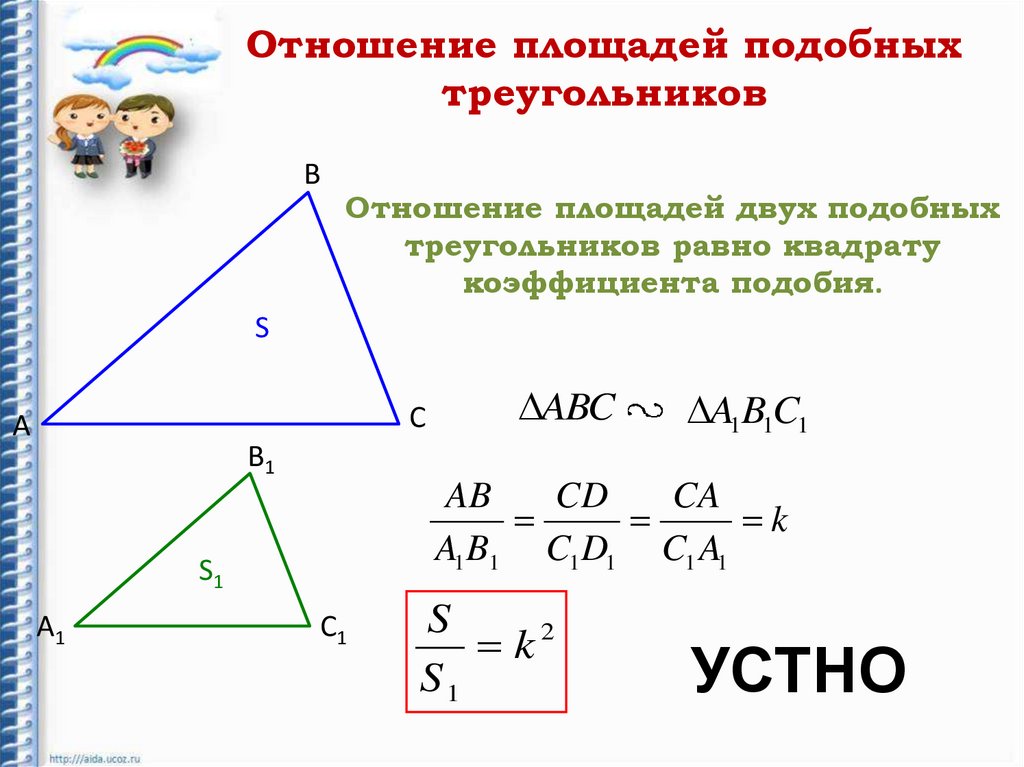
Отношение площадей подобных
треугольников
B
Отношение площадей двух подобных
треугольников равно квадрату
коэффициента подобия.
S
С
А
ABC
A1B1C1
B1
AB
CD
CA
k
A1 B1 C1 D1 C1 A1
S1
А1
С1
S
k2
S1
УСТНО

5.

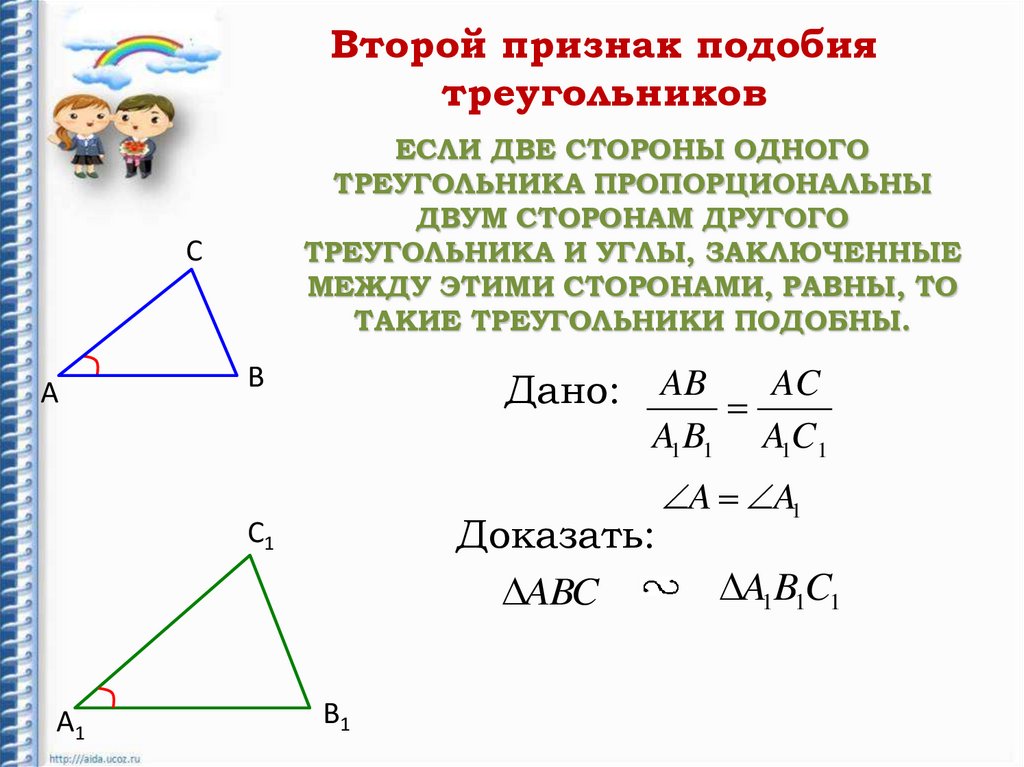
Второй признак подобия
треугольников
ЕСЛИ ДВЕ СТОРОНЫ ОДНОГО
ТРЕУГОЛЬНИКА ПРОПОРЦИОНАЛЬНЫ
ДВУМ СТОРОНАМ ДРУГОГО
ТРЕУГОЛЬНИКА И УГЛЫ, ЗАКЛЮЧЕННЫЕ
МЕЖДУ ЭТИМИ СТОРОНАМИ, РАВНЫ, ТО
ТАКИЕ ТРЕУГОЛЬНИКИ ПОДОБНЫ.
С
А
B
Дано:
Доказать:
ABC
С1
А1
AB
AC
A1 B1 A1C 1
B1
A A1
A1B1C1

6.

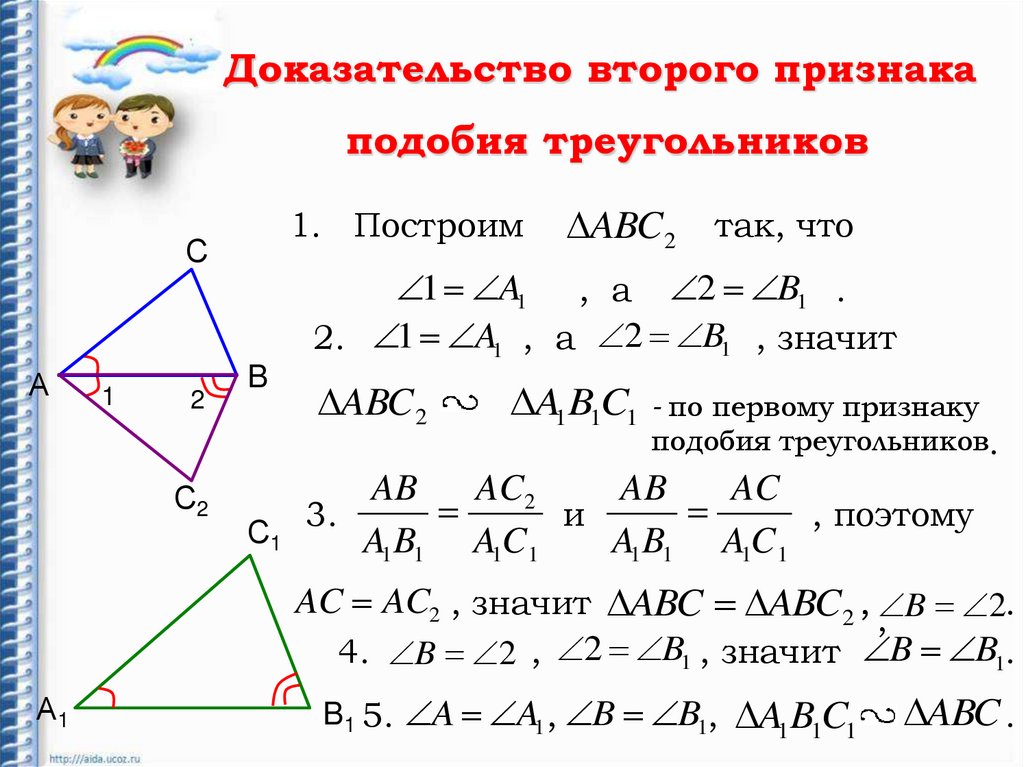
Доказательство второго признака
подобия треугольников
1. Построим
С
А
1
2
С2
ABC 2 так, что
1 A1 , а 2 B1 .
2. 1 A1 , а 2 B1 , значит
B
ABC 2
A1B1C1 - по первому признаку
подобия треугольников.
AB
AC2
AB
AC
3.
и
, поэтому
С1
A1 B1 A1C 1
A1 B1 A1C 1
AC AC2 , значит ABC ABC2 , B 2.
,
4. B 2 , 2 B1 , значит B B1.
А1
B1 5. A A1 , B B1, A1 B1C1
ABC .

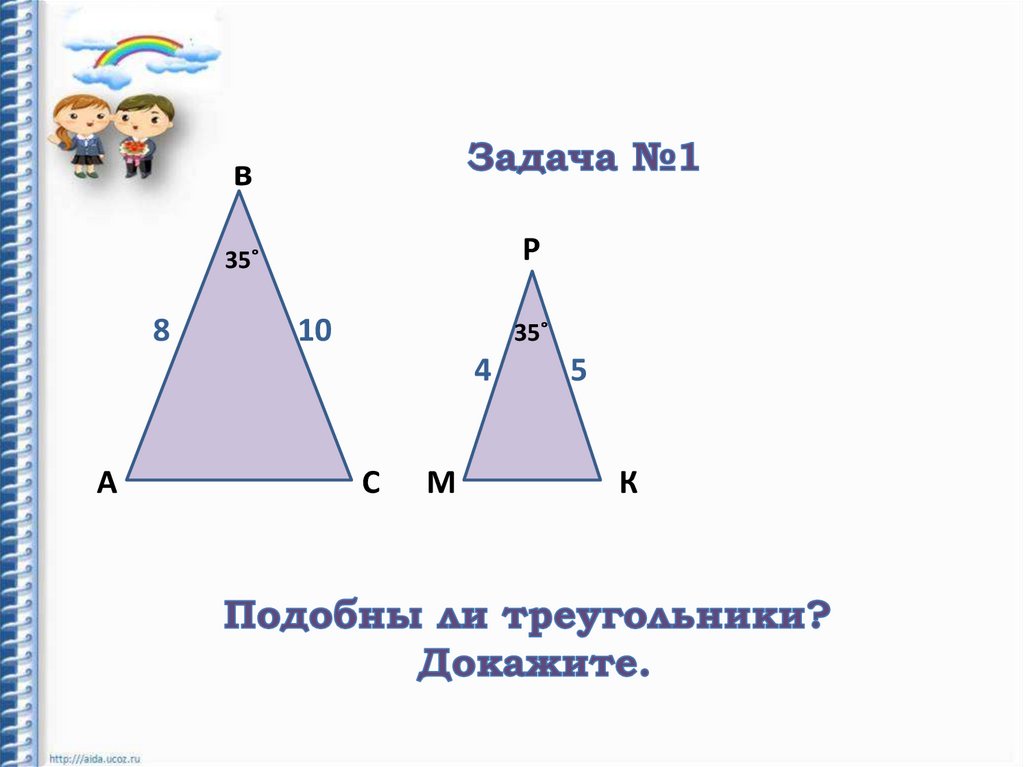
7.

в
Р
35˚
8
10
35˚
4
А
С
М
5
К

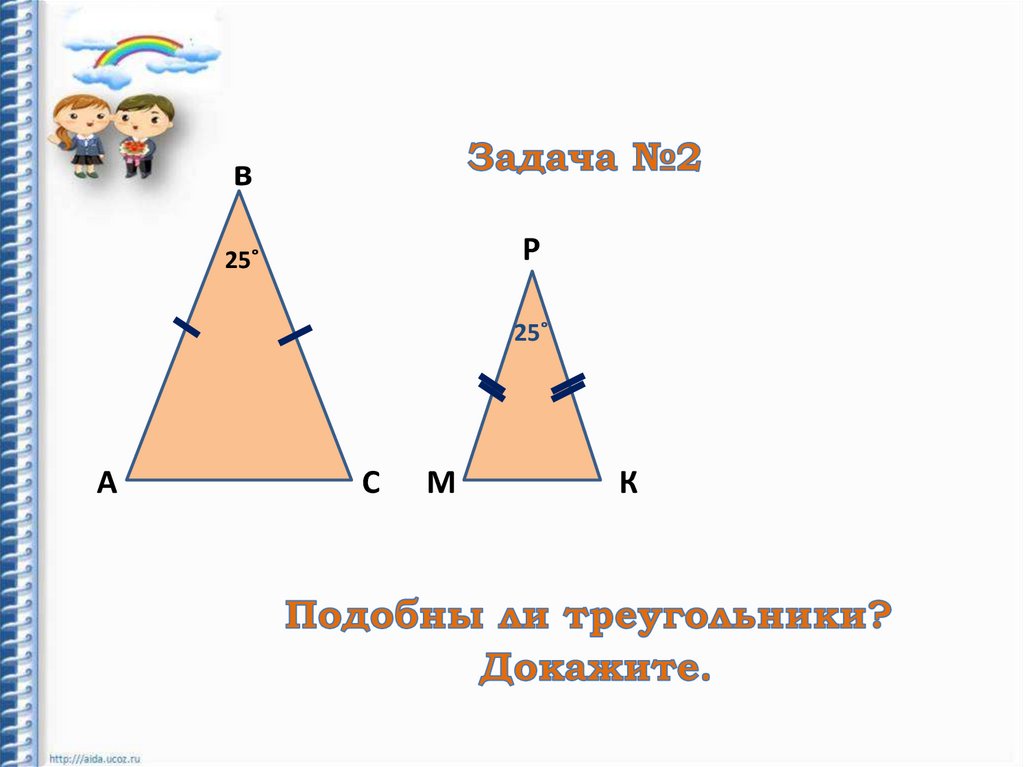
8.

в
Р
25˚
25˚
А
С
М
К