Лекция Закон больших чисел. Непрерывная случайная величина

1.

Составитель: Самойлова О.А.

2.

Составитель: Самойлова О.А.

3.

Составитель: Самойлова О.А.

4.

Составитель: Самойлова О.А.

5.

Составитель: Самойлова О.А.

6. Функция распределения вероятностей случайных величин

Ряд распределения является удобной формой
представления закона распределения ДСВ с конечным
числом возможных значений. Он неприменим для
непрерывных случайных величин, т.к. они имеют
бесконечное число значений и их нельзя перечислить в
какой-либо таблице.
Наиболее общей формой закона распределения СВ X
(как дискретной, так и непрерывной) является функция
распределения.
Составитель: Самойлова О.А.

7.

Определение: Функцией распределения называют
функцию F x , определяющую для каждого значения x
вероятность того, что случайная величина X примет
значение, меньшее x, т.е.
F x P X x
F x ,
Геометрически это равенство означает, что функция
есть вероятность того, что СВ X примет значение, которое
изображается на числовой оси точкой, лежащей левее
точки x
x
X
Часто вместо термина «функция распределения»
используют термин «интегральная функция
распределения».
Составитель: Самойлова О.А.

8.

Свойства функции распределения :
1) Значения функции распределения принадлежат
отрезку 0;1 :
0 F x 1.
2) Функция распределения есть неубывающая функция:
F x2 F x1 ,
если
x2 x1.
3) Вероятность того, что случайная величина X примет
b ,
a,равна
значение, заключенное в интервале
приращению функции распределения на этом интервале:
P a X b F b F a .
Составитель: Самойлова О.А.

9.

4) Вероятность того, что непрерывная случайная
величина X примет одно определенное значение,
например x1равна нулю:
P X x 1 0.
Т.е. нет смысла говорить о том, что НСВ примет одно
определенное значение, а есть смысл говорить о
вероятности попадания в заданный интервал.
5) Если все возможные значения случайной величины X
принадлежат интервалу
a, b то,
F x 0 при x a;
F x 1 при x b.
Составитель: Самойлова О.А.

10.

Нормальный закон распределения
Определение: Нормальным называют распределение
вероятностей непрерывной случайной величины X,
плотность которого имеет вид
1
f ( x)
e
2
где
( x a )2
2 2
,
a – математическое ожидание;
– среднее квадратическое отклонение X.
Составитель: Самойлова О.А.

11.

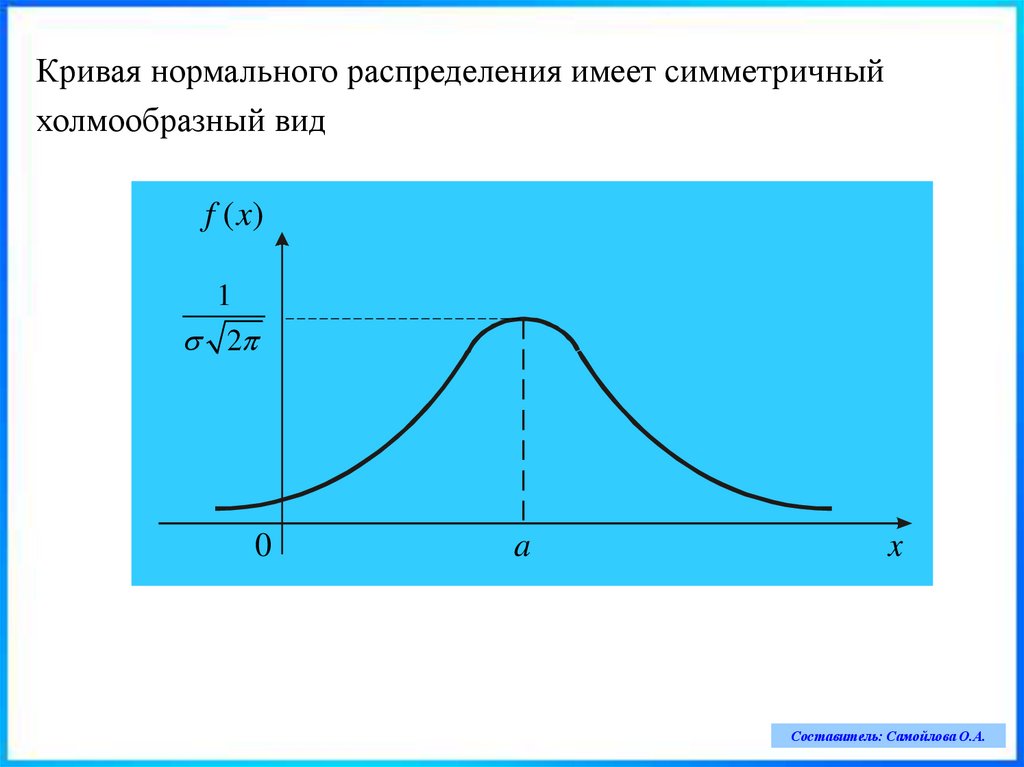
Кривая нормального распределения имеет симметричный
холмообразный вид
f ( x)
1
2
0
a
x
Составитель: Самойлова О.А.

12.

Интегральная функция нормального распределения
записывается следующим образом
x
1
F ( x)
e
2
( x a )2
2 2
dx.
Математическое ожидание нормально распределенной
2
D
(
X
)
случайной величины
,
а
дисперсия
.
М (Х ) a
Пример: Математическое ожидание нормально
распределенной случайной величины X равно 6 и среднее
квадратическое отклонение
плотность
Написать
3.
вероятности X .
Составитель: Самойлова О.А.

13.

Решение:
По условию задачи
Тогда
a 6, 3.
1
f x
e
2
2
x a
2 2
1
e
3 2
( x 6) 2
18
.
Задание: Известно, что случайная величина X подчинена
нормальному закону распределения с функцией плотности
1
f x
e
10 2
( x 15)2
200
.
Найти математическое ожидание и дисперсию СВ X.
Составитель: Самойлова О.А.