Похожие презентации:
предел
1. Предел и непрерывность функции.
2. Предел функции
Предел–
одно
из
основных
понятий
математического анализа. Понятие предела использовалось
еще Ньютоном во второй половине XVII века и математиками
XVIII века, такими как Эйлер и Лагранж, однако они понимали
предел интуитивно. Первые строгие определения предела дали
Больцано в 1816 году и Коши в 1821 году.
предел функции в точке и предел
функции на бесконечности
3.
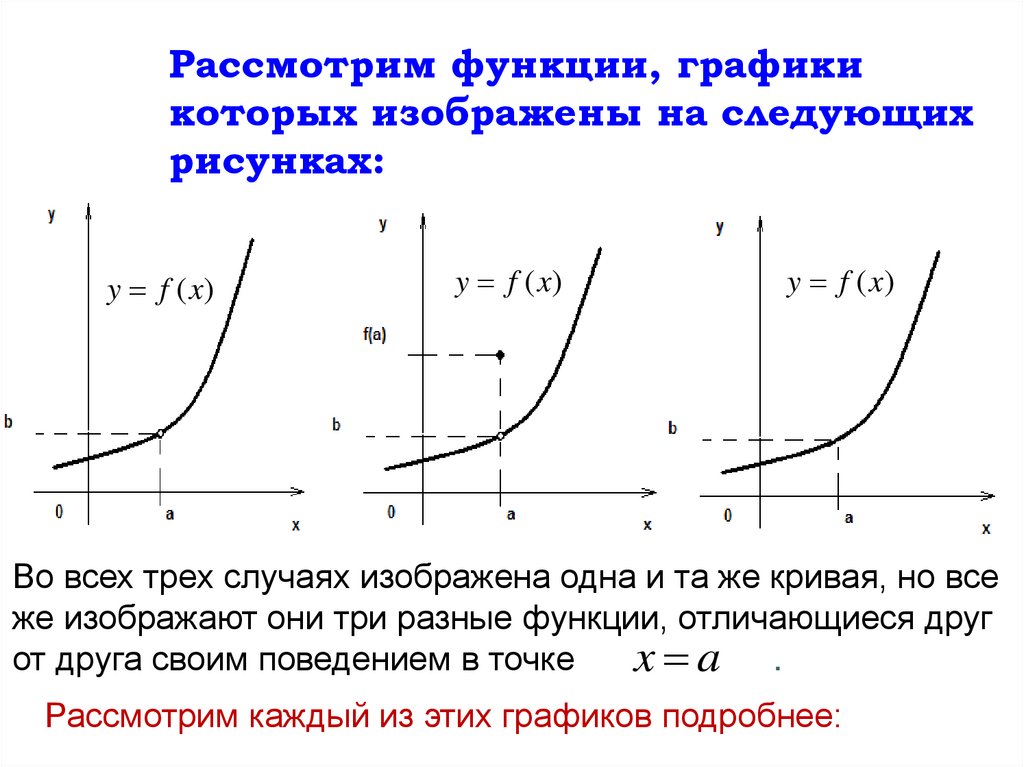
Рассмотрим функции, графикикоторых изображены на следующих
рисунках:
y f (x)
y f (x)
y f (x)
Во всех трех случаях изображена одна и та же кривая, но все
же изображают они три разные функции, отличающиеся друг
от друга своим поведением в точке
x a .
Рассмотрим каждый из этих графиков подробнее:
4.
Для всех трех случаев используется одна ита же запись:
lim f ( x) b,
x а
которую читают: «предел функции y f (x) при
стремлении x к a равен b ».
Содержательный смысл этой фразы следующий: если значения
аргумента выбирать все ближе и ближе к значению
x a, то значения функции все меньше и меньше
отличаются от предельного значения b.
Или можно сказать так: в достаточно малой окрестности
точки a справедливо приближенное равенство:
f ( x) a
При этом сама точка x a исключается из рассмотрения.
5.
Функцию y f (x)называют непрерывной
на промежутке
X , если она непрерывна в
каждой точке этого промежутка.
Примерами непрерывных функций на всей числовой
2
y
ax
by c,
y
kx
b
,
y
C
,
прямой являются:
y | x |, y x n , n ,
Функция
y x непрерывна на луче [0, ), а
n
y
x
, n непрерывна на промежутках
функция
( , 0) (0, ).
6. Предел функции в точке
Пусть функция y = f(x) определена в некоторой окрестности точкиx0, кроме, быть может самой точки x0.
Число А называют пределом функции в точке x0 (или при x x0),
если для любого положительного ε найдется такое положительное
число δ, что для всех х из δ – окрестности точки x0 справедливо
неравенство:
f (x) A
0; 0; x : x x0 f ( x ) A
lim f ( x ) A
x x0
7. Теорема.
Если функция f (x) имеет предел в точке х0, тоэтот предел единственный.
8. Бесконечно малая функция и бесконечно большая функция.
• Функция α (x) называется бесконечно малой при x → a(здесь a – конечное число или ∞), если
• Функция f(x) называется бесконечно большой функцией
(или бесконечно большой величиной) при х→а, если
lim f ( x)
x a
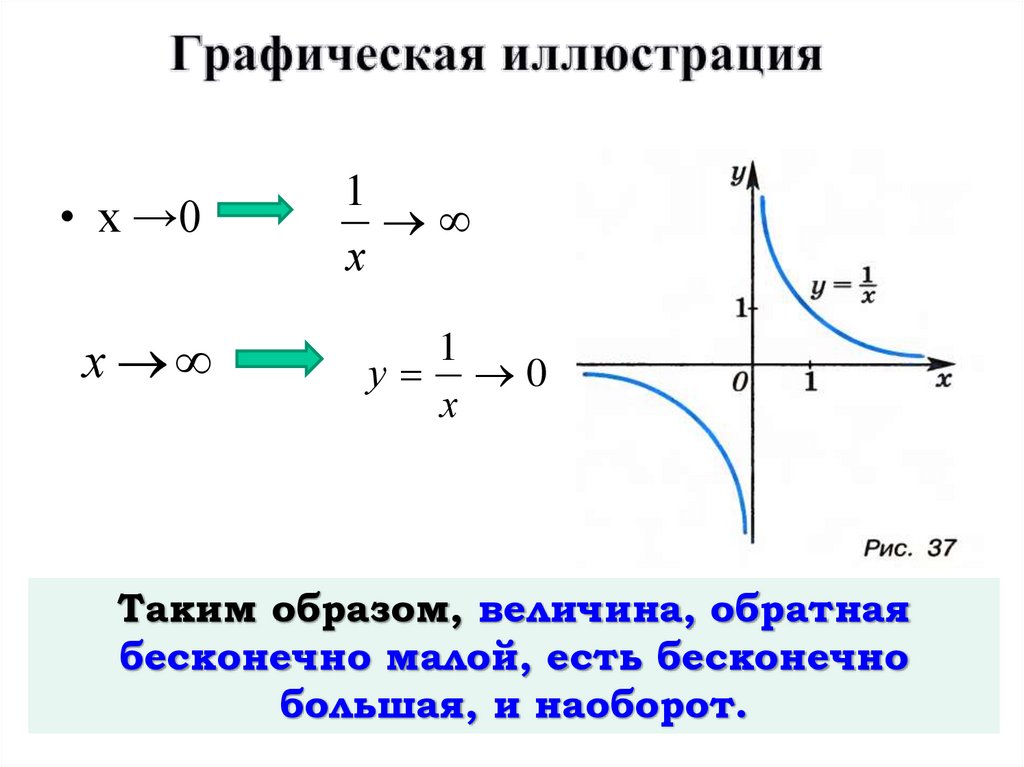
9. Графическая иллюстрация
• х →01
х
х
1
у 0
х
Таким образом, величина, обратная
бесконечно малой, есть бесконечно
большая, и наоборот.
10. Основные теоремы о пределах
1) lim C C , C const2) lim f ( x) g ( x) lim f ( x) lim g ( x)
3) lim f ( x) g ( x) lim f ( x) lim g ( x)
4) lim C f ( x) C lim f ( x)
f ( x) lim f ( x)
5) lim
, lim g ( x) 0
g ( x) lim g ( x)
6) lim f ( x) lim f ( x)
n
n
11. Основные теоремы о пределах
7) Пусть функции f(x), g(x) и h(x) определены внекоторой окрестности точки х0, за исключением
может быть самой точки х0, и функции f(x) и h(x)
имеют в точке х0 предел, равный а, т.е.
lim f ( x) lim h( x) a
x x0
x x0
Пусть, кроме того, выполняется неравенство:
f ( x ) g ( x ) h( x )
Тогда
lim g ( x) a
x x0
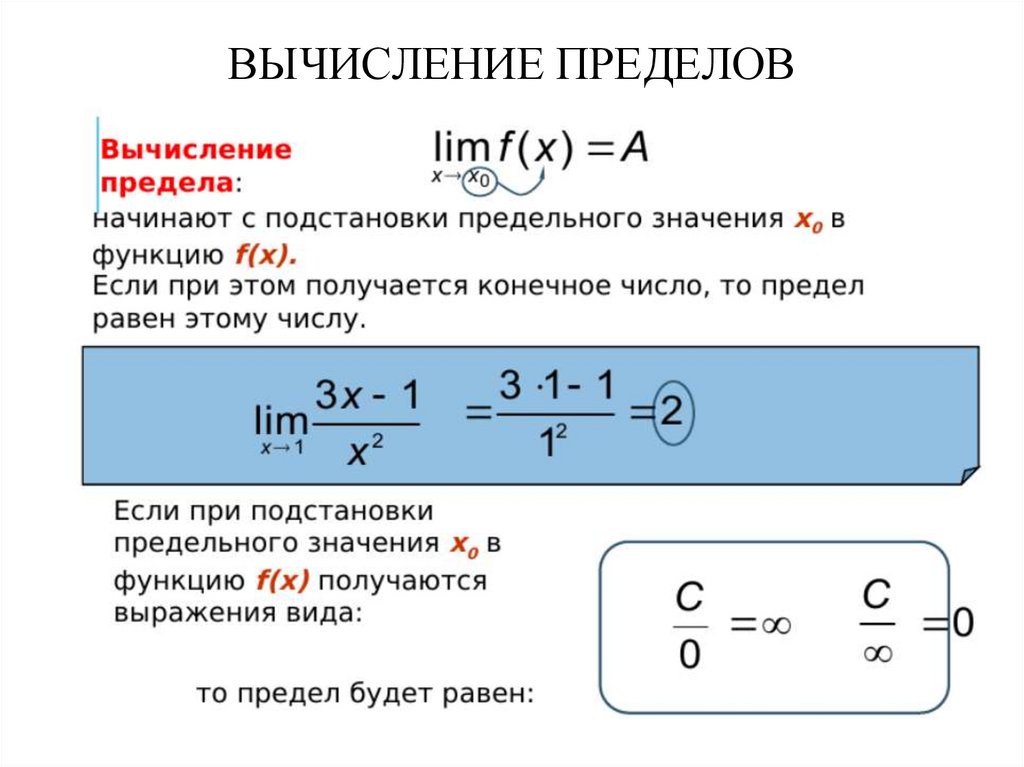
12. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
13. I.Вычисление пределов функций.
1) Вычислитьlim 9 x 2 6 x 8
x 1
14.
15.
16.
17.
18.
19.
20.
21.
sin 4 xlim
x
x 0
1
1
lim
x
x
2 x
















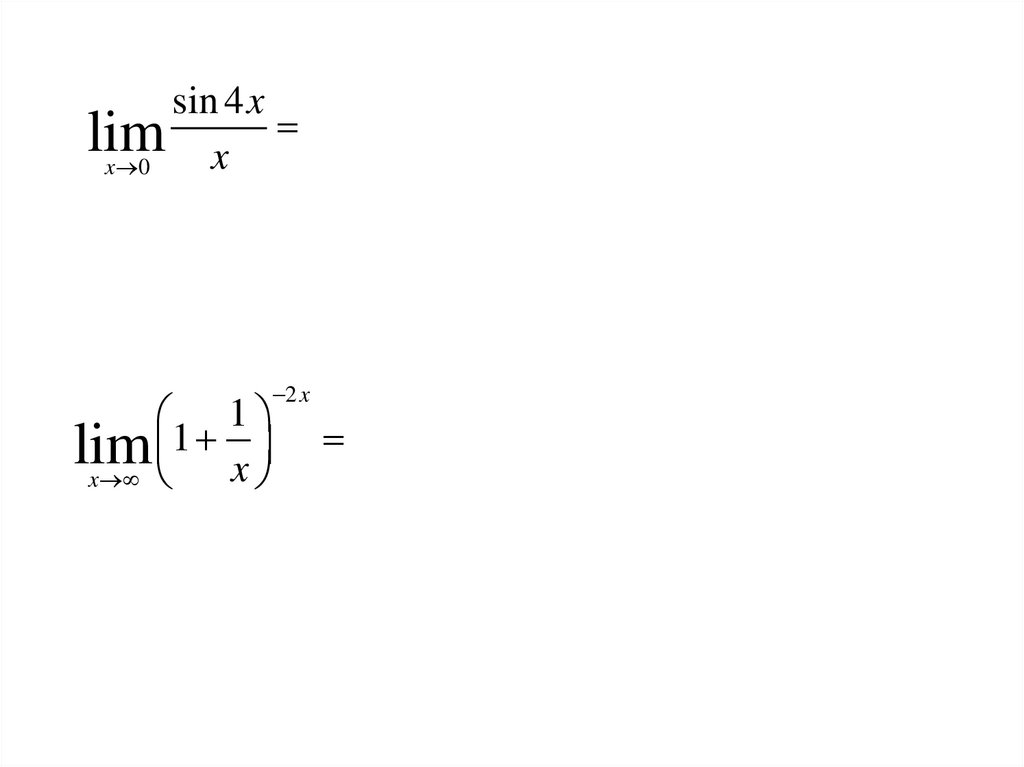


 Математика
Математика








