Односторонние пределы. Эквивалентные функции и их свойства, их применение к вычислению пределов функции в точке

1. Лекция 7. Односторонние пределы. Эквивалентные функции и их свойства, их применение к вычислению пределов функции в точке.

2.

Односторонние пределы
y = f(x)
В этой ситуации а – левый предел функции y = f (x) в точке x0, b –
правый предел функции y = f (x) в точке x0.
Число b называется правым пределом функции y = f (x) в точке x0, если
К R x D( f )( x0 x x0 ) f ( x ) b
Обозначается lim f x
x x0 0
Число a называется левым пределом функции y = f (x) в точке x0, если
R R x D( f )( x0 x x0 ) f ( x ) a
lim f x
Обозначается x x0 0
Смысл следующий: для левого предела – когда x→x0 слева, то f (x)→a;
для правого предела – когда x→x0, то f(x)→b
Высказывание x0 x x0 означает, что x правой полуокружности.
Высказывание x0 x x0 означает, что x левой полуокружности.

3.

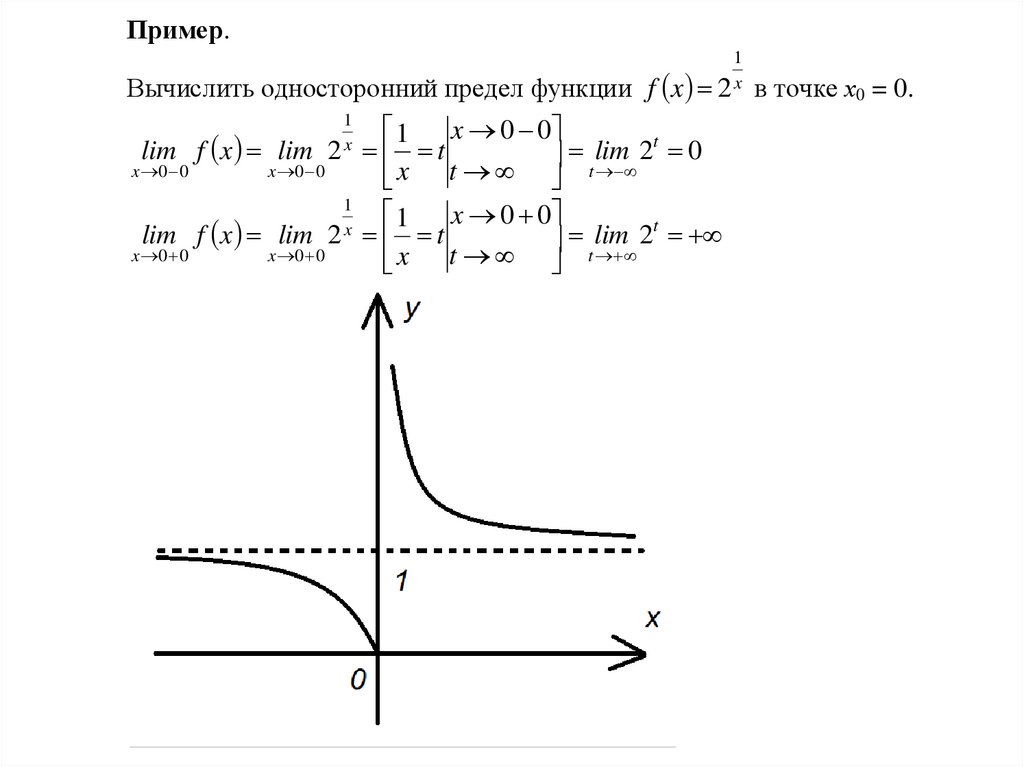
Пример.
Вычислить односторонний предел функции f x
1
2x
x 0 0
1
lim f x lim
t
lim 2t 0
x 0 0
x 0 0
x t t
1
x 0 0
1
t
lim f x lim 2 x t
lim
2
x 0 0
x 0 0
x t t
1
2x
в точке х0 = 0.

4.

Теорема (третий критерий существования предела в точке):
Число b является пределом функции f x тогда и только тогда, когда
x x0
существуют левый и правый пределы и они совпадают, т.е.:
lim f x = lim f x = b
x x0 0
x x0 0
Без доказательства
x
1
lim 1 e
x
x
1
lim 1 e
0
Замечание: логарифмы по основанию e называются натуральными
log e x ln x .

5.

Понятие непрерывной функции.
Df 1. Функция у = f(x) называется непрерывной в точке x0 D f , если
lim f x равен значению функции в этой точке (предел функции в точке
x x0
равен значению функции в этой точке).
Df 1'. Функция у = f(x) называется непрерывной в точке x0 D f , если
R R x D( f )( x x0 f ( x ) f x0 )
Df 1''. Функция у=f(x) называется непрерывной в точке x0 D f , если
x x0 x x0
x0 x x0
x x0 ; x0
x Ơ x0 ;
Рассмотрим:
f ( x ) f x0
f ( x ) f x0
f x0 f ( x ) f x0
f x0 f x0 ; f x0
x Ơ f x0 ;

6.

Грубо говоря, Ơ f x0 ; Ơ x0 ; (f (Ơ x0 ; ) f (Ơ f x0 ; )
Пусть
x x x0 - приращение аргумента х в точке х0
y = f(x)
y f x f x0 . Пусть функция непрерывна в точке х0. Это значит,
что lim f x f x x x0 f x f x0
x x0 0
x x0 0 f x f x0 0 x 0 y 0 ,
т.е бесконечно
малому аргументу соответствует бесконечно малое приращение функции, и
так получаем следующее равносильное предыдущим определения:
Df 1'''. Функция у = f (x) называется непрерывной в точке x0 D f ,
если бесконечно малому приращению аргумента в этой точке соответствует
бесконечно малое приращение функции.
Все 4 определения Df- Df 1''' равносильны между собой.

7.

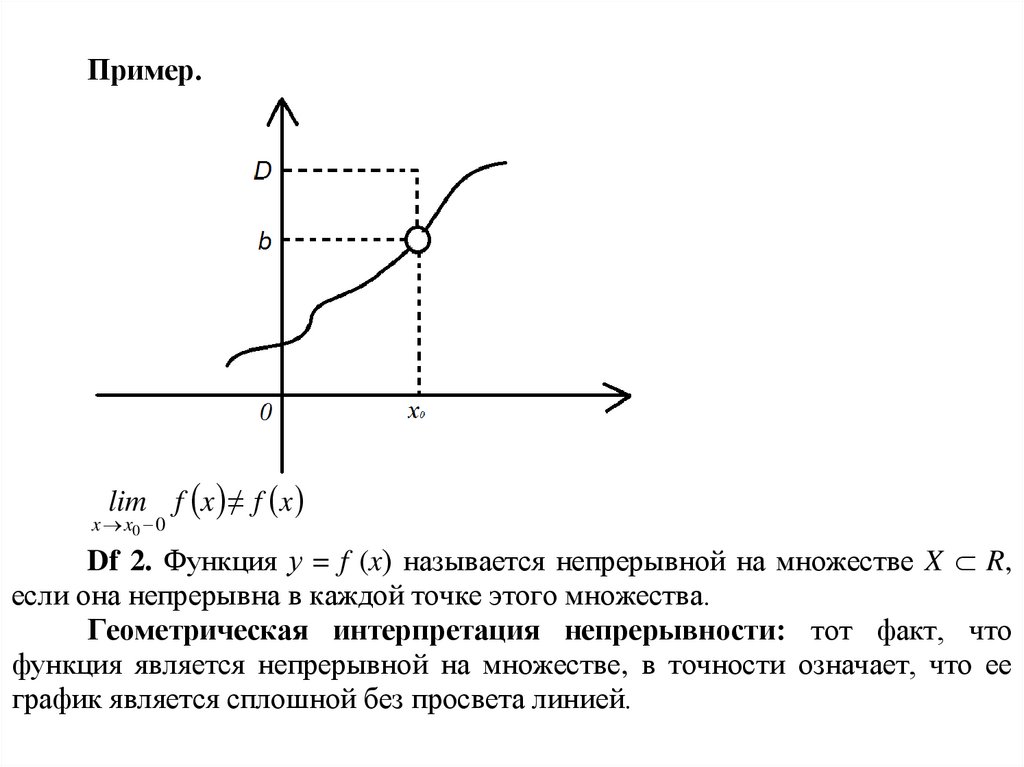
Пример.
lim f x ≠ f x
x x0 0
Df 2. Функция у = f (x) называется непрерывной на множестве X R,
если она непрерывна в каждой точке этого множества.
Геометрическая интерпретация непрерывности: тот факт, что
функция является непрерывной на множестве, в точности означает, что ее
график является сплошной без просвета линией.

8.

Th (критерий непрерывности функции в точке):
Функция у = f (x) является непрерывной в точке x0 тогда и только тогда,
когда lim f x = lim f x f x .
x x0 0
x x0 0
Это сразу же получается из Df 1 и третьего критерия существования
предела функции в точке.
Th (о непрерывности суммы, произведения и частного):
Пусть функции у = f (x) и у = g(x) непрерывны в т.х0, тогда функции f±g,
f
f·g и
тоже непрерывны в этой точке, иными словами, сумма, произведение
g
и частное непрерывных функций есть непрерывная функция.
Доказательство.
Рассмотрим для f+g
Пусть h(x)= f(x)+ g(x)
! lim h x h x0
x x0
lim h x lim f x g x lim f x lim g x f x0 g x0 h x0
x x0
Ч.т.д.
x x0
x x0
x x0

9.

Докажем для
f
g
f x
g(x)≠0
g x
! lim h x h x0
Пусть h x
x x0
lim f x
f x x x0
f x0
lim h x lim
lim g x g x h x0
x x0
x x0 g x
x x
0
0
Ч.т.д.
Для f·g
Пусть h(x)= f(x)·g(x) (!) lim h x h x0
x x0
Замечание: эта теорема оказывается справедливой для любого
конечного числа слагаемых функции и сомножителей.

10.

Следствия:
1-е следствие: любой одночлен x n n N является непрерывной
функцией x n x x ... x произведения и сомножителей.
2-е следствие: f x 0 1 x 2 x 2 ... n x n непрерывны на всей
числовой оси как конечная сумма одночленов
P x
3-е следствие: рациональная функция
является
f x n
Qm x
непрерывной в своей области определения.
Точки разрыва
Df 1. Рассмотрим функцию у = f (x). Точка x0 D f называется точкой
разрыва этой функции, если в данной точке функция не является
непрерывной. Точками разрыва будем также называть точки которые не
принадлежат D f , однозначно функция определена в некоторой проколотой
окрестности этой точки.

11.

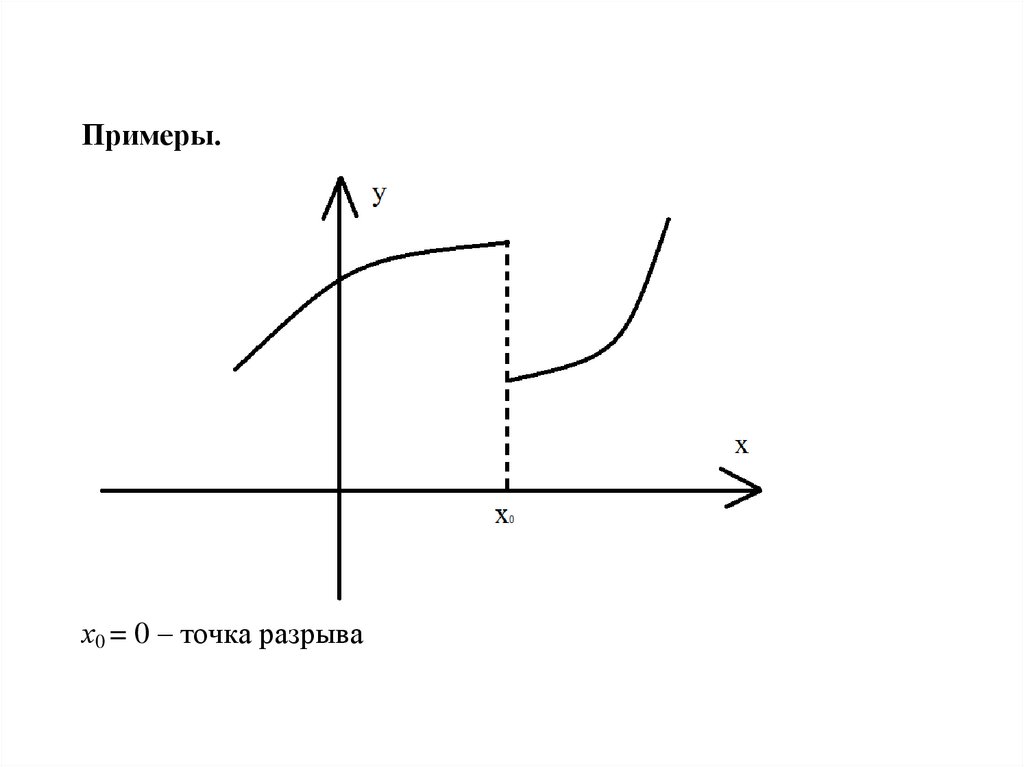
Примеры.
х0 = 0 – точка разрыва

12.

1
x
х0 = 0 – точка разрыва
y

13.

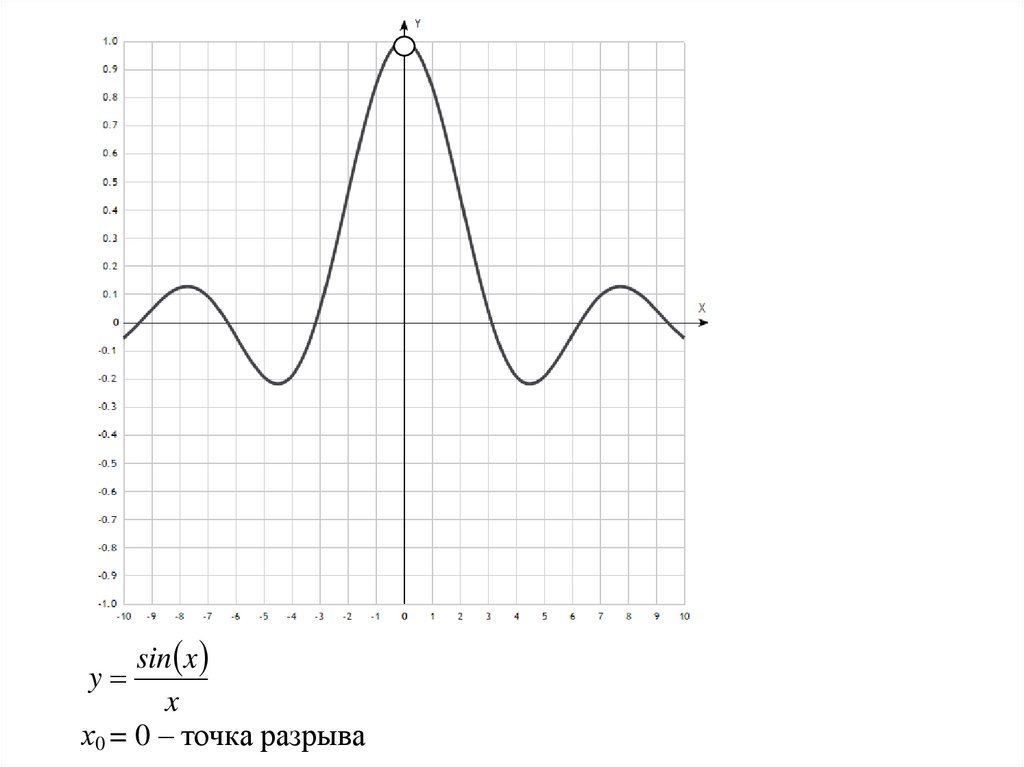
sin x
x
х0 = 0 – точка разрыва
y

14.

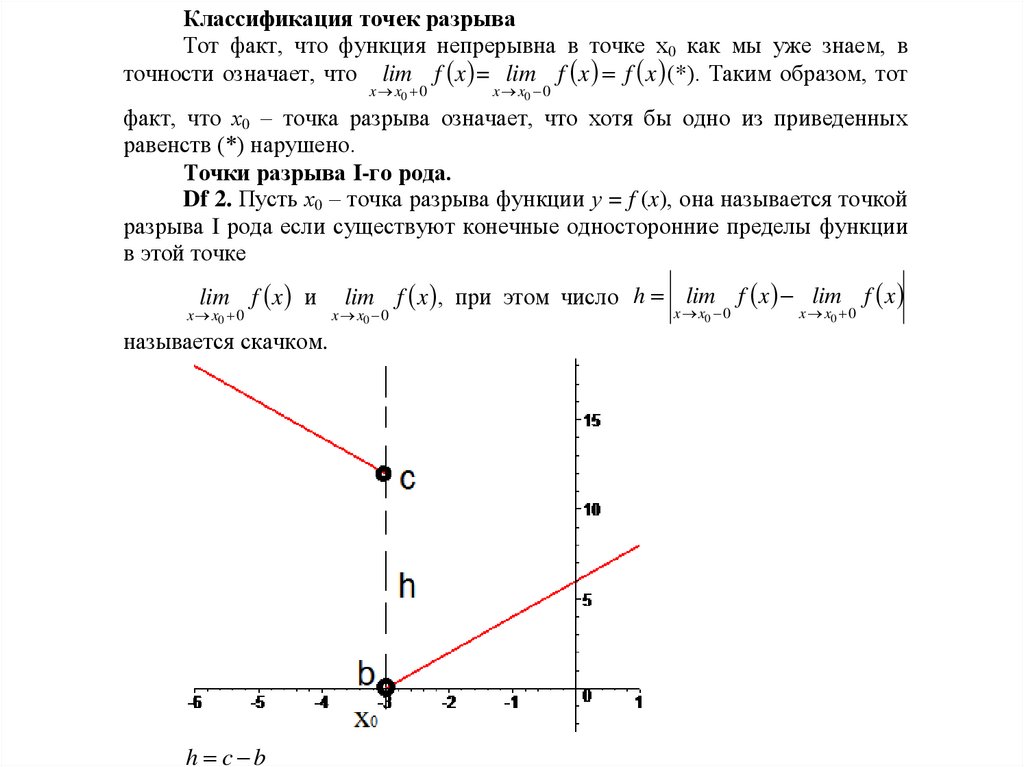
Классификация точек разрыва
Тот факт, что функция непрерывна в точке х0 как мы уже знаем, в
точности означает, что lim f x = lim f x f x (*). Таким образом, тот
x x0 0
x x0 0
факт, что х0 – точка разрыва означает, что хотя бы одно из приведенных
равенств (*) нарушено.
Точки разрыва I-го рода.
Df 2. Пусть х0 – точка разрыва функции у = f (x), она называется точкой
разрыва I рода если существуют конечные односторонние пределы функции
в этой точке
lim f x и
x x0 0
называется скачком.
h c b
lim f x , при этом число h lim f x lim f x
x x0 0
x x0 0
x x0 0

15.

Точки разрыва I рода бывают 2-х видов:
а) h≠0 – х0 – точка разрыва со скачком
б) h=0 – х0 – точка устранимого разрыва
sin x
Примем f x
x
x0 = 0
lim f x - существует lim f x lim f x
x 0
x 0 0
x 0 0
Однако, х0 – точка разрыва. Грубо говоря, одной единственной точкой
можно «заткнуть дырку» в графике.
В общем случае, в случае устранимого разрыва функцию f(x) можно
доопределить в точке х0 так, что она станет непрерывной, а именно:
f x : x x0
F x lim f x : x x
0
x x0
В нашем примере:
sin x
:x 0
F x x
1 : x 0

16.

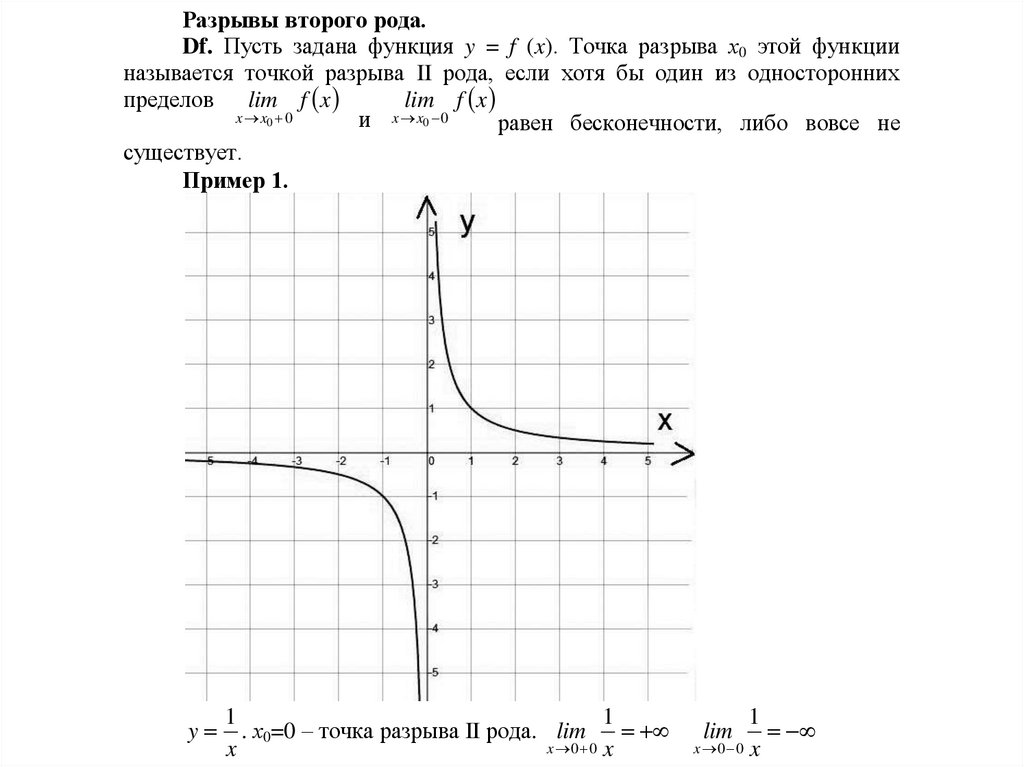
Разрывы второго рода.
Df. Пусть задана функция y = f (x). Точка разрыва х0 этой функции
называется точкой разрыва II рода, если хотя бы один из односторонних
lim f x
пределов lim f x
x x0 0
и x x0 0
равен бесконечности, либо вовсе не
существует.
Пример 1.
y
1
1
. х0=0 – точка разрыва II рода. lim
x 0 0 x
x
1
x 0 0 x
lim

17.

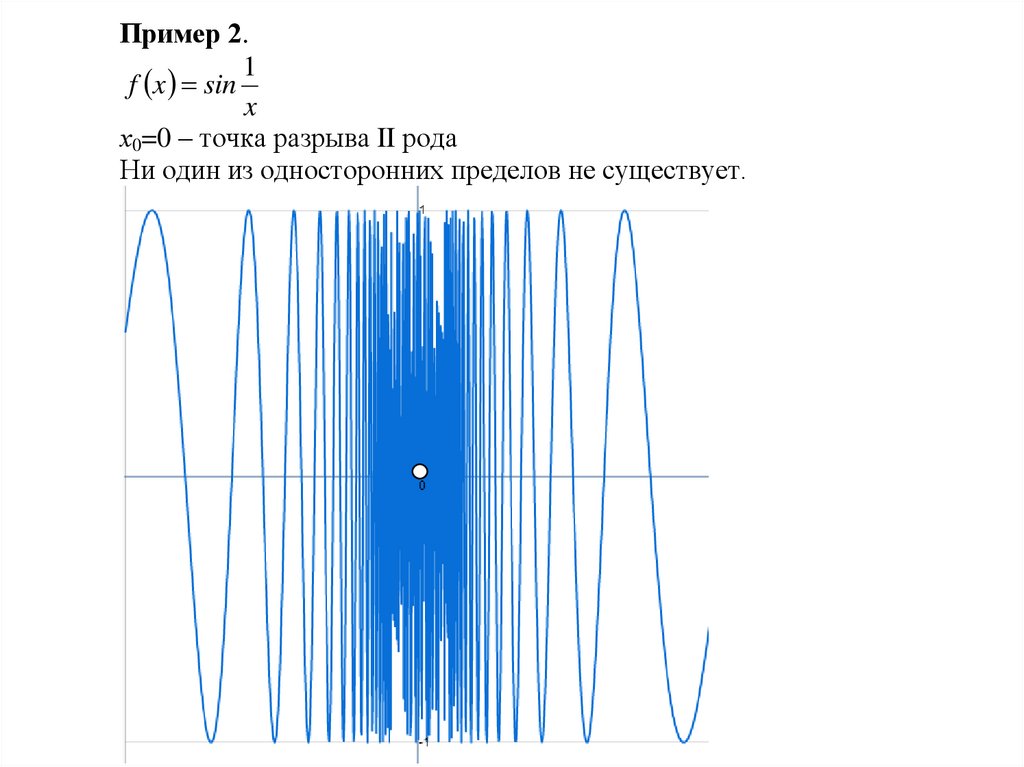
Пример 2.
1
f x sin
x
х0=0 – точка разрыва II рода
Ни один из односторонних пределов не существует.

18.

Замечание:
Пусть функция y = f (x) непрерывна в точке х0. Это означает, что
lim f x = f x0 f lim x
x x0
x x0
Иными
словами,
мы
получили
следующее
отношение
lim f x f lim x lim f f lim
x x0
x x0
Получили правило, которое лежит в основе самой непрерывности:
можно переходить к пределу под знаком непрерывной функции.
Пример.
lim e
x x0
x
e
lim x
x x0
lim tg x tg lim x
x x0
x x0

19.

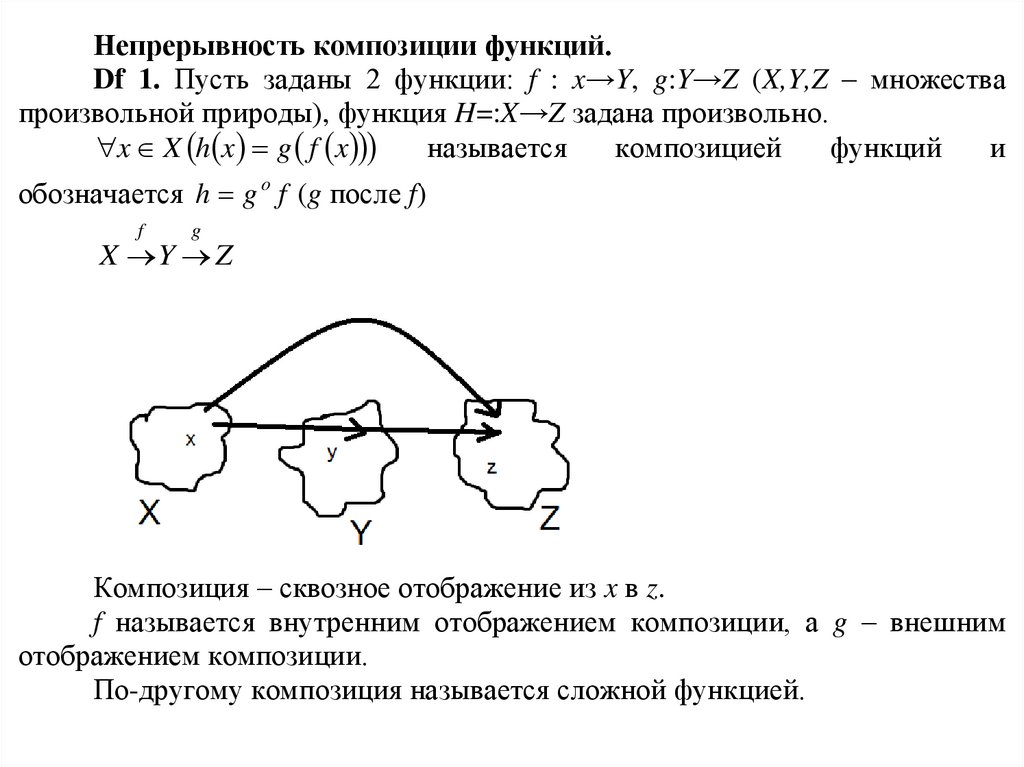
Непрерывность композиции функций.
Df 1. Пусть заданы 2 функции: f : x→Y, g:Y→Z (X,Y,Z – множества
произвольной природы), функция H=:X→Z задана произвольно.
x X h x g f x
называется
композицией
функций
и
обозначается h g o f (g после f)
f
g
X Y Z
Композиция – сквозное отображение из x в z.
f называется внутренним отображением композиции, а g – внешним
отображением композиции.
По-другому композиция называется сложной функцией.

20.

Пример 1.
y sin x
z y2
z y 2 - внешняя
y sin x - внутренняя
Пример 2.
y x2
z sin y
z sin x 2
z sin y - внешняя

21.

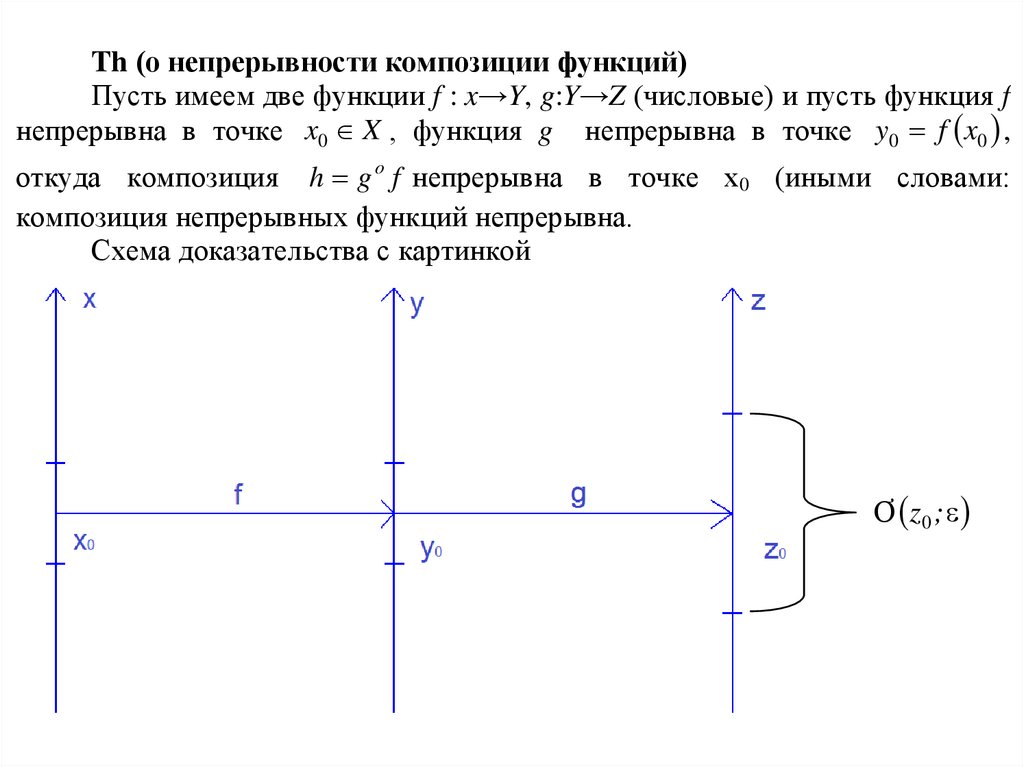
Th (о непрерывности композиции функций)
Пусть имеем две функции f : x→Y, g:Y→Z (числовые) и пусть функция f
непрерывна в точке x0 X , функция g непрерывна в точке y0 f x0 ,
откуда композиция h g o f непрерывна в точке х0 (иными словами:
композиция непрерывных функций непрерывна.
Схема доказательства с картинкой
Ơ z0 ;

22.

Надо показать, что для Ơ z 0 ; Ơ x0 ; (h Ơ x0 ; Ơ z0 ; )
g непрерывна в точке y0 Ơ y0 ; 1 (g Ơ y0 ; 1 Ơ z0 ; )
f непрерывна в точке x0 , Ơ x0 ; (f Ơ x0 ; Ơ y0 ; 1 )
(h Ơ x0 ; Ơ z0 ; )
Мы рассмотрели композицию двух функций. Может быть композиция
большего числа функций.
f
g
X Y Z T
h o g o f
Замечание:
Композиция любого
непрерывна.
конечного
числа
непрерывных
функций

23.

10.3. Сравнение функций
Пусть f(x) и (х) - определены в некоторой U~( x0 ) , проколотой
окрестности т. х0.
Определение. Функций ограниченных в сравнении
Если c>0 и >0 : для х из 0< x-x0 < f(x) c (x) , то говорят,
что функция f ограничена в окрестности т. х0 по сравнению с функцией и
пишут f ( x ) О( ( x )), х х0.
Определение. Функций одного порядка
Если lim f К K 1, K 0 то говорят, что функции f и - одного порядка,
x x0
х х0 и пишут f , х х0.
Определение. Функций эквивалентных
Если xlim
x
0
f
1, то говорят, что функции f и - эквивалентны при х х0 и
обозначают f , х х0.
Определение. Функций бесконечно малых в сравнении
Если xlim
x
0
f
0, то говорят, что функция f является бесконечно малой по
отношению к функции при х х0 и пишут f о( ), х х0.
Примечание.
Точка х0 может быть и бесконечно удаленной.

24.

Примеры:
x2
lim
0. x 2 о( x ), x 0
x 0 x
x
lim 2 0 x о( x 2 ), x
x x
2 x2 3 2
2
2
lim
2
x
3
3
x
2, x
3
x 3 x 2 2
sin x
lim
1 x sin x, x 0
x 0 x
Пусть рассматриваемые функции бесконечно малые при х х0
( x) о(1), ( x) о(1), 1( x) о(1), 1( x) о(1), х х0.

25.

Теоремы о замене эквивалентных бесконечно малых функций при
нахождении пределов.
Теорема. О пределе частного.
Если
1 ,
х х0,
1 , х х0, и lim
x x
0
1
, тогда
1
Доказательство.
1 1
lim lim 1 1 lim 1 .
1 1
x x 0
x x 0 1 1
x x 0 1
Теорема. Об эквивалентности.
Если f g , х х0, g , х х0, то
Пример.
sin x x, x 0
x sin x tgx, x 0 .
tgx x, x 0
f ,
х х0.
lim
x x0
lim 1 .
x x 1
0

26.

Таблица эквивалентных бесконечно малых функций
def
sin
lim
1
0
tg
lim
1
0
arcsin
lim
1
0
sin , 0.
tg , 0.
arcsin , 0.
arctg 0 t = arctg
t
,
lim
1
0
0 = tg t t 0 tg t
lim
arctg , 0.
1
ln(lim(1 ) ) ln e = 1. Тогда
0
lim
0
1
(ln(1 ) ) 1;
ln(1 )
1
0
ln(1 ) ln a
(log € (1 )) ln a
lim
1
0
0
ln a
lim
ln(1 ),
lim
0
ln a log € (1 ) , 0 .
ln(1 ) ln(1 ) t, (1 ) e t
t
lim
.
lim
1
t
0
t 0 e t 1
e
1
,
0
,
t
0
e t 1 t , t 0.
a 1 a 1 t, t 0
t ln a
lim
lim
ln a.
t 0
0
(loga (1 t ) ln a
loga (1 t )
a 1
a 1
Значит, lim
, 0.
1
ln a
0 ln a
(1 ) m 1
Полезно помнить, что
, 0.
m