Похожие презентации:
17 лк. несин. токи
1. 17 лекция
Негармонические периодическиенапряжения и токи в линейных
цепях
© 2001 Томский политехнический университет, кафедра ТОЭ, автор Носов Геннадий Васильевич
2. Негармонические периодические напряжения и токи
23. Негармонические периодические напряжения и токи применяются в различных устройствах радиотехники, автоматики и вычислительной
техники3
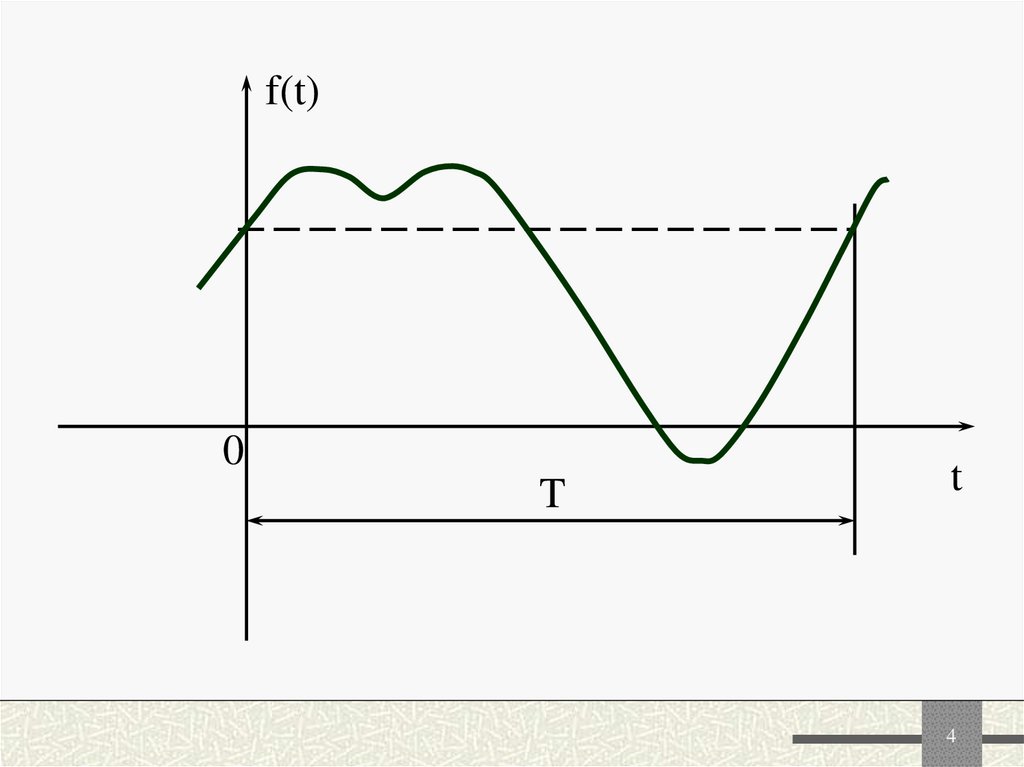
4.
f(t)0
T
t
4
5. В электроэнергетике такие напряжения и токи могут появляться при насыщении стальных магнитопроводов трансформаторов и при
использовании нелинейныхустройств, например,
полупроводниковых
преобразователей
5
6. Негармонические периодические напряжения и токи как функции времени f(t) с периодом Т могут быть представлены в виде
тригонометрического рядаФурье
6
7. Ряд Фурье:
к 1к 1
f (t ) A 0 Bк sin к t Cк cos к t
A 0 Amк sin( к t к )
к 1
7
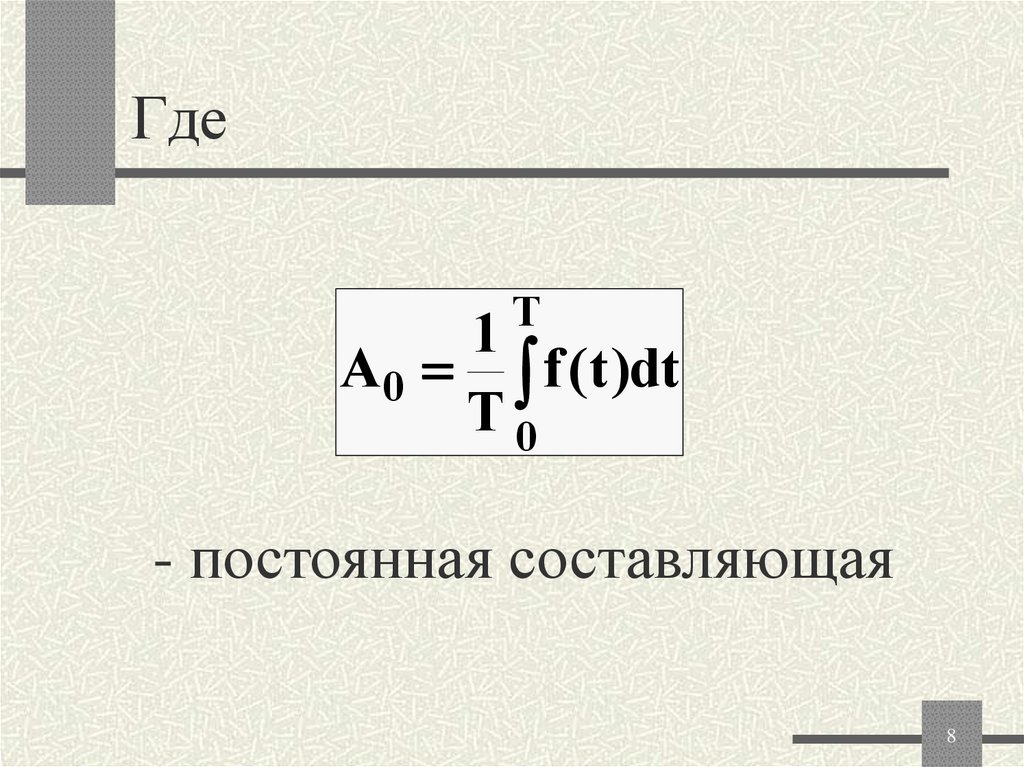
8. Где
Т1
A 0 f (t )dt
T0
- постоянная составляющая
8
9. - амплитуда синусной составляющей к - гармоники
T2
Bк f (t ) sin( к t ) dt
T0
- амплитуда синусной
составляющей к - гармоники
9
10. - амплитуда косинусной составляющей к - гармоники
T2
Cк f (t ) cos(к t ) dt
T0
- амплитуда косинусной
составляющей к - гармоники
10
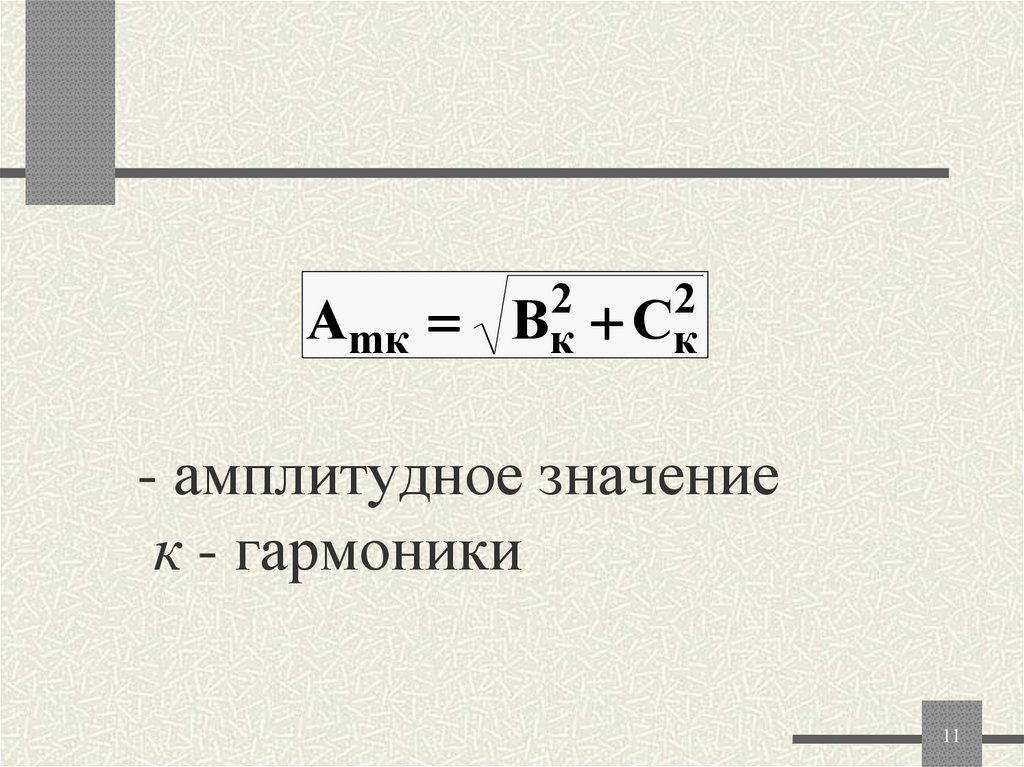
11. амплитудное значение к - гармоники
Amк2
2
Bк Ск
- амплитудное значение
к - гармоники
11
12. - начальная фаза к –гармоники, причем 180 градусов учитывается при Bk<0
Cкк ( 180 ) arctg
Вк
- начальная фаза к –гармоники,
причем 180 градусов
учитывается при Bk<0
12
13. - порядковый номер гармоники
к 1,2,3...- порядковый номер гармоники
13
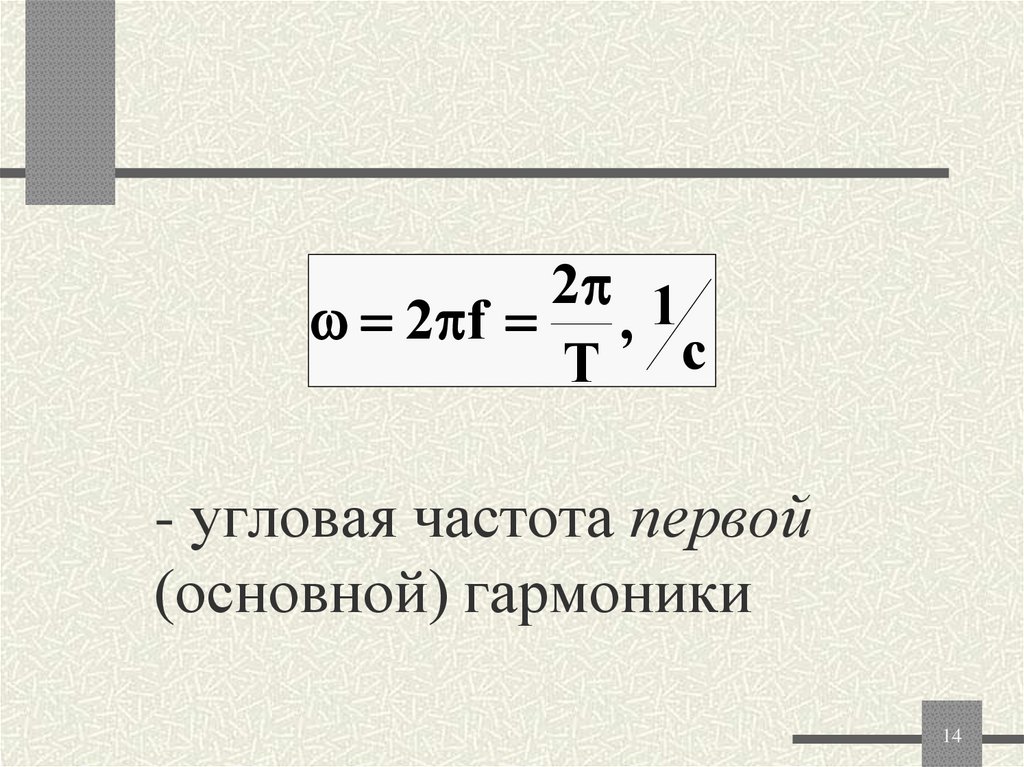
14. - угловая частота первой (основной) гармоники
2 12 f ,
T c
- угловая частота первой
(основной) гармоники
14
15. Дискретные спектры
1516. Гармонический состав f(t) можно задать при помощи дискретных спектров амплитуд и фаз, причем разложение в ряд Фурье f(t) может
осуществлятьсяаналитически, приближенно
по специальным формулам
и при помощи ЭВМ
16
17. После разложения f(t) в ряд Фурье учитываются постоянная составляющая и несколько наибольших по амплитуде гармоник, а остальные
гармоникиотбрасываются
17
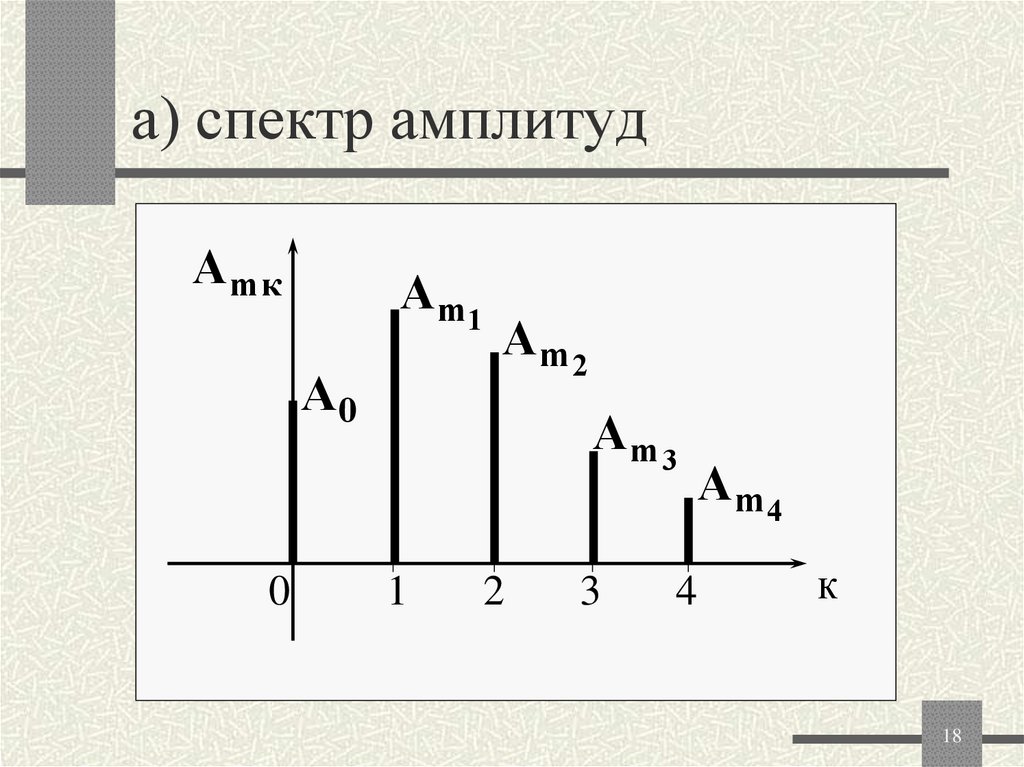
18. а) спектр амплитуд
А mкАm1
А0
0
Аm 2
Аm 3
1
2
3
4
Аm4
к
18
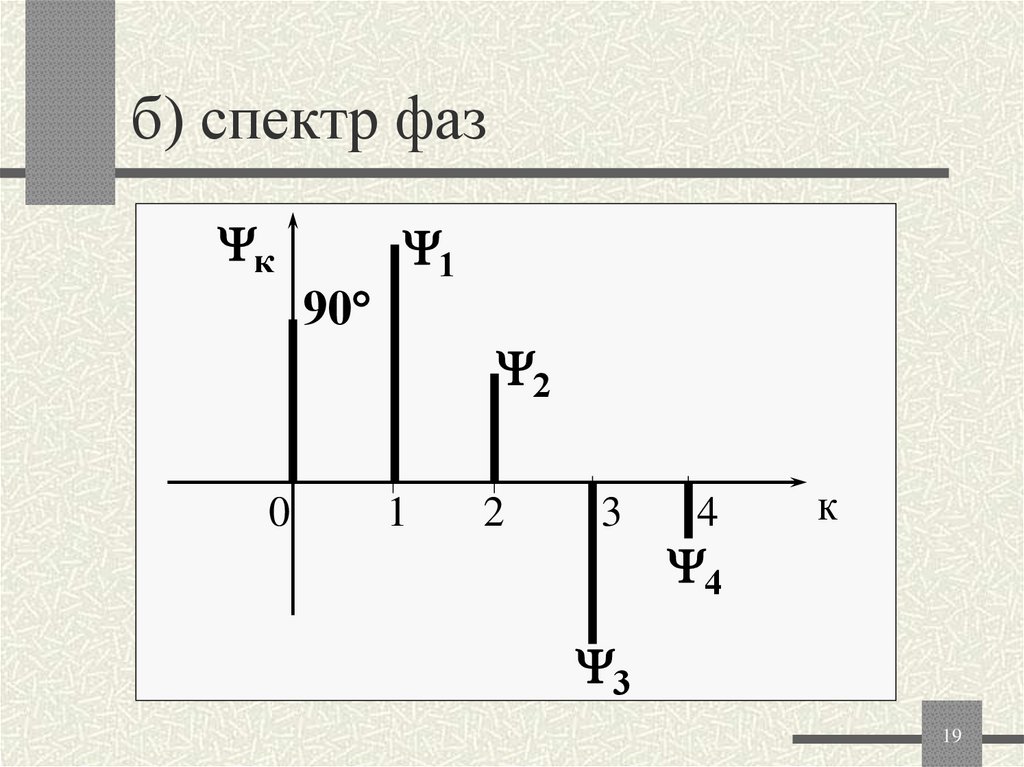
19. б) спектр фаз
к90
1
2
0
1
2
3
4
к
4
3
19
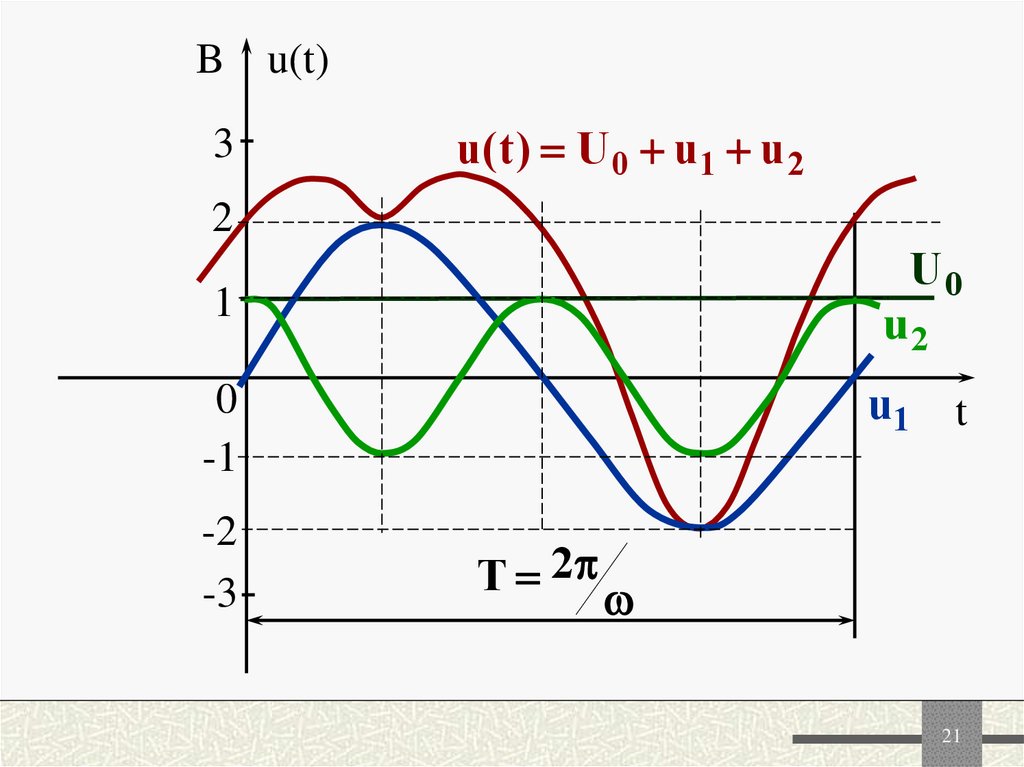
20. Пример
u(t ) 1 2 sin t 1sin( 2 t 90 ), Bгде
U0 1 B
Um1 2 B
1 0
2 90
Um 2 1 B
20
21.
B3
u(t)
u ( t ) U 0 u1 u 2
2
U0
1
u2
0
-1
u1 t
-2
-3
T 2
21
22. Значения негармонических периодических напряжений и токов
2223. Представленных в виде
f (t ) A0 Am1 sin( t 1 )Am 2 sin( 2 t 2 ) ...
23
24. 1. Среднее за период значение
T1
A 0 f (t )dt
T0
- это постоянная составляющая
24
25. 2. Среднее по модулю значение
T1
Aср f (t ) dt
T0
25
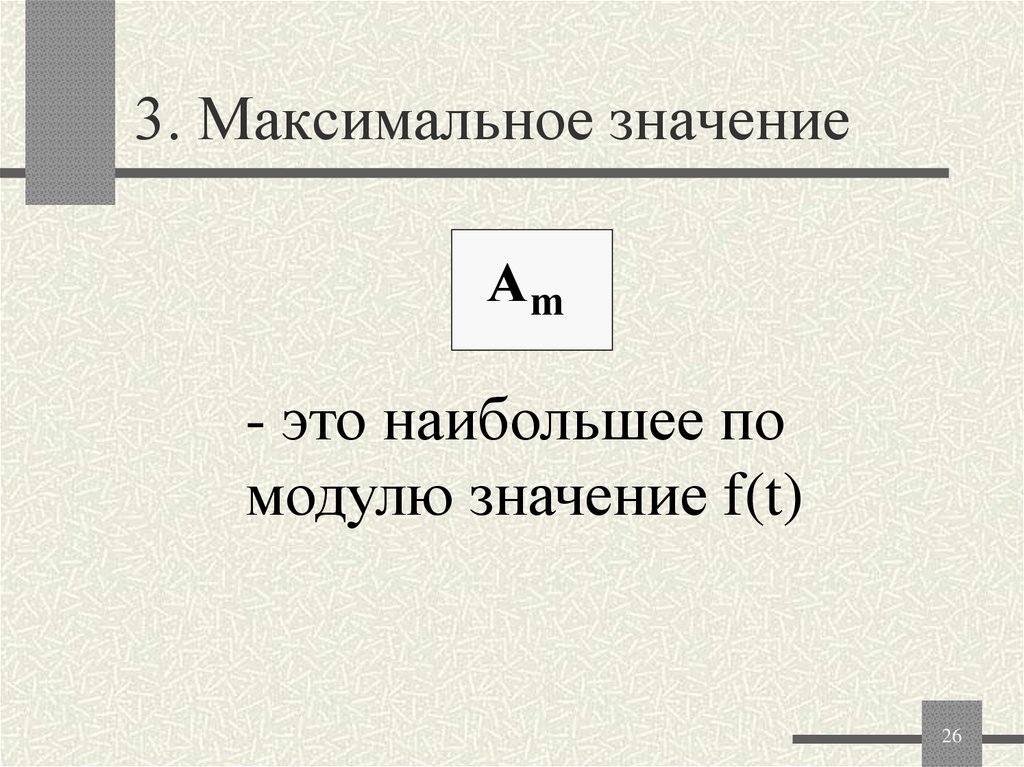
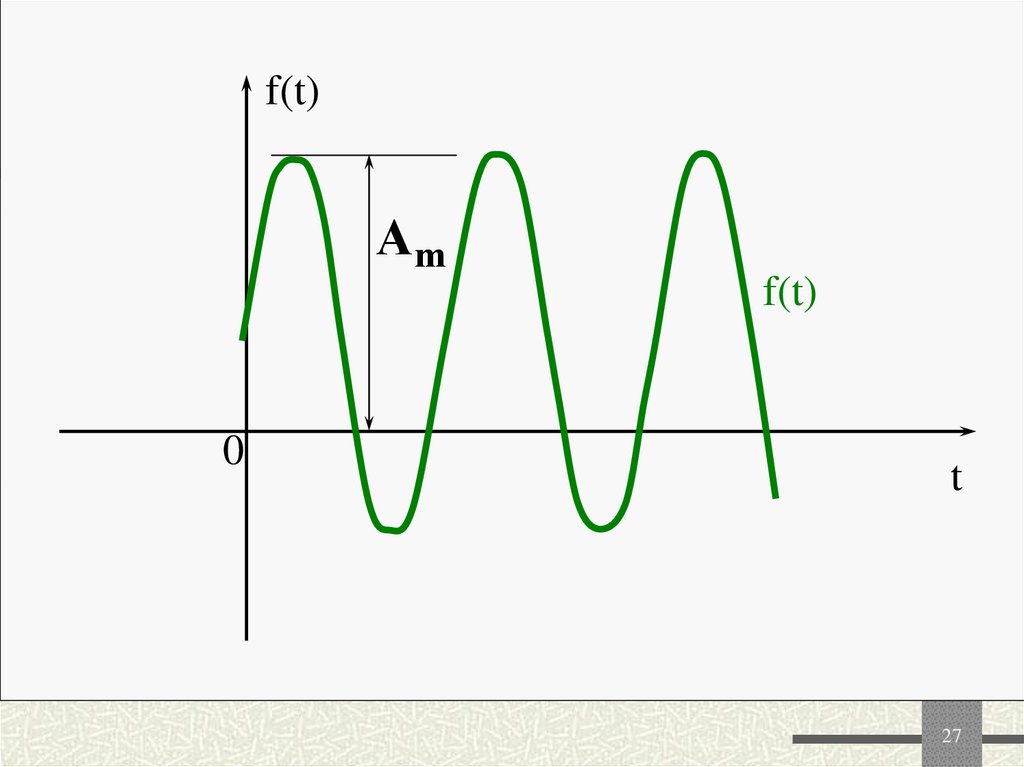
26. 3. Максимальное значение
Am- это наибольшее по
модулю значение f(t)
26
27.
f(t)Am
f(t)
0
t
27
28. 4. Действующее значение
A- это среднеквадратичное
значение f(t) за период Т
28
29.
T1 2
A
f (t ) dt
T0
2
2
2 A m1 A m 2
A0
...
2
2
2
2
2
A 0 A1 A 2 ...
29
30. Где
Am1Am 2
A1
, A2
...
2
2
- действующие значения
отдельных гармоник
30
31. Например:
i(t ) 6 8 2 sin( t 30 )7.07 sin( 3 t 60 ), A
2
7.07
I 6 8
11.18 A
2
2
2
31
32.
u(t ) 3 4 2 sin( t 90 ), B2
2
U 3 4 5B
32
33. Действующие значения тока (I) и напряжения (U) характеризуют тепловую мощность в R:
2U
P I R
, Вт
R
2
33
34. Измерения величин периодических напряжений и токов
3435. Действующие значения могут быть измерены вольтметрами и амперметрами следующих систем:
1. Действующие значениямогут быть измерены
вольтметрами и
амперметрами следующих
систем:
35
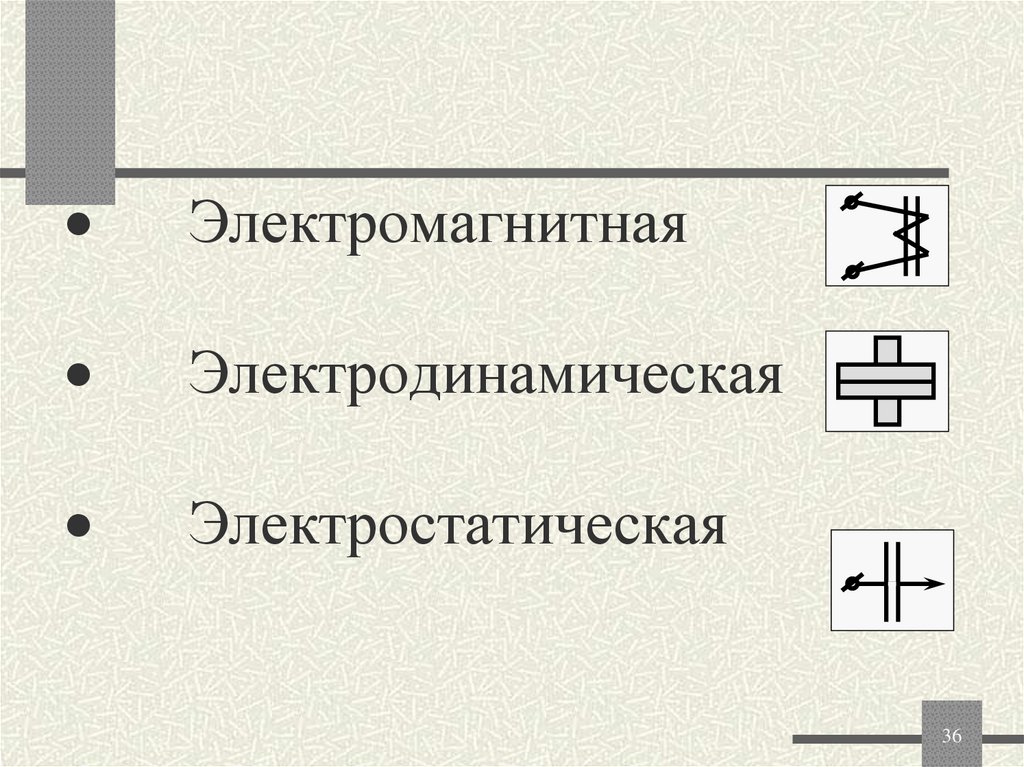
36. · Электромагнитная · Электродинамическая · Электростатическая
ЭлектромагнитнаяЭлектродинамическая
Электростатическая
36
37. 2. Постоянные составляющие измеряются вольтметрами и амперметрами магнитоэлектрической системы:
3738. 3. Средние по модулю значения напряжений и токов фиксируются при помощи вольтметров и амперметров магнитоэлектрической системы
с выпрямителем:38
39. Максимальные и мгновенные значения (в функции времени) напряжений и токов измеряются при помощи осциллографов
4. Максимальные имгновенные значения
(в функции времени)
напряжений и токов
измеряются при помощи
осциллографов
39
40. Коэффициенты негармонических периодических напряжений и токов
4041. Коэффициенты периодических напряжений и токов используются для оценки отличия их от гармонических функций
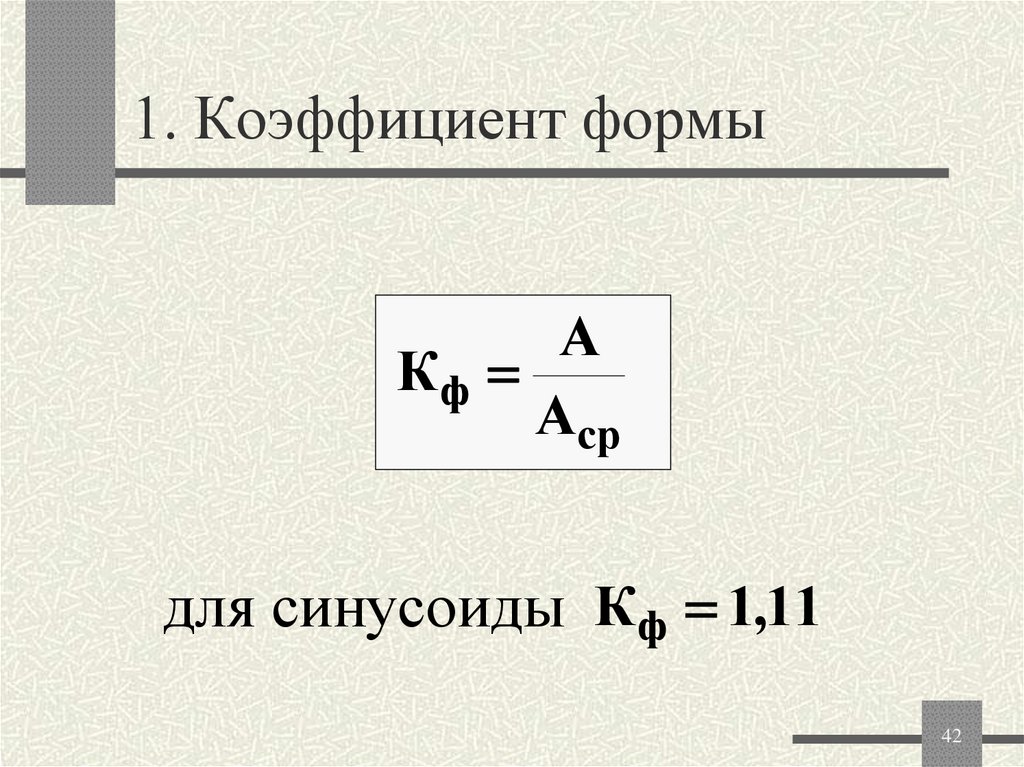
4142. 1. Коэффициент формы
АКф
Аср
для синусоиды Кф 1,11
42
43. 2. Коэффициент амплитуды
АmКа
A
для синусоиды Ка 2 1,41
43
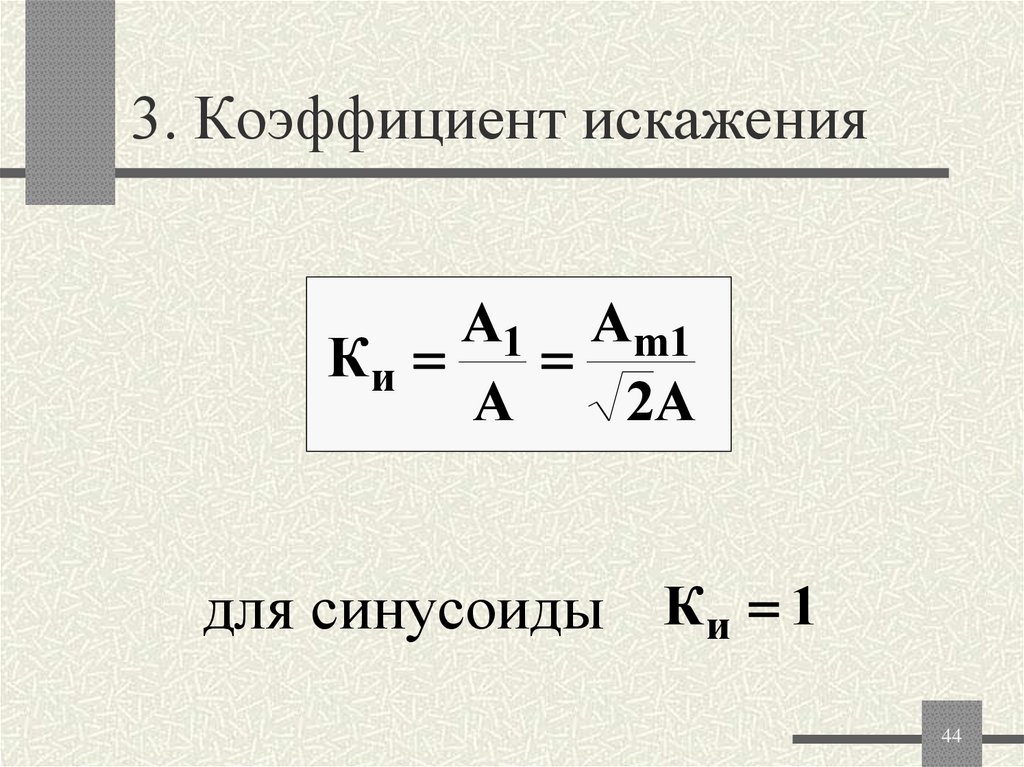
44. 3. Коэффициент искажения
А1 Аm1Ки
А
2A
для синусоиды Ки 1
44
45. 4. Коэффициент гармоник
( А0 0)Кг
2
2
А 2 А 3 ...
А1
для синусоиды Кг 0
45
46. Для практически синусоидальных токов и напряжений:
Кг 0,0546
47. Мощность при периодических напряжениях и токах
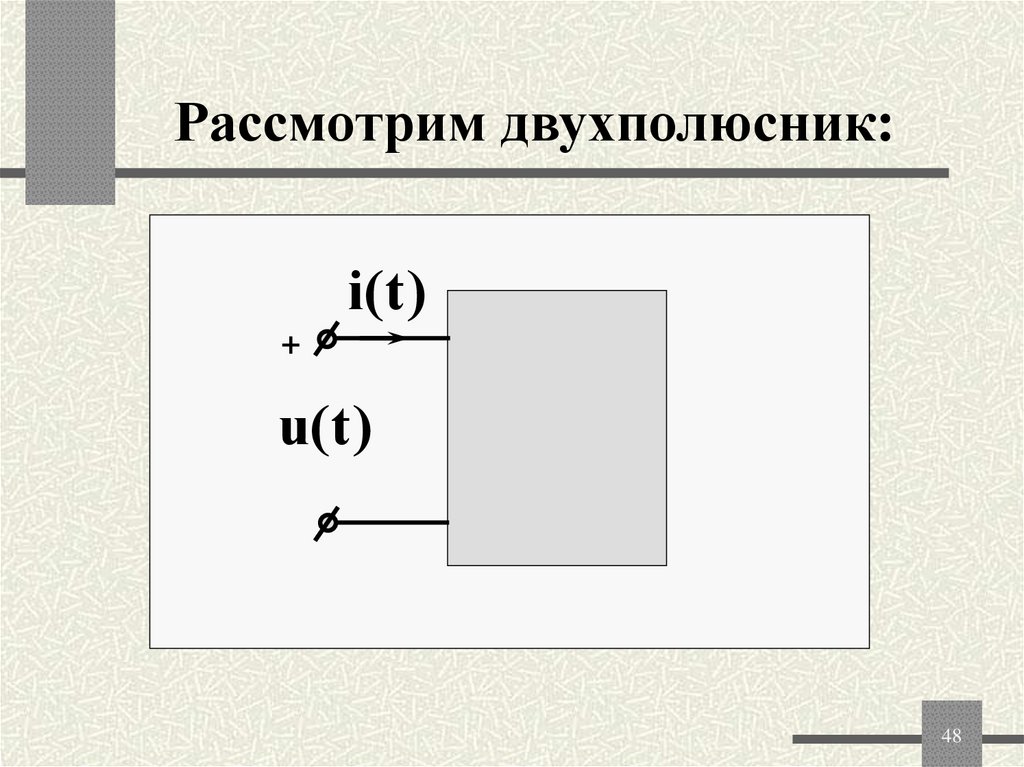
4748.
Рассмотрим двухполюсник:i( t )
+
u(t )
48
49.
Напряжение и ток двухполюсникаu(t ) U 0 2U1 sin( t 1 )
2U 2 sin( 2 t 2 ) ...
i(t ) I 0 2I1 sin( t 1 )
2I 2 sin( 2 t 2 ) ...
49
50. 1. Активная мощность Р характеризует тепловую энергию
W P t P n T, Джгде
n 1, 2, 3...
2
T
50
51.
При этомP P0 P1 P2 ... U0I 0
U1I1 cos 1 U 2I 2 cos 2 ... , Вт
где
1 1 1
2 2 2
51
52. 2. Реактивная мощность Q (условная величина):
Q Q1 Q 2 ...U1I1 sin 1 U 2I 2 sin 2 ... , вар
52
53. 3. Полная мощность S (условная величина):
S UI2
2
2
U 0 U1 U 2 ...
2
2
2
I 0 I1 I 2 ... , ВА
53
54. Причем в большинстве случаях для негармонических функций
2S P Q
2
54
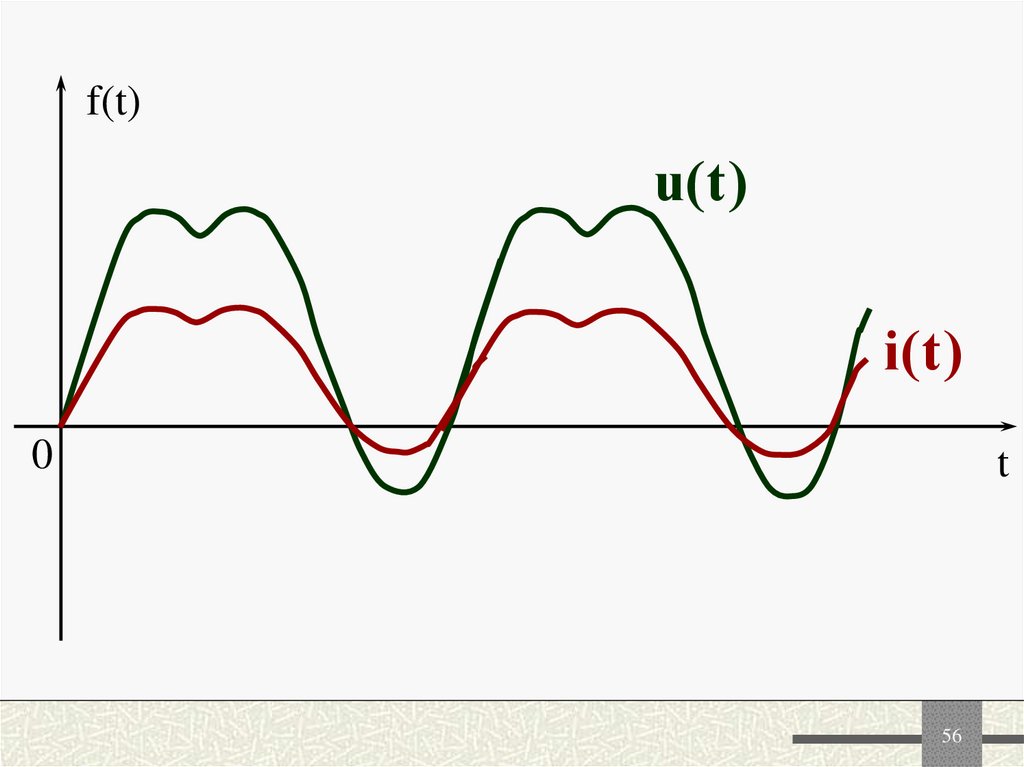
55. Если то формы и одинаковы
Если2
S P Q
то формы
одинаковы
2
u(t ) и i(t )
55
56. f(t)
u( t )i( t )
0
t
56
57. 4. Коэффициент мощности
Pcos 1
S
P
где arccos
S
57
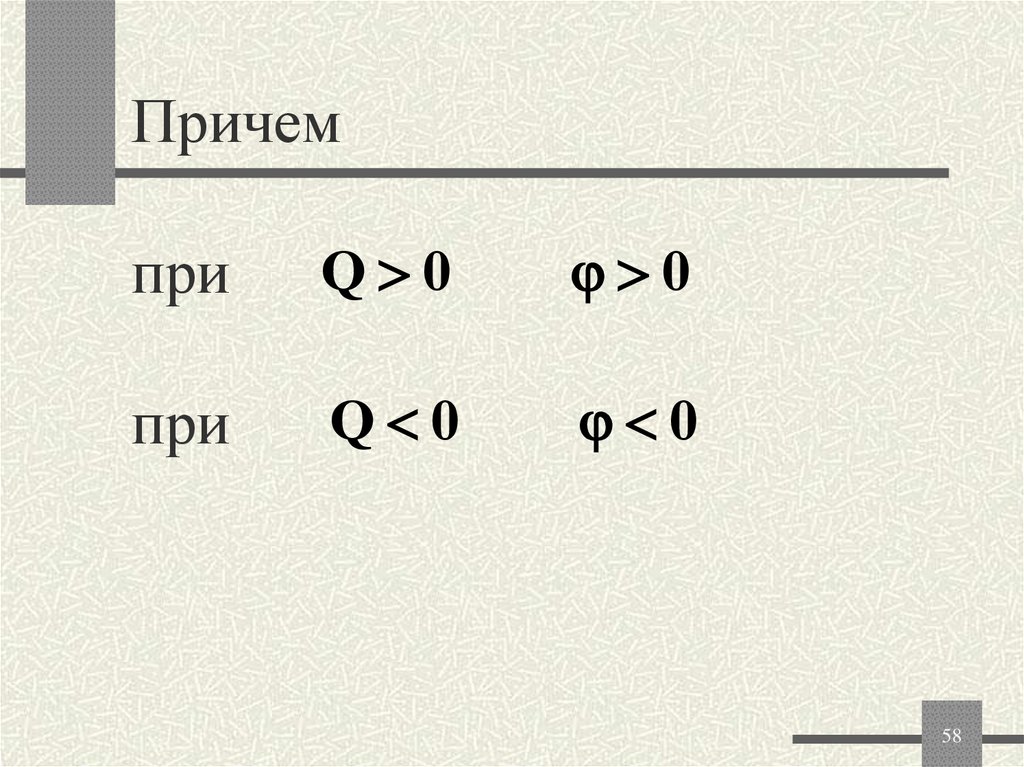
58. Причем при при
Причемпри
Q 0
0
при
Q 0
0
58
59. Эквивалентные синусоиды
u(t ) 2U sin( t 1 )i(t ) 2I sin( t 1 )
где:
U
I
2
2
2
U 0 U1 U 2
2
2
2
I 0 I1 I 2
59
60. Расчет линейных цепей при периодических напряжениях и токах
6061. После разложения периодических ЭДС и токов источников тока в ряд Фурье линейную цепь можно рассчитывать методом наложения, т.е.
рассчитывать постояннуюсоставляющую и каждую
гармонику напряжений и
токов по отдельности
61
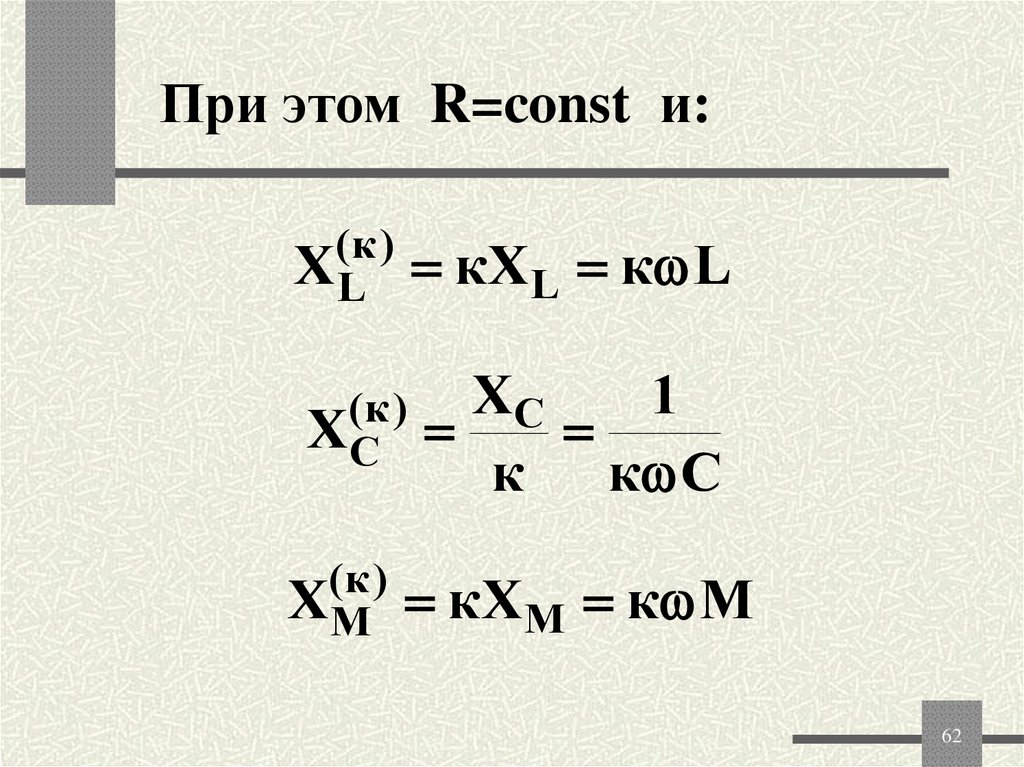
62.
При этом R=const и:(к )
ХL кXL к L
ХС
(к )
ХС
к
1
к C
(к )
ХМ кXМ к М
62
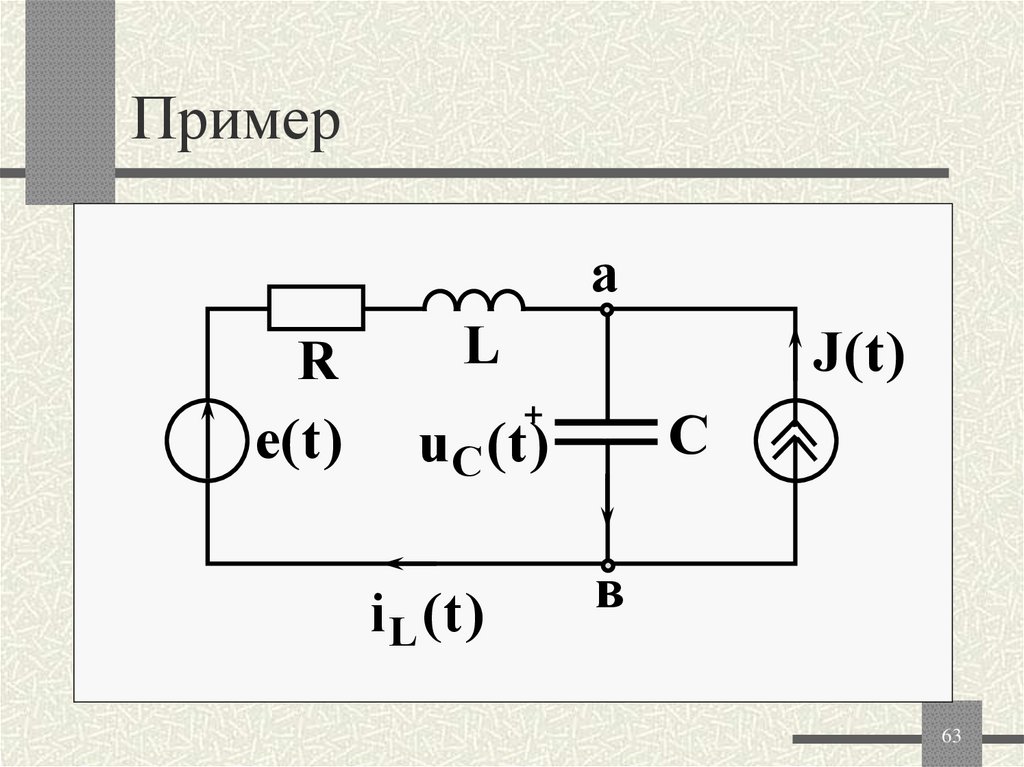
63. Пример
аR
e(t )
L
J(t )
+
С
uC ( t )
i L (t )
в
63
64. Дано:
e(t ) E0 2E1 sin( t 1 )J (t ) J 0 2J 2 sin( 2 t 2 )
, R, L, C
64
65. Определить:
i L ( t ) , uC ( t )65
66. 1. Расчет постоянных составляющих (к=0)
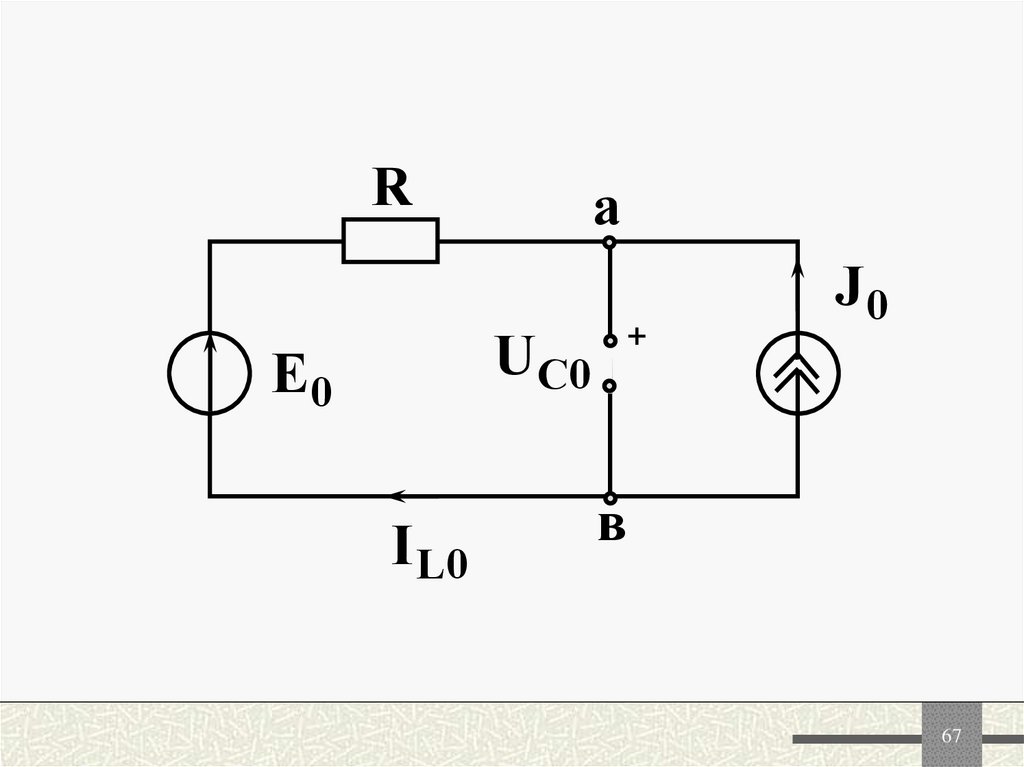
6667.
Rа
U C0
Е0
IL0
+
J0
в
67
68.
I L0 J 0U C 0 E0 I L 0 R E0 J 0 R
68
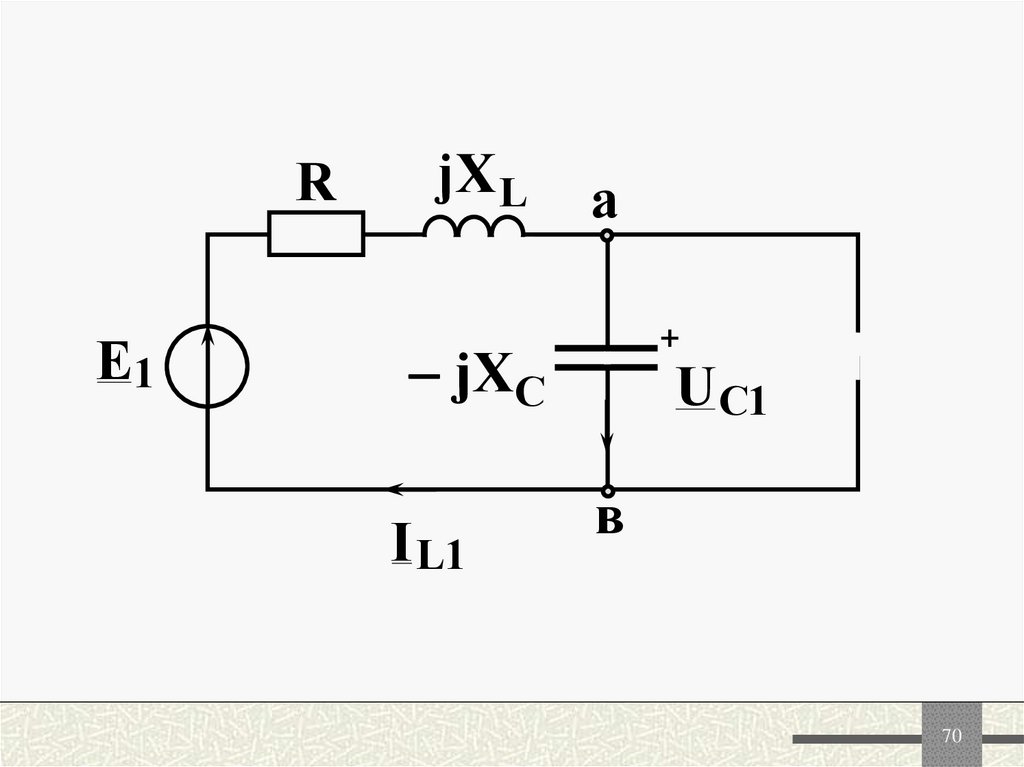
69. 2. Расчет первых гармоник (к=1)
6970.
RЕ1
jXL
а
+
jXC
I L1
U C1
в
70
71.
E1 E1ej 1
1
; X L L
; XC
C
E1
j 1
I L1
I L1e , A
R jXL jXC
UC1 I L1 ( jXC ) UC1e
j 1
,B
71
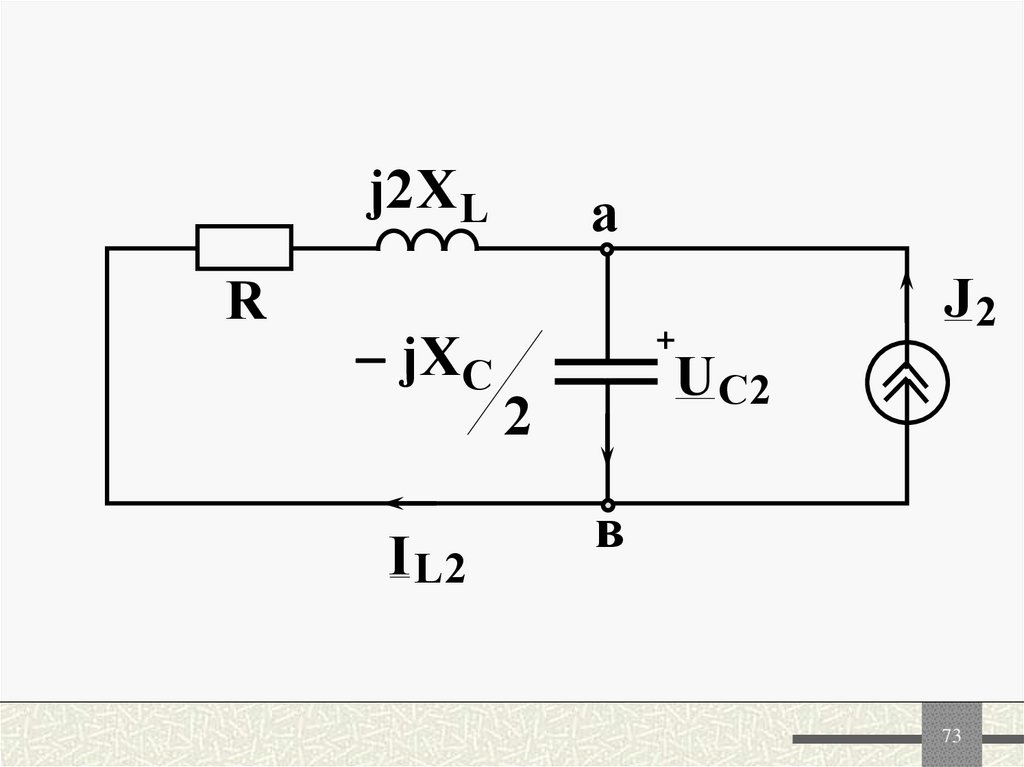
72. 3. Расчет вторых гармоник (к=2)
7273.
j2 X LR
jXC
IL2
а
+
J2
UC2
2
в
73
74.
J 2 J 2ej 2
jXC
2
IL2 J 2
XC
R j2XL j
I L 2e
j 2
,A
2
74
75.
jXC( R j2 XL )
2
UC2 J 2
jXC
R j2 XL
2
U C 2e
j 2
,B
75
76. Окончательный результат
i L (t ) J 0 2I L1 sin( t 1 )2I L 2 sin( 2 t 2 ), A
uC (t ) UC0 2UC1 sin( t 1 )
2UC2 sin( 2 t 2 ), В
76
77. Резонансные явления при периодических напряжениях и токах
7778. Резонансные явления могут наблюдаться при наличии в цепи индуктивностей и емкостей, причем резонанс может возникать на одной
или нескольких гармоникахнапряжений и токов
78
79. При этом входное сопротивление или входная проводимость цепи для этих гармоник становится вещественной (активной) и может быть
близкой к 0 илиРазличают для к-гармоник
резонансы напряжений и
токов, а также резонансы в
сложной цепи
79
80. Резонансные явления могут использоваться в специальных цепях (фильтрах) для пропускания в нагрузку определенных гармоник тока и
напряжения.Рассмотрим такие цепи без
учета активных
сопротивлений катушек
80
81. Пример 1:
даноu1 (t ) U 0 2U1 sin( t 1 )
нужно получить
u 2 (t ) 2U1 sin( t 1 )
81
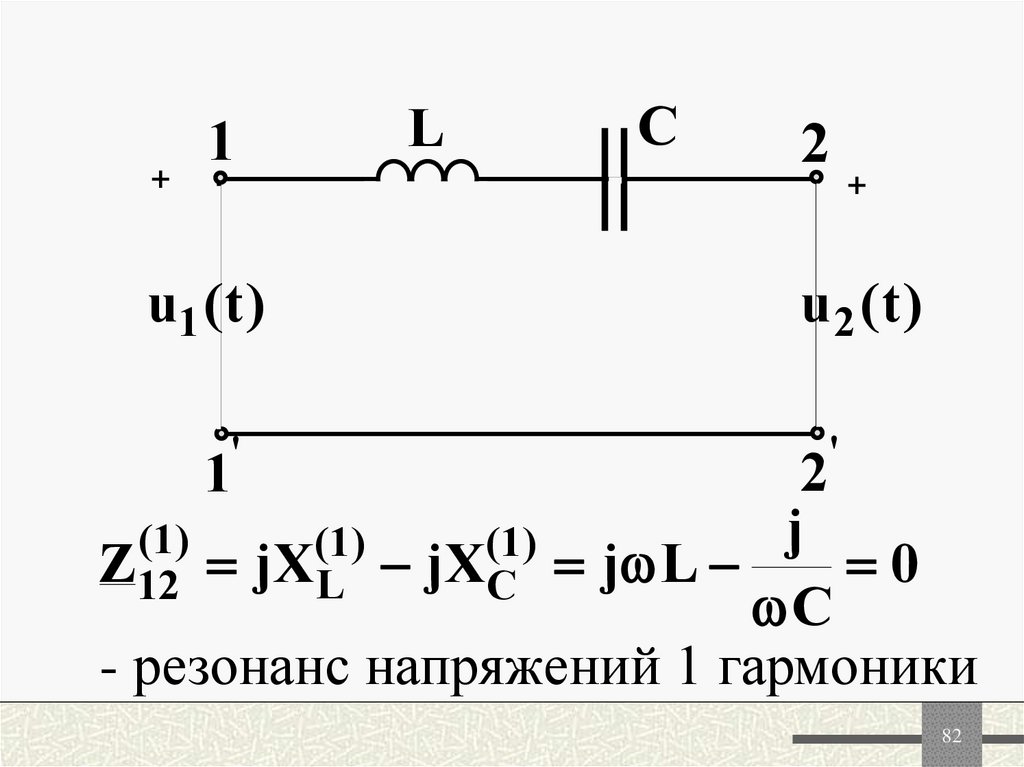
82.
1+
L
C
2
+
u1 ( t )
u 2 (t )
'
'
2
j
(1 )
(1 )
(1 )
Z12 jXL jXC j L
0
C
- резонанс напряжений 1 гармоники
1
82
83. Пример 2:
даноu1 (t ) U 0 2U1 sin( t 1 )
нужно получить
u 2 (t ) U0
83
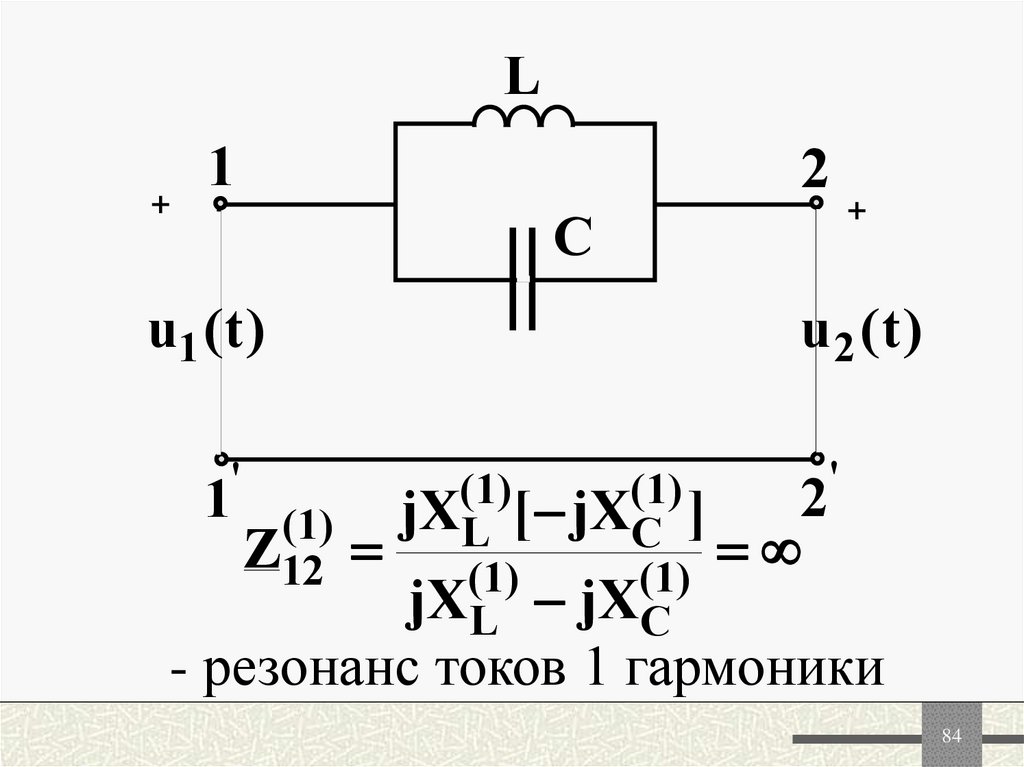
84.
L1
+
u1 ( t )
2
C
+
u 2 (t )
'
(
1
)
(
1
)
2
1 (1) jX [ jX ]
L
C
Z12
(1 )
(1 )
jXL jXC
'
- резонанс токов 1 гармоники
84
85. Пример 3:
даноu1 (t ) U 0 2U1 sin( t 1 )
2U 2 sin( 2 t 2 ) ...
нужно получить
u 2 (t ) 2U1 sin( t 1 )
85
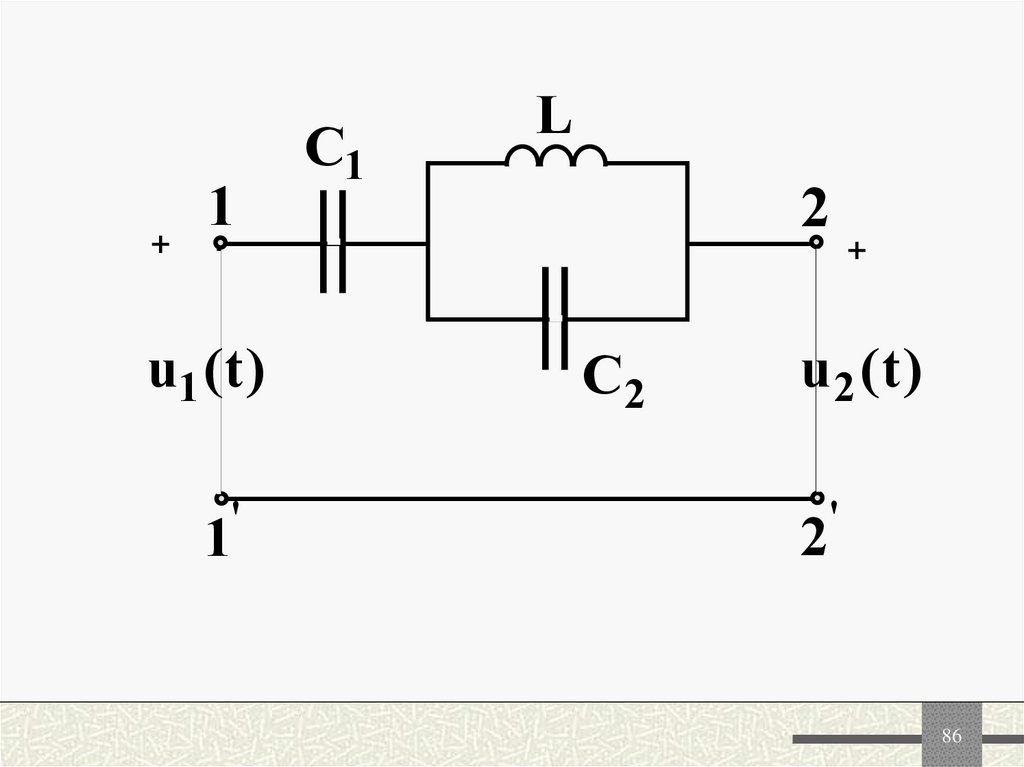
86.
1+
u1 ( t )
'
1
C1
L
2
C2
+
u 2 (t )
2
'
86
87. а) задерживает
а) С1 задерживает U 01
б) 2 L
2 C2
задерживается 2 гармоника
(резонанс токов 2 гармоники)
87
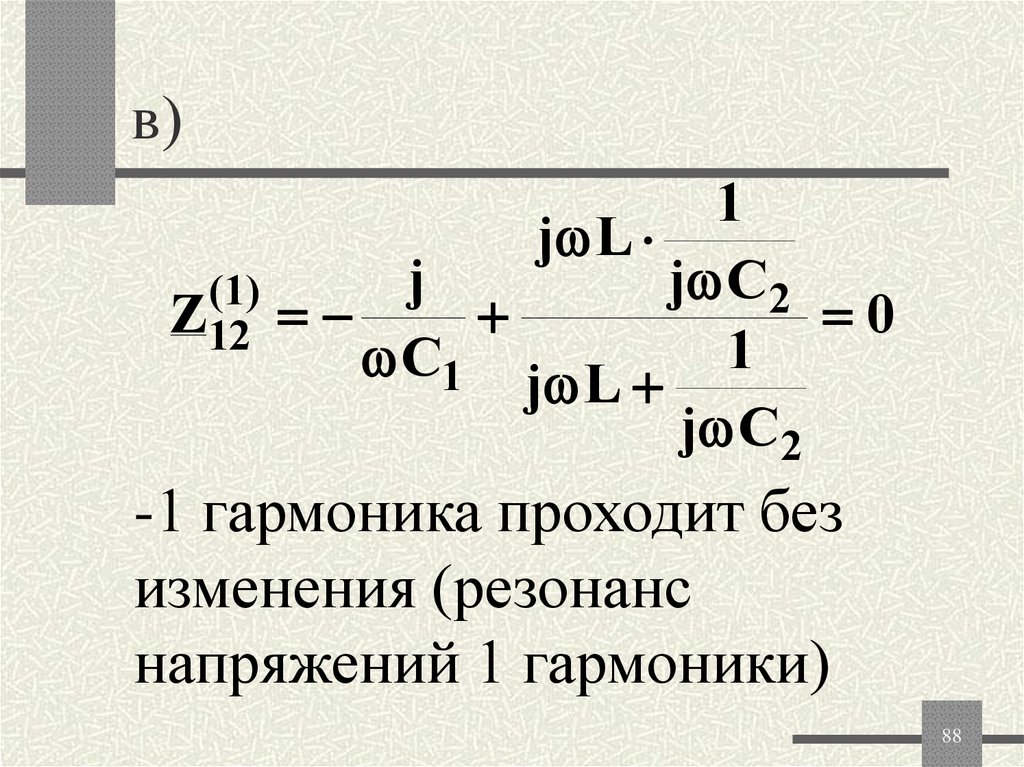
88. в)
1j L
j
j C2
(1 )
Z12
0
C1 j L 1
j C2
-1 гармоника проходит без
изменения (резонанс
напряжений 1 гармоники)
88
89. Высшие гармоники в трехфазных цепях
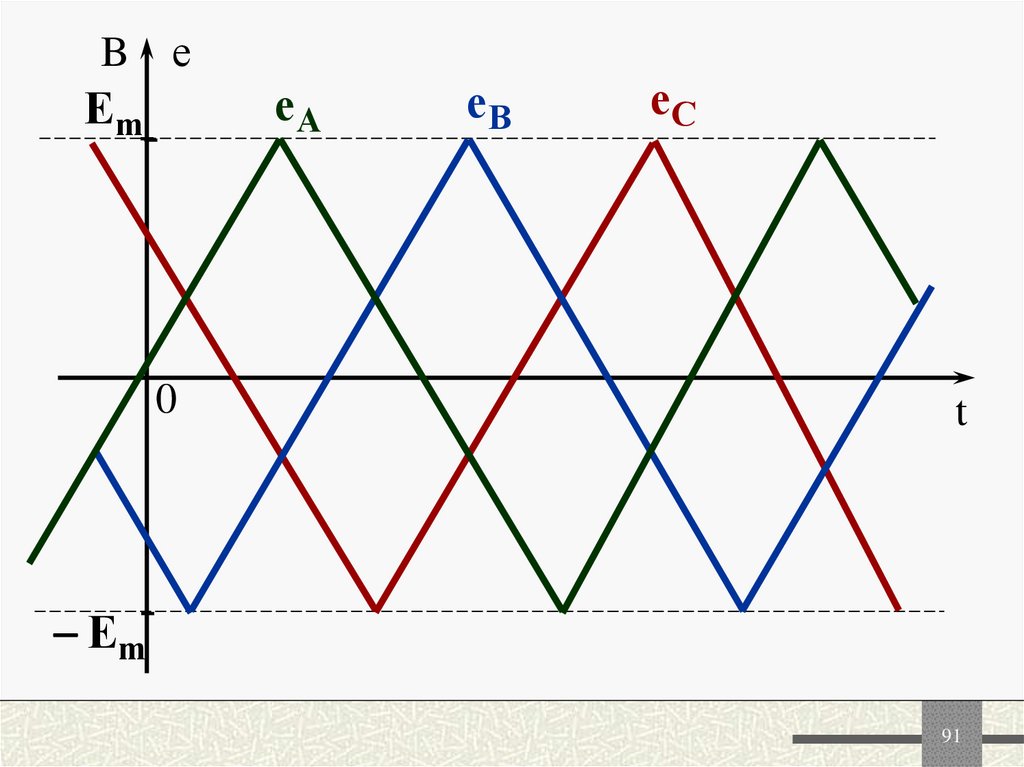
8990. Высшие гармоники в трехфазных цепях появляются за счет негармонических фазных ЭДС генераторов и трансформаторов, которые обычно
одинаковы поформе, сдвинуты на треть
периода и симметричны
относительно оси времени
90
91.
B ееА
Em
0
еВ
еС
t
Em
91
92. Фазные ЭДС содержат нечетные гармоники
e A 2E1 sin( t 1 )2E3 sin( 3 t 3 )
2E5 sin( 5 t 5 ) ...
92
93. Тогда
eВ 2E1 sin( t 1 120 )2E3 sin( 3 t 3 )
2E5 sin( 5 t 5 120 ) ...
93
94. Тогда
eС 2E1 sin( t 1 120 )2E3 sin( 3 t 3 )
2E5 sin( 5 t 5 120 ) ...
94
95. гармоники к = 1, 7, 13 … образуют прямую последовательность
Таким образомгармоники к = 1, 7, 13 …
образуют прямую
последовательность
95
96. Гармоники к = 5, 11, 17 … образуют обратную последовательность
9697. Гармоники к = 3, 9, 15 … образуют нулевую последовательность
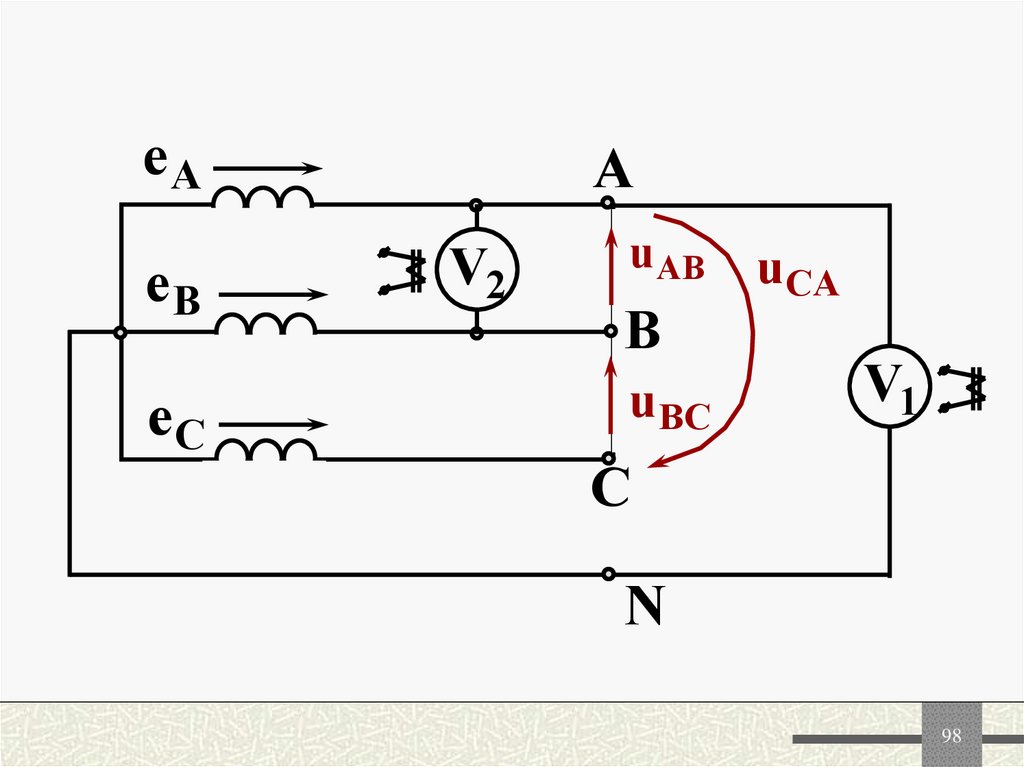
9798.
еАеВ
еС
А
V2
u АВ
В
u ВС
uСА
V1
С
N
98
99. Линейное напряжение
u AB e A eB3 2Е1 sin( t 1 30 )
3 2Е5 sin( 5 t 5 30 ) ...
99
100. Линейное напряжение
uBС eВ eС3 2Е1 sin( t 1 90 )
3 2Е5 sin( 5 t 5 90 ) ...
100
101. Линейное напряжение
uСA eС e А3 2Е1 sin( t 1 150 )
3 2Е5 sin( 5 t 5 150 ) ...
101
102. Действующие значения
U V1 E A EФ2
2
2
E1 E3 E5 ...
U V 2 U АВ U Л 3
2
2
E1 E5 ...
UV2 UЛ
причем
3
U V1 ЕФ
102
103. Линейные напряжения не содержат гармоник кратных трем, причем расчет симметричного режима ведется на одну фазу методом
наложения длякаждой гармоники отдельно
103
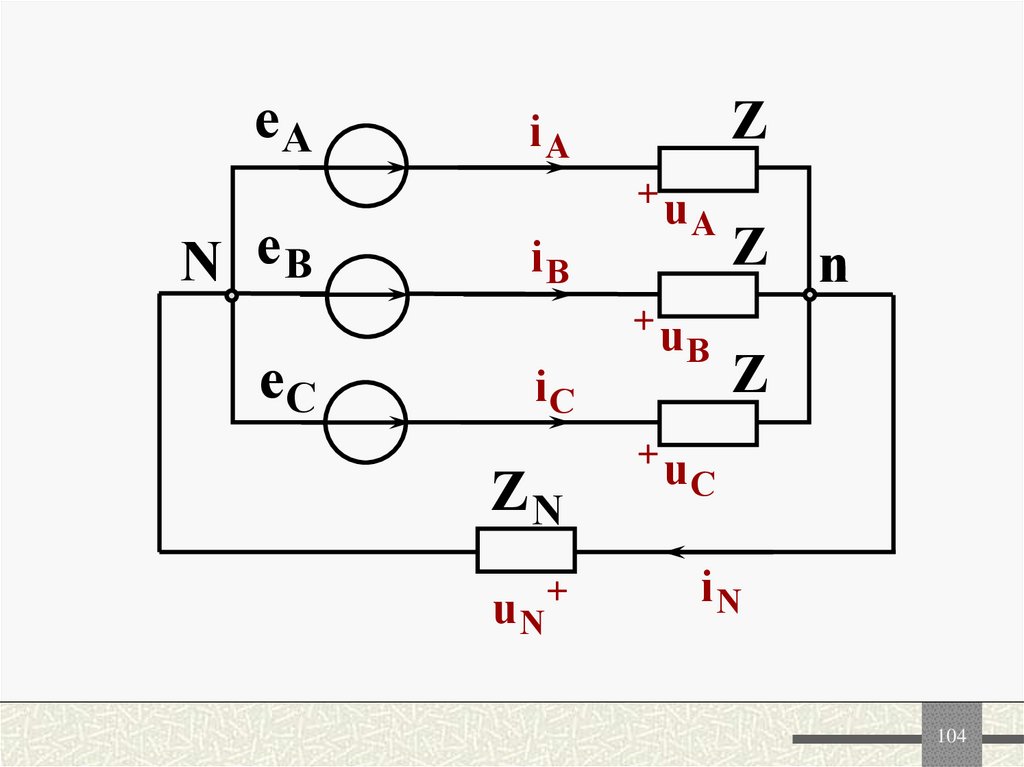
104.
еАZ
iА
N еВ
iB
еС
iС
ZN
uN
uА
uB
Z n
Z
uС
iN
104
105. Дано:
TT
е А ( t ) е B t еC t ,
3
3
2 (1, 3,5 ) ( 3 )
, Т , Z
, ZN
105
106. Определить
i A , u A , i N , uN106
107. Расчет комплексов 1 гармоники фазы А
1. Расчет комплексов1 гармоники фазы А
I1
E1e
Z
U1 Z
j 1
(1 )
(1 )
I1e
j 1
I1 E1e
j 1
107
108. 2. Расчет комплексов 3 гармоники фазы А
I3E3e
Z
( 3)
j 3
I
e
3
( 3)
j 3
3Z N
U3 Z
( 3)
I 3 U 3e
j
108
109. Тогда
( 3)j
U N 3Z N I 3 U N e
I N 3I 3 I Ne
j 3
109
110. 3. Расчет комплексов 5 гармоники фазы А
I5E 5e
Z
U5 Z
j 5
(5)
( 5)
I 5e
j 5
I 5 Е5e
j 5
110
111. 4. Функции времени
i A 2I1 sin( t 1 )2I 3 sin( 3 t 3 )
2I 5 sin( 5 t 5 )
111
112.
u A 2E1 sin( t 1 )2U 3 sin( 3 t )
2E5 sin( 5 t 5 )
112
113.
i N 2I N sin( 3 t 3 )u N 2U N sin( 3 t )
113
114. Примечание:
если( 3)
ZN ,
то
I 3 I N 0,
U N E3 e
U 3 0,
j 3
114






















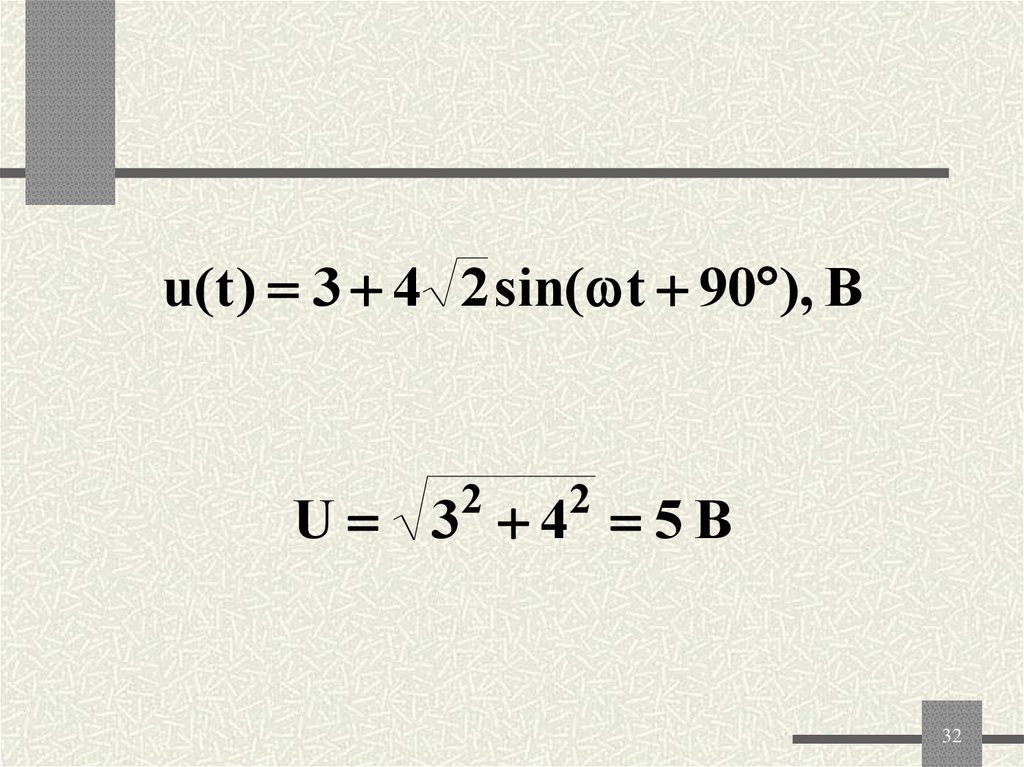























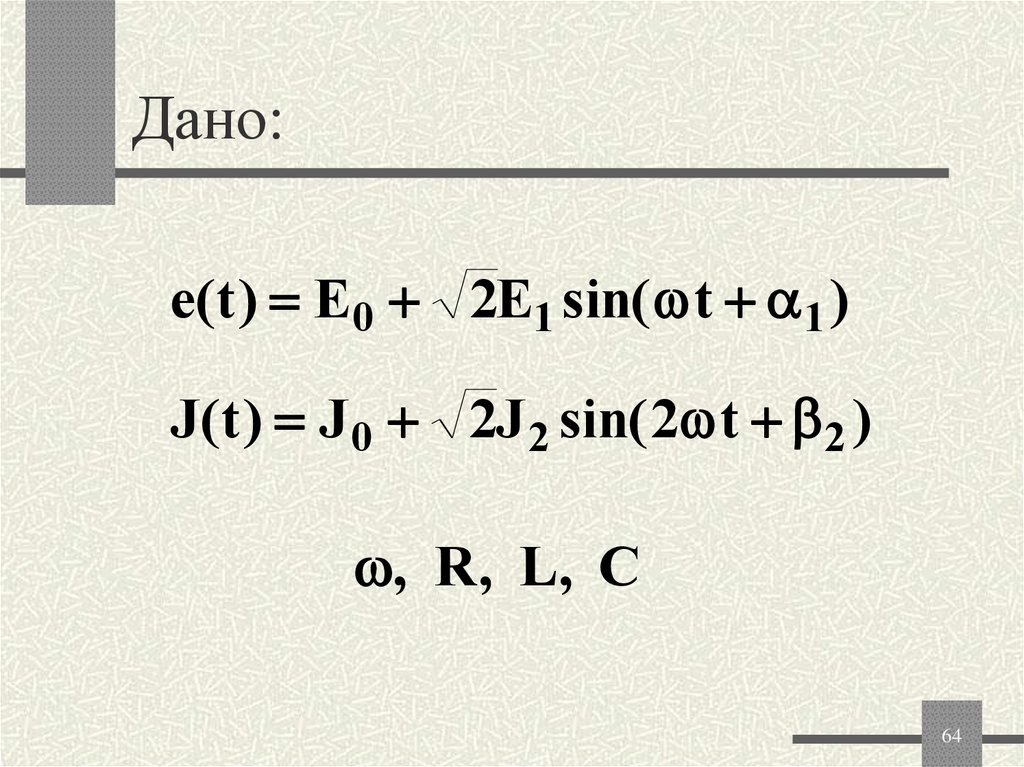
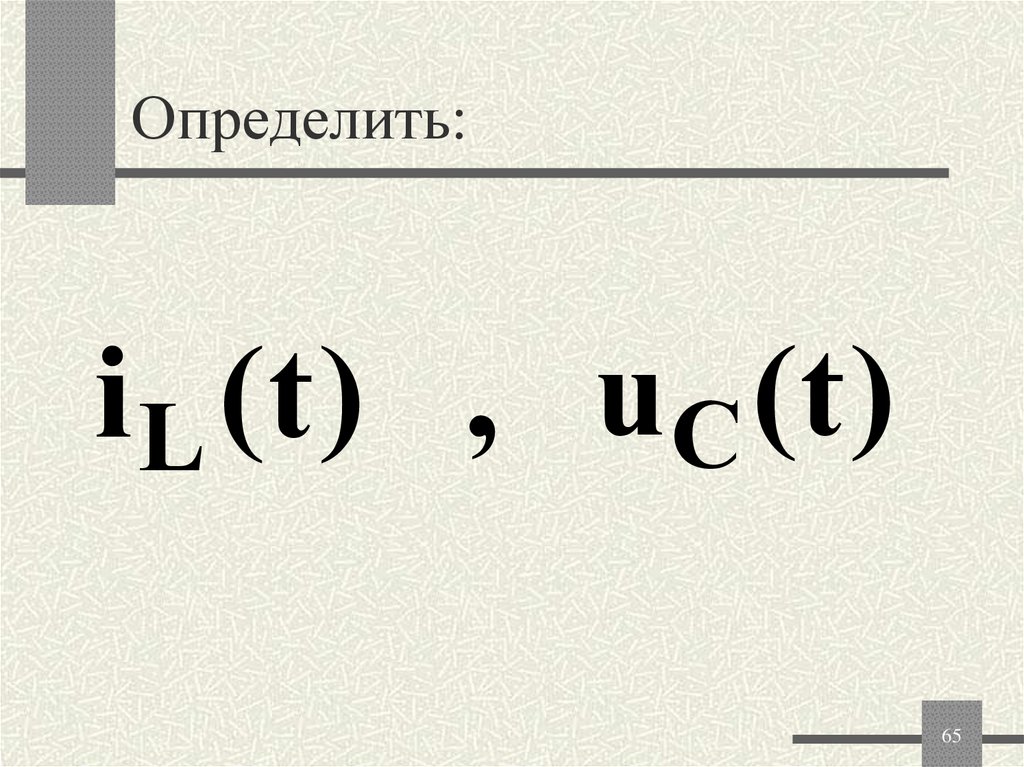

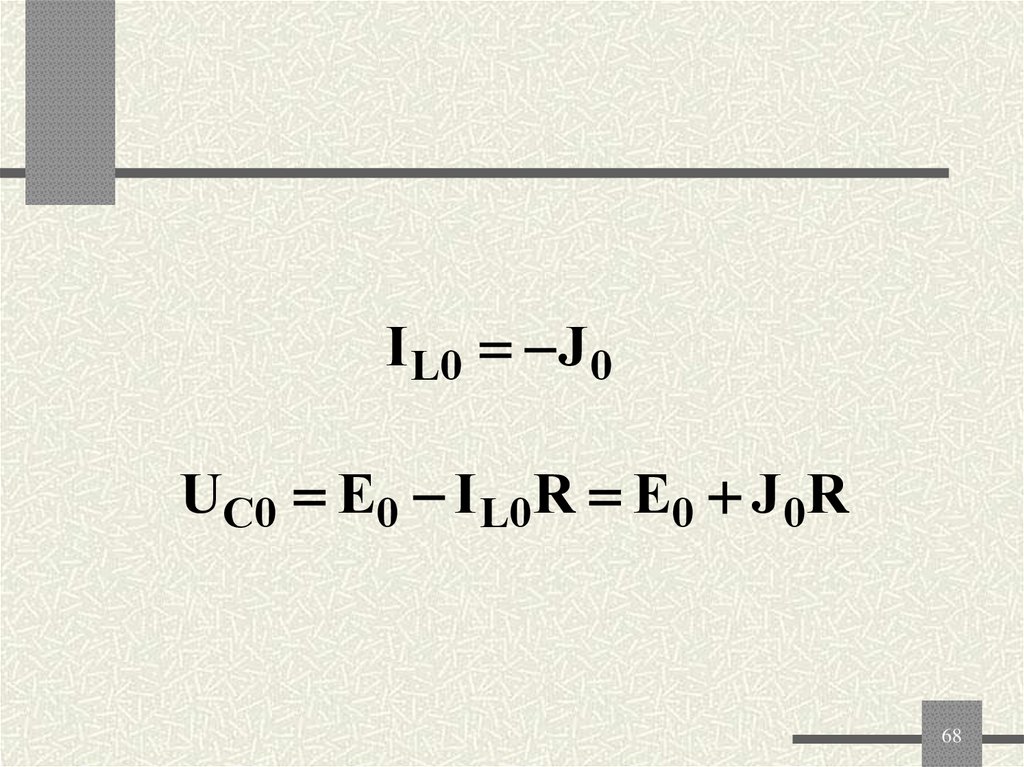

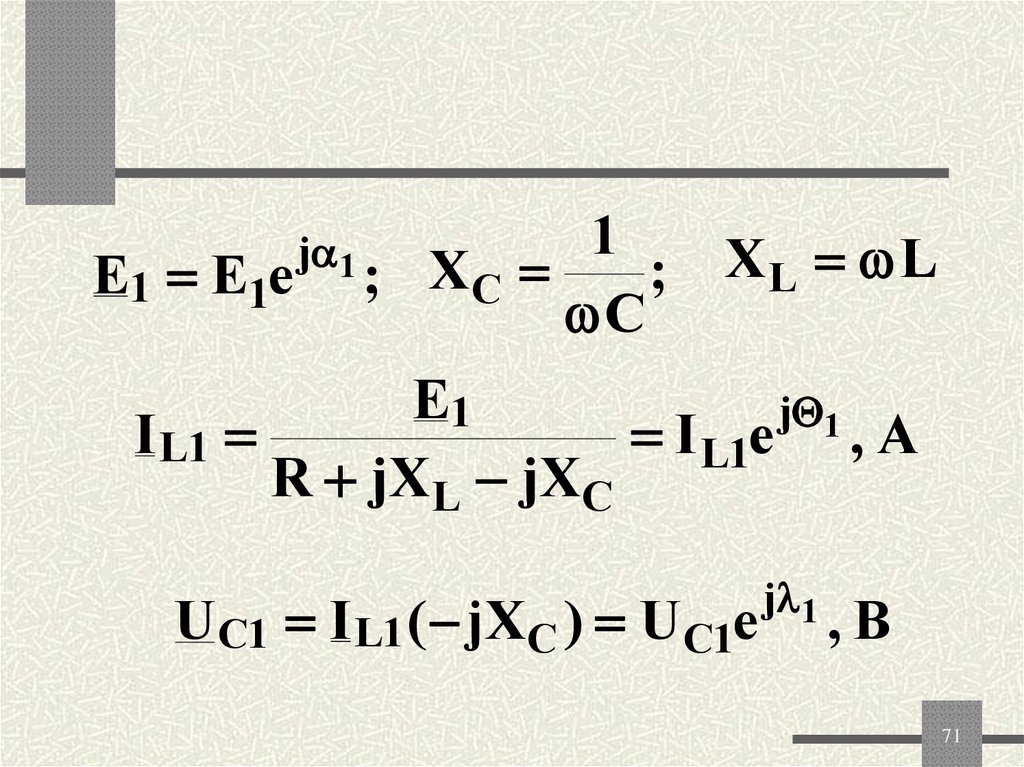

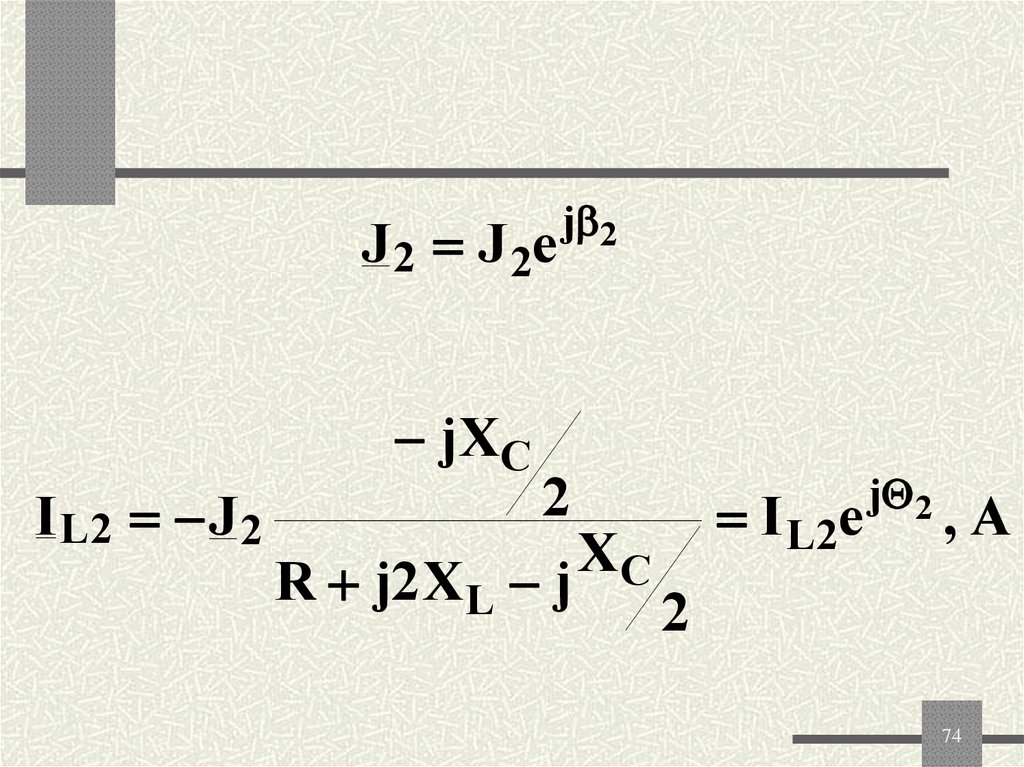
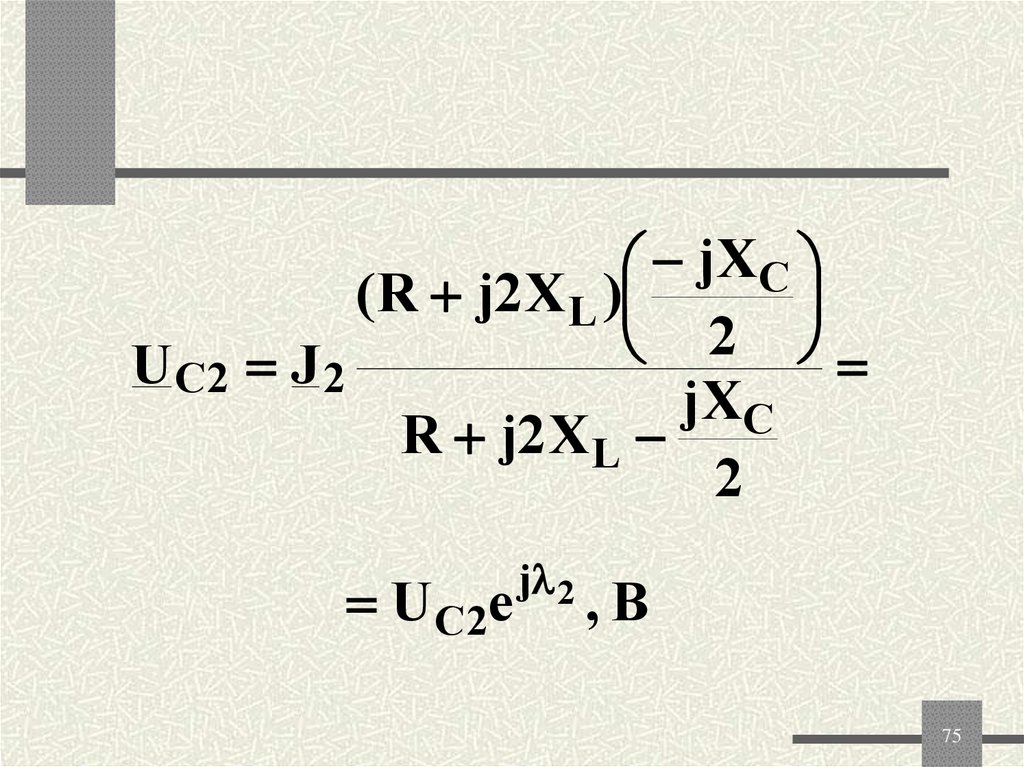






















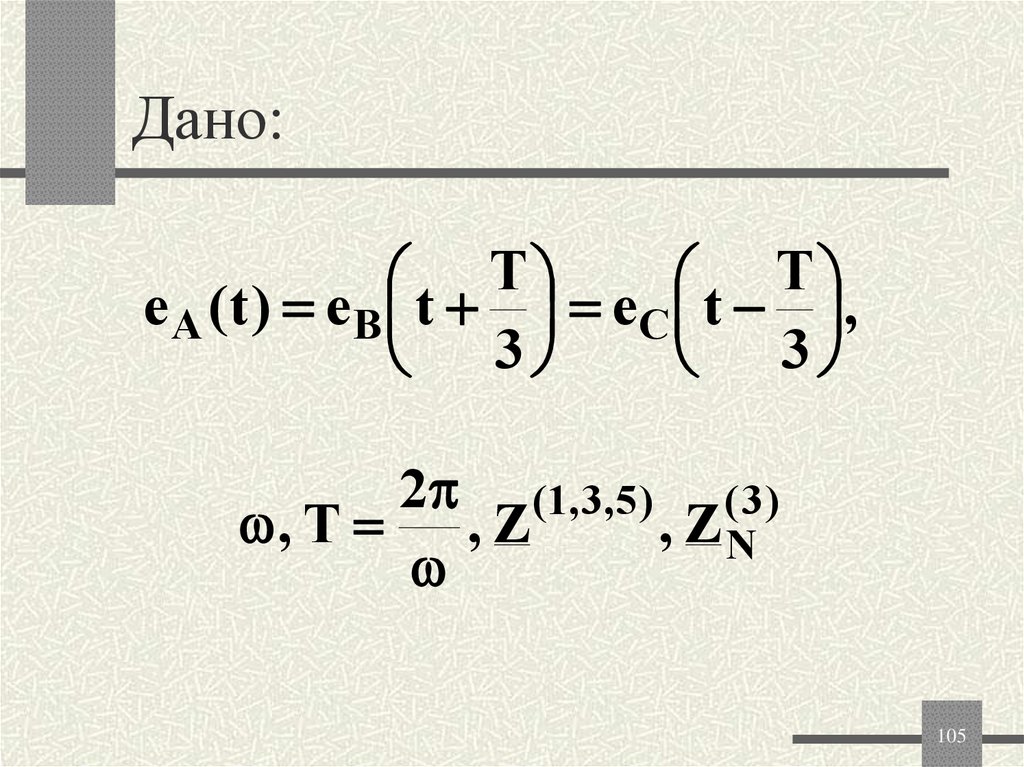






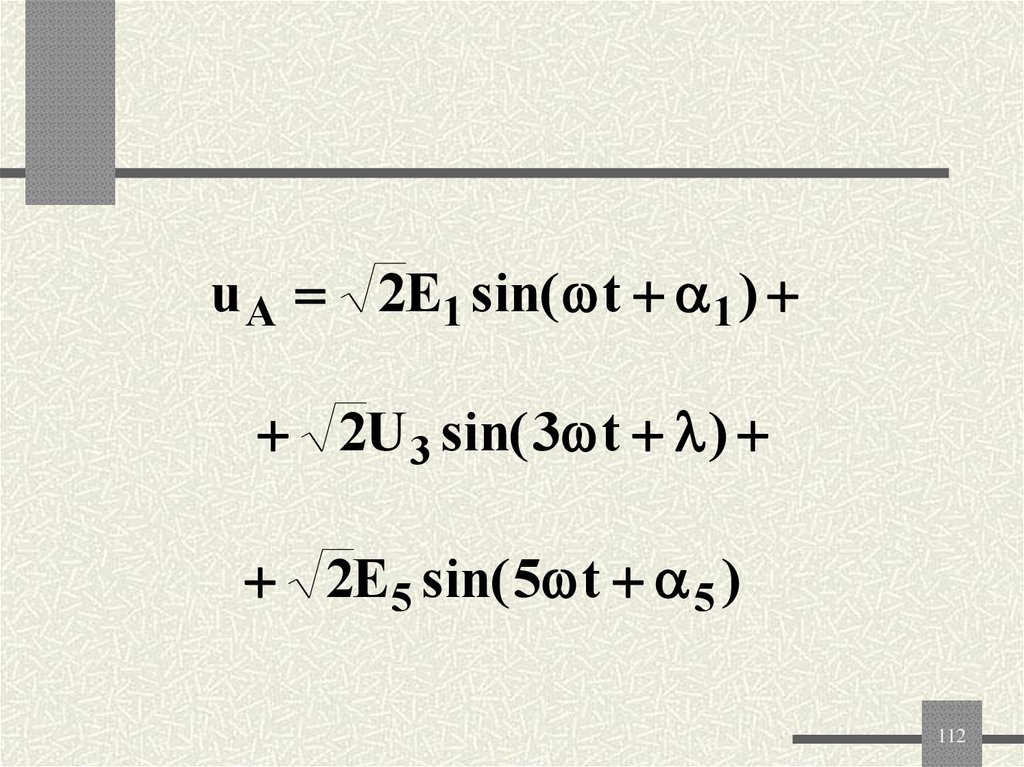
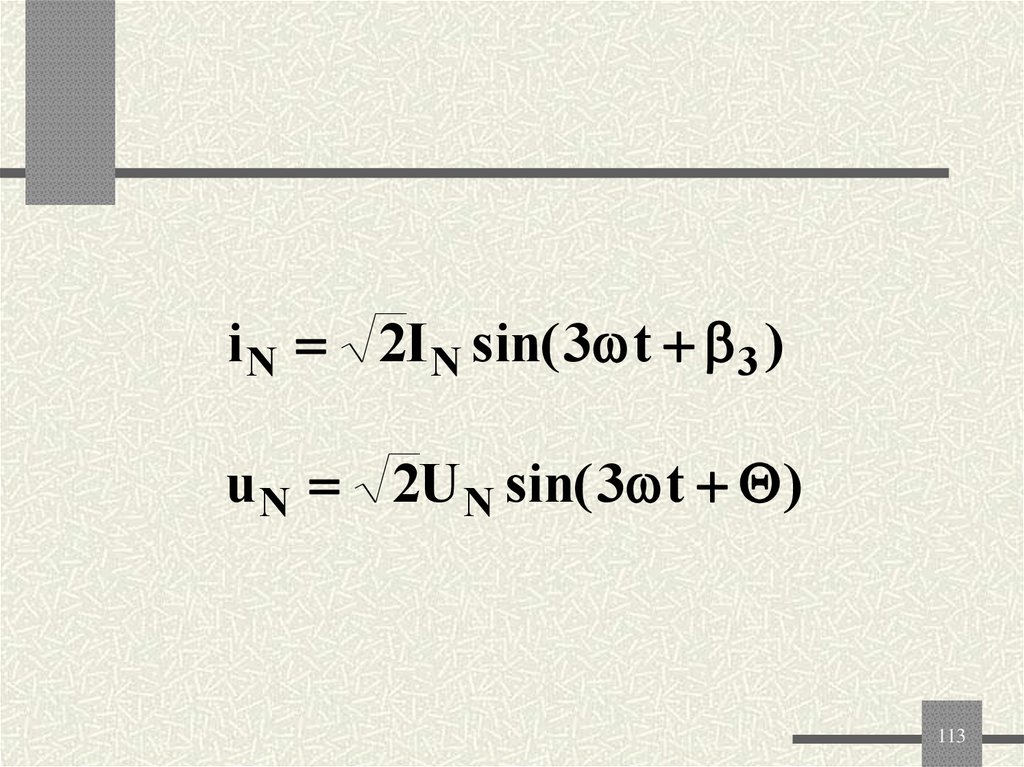

 Физика
Физика








