1ЗЛП-граф (1) (1)

1.

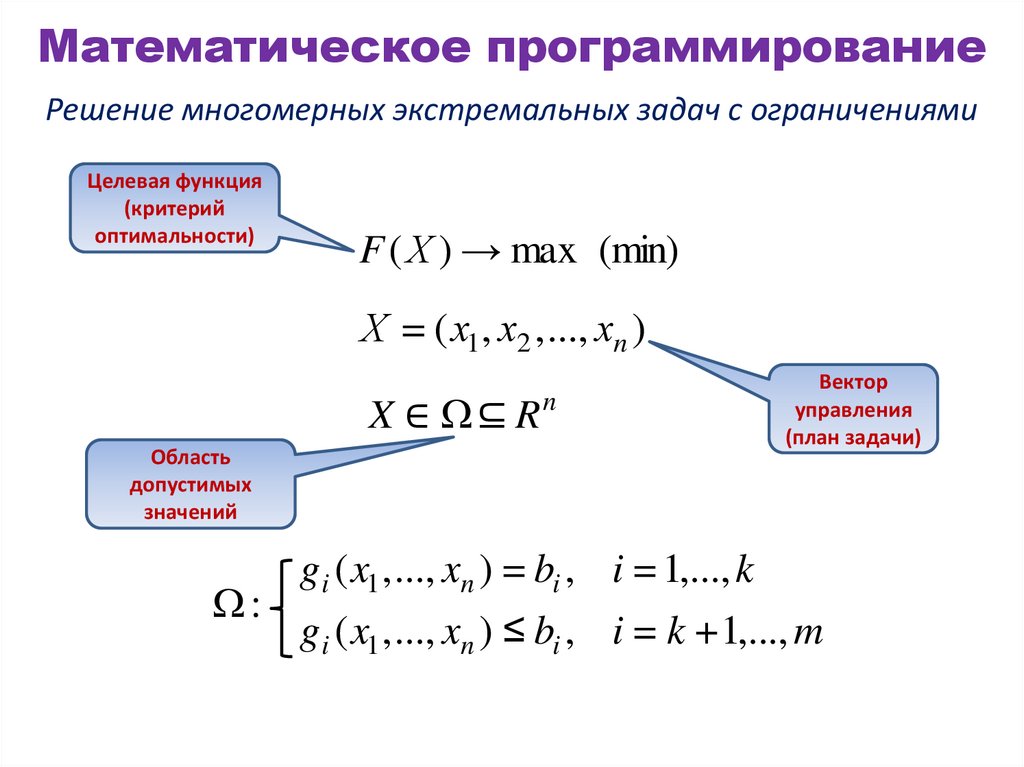
Математическое программирование
Решение многомерных экстремальных задач с ограничениями
Целевая функция
(критерий
оптимальности)
F ( Х ) → max (min)
Х = ( х1, х2 , ..., хn )
X ∈ ⊆ Rn
Область
допустимых
значений
Вектор
управления
(план задачи)
gi ( x1 , ..., xn ) = bi , i = 1,..., k
:
gi ( x1 , ..., xn ) ≤ bi , i = k + 1,..., m

2.

Построение математической модели
1. Для определения каких величин должна быть построена
модель (как идентифицировать переменные задачи)?
2. В чем состоит цель задачи (что является целевой функцией)?
3. Какие ограничения должны быть наложены на переменные,
чтобы выполнялись условия, характерные для моделируемой
системы?
Задача линейного программирования (ЗЛП)
– все функции задачи (и целевая функция, и ограничения)
являются линейными

3.

Задача об использовании ресурсов
(задача планирования производства)
П1, …, Пn – виды выпускаемой продукции
сj – прибыль от реализации единицы j-го вида продукции
Р1, …, Рm – используемые ресурсы
bi – запас i-го ресурса
aij – удельный расход i-го ресурса на единицу
j-го вида продукции
?
Определить оптимальный план
производства продукции, при котором
общая прибыль предприятия будет
максимальной.

4.

хj – количество выпускаемой продукции j-го вида
n
∑ сj хj - общая прибыль предприятия
j =1
n
∑ aij хj - суммарный расход i-го ресурса
j =1
Математическая модель задачи:
F c1x1 c2 x2 ... cn xn max
a11 x1 a12 x2 ... a1n xn b1
a x a x ... a x b
22 2
2n n
2
21 1
....................................
am1x1 am 2 x2 ... amn xn bm
x j 0, i 1, ..., n

5.

Общая постановка задачи
линейного программирования
Найти экстремум (максимум или минимум) линейной
целевой функции при заданных линейных ограничениях и
условии неотрицательности переменных:
n
F c j x j max (min)
j 1
n
aij x j bi , i 1,..., k ;
j 1
n
aij x j bi , i k 1,..., l ;
j 1
n
aij x j bi , i l 1,..., m;
j 1
x j 0, j 1,..., n.

6.

Если система ограничений содержит только неравенства ≤ ,
то ЗЛП называется стандартной, если только равенства –
канонической.
Приведение к каноническому виду:
∑ aij x j ≤ bi
∑ aij x j ≥ bi
j
j
xn+i = bi
∑ aij x j ≥ 0
xn+i = ∑ aij x j
bi ≥ 0
j
j
∑ aij x j + xn+i = bi
∑ aij x j
j
j
xn+i = bi

7.

Графическое решение ЗЛП
F c1x1 c2 x2 max
ai1x1 ai 2 x2 bi , i 1,...,m
x1 0, x2 0
ai1 x1 + ai 2 x2 ≤ bi - полуплоскость
Выпуклое
множество:
x(1) , x( 2) X
[0; 1]
x x(1) (1 ) x( 2) X
1. Полуплоскость – выпуклое множество
2. Пересечение выпуклых множеств – выпуклое множество
Область допустимых решений ЗЛП – выпуклое множество

8.

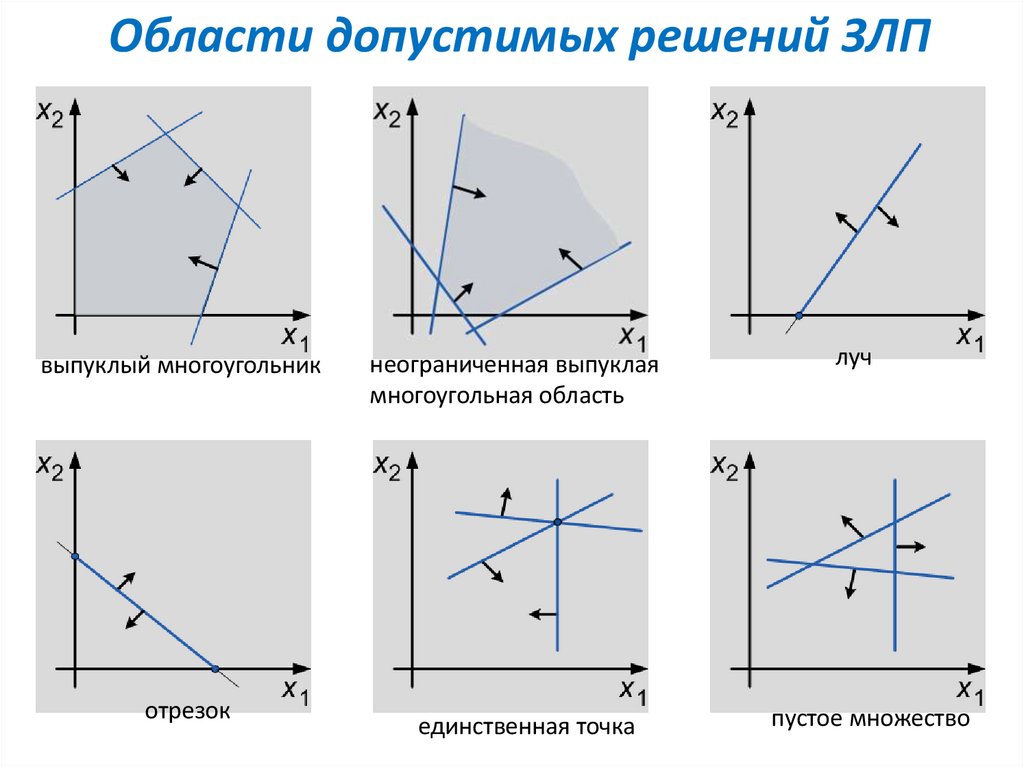
Области допустимых решений ЗЛП
выпуклый многоугольник
отрезок
неограниченная выпуклая
многоугольная область
луч
единственная точка
пустое множество

9.

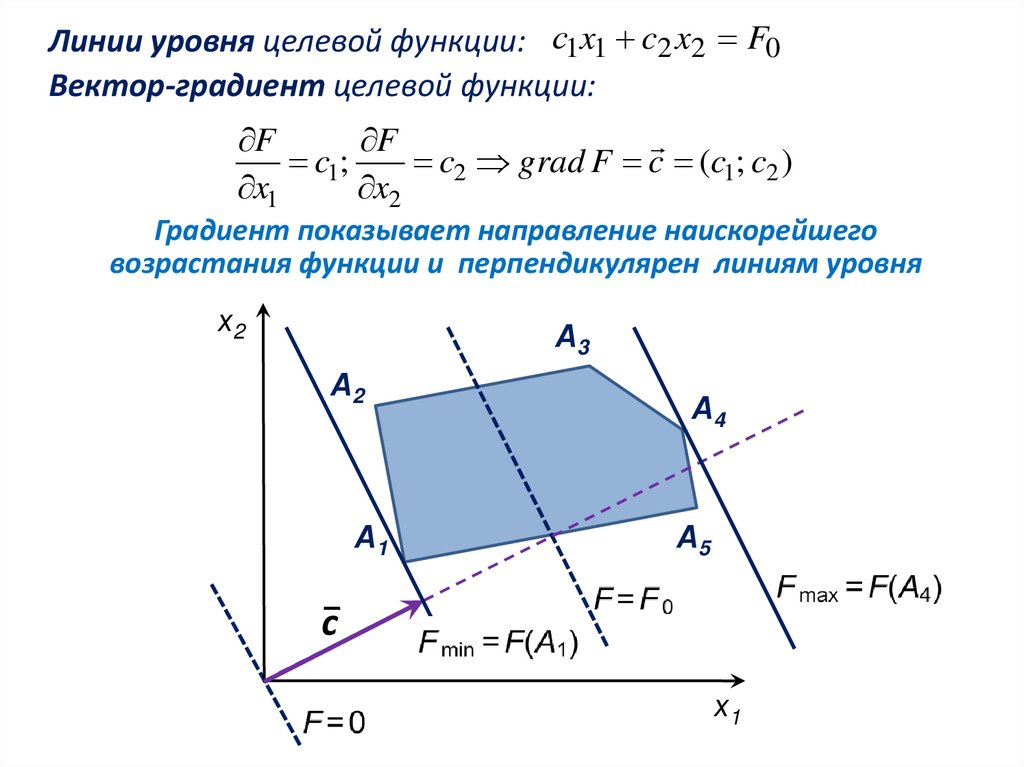
Линии уровня целевой функции: с1x1 c2 x2 F0
Вектор-градиент целевой функции:
F
F
c1;
c2 grad F c (c1; c2 )
x1
x2
Градиент показывает направление наискорейшего
возрастания функции и перпендикулярен линиям уровня
х2
А3
А2
А1
А4
А5
с
х1

10.

Алгоритм графического решения ЗЛП
1. Строим область допустимых решений .
Если область пуста, ЗЛП решений не имеет.
Если область состоит из единственной точки, то это и будет
оптимальное решение.
2. Строим вектор-градиент.
3. Проводим произвольную линию уровня перпендикулярно
градиенту.
4. При решении задачи на максимум перемещаем линию
уровня в направлении градиента так, чтобы она касалась
области допустимых решений в ее крайнем положении
(крайней точке).
В случае решения задачи на минимум линию уровня перемещают
в антиградиентном направлении.
5. Определяем оптимальный план Х* и экстремальное
значение целевой функции F*=f(X*).

11.

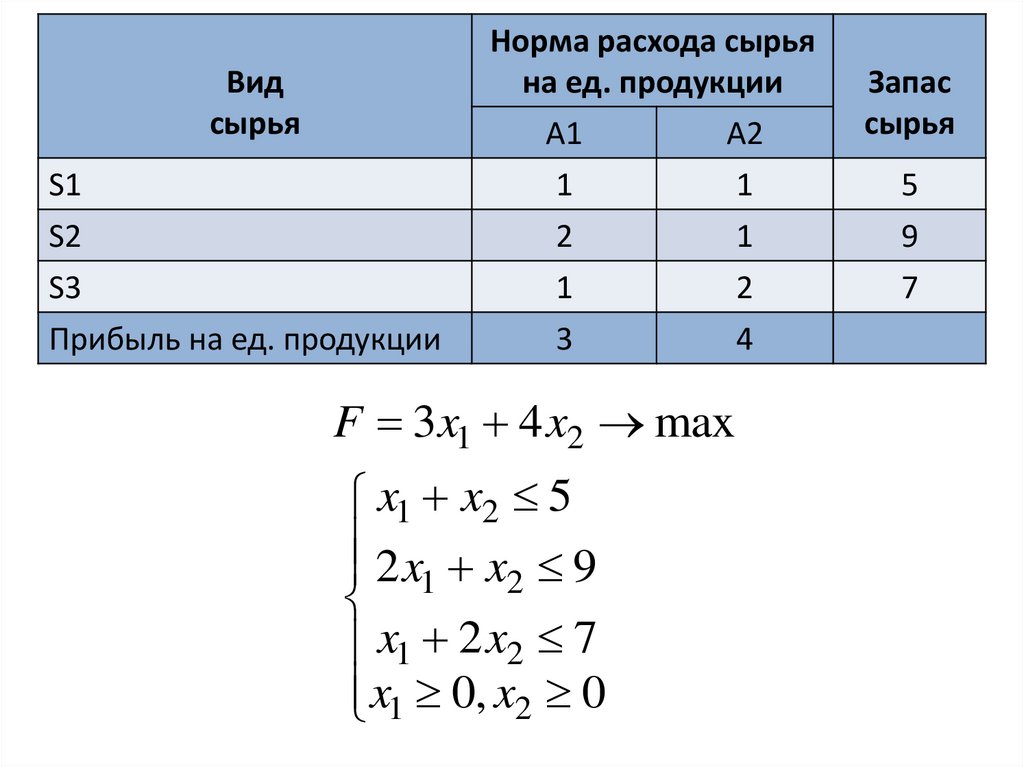
Норма расхода сырья
на ед. продукции
Вид
сырья
S1
S2
А1
1
2
А2
1
1
S3
Прибыль на ед. продукции
1
3
2
4
F 3x1 4 x2 max
x1 x2 5
2 x1 x2 9
x1 2 x2 7
x1 0, x2 0
Запас
сырья
5
9
7

12.

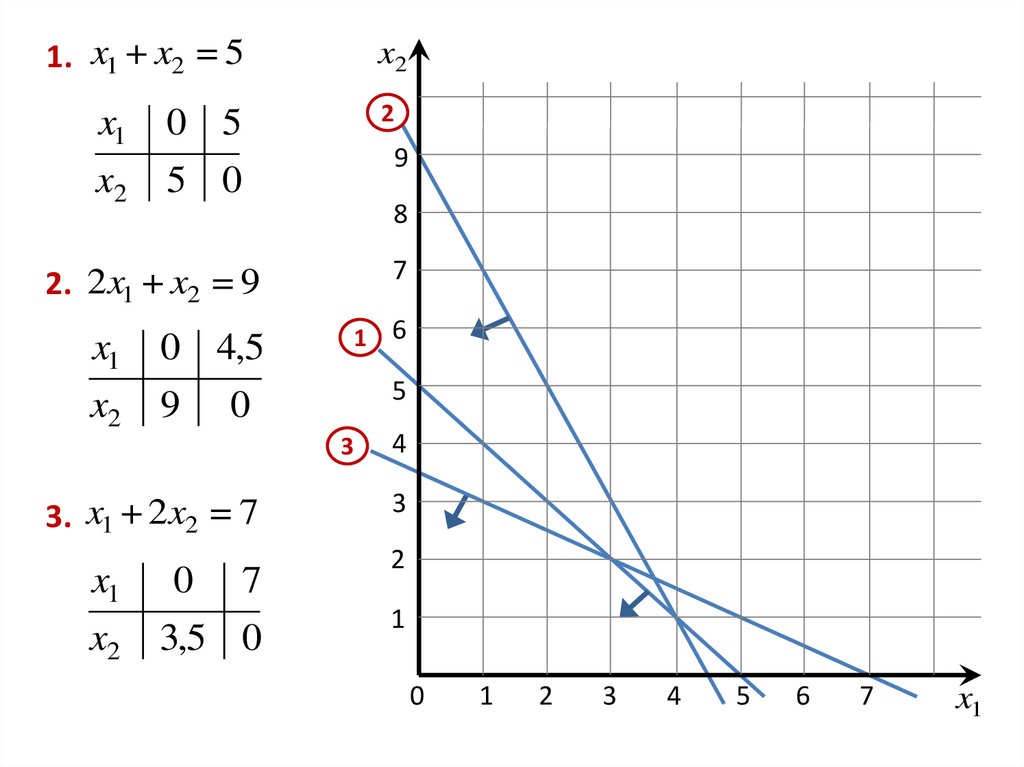
1. x1 + x2 = 5
x1
x2
x2
2
0 5
5 0
9
8
7
2. 2 x1 + x2 = 9
x1
x2
0 4,5
9 0
1 6
5
3
3. x1 + 2 x2 = 7
x1
x2
0 7
3,5 0
4
3
2
1
0
1
2
3
4
5
6
7
x1

13.

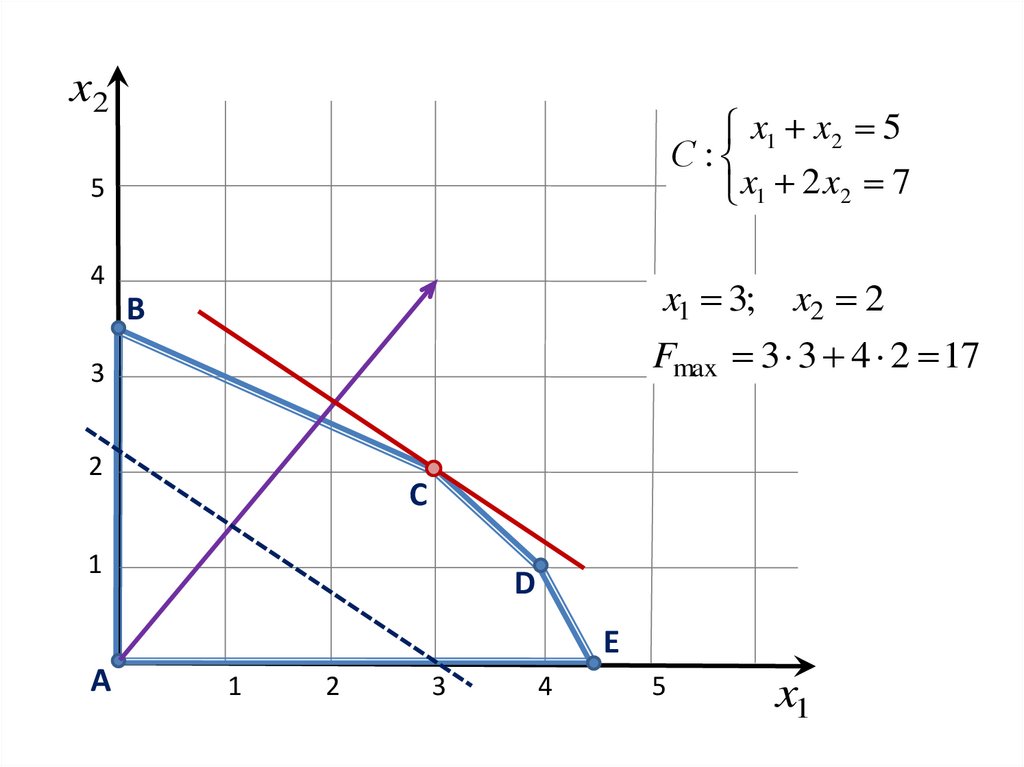
x2
x1 x2 5
С :
x1 2 x2 7
5
4
x1 3;
B
x2 2
Fmax 3 3 4 2 17
3
2
C
1
D
E
A
1
2
3
4
5
x1

14.

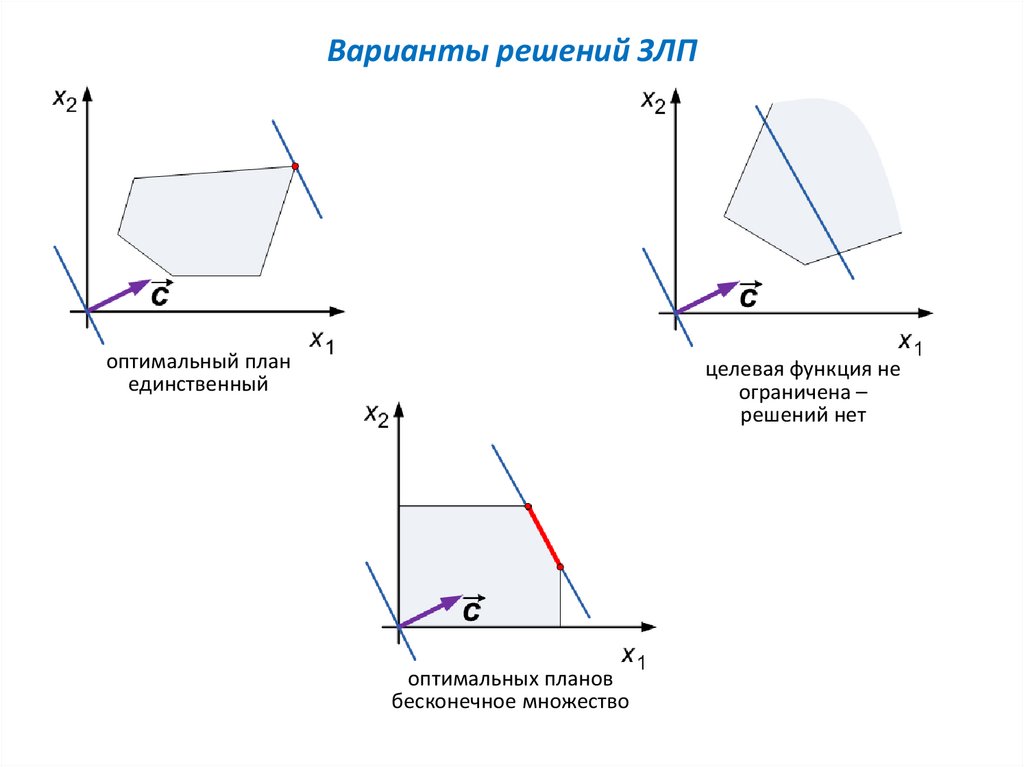
Варианты решений ЗЛП
оптимальный план
единственный
целевая функция не
ограничена –
решений нет
оптимальных планов
бесконечное множество

15.

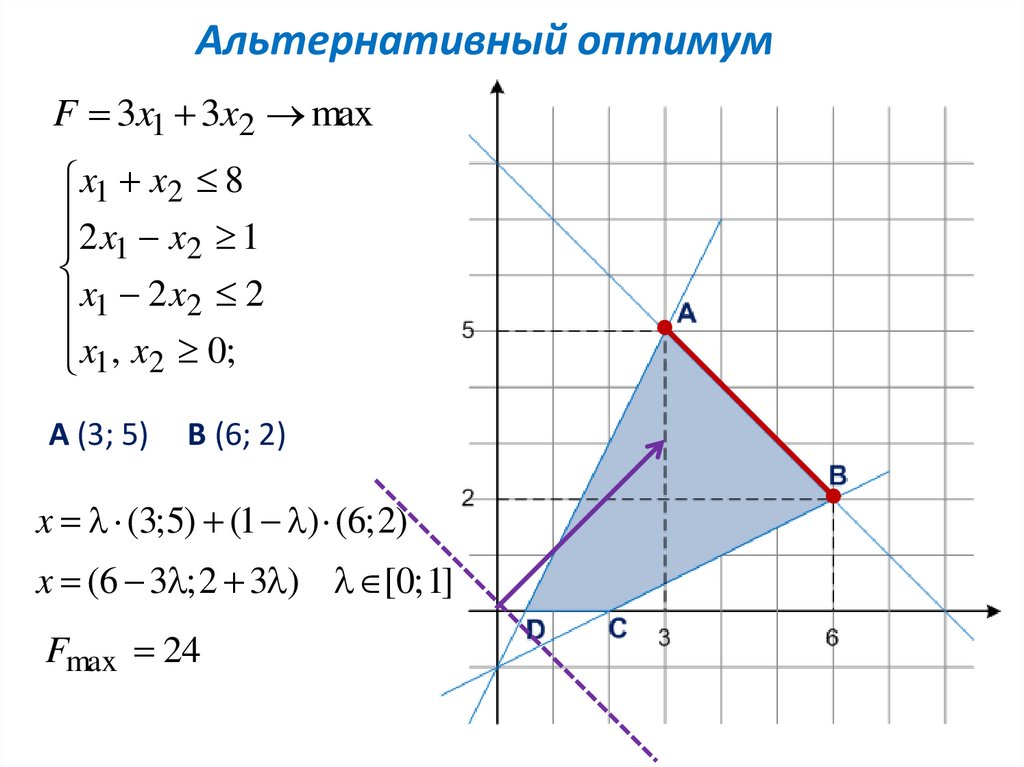
Альтернативный оптимум
F 3x1 3x2 max
x1 x2 8
2 x x 1
1 2
x1 2 x2 2
x1, x2 0;
А (3; 5)
В (6; 2)
x (3; 5) (1 ) (6; 2)
x (6 3 ; 2 3 ) [0; 1]
Fmax 24

16.

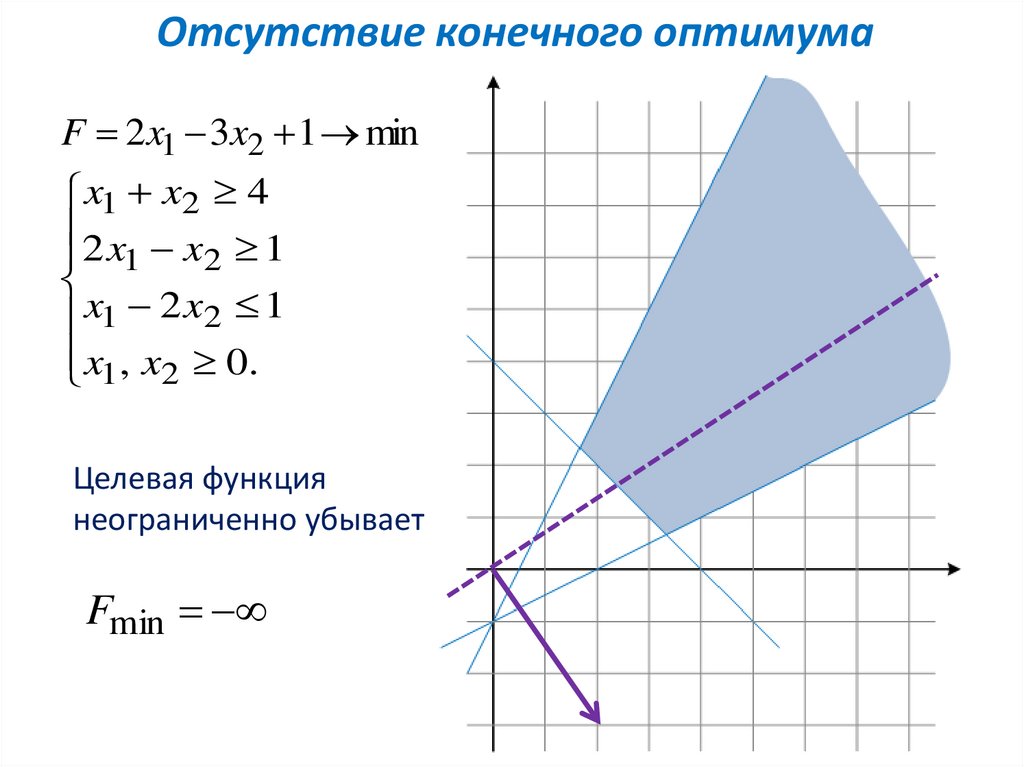
Отсутствие конечного оптимума
F 2x1 3x2 1 min
x1 x2 4
2 x x 1
1
2
x1 2 x2 1
x1, x2 0.
Целевая функция
неограниченно убывает
Fmin

17.

Графические методы анализа
модели на устойчивость
На сколько могут быть увеличены запасы
дефицитных ресурсов для улучшения оптимального
решения при сохранении общей структуры решения?
На сколько могут быть снижены запасы
недефицитных ресурсов при сохранении
оптимальности полученного решения?
Какие дефицитные ресурсы следует увеличивать в
первую очередь?
Каковы пределы изменения коэффициентов
целевой функции, при которых не происходит
изменения оптимального решения?

18.

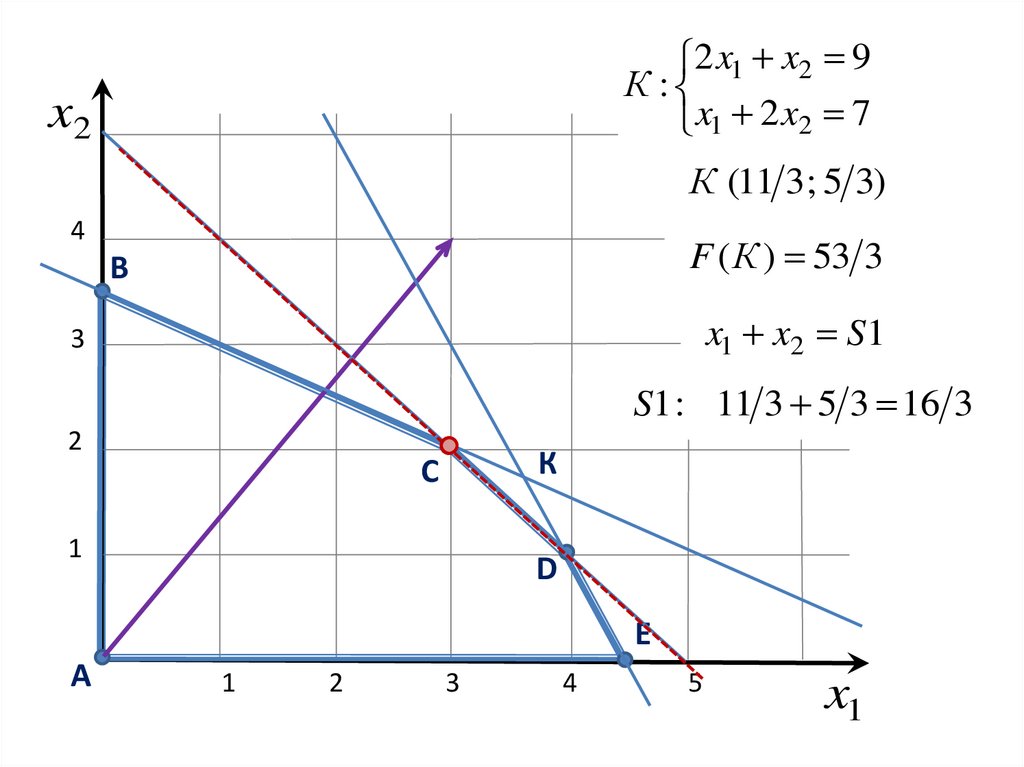
2 x1 x2 9
К :
x1 2 x2 7
x2
К (11 3; 5 3)
4
F ( К ) 53 3
B
x1 x2 S1
3
S1 : 11 3 5 3 16 3
2
К
C
1
D
E
A
1
2
3
4
5
x1

19.

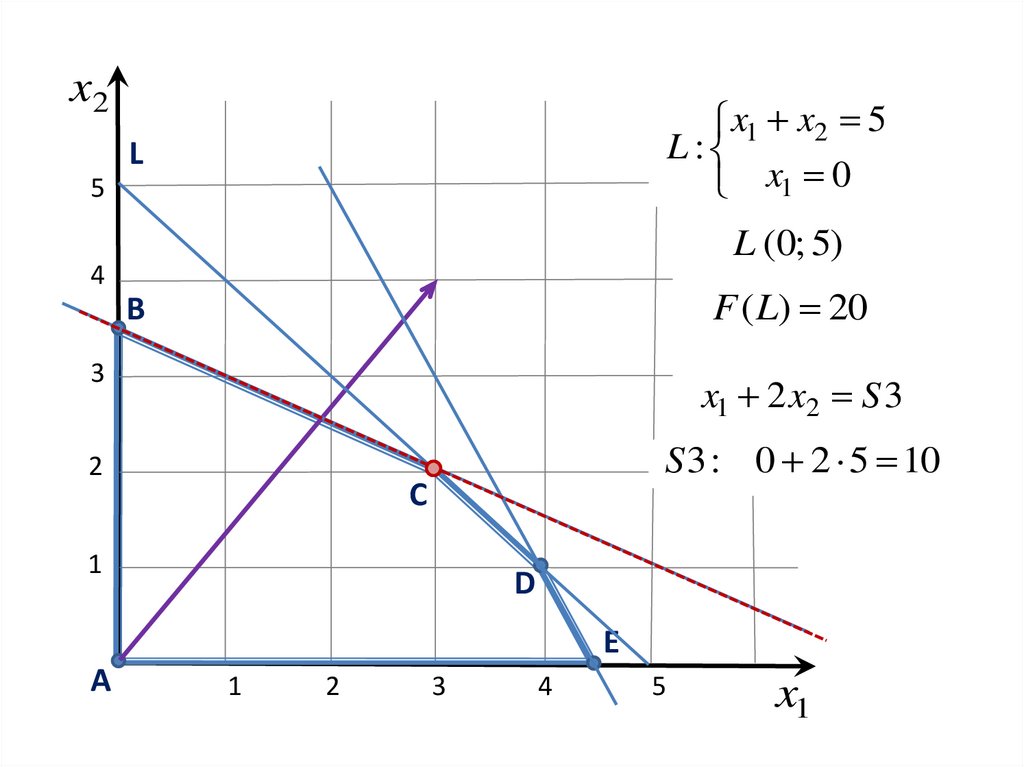
x2
x1 x2 5
L:
x1 0
L
5
L (0; 5)
4
F ( L) 20
B
3
x1 2 x2 S 3
2
S 3 : 0 2 5 10
C
1
D
E
A
1
2
3
4
5
x1

20.

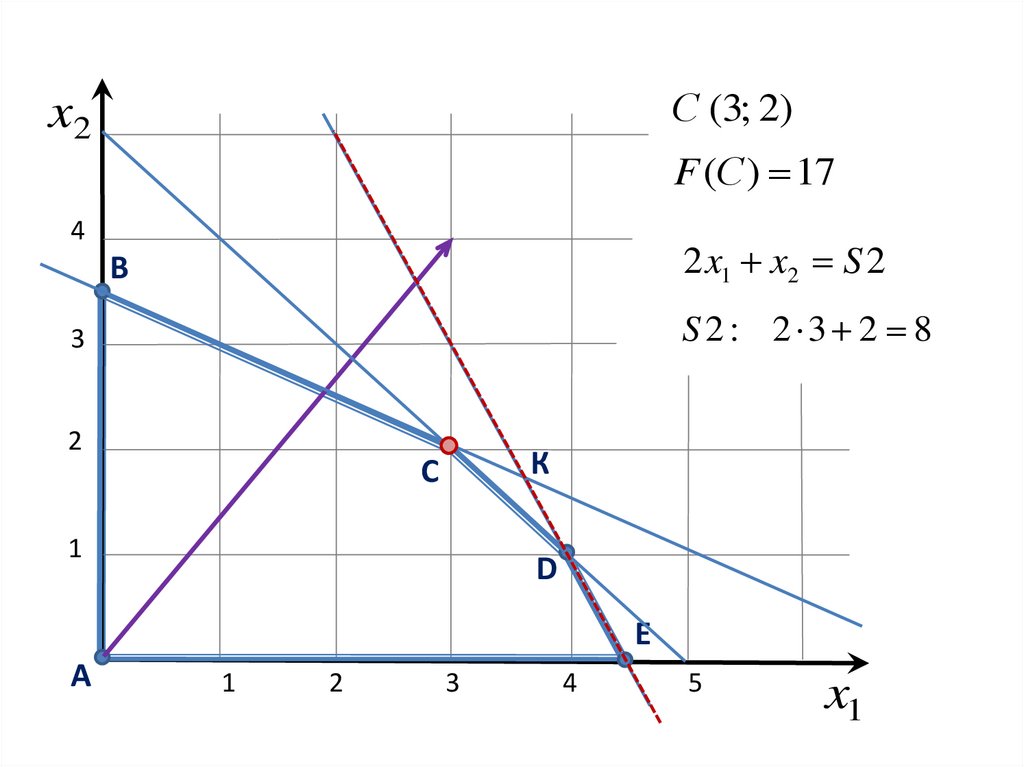
С (3; 2)
x2
F (С ) 17
4
2 x1 x2 S 2
B
S2 : 2 3 2 8
3
2
К
C
1
D
E
A
1
2
3
4
5
x1

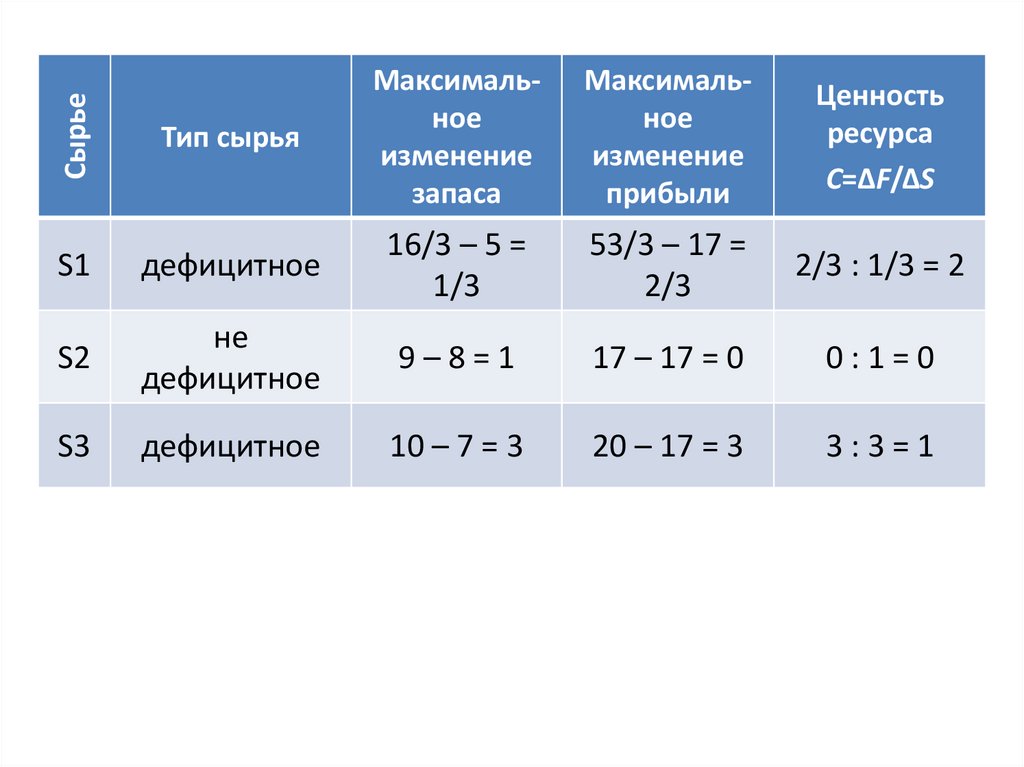
21.

Сырье
Тип сырья
Максимальное
изменение
запаса
Максимальное
изменение
прибыли
Ценность
ресурса
C=ΔF/ΔS
S1
дефицитное
16/3 – 5 =
1/3
53/3 – 17 =
2/3
2/3 : 1/3 = 2
S2
не
дефицитное
9–8=1
17 – 17 = 0
0:1=0
S3
дефицитное
10 – 7 = 3
20 – 17 = 3
3:3=1

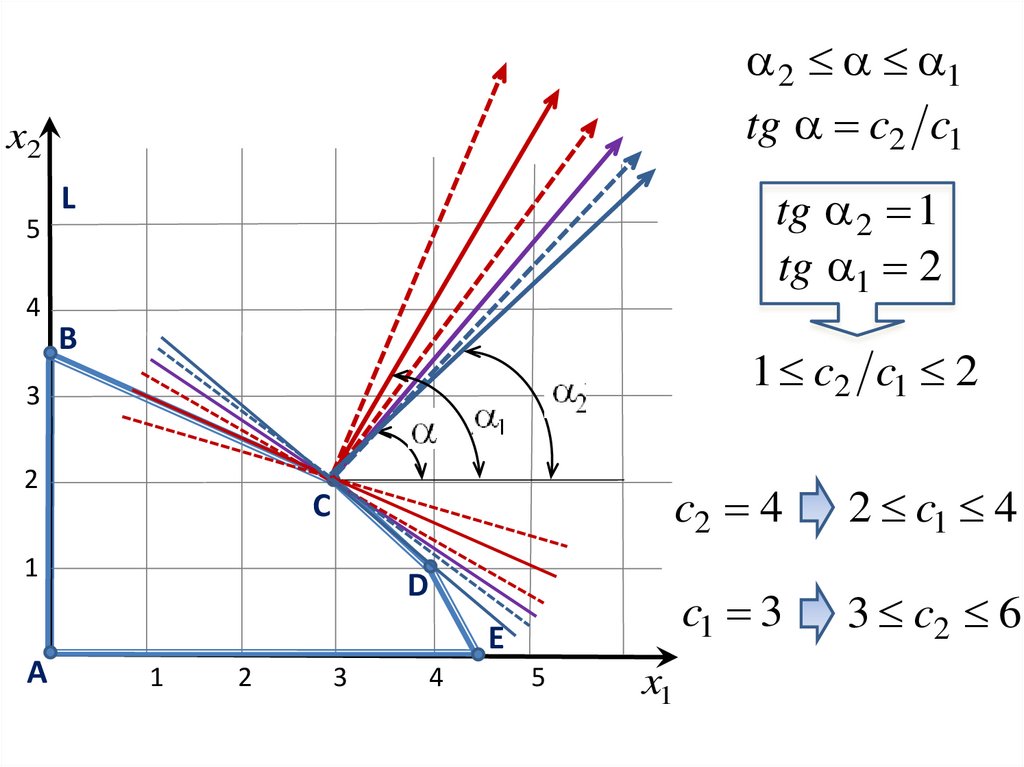
22.

2 1
tg c2 c1
x2
5
4
L
tg 2 1
tg 1 2
B
1 c2 c1 2
3
2
C
1
D
E
A
1
2
3
4
5
x1
c2 4
2 c1 4
c1 3
3 c2 6