л 2-1 матрицы

1.

Дисциплина «МАТЕМАТИКА»
Элементы линейной алгебры
Матрицы. Операции над матрицами

2.

Результаты текущей успеваемости 1 года обучения
за сентябрь
месяц
Учебные
вопросы
1. Определение и классификация матриц.
2. Операции над матрицами.
3. Обратная матрица.

3.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
Определение. Таблица чисел, состоящая из m строк
и n столбцов называется
матрицей размера m n
Числа, из которых матрица составлена, называются
элементами матрицы.
a11
a21
A
.
am1
a12 ... a1n a11 a12 ... a1n
a22 ... a2 n a21 a22 ... a2 n
.
.
.
.
.
.
.
am 2 ... amn am1 am 2 ... amn
a11
a
21
.
am1
a12 ... a1n
a22 ... a2 n
aij
.
.
.
am 2 ... amn

4.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
Классификация матриц
1. Прямоугольная матрица
a11 a12 ... a1n
a21 a22 ... a2 n
A
.
.
.
.
.
am1 am 2 ... amn
Например:
1 5 7 0
A 4 3 2 9 ;
5 1 4 8
2 4 5
;
В
6 8 9
2
С .
6

5.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
2. Квадратная матрица
a11
a
A 21
.
an1
a12 ... a1n
a22 ... a2 n
.
.
.
.
an 2 ... ann
Например:
5 0
;
A
6 2
0 5 12
В 3 4 7 ;
5 9 2
1 0
3
6
С
3 7
0 5
5 4
8 9
.
2 1
8 1

6.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
3. Матрица-строка
Например:
a12
A 2 4 7 9 0 ;
4. Матриц – столбец
Например:
A a11
2
5
A .
7
8
a11
a21
A a31 .
a
n1
a13 ... a1n .

7.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
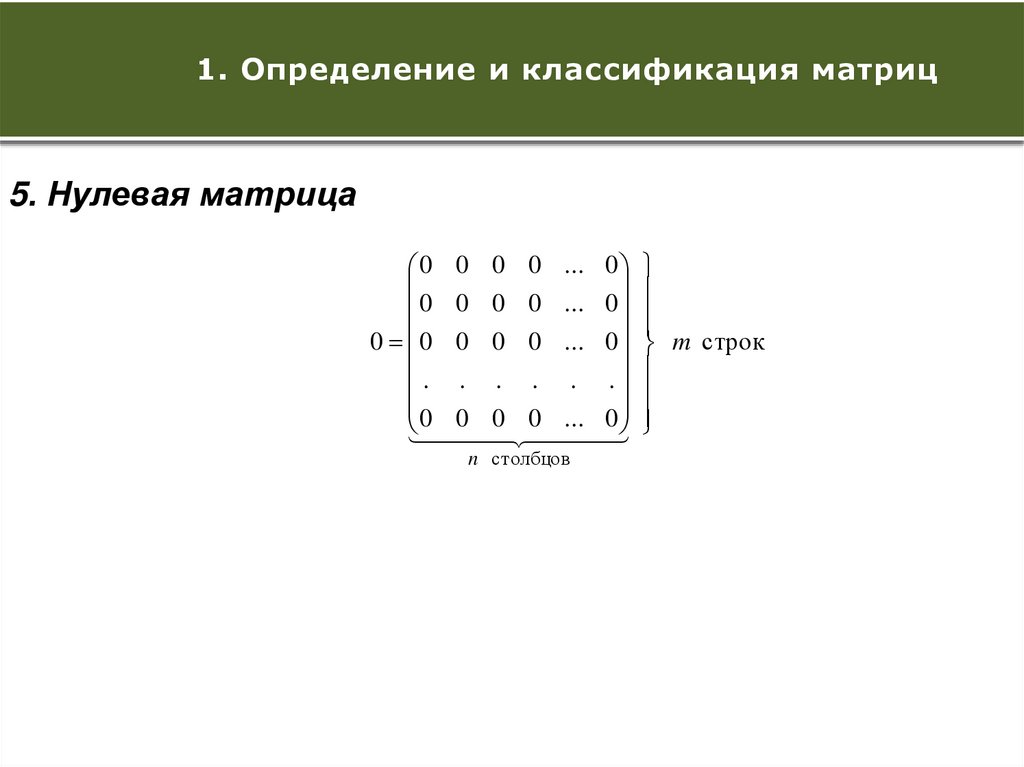
5. Нулевая матрица
0 0 0 0 ... 0
0
0
0
0
...
0
0 0 0 0 0 ... 0 m строк
. . . . . .
0 0 0 0 ... 0
n столбцов

8.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
6. Диагональная матрица
a11
0
A 0
.
0
0
0
a22
0
0
a33
.
0
.
0
0
... 0
... 0 .
.
.
... ann
...
Например:
9 0
;
A
0 7
3 0 0
В 0 2 0 .
0 0 1

9.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
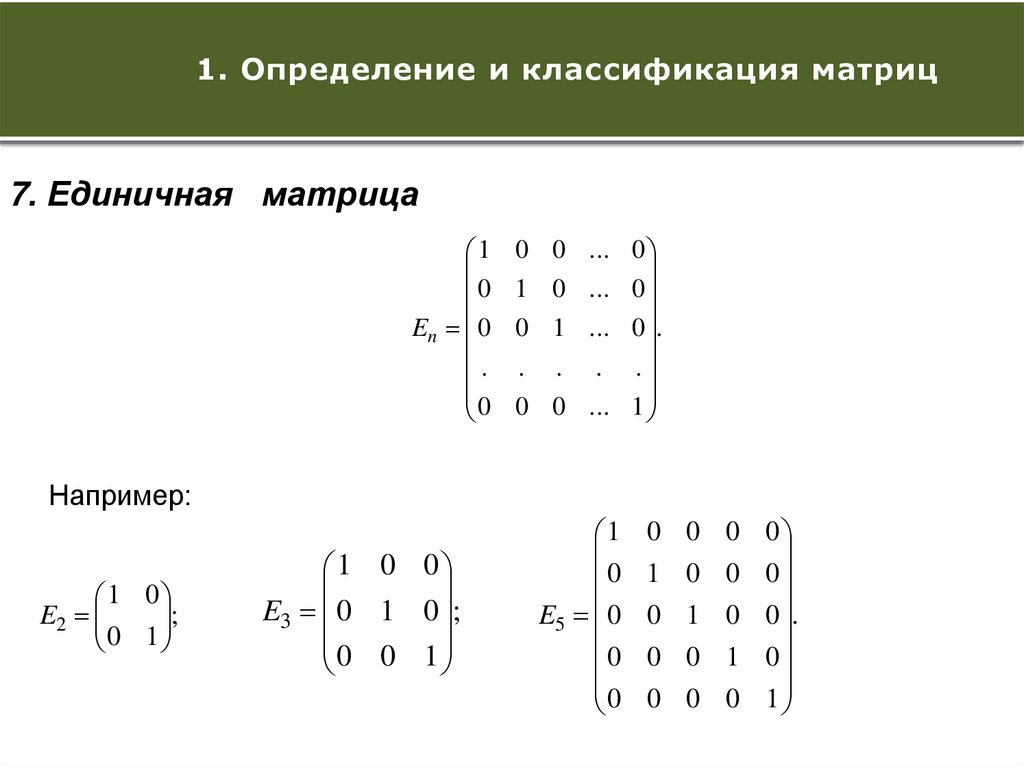
7. Единичная матрица
1
0
En 0
.
0
0 0 ... 0
1 0 ... 0
0 1 ... 0 .
. . . .
0 0 ... 1
Например:
1 0
;
E2
0 1
1 0 0
E3 0 1 0 ;
0 0 1
1
0
E5 0
0
0
0 0 0 0
1 0 0 0
0 1 0 0 .
0 0 1 0
0 0 0 1

10.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
8. Верхняя треугольная матрица
a11
0
A 0
.
0
Например:
1
0
A
0
0
a12
a13
a22
0
a23
a33
.
0
.
0
2 3
5 6
0 4
0 0
4
7
8
5
... a1n
... a2 n
... a3n .
.
.
... ann

11.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
9. Нижняя треугольная матрица
a11 0
a21 a22
A a31 a32
.
.
a
n1 an 2
Например:
2 0 0
A 5 4 0 .
3 8 6
0
0
a33
.
an3
0
... 0
... 0 .
.
.
... ann
...

12.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
Транспонирование матриц
Если в матрице A поменять местами строки и столбцы, то
получится новая матрица, которая по сравнению с матрицей A
называется транспонированной.
Транспонированная матрица обозначается АТ.
a11
a 21
A
.
a m1
a12
a 22
.
am2
... a1n
... a 2 n
.
.
... a mn
Например:
1 2 8 6
A
3 6 7 5
a11
a
AT 12
.
a1n
a21 ... am1
a22 ... am 2
.
.
.
.
a2 n ... amn
3
1
2 6
AT
.
8
7
6 5

13.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
Классификация матриц
1. Прямоугольная матрица
2. Квадратная матрица
3. Матрица-строка
4. Матриц – столбец
5. Нулевая матрица
6. Диагональная матрица
7. Единичная матрица
8. Верхняя треугольная матрица
9. Нижняя треугольная матрица

14.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
Вывод.
Понятие матрицы как таблицы из чисел или элементов
различной природы является одним из основных
математических понятий, имеющих широкую область
приложений.

15.

Количество проведенных
2. Операции
матрицами
контрольныхнад
проверок
Операции над матрицами
линейные операции
нелинейные операции
сложение (вычитание) матриц,
произведение матриц,
умножение матриц на число,
возведение матрицы в целую
положительную степень.
линейная комбинация матриц.

16.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
Равные матрицы
Если
то
a11
A
a21
A B
a12
,
a22
тогда, когда
b11 b12
,
B
b21 b22
a11 b11 ,
a12 b12 ,
a21 b21 ,
a22 b22 .

17.

Количество проведенных
2. Операции
матрицами
контрольныхнад
проверок
Линейные операции над матрицами
1. Сложение (вычитание) матриц.
Суммой двух матриц
Ат п а ij
называется матрица
Ст п c ij ,
сij aij bij
Вт п b ij
и
i 1, т,
такая, что
j 1, п
Свойства:
1) А+В=В+А
(коммутативность);
2) (А+В) + С = А+ (В+С) = А+В+С
(ассоциативность).

18.

Количество проведенных
2. Операции
матрицами
контрольныхнад
проверок
Линейные операции над матрицами
2. Умножение на число.
Произведением матрицы
называется матрица
Вт п b ij
Ат п а ij
такая, что
на число
b ij a ij
i 1, т,
λ
j 1, п .
Свойства:
1) λ ∙ (μ ∙А) = (λ ∙ μ) ∙А
(ассоциативность);
2) λ ∙ (А+В) = λ ∙А +λ ∙В (дистрибутивность относительно
сложения матриц);
3) (λ+μ)∙А = λ ∙А+μ ∙А
(дистрибутивность относительно
сложения чисел ).

19.

Количество проведенных
2. Операции
матрицами
контрольныхнад
проверок
Линейные операции над матрицами
3. Линейная комбинация матриц.
Пример.
Найти линейную комбинацию матриц 2А+3В, где
1 2 3
,
A
0 1 1
2 3 0
.
В
2 1 1

20.

Количество проведенных
2. Операции
матрицами
контрольныхнад
проверок
Элементарные преобразования матриц:
- перестановка местами двух столбцов (строк) матрицы;
- умножение всех элементов столбца (строки) на число,
отличное от нуля;
- прибавление ко всем элементам столбца (строки) матрицы
соответствующих элементов столбца (строки), умноженных на
одно и то же число.
Определение.
Две матрицы А и В называются эквивалентными, если одна из них
получается из другой с помощью элементарных преобразований.
Обозначение: А~В.

21.

Количество проведенных
2. Операции
матрицами
контрольныхнад
проверок
Нелинейные операции над матрицами
1. Произведение матриц.
Определение.
Две матрицы
Ат п
и
Вn p
называются согласованными, если число столбцов матрицы А
совпадает с числом строк матрицы В.
Определение.
Матрицы для которых выполняется условие
перестановочными.
А∙В=В∙А, называются

22.

Количество проведенных
2. Операции
матрицами
контрольныхнад
проверок
Нелинейные операции над матрицами
Свойства:
1) (А ∙ В) ∙ С = А ∙ (В ∙ С) = А ∙ В ∙ С (ассоциативность);
2) (А + В) ∙ С = А ∙ С + В ∙ С
(дистрибутивность);
3) А ∙ (В + С) = А ∙ С + В ∙ С
(дистрибутивность);
4) А ∙ В ≠ В ∙ А;
5) А ∙Е = Е ∙ А = А,
А ∙ 0 = 0 ∙ А = 0;
6) (А ∙ В)Т = ВТ ∙ АТ, (А + В)Т = АТ + ВТ.

23.

Количество проведенных
2. Операции
матрицами
контрольныхнад
проверок
Нелинейные операции над матрицами
Пример.
Найти произведение матриц
2 1
A 0 3 ,
4 2
А∙В
1 3 4
В
0 6 5

24.

Количество проведенных
2. Операции
матрицами
контрольныхнад
проверок
Нелинейные операции над матрицами
2. Возведение матрицы в степень.
Целая неотрицательная степень матрицы определяется равенством
An А А ... А Аn 1 А А Аn 1.
Свойства:
Пример.
п раз
1)
A0 1;
2)
A p Aq A p q .
Найти
n
A
для матрицы
1 1
.
A
0 1

25.

Количество проведенных
2. Операции
матрицами
контрольныхнад
проверок
Выводы по вопросу:
1. Линейные операции над матрицами: умножение матрицы на число и
сложение нескольких матриц проводятся аналогично соответствующим
операциям над числами.
2. В отличие от произведения чисел произведение двух матриц не
обладает свойством коммутативности (переместительному закону) и,
более того, не всегда возможно.
3. Умножение единичной матрицы на матрицу той же размерности
обладает свойством коммутативности и выполняется так же, как
умножение на обычную единицу.

26.

Количество проведенных
3. Обратная
матрица
контрольных
проверок
Определение.
Матрица А-1 называется обратной матрице А, если выполняется условие:
A A 1 A 1 A E
где Е – единичная матрица того же порядка, что и матрица А.
Свойства:
1) (А ∙ В)-1=В -1∙А -1;
2) (А -1)Т= (АТ) -1.
Определение.
Матрица А называется ортогональной, если выполняется условие
А∙АТ=Е, или АТ=А- 1.
Пример.
1
1
2
Проверить, является ли матрица
обратной матрице
2 1 1
2
3 1
.
4 2

27.

Результаты текущей успеваемости 1 года обучения
за сентябрь
месяц
Учебные
вопросы
1. Определение и классификация матриц.
2. Операции над матрицами.
3. Обратная матрица.

28.

Количество проведенных
1. Определение
и классификация
матриц
контрольных
проверок
Классификация матриц
1. Прямоугольная матрица
2. Квадратная матрица
3. Матрица-строка
4. Матриц – столбец
5. Нулевая матрица
6. Диагональная матрица
7. Единичная матрица
8. Верхняя треугольная матрица
9. Нижняя треугольная матрица

29.

Количество проведенных
2. Операции
матрицами
контрольныхнад
проверок
Операции над матрицами
линейные операции
нелинейные операции
сложение (вычитание) матриц,
произведение матриц,
умножение матриц на число,
возведение матрицы в целую
положительную степень.
линейная комбинация матриц.

30.

Количество проведенных
3. Обратная
матрица
контрольных
проверок
Матрица А-1 называется обратной матрице А, если выполняется условие:
A A 1 A 1 A E
где Е – единичная матрица того же порядка, что и матрица А.