Линейная алгебра. Введение

1. Линейная алгебра

Лекция 1
Введение

2. Контакты

Лектор:
Контакты
Фаизова Анна Андреевна,
ассистент каф. Управления рисками и
страхования
[email protected]
[email protected]
Введение
2

3. ОСНОВНЫЕ РАЗДЕЛЫ КУРСА

• Матрицы. Определители. Обратные
матрицы
• Системы линейных уравнений
• Векторы
• Базисы и размерность
• Примеры экономических приложений
Введение
3

4. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Основная
• З.И.Боревич. Определители и матрицы.М.2004.
• Н.Ш.Кремер. Высшая математика для
экономистов. Москва. 1997.
• Д.К.Фаддеев. Лекции по алгебре.Наука.М.1984.
• Учебные и контрольные задания по математике
(высшая алгебра). Изд. ЭСФ СПбГУ. 2005.
Дополнительная
• Н.А.Вавилов, В.Г.Халин. «MATHEMATICA 5.* для
нематематика.» Выпуски 1 и 2. СПб.: ОЦЭиМ,
2005.экономике. М. 2002.
Введение
4

5. КОНТРОЛЬ ЗНАНИЙ И НАВЫКОВ

1. Письменные контрольные работы (1 и 2).
2. Индивидуальные контрольные задания.
Введение
5

6. ЭКЗАМЕН

• Теоретическая часть: знание всех определений и
формулировок;
• Практическая часть: навыки решения задач,
предусмотренных программой.
Использование пособий, учебников, конспектов и
технических устройств не допускается.
Введение
6

7. КРИТЕРИИ ОЦЕНКИ

• Экзамен письменный. 10 заданий: 5 теоретических
вопросов и 5 задач. Каждый оценивается из 7
баллов - итого 70 баллов
• Правильное выполнение индивидуальных
3 контрольных заданий –10 баллов (5 работ по 2
балла каждая)
• Письменные контрольные работы – 20 баллов (по
10 баллов каждая)
Дополнительно:
Активность на практических занятиях, решение задач
повышенной сложности, выполнение домашних
заданий
Введение
7

8. ШКАЛА ОЦЕНОК

«отлично» (A) – 90-100 баллов,
«очень хорошо» (B) – 80-89 баллов,
«хорошо» (C) – 70-79 баллов,
«удовлетворительно» (D) –60-69 баллов,
«посредственно» (E) – 50-59 баллов,
«неудовлетворительно» (F) – менее 50
баллов

9. Линейная алгебра

Лекция 1
Матрицы. Действия над
матрицами

10. ПЛАН ЛЕКЦИИ

Матрицы.
Матрицы специального вида.
Операции над матрицами:
сложение матриц;
умножение матрицы на число;
умножение матриц;
транспонирование матриц.
25.06.2018
Свойства операций над матрицами.
Матрицы
10

11. МАТРИЦЫ. Пример.

Определение
МАТРИЦЫ. Пример.
Матрицей размера m х n называется прямоугольная таблица из
чисел
a ij
i 1, 2, ... , m ,
(элементов матрицы),
a1 1
a2 1
A
...
a
m1
a1 2
a2 2
...
am 2
j 1, 2, ... , n ,
... a1n
... a2 n
... ...
... amn
Обозначения:
A aij
A aij
Примеры
1 2
1,2 2,25 0,5
1,5
A 3 2 ; B 30 6,7 2 ; C 2 ; D 1 2 0 1 .
0 1
0,4 0,22 1
3,3
Матрицы
11

12. КВАДРАТНАЯ МАТРИЦА

Определение
Если число столбцов матрицы равно числу строк (m=n),
то матрица называется квадратной.
Примеры.
1,2
B 30
0,4
2,25
6,7
0,22
0,5
2 ;
1
Матрицы специального вида
1 0
E
0 1
12

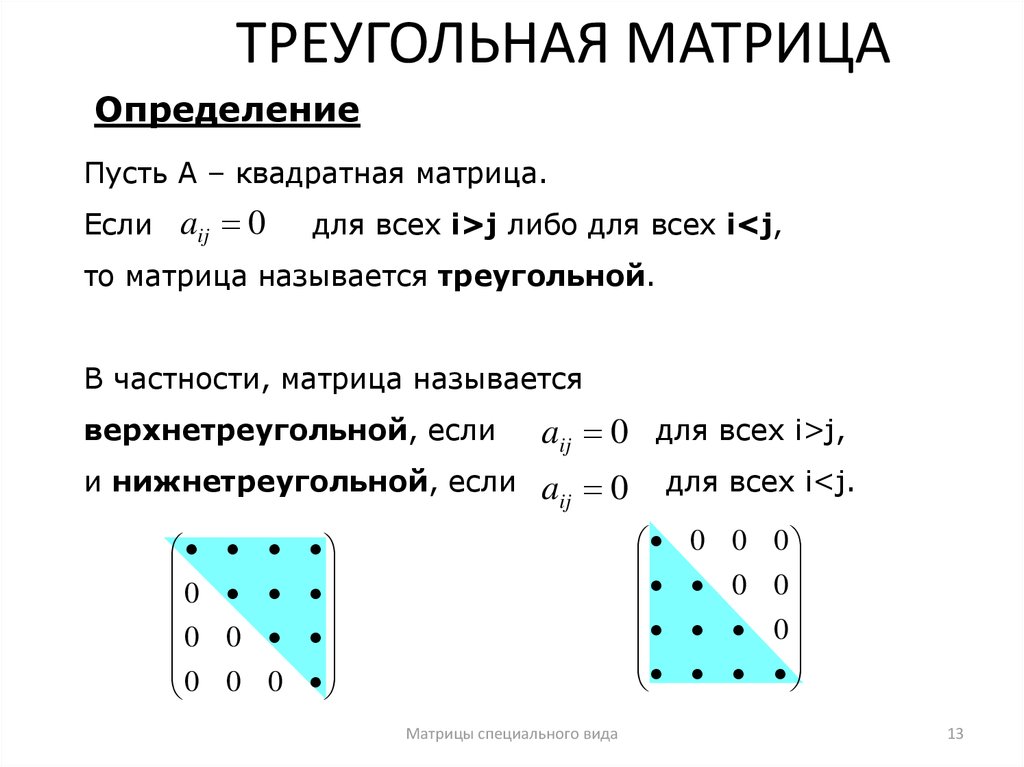
13. ТРЕУГОЛЬНАЯ МАТРИЦА

Определение
Пусть А – квадратная матрица.
Если
aij 0
для всех i>j либо для всех i<j,
то матрица называется треугольной.
В частности, матрица называется
верхнетреугольной, если
aij 0 для всех i>j,
и нижнетреугольной, если
aij 0
0
0
0
для всех i<j.
0
0 0
Матрицы специального вида
0 0 0
0 0
0
13

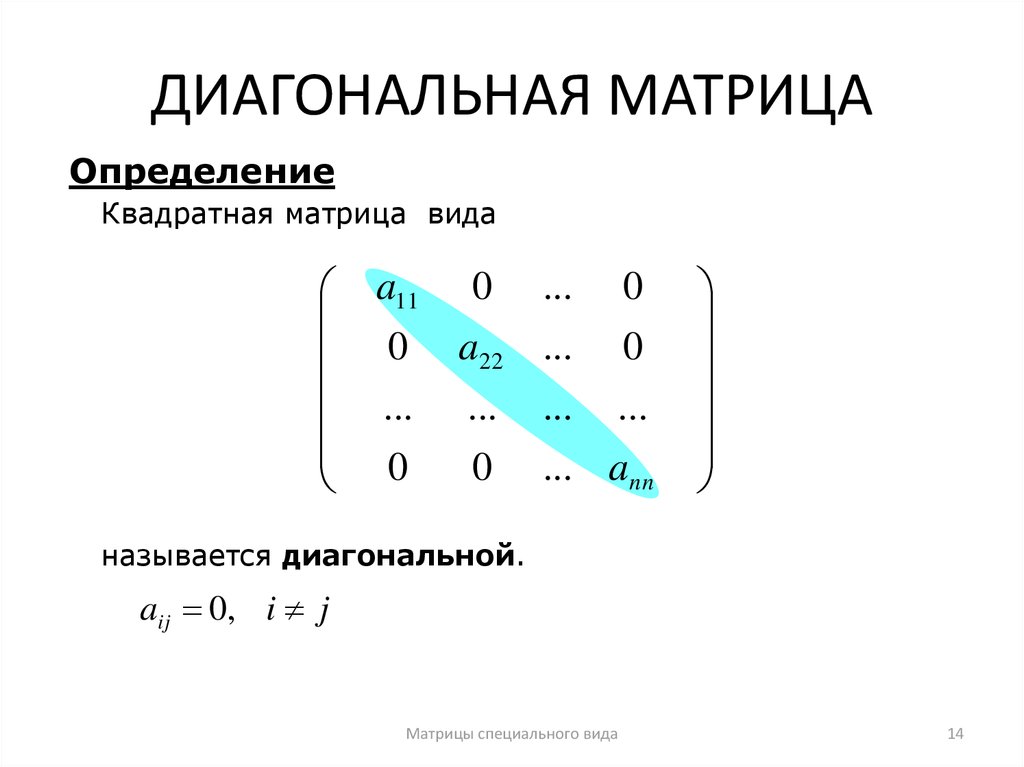
14. ДИАГОНАЛЬНАЯ МАТРИЦА

Определение
Квадратная матрица вида
a11
0
...
0
0
a22 ...
0
...
...
...
...
0
0
... ann
называется диагональной.
aij 0, i j
Матрицы специального вида
14

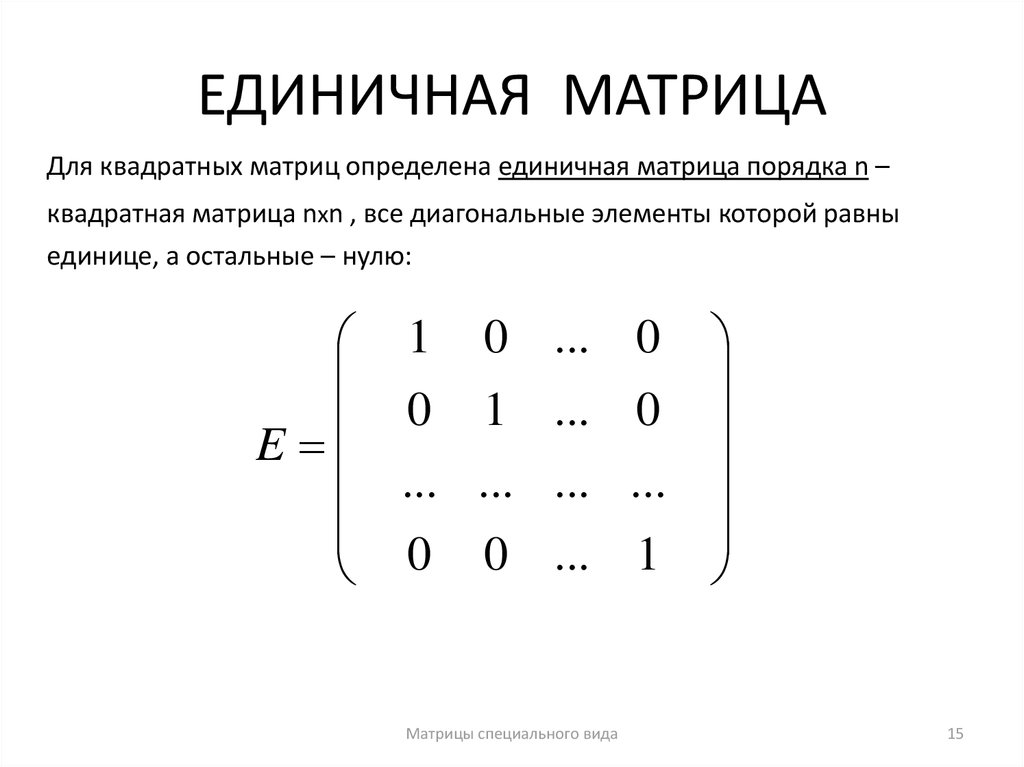
15. ЕДИНИЧНАЯ МАТРИЦА

Для квадратных матриц определена единичная матрица порядка n –
квадратная матрица nxn , все диагональные элементы которой равны
единице, а остальные – нулю:
1 0
0 1
E
... ...
0 0
... 0
... ...
... 1
... 0
Матрицы специального вида
15

16. СИММЕТРИЧЕСКАЯ МАТРИЦА

Определение.
Пусть A – квадратная матрица.
Если
aij a ji
, то матрица называется симметрической.
Примеры
2 1 5
1 3 6 ;
5 6 4
1
0
0
0
0 0 0
1 0 0
.
0 1 0
0 0 1
Матрицы специального вида
16

17. СЛОЖЕНИЕ МАТРИЦ

Суммой
A+B
матриц размера mхn A aij и B bij
называется матрица C cij того же размера, каждый элемент которой
равен сумме соответственных элементов матриц A и B :
i 1,2,..., m ,
j 1,2,..., n ,
cij aij bij ,
Пример
1 2 0
3 5 0,5
A 3 6 2 ; B 0 7 2 ;
4 0 1
4 2
1
Операции над матрицами
4 7 0,5
A B 3 1 4
8 2
2
17

18. УМНОЖЕНИЕ ЧИСЛА НА МАТРИЦУ

Произведением A числа и матрицы A a
ij
называется матрица B bij , получающаяся из матрицы A
умножением всех ее элементов на
:
bij aij ,
Пример
i 1,2,..., m ,
j 1,2,..., n ,
1 2 0
3 6 0
A 3 6 2 ; 3 A 9 18 6
4 0 1
12 0 3
25.06.2018
Операции над матрицами
18

19. УМНОЖЕНИЕ МАТРИЦ

Произведением АВ матрицы A aij
и матрицы B bij
размера mхn
размера nхk называется
матрица C cij
размера mхk , элемент которой
равен сумме произведений соответственных
элементов i-ой строки матрицы A и j-го столбца
n
матрицы B :
Пример
cij aisbsj ,
s 1
i 1, 2, ..., m ,
j 1, 2, ..., k .
2 1
1 1 0
; B 0 3 ;
A
2 1 2
1 2
Операции над матрицами
cij
2 4
AB
6 3
19

20. НЕКОММУТАТИВНОСТЬ УМНОЖЕНИЯ МАТРИЦ

Для матриц, вообще говоря,
АВ ≠ ВА
Пример:
2 1 1 1 3 1
1 1 2 1 1 1
;
3 2 1 1 5 1
1 1 3 2 5 3
3 1 1 1
5 1 5 3
Если АВ = ВА, матрицы А и В называются
коммутирующими.
25.06.2018
Свойства операций над матрицами
20

21. СВОЙСТВА ОПЕРАЦИЙ НАД МАТРИЦАМИ

1) А+В = В+А
2) (A+B)+C = A+(B+C)
3) λ(A+B) = λA+λB
4) A(B+C) = AB + AC
5) (A+B)C = AC + BC
6) λ(AB)=(λA)B=A(λB)
7) А(ВС)=(АВ)С
25.06.2018
Свойства операций над матрицами
21

22. СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ

Для любой квадратной матрицы А выполнено:
АЕ = ЕА = А
Пример:
1 2 3 1 0 0 1 2 3
0 7 2 0 1 0 0 7 2
2 9 4 0 0 1 2 9 4
1 0 0 1 2 3 1 2 3
0 1 0 0 7 2 0 7 2
0 0 1 2 9 4 2 9 4
25.06.2018
Матрицы
22

23. ТРАНСПОНИРОВАНИЕ МАТРИЦ

a11
a21
A
...
a
m1
am 2
a11
a12
A
...
a
1n
a21 ... am1
a22 ... am 2
... ... ...
a2 n ... amn
a12
a22
...
a1n
... a2 n
... ...
... amn
...
A - матрица размера m x n
- матрица размера n x m ,
называется
транспонированной
для
A
T
Обозначения: ' , .
Операции над матрицами
23

24. НЕКОТОРЫЕ СВОЙСТВА ОПЕРАЦИИ ТРАНСПОНИРОВАНИЯ МАТРИЦ

Α'' (A')' Α
(Α Β)' Β Α
Свойства операций над матрицами
24