Преобразование графиков тригонометрических функций

Содержание

y = f(x) + b Параллельный перенос вдоль оси ординат

y = f(x + a) Параллельный перенос вдоль оси ординат

y = mf(x), где m>1 Растяжение от оси х с коэффициентом m

y = mf(x), где 0<m<1 Сжатие к оси х с коэффициентом 1/m

y = mf(x), где m=-1 Преобразование симметрии относительно оси х

y = mf(x), где m<0

y = f(kx), где k>1 Сжатие к оси у с коэффициентом k

y = f(kx), где 0<k<1 Растяжение от оси у с коэффициентом 1/k

y = f(kx), где k=-1 Преобразование симметрии относительно оси y

y = f(kx), где k<0

Построить графики функций

Составить аналитическую запись функции по её графику

Составить аналитическую запись функции по её графику

Составить аналитическую запись функции по её графику

Составить аналитическую запись функции по её графику

Самостоятельная работа

литература

Преобразование графиков тригонометрических функций

Содержание

y = f(x) + b Параллельный перенос вдоль оси ординат

y = f(x + a) Параллельный перенос вдоль оси ординат

y = mf(x), где m>1 Растяжение от оси х с коэффициентом m

y = mf(x), где 0<m<1 Сжатие к оси х с коэффициентом 1/m

y = mf(x), где m=-1 Преобразование симметрии относительно оси х

y = mf(x), где m<0

y = f(kx), где k>1 Сжатие к оси у с коэффициентом k

y = f(kx), где 0<k<1 Растяжение от оси у с коэффициентом 1/k

y = f(kx), где k=-1 Преобразование симметрии относительно оси y

y = f(kx), где k<0

Построить графики функций

Составить аналитическую запись функции по её графику

Составить аналитическую запись функции по её графику

Составить аналитическую запись функции по её графику

Составить аналитическую запись функции по её графику

Самостоятельная работа

литература

963.69K

Похожие презентации:

Построение графиков функций с помощью сдвигов и деформаций

Построение графиков функций с помощью сдвигов и деформаций

Предел функции на бесконечности. (10 класс)

Предел функции на бесконечности. (10 класс)

Дробно-линейная функция и ее график

Построение графиков квадратичной функции, содержащей модуль

Построение графиков квадратичной функции, содержащей модуль

Преобразования графика функции f(x)=x2

Преобразования графика функции f(x)=x2

Преобразование графиков тригонометрических функций

Логарифмическая функция, её свойства и график

Логарифмическая функция, её свойства и график

Функция y=ах2+bx+c, ее свойства и график

Функция y=ах2+bx+c, ее свойства и график

Предел функции в точке

Предел функции в точке

Преобразование графиков тригонометрических функций

Преобразование графиков тригонометрических функций

545937_545894_trigonometriya_funkc

1. Преобразование графиков тригонометрических функций

Малыш Наталья Юрьевна,
учитель математики и информатики
МАОУ «СОШ № 24», г. Сыктывкар
Преобразование графиков
тригонометрических функций

2. Содержание

Теория
Как построить график функции y = f(x) + b
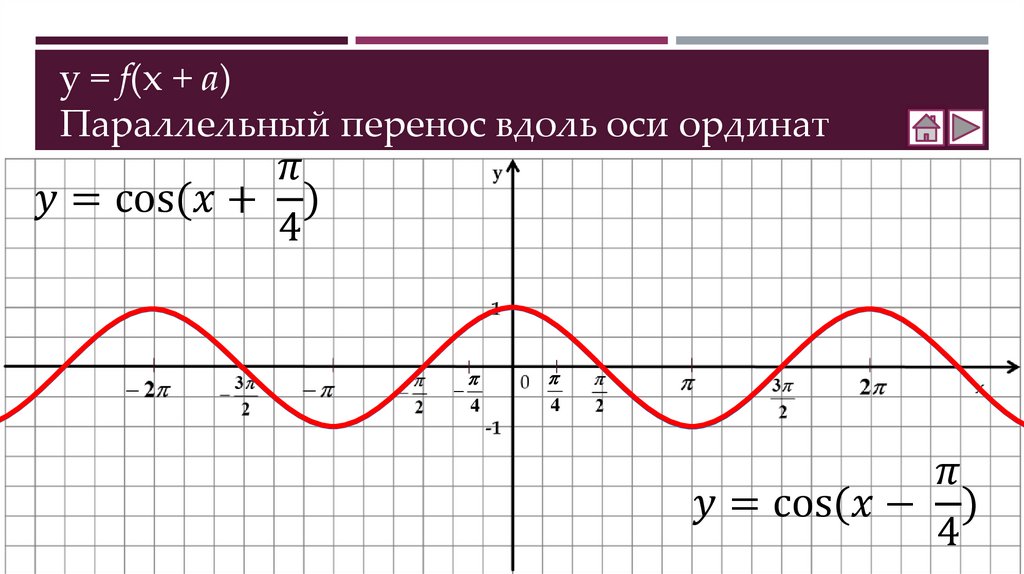
Как построить график функции y = f(x + a)
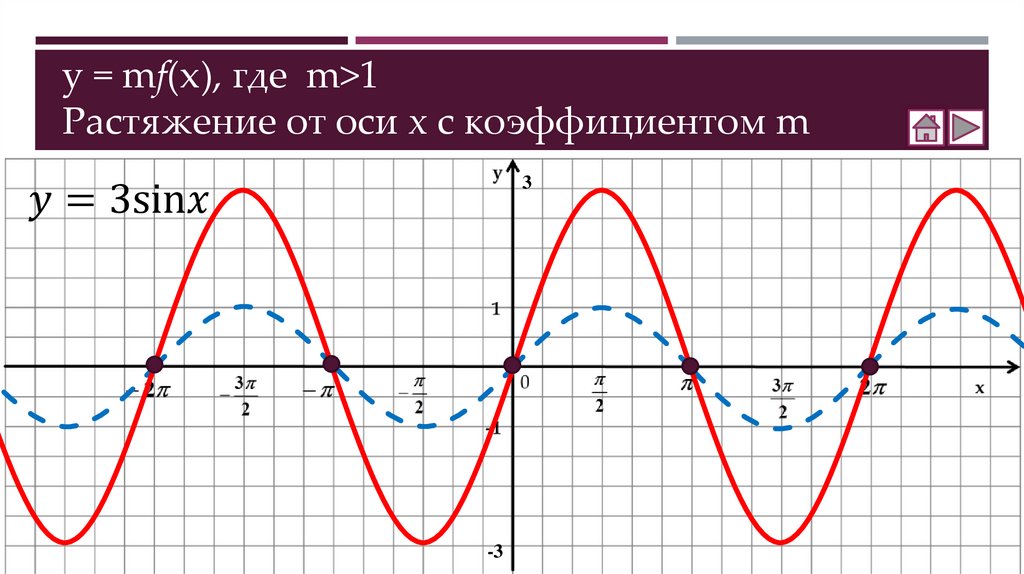
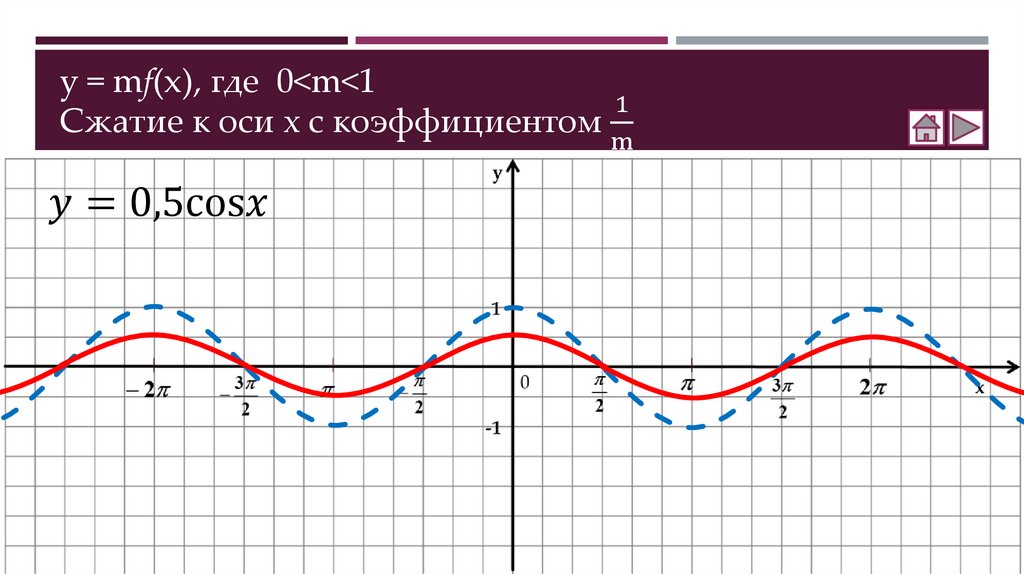
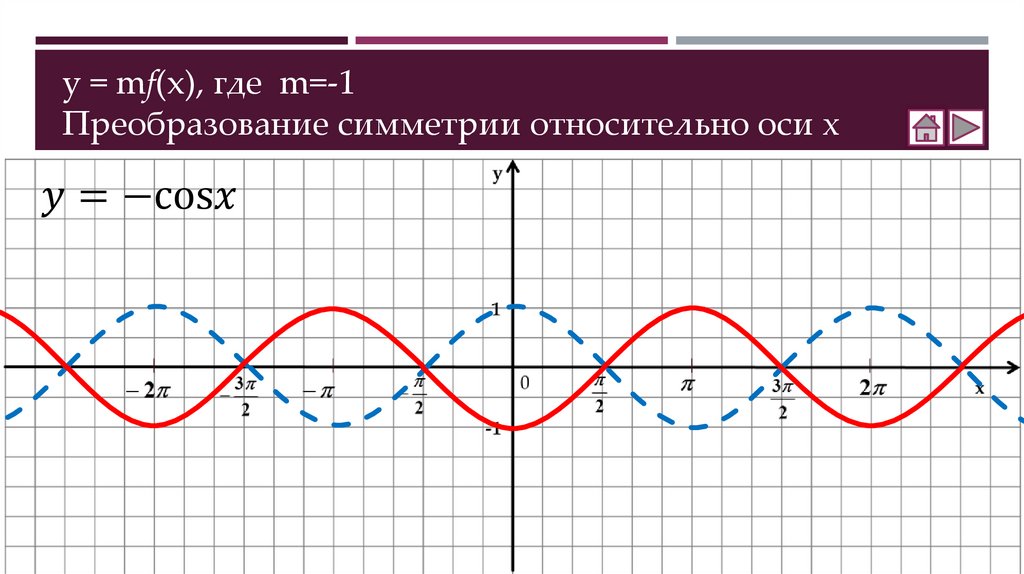
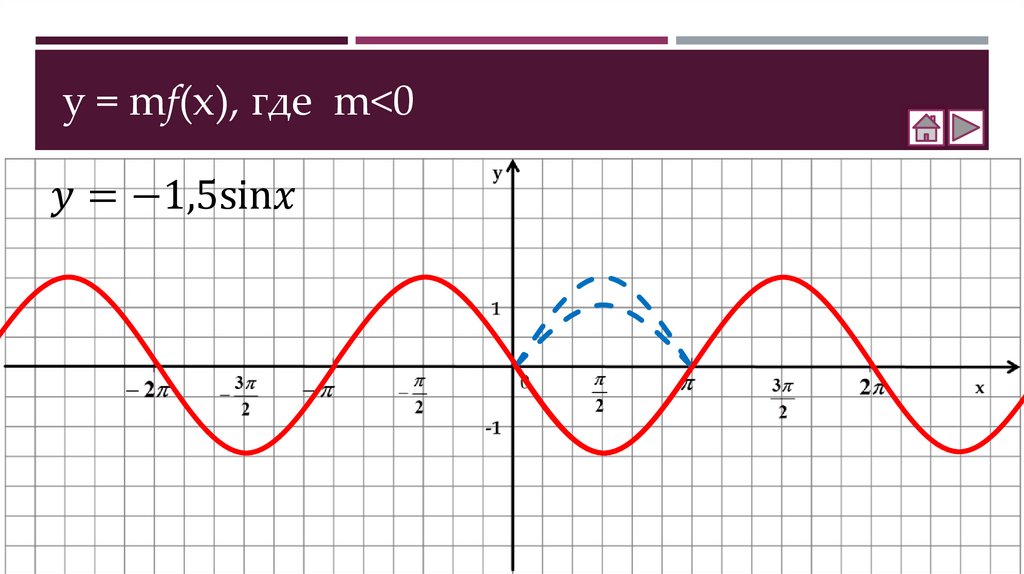
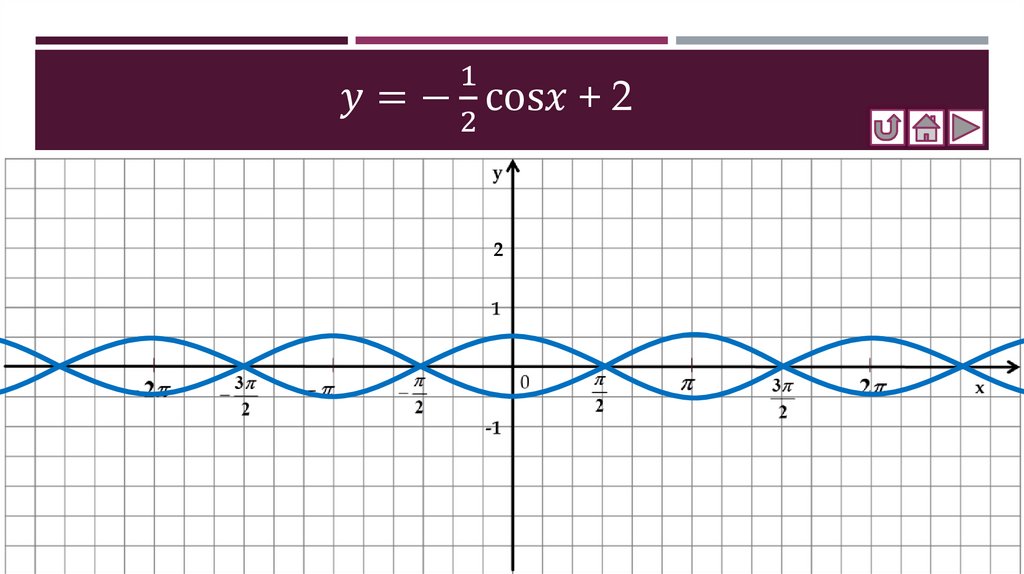
Как построить график функции y = mf(x)
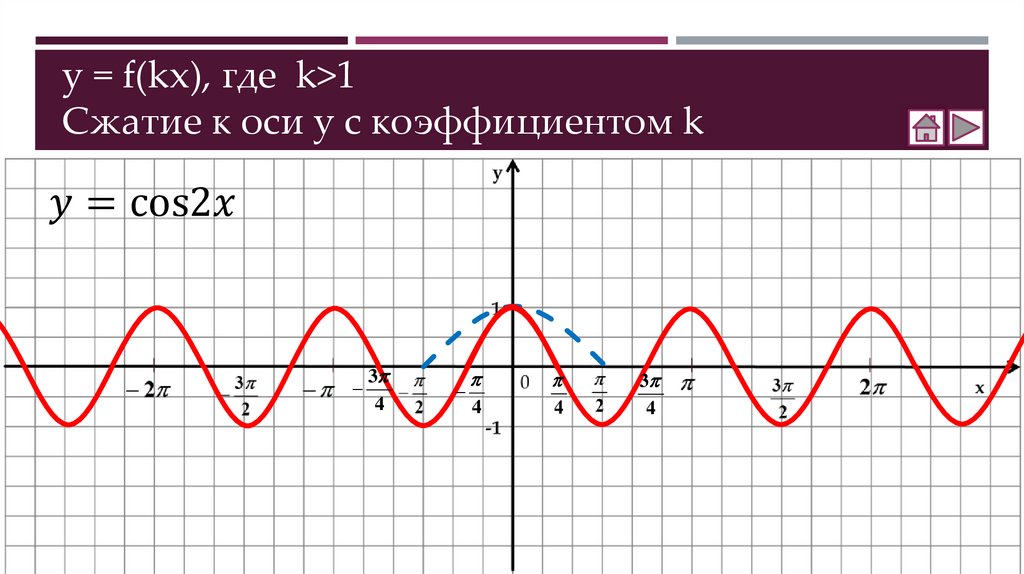
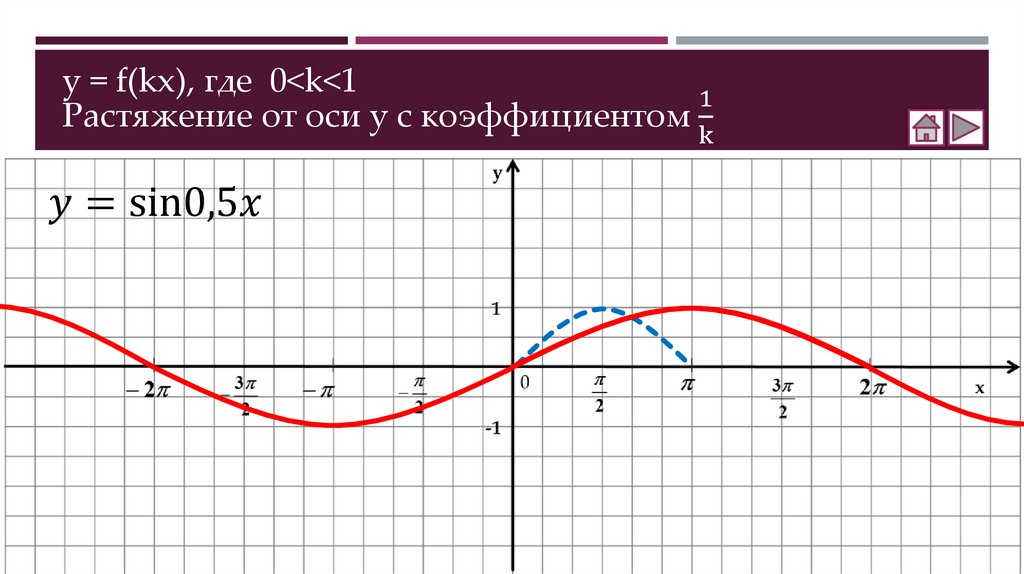
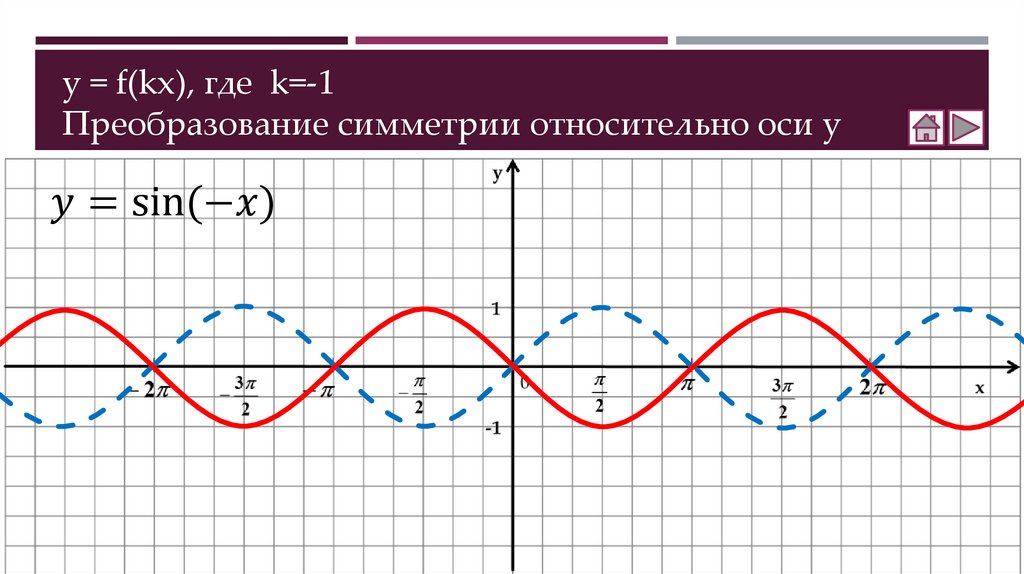
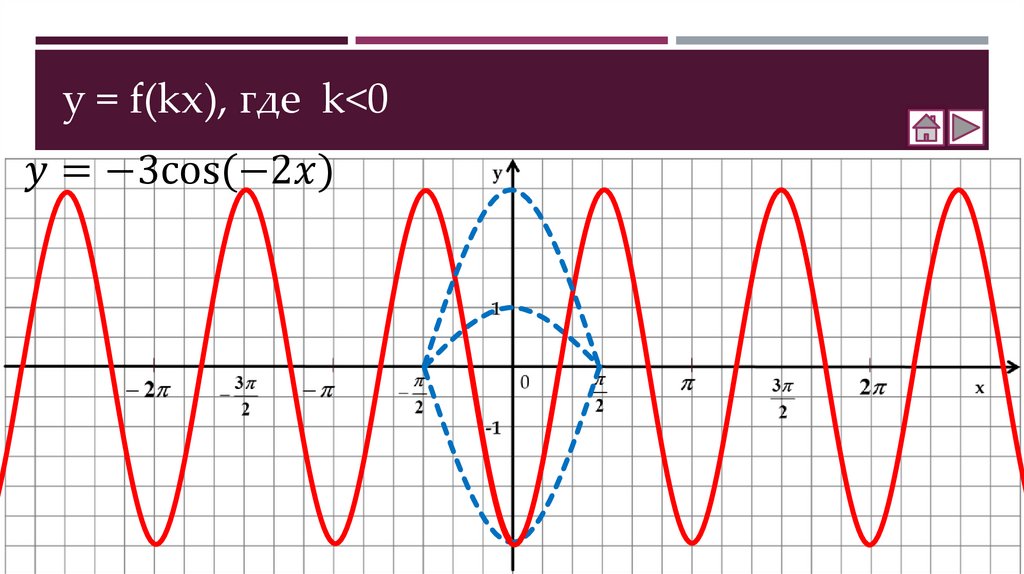
Как построить график функции y = f(kx)
Практика
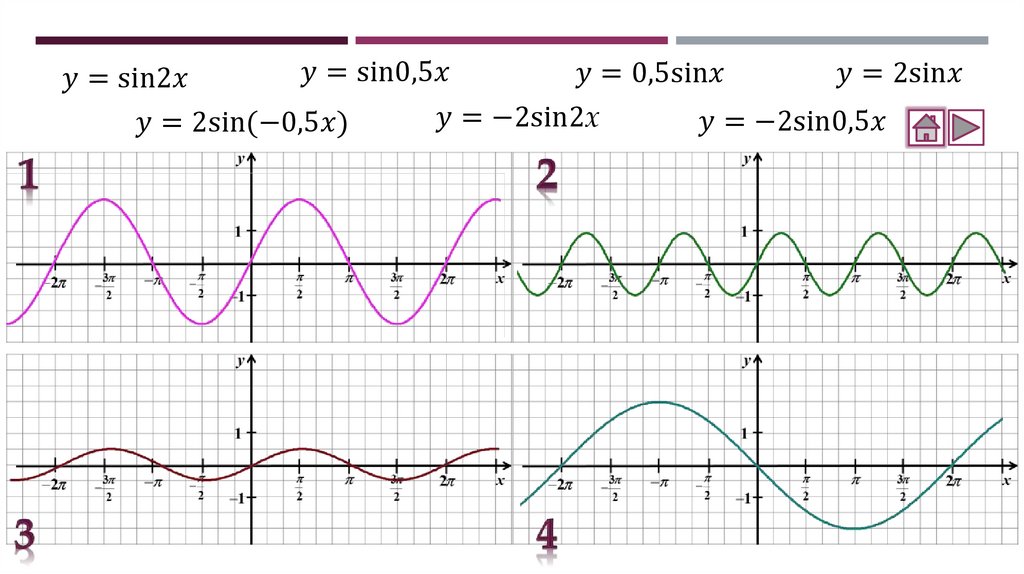
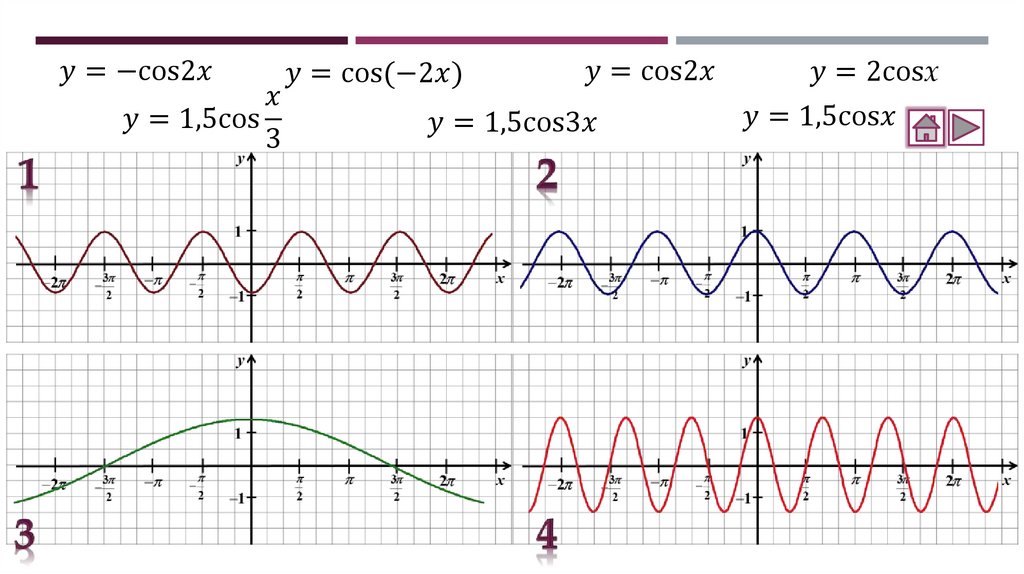
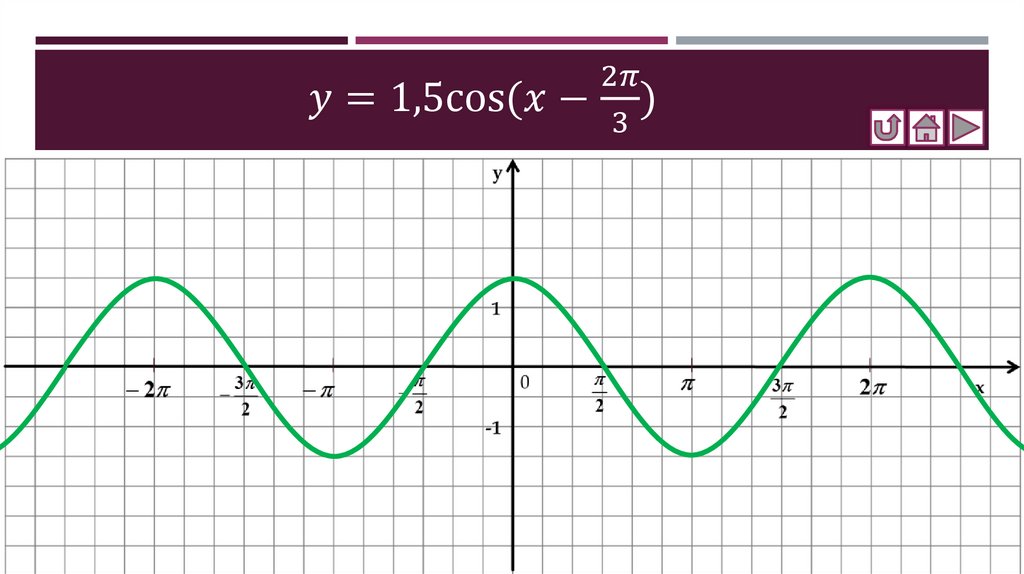
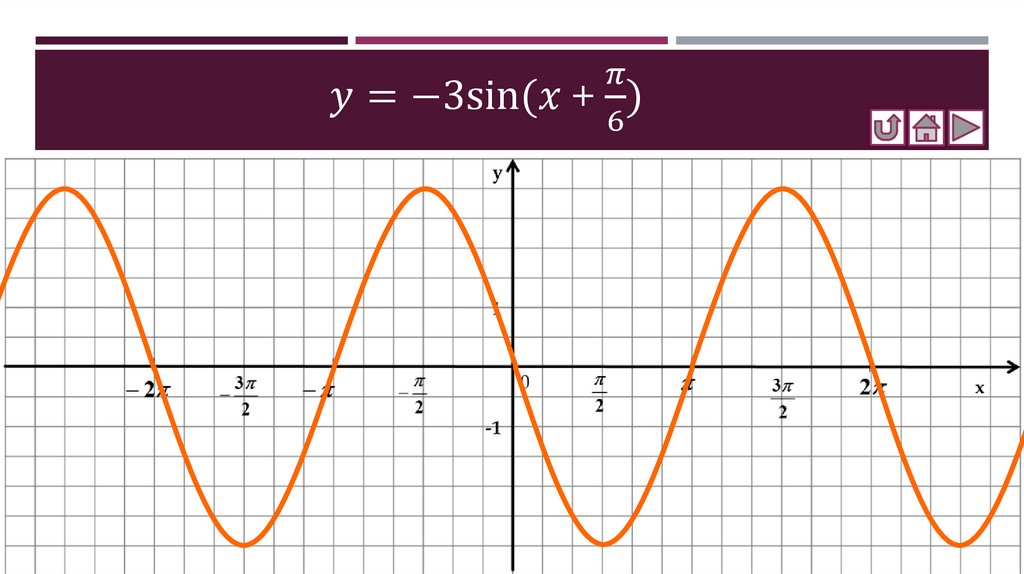
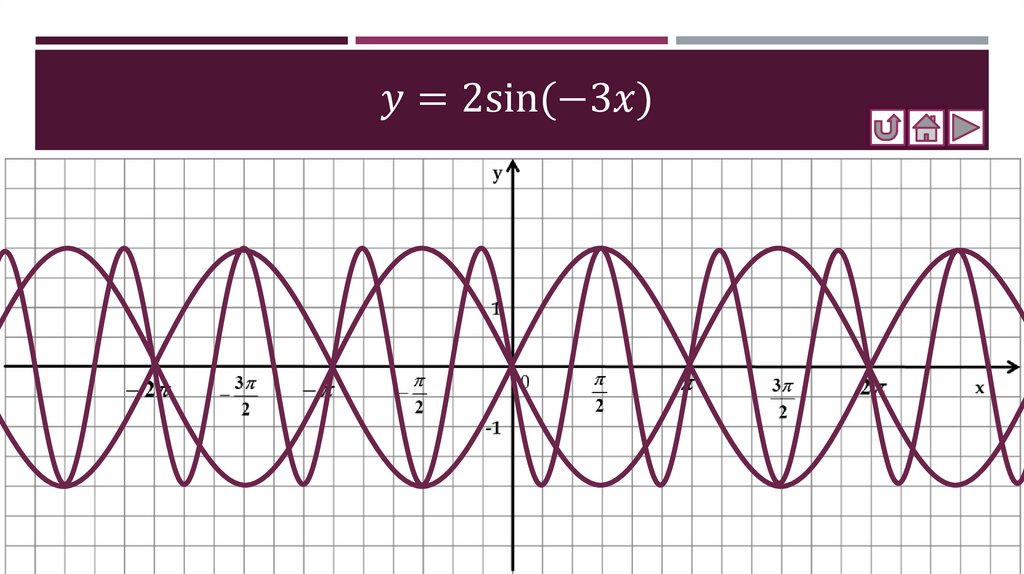
Соотнесение графиков функций с их формулами
Построение графиков функций
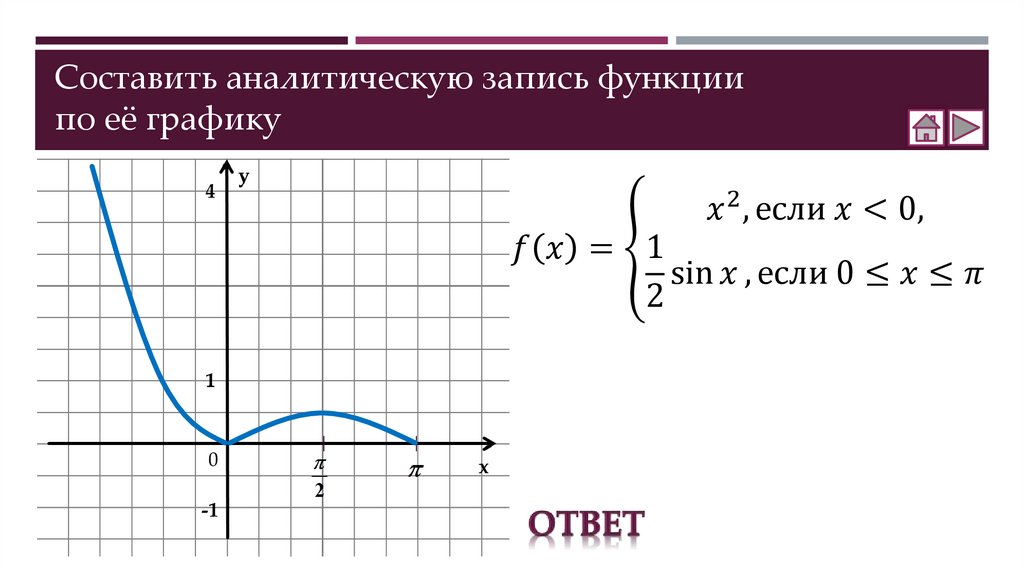
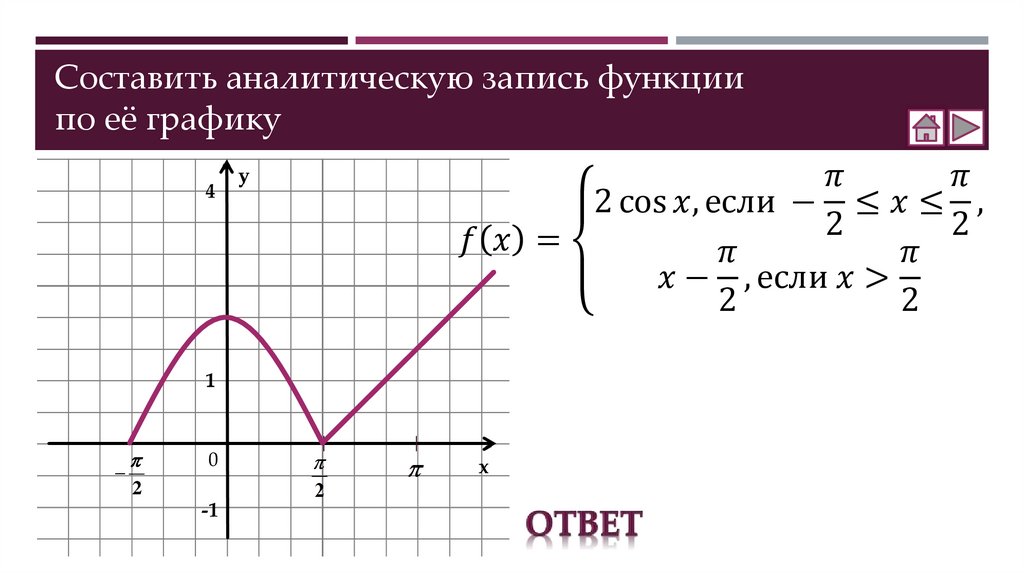
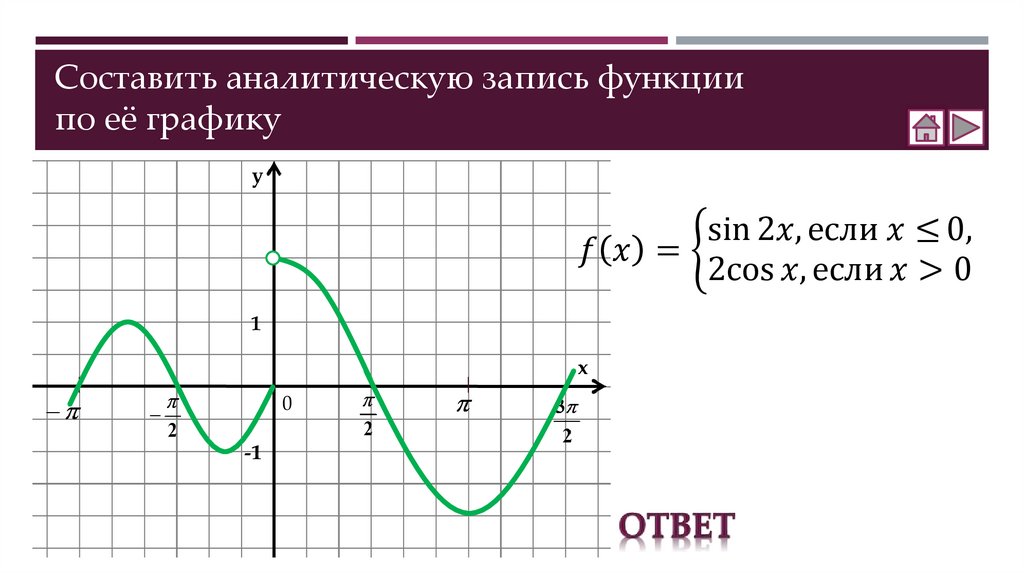
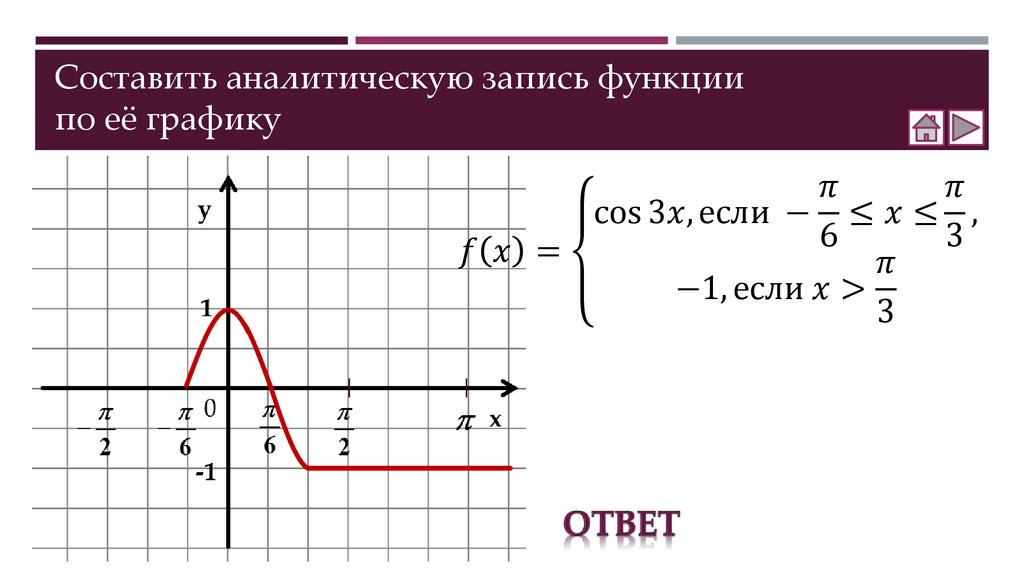
Составление аналитической записи функции по её графику
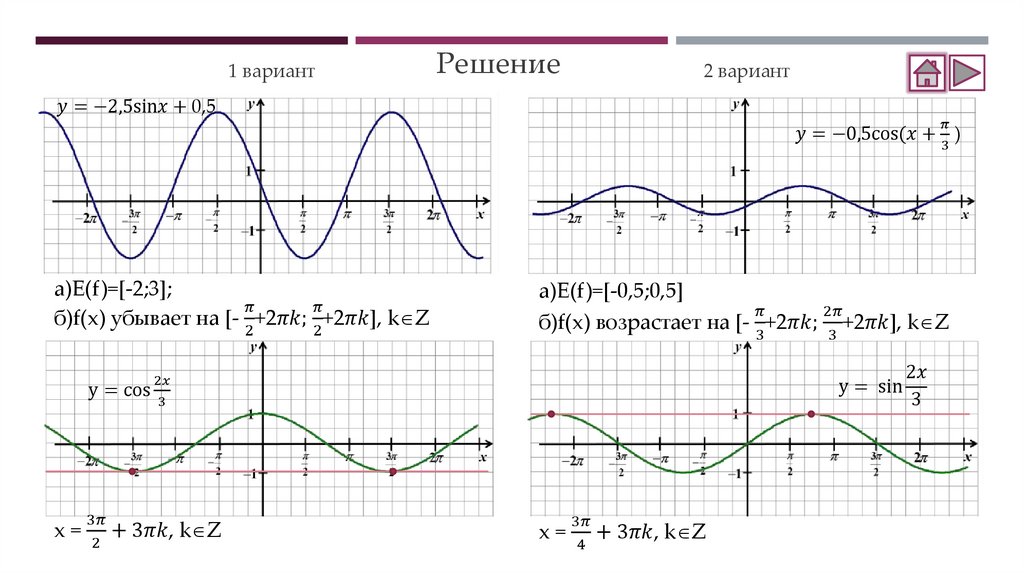
Самостоятельная работа

3. y = f(x) + b Параллельный перенос вдоль оси ординат

3

English Русский Правила