Похожие презентации:
09.12 МЕДИАНЫ, БИССЕКТРИСЫ И ВЫСОТЫ ТРЕУГОЛЬНИКА
1. МЕДИАНЫ, БИССЕКТРИСЫ И ВЫСОТЫ ТРЕУГОЛЬНИКА
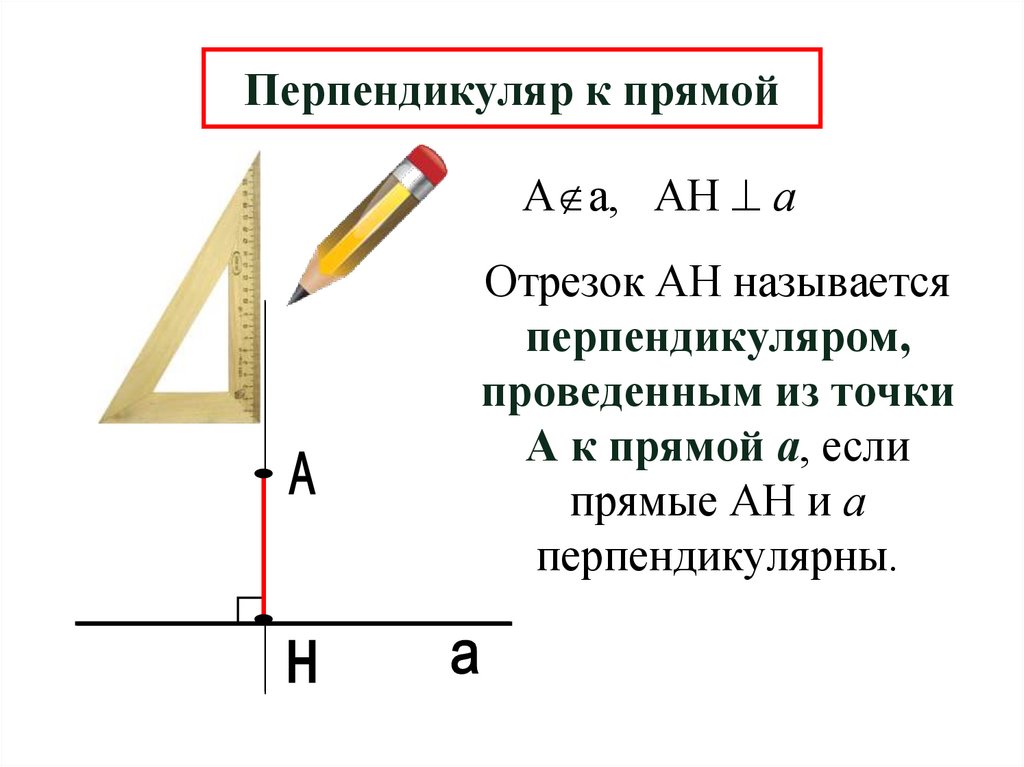
2. Перпендикуляр к прямой
А а, АН аОтрезок АН называется
перпендикуляром,
проведенным из точки
А к прямой а, если
прямые АН и а
перпендикулярны.
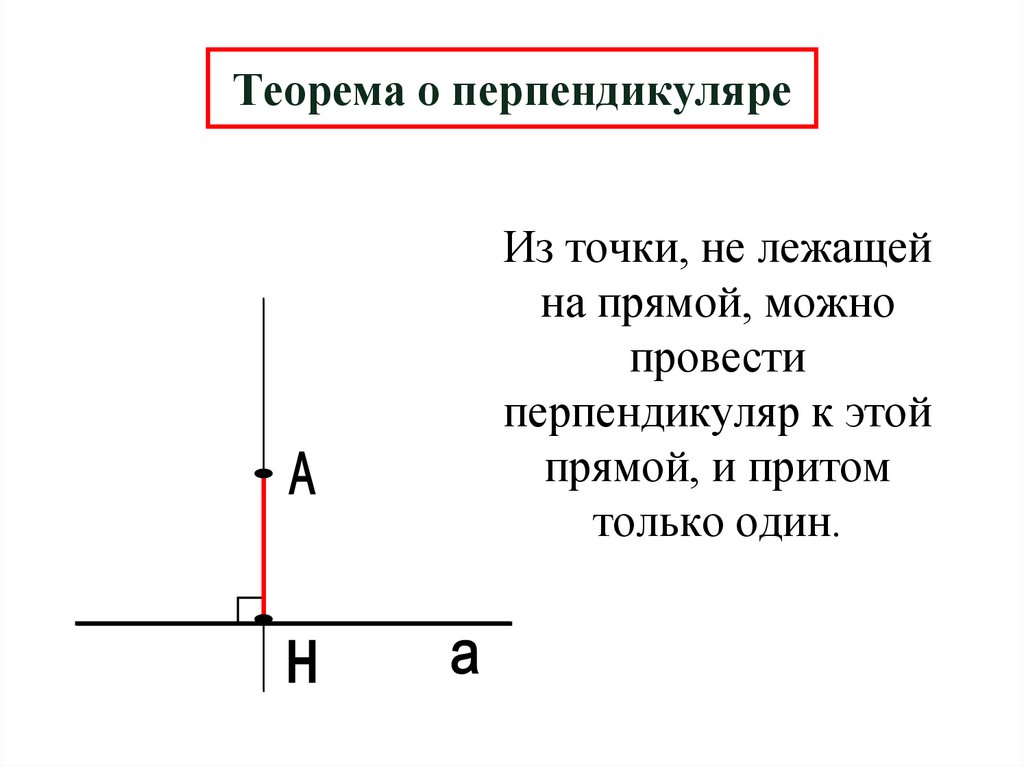
3. Теорема о перпендикуляре
Из точки, не лежащейна прямой, можно
провести
перпендикуляр к этой
прямой, и притом
только один.
4.
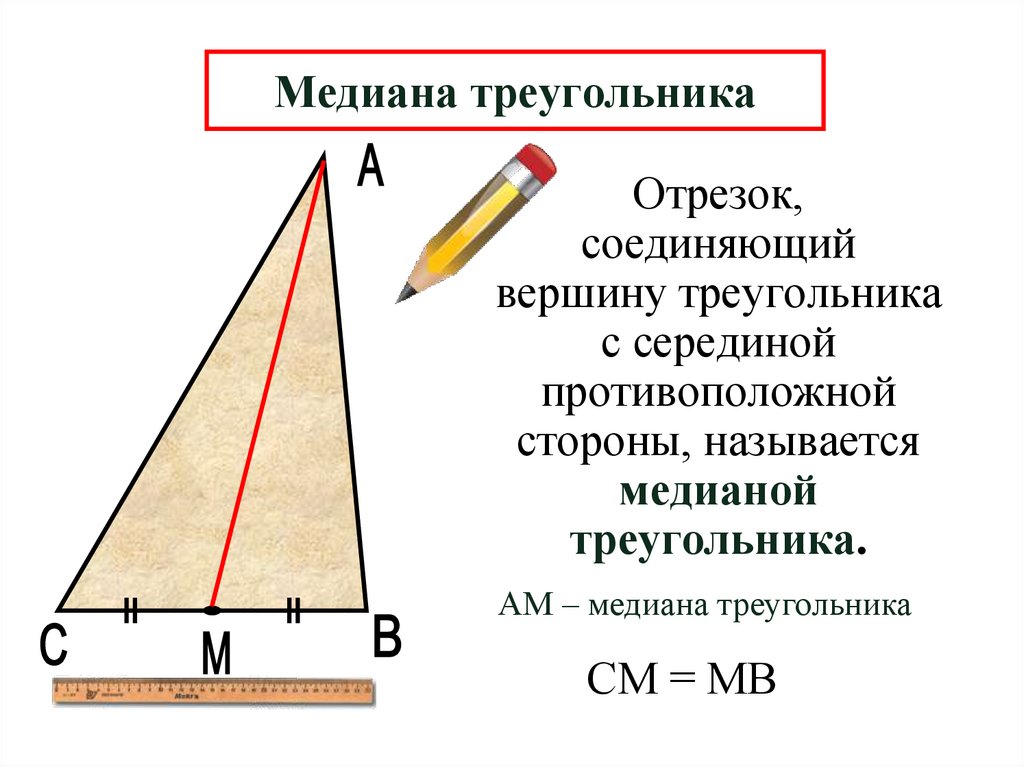
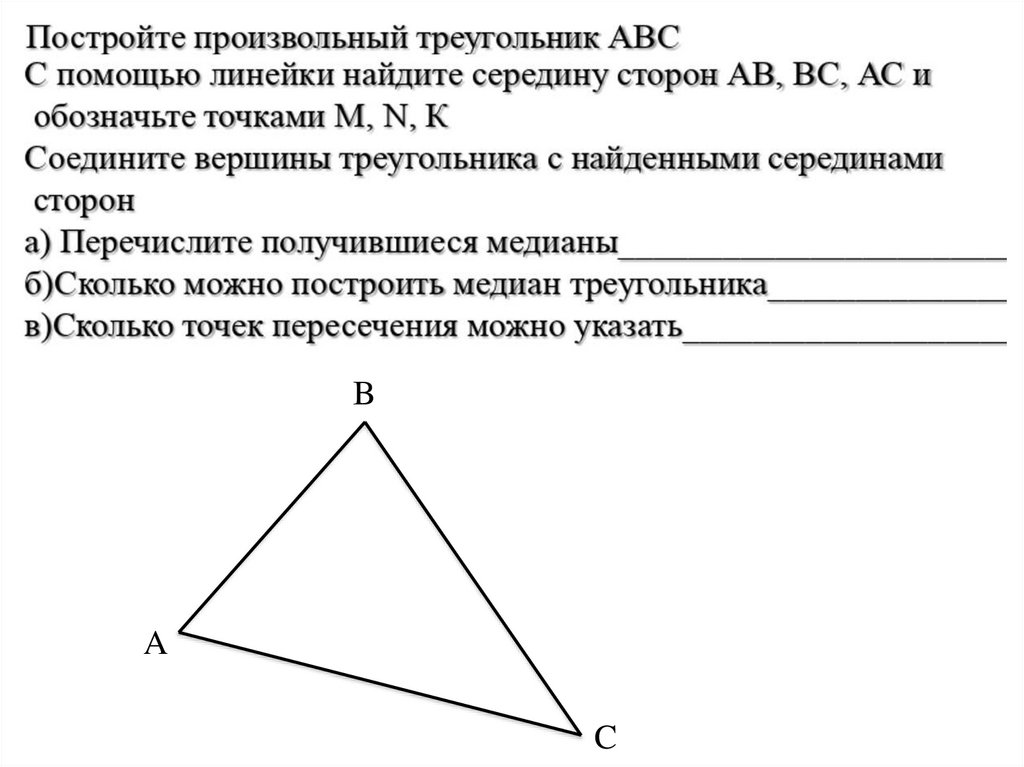
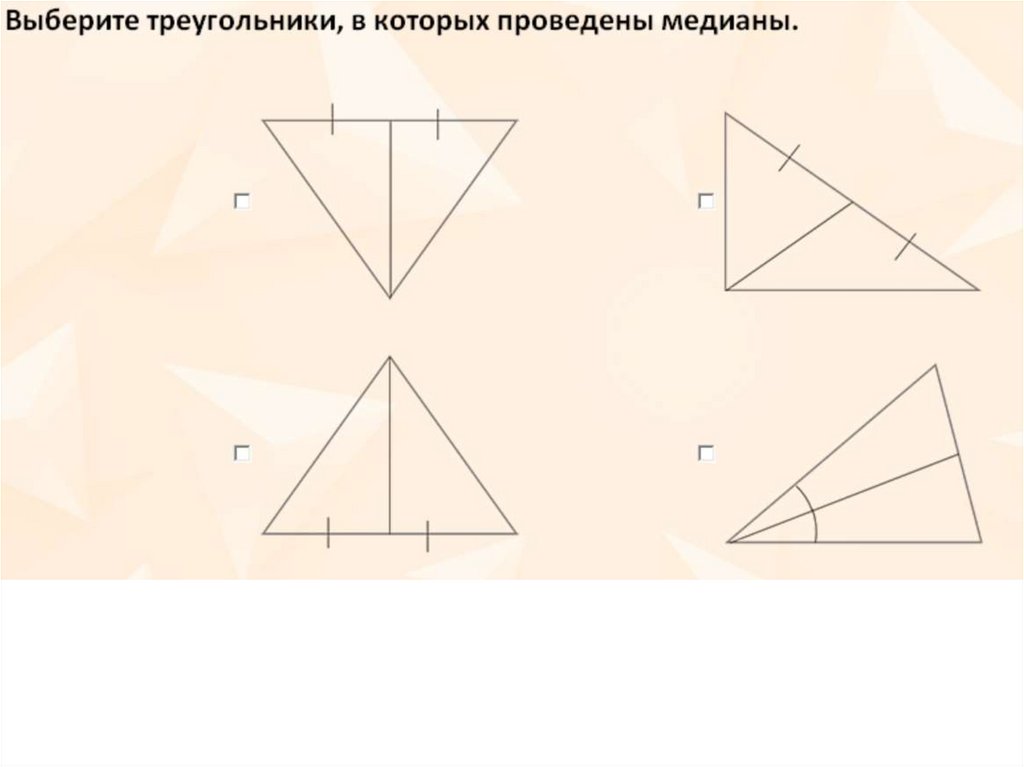
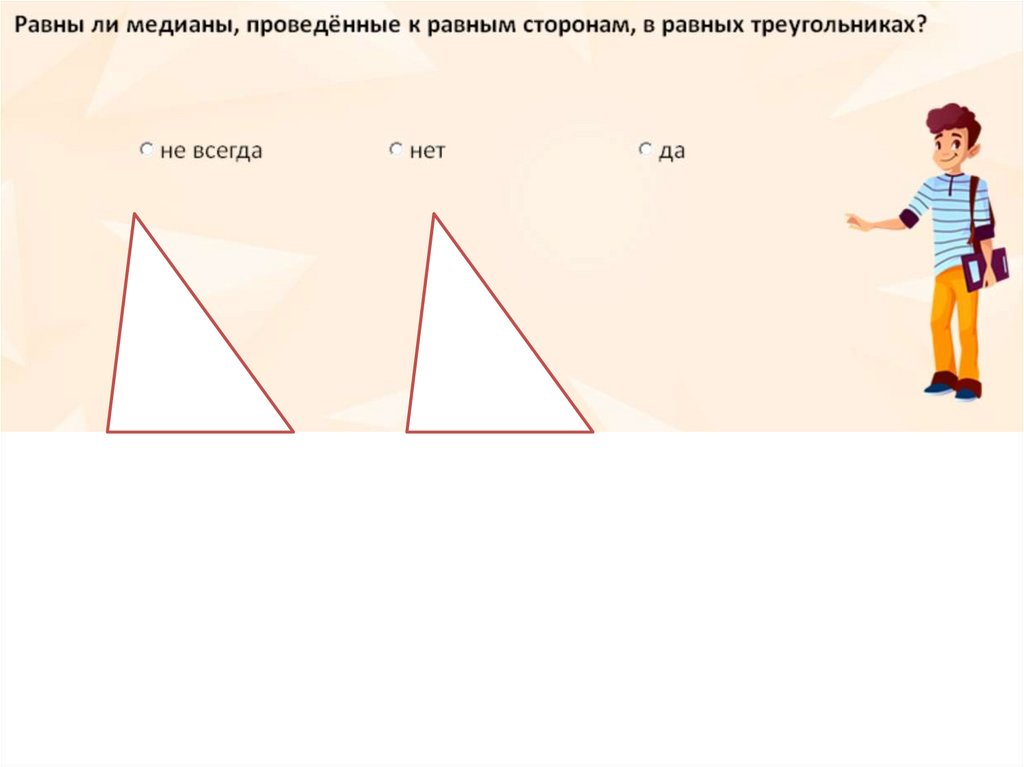
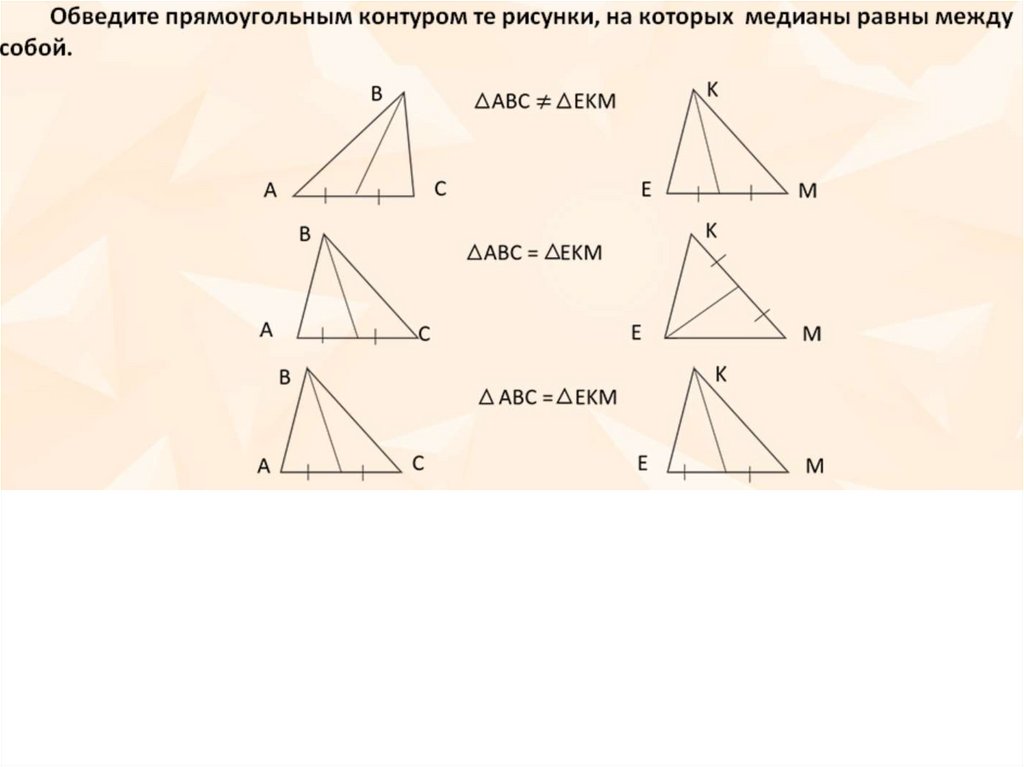
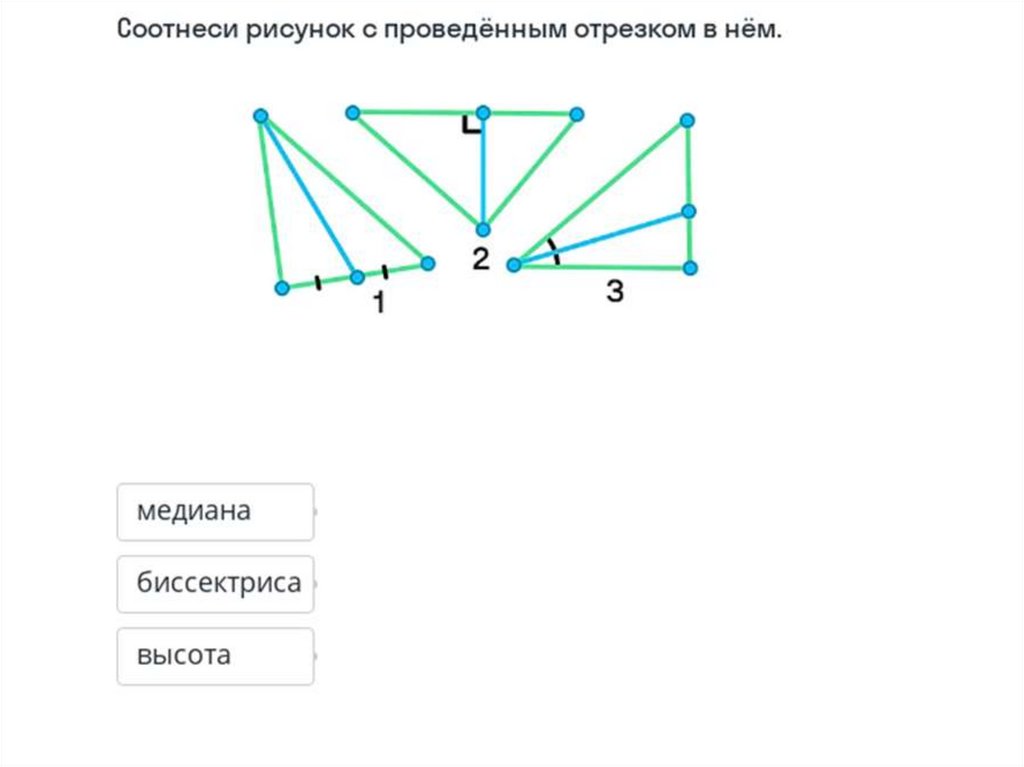
5. Медиана треугольника
Отрезок,соединяющий
вершину треугольника
с серединой
противоположной
стороны, называется
медианой
треугольника.
АМ – медиана треугольника
СМ = МВ
6. Медиана треугольника
Медиана-обезьяна,У которой зоркий глаз,
Прыгнет точно в середину
Стороны против вершины,
Где находится сейчас
7.
BA
C
8.
9.
10.
11.
12.
13.
14.
15.
16.
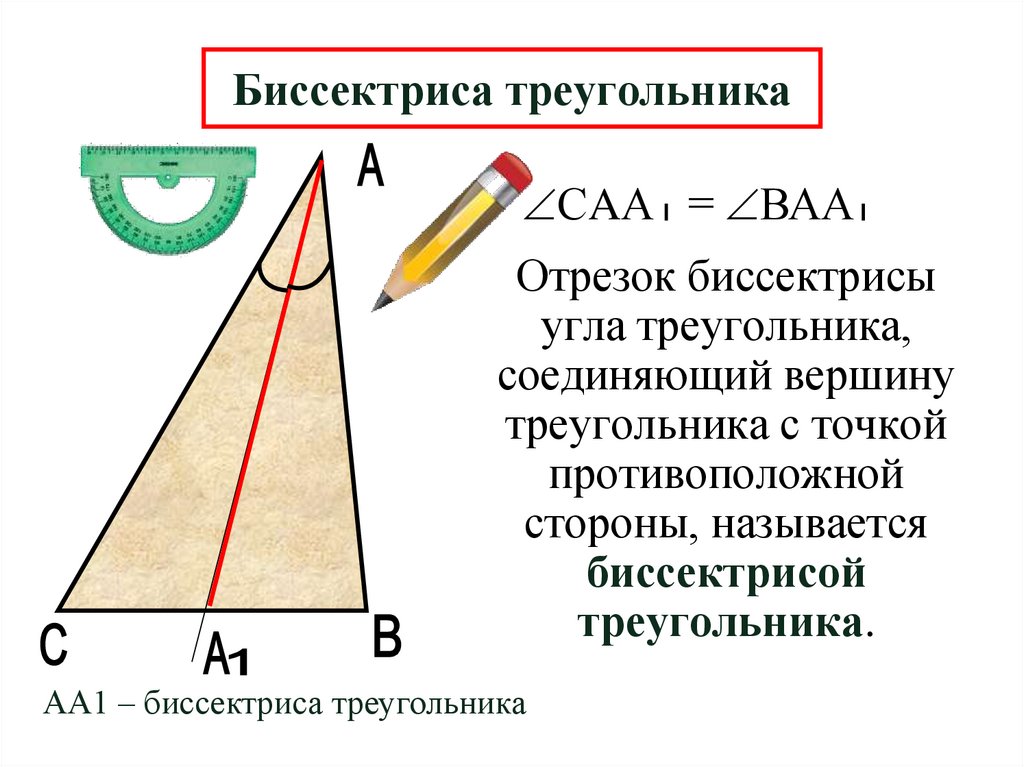
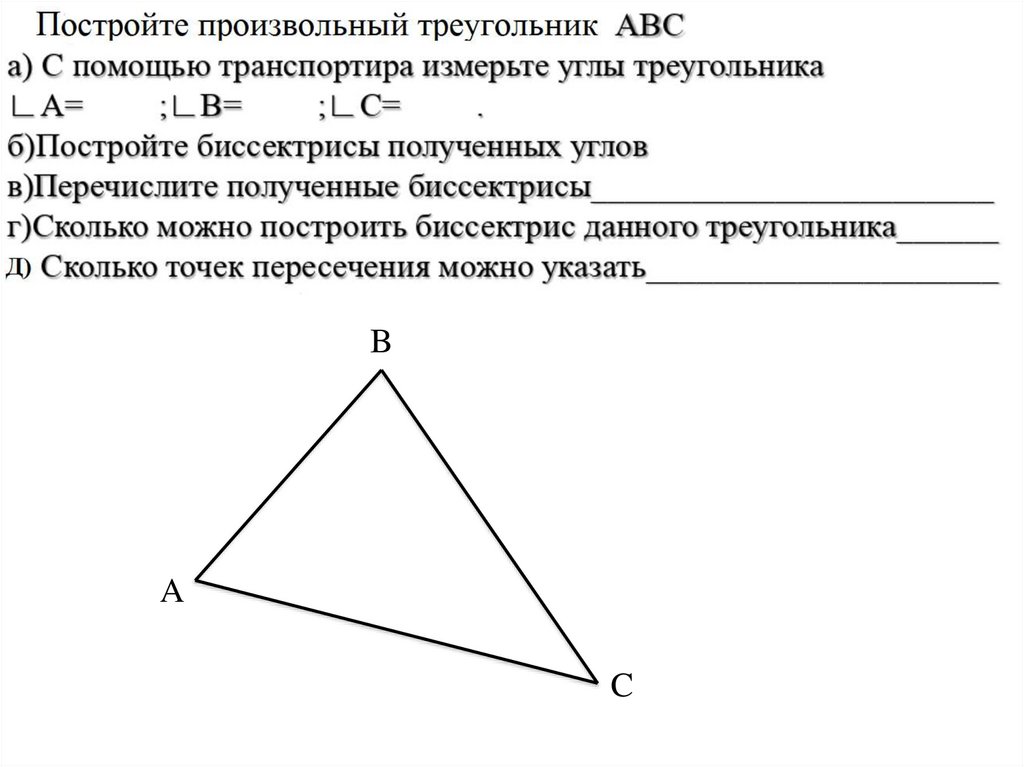
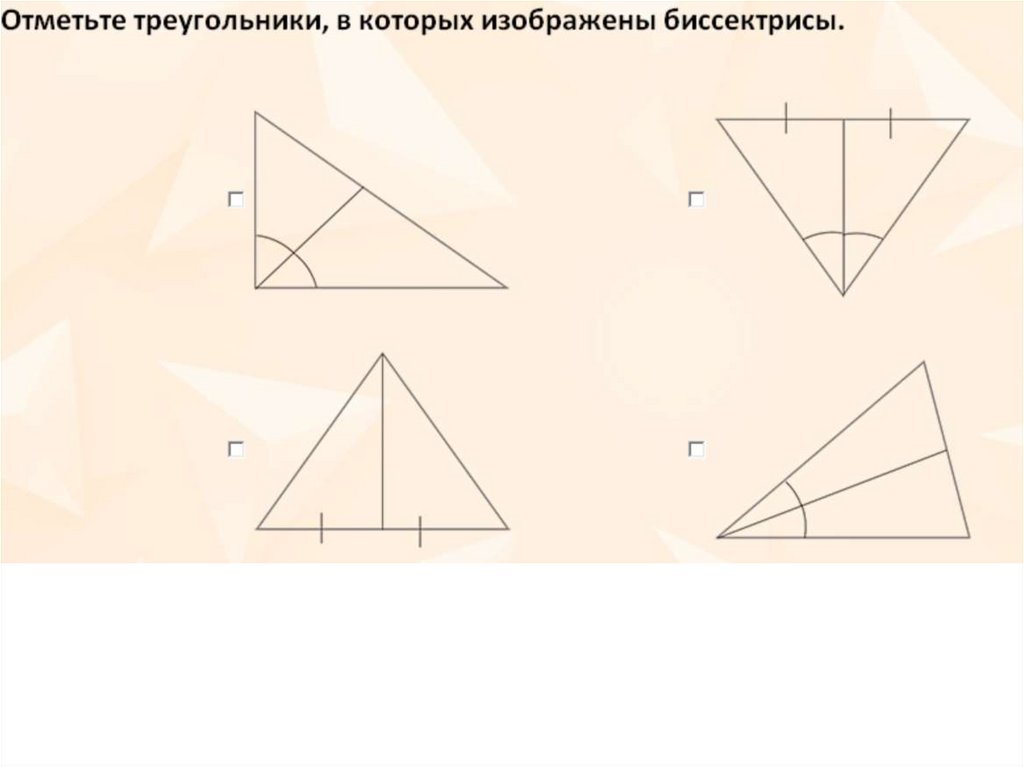
17. Биссектриса треугольника
СAА = ВААОтрезок биссектрисы
угла треугольника,
соединяющий вершину
треугольника с точкой
противоположной
стороны, называется
биссектрисой
треугольника.
АА1 – биссектриса треугольника
18. Биссектриса треугольника
Биссектриса – это крыса,Которая бегает по углам
И делит угол пополам.
19.
20.
BA
C
21.
22.
23.
24.
25.
26.
27.
28.
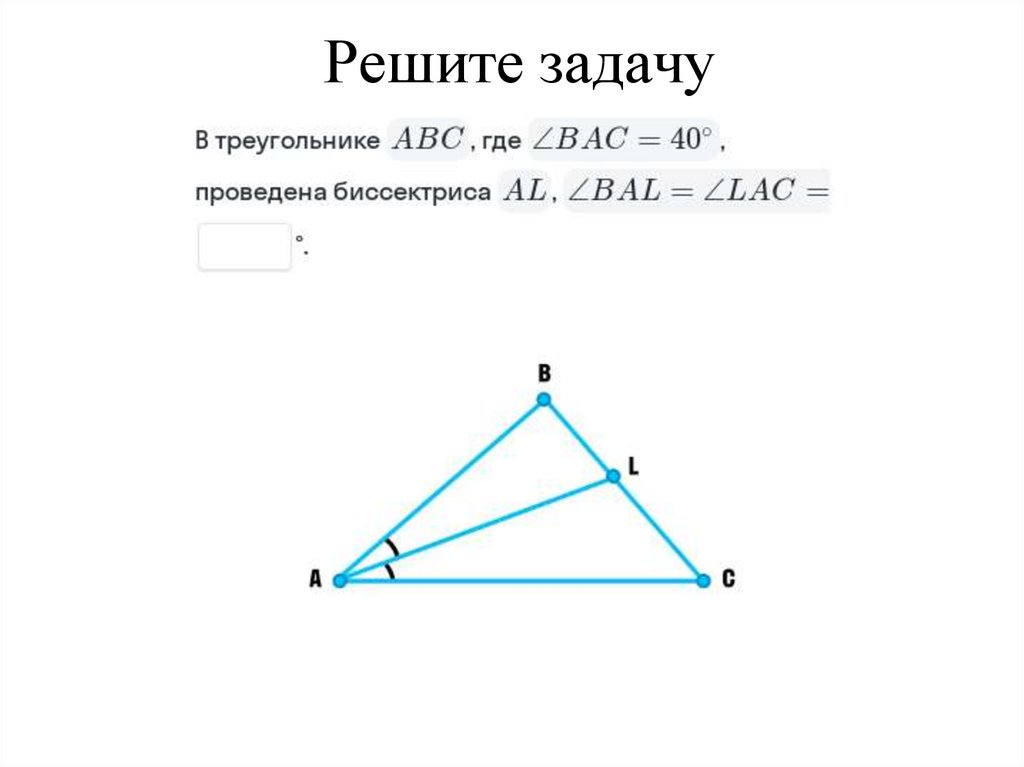
29. Решите задачу
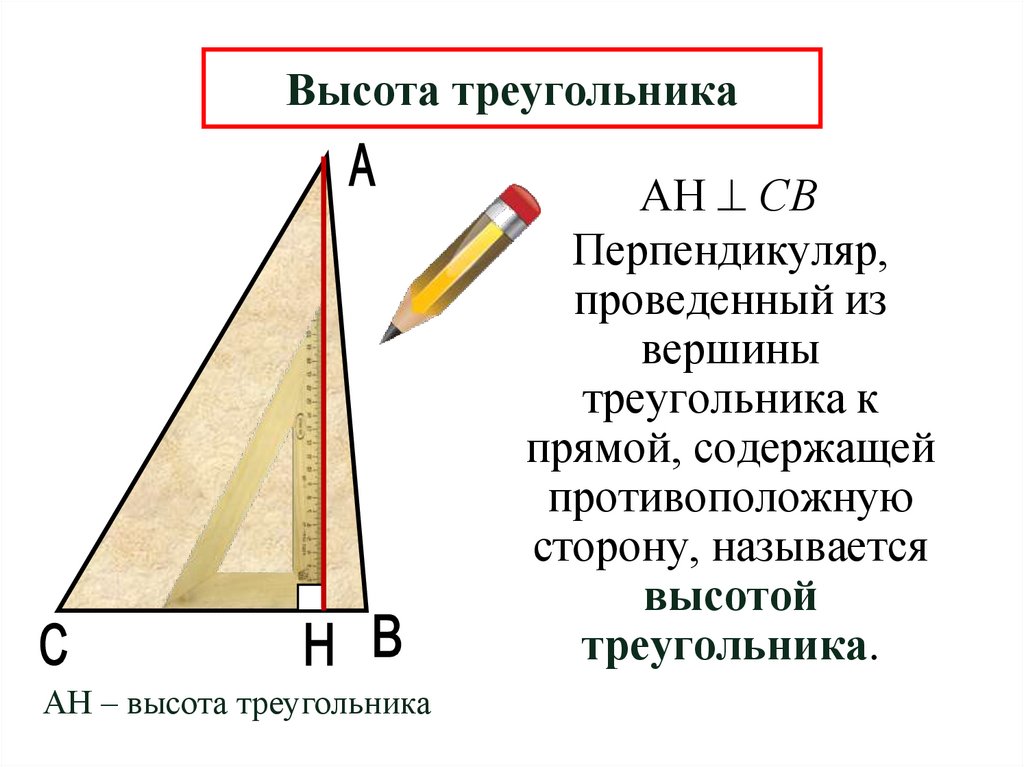
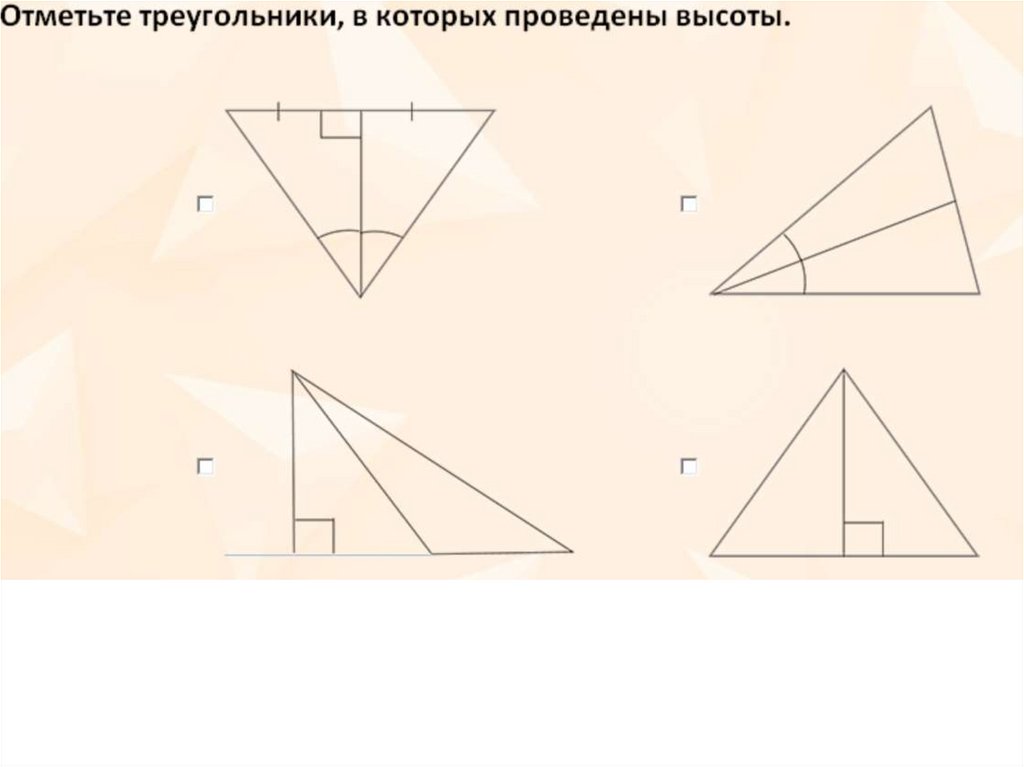
30. Высота треугольника
АН СВПерпендикуляр,
проведенный из
вершины
треугольника к
прямой, содержащей
противоположную
сторону, называется
высотой
треугольника.
АН – высота треугольника
31. Высота треугольника
Высота похожа накота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
32.
АС
В
33.
34.
35.
36.
37.
38.
39.
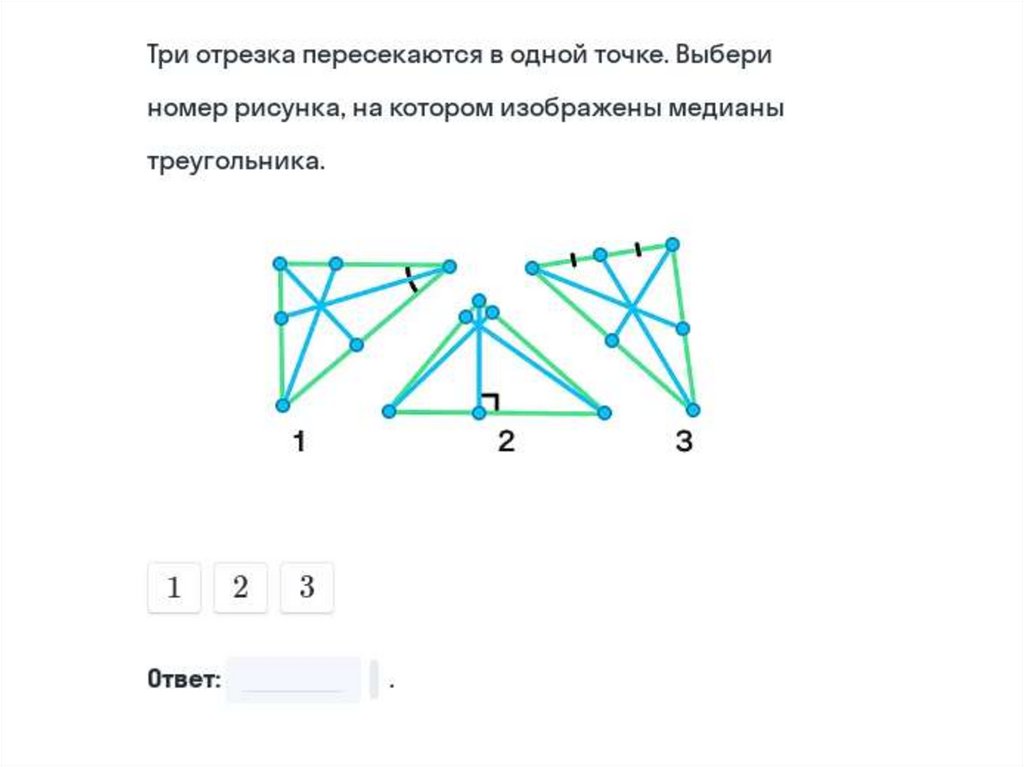
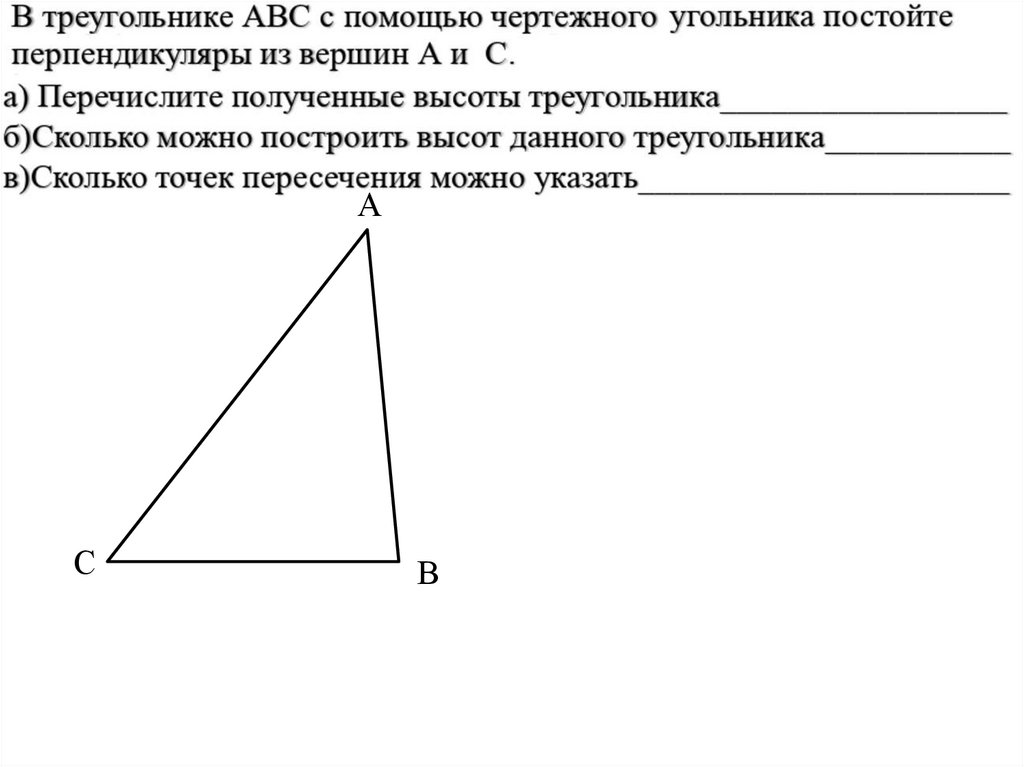
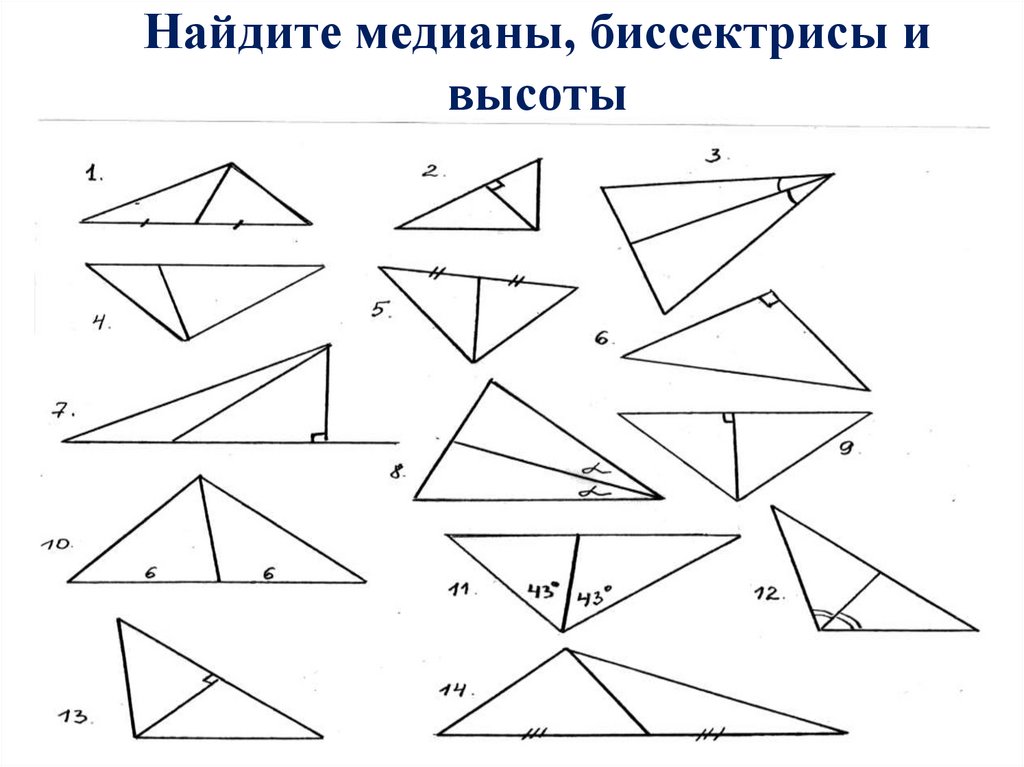
40. Найдите медианы, биссектрисы и высоты
41.
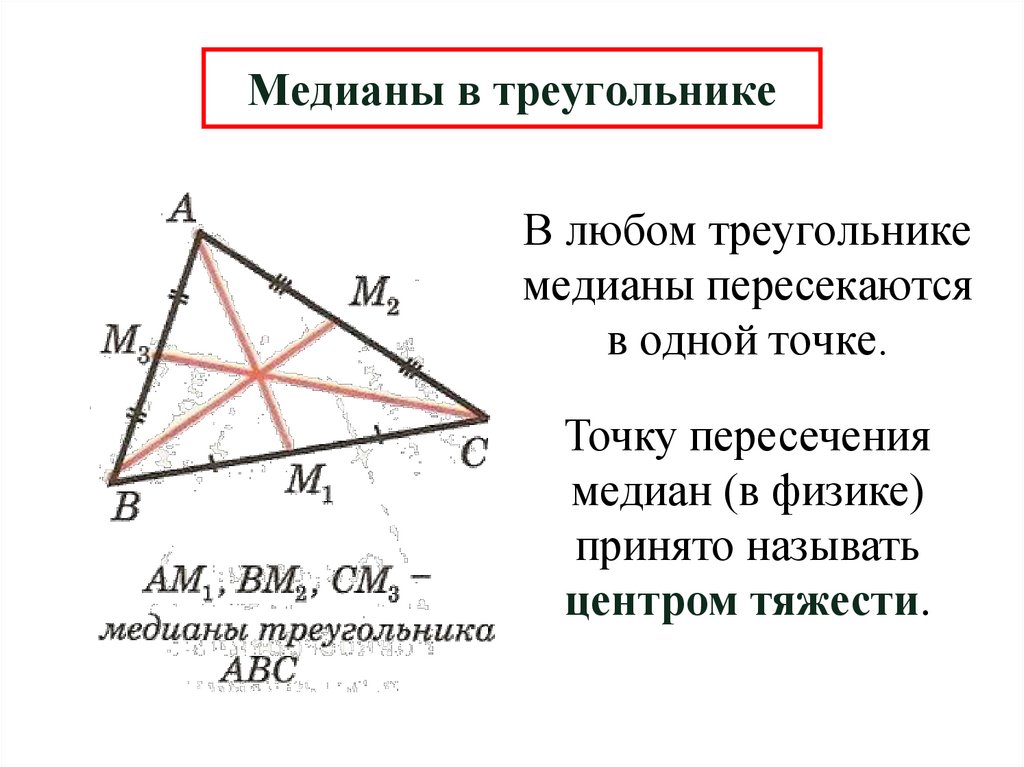
42. Медианы в треугольнике
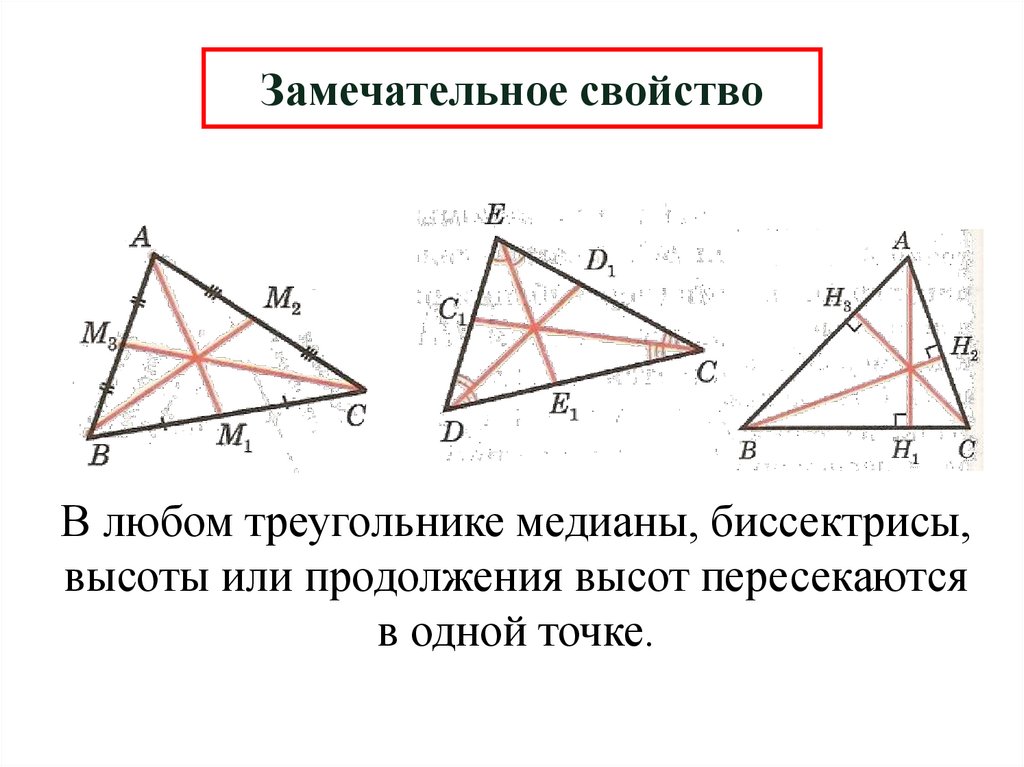
В любом треугольникемедианы пересекаются
в одной точке.
Точку пересечения
медиан (в физике)
принято называть
центром тяжести.
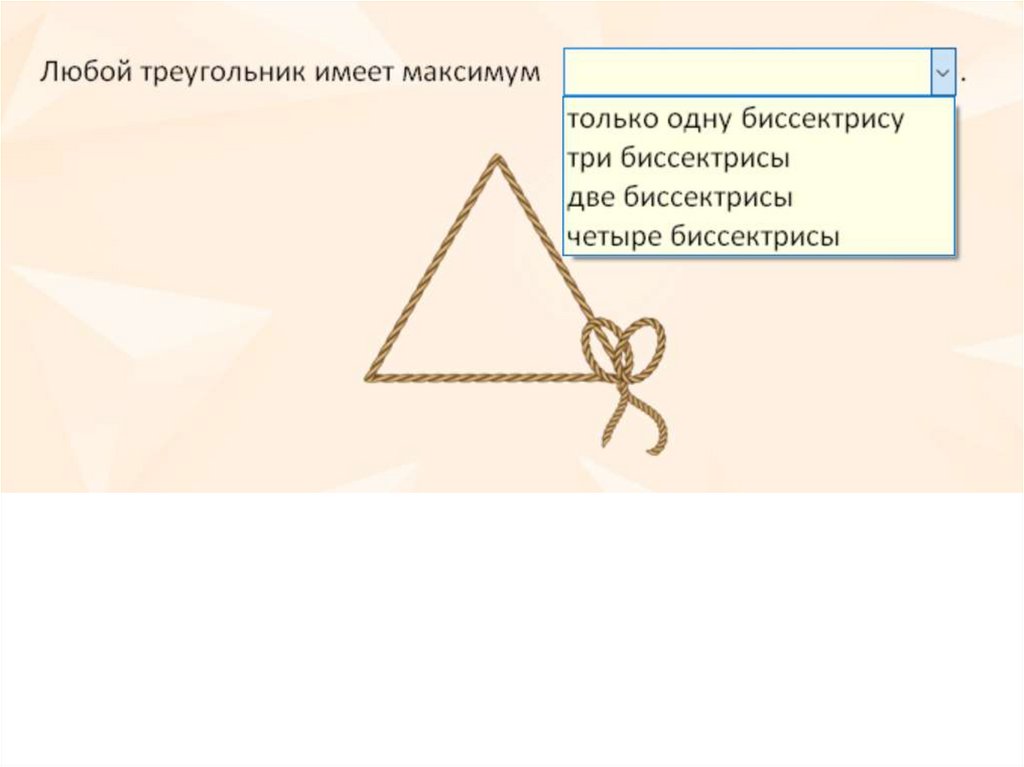
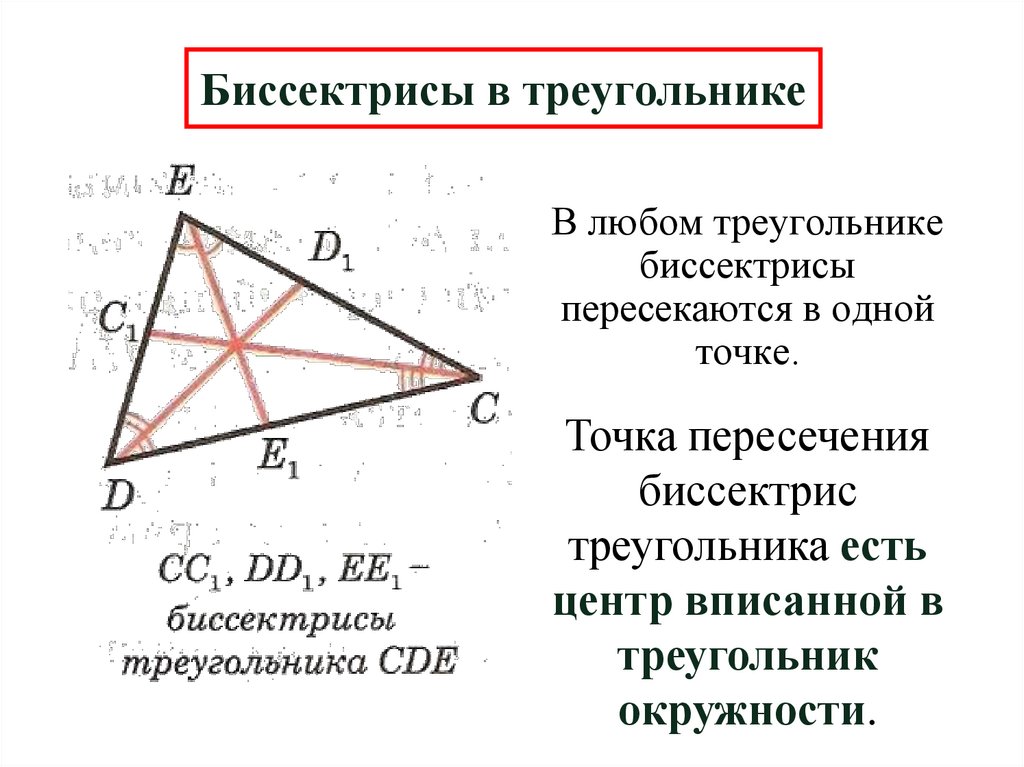
43. Биссектрисы в треугольнике
В любом треугольникебиссектрисы
пересекаются в одной
точке.
Точка пересечения
биссектрис
треугольника есть
центр вписанной в
треугольник
окружности.
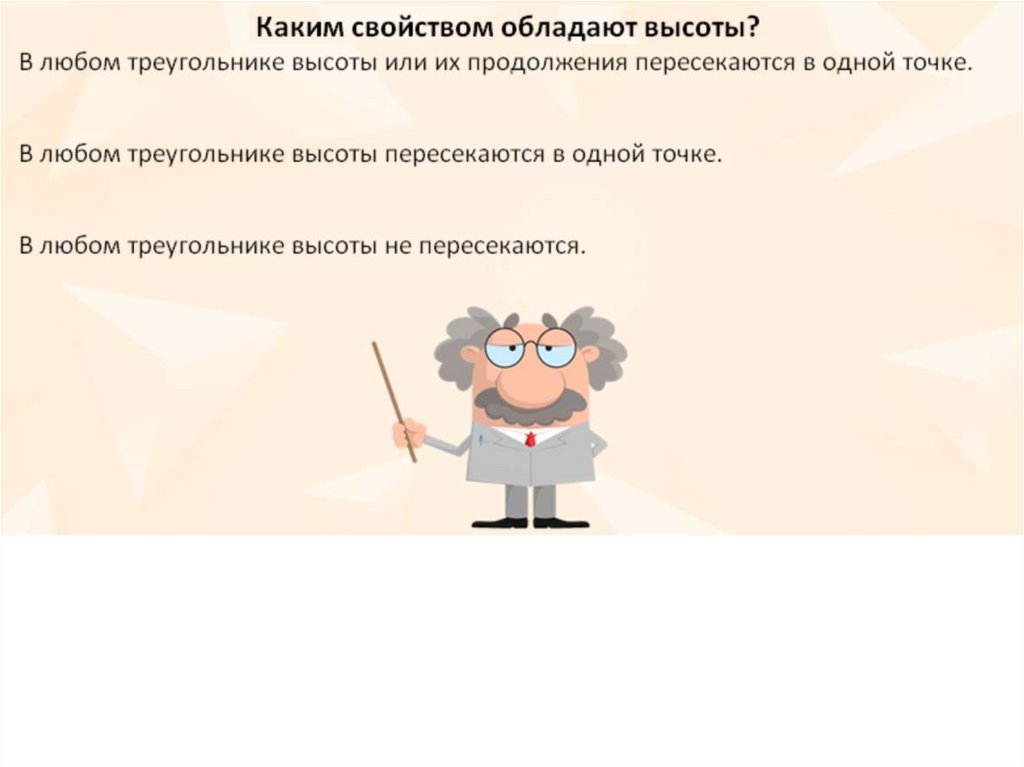
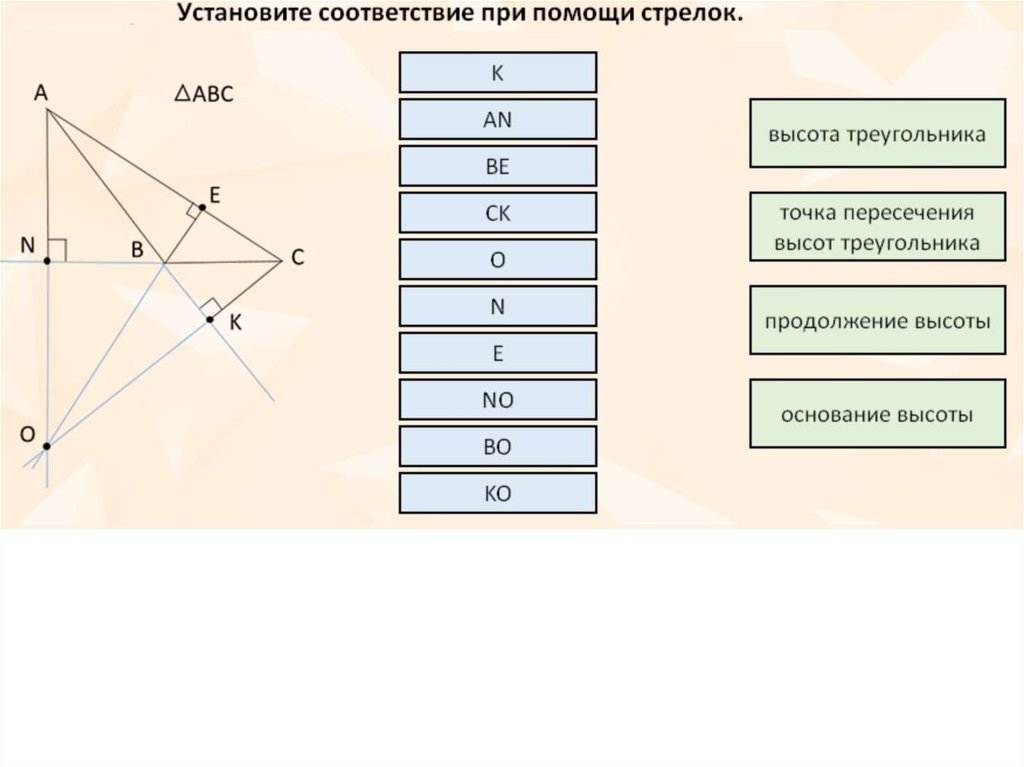
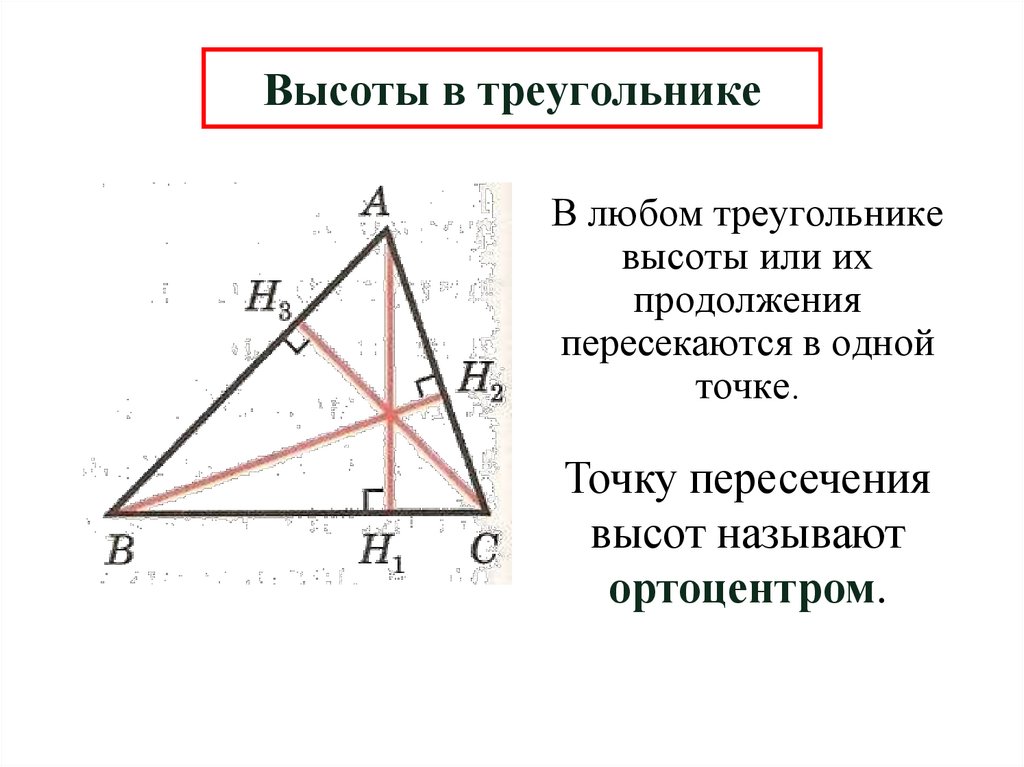
44. Высоты в треугольнике
В любом треугольникевысоты или их
продолжения
пересекаются в одной
точке.
Точку пересечения
высот называют
ортоцентром.
45.
Замечательное свойствоВ любом треугольнике медианы, биссектрисы,
высоты или продолжения высот пересекаются
в одной точке.
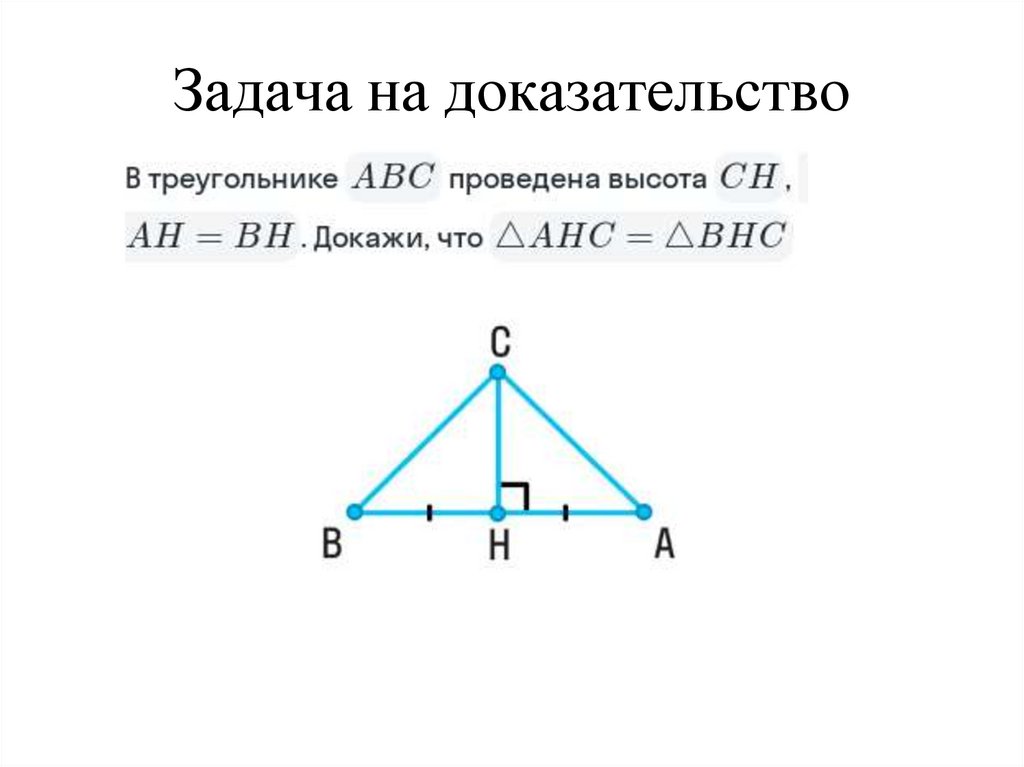
46. Задача на доказательство
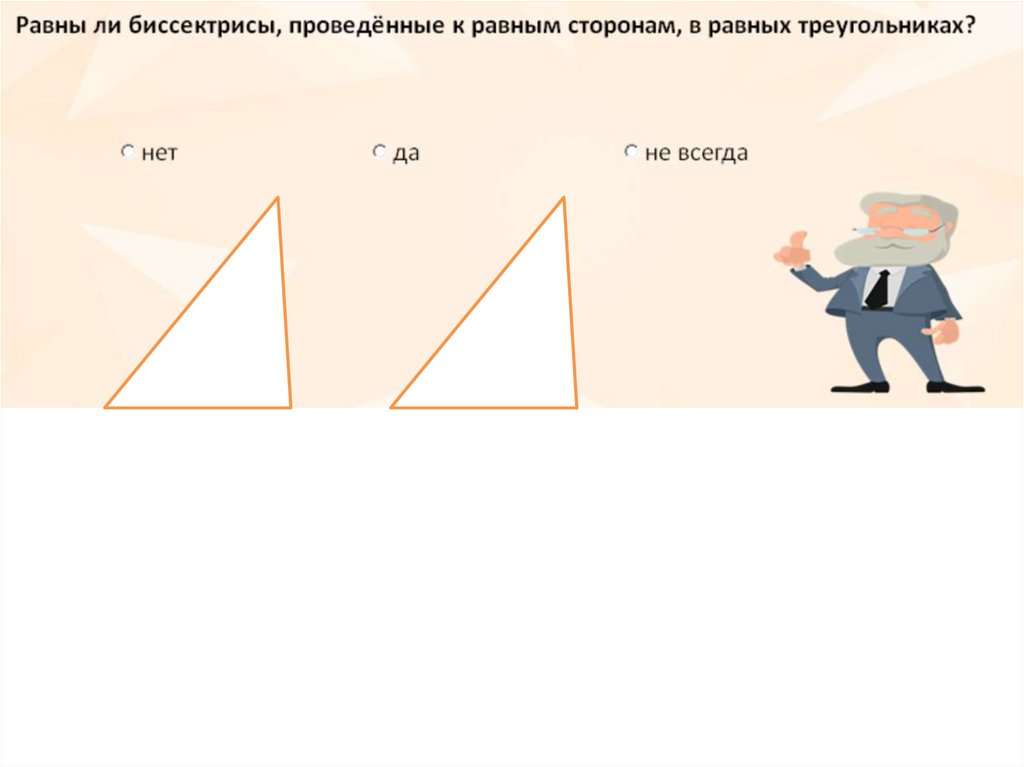
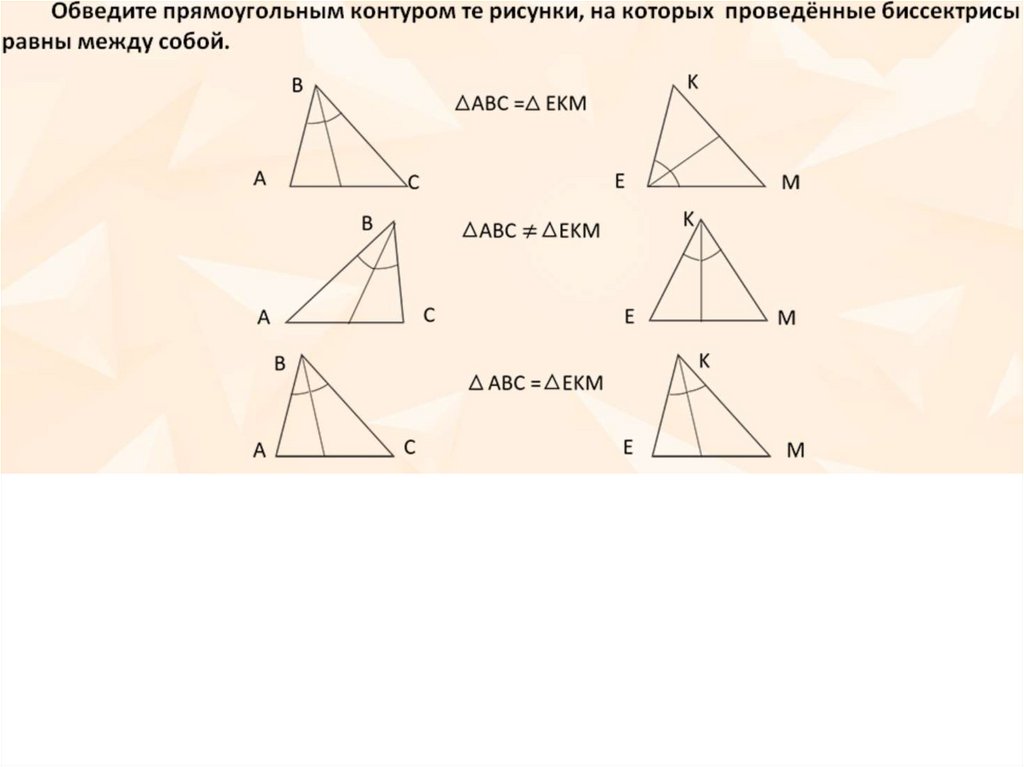
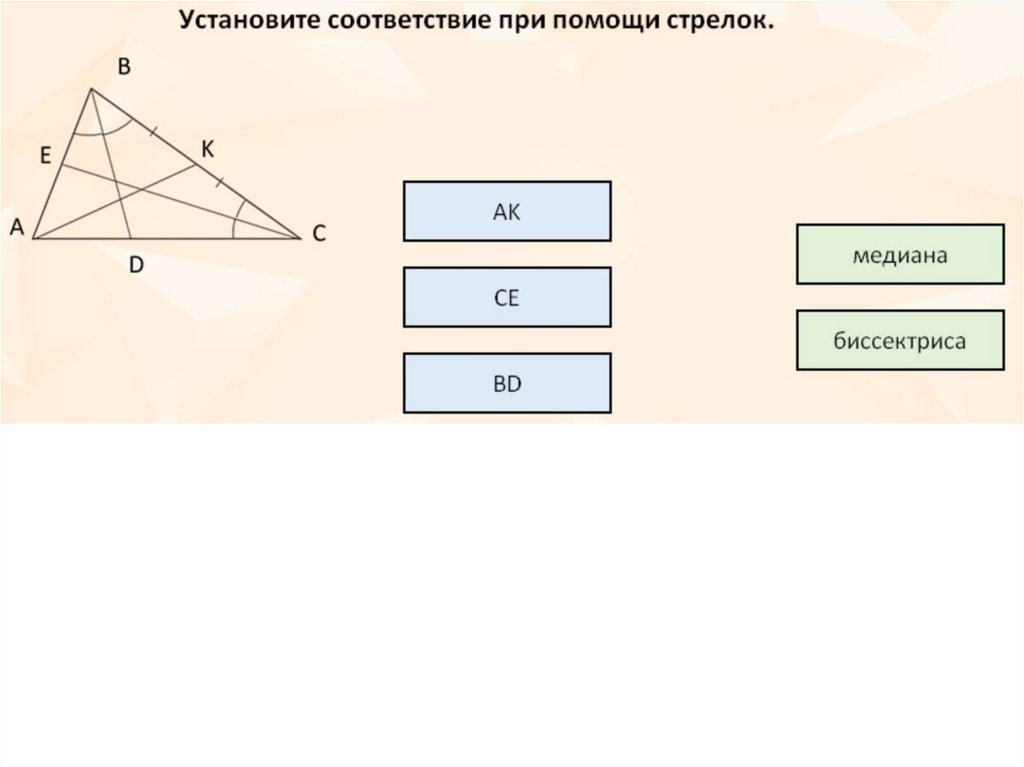
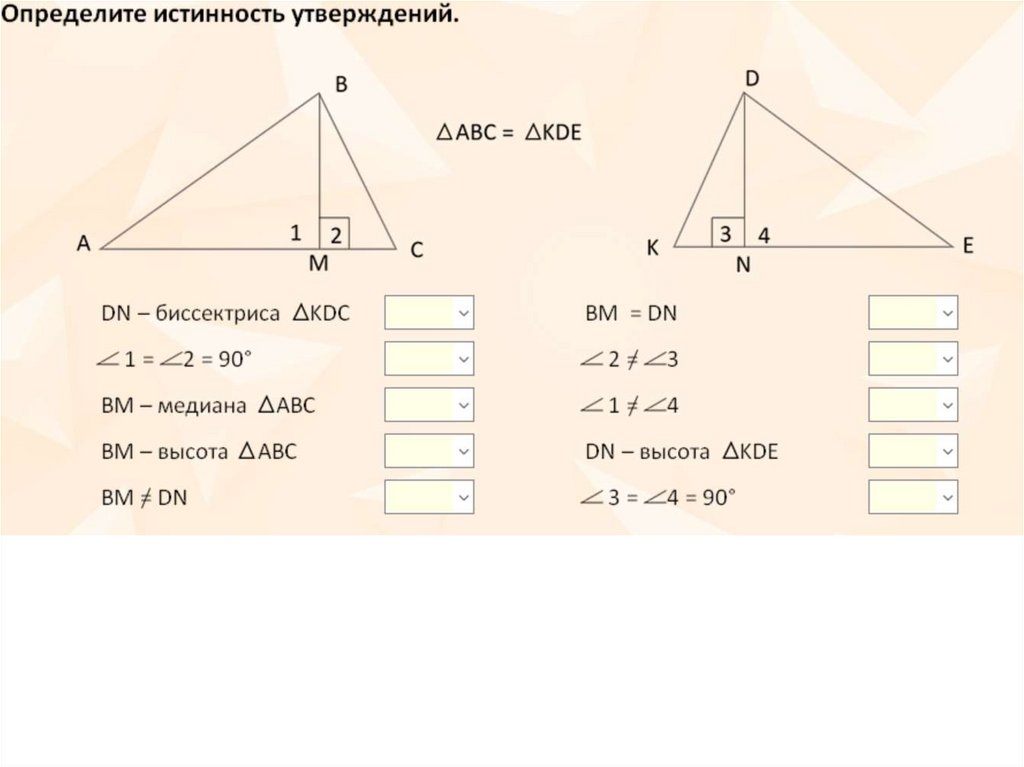
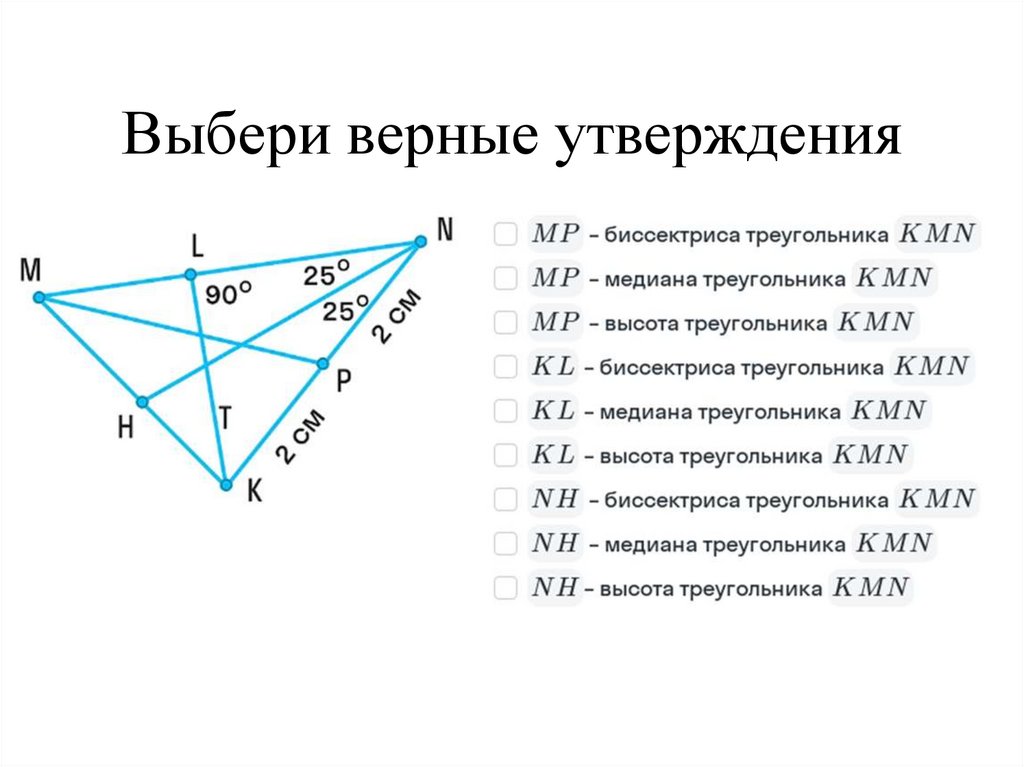
47. Выбери верные утверждения
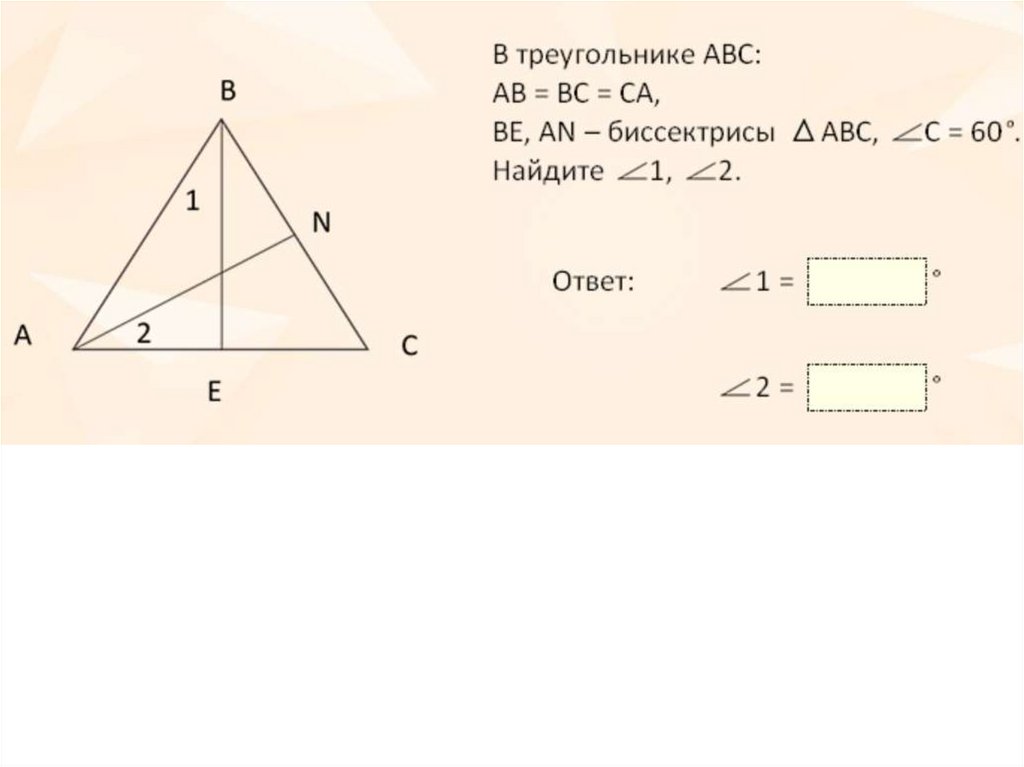
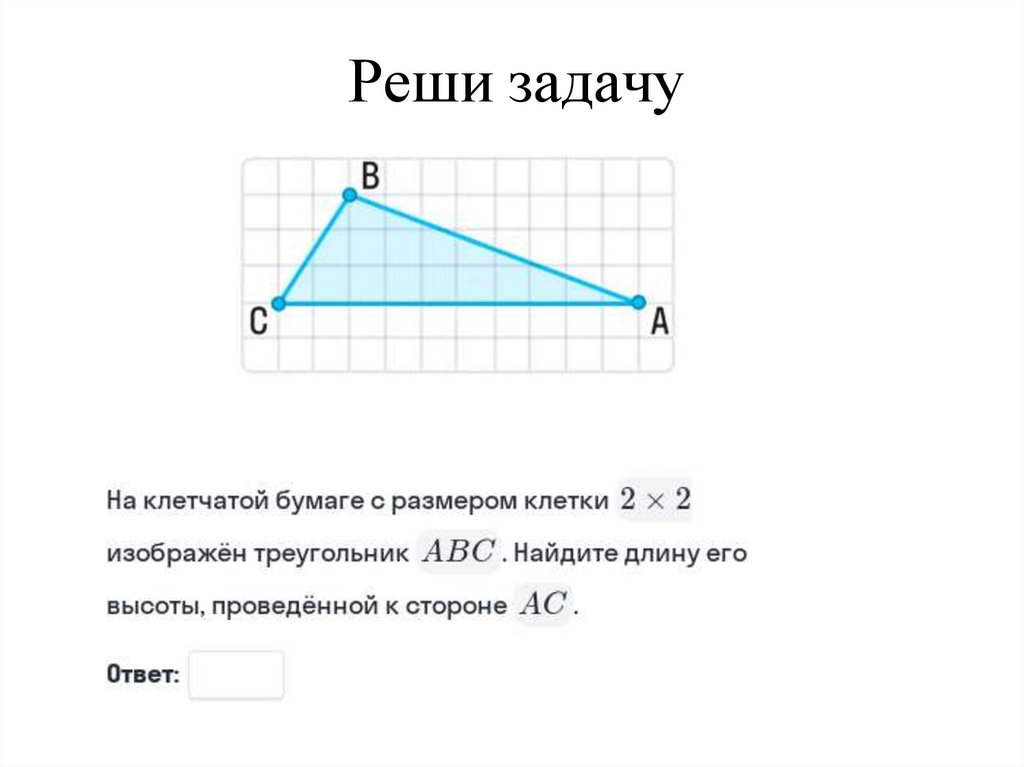
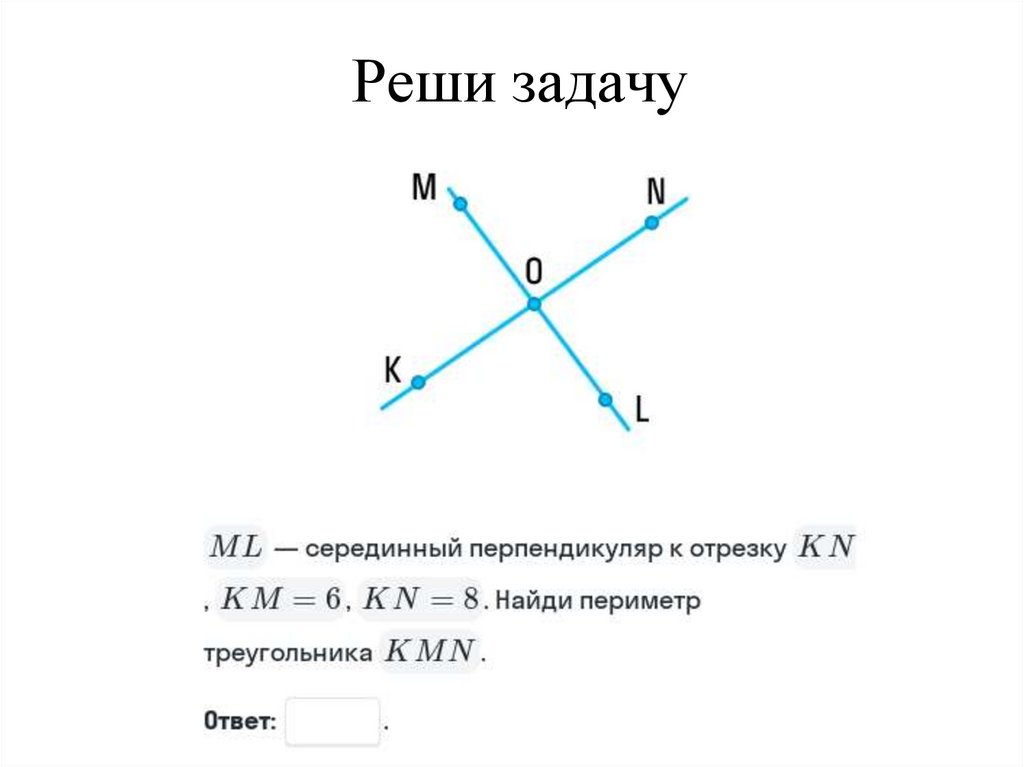
48. Реши задачу
49. Реши задачу
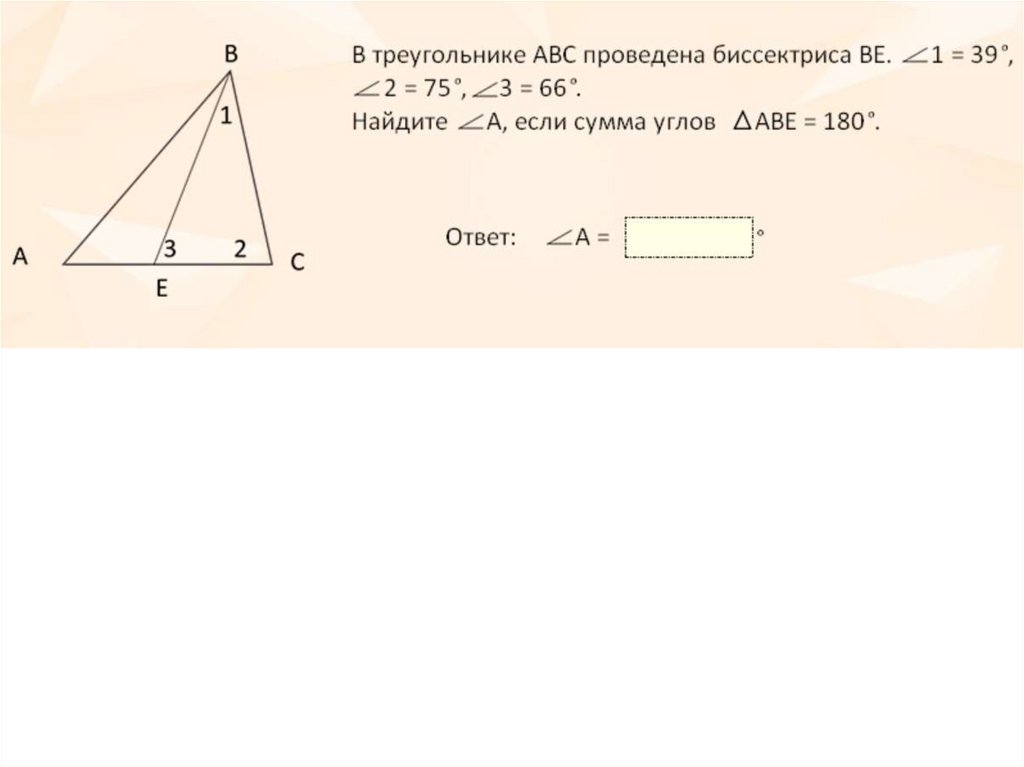
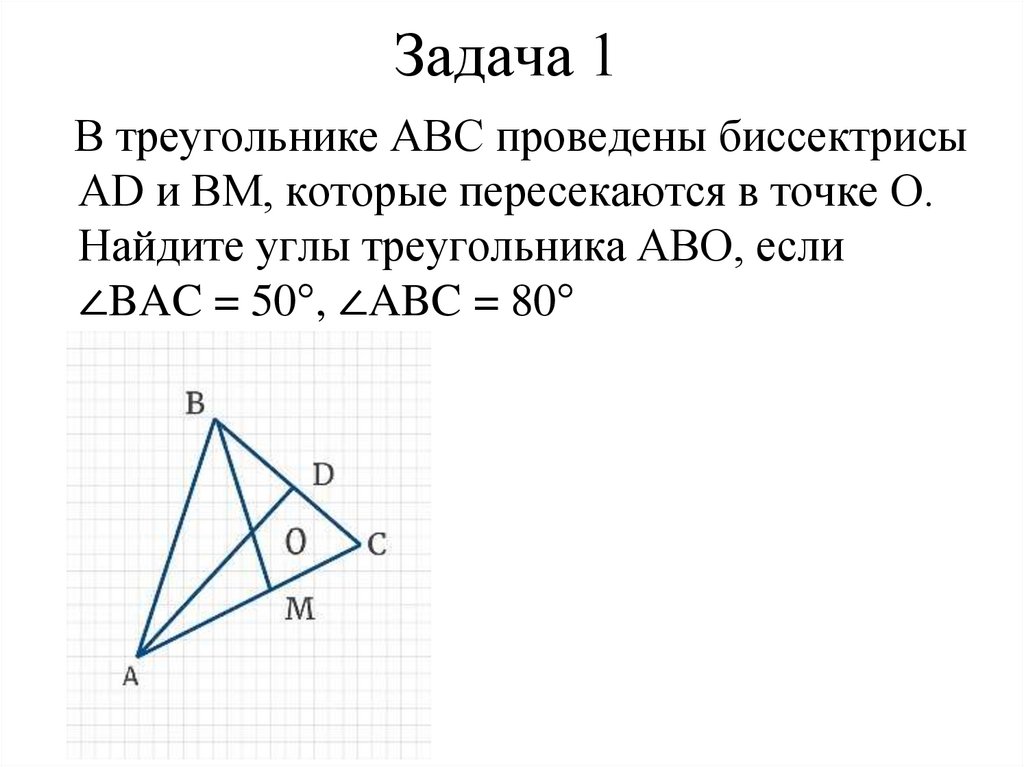
50. Задача 1
В треугольнике ABC проведены биссектрисыAD и BM, которые пересекаются в точке O.
Найдите углы треугольника ABO, если
∠BAC = 50°, ∠ABC = 80°
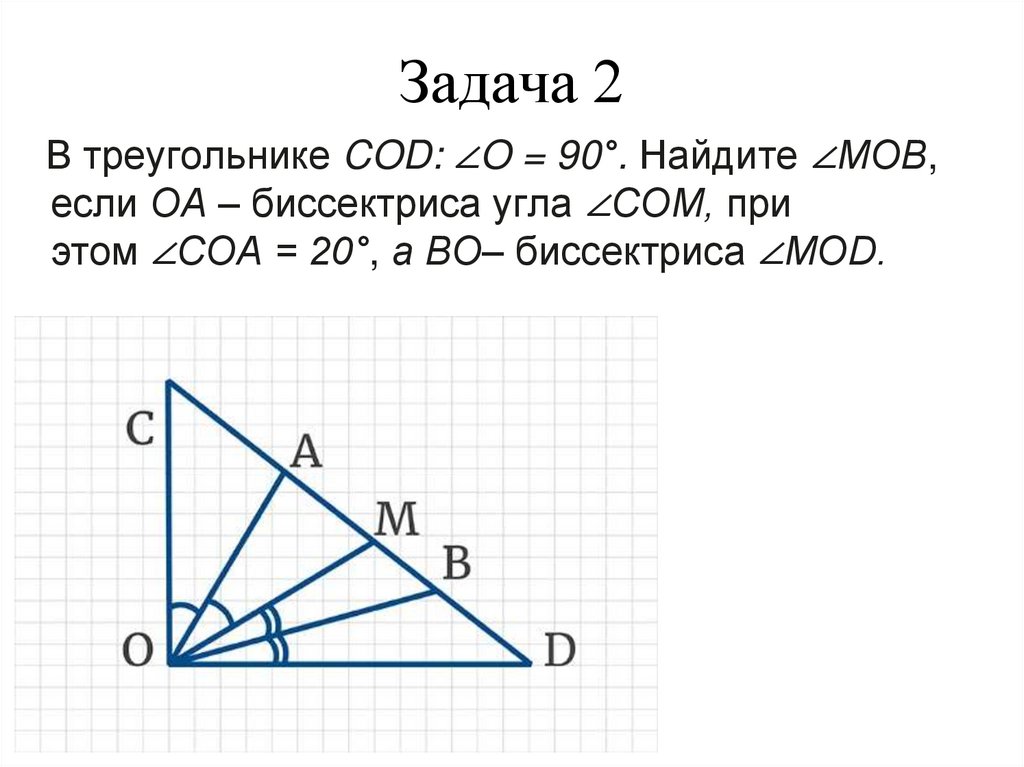
51. Задача 2
В треугольнике COD: ∠O = 90°. Найдите ∠МОВ,если ОА – биссектриса угла ∠СОM, при
этом ∠COА = 20°, а ВО– биссектриса ∠МОD.
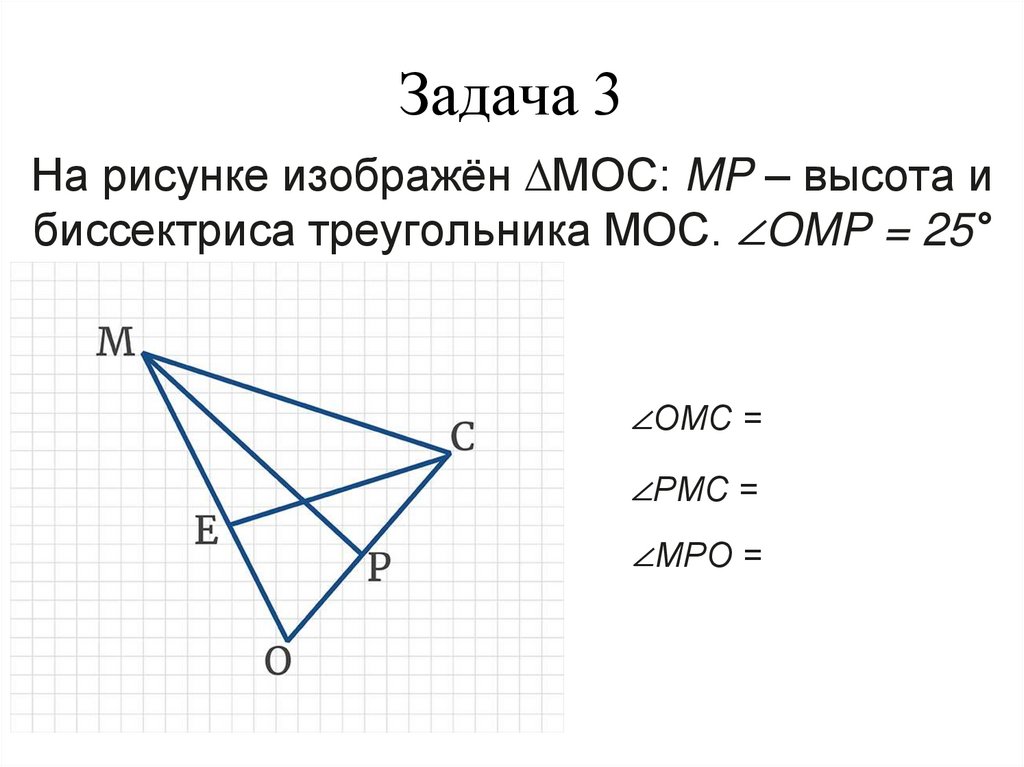
52. Задача 3
На рисунке изображён ∆MOC: MP – высота ибиссектриса треугольника MOC. ∠OMP = 25°
∠OMС =
∠РMС =
∠MРО =
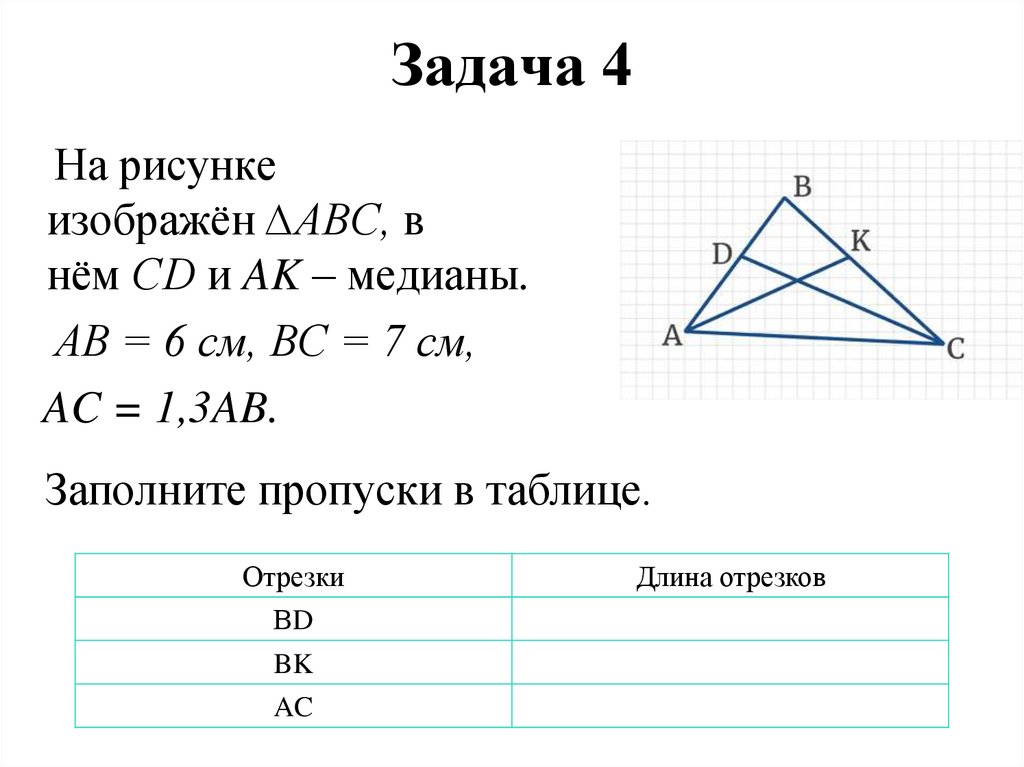
53. Задача 4
На рисункеизображён ∆АBС, в
нём СD и AK – медианы.
AB = 6 см, BC = 7 см,
AC = 1,3AB.
Заполните пропуски в таблице.
Отрезки
ВD
BK
AC
Длина отрезков
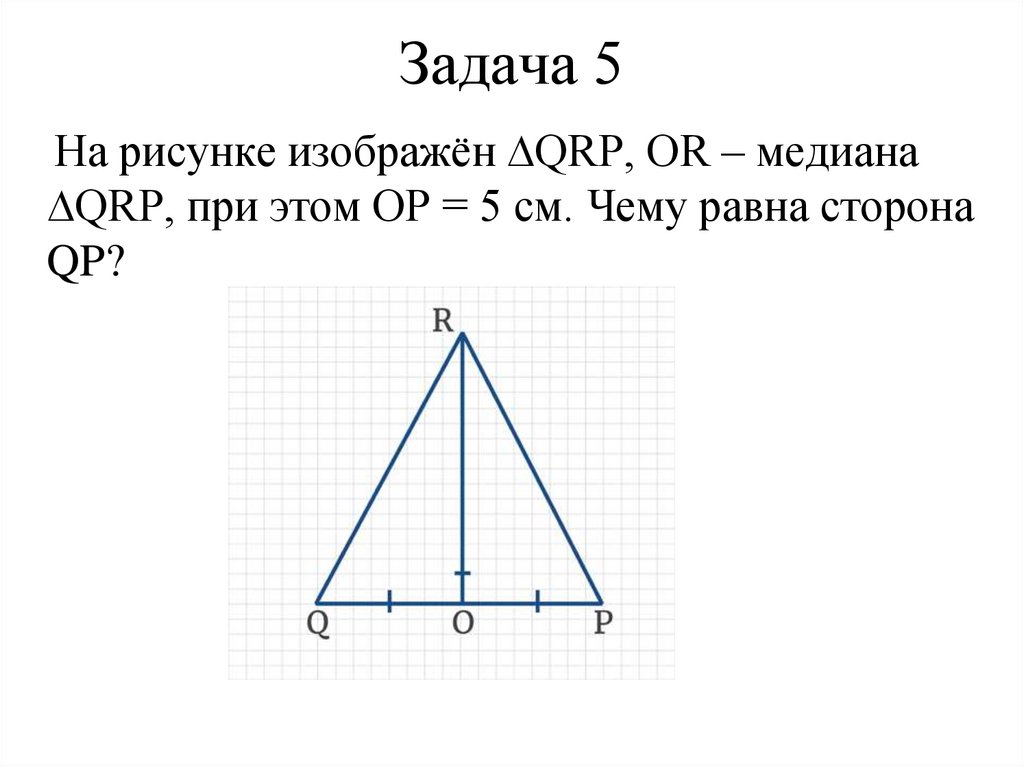
54. Задача 5
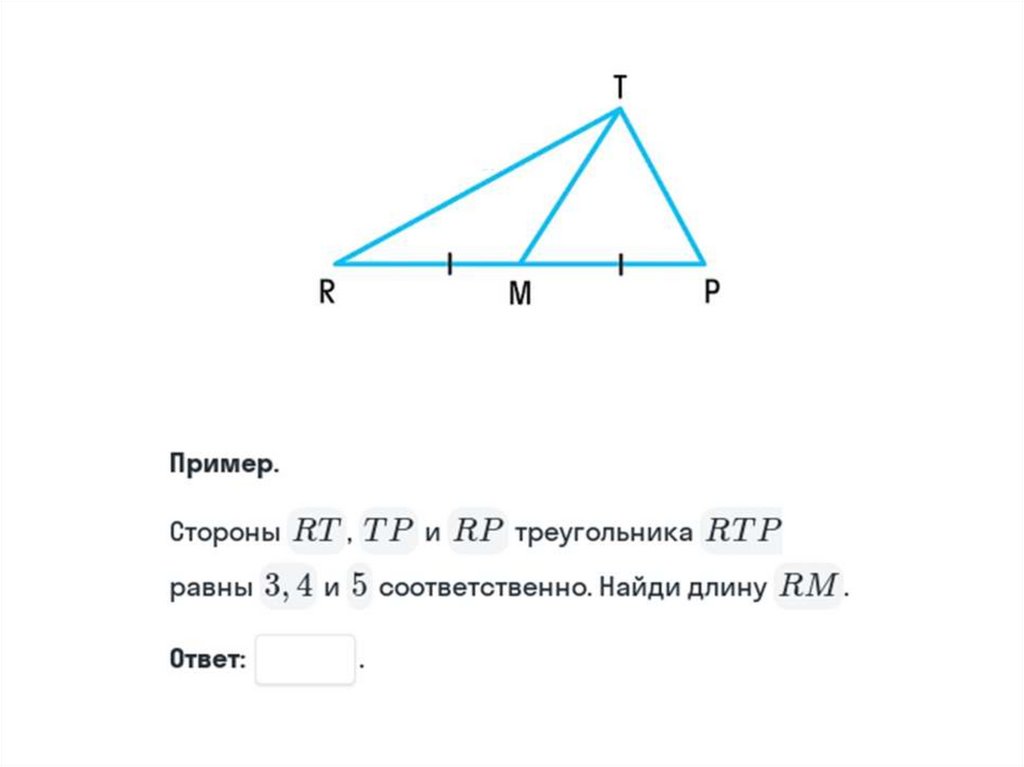
На рисунке изображён ∆QRP, ОR – медиана∆QRP, при этом OP = 5 см. Чему равна сторона
QP?
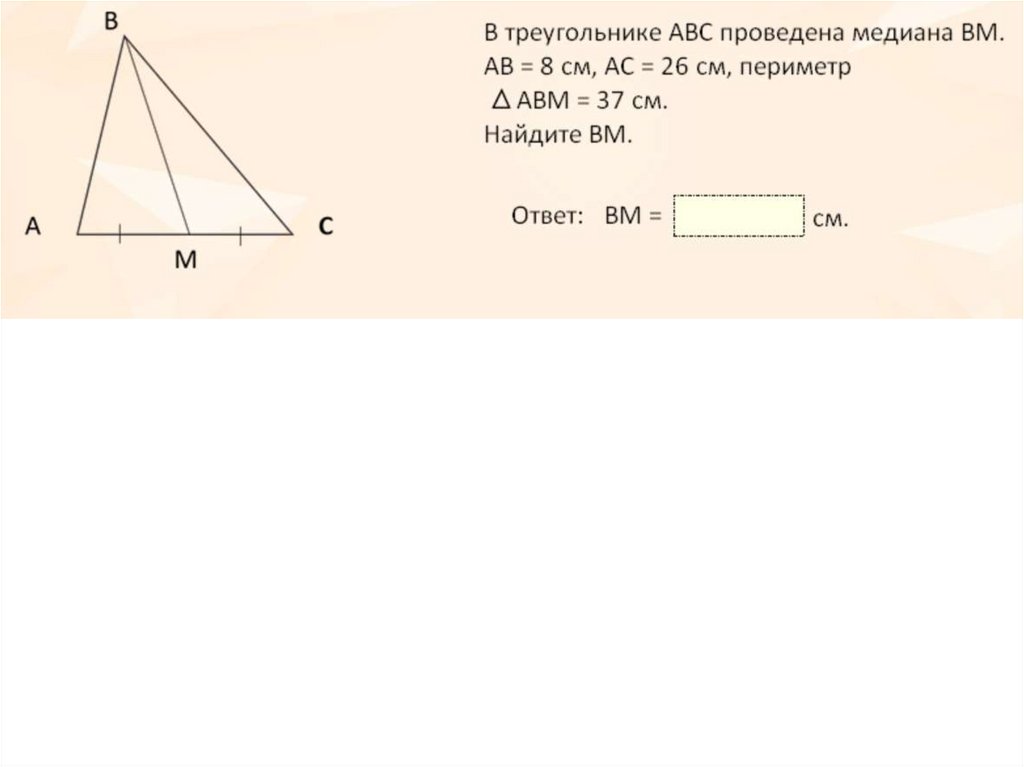
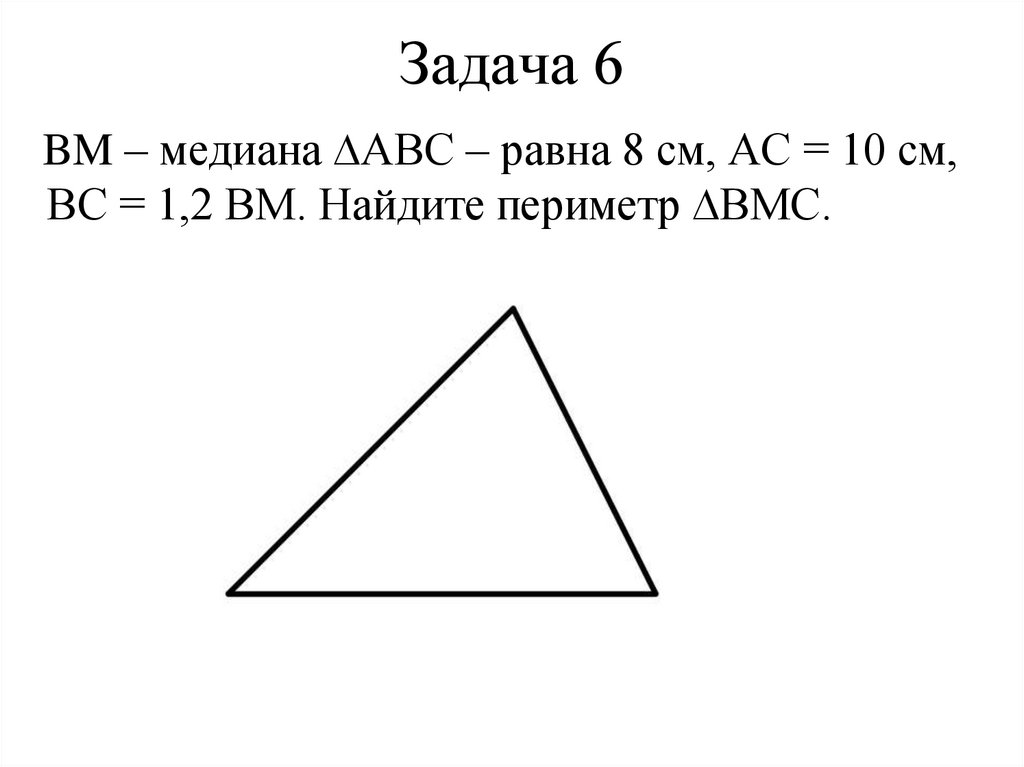
55. Задача 6
BM – медиана ∆ABC – равна 8 см, AC = 10 см,BC = 1,2 ВМ. Найдите периметр ∆BMC.
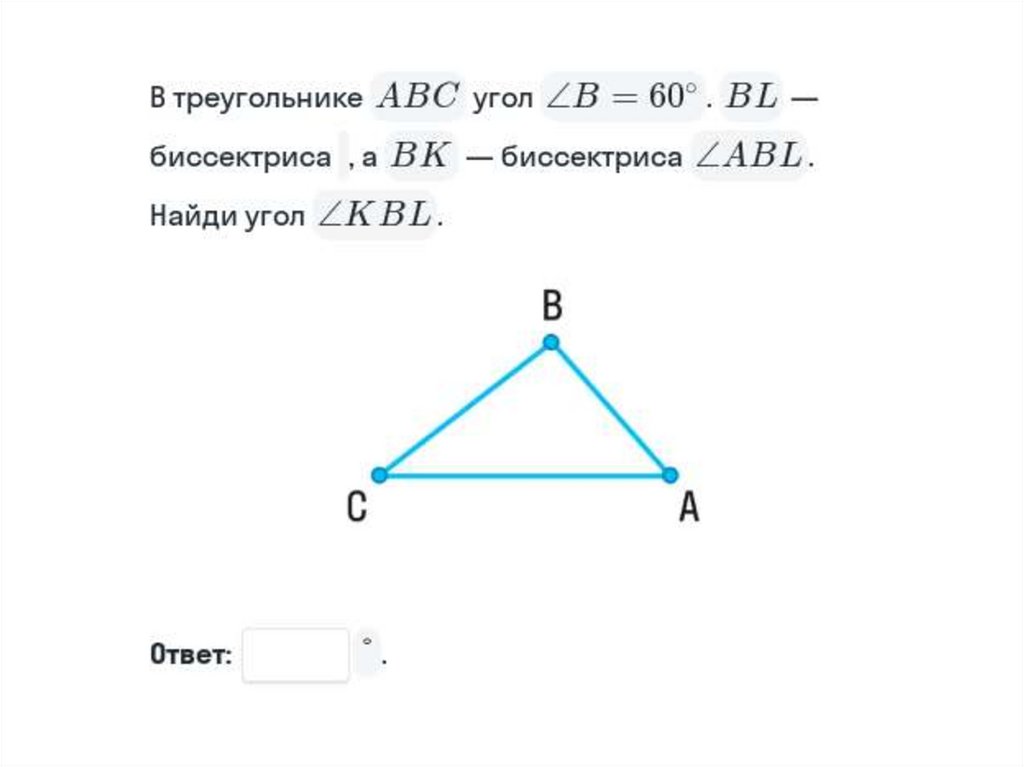
56. Задача 7
На рисунке изображён ∆QRP, в нем RO –высота и медиана треугольника QRP,
сторона QR = RP = 1,4QO. Укажите, чему
равна сторона RP, если сторона QP = 12 см.















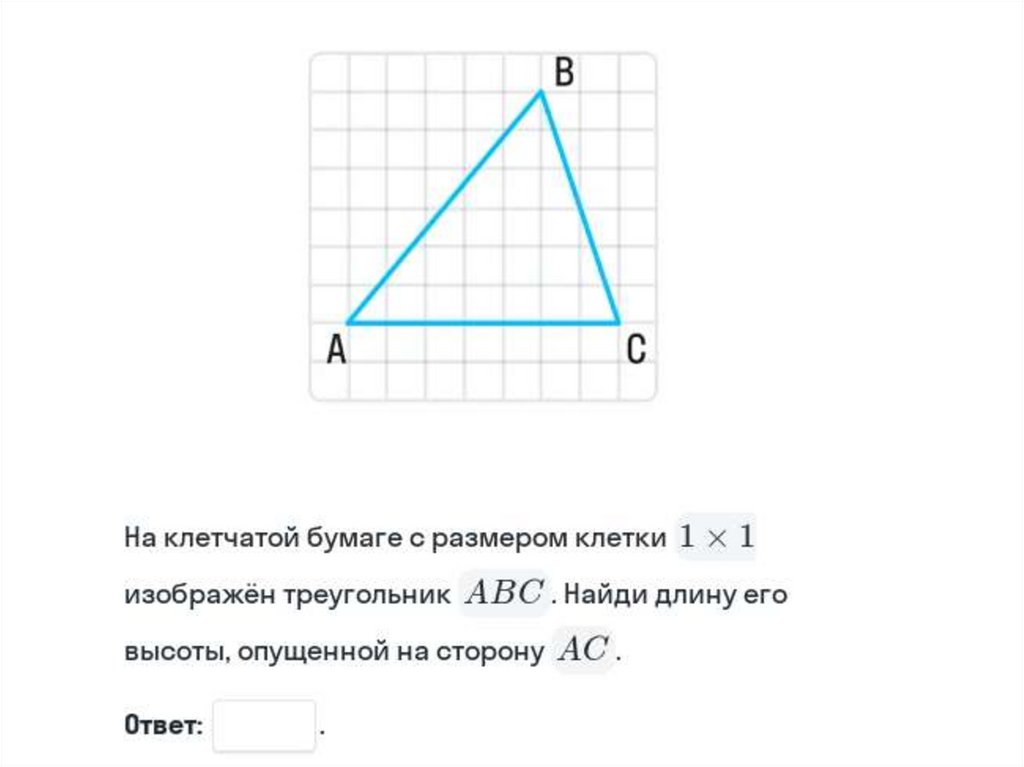
 Математика
Математика