Week13(1)

1.

MathB1001
Mathematics and Statistics I
Lecture 13
Dr. Binru Wei

2. Contents for today

Geometric interpretation of coordinates
Properties of determinants
Cramer’s rule
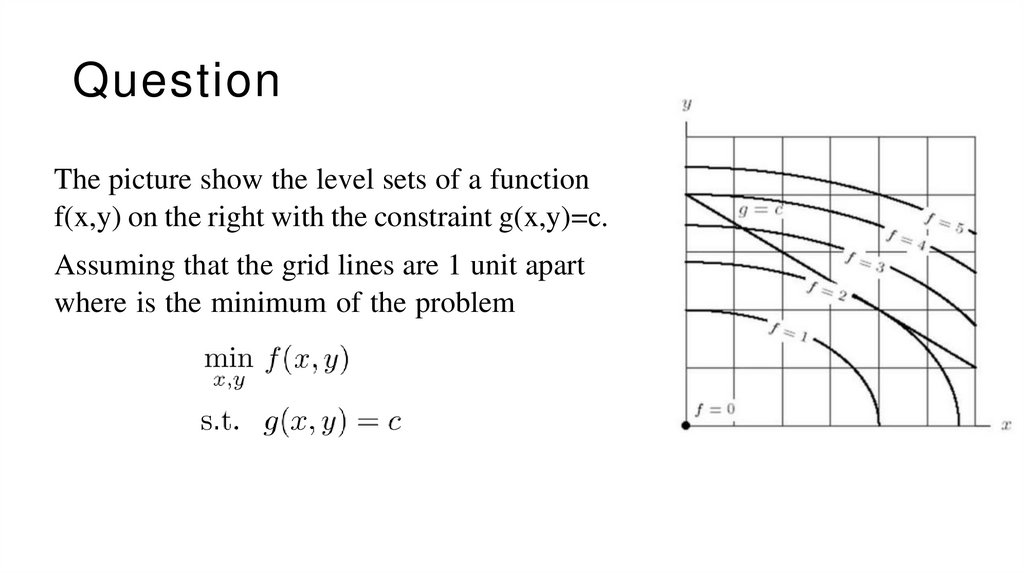
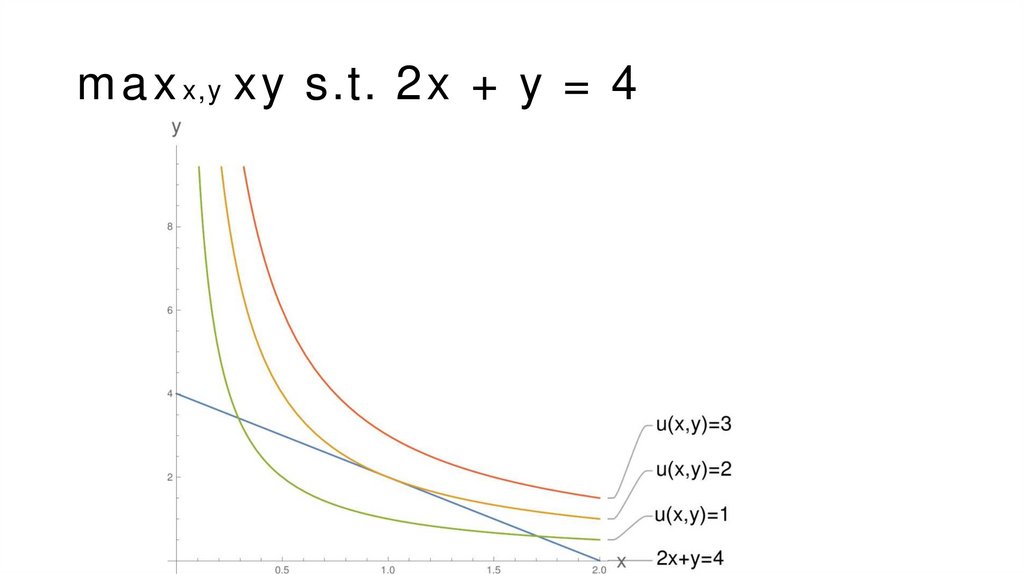
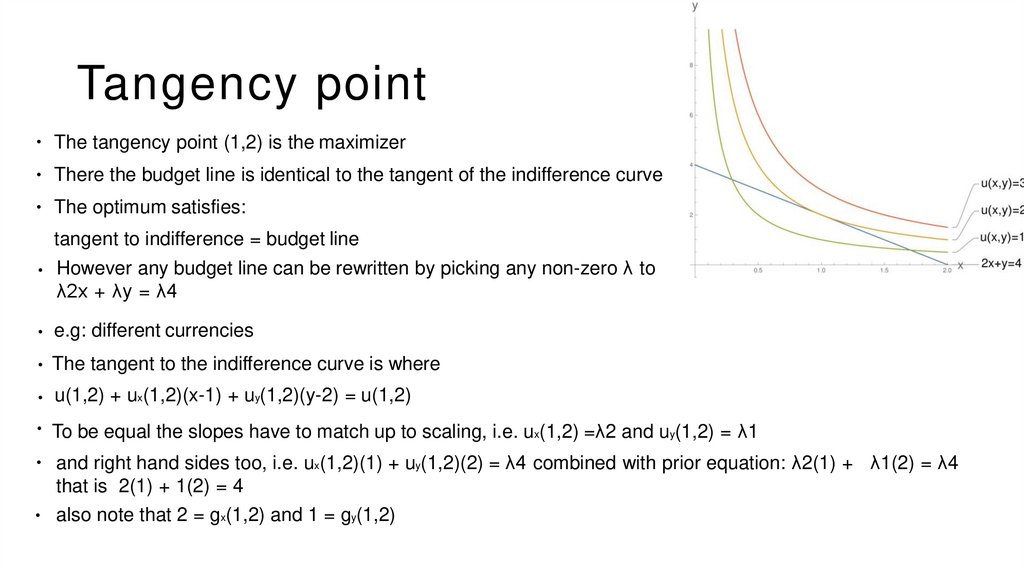
Constrained Optimization
The Lagrangian

3.

Geometric interpretation of
coordinates

4.

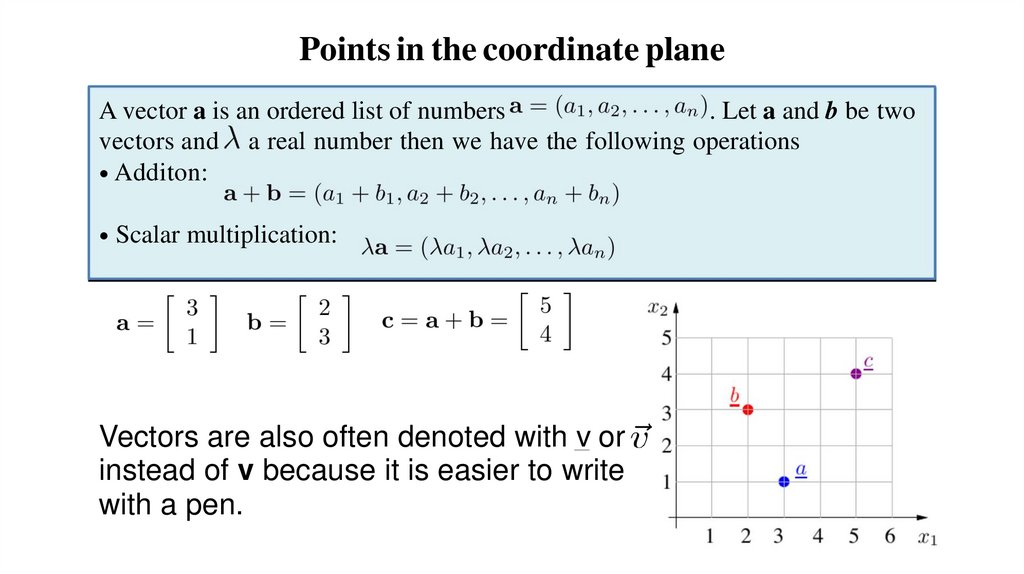
Points in the coordinate plane
A vector a is an ordered list of numbers
. Let a and b be two
vectors and a real number then we have the following operations
● Additon:
● Scalar multiplication:
Vectors are also often denoted with v or
instead of v because it is easier to write
with a pen.

5.

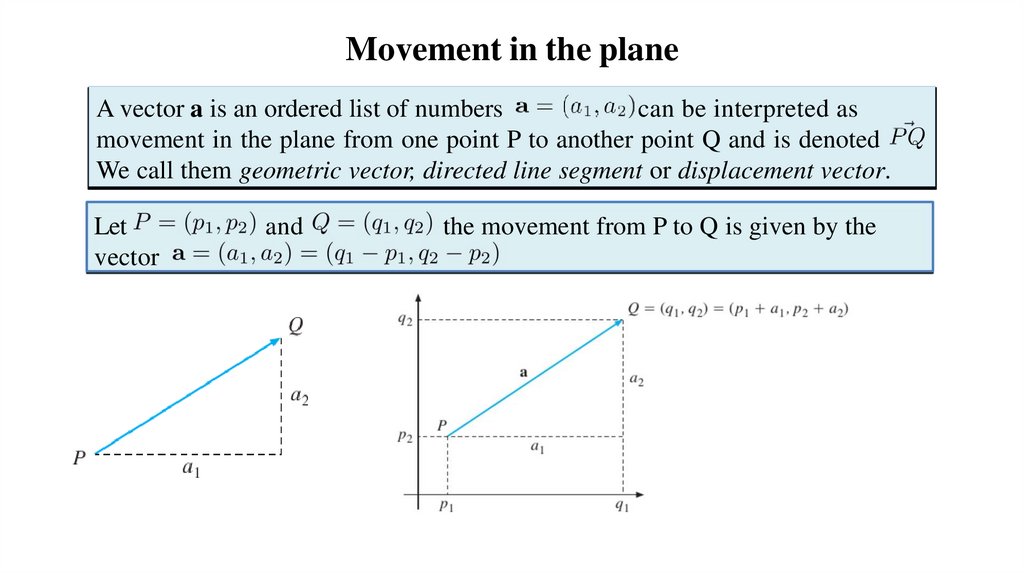
Movement in the plane
A vector a is an ordered list of numbers
can be interpreted as
movement in the plane from one point P to another point Q and is denoted
We call them geometric vector, directed line segment or displacement vector.
Let
vector
and
the movement from P to Q is given by the

6.

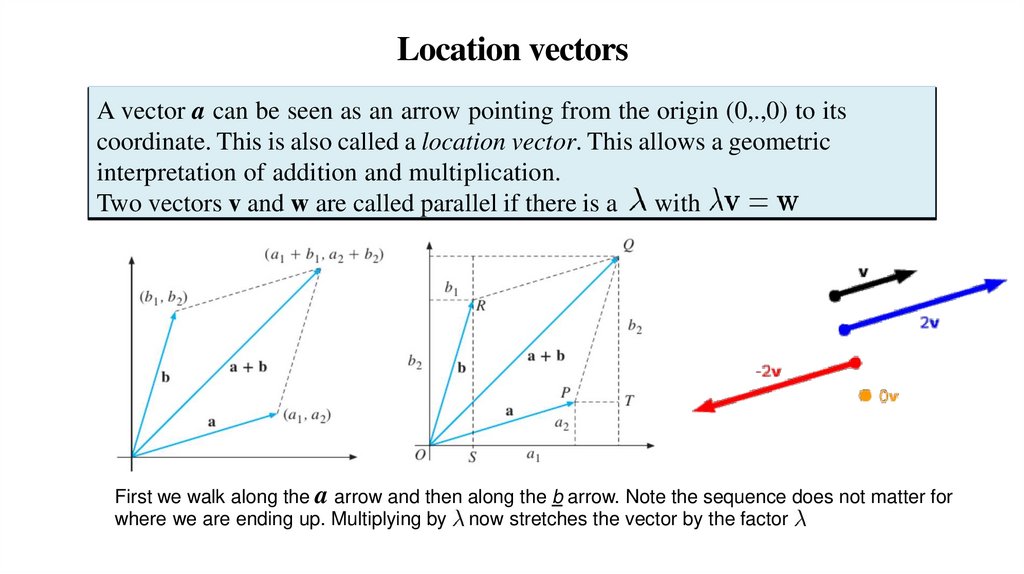
Location vectors
A vector a can be seen as an arrow pointing from the origin (0,.,0) to its
coordinate. This is also called a location vector. This allows a geometric
interpretation of addition and multiplication.
Two vectors v and w are called parallel if there is a with
First we walk along the a arrow and then along the b arrow. Note the sequence does not matter for
where we are ending up. Multiplying by now stretches the vector by the factor

7.

Length of vectors and the standard basis
The length of a vector a (in the Euclidean norm) is
We call the vector a a unit vector if it has length one
The vectors where the i-th entry is one and all other entries are zero is denoted
by e .
In
the vectors e ,e ,.,e are called the standard basis. We can represent
any vector with them.
i
1
For example in
2
n
the standard basis is

8.

Question
Consider a vector in
Find a vector that is
with
1) Parallel but not equal to v
2) Points in the opposite direction of v
3) Has unit length and is parallel to v

9.

Definition of the Dot Product
For any two vectors
The following two definitions of the dot product, or scalar product,