Похожие презентации:
3сем_Лк 7_ЛНДУ с прав частью спец вида (1)
1.
Первое высшее техническое учебное заведение РоссииСанкт-Петербургский горный университет императрицы Екатерины II
Кафедра высшей математики
Лекция 7.
Линейные неоднородные ДУ
с правой частью специального вида
22.12.2025
г. Санкт-Петербург
2025
1|10
2.
Метод неопределенных коэффициентовотыскания частного решения ЛНДУ
y p y q у f (x) (1
ЛНДУ
)
f(x) специального вида:
f ( x) e
a,b
Частное решение:
ax
R ( x) cos bx T ( x) sin bx
n
многочлены степени n и m
R
y ( x) x e
*
m
r ax
P ( x) cos bx Q ( x) sin bx
k
k
многочлены степени k k max(n, m)
Pk ( x) Ak x k Ak 1 x k 1 A1 x A0
Qk ( x) Bk x Bk 1 x
k
k 1
B1 x B0
Найти неопределенные коэффициенты многочленов
2|10
3.
Алгоритм построения частного решения ЛНДУ1. Определить постоянные a, b, n и m.
Записать вспомогательное число
2. Найти показатель степени многочленов:
=a ib
k max(n, m)
3. Составить характеристическое уравнение и найти корни: k1,2 =
4. Сравнить
с корнями и найти показатель r степени хr :
0, если k1 и k2 ;
r 1, если k1 и k2 k1 и k2 ;
2, если k1 k2 .
5. Записать частное решение и подставить в ДУ.
6. Найти неопределенные коэффициенты многочленов и записать
многочлены в формуле частного решения
3|10
i
4.
3xy
5
y
6
y
4 x 5 e
Пример 1. Найти частное решение уравнения
f ( x) e
ax
a 3
R ( x) cos bx T ( x) sin bx 4 x 5 e
n
3x
m
b 0 n 1 m 0 вспомогательное число a ib 3
k max(1, 0) 1
P1 ( x) A1 x A0
Характеристическое уравнение:
k2 3
k 5k 6 0 k1 2,
2
=3– простой корень (кратность 1) k1 k2
Частное решение ДУ имеет вид:
r 1
y xe ( A1 x A0 )
3x
Найдем неопределенные коэффициенты
4|10
A1 , A0
5.
6 y e A1 x A0 x3x
5
y 5 y 6 y 4 x 5 e3 x
2
3x
3x
2
y 3 e ( A x A x) e (2 A x A )
1
y 9 e
3x
1
0
0
A x A x 6 e 3 x 2 A1 x A0 e 3 x 2 A1
2
1
0
2 A1 x A0 2 A1 e
2 A1 4;
A0 2 A1 5
3x
4 x 5 e .
3x
A1 2,
y ( x) e
A0 1
5|10
3x
2 x x
2
6.
ЛНДУ 3-го и 4-го порядка с постояннымикоэффициентами
Общее решение ЛНДУ –
сумма общего решения y (x ) соответствующего ЛОДУ
и частного решения y (x ) ЛНДУ
Пример 2 . Найти общее решение ДУ
f ( x) e
ax
R ( x) cos bx T ( x) sin bx х
n
1. Постоянные a 0
2.
2
y 3y 2 у x
2
m
a ib 0
b 0
n 2 m 0 k max(2, 0) 2
3. Характеристическое уравнение: k1 0
k 3 3k 2 2k 0
k2 1
k3 2
6|10
P2 ( x) А0 х А1 х А2
2
y1 e =1
x
y2 e
x
2x
C
C
e
C
e
2
3
2 x y (x ) 1
y3 e
0
7.
:4. Поскольку
r 1
=0 – простой корень характеристического уравнения
5. Правая часть – многочлен 2-ой степени. Частное решение ищем в виде:
y
х( А0 х 2 А1 х А2 ) А0 х 3 А1 х 2 А2 х
у 3 А х 2 А х А
у 6 А х 2 А
*
2
0
1
0
1
2
*
6 А0 3(6 А0 х 2 А1 ) 2(3 А0 х 2 А1 х А2 ) х .
2
1
A0
6
3
A1
4
y C1 C 2 e C 3 e
x
2x
2
7
A2
4
1 3 3 2 7
х х х
6
4
4
y (x)
y (x)
6|10
8.
Пример 3 . Найти общее решение ДУ yIV
y 4 cos х
Характеристическое ур–е: k 4 1 0
k1 1, k 2 1, k3 i, k4 i.
Общее решение ЛОДУ:
у1 e у 2 e у cos x у sin x
3
3
x
x
y (x) C1e C 2 e
x
x
C3 cos x C 4 sin x.
R 4, T 0.
0х
f
(
x
)
е
( R cos x T sin x)
Правая часть ДУ:
=a
a=0, b=1
ib=
Частное решение искать в виде:
y х( А cos x В sin x).
8|10
i
совпадает с
простым корнем
9.
y х( А cos x В sin x)y y 4 cos х
IV
y ( А cos x В sin x) х( А s inx Вco s x)
( А Bx) cos x ( В Ax) sin x
y B cos x ( A Вx) sin x Asin x ( В Ax) cos x
(2 B Аx) cos x (2 A Вx) sin x
Находим производные 3–го и 4–го порядка
4 А sin x 4 B cos x 4 cos x.
А = 0, В = –1
у C1e C 2 e
x
x
y х sin x.
C 3 cos x C 4 sin x х sin x.
9|10
10.
Спасибо за вниманиеКафедра высшей математики;
Санкт-Петербургский горный
университет императрицы
Екатерины II;
199106, Санкт-Петербург,
Васильевский остров, 21 линия д.2;
Тел.: +7(812) 328-82-31;
E-mail: kafmatem@spmi.ru
10|10








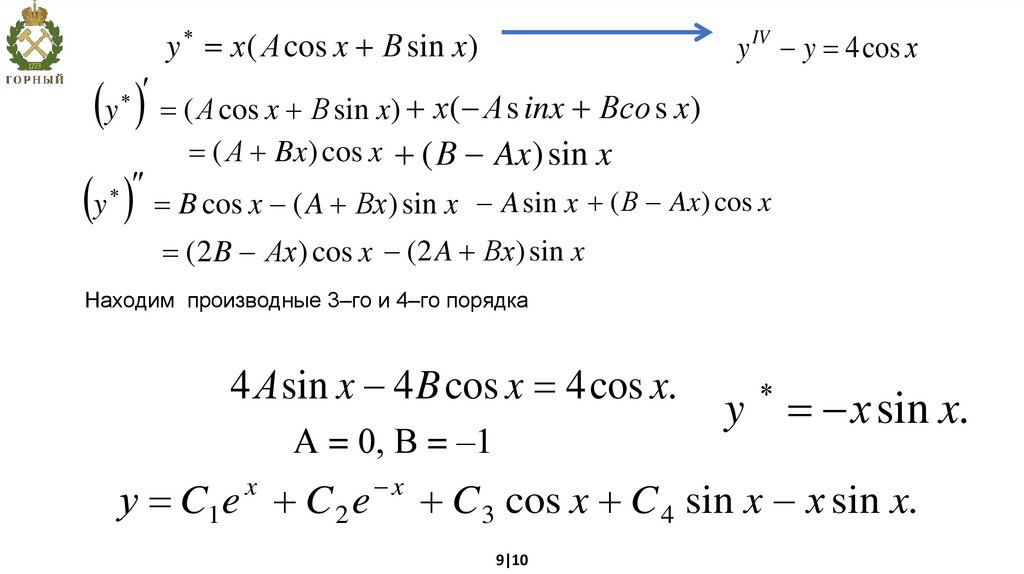

 Математика
Математика








