Похожие презентации:
Линейные ДУ второго порядка с постоянными коэффициентами. Тема 21.8
1.
Рассмотрим случай, когда в уравненииy p( x) y g ( x) y f ( x)
функции p(x) и g(x) – постоянные величины.
2.
Уравнение видаy p y g y f (x)
называется линейным ДУ с
постоянными коэффициентами
9
3.
Где у – искомая функция, p, g – постоянныевеличины.
Если f(х)=0, то уравнение называется
линейным однородным.
Если f (х) не равно 0, то уравнение
называется линейным неоднородным.
4.
Рассмотрим сначала однородное уравнение:y p y g y 0
10
Будем искать решение этого уравнения в виде
y e
kx
Где k - некоторое число.
Находим производные и подставляем в исходное
уравнение:
5.
y k ekx
y k e
2
kx
k e p k e g e 0
2
kx
kx
kx
k p k g 0
2
Это уравнение называется характеристическим
уравнением для уравнения (10).
6.
Вид решения линейного однородного ДУ (10)существенно зависит от того, какие корни
имеет его характеристическое уравнение.
Обозначим эти корни как k1 и k2.
7.
Если корни характеристическогоуравнения вещественные и разные
k1 k2
то общее решение однородного
уравнения (9) имеет вид:
y C1e
k1 x
C2e
k2 x
8.
Если корни характеристическогоуравнения вещественные и равные
k1 k2 k
то общее решение однородного
уравнения (10) имеет вид:
y C1e C2 x e
kx
kx
9.
Если характеристическое уравнениене имеет вещественных корней,
то общее решение однородного
уравнения (10) имеет вид:
y C1e cos x C2e sin x
x
где
x
k1 i
k2 i
-комплексные корни
характеристического уравнения.
10.
1Решить дифференциальное уравнение:
y 5 y 4 y 0
11.
y ek 5k 4 0
5 3
D 25 16 9 k1, 2
2
k1 4
kx
2
k2 1
Корни вещественные и разные, поэтому общее
решение будет иметь вид:
y C1e C2e
x
4x
12.
2Решить дифференциальное уравнение:
y 6 y 9 y 0
13.
y ekx
D 36 36 0
k 6k 9 0
6
k1, 2 3 k
2
2
Корни вещественные и одинаковые, поэтому общее
решение будет иметь вид:
y C1e C2 x e
3x
3x
14.
3Решить дифференциальное уравнение:
y 2 y 2 y 0
15.
y ekx
D 4 8 4
k 2k 2 0
2 4
k1, 2
1 i
2
k1 1 i
2
k2 1 i
Корни комплексные, поэтому общее решение будет
иметь вид:
y C1e x cos x C2e x sin x
16.
Теперь рассмотрим решение неоднородного ЛДУ спостоянными коэффициентами (9).
Общее решение неоднородного ЛДУ
с постоянными коэффициентами
находится как сумма общего решения
однородного уравнения и какого-либо
частного решения неоднородного
уравнения.
17.
Решить дифференциальное уравнение:x
y 3y 2 y e
18.
Сначала находим общее решение однородногоуравнения:
y 3 y 2 y 0
kx
2
y e
k 3k 2 0
D 9 8 1
k1 2
k2 1
3 1
k1, 2
2
19.
Корни вещественные и разные, поэтому общеерешение будет иметь вид:
2x
x
~
y ( x) C1e C2e
Теперь находим частное решение неоднородного
уравнения методом вариации постоянных в виде:
Y ( x) C1 ( x) e C2 ( x) e
2x
2x
Y ( x) C1 ( x) e C1 ( x) 2 e
x
x
C2 ( x) e C2 ( x) e
2x
x
20.
ПустьC1 ( x) e C2 ( x) e 0
2x
x
Тогда
2x
x
Y ( x) C1 ( x) 2e C2 ( x) e
Y C1 ( x) 2e 2 x C1 ( x) 4e 2 x
x
x
C2 ( x) e C2 ( x) e
Подставляем в уравнение:
21.
C1 ( x) 2e 4C1 ( x) e C2 ( x) e2x
2x
x
C2 ( x) e 6C1 ( x) e 3C2 ( x) e
x
2x
x
2C1 ( x) e 2C2 ( x) e e
2x
x
x
Получаем:
C ( x) e 2 x C ( x) e x 0
1
2
2x
x
x
2C1 ( x) e C2 ( x) e e
22.
Вычитаем из второго уравнения первое:C2 ( x ) e e
x
C ( x) e
2x
x
2
Теперь подставляем в первое уравнение:
x
C1 ( x) e e e 0
x
2x
C1 ( x) e x e x 1
23.
Интегрируем эти выражения:C1 ( x) dx x
C2 ( x) e dx e
x
Частное решение
имеет вид:
неоднородного
x
Y xe e e
x
x
2x
уравнения
xe e
x
Общее решение будет:
y C1 e C2 e x e e
x
2x
x
x
x
24.
Частное решение неоднородного уравненияможно найти, используя следующую схему:
25.
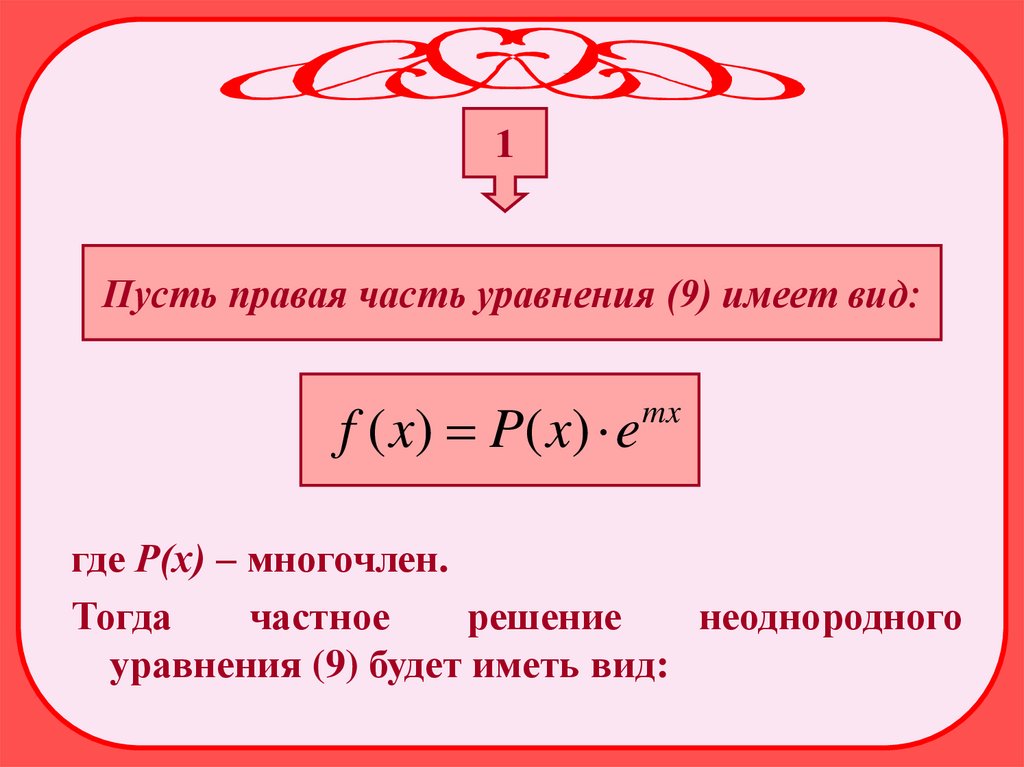
1Пусть правая часть уравнения (9) имеет вид:
f ( x) P( x ) e
mx
где Р(х) – многочлен.
Тогда
частное
решение
неоднородного
уравнения (9) будет иметь вид:
26.
y ( x ) x Q( x ) er
mx
где Q(х) – многочлен той же степени, что и Р(х).
Причем,
если
m
не
является
корнем
характеристического уравнения, то
r=0,
а если является, то r – кратность этого корня.
27.
Решить дифференциальное уравнение:y 2 y y 1 x
28.
Сначала решаем однородное уравнение:y 2 y y 0
y e
kx
D 4 4 0
k 2k 1 0
2
2
k1, 2 1 k
2
Корни вещественные и одинаковые, поэтому общее
решение однородного уравнения будет иметь вид:
x
x
~
y ( x) C1e C2 x e
29.
Теперь решаем неоднородное уравнение. Праваячасть представляет собой рассмотренный
случай:
P( x) 1 x
m 0
m – не является корнем характеристического
уравнения, следовательно r=0. Поэтому частное
решение неоднородного уравнения будем
искать в виде:
Y ( x) A x B
30.
Находим производные и подставляем в исходноеуравнение:
Y ( x ) A
Y ( x ) 0
2 A Ax B 1 x
A 1
B 3
Частное решение неоднородного уравнения имеет
вид:
Y ( x) x 3
31.
Общее решение неоднородного уравнениязапишем
как
сумму
общего
решения
однородного уравнения и частного решения
неоднородного уравнения:
y C1e C2 x e x 3
x
x
32.
2Пусть правая часть уравнения (9) имеет вид:
f ( x) a cos nx b sin nx
33.
Если числа inне являются корнями характеристического
уравнения, то частное решение неоднородного
уравнения (9) будет иметь вид:
y A cos nx B sin nx
Если числа in
являются
корнями
характеристического
уравнения, то частное решение будет иметь вид:
y x A cos nx B sin nx
34.
Решить дифференциальное уравнение:y 4 y 13 y 5 sin 2 x
35.
Сначала решаем однородное уравнение:y 4 y 13 y 0
y e
kx
D 16 52 36
k 4k 13 0
2
4 36
k1, 2
2 3i
2
k1 2 3i
k 2 2 3i
36.
Корни комплексные, поэтому общее решение будетиметь вид:
2 x
~
y ( x) e (C1 sin 3x C2 cos 3x)
Теперь решаем неоднородное уравнение. Правая
часть представляет собой рассмотренный
случай:
n 2
2i
и
–2i
не
являются
корнями
характеристического уравнения, следовательно
частное решение неоднородного уравнения
будем искать в виде:
Y ( x) A cos 2 x B sin 2 x
37.
Находим производные и подставляем в исходноеуравнение:
Y ( x) 2 A sin 2 x 2 B cos 2 x
Y ( x) 4 A cos 2 x 4 B sin 2 x
4 A cos 2 x 4B sin 2 x 8 A sin 2 x 8B cos 2 x
13 A cos 2 x 13B sin 2 x 5 sin 2 x
4 B 8 A 13B 5
4 A 8B 13 A 0
8
A 29
9
B
29
38.
Частное решение неоднородного уравнения имеетвид:
8
9
Y ( x)
cos 2 x
sin 2 x
29
29
Общее
решение
неоднородного
уравнения
запишем
как
сумму
общего
решения
однородного уравнения и частного решения
неоднородного уравнения:
y e
2 x
8
9
(C1 sin 3x C2 cos 3x) cos 2 x sin 2 x
29
29
39.
3Пусть правая часть уравнения (9) имеет вид:
f ( x) e ( P1 ( x) cos nx P2 ( x) sin nx)
mx
где Р1(х) и Р2(х) – многочлены.
40.
Если числа m inне являются корнями характеристического
уравнения, то частное решение неоднородного
уравнения (9) будет иметь вид:
y e ( R1 ( x) cos nx R2 ( x) sin nx)
mx
Если числа m in
являются
корнями
характеристического
уравнения, то частное решение будет иметь вид:
y x e ( R1 ( x) cos nx R2 ( x) sin nx)
mx
41.
где R1(х) и R2(х) – многочлены той же степени, чтои многочлены Р1(х) и Р2(х) .








































 Математика
Математика








