L13_Relativity1_2025_12_01

1.

Общая Физика
Лекция 13
Механика больших скоростей
(Special Relativity)
Лектор:
доцент НИЯУ МИФИ, к.ф.-м.н.,
Ольчак Андрей Станиславович

2.

С чего начинается физика?
Физика начинается с двух догадок.
1. Покой и движение – понятия не абсолютные, а
относительные. Все зависит от того кто и из какой
системы отсчета наблюдает.
- это принцип относительности, который был вполне осознан
только в XVII веке (Коперник, Галилей, и – в окончательной
формулировке - Ньютон
2. Если наблюдать за движением тела из «правильной»
(инерциальной) системы отсчета, и если на тело не
действуют никакие реальные физические силы, то такое
тело будет двигаться с постоянной по величине и
направлению скоростью, либо покоиться. - это т.н. Первый
закон механики Ньютона.

3.

С чего начинается физика?
ЛОГИЧЕСКИЕ СЛЕДСТВИЯ принципа относительности и Первого
закона механики.
• Состояние покоя = состояние движения с неизменной по величине и
направлению скоростью. Состояние с нулевой скоростью ничем
физически не отличается от состояния движения с постоянной, но НЕ
нулевой скоростью
• Все «правильные» наблюдатели (системы отсчета), движущиеся друг
относительно друга равномерно и прямолинейно, физически
равноправны. Во всех «правильных» (инерциальных) системах отсчета
если нет сил – скорость не меняется, а если есть – то меняется.
• Логично предположить, что чем больше сила – тем быстрее меняется
скорость. Это умозаключение выражается формулой
F = mdv/dt

4.

Сложение скоростей.
Преобразования Галилея
Y
Y’
чч:мм:сс
v’ = v - u
V
V’
-u
0’
0
Z’
u
Z
чч:мм:сс
x(t)
x’(t’)
X, X’
x’ = x - ut
t’ = t
x’
t’
1 –u
= 0 1
Матричное умножение - красивая и компактная форма
записи простых и очевидных преобразований Галилея.
В электродинамике тоже есть формулы преобразований.
Очень похожие, да не совсем…
γ(u) = (1 - u2/c2)-½
1 –u
Ey’
= γ(u) -u/c2 1
Bz’
x
t
Galileo GALILEI
1564-1642
Ey
LORENTZ
с – скорость распространенияHendrik
1853-1928
Bz электромагнитных волн (света)

5.

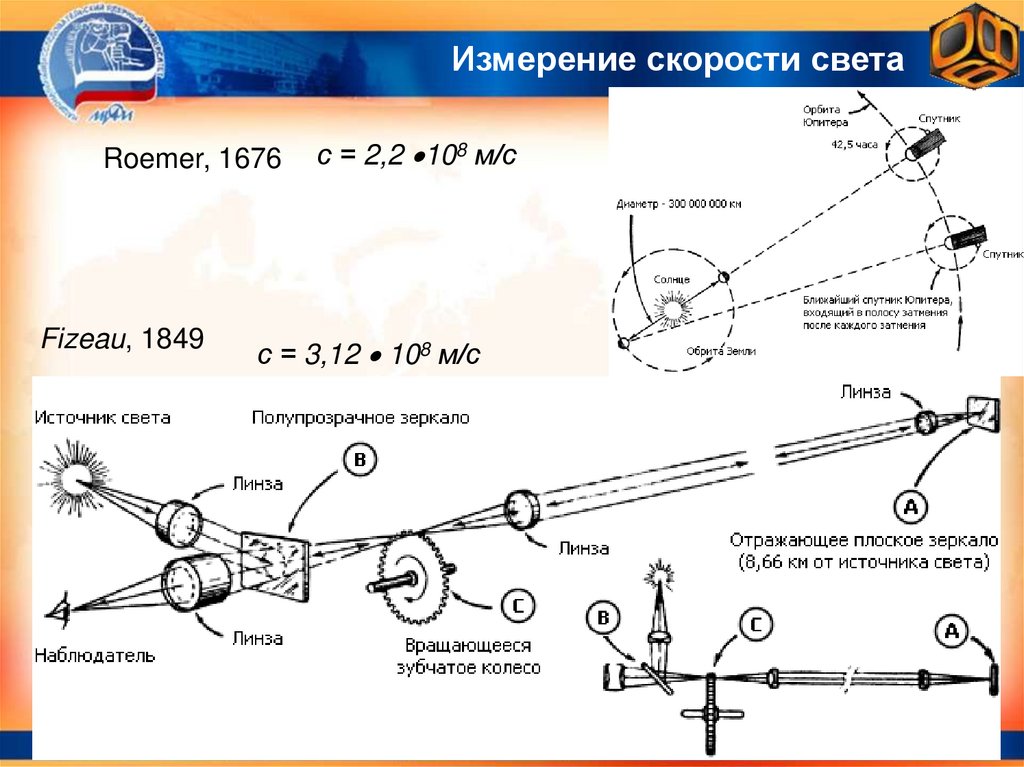
Измерение скорости света
Roemer, 1676
Fizeau, 1849
с = 2,2 108 м/с
с = 3,12 108 м/с

6.

Постоянство скорости света
Michelson & Morley, 1887
Опыт Майкельсона-Морли,
последующие опыты Миллера и др.,
убедительно показали, что скорость
света не зависит ни от направления
движения Земли, ни от направления
распространения света и равна
с = 3 · 108 м/с
http://www.lightandmatter.com/html_books/6mr/
ch01/ch01.html
А. Майкельсон
Э. Морли

7.

Величина скорости света
Наиболее точно измеренное значение скорости света в вакууме
(в единицах системы СИ):
с = 299 792 458 м/с
Погрешность наиболее точных измерений 1975-1978 г.г.: ~1,2 м/с (~4*10-9)
С 1983 года значение скорости с считается точно заданным и само является
основой эталона определения величины метра. :
Приближенное значение с = 3 · 108 м/с является достаточно точным
для большинства расчетов

8.

Преобразования Галилея и Лоренца
Y’
Y
чч:мм:сс
v’ = v - u
V
V’
-u
0’
0
Z’
u
Z
чч:мм:сс
1 –u
Ey’
= γ(u) -u/c2 1
Bz’
x(t)
x’(t’)
X, X’
x’ = x - ut
t’ = t
x’
t’
1 –u
= 0 1
x
t
Galileo GALILEI
1564-1642
γ(u) = (1 - u2/c2)-½
Ey
с – скорость распространения
Bz электромагнитных волн (света)
В чем проблема»? В преобразованиях Галилея нет никаких
ограничений на скорость движения системы отсчета u, а у
Лоренца скоростей u>c быть не может в принципе (!?).
Hendrik LORENTZ
1853-1928

9.

Идея Эйнштейна - Пуанкаре
Идея А. Эйнштейна (1905) и А. Пуанкаре:
Y
применить преобразования типа Лоренца к
механике.
x’
t’
1 –v
= 0 1
x
t
=>
X, X’
0’
0
v
Z
1 –v
x’
=
γ(v)
-v/c2 0
t’
1
Y’
Z’
x(t)
x’(t’)
x
t
γ(v) = (1 - v2/c2)-½
Albert Einstein
1879-1955
Henri Poincare
1854-1912

10.

Идея Эйнштейна - Пуанкаре
Идея А. Эйнштейна и А. Пуанкаре: применить
Y
преобразования типа Лоренца к механике.
x’
t’
1 –v
= 0 1
x
t
=>
Y’
X, X’
0’
0
v
Z
Z’
x(t)
x’(t’)
1 –v
x’
x
2/c2)-½
γ(v)
=
(1
v
=
γ(v)
-v/c2 0 t
t’
1
При v<<c => γ ~= 1 ; -v/c2 -> 0 преобразования Лоренца
превращаются в преобразования Галилея.
Время и координаты выражаются друг через друга, что означает их
неразрывную связь.
Пространство + время = пространство-время (space- time)

11.

События. Уточняем постановку задачи).
Y’
0’
Z’
Y
0
u
X, X’
Z
Y’
Y
0’ 0
Z
u
X, X’
Y
0
Y’
0’
Z
Z’
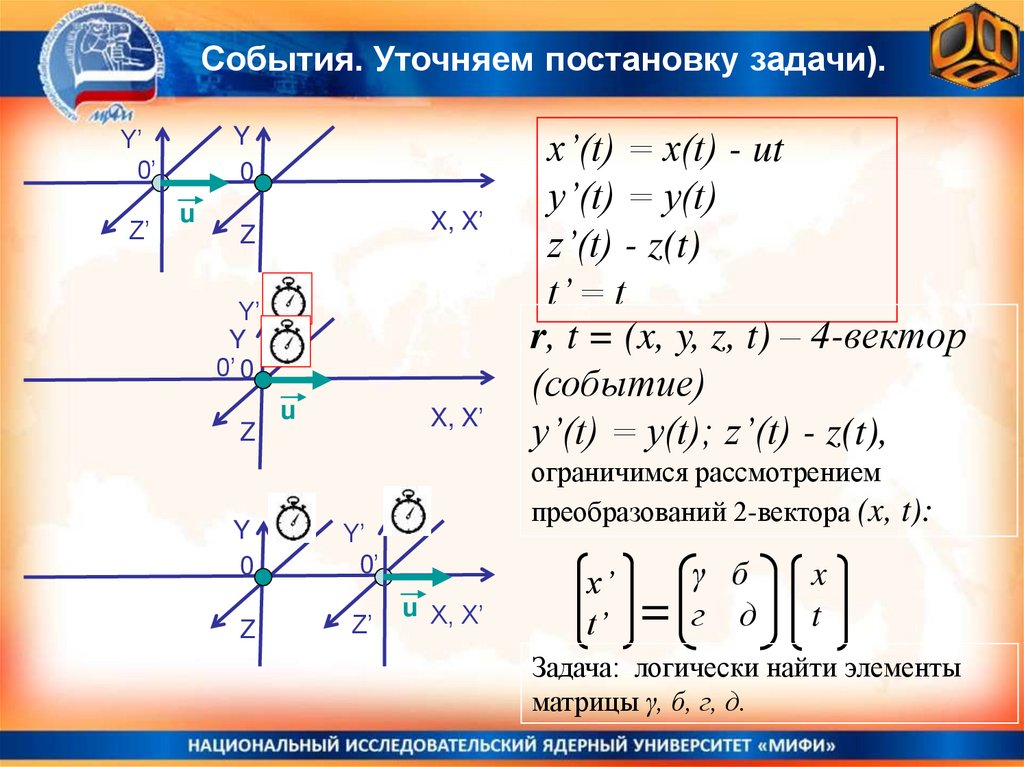
x’(t) = x(t) - ut
y’(t) = y(t)
z’(t) - z(t)
t’ = t
r, t = (x, y, z, t) – 4-вектор
(событие)
y’(t) = y(t); z’(t) - z(t),
ограничимся рассмотрением
преобразований 2-вектора (x, t):
u X, X’
x’
t’
γ б
= г д
x
t
Задача: логически найти элементы
матрицы γ, б, г, д.

12.

События. Уточняем постановку задачи).
Y’
0’
Z’
Y
0
u
X, X’
Z
γ(u) б(u)
= г(u) д(u)
x
t
Задача: логически найти элементы матрицы
γ, б, г, д. Это можно сделать разными
способами. Например
Y’
Y
0’ 0
Z
x’
t’
Шаг 1. Следим из системы К за точкой x’=0.
X, X’ По определению ее координата x = ut, а из
преобразования: 0 = γx + бt = γut + бt =>
u
Y
0
Y’
0’
Z
Z’
б = - γu
Шаг 2. Следим из системы К’ за точкой x=0.
По определению ее координата x’ = -ut’, а
u X, X’ из преобразования: -ut’ = - γut ; t’ = дt =>
д=γ
Шаг 3. γ(u)=γ(-u) – не должно зависеть от
направления скорости

13.

События. Уточняем постановку задачи).
Y’
0’
Z’
Y
0
u
X, X’
Z
γ(u) -uγ(u)
= г(u) γ(u)
x
t
Это вид матрицы после первых трех шагов.
Осталось найти γ(u)= γ (четная функция) и
г(u). Шаг 4: обратное преобразование
Y’
Y
0’ 0
Z
x’
t’
u
X, X’
Y
0
Y’
0’
Z
Z’
x
t
=
γ(u) uγ(u)
г(-u) γ(u)
x'
t'
γ
uγ γ
-uγ
г(-u) γ г(u) γ
u X, X’
=>
1 0
= 0 1
γ2+uγг(u)=1 ; -uγ2 +uγ2 =0
γг(-u)+γг(u)=0 ; γ2- uγг(-u)=1
Вывод: г(и) – функция нечетная

14.

События. Уточняем постановку задачи).
Y’
0’
Z’
Y
0
u
X, X’
Z
γ(u) -uγ(u)
= г(u) γ(u)
x
t
Это вид матрицы после первых 4-х шагов.
Шаг 5. Сделаем замену переменной г(u)= Kuγ
(нечетная функция)
Y’
Y
0’ 0
Z
x’
t’
u
X, X’
Y
0
Y’
0’
Z
Z’
1 -u
x'
t' = γ Ku 1
x
t
Учтем (шаг 4), что γ2+uγг(u)=1 => .
u X, X’
=>
γ2+Ku2γ2 =1 => γ = (1 + Ku2)-1/2
остается неясно, что такое K (константа
или, может быть, четная функция от u).
Можно доказать, что константа
(доказательство громоздкое, опустим)

15.

Преобразования координат событий.
Y’
0’
Z’
u
Y
0
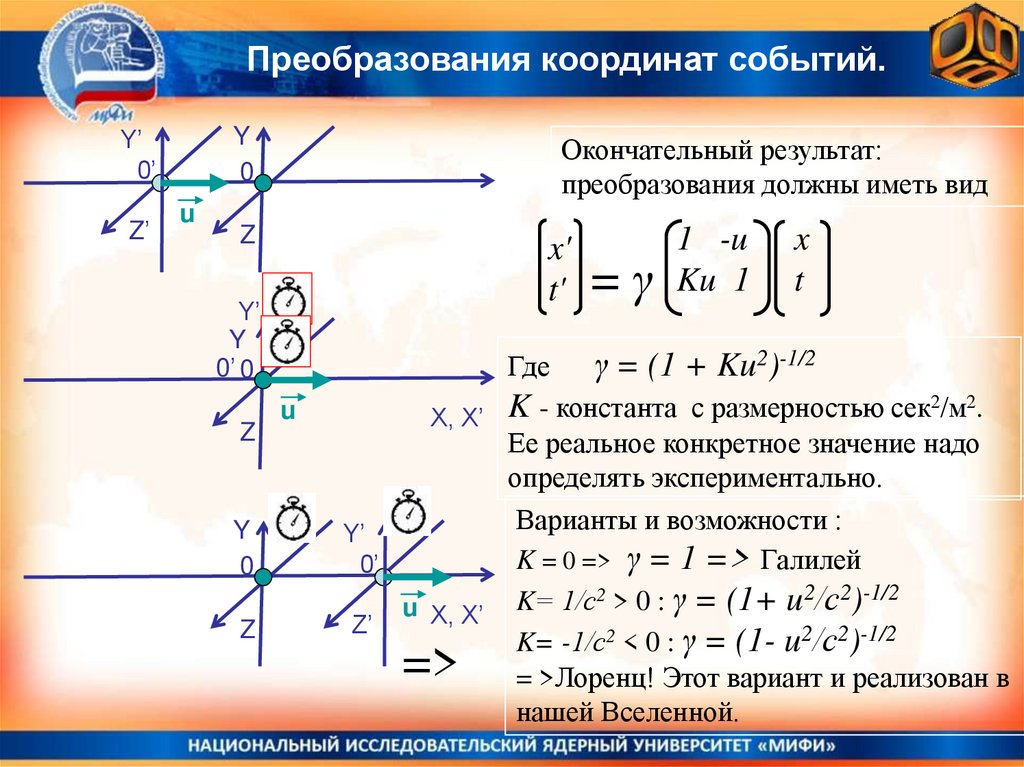
Окончательный результат:
преобразования должны иметь вид
Z
1 -u
x'
t' = γ Ku 1
Y’
Y
0’ 0
Z
Y
0
Z
u
x
t
Где
γ = (1 + Ku2)-1/2
2/м2.
K
константа
с
размерностью
сек
X, X’
Ее реальное конкретное значение надо
определять экспериментально.
Варианты и возможности :
Y’
K = 0 => γ = 1 => Галилей
0’
2 2 -1/2
2
u X, X’ K= 1/с > 0 : γ = (1+ u /с )
Z’
K= -1/с2 < 0 : γ = (1- u2/с2)-1/2
= >Лоренц! Этот вариант и реализован в
нашей Вселенной.
=>

16.

Преобразования Лоренца
x’ = γ (x – ut)
t’ = γ (t - xu/c2)
1
-u
x'
2
t' = γ -u/c 1
γ = (1 - u2/c2 )-1/2
x
t
1
V2
1 2
c
При u << c преобразования Лоренца совпадают с преобразованиями
Галилея. Ньютонова механика была и остается правильной!
При u >c преобразования Лоренца теряют физический смысл => величина с
является предельной скоростью движения и распространения чего-бы то ни
было в природе! Найти конкретное значение с можно экспериментально.
При u < ~ c преобразования Лоренца существенно отличаются от
преобразований Галилея и сильно меняют законы механики. Меняются
правила сложения скоростей, определения импульса и кинетической
энергии.

17.

4-х мерные преобразования Лоренца для механики
В механике больших скоростей движения
надо применять преобразования Лоренца:
Y’’
Y’
Y
X, X’,
0’
0
v
Z
x’ = γ(v) (x - vt)
1
y’ = y
V2
z’ = z
1 2
c
t’ = γ(v)(t - xv/c2)
x’ = γ(v) (x - vt)
t’ = γ(v)(t - xv/c2)
Z’

18.

Следствия преобразований Лоренца для механики
x’ = γ (x – vt)
t’ = γ (t - xv/c2)
1
V2
1 2
c
1. Ход времени в разных системах отсчёта
t’ = γ(v)(t - xv/с 2)
Y
t0= γ(v)(t – v2t/с 2) = t / γ(v)
t = γ(v)t0 > t0 t t0
V2
1 2
c
0
Y’
X=0, Vt, 2Vt, …;
t’ = 0, t0, 2t0…
0’
v
Z
Z’
В движущейся системе отсчета время течет медленнее.
Но какую систему считать движущейся?
x(t)
x’(t’)

19.

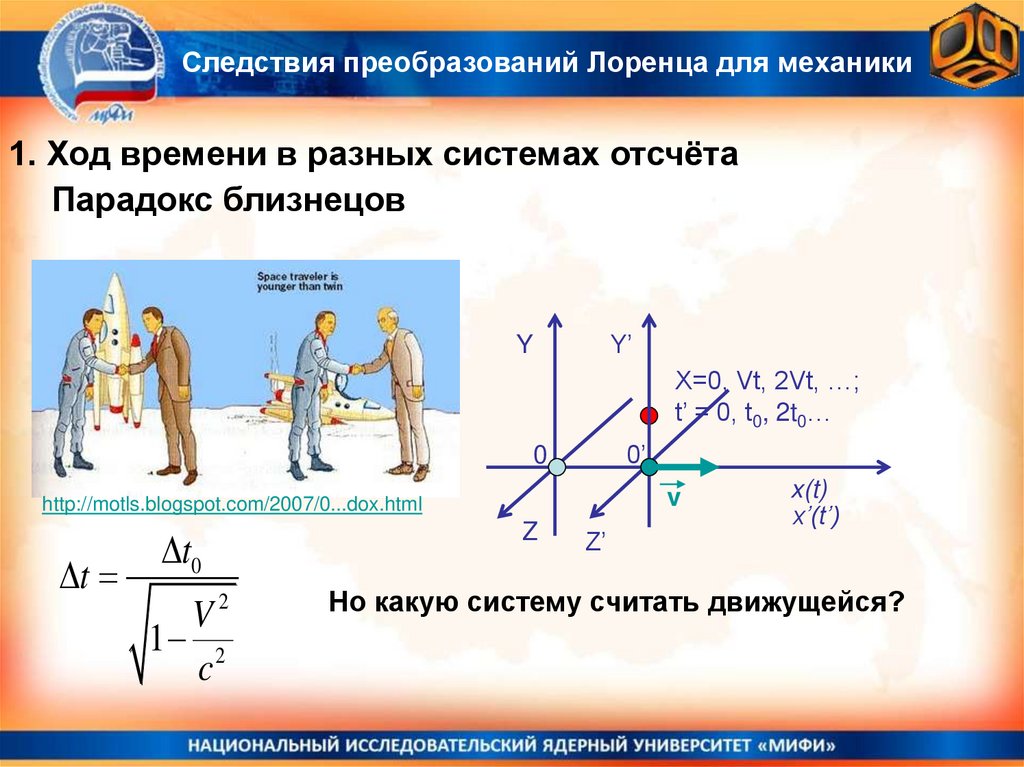
Следствия преобразований Лоренца для механики
1. Ход времени в разных системах отсчёта
Парадокс близнецов
Y’
Y
X=0, Vt, 2Vt, …;
t’ = 0, t0, 2t0…
0’
0
v
http://motls.blogspot.com/2007/0...dox.html
t
t0
V2
1 2
c
Z
Z’
x(t)
x’(t’)
Но какую систему считать движущейся?

20.

Следствия преобразований Лоренца для механики
x’ = γ (x – vt)
t’ = γ (t - xv/c2)
1
V2
1 2
c
2. Неодновременность событий в разных системах
Y’ X= vt, t = t
отсчёта
X=0, t = t Y
t1’ = γ(v)t
X’=0, t2’= ?
X’ = -vt’, t1’= ?
t2’= γ(v)(t – v2t/с2) = t/γ(v)< t1’
0’
0
v
Z
Z’
x(t)
x’(t’)
Если в одной системе отсчета два события кажутся одновременными – в
другой они могут показаться произошедшими в разные моменты времени

21.

Следствия преобразований Лоренца для механики
x’ = γ (x – vt)
t’ = γ (t - xv/c2)
1
V2
1 2
c
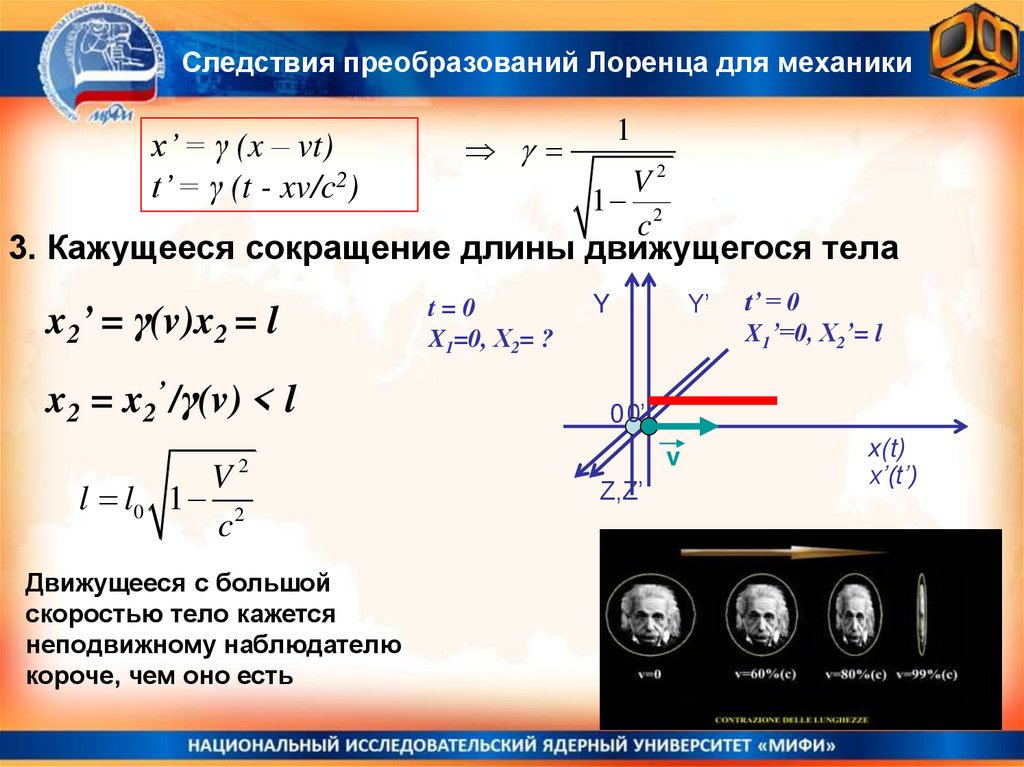
3. Кажущееся сокращение длины движущегося тела
x2’ = γ(v)x2 = l
x2 = x2’ /γ(v) < l
2
V
l l0 1 2
c
Движущееся с большой
скоростью тело кажется
неподвижному наблюдателю
короче, чем оно есть
t=0
X1=0, Х2= ?
Y’
Y
t’ = 0
X1’=0, Х2’= l
0 0’
v
Z,Z’
x(t)
x’(t’)

22.

Следствия преобразований Лоренца для механики
x’ = γ (x – vt)
t’ = γ (t - xv/c2)
Относительная скорость
двух частиц
1
V2
1 2
c
vrel
4. Удивительное сложение скоростей
Y’
Y
Y’’
v3
Y’
Y’’
v1
Y
0’
0
0’’
v1
Z
Z’
0
v2
0’
v2
Z’’
v2 x v1x
,
v1x v2 x
1 2
c
V
Z
Z’
v3 = (v1 + v2)/(1 + v1v2 /с 2) < c
ПРИМЕР: v1 = 0,9c; v2 = 0,9c
cv1 + cv2 < c2 + v1v2
Vrel = (0,9c+0,9c)/(1+0,9 * 0,9)=
=1,8 c/ 1,81 = 0,995c
0 < c2-cv1 –cv2+v1v2 =(c-v1)(c–v2) >0

23.

Преобразования для скоростей
x’ = γ(v) (x - Vt)
y’ = y
z’ = z
t’ = γ(v)(t - xV/c2)
x = γ(v) (x’ + Vt)
y = y’
Y
z = z’
t = γ(v)(t’ + x’/V/c2) 0
γ(v) = (1 - v2/с 2)-1/2
dx dx Vdt
V
dt dt 2 dx
c
dy dy , dz dz
Y’
Y’’
v1
v2
0’
V
Z
dx dy dz
v , , ,
dt dt dt
dx dy dz
v ,
,
dt dt dt
Z’
Относительная скорость
двух частиц
v2 x v1x
vrel
,
v1x v2 x
1 2
c
2
2
v
1
V
c
v z 1 V 2 c 2
vx V
y
vx
, vy
, vz
,
v xV
v xV
v xV
1 2
1 2
1 2
c
c
c

24.

Инварианты преобразований Лоренца. Интервал.
Точечные события:
P1 x1 , y1 , z1 , t1 , P2 x2 , y2 , z2 , t2
s c t1 t2 r ,
2
12
2
2
2
12
где
r x1 x2 y1 y2 z1 z2
2
12
2
2
Интервал инвариант преобразований Лоренца, т.е.
Y’
Y
t = 0, x=0
t’=0, x’=0
0 0’
v
Z,Z’
2
s122 s12 2
x’ = γ (x – vt)
t’ = γ (t - xv/c2)
x=r, t = t
x’= γ(r-vt)
t’= γ(t-vr/c2)
s12 = c2t2 – r2 = c2γ2(t-vr/c2)2 – γ2(r-vt)2=
= γ2((ct-vr/c)2 –(r-vt)2) =
x(t) = γ2(c2t2-2vrt +v2r2/c2 – r2+2rvt-v2t2) =
x’(t’)
= c2 t 2 – r2

25.

Экспериментальные подтверждения СТО в механике
Эксперимент (J.C. Hafele) и R. E. Keating), октябрь 1971
Разность показаний путешествовавших и остававшихся на месте часов, наносекунды
предсказанная
гравитационный вклад
(общая теория относительности)
кинематический вклад
(специальная теория относительности)
измеренная
Всего
на восток
144 ± 14
−184 ± 18
−40 ± 23
−59 ± 10
на запад
179 ± 18
96 ± 10
275 ± 21
273 ± 7

26.

Классические представления
о пространстве и времени
1.
Существует отдельно пространство и независимое от него время.
Пространство является евклидовым, т.е. справедливы аксиомы Евклида.
2.
Существуют инерциальные системы отсчёта, в которых выполняются
второй и третий законы Ньютона.
3.
Справедлив принцип относительности Галилея, который гласит, что во всех
инерциальных системах отсчёта одинаковы все законы механики, а также
свойства пространства и времени.
4.
Справедливы преобразования Галилея координат и времени и абсолютный
характер одновременности событий. Выполняется классический закон
сложения скоростей.

27.

Новые (релятивистские) представления
о пространстве и времени
1. Пространство и время являются двумя проявлениями единой сущности –
пространства-времени. Геометрия пространства-времени не является Евклидовой и
подлежит экспериментальному и теоретическому исследованию.
2. Существуют инерциальные системы отсчёта, в которых, если на тело не действуют
реальные физические силы – оно движется равномерно и прямолинейно.
3. Справедлив принцип относительности Галилея, который гласит, что во всех
инерциальных системах отсчёта одинаковы все законы механики, а также свойства
пространства и времени.
4.
Справедливы
преобразования
Лоренца
для
координат
инвариантом преобразований Лоренца является интервал
и
времени,
причем

28.

Постулаты СТО
Постулаты механики:
1. Все законы природы во
всех ИСО одинаковы
(И. Ньютон).
2) Экспериментальный
факт: существует
максимально возможная
скорость распространения
взаимодействий (скорость
света в вакууме), которая
одинакова во всех
направлениях и не зависит
от скоростей источника и
приемника (А. Эйнштейн)
Nature and nature's laws lay hid in night;
God said "Let Newton be" and all was light
Alexander POPE (1688-1744)
Был этот мир глубокой тьмой окутан.
Да будет свет! И вот явился Ньютон.
(С. Маршак)
It did not last; the devil, howling
"Ho! Let Einstein be!" restored the status quo.
John Squire (1884 -1958)
Но очень скоро чёрт пролаял «Нет!.
Явись. Эйнштейн!» – и снова гаснет
свет…

29.

Курс общей физики НИЯУ МИФИ
Спасибо за внимание!
Продолжение следует!

30.

Пример матричного умножения векторов:
Преобразование координат при повороте СК:
x’ = x cos φ – y sin φ
y’ = x sin φ + y cos φ
x’
y’
cos φ –sin φ
= sin φ cos φ
y’
y
φ
x
0
x
y
x’
x’ = x cos φ – y sin φ + 0*z
y’ = x sin φ + y cos φ + 0*z
z’ = 0*x + 0*y
+z
x’
y’
z'
cos φ –sin φ 0
= sin φ cos φ 0
0
0
1
x
y
z
=>
Mx
Ixx Ixy Ixz
My = Iyx Iyy Iyz
Mz
Izx Izy Izz
ωx
ωy
ωz