Основные_понятия_квантовой_химии_2

1. Основные понятия

ТвГУ
ХТФ
2019

2.

Теории химической связи
• Разные типы химической связи
Взаимодействия характеризуются специфическим распределением электронной плотности (ЭП).
Ковалентные• Поэтому, анализ ЭП
- это прямой метод исследования химической связи.
Ионные
• Однако, рассматривая непосредственно функцию ρ(r), трудно различить детали электронного распределения на фоне
Водородные доминирующего вклада электронных плотностей атомов.
Ван-дер- • Поэтому для анализа ЭП испольВаальсовы зуют вспомогательные функции
2

3.

Взаимодействия = хим. связь
• Х. активность молекул приводит к возникновению
между ними взаимодействий - и образованию стабильной равновесной многоэлектронной системы,
энергия которой ниже, чем сумма энергий составляющих ее молекул, атомов или многоатомных фрагментов в свободном состоянии.
• Нет последовательной математические модели, объясняющей возникновение взаимодействий (нет оператора химической связи).
• Уравнение Шредингера допускает лишь приближенное
деление молекулы или кристалла на фрагменты (атомы, функциональные группы, кластеры и т.д.), свойства и взаимодействия которых используют при объяснении свойств всей системы.
• Единого физически обоснованного подхода к объяснению свойств системы через свойства ее частей в рамках волновой механики на данный момент не существует.
3

4.

Взаимодействия = хим. связь. Аддитивность
• На данный момент есть сложная и непоследовательная
система эмпир. и кв-хим. представлений для объяснения свойств мол-лы через свойства атомов и ат. групп.
• Разработана схема трактовки результатов кв-хим.
расчетов, согласующаяся с идеей аддитивности хим.
свойств.
• Такие схемы имеют разную степень строгости.
• Схемы важны для разработки
основ
Энергиятеоретических
Объём по контуру
Группывеществ
Заряд
3)
создания
с требуемыми
невоз(кДж/моль)свойствами:
0,001 а.е. (Å
можно решить эту задачу без понимания того, как
C1, H2 , H3 , H4
0,008
-104758
32,95
свойства фрагментов определяют свойства системы в
C5, H6 , H7
0,342
-102657
22,99
целом.
N8, H9 , H10
-0,350
-147553
27,96
Итого
0,000
-355057
83,90
4

5.

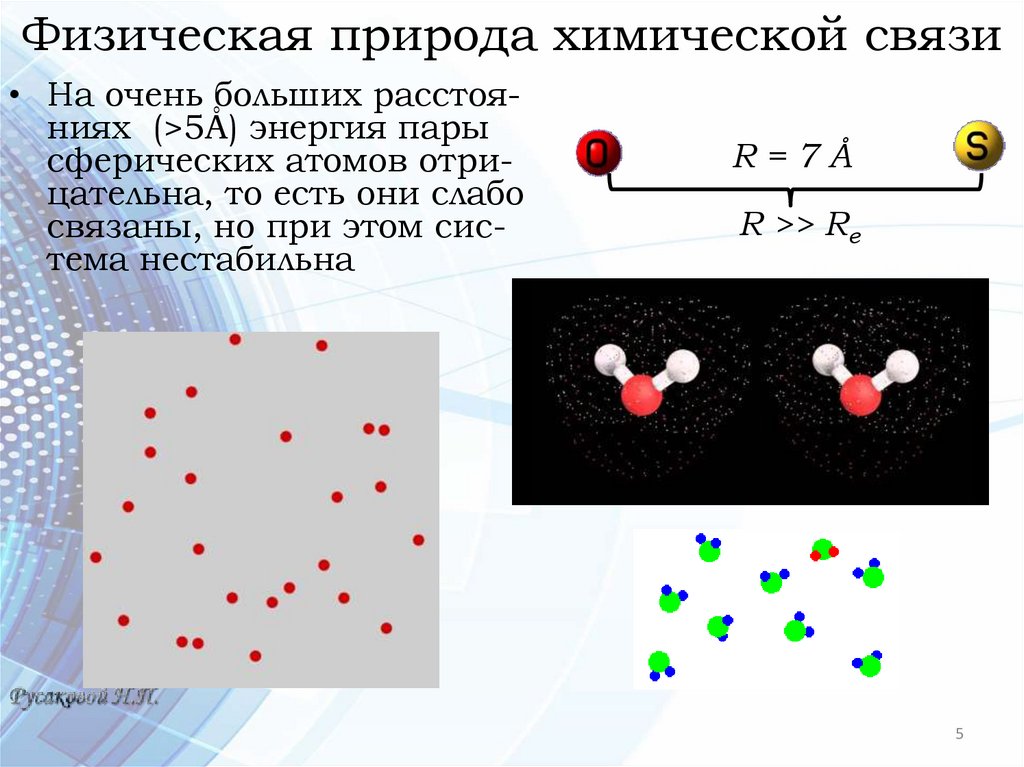
Физическая природа химической связи
• На очень больших расстояниях (>5Å) энергия пары
сферических атомов отрицательна, то есть они слабо
связаны, но при этом система нестабильна
R=7Å
R >> Re
5

6.

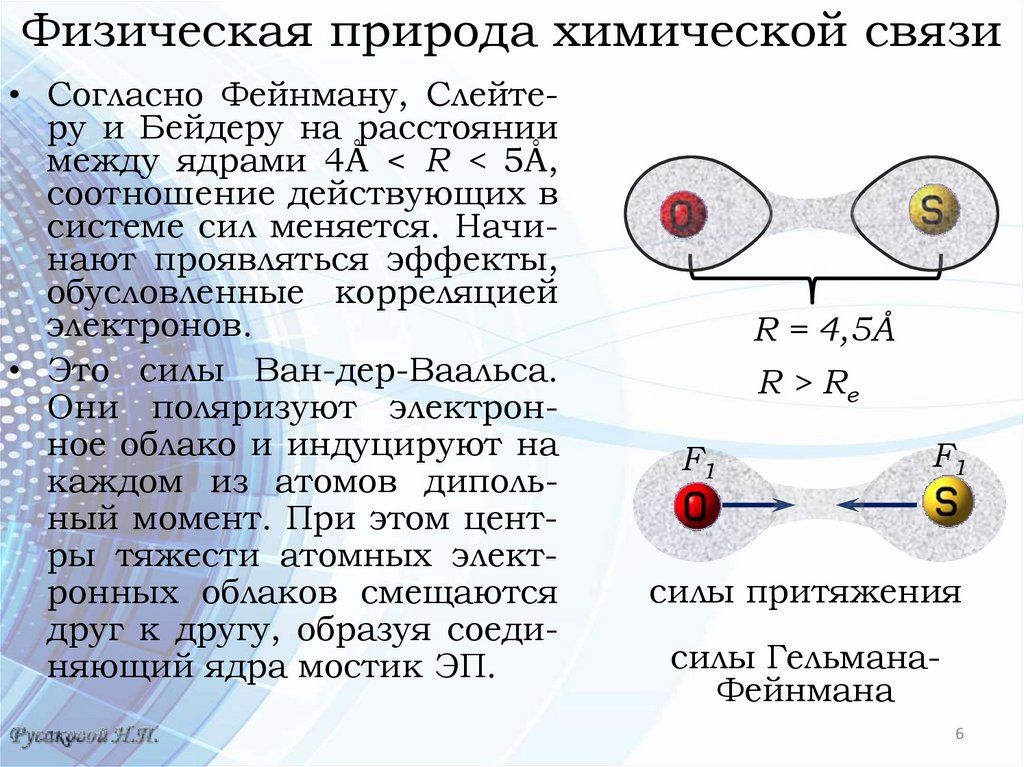
Физическая природа химической связи
• Согласно Фейнману, Слейтеру и Бейдеру на расстоянии
между ядрами 4Å < R < 5Å,
соотношение действующих в
системе сил меняется. Начинают проявляться эффекты,
обусловленные корреляцией
электронов.
• Это силы Ван-дер-Ваальса.
Они поляризуют электронное облако и индуцируют на
каждом из атомов дипольный момент. При этом центры тяжести атомных электронных облаков смещаются
друг к другу, образуя соединяющий ядра мостик ЭП.
R = 4,5Å
R > Re
F1
F1
силы притяжения
силы ГельманаФейнмана
6

7.

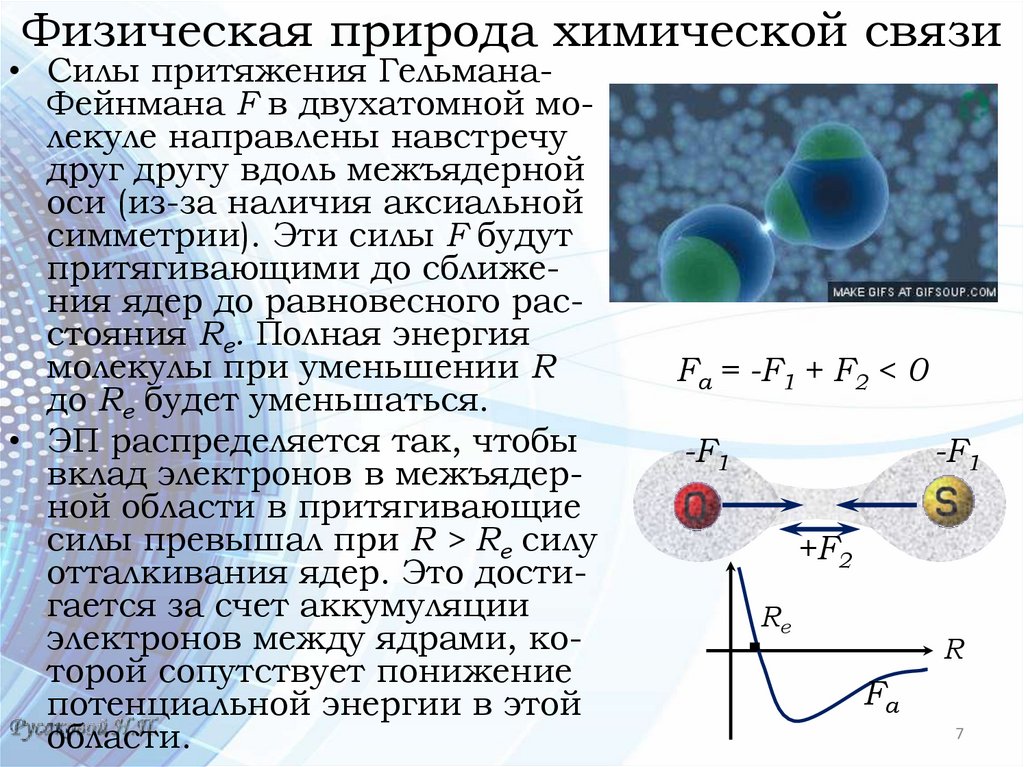
Физическая природа химической связи
• Силы притяжения ГельманаФейнмана F в двухатомной молекуле направлены навстречу
друг другу вдоль межъядерной
оси (из-за наличия аксиальной
симметрии). Эти силы F будут
притягивающими до сближения ядер до равновесного расстояния Rе. Полная энергия
молекулы при уменьшении R
до Rе будет уменьшаться.
• ЭП распределяется так, чтобы
вклад электронов в межъядерной области в притягивающие
силы превышал при R > Rе силу
отталкивания ядер. Это достигается за счет аккумуляции
электронов между ядрами, которой сопутствует понижение
потенциальной энергии в этой
области.
Fа = -F1 + F2 < 0
-F1
-F1
+F2
Re
R
Fа
7

8.

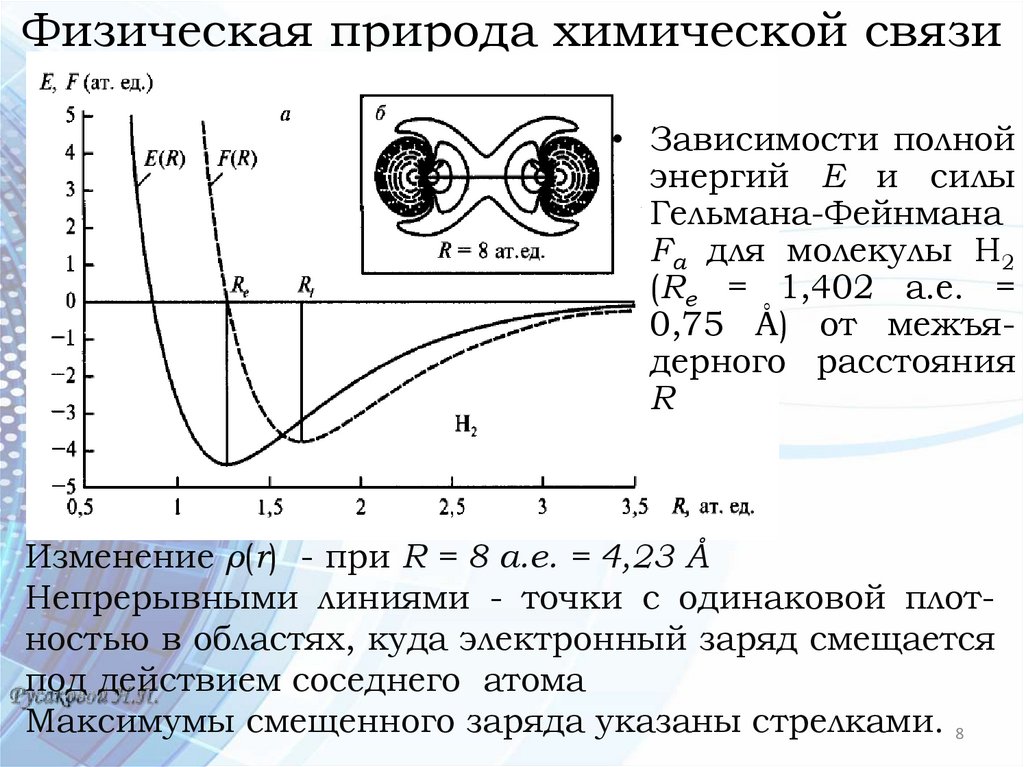
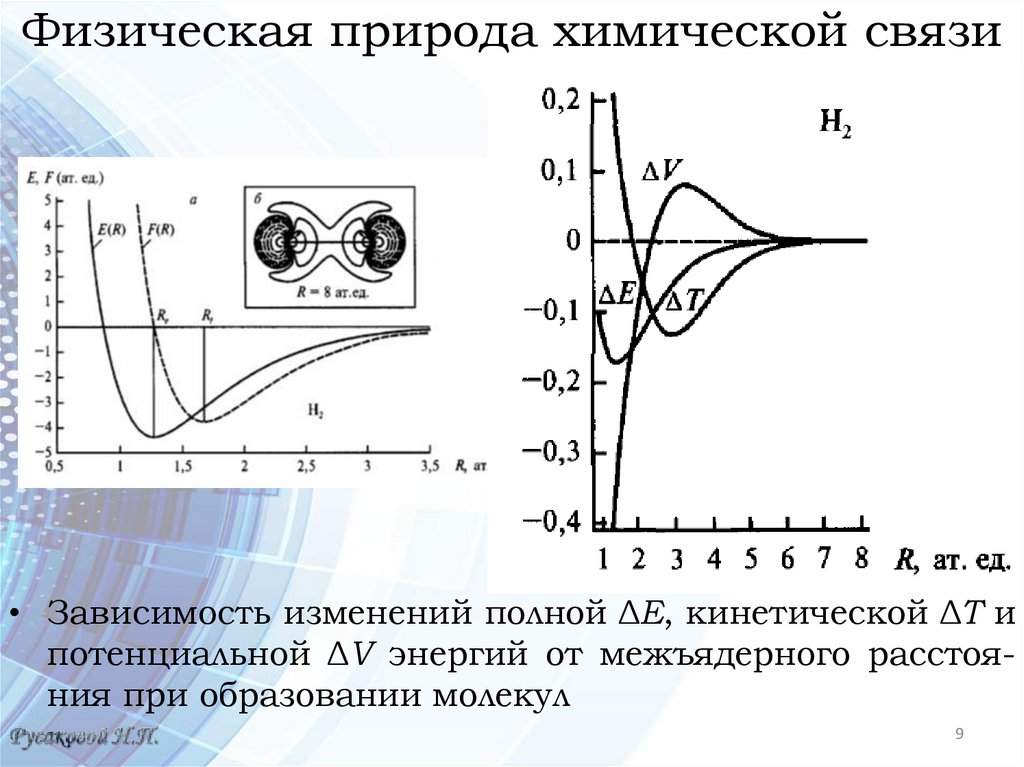
Физическая природа химической связи
• Зависимости полной
энергий Е и силы
Гельмана-Фейнмана
Fа для молекулы Н2
(Rе = 1,402 а.е. =
0,75 Å) от межъядерного расстояния
R
Изменение ρ(r) - при R = 8 а.е. = 4,23 Å
Непрерывными линиями - точки с одинаковой плотностью в областях, куда электронный заряд смещается
под действием соседнего атома
Максимумы смещенного заряда указаны стрелками. 8

9.

Физическая природа химической связи
• Зависимость изменений полной ΔЕ, кинетической ΔТ и
потенциальной ΔV энергий от межъядерного расстояния при образовании молекул
9

10.

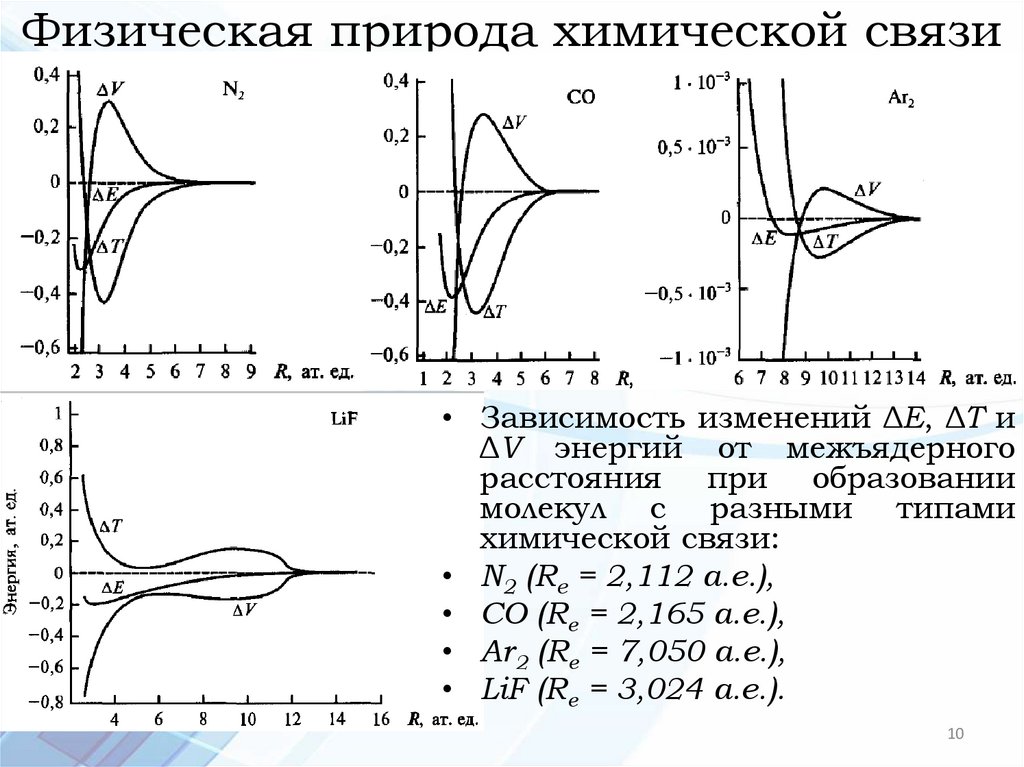
Физическая природа химической связи
• Зависимость изменений ΔЕ, ΔТ и
ΔV энергий от межъядерного
расстояния при образовании
молекул с разными типами
химической связи:
• N2 (Rе = 2,112 а.е.),
• СО (Rе = 2,165 а.е.),
• Ar2 (Rе = 7,050 а.е.),
• LiF (Rе = 3,024 а.е.).
10

11.

Гамильтониан системы. Парные
взаимодействия
Ĥ=Т+V
Отрицательной является только
энергия
электронно-ядерного
взаимодействия Vэя, (притяжение
частиц)
Энергии Vяя и Vээ положительны.
При
образовании
молекул
из
атомов энергия Vэя понижается на
величину, которая превышает по
величине суммарное увеличение Vяя
и Vээ .
11
ΔVэя > ( ΔVяя + ΔVээ )

12.

Гамильтониан системы. Парные
взаимодействия
• Как изменяются парные атомные взаимодействия с
расстоянием? На больших расстояниях, когда обмен
несуществен, доминирующую роль во взаимодействии
атомов играет электростатическое взаимодействие,
которое
является первопричиной образования
химической связи.
• Для сферических атомов сила отталкивания ядер при
любом конечном расстоянии между ними не компенсируется силами электронно-ядерного притяжения изза неполного экранирования ядер электронами. Поэтому силы, действующие на ядра пары сферических
атомов, всегда отталкивающие, а следовательно, такая
система нестабильна
12

13.

Физическая природа химической связи
Таким образом, при образовании молекул можно выделить два отдельных явления:
1. Изменение баланса сил, действующих на атомные ядра со стороны других ядер и электронной плотности
2. Изменение составляющих полной энергии (кинетической и потенциальной) и самой полной энергии системы. Понижение полной электронной энергии по мере
уменьшения межядерного расстояния является общей
закономерностью и не зависит от сорта атомов, образующих молекулу.
Образование химической связи рассматривается с
точки зрения двух подходов:
1. Силового
2. Энергетического
13

14.

Физическая природа химической связи
• Силовой подход объясняет химическую связь через
силы, действующих в молекулах на электроны и ядра.
Эти силы подчиняются закону Кулона, однако
межэлектронные взаимодействия происходят таким
образом, чтобы удовлетворялся принцип Паули
(влияние магнитных сил, обусловленных наличием
электронного и ядерного спинов, на полную энергию
пренебрежимо мало, не говоря уже о гравитационных
силах).
• В энергетическом подходе для объяснения природы
химической
связи
анализируют
изменения
кинетической
и
потенциальной
энергий
при
образовании молекул.
• Оба подхода являются взаимодополняющими и во
многом опираются на три важных теоремы – теорему
Гельмана-Фейнмана, теорему Эренфеста и теорему
вириала.
14

15.

Теоремы о силах.
Сила Гельмана-Фейнмана
Сила, действующая на ядро в молекуле
• для точной и хартри-фоковской волновой функции
справедливо соотношение:
• где λ - некоторый параметр, от которого зависит энергия
(н.п., ядерные координаты λ = Ra)
• Кинетическая энергия электронов Тэ и энергия
межэлектронного взаимодействия Vээ явно не зависят от
координат ядер, а энергии о Vэя и Vяя взаимодействий
зависят.
• Поскольку, сила – градиент потенциальной энергии,
взятый с обратным знаком F= - ∇V, то сила,
действующую в молекуле на ядро а вдоль оси координат
х, имеет следующий вид:
15

16.

Теоремы о силах.
Сила Гельмана-Фейнмана
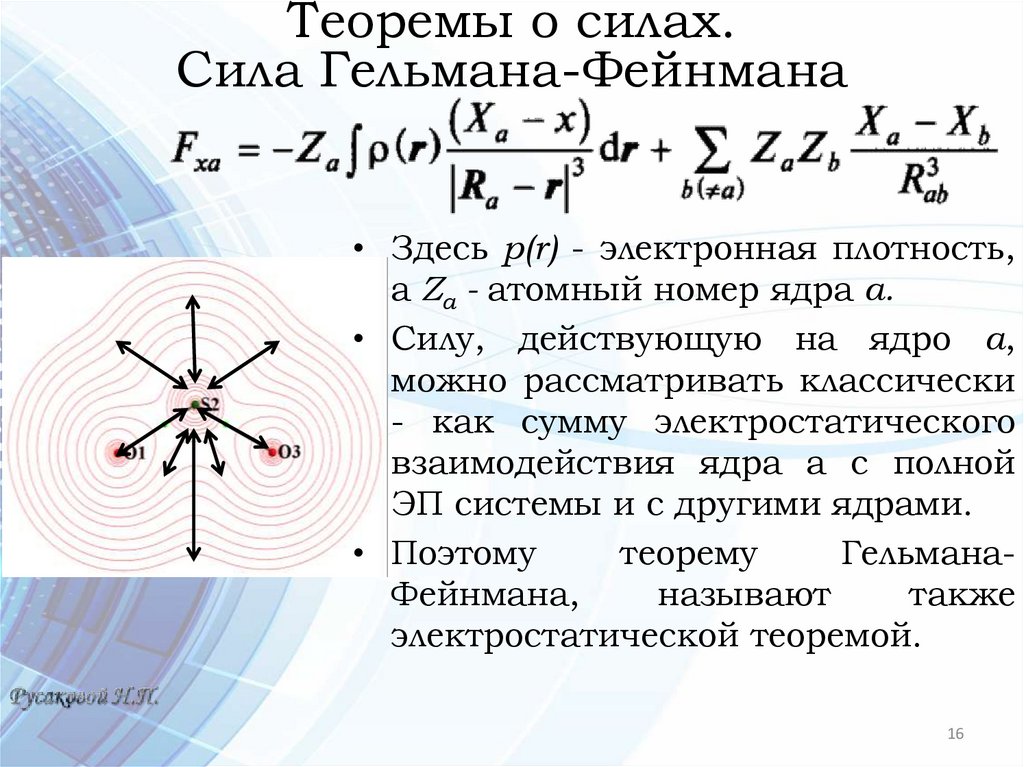
• Здесь p(r) - электронная плотность,
а Za - атомный номер ядра а.
• Силу, действующую на ядро а,
можно рассматривать классически
- как сумму электростатического
взаимодействия ядра а с полной
ЭП системы и с другими ядрами.
• Поэтому
теорему
ГельманаФейнмана,
называют
также
электростатической теоремой.
16

17.

Теоремы о силах.
Сила Гельмана-Фейнмана
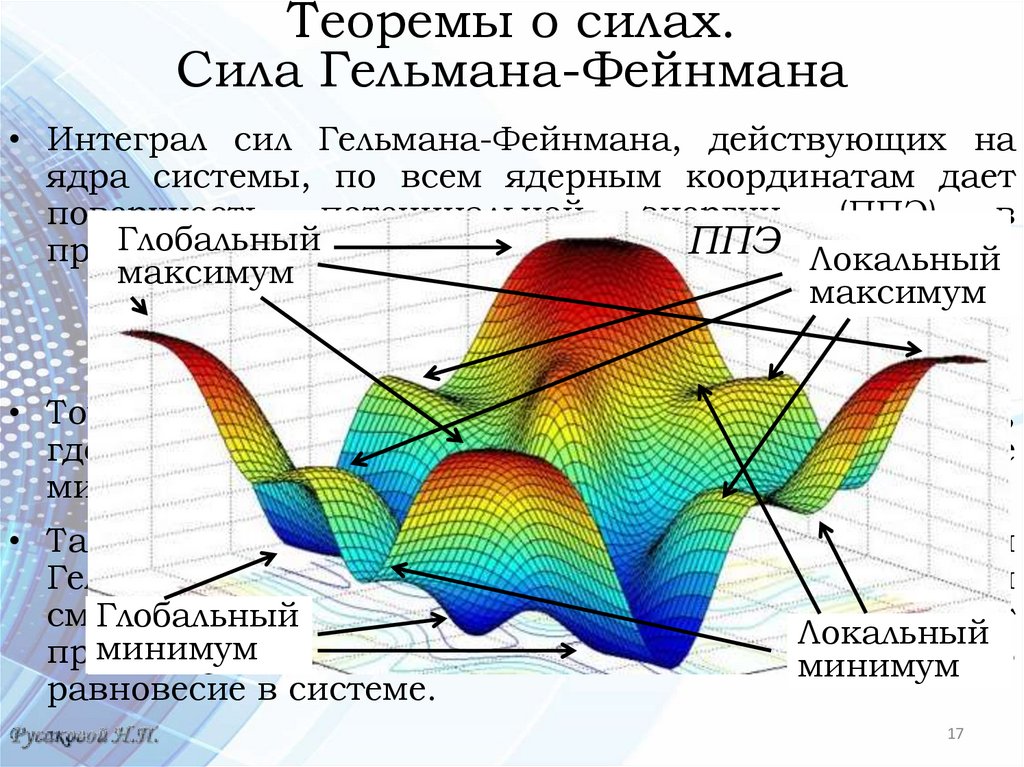
• Интеграл сил Гельмана-Фейнмана, действующих на
ядра системы, по всем ядерным координатам дает
поверхность
потенциальной
энергии
(ППЭ)
в
Глобальный
приближении
Борна-Оппенгеймера. ППЭ Локальный
максимум
максимум
• Точки в ядерном конфигурационном пространстве,
где Fa = 0, для всех ядер определяют положение
минимумов ППЭ.
• Таким образом, в равновесных системах силы
Гельмана-Фейнмана
равны
нулю.
При
любом
смещении
ядер от точек равновесия эти силы носят
Глобальный
Локальный
минимум
притягивающий
характер и стремятся восстановить
минимум
равновесие в системе.
17

18.

Теоремы о силах.
Сила Эренфеста
Сила, действующая на ē со стороны
остальных (N-1) ēē и ядер системы
• Частица описывается гамильтонианом, который не
зависит от времени
• Теорема Эренфеста устанавливает взаимосвязь между
средним значением силы, действующей на частицу, и
производной по времени среднего значения ее
импульса:
, Fэр - коммутатор
• Если р – импульс электрона, то Fэр – это оператор силы
Эренфеста.
• Плотность Fэр, действующей на элемент электронной
плотности в точке r, получаем усреднением по (N- 1)
электронам:
18

19.

Теорема вириала
Cоотношение между средними значениями
V и T компонент Etotal многоēē системы
Etotal = T + V
• Средняя потенциальная энергия ēē определяется как
усреднённый вириал плотности сил Fэр, действующих
на ēē:
, который преобразуется в
• где Ra – радиус-вектор положения ядра а;
- вириал сил, действующих на ядра системы
19

20.

Теорема вириала
Cоотношение между средними значениями
V и T компонент Etotal многоēē системы
• Слейтер:
• Для равновесной ядерной конфиrурации силы, действующие на ядра, равны нулю, следующие соотношения для средних значений компонент полной энергии:
2T + V = 0 или –V = 2T
• А так как E = T + V , то E = -T
• Унифицированная теорема. Выполняется как для
бесконечно удаленных атомов (1), так и для
стабильной молекулы (2):
• изменение компонент при абсолютном нуле равно:
, полной энергии:
20

21.

Волновые процессы атомных
взаимодействий. Интерференция
• Образ-е хим. связи между ат-ми – рез-т электростат.
взаимодействия ēē и ядер (с выполнением принципа
Паули).
• Стабильная хим сис-ма удовл ур-ю Шредингера.
Ĥψ=Eψ – волновое ур-ние, ψ – волновая функция
• Взаимодействие атомов сопров. волновыми процессами, которые описывают взаимное проникновение
атом-ных электронных облаков и их интерференцию,
а также перенос электронов.
• Данные явления хорошо решаются в приближении МО
ЛКАО, в котором каждая молекулярная орбиталь φi(r)
представляется линейной комбинацией атомных
орбиталей χμ(r):
Коэффициенты ciμ – положительные и отрицательные. Они определяют вклад каждой АО χμ(r) в МО φi(r). Одна и та же χμ(r) по-разному
входит в разные φi(r), поэтому ciμ при χμ(r) для каждой φi(r) различ21
ны.

22.

Волновые процессы атомных
взаимодействий. Интерференция
• Мо и АО – это одноэлектронные функции. Они приближенно описывают поведение каждого электрона в
пределах атома или молекулы.
• МО ЛКАО отражает волновую природу электронов и
отвечает принципу суперпозиции. Т.е. МО формируются в результате взаимной интерференции АО.
Интерференция АО может носить как конструктивный, так и деструктивный характер.
• Интерференция - взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких
когерентных волн при их наложении друг на друга
• Когерентные волны - это волны, с одинаковой частотой, постоянной разностью фаз, и колеблющиеся в
одной плоскости
• Конструктивная интерференция - взаимодействие АО
происходит в фазе и коэффициенты ciμ имеют одинаковые знаки
• Деструктивная интерференция АО - в противофазе и
коэффициенты ciμ имеют разные знаки.
22

23.

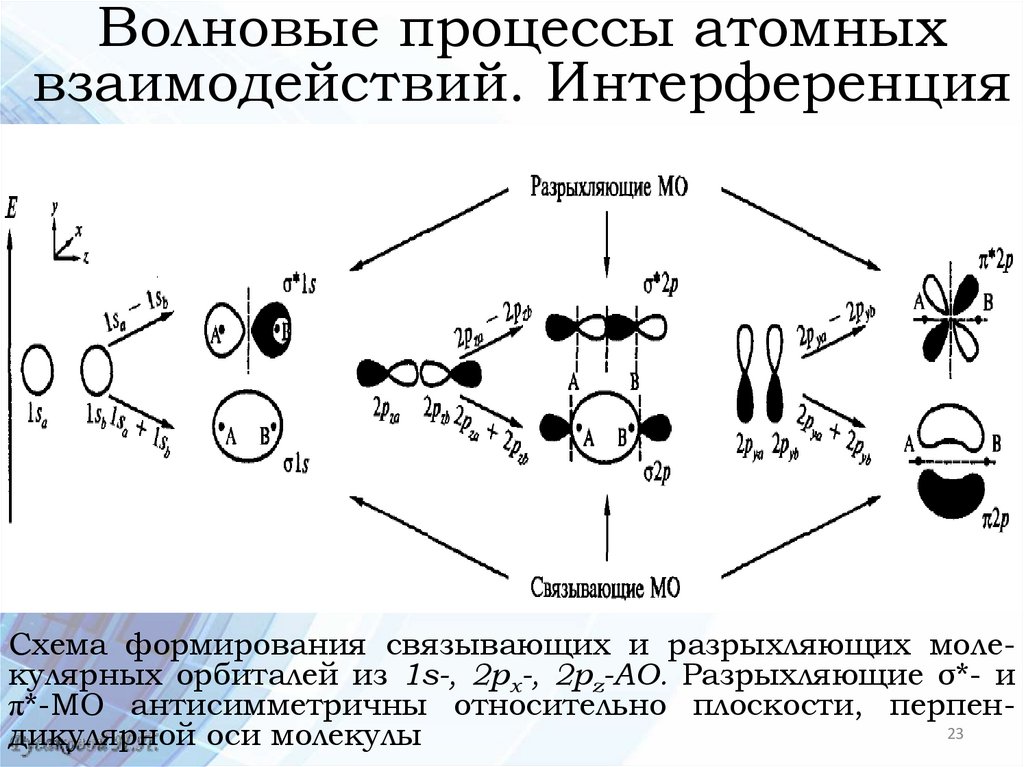
Волновые процессы атомных
взаимодействий. Интерференция
Схема формирования связывающих и разрыхляющих молекулярных орбиталей из 1s-, 2рх-, 2pz-AO. Разрыхляющие σ*- и
π*-МО антисимметричны относительно плоскости, перпен23
дикулярной оси молекулы

24.

Волновые процессы атомных
взаимодействий. Интерференция
• Конструктивная интерференция – МО с более низкой
Е, МО – связывающие
• Деструктивная интерференция - МО с более высокой
Е, МО – разрыхляющие (антисвязывающие)
• Интерференция очень мала (тип не определить) – МО с
такой же Е, МО – несвязывающие (остовные электроны, неподелённые электронные пары)
• Число и тип МО в системе определяется принципом
Паули.
• В многоатомных системах одна и та же МО может
иметь как связывающий, так и разрыхляющий характер в разных точках пространства в зависимости от
характера вклада соответствующих АО.
• Разрыхляющая МО имеет на одну узловую плоскость
больше, чем соответствующая связывающая МО.
24

25.

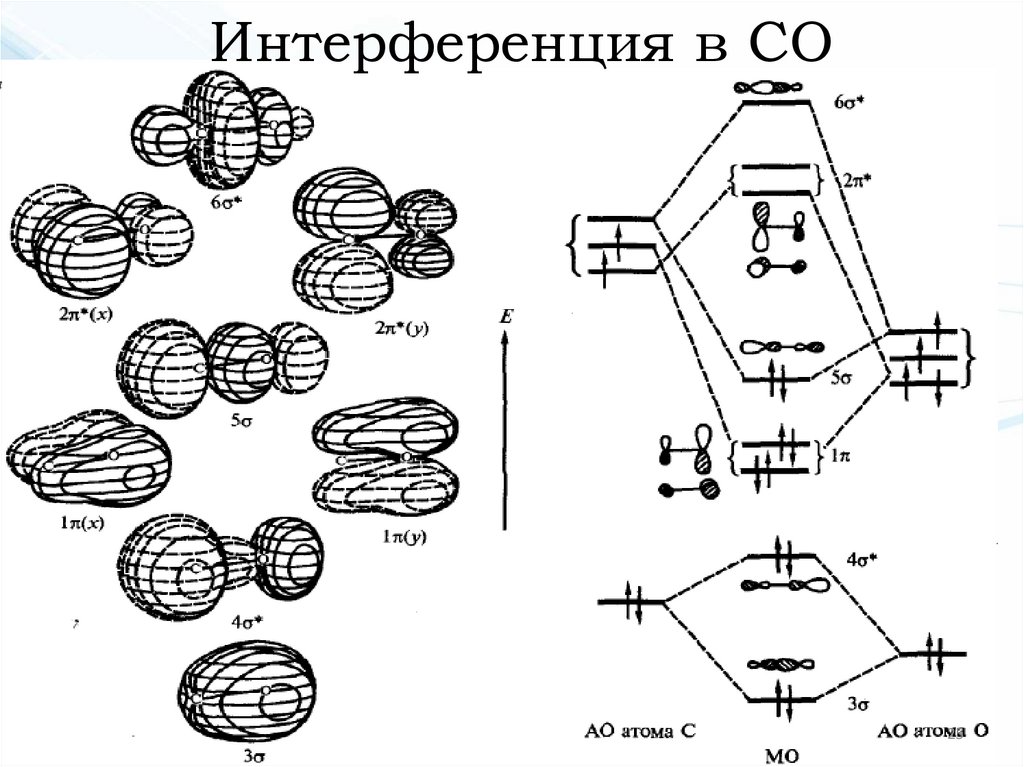
Интерференция в СО
25

26.

Интерференция. МО ЛКАО
• Электронная плотность в МО ЛКАО:
• ЭП молекулы может быть представлена
как сумма вкладов, связанных как с
плотностью электронов на атомных
орбиталях, так и с интерференцией АО.
• Степень
и
характер
взаимного
проникновения
АО
количественно
характеризуют с помощью интегралов
перекрывания
• величина Sμv лежит в пределах
-1 < Sμv < 1.
26

27.

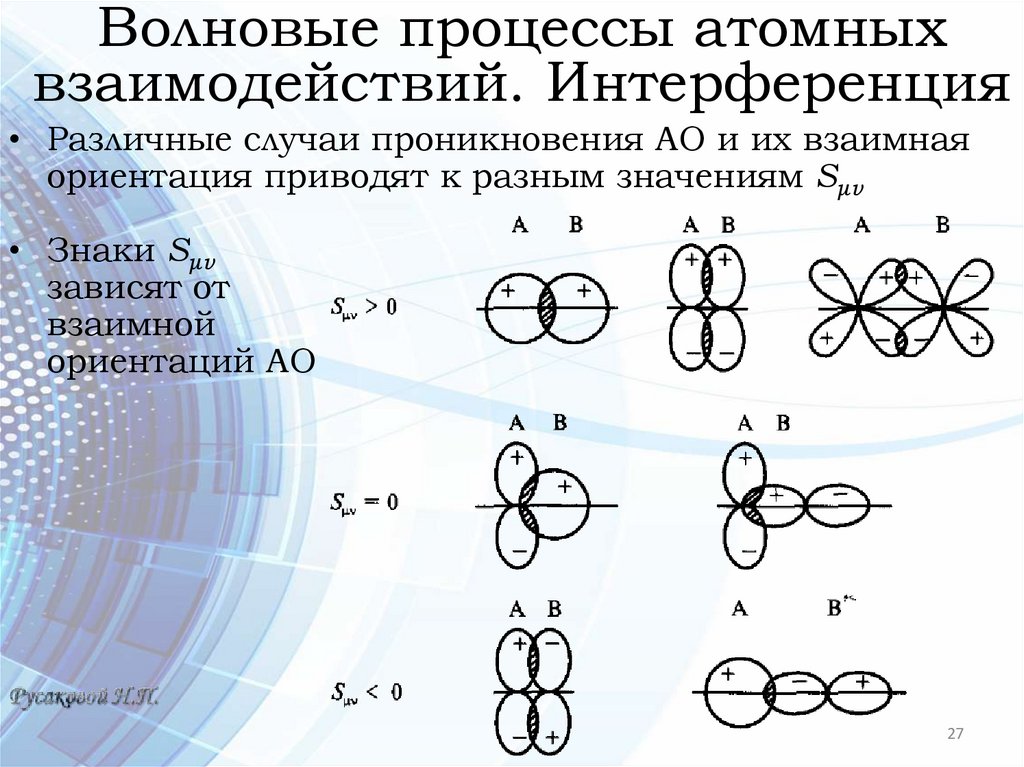
Волновые процессы атомных
взаимодействий. Интерференция
• Различные случаи проникновения АО и их взаимная
ориентация приводят к разным значениям Sμv
• Знаки Sμv
зависят от
взаимной
ориентаций АО
27

28.

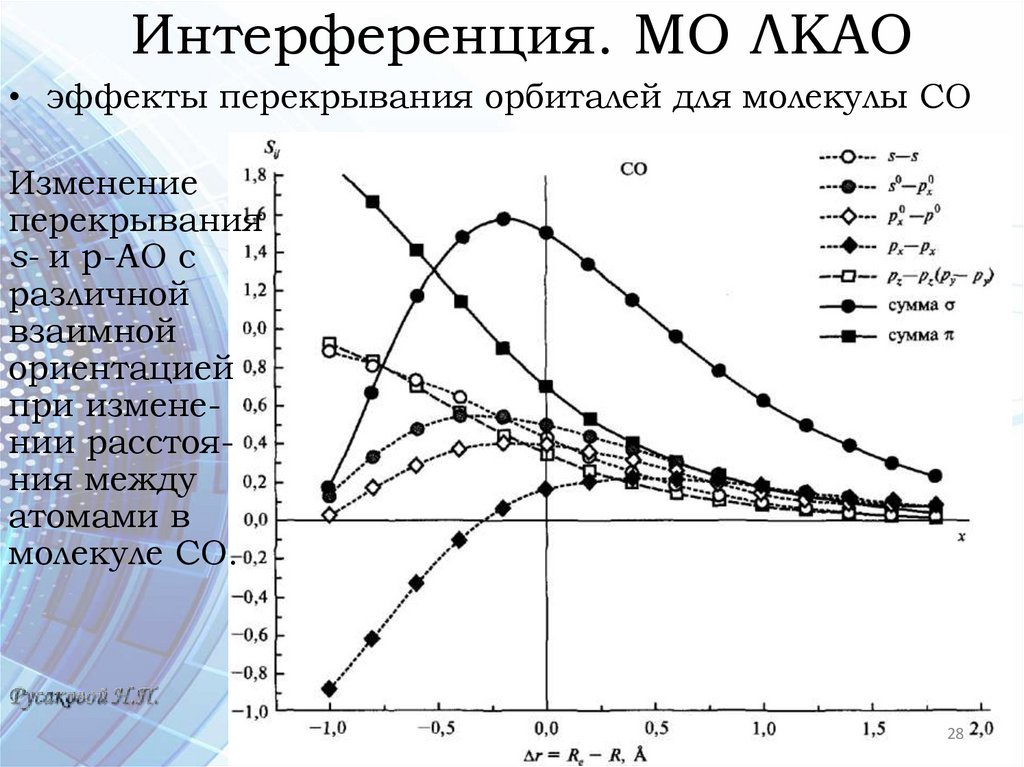
Интерференция. МО ЛКАО
• эффекты перекрывания орбиталей для молекулы СО
Изменение
перекрывания
s- и р-АО с
различной
взаимной
ориентацией
при изменении расстояния между
атомами в
молекуле СО.
28

29.

Интерференция. МО ЛКАО
• Значимость вклада АО в МО определяется выполнением следующих условий:
энергии АО - сравнимы по величине;
АО обладают одинаковыми свойствами симметрии
относительно оси молекулы (т. е., соответствующий Sμv
не равен нулю).
• Основными характеристиками свойств симметрии
являются:
симметрия МО относительно оси молекулы;
симметрия МО относительно плоскости, перпендикулярной оси молекулы;
симметрия МО относительно центра инверсии молекулы;
тип АО, в которые переходят МО при увеличении
межъядерного расстояния.
29

30.

Классификация АО
• По симметрии и обозначения МО на примере гомоядерных
двухатомных молекул типа А2· Величина проекции
орбитального момента импульса каждого электрона в этих
молекулах на молекулярную ось равна ±λħ и определяется
квантовым числом λ, аналогичным магнитному квантовому
числу в атоме.
МО с λ = 0, симметричные относительно отражения в
плоскости молекулы, называют σ-орбиталями,
МО с λ = 1, антисимметричные относительно отражения в
плоскости молекулы, называют π-орбиталями,
МО с λ = 2, 3, …. называют δ-, φ-орбиталями и т. д.
• МО обозначаются индексами g и u (от слов gerade - четный,
иngerade - нечетный). МО g – сохраняет, а и - меняет знак
при инверсии относительно центра симметрии молекулы.
• Четность и нечетность МО лежат в основе правил отбора
разрешенных электронных переходов: возможны переходы
и ↔ g и невозможны переходы и ↔ и и g ↔ g.
30

31.

Функции анализа ЭП
Деформационная ЭП
• После сближения атомов на расстояние менее 4 Å, начинают проявляться квантово-механические эффекты: корреляция электронов, интерференция волновых
функций, делокализация электронов по всей молекуле
и обмен.
• Увидеть результат действия гибридизации и всех этих
факторов на карте полной ЭП невозможно. Чтобы наглядно представить, как изменилось электронное распределение при образовании молекулы из атомов, используют функцию деформационной электронной
плотности:
• где ρмол(r) – ЭП,
- сумма ЭП свободных атомов,
ядра которых расположены в тех же точках, где и
ядра реальной молекулы
31

32.

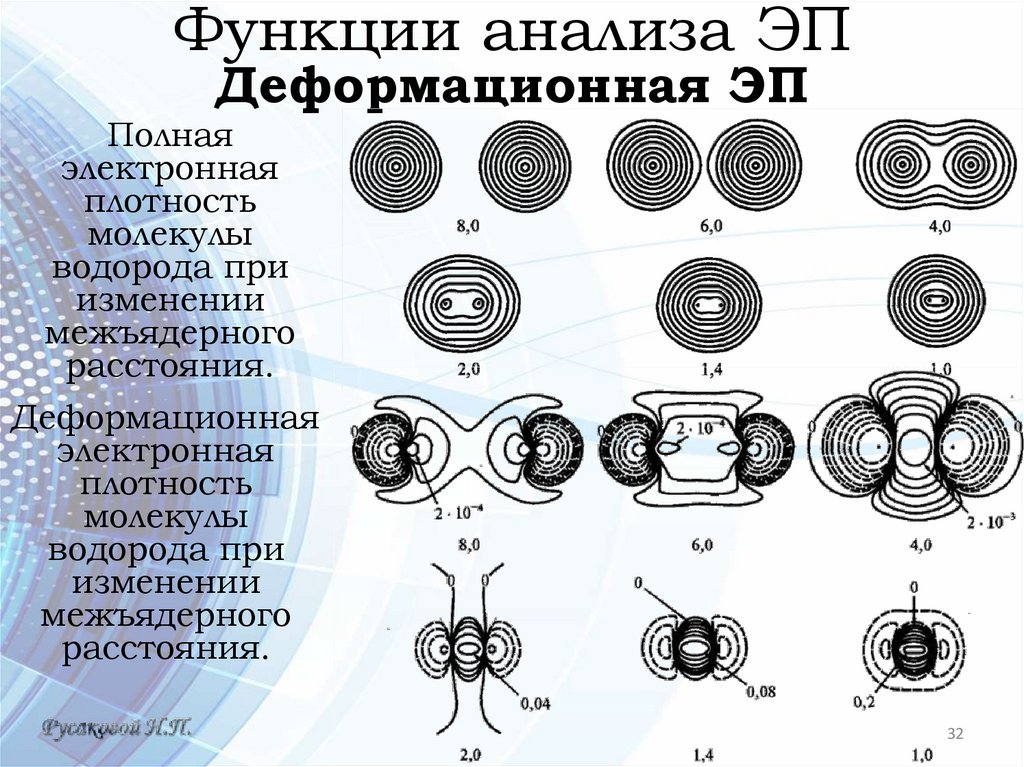
Функции анализа ЭП
Деформационная ЭП
Полная
электронная
плотность
молекулы
водорода при
изменении
межъядерного
расстояния.
Деформационная
электронная
плотность
молекулы
водорода при
изменении
межъядерного
расстояния.
32

33.

Функции анализа ЭП
Деформационная ЭП
• Расчет деформационной ЭП для равновесной ядерной
конфигурации - сумма ЭП свободных атомов называется промолекулой и обозначается ρпром· Промолекула - удобное вспомогательное понятие (модель), не
описывается детерминантом из атомных волновых фций; для нее несправедливы теоремы вириала и
Гельмана-Фейнмана, а также принцип Паули.
• Если промолекулу выбирают в виде совокупности сферических атомов, то δρ - стандартная деформационная ЭП.
• Классическая электростатическая (кулоновская) энергия взаимодействия сферических атомов отрицательна, поэтому промолекула стабильнее, чем набор атомов, удаленных на очень большое расстояние друг от
друга, но является неустойчивой.
33

34.

Деформационная ЭП
• При вычислении ЭП промолекулы следует иметь в виду, что
Ψē свободного атома в основном состоянии может быть:
• пространственно невырожденной (1 ē - «своя» АО (атомы Н,
Li, N, ... );
• n-кратно пространственно вырожденной (спин-орбит.
взаим-я нет).
• Вырождение - в ат-х с частично заполненными ēē р-, dили f-подоболочками (н.п.: В, С, О, F, где n = 3).
• Экспер. определить, какие именно орбитали заняты ēē,
невозможно. Поэтому сост-е таких свободных ат-в
описывается как линейная комбинация основных сост-й с
равной Е, но с разл. размещением ēē на вырожденных АО.
• ЭП таких атомов в промолекуле – стат. среднее по
возможным ē-ным конфигурациям.
Атом C - 3 эл-е конф-ции с равной Е: 1s2 2s2 2p1x2p1y2p0z,
1s2 2s2 2p1x2p0y2p1z и 1s2 2s2 2p0x2p1y2p1z.
Усредненная ē-ная конф-ция ат. С: 1s2 2s2 2p2/3x2p2/3y2p2/3z.
Т.е. электронные заселенности АО в «усредненном» атоме
могут быть нецелочисленными.
34

35.

Деформационная ЭП связи
• Стандартные деформационные плотности ординарных
(этан С2Н6), двойных (этилен С2Н4) 2 и тройных
(ацетилен
2
2/3
2/3
С2Н2) связей С-С. Конф-ция ат. С: 1s 2s 2p x2p y2p2/3z
Вывод анализа карт деформационной ЭП :
1. ēē в мол-ле аккумулируются между ядрами, где имеет
место конструктивная интерференция АО.
2. При наличии π-связей избыточные пики δρ удлиняются
перпендикулярно линии связи.
3. По сравн. с суперпозицией сфер-х ат-в ЭП возрастает
также в областях хорошо локализованных несвязывающих
МО в мол-ле (например, МО, описывающих неподеленные
электронные пары) и некоторых областях разрыхляющих
МО, полностью занятых ēē.
4. Вблизи узловых поверхностей МО ЭП уменьшается по
сравнению с промолекулой.
5. При взаимодействии ат-в разного типа (полярная ков-я
или ионная связь) ЭП смещается к более ЭО атому.
35

36.

Деформационная ЭП
• Деформационная ЭП используется для определения
зарядов на атомах по Хиршфельду: в непрерывном
распределении ЭП молекулы ρ(r) можно выделить «связанный атом» (псевдоатом), его ЭП - ρпсевд(r) пропорциональна относительному вкладу соответствующего
свободного сферического атома ρμ в плотность промолекулы.
• Вводится весовая функция:
• где
-ЭП промолекулы
• тогда ЭП связанного атома μ:
• перейдя к деформационной ЭП:
получаем:
• Интегрируя её по всему пространству получаем заряд
на атоме μ:
36

37.

Функции анализа ЭП
Деформационная ЭП
37