Похожие презентации:
Колебания (продолжение). Лекция № 6
1. Лекция № 6
КОЛЕБАНИЯ(продолжение)
2. Свободные затухающие колебания
В реальных механических колебательныхсистемах энергия постепенно расходуется на
работу
против
сил
m
сопротивления
и сил
x
внутреннего
трения.
k x r x, x Такие системы являются
диссипативными (рис.6.1)
Рис. 6.1
В них механическая
энергия переходит в тепловую, а амплитуда
колебаний уменьшается с течением времени.
3.
Ур-е движения тела под действием силыупругости и силы сопротивления при
c
небольших скоростях F r имеет вид:
y c
ma F F
x:
m x kx rx
:m
r
k
x x x 0
m
m
ДУ свободных затухающих колебаний:
x 2 x
2
0 x
0
(6.1)
4.
Здесьr
2m
k
0
m
– собственная частота
осциллятора,
– коэффициент затухания системы,
r – коэффициент сопротивления.
Решение ур-я (6.1) при ω0 > β имеет вид:
x A0 e
t
cos t
(6.2)
где ω – циклическая частота затухающих
колебаний:
2
2
0
(6.3)
5.
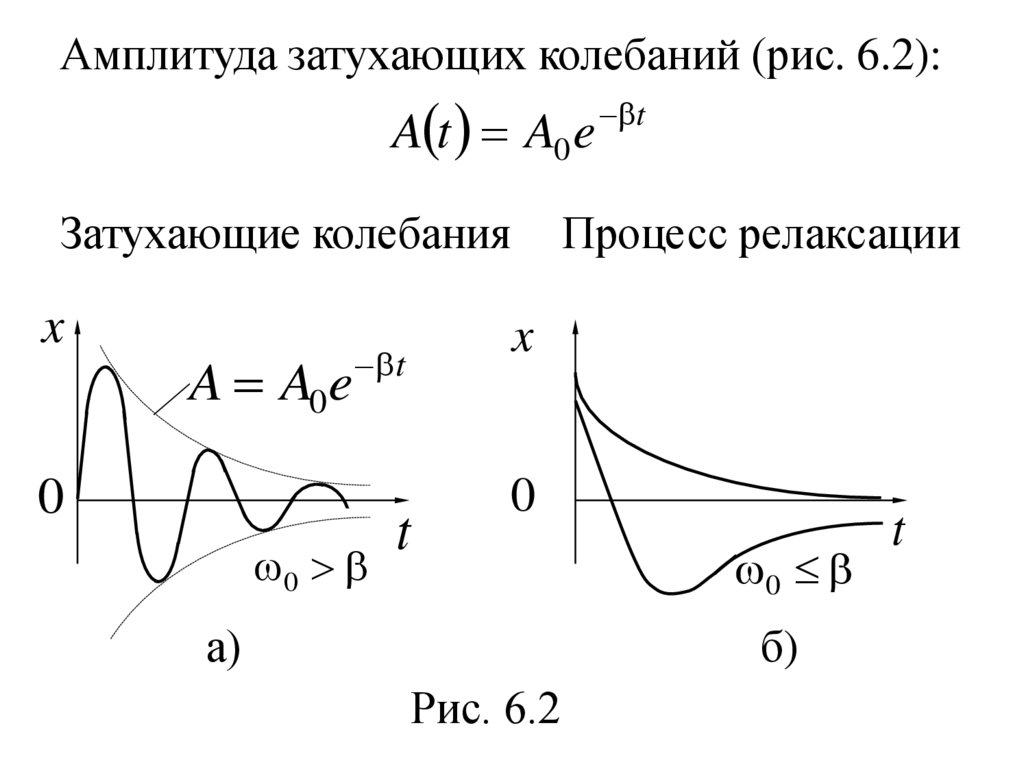
Амплитуда затухающих колебаний (рис. 6.2):A t A0 e
Затухающие колебания
x
A A0e
t
0
0
t
t
Процесс релаксации
x
0
0
а)
б)
Рис. 6.2
t
6.
Период затухающих колебаний2
2
T
2
2
0
Если затухание велико (ω0 β ), то при
выводе системы из положения равновесия
колебания не возникают – она возвращается в
состояние
равновесия
в
процессе,
называемом процессом релаксации.
Декремент затухания характеризует
относительное
уменьшение
амплитуды
колебаний за период
A t
T
D
e
(6.4)
A t T
7.
Логарифмический декремент затухания:D ln D ln e T
T
(6.5)
Время релаксации
1
За это время амплитуда уменьшается в e раз.
Число колебаний, совершаемых системой за
время релаксации
1
1
Ne
T T D
8.
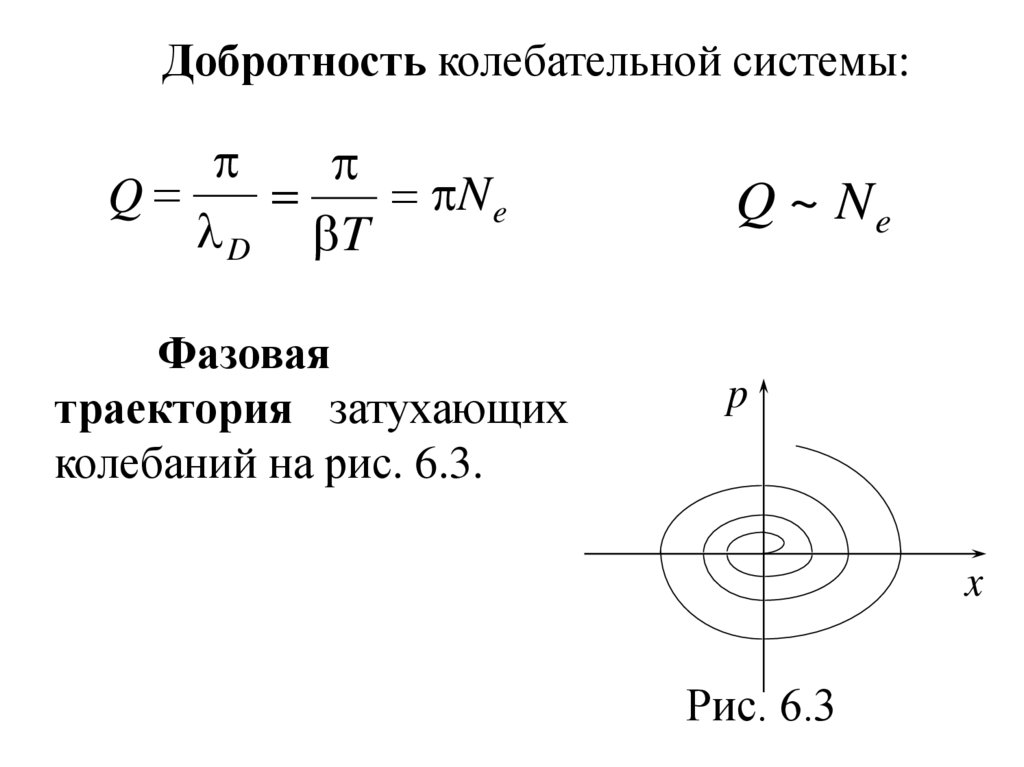
Добротность колебательной системы:N e
Q
D T
Фазовая
траектория затухающих
колебаний на рис. 6.3.
Q ~ Ne
p
x
Рис. 6.3
9. Вынужденные колебания
Чтобывозбудить
в
реальной
колебательной
системе
незатухающие
колебания,
необходимо
компенсировать
потери энергии, обусловленные силами
сопротивления. Для этого на
F t
систему (рис. 6.4) воздействуют
переменной внешней силой F ,
m
x
в простейшем случае
изменяющейся
по
k x r x, x
гармоническому закону:
Рис. 6.4
Fx F0 cos t
10.
где Ω – частота вынуждающей силы.Поведение системы описывается ДУ:
m x rx kx F0 cos t
x 2 x
2
0 x
f 0 cos t
F0
f0
m
(6.6)
11. Установившиеся вынужденные колебания
Опыт показывает, что через некотороевремя после начала действия вынуждающей
силы
в
системе
устанавливаются
гармонические
колебания
с
частотой
вынуждающей силы, но отстающие от нее по
фазе. Общее решение уравнения (6.6) может
быть представлено в виде суммы решения
уравнения свободных затухающих колебаний
и
установившихся
колебаний.
Для
установившихся колебаний имеем:
12.
x A cos t(6.7)
где A – амплитуда колебаний объекта массой
m, α – сдвиг фаз между колебаниями объекта
и внешней силой F(t).
Продифференцируем (6.7) по времени:
x A sin t A cos t ,
2
2
A
cos t
x A cos t
2
13.
Чтобы найти A и α, подставим решение(6.7) в ур-е (6.6):
2
A
cos
t
2 A cos t
2
C1
C
2
F0
t cos t
m
2
0 A cos
C3
(6.8)
C4
Правая часть (6.8) – результат сложения
трех гармонических колебаний, описанных в
его левой части. Сложение произведем при
помощи графического построения.
14.
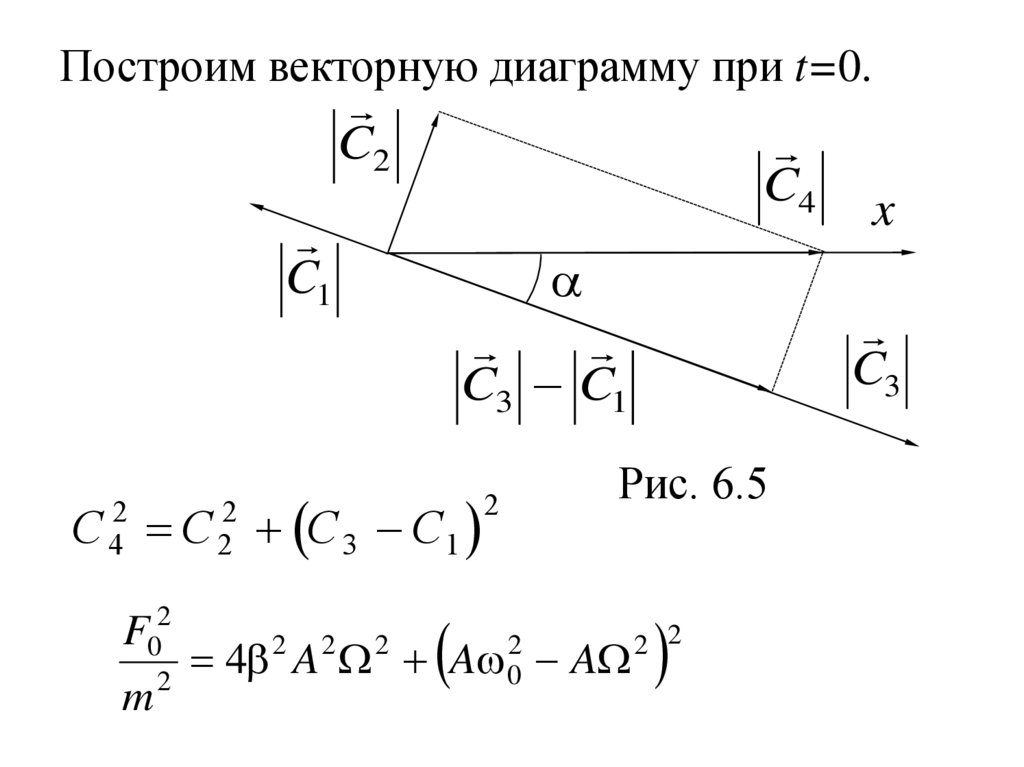
Построим векторную диаграмму при t=0.C2
C4
C1
C3
C3 C1
2
С4
2
С2
2
F0
2
m
С 3 С1
4 A
2
2
2
2
2
A 0
Рис. 6.5
A
x
2 2
15.
откуда значение амплитудыA
F0 m
02
2 2
4 2 2
(6.9)
Из векторного многоугольника (см. рис. 6.5)
находим
C
tg
Начальная фаза
2
C3 C1
2
arctg 2
2
0
16. Механический резонанс
Резонанс – физическое явление,состоящее в резком возрастании амплитуды
установившихся вынужденных колебаний
системы, вызываемое вынуждающей силой с
некоторой характерной частотой, называемой
резонансной.
Из условия экстремума функции A(Ω)
d A
0,
d
определим резонансную частоту.
17.
Найдем частоту вынуждающей силы,при которой амплитуда установившихся
вынужденных
колебаний
будет
максимальной, и, следовательно, выражение в
знаменателе (6.9) примет минимальное
значение.
Исследуем
на
экстремум
знаменатель выражения (6.9).
1
2
2
2
2 0 p 2 p 8 p 0
2
Резонансная частота
p 0 :
18.
42
0
2
p
8
2
0,
02 2p 2 2 0,
откуда резонансная частота
p
2
0
2
2
(6.10)
Подставив (6.10) в (6.9) определим
амплитуду резонанса
Ap
F0 m
2
2
0
2
(6.11)
19.
При β 0 из (6.11) следует, что Ap . Из(6.10) следует, что при 2 2 02 резонанс
не наблюдается (рис. 6.6). При 0,
F0
A
;
2
0
m 0
при , A 0
A
0
F0
02 m
0
0
p 0
Рис. 6.6
2
2
















 Физика
Физика








